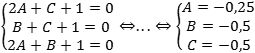Как найти единичный вектор перпендикулярный плоскости

6.2. Найти единичный вектор того же направления что и .

Единичный вектор
находится:
,
где– модуль вектора.

Находим

тогда

Ответ:
.

Примечание.
Координаты единичного вектора должны
быть не больше единицы.

6.3. Найти длину
и направляющие косинусы вектора
.
Сравните с ответом в предыдущем пункте.
Сделайте выводы.

Длина вектора –
это есть его модуль:

,
а направляющие косинусы мы можем найти
по формуле одного из способов задания
векторов:

Из полученного мы
видим, что направляющие косинусы это и
есть координаты единичного вектора.

Ответ:
,,,.

6.4. Найти
.

Необходимо выполнить
действия умножения вектора на число,
сложения и модуль.

Почленно перемножаем
координаты векторов на число.

Почленно складываем
координаты векторов.

Находим модуль
вектора.

Ответ:

6.5. Определить
координаты вектора
,
коллинеарного вектору,
зная, чтои он направлен в сторону, противоположную
вектору.

Вектор
коллинеарен вектору,
значит, его единичный вектор равен
единичному векторутолько со знаком минус, т.к. направлен
в противоположную сторону.

Единичный вектор
имеет длину равную 1, значит, если его
умножить на 5, то его длинна будет равна
пяти.

Находим

Ответ:

6.6. Вычислить
скалярные произведения
и.
Перпендикулярны ли векторыи,имежду собой?

Выполним скалярное
произведение векторов.

Если вектора
перпендикулярны, их скалярное произведение
равно нулю.

Мы
видим, что в нашем случае вектораиперпендикулярны.

Ответ:
,,
векторы не перпендикулярны.

Примечание.
Геометрический смысл скалярного
произведения малоприменим на практике,
но все-таки существует.

Результат такого
действия можно изобразить и вычислить
геометрически.

6.7. Найти работу,
совершённую материальной точкой к
которой приложена сила
,
при перемещении её из точки B в точку С.

Физический смысл
скалярного произведения – это работа.
Вектор силы здесь
,
вектор перемещения – это.
А произведение этих векторов и будет
искомой работой.

Находим работу

Ответ: -3.

6.8. Найти
внутренний угол при вершине A
и внешний угол при вершине C
треугольника ABC.

Из определения,
скалярного произведения векторов
получим формулу нахождения угла:
.

Далее, нам нужно
определить вектора, между которыми
будем искать угол.

Внутренний
угол будем искать как угол между
векторами, выходящими из одной точки.

Для нахождения
внешнего угла нужно совмещать вектора,
таким образом, чтоб они выходили из
одной точки. Рисунок это поясняет.

Стоит заметить,
что
,
только имеют разные начальные координаты.

Находим необходимые
вектора и углы

Ответ: внутренний
угол при вершине А =
,
внешний угол при вершине В =.

Вспомним вектора-орты:
,,.

Проекция находится
также из скалярного произведения

–проекция b
на a.

Ранее полученные
нами вектора

,
,

Находим проекцию

Находим вторую
проекцию

Ответ:
,

Примечание.
Знак минуса при нахождении проекции
означает то, что проекция опускается
не на сам вектор, а в противоположную
сторону, на линию на которой лежит этот
вектор.

6.10. Вычислить
.

Выполним векторное
произведение векторов

Найдем модуль

Синус угла между
векторами найдём из определения
векторного произведения векторов

Ответ:
,,.

6.11. Найти площадь
треугольника ABC
и длину высоты, опушенной из точки С.

Геометрический
смысл модуля векторного произведения
состоит в том, что это площадь
параллелограмма, образованного этими
векторами. А площадь треугольника равна
половине площади параллелограмма.

Площадь треугольника
также можно найти как произведение
высоты, на основание, делённое на два,
из этого можно вывести формулу нахождения
высоты.

Таким образом,
найдём высоту

Ответ:
,.

6.12. Найти
единичный вектор, перпендикулярный
векторам
и.

Результатом
скалярного произведения есть вектор,
который перпендикулярный двум исходным.
А единичный вектор – это вектор, делённый
на его длину.

Ранее, нами было
найдено:

,

Ответ:
.

6.13. Определить
величину и направляющие косинусы момента
силы
,
приложенной к А относительно точки С.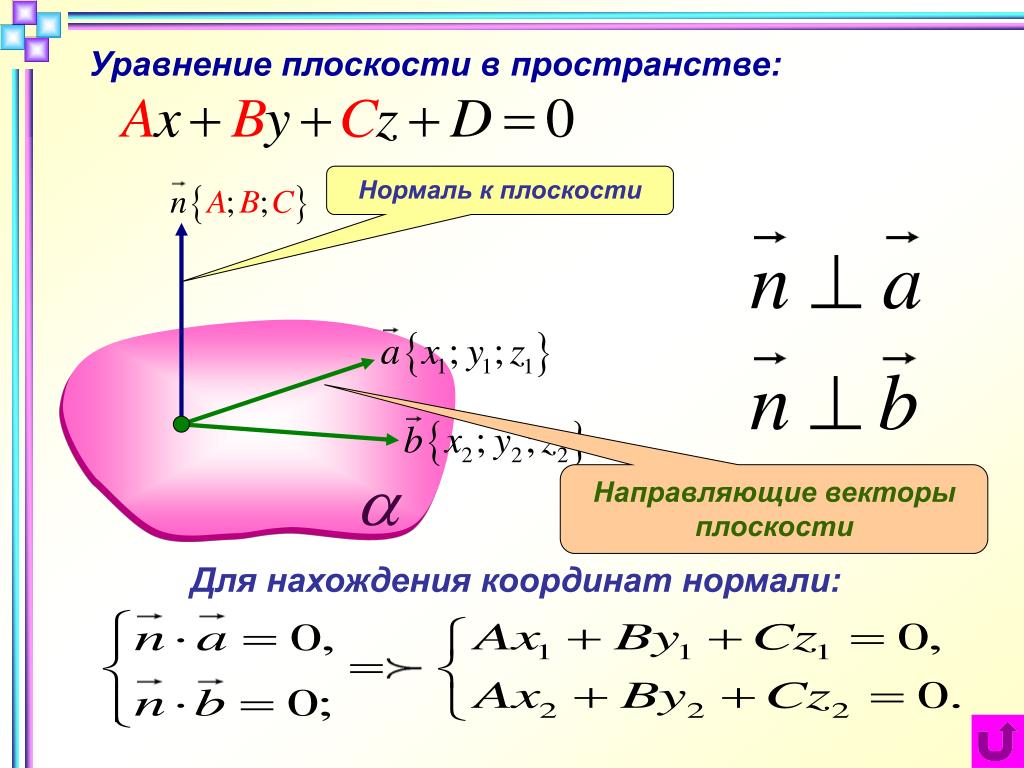

Физический смысл
векторного произведения – это момент
силы. Приведём иллюстрацию к данному
заданию.

Находим момент
силы

Ответ:
.

6.14. Лежат ли
векторы
,ив одной плоскости? Могут ли эти векторы
образовывать базис пространства? Почему?
Если могут, разложите по этому базису
вектор.

Чтобы проверить
лежат ли вектора в одной плоскости
необходимо выполнить смешанное
произведение этих векторов.

Смешанное
произведение не равно нулю, следовательно,
вектора не лежат в одной плоскости (не
компланарные) и могут образовывать
базис. Разложим
по этому базису.

Разложим по базису,
решив уравнение

Ответ: Векторы
,ине лежат в одной плоскости..

6.15. Найти
.
Чему равен объём пирамиды с вершинами
A, B, C, D и её высота, опущенная из точки A
на основание BCD.

Геометрический
смысл смешанного произведения в том,
что это объём параллелепипеда образованного
этими векторами.

Объём же пирамиды
в шесть раз меньше объёма параллелепипеда.

Объём пирамиды,
ещё можно найти так:

Получим формулу
нахождения высоты

Находим

Находим высоту

Ответ: объём = 2.5,
высота =.

6.16. Вычислить
и.

–над этим заданием
предлагаем вам подумать самим.

–выполним
произведение.

Ранее было получено

Ответ:
.

6.17. Вычислить

Выполним действия
по частям

1)

2)

3)

4)

5)

Суммируем полученные
значения

Ответ:
.

6.18. Найти вектор
,
зная, что он перпендикулярен векторами,
а его проекция на векторравна 5.

Разобьем данную
задачу на две подзадачи

1) Найдём вектор,
перпендикулярный векторам
ипроизвольной длинны.

Перпендикулярный
вектор мы получим в результате векторного
произведения

Ранее, нами было
найдено:

Искомый вектор
отличается лишь длинной, от полученного

2) Найдем
через уравнение

Ответ:

6. 19. Найти вектор
,
удовлетворяющий условиям,,.

Рассмотрим более
детально данные условия.

Это система линейных
уравнений. Составим и решим данную
систему.

Ответ:

6.20. Определить
координаты какого-либо вектора
,
компланарного с векторамии,
и перпендикулярного вектору.

В данном задании
два условия: компланарность векторов
и перпендикулярность, выполним сначала
первое условие, а потом второе.

1) Если вектора
компланарны, значит их смешанное
произведение равно нулю.

Отсюда
получим некоторую зависимость координат
вектора

Найдем вектор
.

2) Если вектора
перпендикулярны, значит их скалярное
произведение равно нулю

Мы получили вторую
зависимость координат искомого вектора

Для любого значения
вектор будет удовлетворять условиям.
Подставим.

Ответ:
.

Аналитическая
геометрия

Алгебра векторов, страница 21

Математика
Аналитическая геометрия и линейная алгебра

Задачи
для самостоятельной работы.

1. Упростить выражение (a – b)xc – (a
+ с)xb – (b + с)xa.

2. Найти площадь треугольника,
построенного на векторах 2m + n  и
3m – n,
если |m

| = 4, , .

3. Вычислить длины диагоналей и
площадь параллелограмма, построенного на векторах

a =
i – 2j
+ 2k и b = i – 3j + k.

4. Точки A(-2,
1, 3), B(-1, 3, 0), C(-4,
2, -1) являются вершинами ΔABC. Вычислить
площадь треугольника и длину его высоты, опущенной из вершины С на сторону
АВ.

5. Вектор a
ортогонален оси Oz и вектору c = 2i
– j + 3k,
образует с осью Oy острый угол и . Найти координаты вектора a.

6. Найти координаты вектора p, который ортогонален векторам a  = (5, -2, 3) и c  = (-1, 4, -3) и
удовлетворяет условию , где b = 2

i + j —
k.

6. Сила F = 2i +
j – 3k  приложена к точке N(2, -5, 3). Найти момент этой силы относительно точки P(1, -3, -1).

7. Векторы a, b, c удовлетворяют условию a
+ b + c = 0. Доказать, что axb = bxc = cxa.

8. Найти координаты единичных
векторов, перпендикулярных к плоскости ΔABC,
построенного на векторах  и .

9. Найти |(a – 3c)x(2a + c)|, если
векторы a и c
ортогональны и |a| = 4, |c| = 3.

10. Найти площадь
параллелограмма, диагоналями которого являются векторы 3m + 2n  и

-5m +
4n, если , |n| = 2, .

11. Найти координаты единичного
вектора p, перпендикулярного векторам a = i
– 2j  и

c =
2j + 3k  и образующего с осью Oz тупой угол.

12. Даны
векторы a = 2i +
6j – 3k, b = i + 5j
– k,  c = –i – 3j +
2k. Найти координаты вектора p,
ортогонального векторам b и c, если .

13. Вычислить площадь
треугольника с вершинами в точках  A(2, -2, 3), B(3, -3, 4), C(1, 0, 1) и
длину его высоты, опущенной из вершины B на сторону
AC.

14. Найти площадь
параллелограмма, построенного на векторах m = 2a —
c  и

n =
a + 3c, если .

15. Сила  f = (1, -2, 3) приложена к
точке P(3, 1, 1). Найти момент этой силы
относительно точки A(2, 0, 2).

Скачать файл

Выбери свой ВУЗ

Полный список ВУЗов

Найдите единичный вектор, перпендикулярный плоскости треугольника ABC, где координаты его вершин равны A(3, –1,2), B(1, –1, –3) и C(4, –3, 1) . — Sarthaks eConnect

← Предыдущий вопрос
Следующий вопрос →

спросил
15 марта 2021 г.
в векторах
по
Рупа01
(32,5 тыс. баллов)

закрыто
15 марта 2021 г.
от Rupa01

Найдите единичный вектор, перпендикулярный плоскости треугольника ABC, где координаты его вершин равны A(3, –1, 2), B(1, –1, –3) и C(4, –3, 1) .

• векторная алгебра
• класс-12

1 ответ

+1 голос

← Предыдущий вопрос
Следующий вопрос →

Похожие вопросы

Если вектор a, вектор b, вектор c являются векторами положения вершин A, B и C соответственно треугольника ABC, запишите значение вектора (AB)

спросил
16 мая 2021 г.
в векторах
по
Лакхи
(29,5 тыс. баллов)

• векторная алгебра
• класс-12

Вершины A, B, C треугольника ABC имеют соответственно векторы положения вектор a, вектор b, вектор c относительно данного начала координат O.

спросил
13 мая 2021 г.
в векторах
по
Каина
(30,5 тыс. баллов)

• векторная алгебра
• класс-12

Если вершины A, B, C треугольника ABC являются точками с векторами положения a1 i+a2 j + a3 k, b1i + b2 j + b3k, c2j +c3k

спросил
14 мая 2021 г.
в векторах
по
Лакхи
(29,5 тыс. баллов)

• векторная алгебра
• класс-12

Если вершины A, B, C треугольника ABC равны (1, 2, 3), (-1, 0, 0), (0, 1, 2) соответственно,

спросил
26 февр. 2020 г.
в векторах
по
Звуковой сигнал
(59,1 тыс. баллов)

• векторная алгебра
• класс-12

Напишите единичный вектор, образующий равные острые углы с осями координат.

спросил
16 мая 2021 г.
в векторах
по
Лакхи
(29,5 тыс. баллов)

• векторная алгебра
• класс-12

Категории

• Все категории
• JEE
  (28,1к)
• NEET
  (8,5к)
• Наука
  (748к)
• Математика
  (242к)
  • Система счисления
    (9,8к)
  • Множества, отношения и функции
    (5,5к)
  • Алгебра
    (35,9к)
  • Коммерческая математика
    (7,4к)
  • Координатная геометрия
    (10,4к)
  • Геометрия
    (11,7к)
  • Тригонометрия
    (11,0 к)
  • Измерение
    (6,8к)
  • Статистика
    (4,9к)
  • Вероятность
    (5,3к)
  • Векторы
    (2,8к)
  • Исчисление
    (19,7к)
  • Линейное программирование
    (909)
• Статистика
  (2,8к)
• Наука об окружающей среде
  (3,8к)
• Биотехнология
  (579)
• коммерция
  (62,4к)
• Электроника
  (3,7к)
• Компьютер
  (16,3к)
• Искусственный интеллект (ИИ)
  (1,4к)
• Информационные технологии
  (13,2к)
• Программирование
  (8. 7к)
• Политическая наука
  (6,5к)
• Домашняя наука
  (4,9к)
• Психология
  (3,4к)
• Социология
  (5,6к)
• Английский
  (58,3к)
• хинди
  (23,6к)
• Способность
  (23,7к)
• Рассуждение
  (14,6к)
• ГК
  (25,7к)
• Олимпиада
  (527)
• Советы по навыкам
  (75)
• CBSE
  (722)
• РБСЭ
  (49,1к)
• Общий
  (58,5к)
• МСБШСЭ
  (1,8к)
• Совет Тамилнаду
  (59,3к)
• Совет Кералы
  (24,5к)

математика — Как найти координаты трехмерных точек в плоскости, перпендикулярной заданному вектору

спросил
3 года 10 месяцев назад

Изменено
3 года, 10 месяцев назад

Просмотрено
531 раз

У меня есть две точки в трехмерном пространстве, одна точка (x,0,z), а другая — начало координат (0,0,0), через эти точки проходит линия длиной L, которая начинается от первой точки и продолжая за исходной точкой, в конце этой линии находится перпендикулярная (к линии) плоская доска размерами Ш х В, линия заканчивается посередине этой доски.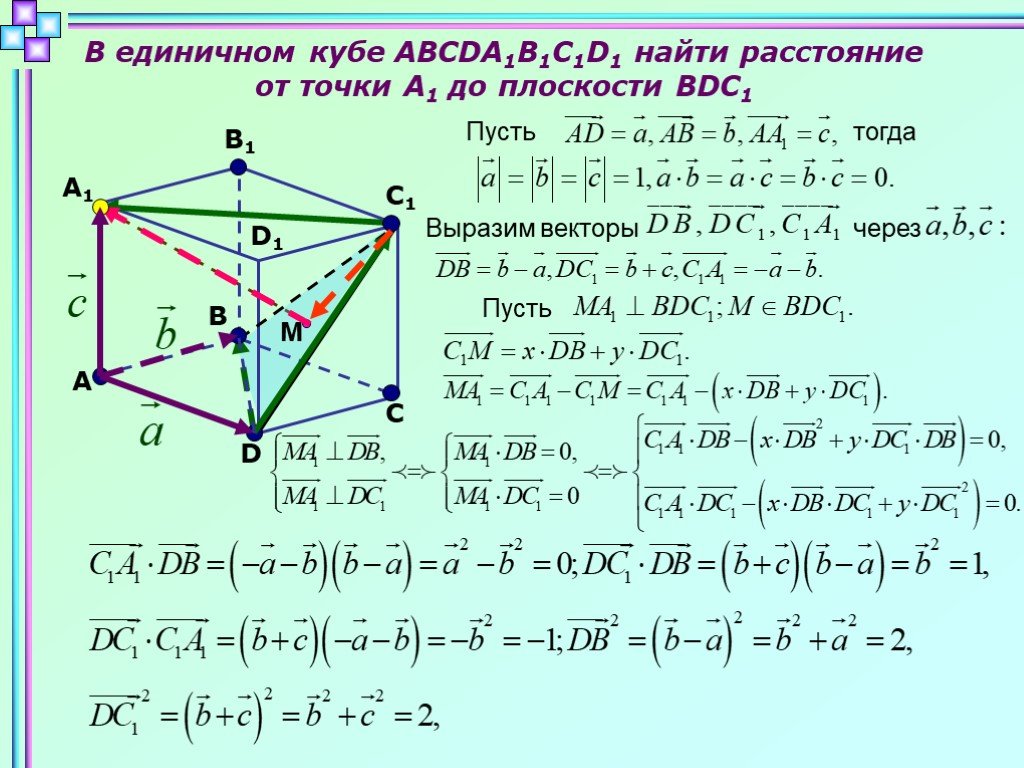

Предположим, что x, z, L, H, W заданы. Мне нужен способ найти все координаты трехмерных точек, где эти точки образуют изображение в пикселях на доске (это означает, что каждая точка имеет расстояние 1 слева от нее, правая, верхняя, нижняя соседние точки).

Прикрепил довольно некрасивый рисунок 🙂 Сделал, пытаясь проиллюстрировать проблему (точки пикселей отметил двумя вопросительными знаками, а мне нужны они все).

Спасибо.

• математика
• вектор
• геометрия
• вычислительная геометрия
• векторная графика

0

Можно определить эту плоскость. Но нет выбранного направления для однозначного построения сетки.

В качестве основы выберем направление OY (потому что нормаль имеет нулевую Y-компоненту).

Итак, мы имеем:

Вектор нормали N = (xx, 0, zz) //Я переименовал значения, чтобы не путать с координатой
переменные

Единичный вектор нормали n = (nx, 0, nz) , где

 nx = xx / Sqrt(xx*xx+zz*zz)
 nz = zz / Sqrt(xx*xx+zz*zz)
 

Базовая точка

 B = (bx, 0, bz) = (xx - nx * L, 0, zz - nz * L)
 

Базовый вектор единицы измерения в плоскости

 dy = (0, 1, 0)
 

Другой базовый вектор

 dc = dy x n // векторное произведение
   = (-бз, 0, бх)
 

Теперь можно генерировать сетку, используя целочисленные индексы i, j в диапазонах (-W/2.

Ортогональные векторы и условие ортогональности

В данной статье мы расскажем, что такое ортогональные векторы, какие существуют условия ортогональности, а также приведем подробные примеры для решения задач с ортогональными векторами.

Ортогональные векторы: определение и условие

Ортогональные векторы — это векторы a ¯ и b ¯ , угол между которыми равен 90 0 .

Необходимое условие для ортогональности векторов — два вектора a ¯ и b ¯ являются ортогональными (перпендикулярными), если их скалярное произведение равно нулю.

Примеры решения задач на ортогональность векторов

Плоские задачи на ортогональность векторов

Если дана плоская задача, то ортогональность для векторов a ¯ = < a x × a y >и b ¯ = < b x × b y >записывают следующим образом:

a ¯ × b ¯ = a x × b x + a y × b y = 0

Задача 1. Докажем, что векторы a ¯ = < 1 ; 2 >и b ¯ = < 2 ; – 1 >ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 1 × 2 + 2 × ( – 1 ) = 2 – 2 = 0

Ответ: поскольку произведение равняется нулю, то векторы являются ортогональными.

Задача 2. Докажем, что векторы a ¯ = < 3 ; – 1 >и b ¯ = < 7 ; 5 >ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 3 × 7 + ( – 1 ) × 5 = 21 – 5 = 16

Ответ: поскольку скалярное произведение не равняется нулю, то и векторы не являются ортогональными.

Задача 3. Найдем значение числа n , при котором векторы a ¯ = < 2 ; 4 >и b ¯ = < n ; 1 >будут ортогональными.

Как решить?

Найдем скалярное произведение данных векторов:

a ¯ × b ¯ = 2 × n + 4 × 1 = 2 n + 4 2 n + 4 = 0 2 n = – 4 n = – 2

Ответ: векторы являются ортогональными при значении n = 2 .

Примеры пространственных задач на ортогональность векторов

При решении пространственной задачи на ортогональность векторов a ¯ = < 1 ; 2 ; 0 >и b ¯ = < 2 ; – 1 ; 10 >условие записывается следующим образом: a ¯ × b ¯ = a x × b x + a y × b y + a z × b z = 0 .

Задача 4. Докажем, что векторы a ¯ = < 1 ; 2 ; 0 >и b ¯ = < 2 ; – 1 ; 10 >являются ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 1 × 2 + 2 × ( – 1 ) + 0 × 10 = 2 – 2 = 0

Ответ: поскольку произведение векторов равняется нулю, то они являются ортогональными.

Задача 5. Найдем значение числа n , при котором векторы a ¯ = < 2 ; 4 ; 1 >и b ¯ = < n ; 1 ; – 8 >будут являться ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 2 × n + 4 × 1 + 1 × ( – 8 ) = 2 n + 4 – 8 = 2 n – 4 2 n – 4 = 0 2 n = 4 n = 2

Ответ: векторы a ¯ и b ¯ будут ортогональными при значении n = 2 .

Найти единичный вектор, ортогональный векторам a = i + j + 2k и b = 2i + j + k Помогите решить пожалуйста срочно надо?

Алгебра | 10 – 11 классы

Найти единичный вектор, ортогональный векторам a = i + j + 2k и b = 2i + j + k Помогите решить пожалуйста срочно надо.

Надо вычислить векторное произведение

Значит вектор с = – i + 3j – k.

Чтобы он был единичным мы должны его нормировать.

Теперь надо поделить каждую координату на длину вектора.

В итоге получим единичный вектор.

Какой угол образует единичные векторы a и b, если известно, что векторы a + 2b и 5a – 4b взаимно перпендикулярны?

Какой угол образует единичные векторы a и b, если известно, что векторы a + 2b и 5a – 4b взаимно перпендикулярны?

Определите координаты единичного вектора, сонаправленного с вектором p( – √7 ; 3)?

Определите координаты единичного вектора, сонаправленного с вектором p( – √7 ; 3).

Найти координаты вектора единичной длины , который направлен противоположно вектору ВА, если даны координаты точек А(7, 4, – 2) и В(1, 2, 1)?

Найти координаты вектора единичной длины , который направлен противоположно вектору ВА, если даны координаты точек А(7, 4, – 2) и В(1, 2, 1).

Найти (вектор m + вектор n ) ^ 2 , если векторы m и n – единичные векторы с углом 120градусов меж ними?

Найти (вектор m + вектор n ) ^ 2 , если векторы m и n – единичные векторы с углом 120градусов меж ними.

Найдите координаты единичного вектора, сонаправленного с вектором a( – 2 ; 6 ; 3)?

Найдите координаты единичного вектора, сонаправленного с вектором a( – 2 ; 6 ; 3).

Найти единичный вектор перпендикулярный плоскости 2x – y + 3z – 5 = 0?

Найти единичный вектор перпендикулярный плоскости 2x – y + 3z – 5 = 0.

Вычислить угол между векторами a = 3p + 2q и b = p + 5q, где p и q, где p и q – единичные взаимно перпендикулярные векторы Помогите кто сможет?

Вычислить угол между векторами a = 3p + 2q и b = p + 5q, где p и q, где p и q – единичные взаимно перпендикулярные векторы Помогите кто сможет.

Пожалуйста ооочень надо?

Пожалуйста ооочень надо!

Даны векторы а и б.

Б! = кореньиз2, угол между векторами а и б = 135 найти : а) координаты вектора а, если он противоположно направлен с вектором с <4 ; – 12 ; 6>б) длинну вектора а – 3б.

Дан вектор а( 2 ; 4 )найти вектор 3а?

Дан вектор а( 2 ; 4 )найти вектор 3а.

Найдите единичный вектор , коллинеарный вектору а (0 ; 4 ; 3)?

Найдите единичный вектор , коллинеарный вектору а (0 ; 4 ; 3).

На этой странице вы найдете ответ на вопрос Найти единичный вектор, ортогональный векторам a = i + j + 2k и b = 2i + j + k Помогите решить пожалуйста срочно надо?. Вопрос соответствует категории Алгебра и уровню подготовки учащихся 10 – 11 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

Держи только 1. А) 4(x – 5) – (7x + 9) = 1 4x – 20 – 7x – 9 – 1 = 0 – 3x – 30 = 0 – 3x = 30 x = – 30 / 3 x = – 10 б) 3y – 11 = 1 – 2y 3y + 2y = 11 + 1 5y = 12 y = 12 / 5 y = 2, 4.

F(x) = x² + 2x – 12lnx f ‘(x) = (x²) ‘ + (2x) ‘ – (12lnx) ‘ = 2x + 2 – 12 / x 2x + 2 – 12 / x = 0 2x² + 2x – 12 = 0 x не = 0 x² + x – 6 = 0 X1 = – 3 X2 = 2.

Вот ваше решение (х – 3)(х – 6)>(х + 4)(х – 5) х ^ 2 – 6х – 3х + 18>х ^ 2 – 5х + 4х – 20 – 6х – 3х + 18> – 5х + 4х – 20 – 9х + 18> – х – 20 – 9х + х> – 20 – 18 – 8х> – 38 | : ( – 8) х.

(x – 3)(x – 6)>(x + 4)(x – 5) x² – 3x – 6x + 18>x² – 5x + 4x – 20 x² – 9x + 18>x² – x – 20 8x.

1) корень из ста = 10 2) корень из 784 = 28 3) корень из 1600 = 40 4) корень из 4 / 1089 = 2 / 33 5) корень из 3 1 / 225 = корень из 3 / 15 6) корень из 12 4 / 5 = 4 корня из 3 / корень из 5 1) 125 2) 1296 3) 64 4) 256 5) 1. 2 * 0, 16 = 0, 192.

(5y – 8) ^ 2 = 25y ^ 2 – 80y + 64.

Ну вот они – Квадрат суммыдвух величин равен квадрату первой плюс удвоенное произведение первой на вторую плюс квадрат второй. (a + b)2 = a2 + 2ab + b2Квадрат разностидвух величин равен квадрату первой минус удвоенное произведение первой на вторую п..

sqrt<2x ^ 2 – 18x + 16>” alt = “x – 4> sqrt<2x ^ 2 – 18x + 16>” align = “absmiddle” > 2x ^ 2 – 18x + 16 ; x – 4>0″ alt = “2x ^ 2 – 18x + 16 geq 0 ; (x – 4) ^ 2>2x ^ 2 – 18x + 16 ; x – 4>0” align = “absmiddle” > Решите неравенствоsqrt(2x ^ 2 – 18x + 16) + 4?

Ответ : решение представлено на фотоОбъяснение .

0, 4 – округление до десятых , погрешность 0, 02.

Ортогональность векторов. Перпендикулярность векторов.

Вектора a и b называются ортогональными, если угол между ними равен 90°. (рис. 1).

рис. 1

Примеры задач на ортогональность векторов

Примеры плоских задач на ортогональность векторов

Так в случае плоской задачи для векторов a = < a_x ; a_y > и b = < b_x ; b_y > , условие ортогональности запишется следующим образом:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) = 2 – 2 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 3 · 7 + (-1) · 5 = 21 – 5 = 16

Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 = 2 n + 4
2 n + 4 = 0
2 n = -4
n = -2

Ответ: вектора a и b будут ортогональны при n = -2.

Примеры пространственных задач на ортогональность векторов

Так в случае пространственной задачи для векторов a = < a_x ; a_y ; a_z > и b = < b_x ; b_y ; b_z >, условие ортогональности запишется следующим образом:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 – 2 + 0 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 + 1 · (-8)= 2 n + 4 – 8 = 2 n – 4
2 n – 4 = 0
2 n = 4
n = 2

Ответ: вектора a и b будут ортогональны при n = 2.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

[spoiler title=”источники:”]

http://algebra.my-dict.ru/q/298834_najti-edinicnyj-vektor-ortogonalnyj-vektoram-a/

http://ru.onlinemschool.com/math/library/vector/orthogonality/

[/spoiler]

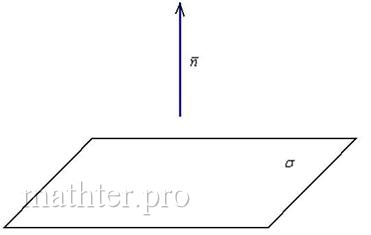
5.2.3. Вектор нормали плоскости (нормальный вектор)

Вектор нормали плоскости – это вектор, который перпендикулярен данной плоскости. Очевидно, что у любой плоскости бесконечно много нормальных векторов.

Но для решения задач нам будет хватать и одного: если плоскость задана общим уравнением в прямоугольной (!) системе координат, то вектор является нормальным вектором данной плоскости.

Просто до безобразия! – всё, что нужно сделать – это «снять» коэффициенты из уравнения плоскости. И чтобы хоть как-то усложнить практику рассмотрим тоже простую, но очень важную задачу, которая часто встречается, причём, не только в геометрии:

Задача 134

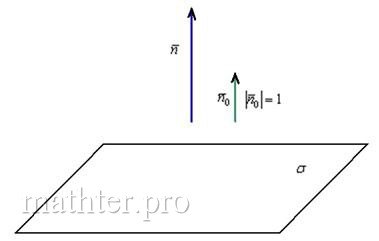
Найти единичный нормальный вектор плоскости .

Решение: принципиально ситуация выглядит так:

Сначала из уравнения плоскости «снимем» вектор нормали: .

И эту задачку мы уже решали: для того чтобы найти единичный вектор , нужно каждую координату вектора разделить на длину вектора .

Вычислим длину вектора нормали:

Контроль:, ОК

Ответ:

Вспоминаем, что координаты этого вектора – есть в точности направляющие косинусы вектора : .

И, как говорится, обещанного три страницы ждут 🙂 – вернёмся к Задаче 130, чтобы выполнить её проверку. Напоминаю, что там требовалось построить уравнение плоскости по точке и двум векторам , и в результате решения мы получили уравнение .

Проверяем:

Во-первых, подставим координаты точки в полученное уравнение:

– получено верное равенство, значит, точка лежит в данной плоскости.

На втором шаге из уравнения плоскости «снимаем» вектор нормали: . Поскольку векторы параллельны плоскости, а вектор ей перпендикулярен, то должны иметь место следующие факты: . Ортогональность векторов элементарно проверяется с помощью скалярного произведения:

Вывод: уравнение плоскости найдено правильно.

В ходе проверки я фактически процитировал следующее утверждение теории: вектор параллелен плоскости в том и только том случае, когда .

Итак, с «выуживанием» нормального вектора разобрались, теперь ответим на противоположный вопрос:

Метод координат в пространстве

Для того, чтобы использовать метод координат, надо хорошо знать формулы. Их три:

Главная формула — косинус угла φ между векторами a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂):

На первый взгляд, выглядит угрожающе, но достаточно немного практики — и все будет работать великолепно.

Задача. Найти косинус угла между векторами a = (4; 3; 0) и b = (0; 12; 5).

Решение. Поскольку координаты векторов нам даны, подставляем их в первую формулу:

Задача. Составить уравнение плоскости, проходящей через точки M = (2; 0; 1), N = (0; 1; 1) и K = (2; 1; 0), если известно, что она не проходит через начало координат.

Решение. Общее уравнение плоскости: Ax + By + Cz + D = 0, но, поскольку искомая плоскость не проходит через начало координат — точку (0; 0; 0) — то положим D = 1. Поскольку эта плоскость проходит через точки M, N и K, то координаты этих точек должны обращать уравнение в верное числовое равенство.

Подставим вместо x, y и z координаты точки M = (2; 0; 1). Имеем:
A · 2 + B · 0 + C · 1 + 1 = 0 ⇒ 2A + C + 1 = 0;

Аналогично, для точек N = (0; 1; 1) и K = (2; 1; 0) получим уравнения:
A · 0 + B · 1 + C · 1 + 1 = 0 ⇒ B + C + 1 = 0;
A · 2 + B · 1 + C · 0 + 1 = 0 ⇒ 2A + B + 1 = 0;

Итак, у нас есть три уравнения и три неизвестных. Составим и решим систему уравнений:

Получили, что уравнение плоскости имеет вид: − 0,25x − 0,5y − 0,5z + 1 = 0.

Задача. Плоскость задана уравнением 7x − 2y + 4z + 1 = 0. Найти координаты вектора, перпендикулярного данной плоскости.

Решение. Используя третью формулу, получаем n = (7; − 2; 4) — вот и все!

Вычисление координат векторов

А что, если в задаче нет векторов — есть только точки, лежащие на прямых, и требуется вычислить угол между этими прямыми? Все просто: зная координаты точек — начала и конца вектора — можно вычислить координаты самого вектора.

Чтобы найти координаты вектора, надо из координат его конца вычесть координаты начала.

Эта теорема одинаково работает и на плоскости, и в пространстве. Выражение «вычесть координаты» означает, что из координаты x одной точки вычитается координата x другой, затем то же самое надо сделать с координатами y и z. Вот несколько примеров:

Задача. В пространстве расположены три точки, заданные своими координатами: A = (1; 6; 3), B = (3; − 1; 7) и C = (− 4; 3; − 2). Найти координаты векторов AB, AC и BC.

Рассмотрим вектор AB: его начало находится в точке A, а конец — в точке B. Следовательно, чтобы найти его координаты, надо из координат точки B вычесть координаты точки A:
AB = (3 − 1; − 1 − 6; 7 − 3) = (2; − 7; 4).

Аналогично, начало вектора AC — все та же точка A, зато конец — точка C. Поэтому имеем:
AC = (− 4 − 1; 3 − 6; − 2 − 3) = (− 5; − 3; − 5).

Наконец, чтобы найти координаты вектора BC, надо из координат точки C вычесть координаты точки B:
BC = (− 4 − 3; 3 − (− 1); − 2 − 7) = (− 7; 4; − 9).

Ответ: AB = (2; − 7; 4); AC = (− 5; − 3; − 5); BC = (− 7; 4; − 9)

Обратите внимание на вычисление координат последнего вектора BC: очень многие ошибаются, когда работают с отрицательными числами. Это касается переменной y: у точки B координата y = − 1, а у точки C y = 3. Получаем именно 3 − (− 1) = 4, а не 3 − 1, как многие считают. Не допускайте таких глупых ошибок!

Вычисление направляющих векторов для прямых

Если вы внимательно прочитаете задачу C2, то с удивлением обнаружите, что никаких векторов там нет. Там только прямые да плоскости.

Для начала разберемся с прямыми. Здесь все просто: на любой прямой найдутся хотя бы две различные точки и, наоборот, любые две различные точки задают единственную прямую.

Кто-нибудь понял, что написано в предыдущем абзаце? Я и сам не понял, поэтому объясню проще: в задаче C2 прямые всегда задаются парой точек. Если ввести систему координат и рассмотреть вектор с началом и концом в этих точках, получим так называемый для прямой:

Зачем нужен этот вектор? Дело в том, что — это угол между их направляющими векторами. Таким образом, мы переходим от непонятных прямых к конкретным векторам, координаты которых легко считаются. Насколько легко? Взгляните на примеры:

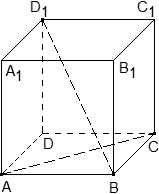
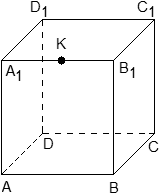
Задача. В кубе ABCDA₁B₁C₁D₁ проведены прямые AC и BD₁. Найдите координаты направляющих векторов этих прямых.

Поскольку длина ребер куба в условии не указана, положим AB = 1. Введем систему координат с началом в точке A и осями x, y, z, направленными вдоль прямых AB, AD и AA₁ соответственно. Единичный отрезок равен AB = 1.

Теперь найдем координаты направляющего вектора для прямой AC. Нам потребуются две точки: A = (0; 0; 0) и C = (1; 1; 0). Отсюда получаем координаты вектора AC = (1 − 0; 1 − 0; 0 − 0) = (1; 1; 0) — это и есть направляющий вектор.

Теперь разберемся с прямой BD₁. На ней также есть две точки: B = (1; 0; 0) и D₁ = (0; 1; 1). Получаем направляющий вектор BD₁ = (0 − 1; 1 − 0; 1 − 0) = (− 1; 1; 1).

Ответ: AC = (1; 1; 0); BD₁ = (− 1; 1; 1)

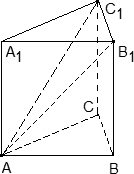
Задача. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, проведены прямые AB₁ и AC₁. Найдите координаты направляющих векторов этих прямых.

Введем систему координат: начало в точке A, ось x совпадает с AB, ось z совпадает с AA₁, ось y образует с осью x плоскость OXY, которая совпадает с плоскостью ABC.

Для начала разберемся с прямой AB₁. Тут все просто: у нас есть точки A = (0; 0; 0) и B₁ = (1; 0; 1). Получаем направляющий вектор AB₁ = (1 − 0; 0 − 0; 1 − 0) = (1; 0; 1).

Теперь найдем направляющий вектор для AC₁. Все то же самое — единственное отличие в том, что у точки C₁ иррациональные координаты. Итак, A = (0; 0; 0), поэтому имеем:

Небольшое, но очень важное замечание насчет последнего примера. Если начало вектора совпадает с началом координат, вычисления резко упрощаются: координаты вектора просто равны координатам конца. К сожалению, это верно лишь для векторов. Например, при работе с плоскостями присутствие на них начала координат только усложняет выкладки.

Вычисление нормальных векторов для плоскостей

Нормальные векторы — это не те векторы, у которых все в порядке, или которые чувствуют себя хорошо. По определению, нормальный вектор (нормаль) к плоскости — это вектор, перпендикулярный данной плоскости.

Другими словами, — это вектор, перпендикулярный любому вектору в данной плоскости. Наверняка вы встречали такое определение — правда, вместо векторов речь шла о прямых. Однако чуть выше было показано, что в задаче C2 можно оперировать любым удобным объектом — хоть прямой, хоть вектором.

Еще раз напомню, что всякая плоскость задается в пространстве уравнением Ax + By + Cz + D = 0, где A, B, C и D — некоторые коэффициенты. Не умаляя общности решения, можно полагать D = 1, если плоскость не проходит через начало координат, или D = 0, если все-таки проходит. В любом случае, координаты нормального вектора к этой плоскости равны n = (A; B; C).

Итак, плоскость тоже можно успешно заменить вектором — той самой нормалью. Всякая плоскость задается в пространстве тремя точками. Как найти уравнение плоскости (а следовательно — и нормали), мы уже обсуждали в самом начале статьи. Однако этот процесс у многих вызывает проблемы, поэтому приведу еще парочку примеров:

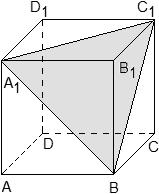
Задача. В кубе ABCDA₁B₁C₁D₁ проведено сечение A₁BC₁. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA₁ соответственно.

Поскольку плоскость не проходит через начало координат, ее уравнение выглядит так: Ax + By + Cz + 1 = 0, т.е. коэффициент D = 1. Поскольку эта плоскость проходит через точки A₁, B и C₁, то координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = − 1;

Аналогично, для точек B = (1; 0; 0) и C₁ = (1; 1; 1) получим уравнения:
A · 1 + B · 0 + C · 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = − 1;
A · 1 + B · 1 + C · 1 + 1 = 0 ⇒ A + B + C + 1 = 0;

Но коэффициенты A = − 1 и C = − 1 нам уже известны, поэтому остается найти коэффициент B:
B = − 1 − A − C = − 1 + 1 + 1 = 1.

Получаем уравнение плоскости: − A + B − C + 1 = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; − 1).

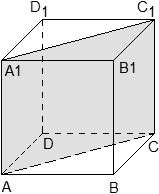
Задача. В кубе ABCDA₁B₁C₁D₁ проведено сечение AA₁C₁C. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA₁ соответственно.

В данном случае плоскость проходит через начало координат, поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz = 0. Поскольку плоскость проходит через точки A₁ и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;

Аналогично, для точки C = (1; 1; 0) получим уравнение:
A · 1 + B · 1 + C · 0 = 0 ⇒ A + B = 0 ⇒ A = − B;

Положим B = 1. Тогда A = − B = − 1, и уравнение всей плоскости имеет вид: − A + B = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; 0).

Вообще говоря, в приведенных задачах надо составлять систему уравнений и решать ее. Получится три уравнения и три переменных, но во втором случае одна из них будет свободной, т.е. принимать произвольные значения. Именно поэтому мы вправе положить B = 1 — без ущерба для общности решения и правильности ответа.

Координаты середины отрезка

Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.

Итак, пусть отрезок задан своими концами — точками A = (x_a; y_a; z_a) и B = (x_b; y_b; z_b). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:

Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.

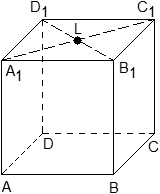
Задача. Единичный куб ABCDA₁B₁C₁D₁ помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA₁ соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A₁B₁. Найдите координаты этой точки.

Поскольку точка K — середина отрезка A₁B₁, ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A₁ = (0; 0; 1) и B₁ = (1; 0; 1). Теперь найдем координаты точки K:

Задача. Единичный куб ABCDA₁B₁C₁D₁ помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA₁ соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A₁B₁C₁D₁.

Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A₁L = C₁L, т.е. точка L — это середина отрезка A₁C₁. Но A₁ = (0; 0; 1), C₁ = (1; 1; 1), поэтому имеем:

Нормальный вектор плоскости, координаты нормального вектора плоскости

Существует ряд заданий, которым для решения необходимо нормальный вектор на плоскости, чем саму плоскость. Поэтому в этой статье получим ответ на вопрос определения нормального вектора с примерами и наглядными рисунками. Определим векторы трехмерного пространства и плоскости по уравнениям.

Нормальный вектор плоскости – определение, примеры, иллюстрации

Чтобы материал легко усваивался, необходимо предварительно изучить теорию о прямой в пространстве и представление ее на плоскости и векторы.

Нормальным вектором плоскости считается любой ненулевой вектор, который лежит на перпендикулярной к данной плоскости прямой.

Отсюда следует, что имеет место существование большого количества нормальных векторов в данной плоскости. Рассмотрим на рисунке, приведенном ниже.

Нормальные векторы располагаются на параллельных прямых, поэтому они все коллинеарны. То есть, при нормальном векторе n → , расположенном в плоскости γ , вектор t · n → , имея ненулевое значение параметра t , также нормальный вектор плоскости γ . Любой вектор может быть рассмотрен как направляющий вектор прямой, которая перпендикулярна этой плоскости.

Имеются случаи совпадения нормальных векторов плоскостей из-за перпендикулярности одной из параллельных плоскостей, так как прямая перпендикулярна и второй плоскости. Отсюда следует, что нормальные векторы перпендикулярных плоскостей должны быть перпендикулярными.

Рассмотрим на примере нормального вектора на плоскости.

Задана прямоугольная система координат О х у z в трехмерном пространстве. Координатные векторы i → , j → , k → считаются нормальными векторами плоскостей O y z , O x z и O x y . Это суждение верно, так как i → , j → , k → ненулевые и расположены на координатных прямых O x , O y и O z . Эти прямые перпендикулярны координатным плоскостям O y z , O x z и O x y .

Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости

Статья предназначена для того, чтобы научить находить координаты нормального вектора плоскости при известном уравнении плоскости прямоугольной системы координат О х у z . Для определения нормального вектора n → = ( A , B , C ) в плоскости необходимо наличие общего уравнения плоскости, имеющее вид A x + B y + C z + D = 0 . То есть достаточно иметь уравнение плоскости, тогда появится возможность для нахождения координат нормального вектора.

Найти координаты нормального вектора, принадлежащего плоскости 2 x — 3 y + 7 z — 11 = 0 .

По условию имеем уравнение плоскости. Необходимо обратить внимание на коэффициенты, так как они и являются координатами нормального вектора заданной плоскости. Отсюда получаем, что n → = ( 2 , — 3 , 7 ) — это нормальный вектор плоскости. Все векторы плоскости задаются при помощи формулы t · n → = 2 · t , — 3 · t , 7 · t , t является любым действительным числом не равным нулю.

Ответ: n → = ( 2 , — 3 , 7 ) .

Определить координаты направляющих векторов заданной плоскости x + 2 z — 7 = 0 .

По условию имеем, что дано неполное уравнение плоскости. Чтобы увидеть координаты, необходимо преобразовать уравнение x + 2 z — 7 = 0 к виду 1 · x + 0 · y + 2 z — 7 = 0 . Отсюда получим, что координаты нормального вектора данной плоскости равны ( 1 , 0 , 2 ) . Тогда множество векторов будет иметь такую форму записи ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .

Ответ: ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .

При помощи уравнения плоскости в отрезках, имеющего вид x a + y b + z c = 1 , и общего уравнения плоскости возможна запись нормального вектора этой плоскости, где координаты равны 1 a , 1 b , 1 c .

Знания о нормальном векторе позволяют с легкостью решать задачи. Часто встречающимися задачами являются задания с доказательствами параллельности или перпендикулярности плоскостей. Заметно упрощается решение задач на составление уравнений заданной плоскости. Если имеется вопрос о нахождении угла между плоскостями или между прямой и плоскостью, то формулы нормального вектора и нахождения его координат помогут в этом.

Данная статья раскрывает смысл перпендикулярности двух векторов на плоскости в трехмерном пространстве и нахождение координат вектора, перпендикулярному одному или целой паре векторов. Тема применима для задач, связанных с уравнениями прямых и плоскостей.

Мы рассмотрим необходимое и достаточное условие перпендикулярности двух векторов, решим по методу нахождения вектора, перпендикулярному заданному, затронем ситуации по отысканию вектора, который перпендикулярен двум векторам.

Необходимое и достаточное условие перпендикулярности двух векторов

Применим правило о перпендикулярных векторах на плоскости и в трехмерном пространстве.

При условии значения угла между двумя ненулевыми векторами равным 90°( π2 радиан) называют перпендикулярными.

Что это значит, и в каких ситуациях необходимо знать про их перпендикулярность?

Установление перпендикулярности возможно через чертеж. При отложении вектора на плоскости от заданных точек можно геометрически измерить угол между ними. Перпендикулярность векторов если и будет установлена, то не совсем точно. Чаще всего данные задачи не позволяют делать это при помощи транспортира, поэтому данный метод применим только в случае, когда ничего больше о векторах неизвестно.

Большинство случаев доказательства перпендикулярности двух ненулевых векторов на плоскости или в пространстве производится с помощью необходимого и достаточного условия перпендикулярности двух векторов.

Скалярное произведение двух ненулевых векторов a→ и b→ равном нулю для выполнения равенства a→, b→=0 достаточно для их перпендикулярности.

Условие перпендикулярности на координатной плоскости

Раздел скалярного произведения в координатах демонстрирует неравенство (a→, b→)=ax·bx+ay·by, справедливое для векторов с координатами a→=(ax, ay) и b→=(bx, by), на плоскости и (a→,b→)=ax·bx+ay·by для векторов a→=(ax, ay, az) и b→=(bx, by, bz) в пространстве. Необходимым и достаточным условием перпендикулярности двух векторов в координатной плоскости имеет вид ax·bx+ay·by=0, для трехмерного пространства ax·bx+ay·by+az·bz=0.

Применим на практике и рассмотрим на примерах.

Имеются случаи, когда вопрос о перпендикулярности невозможен даже при необходимом и достаточном условии. При известных данных о трех сторонах треугольника на двух векторах, возможно, найти угол между векторами и проверить его.

Нахождение вектора, перпендикулярного данному

Важно научиться находить координаты вектора, перпендикулярного заданному. Это возможно как на плоскости, так и в пространстве при условии перпендикулярности векторов.

Нахождение вектора, перпендикулярного данному в плоскости.

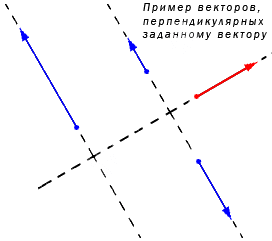
Ненулевой вектор a→ может иметь бесконечное количество перпендикулярных векторов на плоскости. Изобразим это на координатной прямой.

Задан ненулевой вектор a→, лежащий на прямой а. Тогда заданный b→, расположенный на любой прямой, перпендикулярной прямой а, становится перпендикулярным иa→. Если вектору i→ перпендикулярен вектор j→ или любой из векторов λ·j→при λ равной любому действительному числу кроме нуля, то нахождение координат вектора b→, перпендикулярному a→=(ax, ay), сводится к бесконечному множеству решений. Но необходимо найти координаты вектора, перпендикулярного a→=(ax, ay). Для этого необходимо записать условие перпендикулярности векторов в такой форме ax·bx+ay·by=0. Имеем bx и by , являющиеся искомыми координатами перпендикулярного вектора. Когда ax≠0, значение by является ненулевым, а bx вычислим из неравенства ax·bx+ay·by=0 ⇔bx=-ay·byax. При ax=0 и ay≠0 присваиваем bx любое значение кроме нуля, а by находим из выражения by=-ax·bxay.

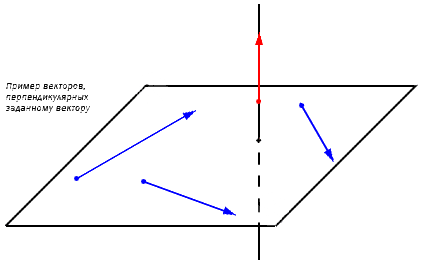
Если ставится вопрос о трехмерном пространстве, задача решается по такому же принципу. При заданном векторе a→=(ax, ay, az) существует бесконечное множество перпендикулярных векторов. Зафиксирует это на координатной трехмерной плоскости. Дана a→ , лежащая на прямой a. Перпендикулярную прямой a плоскость обозначаем α. В этом случае любой ненулевой вектор b→ из плоскости α перпендикулярен a→.

Необходимо найти координаты b→, перпендикулярного ненулевому вектору a→=(ax, ay, az).

Пусть задан b→ с координатами bx, by и bz. Чтобы найти их, необходимо применить определение условия перпендикулярности двух векторов. Равенство ax·bx+ay·by+az·bz=0 должно выполняться. Из условия a→ – ненулевой, значит, одна из координат имеет значение не равное нулю. Предположим, что ax≠0, ( ay≠0 или az≠0). Следовательно, имеем право разделить на эту координату все неравенство ax·bx+ay·by+az·bz=0, получим выражениеbx+ay·by+az·bzax=0⇔bx=-ay·by+az·bzax. Присваиваем координатам by и bx любое значение, вычисляем значение bx, исходя из формулы, bx=-ay·by+az·bzax. Искомый перпендикулярный вектор будет иметь значение a→=(ax, ay, az).

Рассмотрим доказательство на примере.

Нахождение координат вектора, перпендикулярного двум заданным векторам

Нужно найти координаты вектора в трехмерном пространстве. Он перпендикулярен не коллинеаренным векторамa→(ax, ay, az) и b→=(bx, by, bz). При условии коллинеарности векторов a→ и b→ в задаче достаточно будет найти вектор, перпендикулярный a→ или b→.

При решении применяется понятие векторного произведения векторов.

Векторным произведением векторов a→ и b→ называют вектор, одновременно перпендикулярный и a→ и b→. Для решения данной задачи применяется векторное произведение a→×b→. Для трехмерного пространства имеет вид a→×b→=a→j→k→axayazbxbybz

Разберем подробнее векторное произведение на примере задачи.