Запомните!
![]()
Периметр — это сумма длин всех сторон многоугольника.
Иногда для вычисления периметра геометрических фигур используются специальные формулы,
в которых периметр обозначается заглавной латинской буквой «P».
Периметр измеряется в единицах длины: мм, см, м, км и т.д.
При нахождении периметра мы рекомендуем писать название фигуры маленькими
буквами под знаком «P», чтобы не забывать чей периметр вы находите.
Запомните!
![]()
Периметр прямоугольника — это сумма длины и ширины, умноженная на «2».
P = (a + b) · 2
,
где «a» — длина прямоугольника, «b» — ширина прямоугольника.
Стороны прямоугольника, которые лежат друг против друга (противолежащие), мы
называем длиной и шириной.
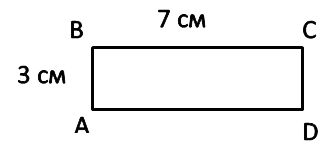
AB = 3 см, BC = 7 см
PABCD = (AB + BC) · 2
PABCD = (7 + 3) · 2 = 10 · 2 = 20 (см)
Запомните!
![]()
Периметр квадрата — это длина стороны квадрата, умноженная на «4».
P = a · 4
, где a — длина стороны квадрата.
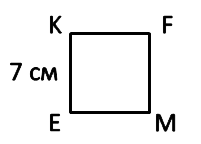
KE = 7 см
PEKFM = 4 · KE
PEKFM = 4 · 7 = 28 (см)
Как найти периметр многоугольника
Периметр любого многоугольника (в том числе и периметр треугольника)
рассчитывается по определению периметра.
Для этого надо просто сложить длины всех сторон многоугольника.
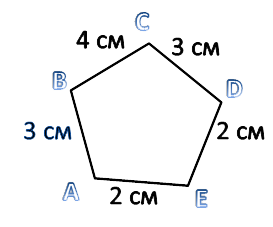
PABCDE = AB + BC + CD + DE + EA = 3 + 4 + 3 + 2 + 2 = 14 (см)
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
20 апреля 2017 в 17:19
Надежда Григоренко

Профиль
Благодарили: 0
Сообщений: 1

Надежда Григоренко
Профиль
Благодарили: 0
Сообщений: 1
длина прямоугольника 720м а ширина 18м меньше.найти ширину прямоугольника и его периметр
0
Спасибо
Ответить
26 апреля 2017 в 20:06
Ответ для Надежда Григоренко
Ярослав Мудрый

Профиль
Благодарили: 0
Сообщений: 1

Ярослав Мудрый
Профиль
Благодарили: 0
Сообщений: 1
Нужно из 720 вычесть 18, а потом 720 · 2 + 702 · 2
0
Спасибо
Ответить
17 мая 2017 в 22:22
Ответ для Надежда Григоренко
София Нгуен

Профиль
Благодарили: 0
Сообщений: 2

София Нгуен
Профиль
Благодарили: 0
Сообщений: 2
720-18=702-ширина
Р=2(720+702)=2844
0
Спасибо
Ответить
5 февраля 2017 в 12:17
Лев Дубров

Профиль
Благодарили: 0
Сообщений: 1

Лев Дубров
Профиль
Благодарили: 0
Сообщений: 1
на сколько изменится периметр прямоугольника если его длину увелисчить на 5.1/6 сантиметров, а ширину уменьшить на 1.1/2 сантиметров?
0
Спасибо
Ответить
11 февраля 2017 в 13:46
Ответ для Лев Дубров
Алексей Карапов

Профиль
Благодарили: 0
Сообщений: 9

Алексей Карапов
Профиль
Благодарили: 0
Сообщений: 9
Формула прямоугольника после изменений
В которой
Р -Периметр
Р + (5.1/6 + 5.1/6) + (1.1/2 + 1.1/2)
Разкажу более подробней
Р + 10.2/6 +3 = Р + 13Целых и 2/6
ИЛИ
Периметр + сума в первых скобках + сума во вторых скобках
0
Спасибо
Ответить
19 января 2017 в 18:22
София Желнаркевич

Профиль
Благодарили: 0
Сообщений: 1

София Желнаркевич
Профиль
Благодарили: 0
Сообщений: 1
Периметр равнобедренного треугольника равен 15 см 8 мм.Основание треугольника 7 см 8 мм. Найдите боковые стороны треугольника.
0
Спасибо
Ответить
20 февраля 2017 в 17:43
Ответ для София Желнаркевич
Алексей Карапов

Профиль
Благодарили: 0
Сообщений: 9

Алексей Карапов
Профиль
Благодарили: 0
Сообщений: 9
РЕШЕНИЕ: 15см8мм ? 7см8мм=8см8мм-2 боковые стороны;
8см8мм :2=4см4мм-1 боковая сторона
0
Спасибо
Ответить
13 декабря 2016 в 19:36
Марина Ребрикова

Профиль
Благодарили: 0
Сообщений: 1

Марина Ребрикова
Профиль
Благодарили: 0
Сообщений: 1
стороны прямоугольника равны 12 см и 25 см, Вычислите его: а) периметр б) площадь
0
Спасибо
Ответить
14 декабря 2016 в 16:37
Ответ для Марина Ребрикова
Руслан Потапов

Профиль
Благодарили: 0
Сообщений: 2

Руслан Потапов
Профиль
Благодарили: 0
Сообщений: 2
периметр р=2(а+в)=2(12+25)=74
площадь s=ав=300
0
Спасибо
Ответить
20 декабря 2016 в 22:45
Ответ для Марина Ребрикова
Сарра Черенкова

Профиль
Благодарили: 0
Сообщений: 1

Сарра Черенкова
Профиль
Благодарили: 0
Сообщений: 1
Периметр находится так, нужно сложить сторону А и сторону В и умножить их на 2. Это, (12+25) · 2= 37 · 2=74 см. Площадь находится умножением стороны А на В. 12 · 25=300 см.
0
Спасибо
Ответить
21 ноября 2016 в 20:55
Никита Зимоха

Профиль
Благодарили: 0
Сообщений: 1

Никита Зимоха
Профиль
Благодарили: 0
Сообщений: 1
длина прямоугольника в 4 раза больше ширины нйдите стороны прямоугольника, если уго периметр равен 130 дм.
0
Спасибо
Ответить
23 ноября 2016 в 8:48
Ответ для Никита Зимоха
Владимир Баженов

Профиль
Благодарили: 0
Сообщений: 1

Владимир Баженов
Профиль
Благодарили: 0
Сообщений: 1
привет Никита .
4х+1х+4х+1х=130
10х=130
х=13 -длина маленькой стороны
4х=4*13=52 -длина большой стороны
Никита мне нужна твоя помощ. Напиши мне на почту hihkore2@yandex.ru
0
Спасибо
Ответить
9 апреля 2016 в 17:37
Матвей Гамзиков

Профиль
Благодарили: 0
Сообщений: 3

Матвей Гамзиков
Профиль
Благодарили: 0
Сообщений: 3
Учебник геометрии 7 класс (Александров Вернер…) задача 7.35 Периметр прямоугольника равен 1. Найти стороны прямоугольника если: а)одна сторона больше другой в 2 раза, б) одна сторона больше другой на 0,1 в) одна сторона составляет 25% от другой. Вопросов по решению а и в нет. Выражаем одну сторону через другую составляем уравнение вычисления периметра и готово. Тогда как в варианте б не корректно поставлено условие, которое допускает два решения. По логике решения а и в X-одна сторона вторая равна X+0.1X=1.1X В ответе стороны равны 10/42 и 11/42. Сумма всех торон дает единицу. Но учитель утверждает что формула вычисления выглядит так 2X+2(X+0.1)=1 Т.е. согласно этого решения одна сторона больше другой на 0,1 периметра. но этого в условии не указано. Еще одно утверждение учителя что сторона больше другой на 0,1 единичного отрезка тоже никак не отражено в условии. Решение этого уравнения дает размеры сторон 2/10 и 3/10 сумма тоже равна 1 Ответ в учебнике именно этот. Так где-же логика которая от математики не должна отходить ни на шаг? Может я чего-то не понимаю? <col />
0
Спасибо
Ответить
10 апреля 2016 в 9:26
Ответ для Матвей Гамзиков
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Большое спасибо, за попытку разобраться-это стоит многого! Кажется вопрос во внимательности. Если процитировать задачу, то пункт б) звучит именно так: «б) одна сторона больше другой на 0,1». И дальше вы сами же себе противоречите, говоря, что этого нет в задаче =).
Утверждение учителя, относительно формулы-абсолютно верное. Х-одна сторона. Вторая на 0,1 больше, следовательно Х+0,1. В прямоугольнике по две стороны каждой длины, а значит и периметр вычисляем умножив каждую на 2. 2Х+2(Х+0,1). По условию задачи, периметр равен 1. Составляем и решаем. 2/10 и 3/10 — ответ абсолютно верный. Есть второй момент, который может Вам помочь: Вы написали:«По логике решения а и в X-одна сторона вторая равна X+0.1X=1.1X ». В этом выражении присутствует ошибка. Если перевести его в текст, то условие задачи было бы: «Одна сторона больше другой в 0,1 раз». «В» — это умножение, а «На»-это сложение. Вот и получается, что учитель дал вам совершенно правильное уравнение для периметра. Удачи, надеюсь не сильно запутал!
0
Спасибо
Ответить
10 апреля 2016 в 10:23
Ответ для Матвей Гамзиков
Матвей Гамзиков

Профиль
Благодарили: 0
Сообщений: 3

Матвей Гамзиков
Профиль
Благодарили: 0
Сообщений: 3
Спасибо за ответ. Тогда объясните с этой же позиции Одна сторона больше другой в 2раза.
Т.е. одна =Х, другая Х*2=2Х
одна сторона больше другой в 0,1
одна=Х, другая Х*0,1= 0,1Х т.е полусчается противоречие -сторона в еденицах измерения меньше первой. Для того что-бы на писать «в» нужно указать что одна сторона больше другой «в 1.1 раза
Поэтому в условии и сказано чтобольше на 0,1 только не указано от чего.
0,1 стороны прямоугольника или 0,1 периметра. Я еще раз настаиваю на не корректной постановки задачи. если задачу с этим условием незначительно изменить, то она получает не 2 а 3 решения и все три правильные.
Если периметр будет равен 3 а остальные условия останутся прежними: в случае относительно сторон одна сторона = , вторая = , периметр=3,
вслучае относительно периметра одна сторона=0,6, вторая=0,9, периметр= 3,
вслучае решения по учебнику одна сторона= , вторая = , периметр=3,
Математика наука точная постановки задач в математике должны быть точными и корректными, не допускающими двойного толкования. Тогда у нас небудуть падать спутники и сталкиваться в лобовую поезда. Внимательно и с удовольствием выслушаю все доказательства того, что вариант решения по учебнику единственно правильный.
Попробуйте решить простую задачу: одна сторона прямоугольника= 1фут другая на 0,1 больше напишите размеры сторон в сантиметрах
0
Спасибо
Ответить
10 апреля 2016 в 17:25
Ответ для Матвей Гамзиков
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
И снова добрый день. Вот здесь и есть недопонимание: «Поэтому в условии и сказано чтобольше на 0,1 только не указано от чего.
0,1 стороны прямоугольника или 0,1 периметра. Я еще раз настаиваю на не корректной постановки задачи. если задачу с этим условием незначительно изменить, то она получает не 2 а 3 решения и все три правильные.»
Больше на 0,1. Значит, что больше на 0,1 условную единицу. Задайте себе вопрос, почему Вас не смущает в условии: «Периметр равен 1»? Не 1 см, не 1фут. а просто 1. Ровно из тех же соображений, написано больше на 0,1.
По мимо того, что математика наука точная, она учит ещё и абстрактному мышлению и принятию некоторых условий. Если не указана единица измерения, то берётся некоторая абстрактная условная единица, просто об этом не пишут.
А Ваша задача решается предельно просто:
Т.к. размер одной стороны 1 фут, а вторая больше неё на 0,1 ПРЕДПОЛОЖИМ, что больше она на 0,1 фут. Следовательно размер второй стороны 1,1 фут.
1фут=30,48 см.
1,1фут=33,528см.
Если же ПРЕДПОЛОЖИТЬ, что больше на 0,1 см, то сначала выражаем первую сторону в см, а потом прибавляем 0,1см.
1фут=30,48см
30,48см+0,1см=30,58см.
Ни один преподаватель после такого объяснения и описания вам не скажет ничего осуждающего, а только похвалит.
Стоит отметить, что в исходной задче не указаны единицы измерения, а вы их сами взяли и смешали, так что сравнение некорректное.
И ещё маленькое уточнение: В этом мире, к сожалению, всего знать невозможно. Если Вы считаете, что в учебнике ошибка-напишите в редакцию, подробно опишите проблему и Вам наверняка ответят. благо современные средства связи позволяют.
Боритесь за свою правоту! Главное-умейте признавать ошибки! =)
Всего доброго! =)
0
Спасибо
Ответить
10 апреля 2016 в 18:22
Ответ для Матвей Гамзиков
Матвей Гамзиков

Профиль
Благодарили: 0
Сообщений: 3

Матвей Гамзиков
Профиль
Благодарили: 0
Сообщений: 3
Приятно получить исчерпывающий ответ. Я поэтому и задал вопрос об 1футе. Стоит ввести небольшое уточнение как задача теряет единственность решения. Это уже ближе вероятному решению А если взадаче указать 0,1 от периметра то единственностьрешения не измениться при любых вводных условиях. Приятно было общаться.
0
Спасибо
Ответить
14 июня 2016 в 19:50
Ответ для Матвей Гамзиков
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Не морочь людям голову.
Задача ясно и однозначно поставлена.
В учебнике ответ и .
0
Спасибо
Ответить
3 апреля 2016 в 12:15
Димка Шаменков

Профиль
Благодарили: 0
Сообщений: 1

Димка Шаменков
Профиль
Благодарили: 0
Сообщений: 1
? 1/12 части квадрата 3см? Найти ? всего квадрата
0
Спасибо
Ответить
4 апреля 2016 в 8:15
Ответ для Димка Шаменков
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Если площадь части квадрата 3, то площадь всего квадрата в 12 раз больше. Т.е. 12 · 3= 36.
36см2-площадь всего квадрата.
0
Спасибо
Ответить
17 января 2016 в 15:47
Сергей Малярчук

Профиль
Благодарили: 0
Сообщений: 1

Сергей Малярчук
Профиль
Благодарили: 0
Сообщений: 1
периметр прямоугольника равен 36см. найдите площадь прямоугольника, если известно, что его стороны относятсякак: а1:5 б1:3 в1:2 г1:1.как меняется площадь прямоугольника от первого к последнему случаю? у какого прямоугольника площадь наибольшая?
0
Спасибо
Ответить
19 сентября 2016 в 11:40
Ответ для Сергей Малярчук
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Периметр прямоугольника.
P=2(a+b)
Площадь прямоугольника.
S=a · b
a)36=2(x+5x)
36=12x
x=3
a=3
b=5 · 3=15
S=a · b =3 · 15=45
Далее логика аналогичная:
б)36=2(x+3x)
a=4,5
b=13,5
S=60,75
в)36=2(x+2x)
a=6
b=12
S=72
г)36=2(x+x)
a=12
b=12
S=144
Площадь прямоугольника увеличивается. Площадь прямоугольника г) — наибольшая. Прямоугольник г) также является квадратом. т.к. стороны равны.
0
Спасибо
Ответить
12 января 2016 в 18:45
Артем Василенко

Профиль
Благодарили: 0
Сообщений: 1

Артем Василенко
Профиль
Благодарили: 0
Сообщений: 1
Знайди периметр трикутника зі сторонами 2 см 8мм, 3 см 4мм,1 см 7 мм.
0
Спасибо
Ответить
12 января 2016 в 18:50
Ответ для Артем Василенко
Кирилл Нечаев

Профиль
Благодарили: 0
Сообщений: 3

Кирилл Нечаев
Профиль
Благодарили: 0
Сообщений: 3
р
0
Спасибо
Ответить
12 января 2016 в 18:51
Ответ для Артем Василенко
Кирилл Нечаев

Профиль
Благодарили: 0
Сообщений: 3

Кирилл Нечаев
Профиль
Благодарили: 0
Сообщений: 3
34417
0
Спасибо
Ответить
12 января 2016 в 18:52
Ответ для Артем Василенко
Кирилл Нечаев

Профиль
Благодарили: 0
Сообщений: 3

Кирилл Нечаев
Профиль
Благодарили: 0
Сообщений: 3
34417
0
Спасибо
Ответить
19 сентября 2016 в 10:35
Ответ для Артем Василенко
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Чтобы найти периметр треугольника(если я правильно понял название фигуры) нужно сложить длины его сторон. Нужно учитывать, что в 1см=10мм. Переведём всё в мм и сложим. P=a+b+c=28+34+17=79мм=7см9мм.
0
Спасибо
Ответить
11 ноября 2015 в 17:47
Дианочка Лазарева

Профиль
Благодарили: 0
Сообщений: 1

Дианочка Лазарева
Профиль
Благодарили: 0
Сообщений: 1
Длина прямоугольника в 8 раз больше ширины.найдите площадь и периметр прямоугольника, если ширина на 42 см меньше длины
0
Спасибо
Ответить
16 сентября 2016 в 13:37
Ответ для Дианочка Лазарева
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Обозначим:
a-длина
b-шрина
Длина в 8 раз больше ширины: a=8b
Ширина на 42см меньше длины: a=b + 42
Вычислим отсюда b: b + 42=8b
7b=42
b=6 — ширина равна 6, тогда длина a=6 · 8 = 48.
Периметр прямоугольника P = 2a + 2b = 2 · 6 + 2 · 48 = 108
Площадь прямоугольника S = a · b = 2 · 48 = 96
0
Спасибо
Ответить
23 октября 2015 в 10:20
Галина Тимичева

Профиль
Благодарили: 0
Сообщений: 2

Галина Тимичева
Профиль
Благодарили: 0
Сообщений: 2
периметр квадрата равен 12см. найдите сторону квадрата и начертите его.
0
Спасибо
Ответить
23 октября 2015 в 10:23
Ответ для Галина Тимичева
Галина Тимичева

Профиль
Благодарили: 0
Сообщений: 2

Галина Тимичева
Профиль
Благодарили: 0
Сообщений: 2
периметр квадрата равен 12см. найдите сторону квадрата и начертите его.
0
Спасибо
Ответить
23 октября 2015 в 17:59
Ответ для Галина Тимичева
Марина Реснянская

Профиль
Благодарили: 0
Сообщений: 4

Марина Реснянская
Профиль
Благодарили: 0
Сообщений: 4
И ТАК 12: 4 =3СМ СТОРОНА КВАДРАТА И ЧЕРЧИШЬ КВАДРАТ 3*3
0
Спасибо
Ответить
23 октября 2015 в 18:00
Ответ для Галина Тимичева
Марина Реснянская

Профиль
Благодарили: 0
Сообщений: 4

Марина Реснянская
Профиль
Благодарили: 0
Сообщений: 4
И ТАК 12: 4 =3СМ СТОРОНА КВАДРАТА И ЧЕРЧИШЬ КВАДРАТ 3*3
0
Спасибо
Ответить
23 октября 2015 в 21:21
Ответ для Галина Тимичева
Елизавета Яременко

Профиль
Благодарили: 0
Сообщений: 5

Елизавета Яременко
Профиль
Благодарили: 0
Сообщений: 5
Мне кажется, что:
1)12:4=3(см)-сторона квадрата.
0
Спасибо
Ответить
27 октября 2015 в 15:27
Ответ для Галина Тимичева
Марина Доценко

Профиль
Благодарили: 0
Сообщений: 3

Марина Доценко
Профиль
Благодарили: 0
Сообщений: 3
1)12: 4=3(см)-сторона квадрата
0
Спасибо
Ответить
9 ноября 2015 в 18:48
Ответ для Галина Тимичева
София Тышкевич

Профиль
Благодарили: 0
Сообщений: 2

София Тышкевич
Профиль
Благодарили: 0
Сообщений: 2
согласна что тут непонятного
0
Спасибо
Ответить
9 ноября 2015 в 18:49
Ответ для Галина Тимичева
София Тышкевич

Профиль
Благодарили: 0
Сообщений: 2

София Тышкевич
Профиль
Благодарили: 0
Сообщений: 2
согласна что тут непонятного
0
Спасибо
Ответить
14 ноября 2015 в 19:05
Ответ для Галина Тимичева
Максим Бычков

Профиль
Благодарили: 0
Сообщений: 2

Максим Бычков
Профиль
Благодарили: 0
Сообщений: 2
12: 4=3
0
Спасибо
Ответить
22 октября 2015 в 15:34
Эльза Прокофьева

Профиль
Благодарили: 0
Сообщений: 1

Эльза Прокофьева
Профиль
Благодарили: 0
Сообщений: 1
Пожалуйста помогите с Домашним Заданием для 3 класса!![]() Ширина прямоугольника 3 см, а длина в 4 раза больше. Найди периметр и площадь прямоугольника.
Ширина прямоугольника 3 см, а длина в 4 раза больше. Найди периметр и площадь прямоугольника.
0
Спасибо
Ответить
23 октября 2015 в 13:47
Ответ для Эльза Прокофьева
Елизавета Яременко

Профиль
Благодарили: 0
Сообщений: 5

Елизавета Яременко
Профиль
Благодарили: 0
Сообщений: 5
3 · 4 Это площадь3 + 4 + 3 + 4 Это периметр
0
Спасибо
Ответить
23 октября 2015 в 13:48
Ответ для Эльза Прокофьева
Елизавета Яременко

Профиль
Благодарили: 0
Сообщений: 5

Елизавета Яременко
Профиль
Благодарили: 0
Сообщений: 5
Ну как?
я 5 класс
спрашивай если что
0
Спасибо
Ответить
23 октября 2015 в 18:03
Ответ для Эльза Прокофьева
Марина Реснянская

Профиль
Благодарили: 0
Сообщений: 4

Марина Реснянская
Профиль
Благодарили: 0
Сообщений: 4
1)ДЛИНА=3 УМНОЖИТЬ НА 2 =6
р=2*6=12 СМ
2)24:3=4
0
Спасибо
Ответить
23 октября 2015 в 18:03
Ответ для Эльза Прокофьева
Марина Реснянская

Профиль
Благодарили: 0
Сообщений: 4

Марина Реснянская
Профиль
Благодарили: 0
Сообщений: 4
НАЙДИ В ЯНДЕКСЕ.
0
Спасибо
Ответить
26 октября 2015 в 11:59
Ответ для Эльза Прокофьева
Иван Мудрак

Профиль
Благодарили: 0
Сообщений: 1

Иван Мудрак
Профиль
Благодарили: 0
Сообщений: 1
я тож пятый класс![]()
0
Спасибо
Ответить
27 октября 2015 в 15:24
Ответ для Эльза Прокофьева
Марина Доценко

Профиль
Благодарили: 0
Сообщений: 3

Марина Доценко
Профиль
Благодарили: 0
Сообщений: 3
3*4=12cм — площадь
(3+4)*2=14см — периметр
0
Спасибо
Ответить
27 октября 2015 в 15:25
Ответ для Эльза Прокофьева
Марина Доценко

Профиль
Благодарили: 0
Сообщений: 3

Марина Доценко
Профиль
Благодарили: 0
Сообщений: 3
Лиза я тоже в 5 классе
0
Спасибо
Ответить
29 октября 2015 в 15:55
Ответ для Эльза Прокофьева
Марья Голдобина

Профиль
Благодарили: 0
Сообщений: 4

Марья Голдобина
Профиль
Благодарили: 0
Сообщений: 4
3 · 4=12-длина
12 · 3=36-S
12+3+36=51-P
точно не помню не судите строго
0
Спасибо
Ответить
30 марта 2016 в 15:52
Ответ для Эльза Прокофьева
Галина Петухова

Профиль
Благодарили: 0
Сообщений: 1

Галина Петухова
Профиль
Благодарили: 0
Сообщений: 1
незнаю когда это было но девочке 2 поставели потому что:
3*4=12 это длина прямоугольника
(3+12)*2=30см а не 12 это p
3*12=36 кв см это S
всё!!!!!!!!!!!!
0
Спасибо
Ответить
15 сентября 2016 в 10:46
Ответ для Эльза Прокофьева
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Вот это неразбериха! Хотя ответ правильный уже дан, может понятнее будет+приведу ссылки на объяснение на сайте.
1) найдём длину прямоугольника. Т.к. она в 4 раза больше ширины, значит нужно длину умножить на 4.
3 · 4 = 12 (см) — длина прямоугольника.
2) Периметр прямоугольника — сумма всех его сторон. У прямоугольника 2 длины и две ширины. Подробнее здесь.
P=2a+2b
P=2 · 3 + 2 · 12 = 6 + 24 = 30 (см) — периметр прямоугольника.
3) Площадь прямоугольника это произведение ширины на длину. Подробнее здесь.
S=a · b
S=3 · 12 = 36 (см2) — площадь прямоугольника.
Ответ: P=30см, S=36см2
0
Спасибо
Ответить
16 сентября 2015 в 18:25
Света Шульга

Профиль
Благодарили: 0
Сообщений: 1

Света Шульга
Профиль
Благодарили: 0
Сообщений: 1
Из двух листов картона, имеющих форму квадрата, длина стороны которого 30 см, вырезали два круга. Найдите площадь обрезков картона, если 3,14
0
Спасибо
Ответить
8 сентября 2016 в 16:24
Ответ для Света Шульга
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Т.к. мы имеем два одинаковых листа картона и два одинаковых круга, которые из них вырезают, то найдём площадь обрезков от одного и умножим на 2. ПРЕДПОЛОЖИМ, что круг вырезают максимально возможного радиуса. В таком случае, радиус круга равен половине длины стороны квадрата (лучший сопсоб это представить-вырезать из реальной бумаги.) Что такое обрезки? это то, что осталось, после вырезания круга, т.е. разница между площадью квадрата(листа картона) и площадью круга, который вырезают из этого листа.
Площадь квадрата S=a2
Площадь круга S=?r2=?()2=
Площадь обрезков S=a2 ?
0
Спасибо
Ответить
8 сентября 2016 в 16:29
Ответ для Света Шульга
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
S=900 ? =900 ? 3,14 · 225 = 193,5
Т.к. квадратов 2, то полученный результат умножаем на 2. 193,5 · 2 = 387
Ответ: Площадь обрезков равна 387 см2P.S. Данное решение будет верным, в случае нашего ПРЕДПОЛОЖЕНИЯ
0
Спасибо
Ответить
4 сентября 2015 в 15:35
Игорь Винников

Профиль
Благодарили: 0
Сообщений: 2

Игорь Винников
Профиль
Благодарили: 0
Сообщений: 2
Периметр прямоугольника 36см, одна из сторон12см. Чему равны другие три стороны?
0
Спасибо
Ответить
1 сентября 2016 в 10:15
Ответ для Игорь Винников
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Периметр это сумма длин сторон. В прямоугольнике противоположные стороны равны по длине. Предположим, что одна сторона равна a, а другая b.
Периметр прямоугольника вычисляется по формуле:
P=a+a+b+b=2a+2b. Допустим, что сторона a=12см. Подставим значения в формулу:
36 = 2 · 12 + 2 · b
2 · b = 36 ?2 · 12
2 · b = 12
b = 6
Произведем проверку, подставив значения в формулу перметра.
2 · 12 +2 · 6 = 24 + 12 = 36
Следовательно, ответ был получен верно.
Ответ: оставшиеся стороны прямоугольника равны 12см, 6см, 6см.
0
Спасибо
Ответить
26 августа 2015 в 21:11
Таня Грига

Профиль
Благодарили: 0
Сообщений: 2

Таня Грига
Профиль
Благодарили: 0
Сообщений: 2
Петерсон. 5 класс 1 часть №102
Одна из сторон прямоугольника на 10 см меньше другой. Если меньшую сторону увеличить на 15 см, а большую увеличить на 20 см, то площадь прямоугольникаувеличиться в 5 раз. Чему равна ширина данного прямоугольника?
0
Спасибо
Ответить
26 августа 2015 в 21:13
Ответ для Таня Грига
Таня Грига

Профиль
Благодарили: 0
Сообщений: 2

Таня Грига
Профиль
Благодарили: 0
Сообщений: 2
Какую из сторон брать за Х?
0
Спасибо
Ответить
1 сентября 2016 в 9:41
Ответ для Таня Грига
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Не принципиален выбор стороны за X. Обозначим большую сторону за X, тогда другая сторона будет X-10, т.е. на 10 см меньше. Если обозначить за X меньшую сторону, то другая сторона будет X+10.
Рассмотрим первый вариант.
Одна сторона — X, другая сторона X-10.
Площадь прямоугольника равна произведению длины на ширину(a · b) или X · (X-10). Обозначим площадь за S.
Учитывая второе условие составим ещё одно уравнение:
(X +20) · (X ?10 + 15) = 5 · S
S =
Выразив S из каждого уравнения, приравняем их и вычислим значение X.
X · (X ?10) =
5 · X2 ? 50 · X = X2+ 5 · X + 20 · X + 100
4 · x2 ? 75 · x ? 100 = 0
Решим квадратное уравнение:
D = (-75)2 ? 4 · 4 · (-100) = 5625 + 1600 = 7225
x1=
= — 1,25
x2 = = 20
Т.к. длина стороны не может быть выражена отрицательным значением, то остаётся только один ответ: 20. Следовательно длина прямоугольника равна 20, а ширина 20-10=10, а площадь соотвественно 20 · 10 = 200.
Проверим получившиеся значения, применив известное по задаче условие:
(20+20) · (10+15) = 40 · 25 = 1000
1000: 5 =200
Условие выполняется, а значит ответ подобран верно.
Ответ: ширина данного прямоугольника равна 10 см.
0
Спасибо
Ответить
14 мая 2015 в 18:17
Настя Фадеева

Профиль
Благодарили: 0
Сообщений: 1

Настя Фадеева
Профиль
Благодарили: 0
Сообщений: 1
Сторона квадрата равна 14 мм. Чему равна его площадь
0
Спасибо
Ответить
14 мая 2015 в 21:45
Ответ для Настя Фадеева
Ярик Кравченко

Профиль
Благодарили: 0
Сообщений: 3

Ярик Кравченко
Профиль
Благодарили: 0
Сообщений: 3
14мм *14мм= 196мм= 190,6 см
0
Спасибо
Ответить
19 мая 2015 в 15:04
Ответ для Настя Фадеева
Мадина Зиямидинова

Профиль
Благодарили: 0
Сообщений: 1

Мадина Зиямидинова
Профиль
Благодарили: 0
Сообщений: 1
14 * 14*14*14 = 56
0
Спасибо
Ответить
23 октября 2015 в 21:37
Ответ для Настя Фадеева
Елизавета Яременко

Профиль
Благодарили: 0
Сообщений: 5

Елизавета Яременко
Профиль
Благодарили: 0
Сообщений: 5
14-1сторона квадрата
всего их 4 поэтому умножаем на 4
1)14.4=56мм-4стороны квадрата)))))))
0
Спасибо
Ответить
17 апреля 2016 в 16:22
Ответ для Настя Фадеева
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Площадь квадрата — это квадрат его стороны. А периметр квадрата, это сумма длин его сторон. Т.е. сторона умноженная на 4. Следовательно, ответ данный Яриком Кравченко-абсолютно верный, за исключением перевода в см: 14*14 = 196(мм) = 19,6 см.
Остальные ответы не верные даже в расчете.
0
Спасибо
Ответить
21 апреля 2015 в 8:42
Надежда Григорьева

Профиль
Благодарили: 0
Сообщений: 1

Надежда Григорьева
Профиль
Благодарили: 0
Сообщений: 1
Длина прямоугольника 2,8 дм, а ширина в 4 раза меньше длины. Найдите длину стороны квадрата, площадь которого равна площади прямоугольника
0
Спасибо
Ответить
14 апреля 2016 в 11:54
Ответ для Надежда Григорьева
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
1) Найдём ширину прямоугольника: 2,8/4=0,7.
2) Найдём площадь прямоугольника: S=a · b = 2,8 · 0,7 = 1,96
3) Площадь квадрата: S=a2. Следовательно сторона: а=?S
a=?1,96=±1,4. Длина стороны не может быть отрицательной, а значит равна 1,4.
Ответ 1,4дм
0
Спасибо
Ответить
![]()
Периметр — длина контура замкнутой плоской фигуры, длина границы.
Пери́метр (др.-греч. περίμετρον — окружность, др.-греч. περιμετρέο — измеряю вокруг) — общая длина границы фигуры (чаще всего на плоскости). Имеет ту же размерность величин, что и длина.
Иногда периметром называют границу геометрической фигуры.
Вычисление периметра имеет существенное практическое значение. Например, для вычисления длины ограды вокруг сада или участка. Периметр колеса (окружности) определяет, насколько далеко оно продвинется при полном обороте. Таким же образом, длина нитки, намотанной на катушку, тесно связана с периметром катушки.
Формулы[править | править код]
| фигура | формула | переменные |
|---|---|---|
| окружность |  |
где  — радиус окружности, а — радиус окружности, а  — диаметр. — диаметр.
|
| треугольник |  |
где  , ,  и и  — длины сторон треугольника. — длины сторон треугольника.
|
| квадрат/ромб |  |
где  — длина стороны. — длина стороны.
|
| прямоугольник |  |
где  — длина (основания), а — длина (основания), а  — ширина. — ширина.
|
| равносторонний многоугольник |  |
где  — число сторон, а — число сторон, а  — длина сторон. — длина сторон.
|
| правильный многоугольник |  |
где  — число сторон, а — число сторон, а  — расстояние от центра многоугольника до одной из вершин многоугольника. — расстояние от центра многоугольника до одной из вершин многоугольника.
|
| общий многоугольник |  |
где  — длина — длина  -й (1, 2, 3 … n) стороны n-угольника. -й (1, 2, 3 … n) стороны n-угольника.
|
Многоугольники[править | править код]

Многоугольники являются основными фигурами для определения периметров, и не только потому, что они являются простейшими фигурами, но и потому, что периметры многих фигур вычисляются путём аппроксимации их последовательностью многоугольников. Первым известным математиком, который использовал этот подход, был Архимед, который аппроксимировал периметр окружности путём описывания около неё правильных многоугольников.
Периметр многоугольника равен сумме длин его сторон. В частности, периметр прямоугольника, имеющего ширину 


Равносторонний многоугольник — это многоугольник, имеющий равные длины сторон (например ромб — это равносторонний многоугольник с 4 сторонами). Чтобы вычислить периметр равностороннего многоугольника, нужно умножить число сторон на общую длину стороны.
Периметр правильного многоугольника можно вычислить по числу сторон и его радиусу, то есть расстоянию от центра до вершин. Длину стороны можно вычислить, используя тригонометрию. Если R — радиус многоугольника, а n — число сторон, периметр равен
Периметр окружности[править | править код]

Если диаметр окружности равен 1, её периметр равен π.
Периметр окружности пропорционален её диаметру (и радиусу). То есть, существует константа π такая, что если P — периметр окружности, а D — её диаметр, то:
Для радиуса r окружности формула превращается в
Для вычисления периметра окружности знание радиуса или диаметра и числа π достаточно. Проблема заключается в том, что π не является рациональным (его нельзя выразить в виде дроби двух целых чисел) и даже не является алгебраическим (оно не является корнем никакого полиномиального уравнения с рациональными коэффициентами). Таким образом, получение точного приближения к π важно для вычислений. Нахождение знаков π относится ко многим областям, таким как математический анализ и теория алгоритмов.
Осмысление периметра[править | править код]

Чем мельче структура фигуры, тем меньше площадь и тем больше периметр. Выпуклая оболочка остаётся той же самой.

Периметр и площадь являются двумя основными измерениями геометрических фигур, их часто[насколько?] путают[кто?]. Нередко также считают[кто?], что увеличение одной из этих величин приводит к увеличению другой. Действительно, увеличение (или уменьшение) размера фигуры приводит к увеличению (или уменьшению) её площади, так же как и её периметра. Так, например, если нарисовать карту поля в масштабе 1/10 000, действительные размеры периметра можно вычислить простым умножением на 10 000. Действительная площадь будет в 10 0002 раз больше площади фигуры на карте.
Тем не менее, нет никакой связи между площадью и периметром фигур[источник не указан 346 дней]. Например, периметр прямоугольника шириной 0,001 и длиной 1000 чуть больше 2000, в то время, как периметр прямоугольника шириной 0,5 и длиной 2 равен 5. Площади обеих фигур равны 1.
Прокл (V-й век) писал, что греческие крестьяне делили поля, опираясь на периметры[1], однако урожай с поля пропорционален площади, а не периметру, и много наивных крестьян получали поля с большим периметром, но малой площадью.
Если удалить часть фигуры, её площадь уменьшится, а вот периметр может и не уменьшиться. В случае очень неправильных фигур некоторые могут спутать периметр с выпуклой оболочкой. Выпуклую оболочку визуально можно представить как резинку, натянутую вокруг фигуры. На рисунке слева все фигуры имеют одну выпуклую оболочку (шестиугольник).
Изопериметрическая задача[править | править код]
Изопериметрическая задача — это задача нахождения фигуры с максимальной площадью среди фигур, имеющих заданный периметр.
Решение интуитивно — это окружность. В частности поэтому капли жира в бульоне имеют форму кружочков.
Задача выглядит простой, но строгое математическое доказательство сложно. Изопериметрическая задача иногда упрощается — найти четырёхугольник, треугольник или другую определённую фигуру с наибольшей площадью среди имеющих заданный периметр. Решение изопериметрической задачи для четырёхугольников — квадрат, для треугольников — правильный треугольник. В общем случае, многоугольник с n сторонами имеет максимальную площадь при заданном периметре, если он является правильным, что ближе к окружности по сравнению с неправильными многоугольниками.
Вариации и обобщения[править | править код]
- Полупериметр — половина периметра. Употребляется в основном в геометрии треугольника.
См. также[править | править код]
- Длина кривой
- Площадь фигуры
- Задача Дидоны
- Множество Каччопполи[en]
- Парадокс береговой линии
- Изопериметрическая задача
- Теорема Пифагора
- Смоченный периметр
Примечания[править | править код]
- ↑ Heath, 1981, с. 206.
Литература[править | править код]
- T. Heath. A History of Greek Mathematics. — Dover Publications, 1981. — Т. 2. — ISBN 0-486-24074-6.
Ссылки[править | править код]
- Weisstein, Eric W. Perimeter (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Semiperimeter (англ.) на сайте Wolfram MathWorld.
Содержание материала
- Формула
- Видео
- Периметр треугольника
- Что такое периметр?
- Площадь квадрата
- Перевод единиц измерения площади
- Нахождение периметра параллелограмма
- Нахождение периметра многоугольника
- Решение задач
Формула
Чтобы найти периметр треугольника $ABC$, необходимо сложить длины всех его сторон.
Напомним, что периметр треугольника — это сумма длин всех его сторон. То есть если задан произвольный треугольник $ABC$ и длины его сторон соответственно равны $AB=c$, $AC=b$, $BC=a$, то периметр треугольника вычисляется по формуле:
$$P_{Delta A B C}=a+b+c$$

Видео
Периметр треугольника
Треугольником следует называть геометрическую фигуру, имеющую три угла (как разного значения, так и одинакового) и состоящую из отрезков, образованных от точек пересечения лучей, образующих углы. Треугольник имеет три стороны и три угла. В нем могут быть из трех равны две стороны. Такой треугольник следует считать равнобедренным. Бывают такие фигуры, в которых равны все три стороны между собой. Принято такие треугольники называть равносторонними.
Что такое периметр треугольника? Его вычисление можно провести по аналогии с периметром четырехугольника. Равен периметр треугольника суммарной длине длин его сторон. Вычисление периметра треугольника, в котором две стороны равны – равнобедренного – упрощается умножением одной длины равных сторон на два. К полученному значению необходимо прибавить значение длины третьей стороны. Вычисление периметра треугольника с равными сторонами можно свести к простому вычислению произведения одной длины стороны треугольника на три.
Читать еще: Тест нарисовать дом дерево человека расшифровка пример. Методика исследования личности «Дом-дерево-человек» Дж

Что такое периметр?
Периметром называют суммарную длину всех сторон геометрической фигуры. Для его обозначения используется буква латинского алфавита «Р». Проще говоря, чтобы найти периметр, необходимо измерить длины всех сторон геометрической фигуры и сложить полученные значения. Длина вычисляется обычным измерительным прибором, таким как линейка, рулетка, сантиметровая лента и прочее.
Единицей измерения соответственно являются сантиметры, метры, миллиметры и другие меры длины. Длина стороны многоугольника вычисляется путем прикладывания измерительного прибора от одной вершины к другой. Начало шкалы деления прибора должно совпадать с одной из вершин. Второе числовое значение, на которое попадает другая вершина и является длиной стороны многоугольника. Таким же образом необходимо измерить все длины сторон фигуры и полученные значения сложить. Единицей измерения периметра является та же самая единица, которая используется для измерения стороны фигуры.
Площадь квадрата
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см

Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.
Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см
3 × 3 = 9
В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:

Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 32.
Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.
Перевод единиц измерения площади
Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.
1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.

Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см

Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100
S = 1002 = 10 000 см2
Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.
1 м2 = 10 000 см2
Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.
Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.
А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.
Например, переведём 100 000 см2 в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см2 это один квадратный метр, то сколько раз 100 000 см2 будут содержать по 10 000 см2»
100 000 см2 : 10 000 см2 = 10 м2
Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км2 в квадратные метры.
Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000
S = 10002 = 1 000 000 м2
Получается, что на один квадратный километр приходится один миллион квадратных метров:
1 км2 = 1 000 000 м2
Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.
Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.
Итак, вернёмся к нашей задаче. Требовалось перевести 2 км2 в квадратные метры. Умножим 2 км2 на 1 000 000
2 км2 × 1 000 000 = 2 000 000 м2
А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.
Например, переведём 3 500 000 м2 в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м2 это один квадратный километр, то сколько раз 3 500 000 м2 будут содержать по 1 000 000 м2»
3 500 000 м2 : 1 000 000 м2 = 3,5 км2
Пример 2. Выразить 7 м2 в квадратных сантиметрах.
Умножим 7 м2 на 10 000
7 м2 = 7 м2 × 10 000 = 70 000 см2
Пример 3. Выразить 5 м2 13 см2 в квадратных сантиметрах.
5 м2 13 см2 = 5 м2 × 10 000 + 13 см2 = 50 013 см2
Пример 4. Выразить 550 000 см2 в квадратных метрах.
Узнаем сколько раз 550 000 см2 содержит по 10 000 см2. Для этого разделим 550 000 см2 на 10 000 см2
550 000 см2 : 10 000 см2 = 55 м2
Пример 5. Выразить 7 км2 в квадратных метрах.
Умножим 7 км2 на 1 000 000
7 км2 × 1 000 000 = 7 000 000 м2
Пример 6. Выразить 8 500 000 м2 в квадратных километрах.
Узнаем сколько раз 8 500 000 м2 содержит по 1 000 000 м2. Для этого разделим 8 500 000 м2 на 1 000 000 м2
8 500 000 м2 × 1 000 000 м2 = 8,5 км2
Нахождение периметра параллелограмма
Определение
Параллелограмм – это такой четырехугольник, у которого противоположные стороны порно параллельны.
Характеристики:
- Противоположные стороны равны.
- Противоположные углы равны.
- Диагонали в точке пересечения делятся пополам.
- Как и в прямоугольнике, диагональ параллелограмма делит его на 2 треугольника.
- Два угла на одной стороне равны 180°

Периметр параллелограмма находится точно так же, как и периметр прямоугольника:
[P = a + a + b + b]
[P = 2(a + b)]
[P = 2a + 2b]
Нахождение периметра многоугольника
Определение
Многоугольник – это геометрическая фигура, которая со всех сторон ограничена ломанной линией.
Характеристики:
- Название многоугольника определяется количеством его вершин. Если у многоугольника количество вершин равно n, то он называется n-угольником.
- Многоугольником являются такие фигуры, как: квадрат, ромб, параллелограмм и т.д.
- Если углы с отрезками равны, то это правильный многоугольник.

Чтобы найти периметр n-угольника, нужно сложить всего длины его сторон:
[P = a1 + a2 + … an]
А для правильного n-угольника можно выделить еще одну формулу, потому как его стороны равны:
P = na
Здесь мы умножаем длину одной стороны на n.
Пример 1
Найдите периметр правильного многоугольника, если у него 5 вершин, а длина его одной стороны равна 7.
Решение:
Здесь воспользуемся этой формулой:
P = na
7 × 5 = 35 (см)
Ответ: периметр многоугольника равняется 35 см.
Решение задач
Площадь прямоугольника равна 80 см2, длина составляет 10 см. Чему равен периметр фигуры?
Как решаем:
- Для использования формулы P = 2 × (a + b), нам нужно найти ширину;
- Так как S = a × b, для поиска одной стороны необходимо разделить площадь на известную сторону: 80 : 10 = 8 см;
- Далее подставляем известные данные в формулу: (10 + 8) × 2 = 36 см;
Ответ: 36 см.
Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?
Как решаем:
- Мы знаем, что периметр — это сумма длин всех сторон, а значит, если вычесть из данного периметра сторону основания — получим сумму двух оставшихся сторон: 40 − 6 = 34 см;
- Известно, что равнобедренный треугольник имеет две равные стороны;
- Далее делим получившуюся сумму на два: 34 : 2 = 17 см;
Ответ: две другие стороны равны по 17 см.
Радиус окружности равен периметру равностороннего пятиугольника со стороной 4 см. Найдите длину окружности.
Как решаем:
- Периметр равностороннего пятиугольника равен 4 × 5 = 20 см, значит, радиус окружности равен 20 см;
- Длина окружности равна π × 2 × 20 = 40π см;
Ответ: 40π см.
Еще больше практических заданий — на курсах по математике в онлайн-школе Skysmart!
Теги
В данной публикации мы рассмотрим, что такое периметр геометрической фигуры, как он считается, а также разберем примеры для демонстрации практического применения теоретических знаний.
- Определение периметра
- Формулы периметра распространенных фигур
- Примеры нахождения периметра
Определение периметра
Периметр – это сумма длин всех сторон геометрической фигуры (треугольника, квадрата, трапеции, ромба и т.д.).
Для измерения периметра используются единицы длины: миллиметры (мм), сантиметры (см), метры (м), километры (км) и т.д.
Общепринятое обозначение периметра – это латинская буква “P“, под которой можно добавить сокращенное название фигуры или ее обозначение. Например:
- Периметр треугольника можно записать как “Pтреуг.“ или “P△“;
- Периметр квадрата – “Pквадр.“ или “P□“
Формулы периметра распространенных фигур
Периметр произвольного многоугольника находится путем сложения длин всех его сторон.
Примеры нахождения периметра
Пример 1
Найдем периметр квадрата с длиной стороны 5 см.

Pквадр. = 5 + 5 + 5 + 5 = 4 ⋅ 5 = 20 см.
Пример 2
Вычислим периметр прямоугольника с длиной 8 см и шириной 6 см.

Pпрямоуг. = 6 + 8 + 6 + 8 = (6 + 8) ⋅ 2 = 28 см.
Пример 3
Найдем периметр шестиугольника ниже.

P = AB + BC + CD + DE + EH + HA = 5 + 3 + 5 + 4 + 6 + 5 = 28.
Данный материал содержит геометрические фигуры с измерениями. Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.
Периметр геометрической фигуры
Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.
Вычислим периметр следующей фигуры:
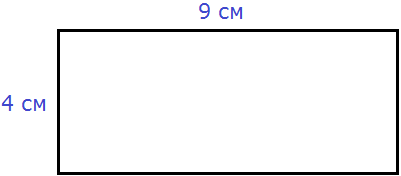
Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.
У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:
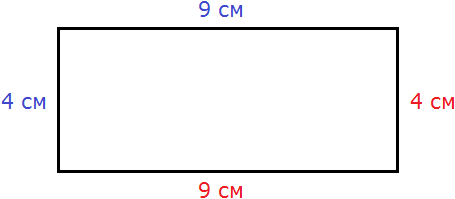
Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters). Тогда получим:
P = 9 см + 4 см + 9 см + 4 см = 26 см.
Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»
P = 2 × (9 + 4) = 18 + 8 = 26 см.
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»
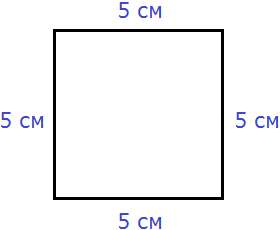
Чтобы вычислить периметр, сложим все стороны:
P = 5 см + 5 см + 5 см + 5 см = 20 см
Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза
P = 5 см × 4 = 20 см
Площадь геометрической фигуры
Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.
Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.
Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.
Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.
Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:
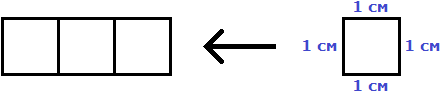
Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.
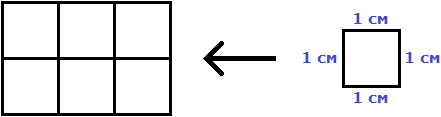
Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:
Допустим, потребовалось измерить площадь следующей комнаты:

Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:
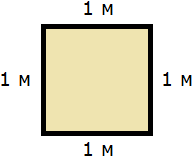
Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:

Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.
Площадь прямоугольника
В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.
Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.
Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.
Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:
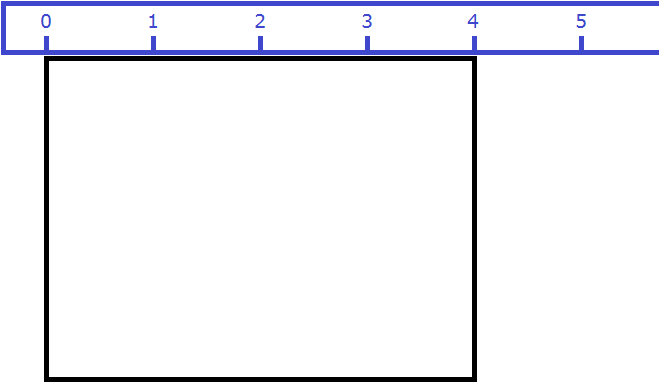
Теперь измерим ширину. Пусть она составила 3 метра:
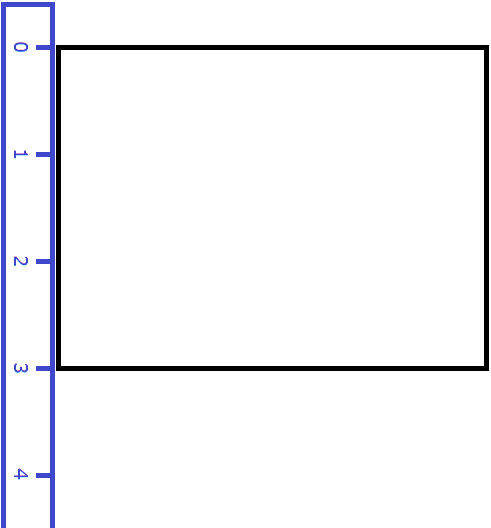
Умножим длину (4 м) на ширину (3 м).
4 × 3 = 12
Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:
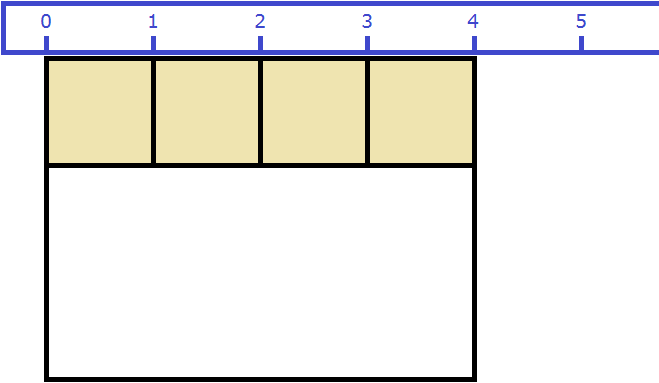
Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:
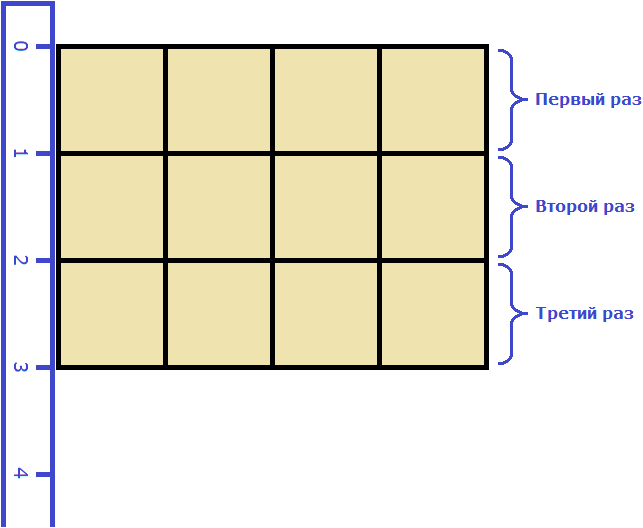
Площадь квадрата
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см
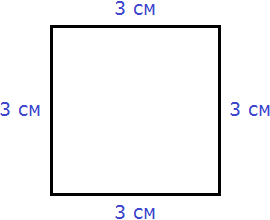
Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.
Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см
3 × 3 = 9
В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
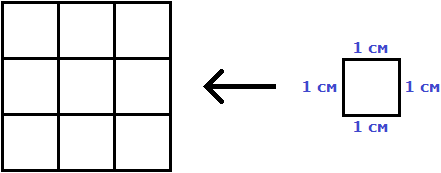
Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 32.
Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.
Обозначения
Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу
S = a2
где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.
Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см2. Это обозначение заменяет словосочетание «квадратный сантиметр».
Например, вычислим площадь квадрат со стороной 2 см.
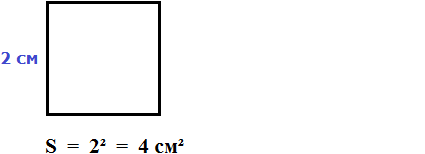
Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:
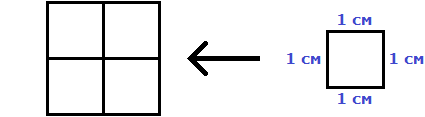
Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м2. Это обозначение заменяет словосочетание «квадратный метр».
Вычислим площадь квадрата со стороной 3 метра
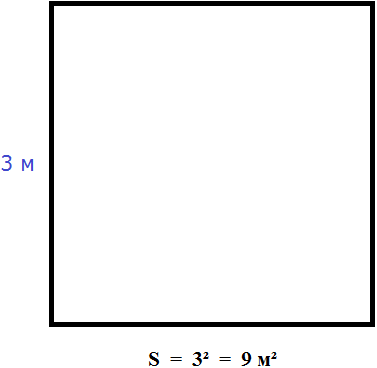
Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:
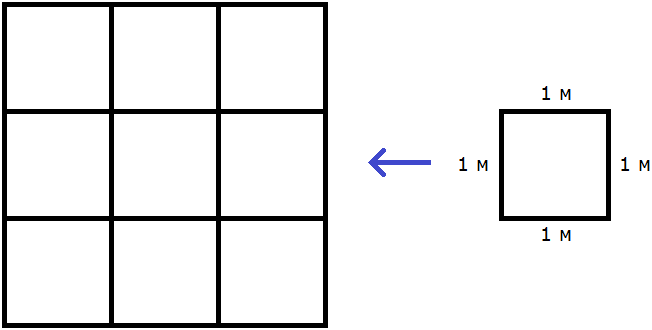
Аналогичные обозначения используются при вычислении площади прямоугольника. Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
S = a × b
Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см2, м2, км2. Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.
Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см
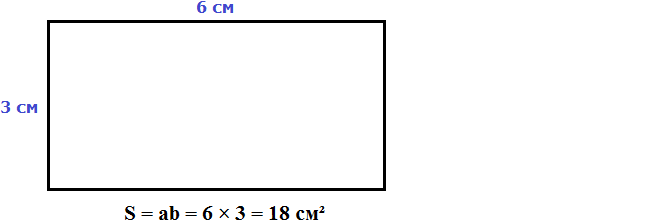
Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:
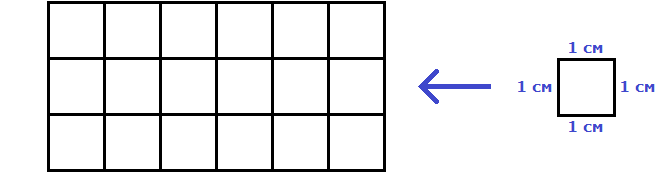
В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).
Перевод единиц измерения площади
Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.
1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.
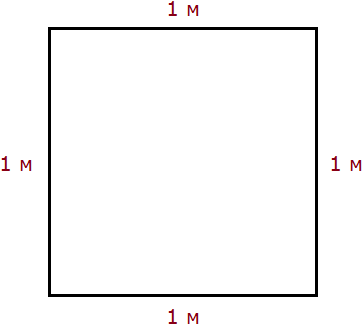
Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см
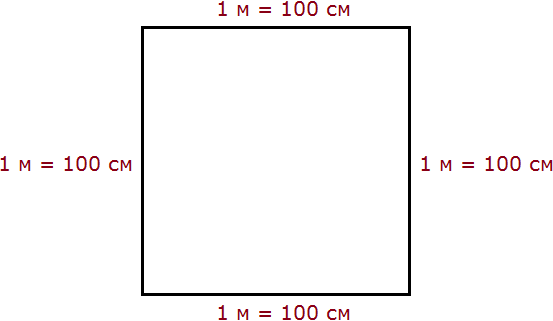
Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100
S = 1002 = 10 000 см2
Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.
1 м2 = 10 000 см2
Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.
Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.
А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.
Например, переведём 100 000 см2 в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см2 это один квадратный метр, то сколько раз 100 000 см2 будут содержать по 10 000 см2»
100 000 см2 : 10 000 см2 = 10 м2
Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км2 в квадратные метры.
Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000
S = 10002 = 1 000 000 м2
Получается, что на один квадратный километр приходится один миллион квадратных метров:
1 км2 = 1 000 000 м2
Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.
Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.
Итак, вернёмся к нашей задаче. Требовалось перевести 2 км2 в квадратные метры. Умножим 2 км2 на 1 000 000
2 км2 × 1 000 000 = 2 000 000 м2
А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.
Например, переведём 3 500 000 м2 в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м2 это один квадратный километр, то сколько раз 3 500 000 м2 будут содержать по 1 000 000 м2»
3 500 000 м2 : 1 000 000 м2 = 3,5 км2
Пример 2. Выразить 7 м2 в квадратных сантиметрах.
Умножим 7 м2 на 10 000
7 м2 = 7 м2 × 10 000 = 70 000 см2
Пример 3. Выразить 5 м2 13 см2 в квадратных сантиметрах.
5 м2 13 см2 = 5 м2 × 10 000 + 13 см2 = 50 013 см2
Пример 4. Выразить 550 000 см2 в квадратных метрах.
Узнаем сколько раз 550 000 см2 содержит по 10 000 см2. Для этого разделим 550 000 см2 на 10 000 см2
550 000 см2 : 10 000 см2 = 55 м2
Пример 5. Выразить 7 км2 в квадратных метрах.
Умножим 7 км2 на 1 000 000
7 км2 × 1 000 000 = 7 000 000 м2
Пример 6. Выразить 8 500 000 м2 в квадратных километрах.
Узнаем сколько раз 8 500 000 м2 содержит по 1 000 000 м2. Для этого разделим 8 500 000 м2 на 1 000 000 м2
8 500 000 м2 × 1 000 000 м2 = 8,5 км2
Единицы измерения площади земельных участков
Площади небольших земельных участков удобно измерять в квадратных метрах.
Площади более крупных земельных участков измеряются в арах и гектарах.
Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м2). В виду частого распространения такой площади (100 м2) она стала использоваться, как отдельная единица измерения.
Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м2 каждый, то есть:
3 а = 100 м2 × 3 = 300 м2
В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м2. Примеры:
1 сотка = 100 м2
2 сотки = 200 м2
10 соток = 1000 м2
Гектар (сокращенно: га) — это площадь, равная 10 000 м2. Например, если сказано что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м2 каждый, то есть:
20 га = 10 000 м2 × 20 = 200 000 м2
Прямоугольный параллелепипед и куб
Прямоугольный параллелепипед — это геометрическая фигура, состоящая из грáней, рёбер и вершин. На рисунке показан прямоугольный параллелепипед:
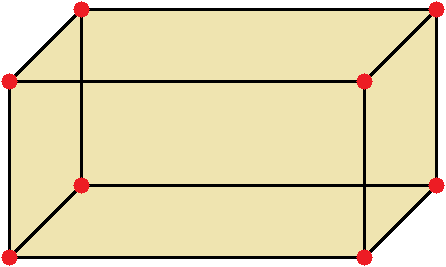
Желтым цветом показаны грáни параллелепипеда, чёрным цветом — рёбра, красным — вершины.
Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:
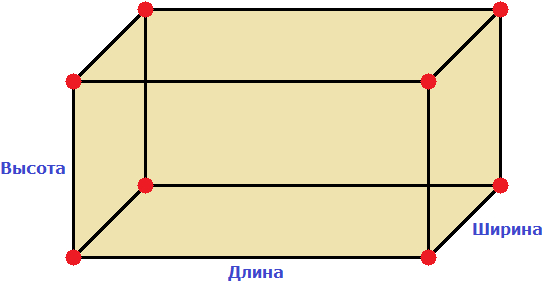
Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:
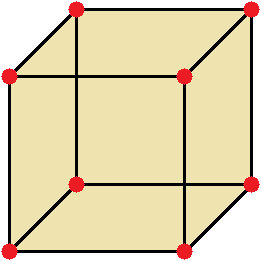
Объём геометрической фигуры
Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.
Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.
Измерить объём какой-нибудь фигуры означает выяснить сколько кубических единиц вмещается в данную фигуру.
Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:
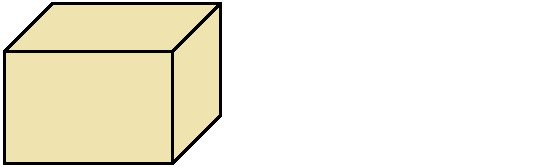
Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:
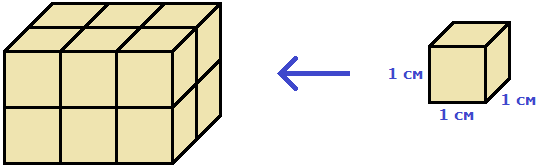
Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
V = 12 см3
Объём любого параллелепипеда вычисляют следующим образом: перемножают его длину, ширину и высоту .
Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
V = abc
где, a — длина, b — ширина, c — высота
Так, в предыдущем примере мы визуально определили, что объём параллелепипеда равен 12 см3. Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат
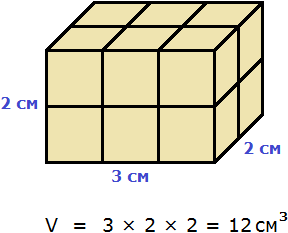
Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.
Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
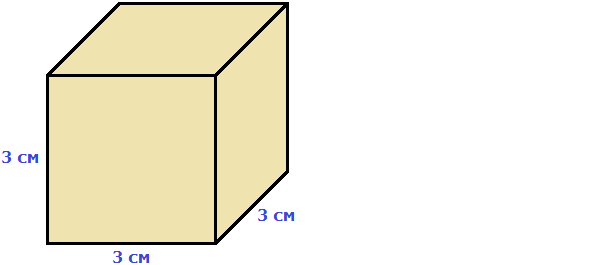
Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:
V = 3 × 3 × 3 = 27 см³
Действительно, в исходный куб вмещается 27 кубиков длиной 1 см
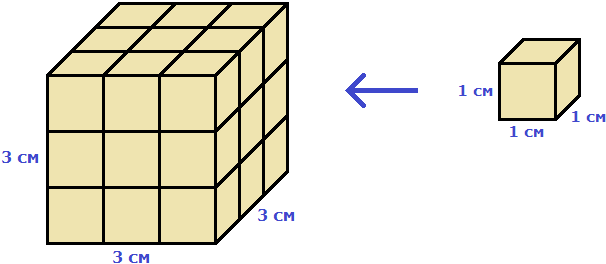
При вычислении объёма данного куба мы перемножили длину, ширину и высоту. Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 33.
V = 33 = 27 см3
Поэтому третью степень числа называют кубом числа. При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.
Таким образом, объём куба вычисляется по следующему правилу:
V = a3
Где a — длина куба.
Кубический дециметр. Кубический метр
Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах (м3). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах (дм3).
Другое название одного кубического дециметра – один литр.
1 дм3 = 1 литр
Перевод единиц измерения объёма
Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 кубический метр в кубических сантиметрах.
Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.
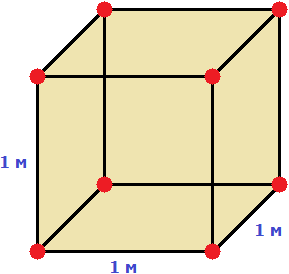
Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см
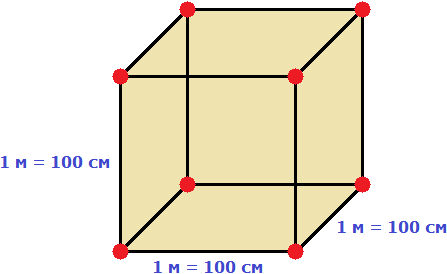
Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:
V = 1003 = 1 000 000 см3
Получается, что на один кубический метр приходится один миллион кубических сантиметров:
1 м3 = 1 000 000 см3
Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.
Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.
А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.
Например, переведём 300 000 000 см3 в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см3 это один кубический метр, то сколько раз 300 000 000 см3 будут содержать по 1 000 000 см3»
300 000 000 см3 : 1 000 000 см3 = 300 м3
Пример 2. Выразить 3 м3 в кубических сантиметрах.
Умножим 3 м3 на 1 000 000
3 м3 × 1 000 000 = 3 000 000 см3
Пример 3. Выразить 60 000 000 см3 в кубических метрах.
Узнаем сколько раз 60 000 000 см3 содержит по 1 000 000 см3. Для этого разделим 60 000 000 см3 на 1 000 000 см3
60 000 000 см3 : 1 000 000 см3 = 60 м3
Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.
1 литр = 1 дм3
Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм3. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.
Пример 1. Перевести 5 литров в кубические дециметры.
Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1
5 л × 1 = 5 дм3
Пример 2. Перевести 6000 литров в кубические метры.
Шесть тысяч литров это шесть тысяч кубических дециметров:
6000 л × 1 = 6000 дм3
Теперь переведём эти 6000 дм3 в кубические метры.
Длина, ширина и высота одного кубического метра равны 10 дм
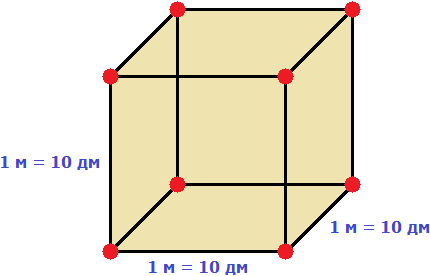
Если вычислить объём этого куба в дециметрах, то получим 1000 дм3
V = 103= 1000 дм3
Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм3 содержит по 1 000 дм3
6 000 дм3 : 1 000 дм3 = 6 м3
Значит, 6000 л = 6 м3.
Таблица квадратов
В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.
Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.
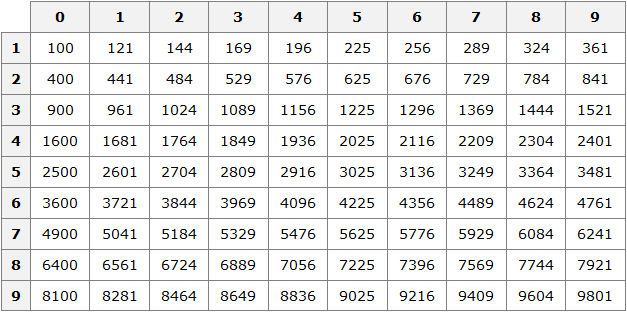
Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.
Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.
Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576
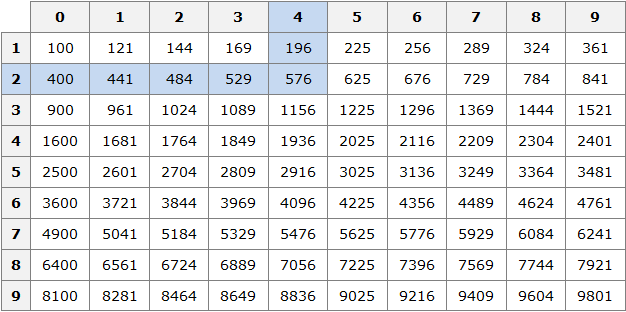
242 = 576
Таблица кубов
Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.
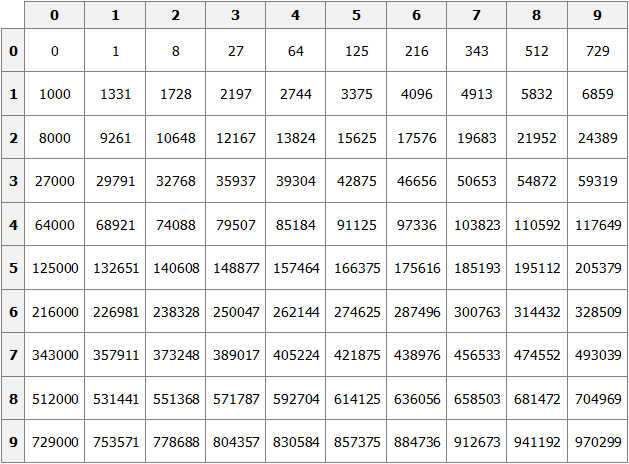
Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
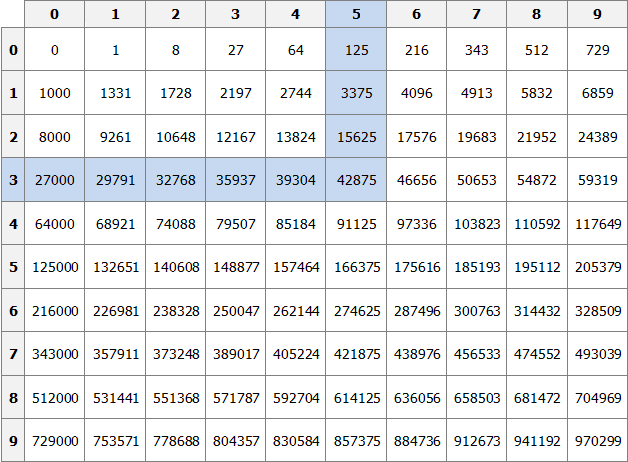
353 = 42875
Задания для самостоятельного решения
Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.
Решение
P = 2(a + b)
a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см
Ответ: периметр прямоугольника равен 16 см.
Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.
Решение
S = ab
a = 6, b = 2
S = 6 × 2 = 12 см2
Ответ: площадь равна 12 см2.
Задача 3. Площадь прямоугольника составляет 12 см2. Длина составляет 6 см. Найдите ширину прямоугольника.
Решение
S = ab
S = 12, a = 6, b = x
12 = 6 × x
x = 2
Ответ: ширина прямоугольника составляет 2 см.
Задача 4. Вычислите площадь квадрата со стороной 8 см
Решение
S = a2
a = 8
S = 82 = 64 см2
Ответ: площадь квадрата со стороной 8 см равна 64 см2
Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.
Решение
V = abc
a = 6, b = 4, c = 3
V = 6 × 4 × 3 = 72 см3.
Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см3
Задача 6. Объем прямоугольного параллелепипеда составляет 200 см3. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см
Решение
V = abc
V = 200, a = 10, b = 5, c = x
200 = 10 × 5 × x
200 = 50x
x = 4
Ответ: высота прямоугольного параллелепипеда равна 4 см.
Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га
Решение
Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.
Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.
Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза
4 × 3 = 12 га
Ответ: пшеницей засеяно 12 га.
Задача 8. Длина зернохранилища 42 м, ширина составляет  длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м3 его весит 740 кг.
длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м3 его весит 740 кг.
Решение
a — длина
b — ширина
c — высота
a = 42 м
b = 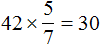 м
м
c = 42 × 0,1 = 4,2 м
Определим объем зернохранилища:
V = abc = 42 × 30 × 4,2 = 5292 м3
Определите сколько тонн зерна вмещает зернохранилище:
5292 × 740 = 3916080 кг
Переведём килограммы в тонны:
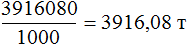
Ответ: зернохранилище вмещает 3916,08 тонн зерна.
Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.
Решение
Определим сколько литров в минуту вливается через вторую трубу:
25 л/мин × 0,75 = 18,75 л/мин
Определим сколько литров в минуту вливается в бассейн через обе трубы:
25 л/мин + 18,75 л/мин = 43,75 л/мин
Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин
43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л
1 л = 1 дм3
35 525 л = 35 525 дм3
Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:
35 525 дм3 : 1000 дм3 = 35,525 м3
Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:
V = 35,525
a = 5.8
b = 3.5
c = x
35,525 = 5,8 × 3,5 × x
35,525 = 20,3 × x
x = 1,75 м
с = 1,75
Ответ: высота (глубина) бассейна составляет 1,75 м.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже





