План урока:
Луч, угол, отрезок
Измерение отрезков. Сантиметр. Дециметр
Геометрические фигуры. Треугольник. Четырехугольник. Многоугольники
Килограмм
Литр
Начинаем наш урок
Пусть тебе пойдет он впрок.
Будем вместе рассуждать,
Наблюдать и измерять.
Наверное, каждый ребенок мечтает быть изобретателем или исследователем. Надеюсь, ты тоже, ведь наш урок мы проведем в лаборатории.
Там мы будем моделировать, проводить разные опыты и измерения. Ты узнаешь много нового, познакомишься с различными измерительными инструментами. Я научу тебя как нужно ими пользоваться. Итак, приступим.
Луч, угол, отрезок
Давай вспомним материал из нашего первого урока. Мы знакомились с некоторыми геометрическими понятиями и выучили названия основных геометрических фигур. Посмотри на картинку и попробуй назвать, что здесь изображено.
Проверь, все ли ты правильно вспомнил.
Замечательно. А теперь мы приступим к изучению нового. Начнем с самого простого.
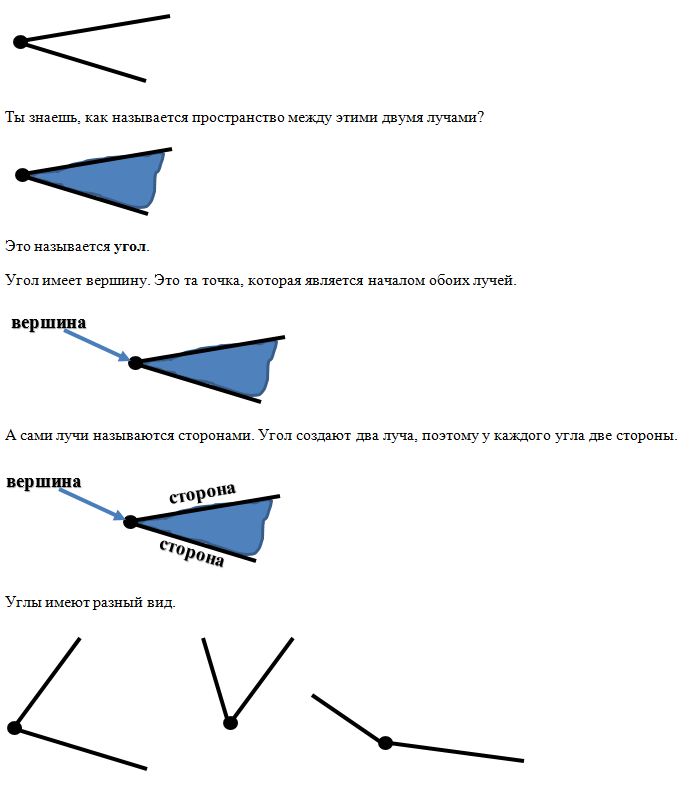
Это луч.
Как ты думаешь, почему его так называют?
Если присмотреться, то мы можем представить, что точка – это солнышко. Оно испускает лучи.
Обрати внимание, что все лучи исходят из центра солнца. У них общее начало.
Мы возьмем только два луча, которые исходят из одной точки.
Теперь давай поэкспериментируем. Сделаем модель угла. Нужно две палочки. Это могут быть счетные палочки, палочки для мороженого или обычные зубочистки.
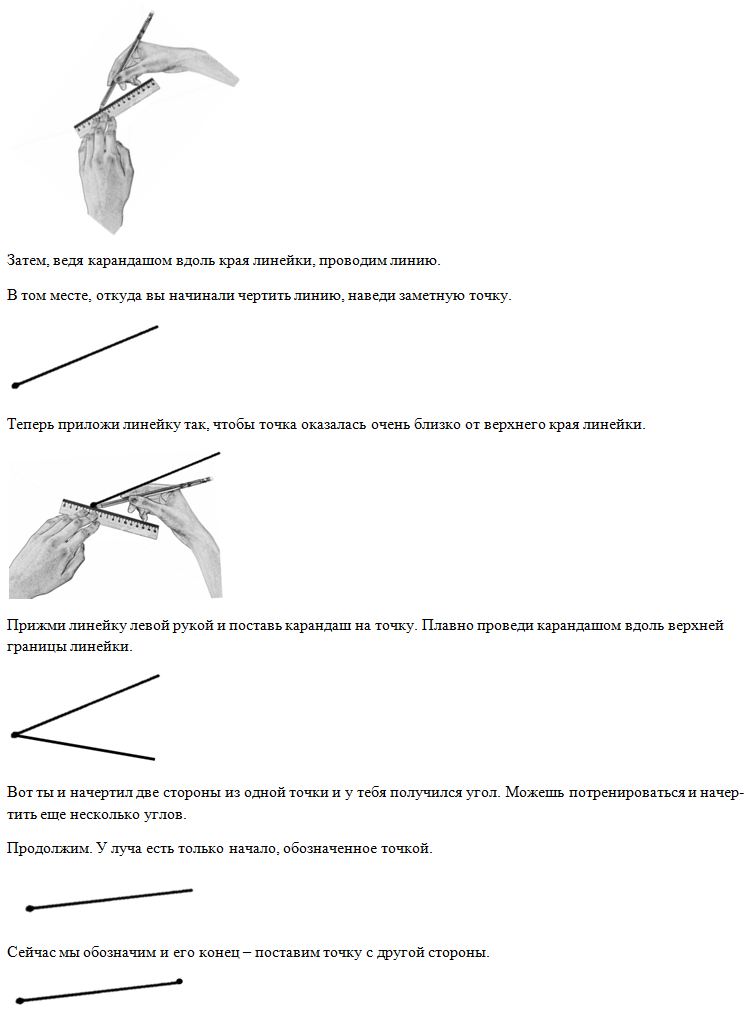
Теперь поучимся чертить угол в тетради. Для этого нам понадобится линейка и карандаш.
Нужно положить линейку на лист и крепко прижать ее левой рукой. Поставь карандаш возле ее верхнего края.
У нас получился отрезок. Это часть прямой, которая с двух сторон ограничена точками. Значит, у отрезка должно быть две точки.
Создадим модель отрезка. Сделай два шарика из пластилина и прикрепи их с обеих сторон палочки.
Готово. Правда, это было легко?
Чертить отрезок в тетради тоже не сложно. Действуем так же, как и при черчении луча.
После того как проведем под линейку прямую линию, отметим точками начало и конец отрезка.
Длина отрезка может быть разной. Его можно начертить совсем маленьким или продлить на всю страничку и даже выйти за нее. Потренируйся чертить разные отрезки в разном направлении.
Скажи, ты можешь определить, какой отрезок больше? Какой самый маленький? Есть ли здесь равные отрезки? На сколько один отрезок больше, чем другой? Как начертить отрезок, который будет заданной длины?
На все эти вопросы мы ответим после работы в нашей лаборатории.
Измерение отрезков. Сантиметр. Дециметр
Чтобы сравнивать, нам нужно научиться измерять отрезки. Это можно делать и с помощью обычной палочки. Найди себе подходящую палочку, и мы вместе проведем измерения.
Следует приложить ее начало к началу отрезка и отметить на палочке конец отрезка.
Теперь эту же палочку приложим к другому отрезку, тоже соединив их начало. И отметим конец этого отрезка.
Мы получили на палочке две отметки. Чья отметка находится дальше, тот отрезок и больше по длине.
Мы можем с помощью этой палочки чертить равные отрезки. Нужно только приложить ее к листу тетради и провести вдоль нее линию от начала и до нужной отметки.
Попробовал? Мы получили точно такой же отрезок, как и тот, что измеряли первым и отметили его длину красной черточкой.
Однако, измеряя отрезки палочкой мы получаем о них очень мало информации, которую нельзя никому передать или записать. Например, как ты расскажешь своему другу о своих измерениях в нашей лаборатории? Какой длины оказались твои отрезки? Кусочек палочки?
Это похоже на то, как герои мультфильма пытались измерить длину удава, считая ее шагами, попугаями и даже мартышками.
Но мы с тобой занимаемся научными исследованиями, а значит, все измерения должны быть точными и правильно записанными. Поэтому сейчас познакомимся с инструментами и единицами измерения, необходимыми для определения длины отрезков.
Ты уже знаком с линейкой. Возьми ее и положи перед собой.
Мы ее использовали для проведения прямых линий. Но линейка является измерительным инструментом. Рассмотри ее. На ней нанесены штрихи и цифры. Обрати внимание, что штрихи разной длины, а цифры написаны только возле самых длинных черточек.
Это шкала измерений. Начало отсчета обозначено числом 0, а дальше идут числа по порядку, как в числовом ряду, который тебе уже знаком.
Особенность шкалы заключается в том, что расстояние между схожими штрихами одинаковое. Сегодня мы будем изучать только длинные черточки. Часть шкалы от одной длинной черточки до соседней длинной черточки называется сантиметр. Отметим на рисунке 1 сантиметр.
Сантиметр – это единица измерения длины отрезков. Вся шкала на линейке разделена на сантиметры.
Давай посчитаем каждый сантиметр на линейке. Например, здесь мы отметили пять сантиметров и остановились на числе 5.
Числа указывают сколько сантиметров отсчитано от числа 0. Поэтому мы, начиная измерять или чертить отрезок, обязательно совмещаем его начало с черточкой возле числа 0.
Например, выполним измерение отрезка. Приставим к точке, которая отмечает начало отрезка, черточку возле числа 0. Линейку нужно положить ровно вдоль линии.
После такого совмещения посмотрим на точку, которая отмечает конец отрезка. Она находится возле черточки, внизу которой написано число 7. Значит длина этого отрезка составляет 7 сантиметров.
Все довольно просто. Главное – соблюдать точность.
Чтобы записать длину отрезка будем использовать короткую запись см. Пишем так:
7 см
Сейчас мы используем полученные навыки для проведения опыта. Нам нужно найти равные отрезки.
Глядя на отрезки, нельзя сразу сказать, какие из них одинаковые. Чтобы найти равные отрезки, нужно провести их измерения. Посмотри, как мы это сделали.
Определи размеры каждого отрезка в сантиметрах.
Я тоже это сделала. У меня получилось так.
Итак, мы опытным путем установили, что здесь два одинаковых отрезка, длина которых 12 см.
Никаких сомнений быть не может – все точно.
Потренируйся проводить самостоятельные измерения. Попроси кого-то из взрослых начертить тебе несколько отрезков, а ты измерь их длину.
А сейчас ты и сам научишься чертить отрезки. Это тоже легко. Например, начертим отрезок длиной 4 см.
Приложим линейку. Поставим точку напротив числа 0.
Не сдвигая линейку, поставим точку напротив числа, соответствующего длине отрезка. В нашем случае это число 4.
Теперь крепко прижмем линейку. Убедимся, что обе точки находятся непосредственно у верхнего края линейки. Поставим карандаш на первую точку и плавно проведем линию до второй точки.
Теперь линейку можно убирать. Отрезок готов.
Теперь твоя очередь. Выполни аналогичные действия в такой же последовательности, чтобы начертить отрезок длиной 6 см.
А теперь взгляни на рисунок и скажи, сколько сантиметров составляет длина этого отрезка.
Итак, мы установили, что длину отрезка можно записать, как 13 см, а можно, как 1 дм 3 см. Это можно делать с любым отрезком, если его длина выражена двузначным числом. Подумай, как можно еще записать длину отрезка, если мы определили, что она составляет 17 см.
Правильно, это будет 1 дм 7 см.
Замечательно. Ты усвоил много новой информации об угле, отрезке и единицах измерения длины. Дальше будет проще, потому что основное ты уже знаешь.
Геометрические фигуры. Треугольник. Четырехугольник. Многоугольники
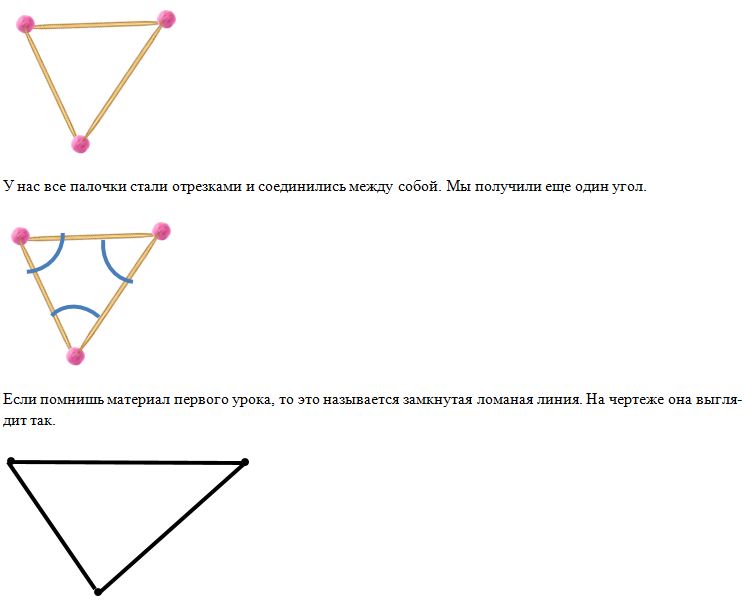
Давай вернемся к нашей модели угла.
Такие замкнутые ломаные линии являются геометрическими фигурами. Мы уже с тобой посчитали, что в этой фигуре три угла. Каждый угол имеет вершину – точку, в которой соединяются две стороны угла. Значит вершин тоже три. А теперь посчитай, сколько палочек мы использовали.
И палочек тоже три, т.е. у фигуры три стороны.
Такая фигура называется треугольник. Ты уже знаешь это название и знаешь, как выглядит треугольник. Сегодня мы выучили основные характеристики этой фигуры. Треугольники бывают разные и по размеру, и по виду.
Главное, что у треугольника три угла, три вершины и три стороны. Наверное, и название у него такое, потому что у него всего по три.
Вокруг нас есть много предметов, которые имеют треугольную форму. Например, крыши домов.
Убедись, что это треугольник – посчитай стороны крыши. Их три, значит, красная фигура является треугольником.
Вспомни, что еще похоже на треугольник.
А сейчас давай продолжим моделировать. Разъедини две палочки и сделай их все отрезками.
Посчитай углы каждого четырехугольника.
Убедился? Любая фигура, у которой есть четыре угла, является четырехугольником. Мы знаем очень много предметов, которые имеют четырехугольную форму. Например, тетрадь и книга.
Все эти предметы имеют по четыре стороны, а значит они четырехугольники.
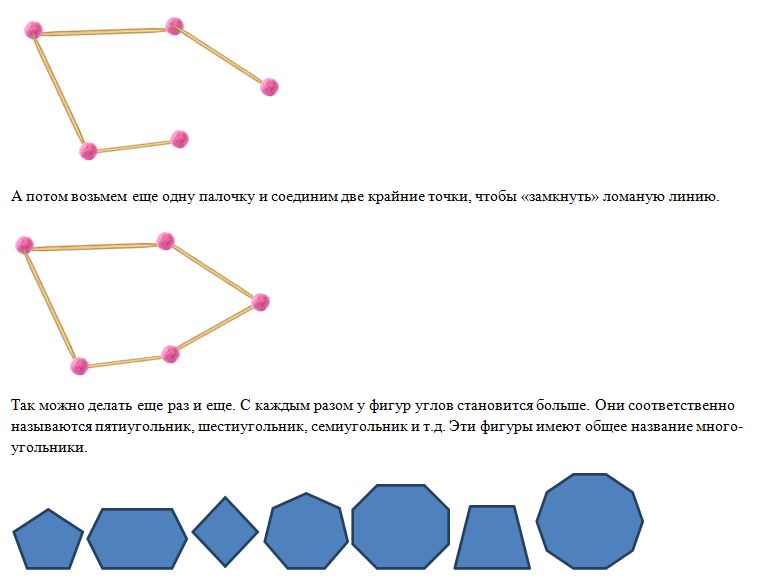
Надеюсь, ты уже понял связь между названием и строением фигуры. Подумай, какую фигуру называют пятиугольником?
Правильно, это фигура, у которой пять углов, пять вершин и пять сторон. Знаешь, как его смоделировать?
Сначала разъединим любые две палочки.
Посчитай углы и стороны каждого многоугольника и назови их. Найди среди этих фигур четырехугольники.
Обрати внимание, что сторонами фигур являются отрезки. Значит, их можно измерять. Для этого нужна линейка. Ты уже знаешь, как ею пользоваться.
Давай измерим каждую сторону треугольника.
Длина третей стороны 13 см. Это тоже можно записать в другом виде: 1 дм 3 см.
Мы отлично справились. Наша работа не прошла в пустую. Теперь ты можешь правильно назвать почти любую геометрическую фигуру.А с помощью линейки сумеешь измерить стороны у любой фигуры.
Килограмм
Продолжим. Будем снова измерять. Только уже совсем по-другому. Нам нужно сравнить два предмета.
Что ты можешь сказать? Чем они отличаются?
Конечно, они отличаются по цвету, но ведь мы изучаем математические понятия. Поэтому поговорим о других параметрах.
Ты уже, наверное, догадался, о чем речь. Арбуз тяжелый, а мяч легкий. Это значит, что у них разная масса. Итак, мы поговорим о том, что у предметов можно измерять массу, т.е. узнавать, сколько они весят. Какой измерительный инструмент нам нужен для определения массы?
Это весы. Они бывают разных видов.
Есть весы с чашами. Они называются механическими.
На одну чашу нужно положить сам предмет, а на другую чашу ставят гири. Следует подобрать такие гири, чтобы чаши весов оказались на одном уровне.
А сколько весит арбуз? Определи общее количество килограммов на гирях.
Правильно, 5 и 2 будет 7. Значит, арбуз весит 7 кг.
Все очень просто и интересно. Попроси родителей купить себе такой набор и потренируйся взвешивать разные предметы, которые есть в твоей комнате.
Запомни, что их масса измеряется в килограммах.
Литр
А теперь нам нужно измерить молоко. Как мы будем наливать его на чашу весов? Что произойдет?
Верно, если лить молоко, то оно разольется по столу и ничего измерить не получится. Молоко нужно лить в посуду: бутылку, стакан, банку.
Как же измерить, сколько молока вместилось в бидон или кувшин? Для этого есть еще одна единица измерения – литр. Она нужна для измерения вместимости. При этом используется специальная мерная посуда, на которой нанесена шкала.
Чтобы определить, сколько литров молока находится в кувшине, надо перелить его в мерную посуду и посмотреть какой метки достигнет его уровень.Таким образом, мы можем измерить не только количество молока, но и любой другой жидкости.
Есть емкости, которые имеют определенный объем. Например, вот посуда, которая вмещает 1 литр.
Записывается так:
1 литр – 1 л
Вот мы и закончили наш урок. Ты узнал много нового. Теперь ты знаешь, как начертить многоугольник.
А главное, мы выучили единицы измерения. Вот что ты должен запомнить.
Сегодня мы сделали только первый шаг в деле исследования. Надеюсь, тебе понравилось проводить опыты, моделировать и ты продолжишь это делать самостоятельно.А сейчас выполни несколько проверочных заданий.
Измерение — это сравнение объекта измерения с выбранной единицей измерения.
Хорошее представление об измерении даёт милый мультфильм «(38) попугаев». В нём была решена проблема измерения длины удава.
В попугаях длина удава составляла 38 попугаев, в мартышках — 5 мартышек, а в слонёнках — только (2) слонёнка. Естественно, удаву больше нравилось то, что в попугаях он длиннее. Значит, в измерении очень важно выбрать единицу измерения.
Обрати внимание!
Если мы хотим измерять несколько объектов и сравнивать результаты измерения, то очень важно измерить эти объекты в одинаковых единицах.
Если нужно измерить длину двух удавов, то обоих надо мерить или в попугаях, или в мартышках, или в слонёнках.
Измеряя объект, мы узнаём, насколько измеряемый объект больше (или меньше) единицы измерения. Может оказаться, что принятая единица измерения не укладывается целое число раз в измеряемый объект. Тогда единицу измерения делят на части, а части можно продолжать делить на меньшие части для получения более точного результата. Результат в зависимости от ситуации также можно округлить и использовать приближённо.
Продолжая рассказ об измерении удава, вспомним, что точный результат измерения в попугаях был следующим: 38 попугаев и одно крылышко — но было принято решение результат округлить до целых единиц.
Для измерения отрезка чаще всего как инструмент измерения используют линейку (линейки бывают очень разные — как для очень мелких измерений, так и для крупных).
Рис. (1). Линейка.
Очень часто используемые единицы измерения: (1) (км), (1) (м), (1) (дм), (1) (см), (1) (мм).
1км =1000 м;1 м=10 дм;1 дм=10 см;1 см=10 мм.
Свойства длины отрезка
1. Равные отрезки имеют равные длины.
2. Часть отрезка всегда имеет длину, которая меньше длины отрезка.
3. Если точки на отрезке делят отрезок на части, то длина отрезка равна сумме длин этих частей.
Независимо от измеряемого объекта измеряемая величина имеет такие же свойства.
Свойства величины угла
1. Равные углы имеют равные величины.
2. Часть угла всегда имеет величину, которая меньше величины угла.
3. Если лучи, выходящие из вершины угла, делят угол на части, то величина угла равна сумме величин этих частей.
Один из инструментов измерения, которые используются для измерения угла, называется транспортир.
Рис. (2). Транспортир.
Совсем особенная единица измерения угла — градус.
Это не тот градус, который используют для измерения температуры.
Для измерения угла как единицу измерения принимают
1180
часть развёрнутого угла, таким образом:
величина развёрнутого угла — (180) таких единиц, или градусов.
Рис. (3). Развёрнутый угол.
Это записывается:
∠AOB=180°
.
Можем представить и угол, величина которого —
0°
.
Рис. (4). Нулевой угол.
Одна четвёртая часть полного угла, или половина развёрнутого угла, называется прямой угол с величиной
∠AOB=90°
и особым знаком во внутренней части угла.
Рис. (5). Прямой угол.
Угол, величина которого
0°<∠AOB<90°
, называют острым углом.
Рис. (6). Острый угол.
Угол, величина которого
90°<∠AOB<180°
, называют тупым углом.
Рис. (7). Тупой угол.
Источники:
Рис. 1. Указание авторства не требуется: образование, 2017-01-11, бесплатно для коммерческого использования, https://clck.ru/V4pwr.
Рис. 2. Mayyskiyysergeyy, CC BY-SA 4.0 <https://creativecommons.org/licenses/by-sa/4.0>, через Викисклад.
Рис. 3-7. Углы, © ЯКласс.
Дисциплина: Математика
«Измерения в геометрии»
учебно-методические рекомендации для студентов
Составитель: преподаватель математики Р.Х.Бичурина
ТЕОРИЯ
Объем — это одна из характеристик трехмерных геометрических фигур.
Объем обозначается большой латинской буквой V («вэ»). Величины объема взаимосвязаны (одну кубическую единицу объема можно заменить ругой).
Правило. Объем прямоугольного параллелепипеда равен произведению трех его измерений.
Единицами измерения объема служат:
а) стандартные единицы длины в кубе:
1 см3 = 1 000 мм3
1 дм3 = 1 000 см3 = 1 000 000 мм3
1 м3 = 1 000 дм3 = 1 000 000 см3= 1 000 000 000 мм3
1 км3=1 000 000 000 м3
б) специальная единица объема (литр):
1 л = 1 дм3 = 1 000 см3.
В качестве единицы измерения выбирают кубик с ребром, равным какой-нибудь единице длины, например 1 см. Тогда единицей измерения объема будет объем такого кубика .
Например, объем прямоугольного параллелепипеда (рис. 65) равен 24 см3. Это значит, что его объем содержит 24 кубика объемом по 1 см3. Этот же результат можно получить, если измерить длину a, ширину b и высоту c тела, а затем их значения перемножить.
Объем обозначается латинской буквой V:
V = abc
В СИ единицей объема является 1 м3.
Другие единицы: дм3, см3, мм3— дольные единицы м3.
1м3 =1000дм3 =1•103дм3;
1дм3 =1000см3 =1•103 см3;
1см3 =1000мм3 =1•103 мм3;
1дм3 =0,001м3 =1•10-3 м3;
1см3 =0,001дм3 =0,000001м3 =1•10-6 м3;
1мм3 =0,001см3 =1•10-3 см3;
1мм3 =0,000001дм3 =1•10-6 дм3;
1 мм3 = 0,000000001м3 = 1 • 10-9 м3
Изучение стереометрии начинается со знания формул. Для решения задач по стереометрии на нахождение объемов и площадей поверхностей многогранников и тел вращения в основном нужны: формулы объёмов, формулы площадей поверхностей, формулы площадей плоскостных фигур и
элементарная логика.
Многогранники.
Формулы объёмов и формулы площадей поверхностей многогранников даны в таблице.
Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».
Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.
Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.
Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.
Тела вращения
Цилиндр, конус и шар относятся к объемным (трехмерным) геометрическим фигурам вращения.
Так, цилиндр — это фигура, полученная от вращения прямоугольника вокруг одной из его сторон как оси; конус — вращением прямоугольного треугольника вокруг его катета как оси, шар — вращением полукруга вокруг его диаметра как оси.
Объемные фигуры бывают прямые (прямой цилиндр, прямой конус) и наклонные (наклонный цилиндр, наклонный конус), что зависит от вида той плоской геометрической фигуры, которая их образует.
В нашем курсе математики рассматриваются только прямые цилиндры и конусы.
Определение. Цилиндр — это тело (объемная геометрическая фигура), полученное вращением прямоугольника вокруг одной из его сторон как оси.
Определение. Конус (прямой) — это тело (объемная геометрическая фигура), полученное вращением прямоугольного треугольника вокруг его катета как оси.
Определение. Шар — это тело (объемная геометрическая фигура), полученное вращением полукруга вокруг его диаметра как оси.
Развертки цилиндра и конуса
Разверткой геометрической фигуры называется изображение плоскости, ограничивающей фигуру, в одной плоскости листа по размерам фигуры.
Развертка цилиндра приведена схематически.
Развертка конуса приведена схематически.
Площади боковой поверхности цилиндра и конуса
Правило. Площадь боковой поверхности цилиндра равна произведению длины окружности основания и высоты цилиндра.
где C — длина окружности, H — высота цилиндра, R — радиус окружности основания.
Правило. Площадь боковой поверхности конуса равна произведению половины длины окружности основания и образующей конуса.
где C — длина окружности основания, l — длина образующей конуса, R — радиус основания.
Площадь поверхности шара
Правило. Площадь поверхности шара равна учетверенной площади большого круга шара.
где R — радиус шара
Объемы цилиндра, конуса и шара
Правило. Объем цилиндра равен произведению площади основания н высоты.
где R — радиус основания, H — высота цилиндра.
Правило. Объем конуса равен одной трети произведения площади основания и высоты конуса.
где R — радиус основания, H — высота конуса.
Правило. Объем шара равен четырем третям
произведения числа Пи на куб радиуса.
где R — радиус шара
Цилиндр
Площадь боковой поверхности:
Площадь полной поверхности:
Объем:
Конус
Площадь боковой поверхности:
Площадь полной поверхности:
Объем:
Усеченный конус Шар
Подобие тел
Подобные тела. Зеркально подобные тела и фигуры.
Два тела подобны, если одно из них может быть получено из другого путём увеличения (или уменьшения ) всех его линейных размеров в одном и том же отношении. Автомобиль и его модель – подобные тела. Два тела (фигуры) зеркально подобны, если одно из них подобно зеркальному отражению другого. Например, картина и её фотонегатив зеркально подобны друг другу.
В подобных и зеркально подобных фигурах все соответственные углы (линейные и двугранные) равны.
В подобных телах многогранные и телесные углы равны; в зеркально подобных телах они зеркально равны.
Если два тетраэдра (две треугольные пирамиды) имеют соответственно пропорциональные рёбра ( или соответственно подобные грани ), то они подобны или зеркально подобны. Например, если грани первой пирамиды вдвое больше, чем у второй, то высоты, апофемы, радиус описанного круга первой пирамиды также вдвое больше, чем у второй. Эта теорема не имеет места для многогранников с большим числом граней. Предположим, что мы соединили все рёбра куба в его вершинах посредством шарниров; тогда мы можем изменить форму этой фигуры, не растягивая её стержни, и получить из начального куба параллелепипед.
Две правильные призмы или пирамиды с одинаковым числом граней подобны, если радиусы их оснований пропорциональны их высотам. Два круглых цилиндра или конуса подобны, если радиусы их оснований пропорциональны их высотам.
Если два и более тел подобны, то площади всех соответствующих плоских и кривых поверхностей этих тел пропорциональны квадратам любых соответствующих отрезков.
Если два и более тел подобны, то их объёмы, а также объёмы любых их соответствующих частей, пропорциональны кубам любых соответствующих отрезков.
РЕШЕНИЕ ЗАДАЧ
Формула для расчета объема прямоугольного параллелепипеда:
V = a * b * c
где а — длина, Ь — ширина, с — высота.
Так как у куба все измерения равны (а = Ь = с), то формула для вычисления объема куба V = а3.
Примеры
1.Вычислить объем прямоугольного параллелепипеда длиной 6 м, шириной 4 м и высотой 8 м.
Решение. Так как длина, ширина и высота измеряются одной и той же единицей длины (м), то подставим их в формулу V=а*Ь*с и вычислим объем:
V = 6 * 4 * 8 = 192 (м3)
Ответ: 192 м3.
2.Вычислите объем куба со стороной основания 10 см.
Решение. Подставим численное значение стороны куба в формулу вычисления объема V=а3 и вычислим:
V = 10 * 10 * 10 = 103 = 1 000 (см3) — 1 л.
Ответ: 1 000 см3, или 1 л.
Некоторые задачи по стереометрии решаются вообще без формул!
Например.
3.Объём куба равен 12. Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Обойдёмся без формул!
Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб 🙂
Площадь поверхности многогранника — это сумма площадей всех его граней.
4.В некоторых задачах каждое ребро многогранника увеличили, например, в три раза. Очевидно, что при этом площадь поверхности увеличится в девять раз, а объём — в 27раз.
5.Чашка диаметром 8 см и высотой 10 см вмещает 0.5 литра воды. Каких размеров должна быть подобная чашка, вмещающая 4 литра воды ?
Решение
|
Поскольку чашки – подобные цилиндры, то отношение их объёмов равно отношению кубов соответствующих отрезков ( в нашем случае – высот и диаметров чашек ). Следовательно, высота h новой чашки находится из отношения: ( h / 10 ) 3 = 4 / 0.5, то есть h 3 = 8 · 10 3, откуда h = 20 см; аналогично, для диаметра d получим: ( d / 8 ) 3 = 4 / 0.5 , то есть d 3 = 8 · 8 3, откуда d = 16 см . |
Задания для самостоятельной работы
- В каком отношении делится боковая поверхность правильной треугольной призмы плоскостью, проходящей через среднюю линию ее основания.(2 балла)
- В прямоугольном параллелепипеде стороны основания 3 и 4, а диагональ наклонена к плоскости основания под углом 45°.Найдите площадь поверхности параллелепипеда.(4 балла)
- Найдите площадь боковой поверхности прямоугольного параллелепипеда, у которого стороны основания 5 и 6,а боковые ребра 7. (4 балла)
- В правильной четырехугольной пирамиде сторона основания равна 6. Боковая грань наклонена к плоскости основания под углом 45°. Какова площадь поверхности пирамиды? (4 балла)
- Можно ли из куска жести прямоугольной формы размером 31х11см сделать открытую сверху коробку, имеющую форму прямоугольного параллелепипеда размером 10х10х6см? (5 баллов)
- Стороны прямоугольника 4 и 5.Какова площадь поверхности тела , полученного вращением этого прямоугольника вокруг меньшей стороны? (4 балла)
- Из скольки кубиков, с ребром 3 см каждый можно составить куб ,с ребром 15 см?(2 балла)
- Каков объем прямоугольного параллелепипеда, у которого ребра основания 6 и 8, а диагональ наклонена к плоскости основания под углом 30°? (3 балла)
Эталоны ответов
- 1:4
- 94
- 147
- Нет
- 96π
- 375
- 160
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Начальные геометрические сведения
- Единицы измерения длины, расстояний
Для измерения длин отрезков и нахождения расстояний между объектами используют различные единицы измерения.
В международной системе единиц основной единицей измерения является метр (м).
Существуют и другие единицы измерения расстояний: миллиметр (мм), сантиметр (см), дециметр (дм), километр (км) и др.:
- При измерении расстояний между двумя точками, изображенными на листе бумаги, удобно использовать сантиметры или миллиметры.
- При измерении расстояний между предметами в помещениях, удобно использовать метры.
- При измерении расстояний между городами, используют километры.
Чтобы измерять расстояния в различных случаях пользуются специальными инструментами, например:
- Масштабная миллиметровая линейка служит для измерения расстояний между точками на листе бумаги, выполнения чертежей (Рис.1);
- Рулетка – для измерения расстояний в помещении, на местности (Рис. 2);
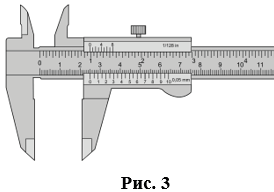
- Штангенциркуль – для измерения диаметров (Рис.3).
Соотношение мер длины:
1 см = 10 мм; 1 м = 10 дм;
1 дм = 10 см; 1 м = 1000 мм;
1 м = 100 см; 1 км = 1000 м.
Советуем посмотреть:
Точки, прямые, отрезки
Провешивание прямой на местности
Луч
Угол
Равенство геометрических фигур
Сравнение отрезков
Сравнение углов
Длина отрезка
Градусная мера угла
Измерение углов на местности
Смежные углы
Вертикальные углы
Перпендикулярные прямые
Построение прямых углов на местности
Начальные геометрические сведения
Правило встречается в следующих упражнениях:
7 класс
Задание 24,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 25,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 13,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 533,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 6,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 октября 2020 года; проверки требует 1 правка.
Геометрическая система единиц — это система естественных единиц, в которой основные физические единицы выбраны таким образом, что скорость света в вакууме с, и гравитационная постоянная G принимаются равными единице.
Геометрическая система единиц измерения не является полностью определённой системой. Некоторые другие системы являются геометрическими системами единиц в том смысле, что они определяют их в дополнение к другим константам, для полноты, например стоуновские единицы и планковские единицы.
Эта система применяется в физике, особенно в специальной и общей теориях относительности. Все физические величины отождествляются с геометрическими величинами, такими как площади, длины, безразмерные числа, кривизны траектории или кривизны сечения.
Многие уравнения в релятивистской физике приобретают более простой вид, когда выражаются в геометрических единицах, потому что все вхождения G и c выпадают. Например, радиус Шварцшильда невращающейся незаряженной чёрной дыры с массой m становится r = 2m. По этой причине во многих книгах и статьях по релятивистской физике используются геометрические единицы. Альтернативной системой геометрических единиц, часто используемой в физике элементарных частиц и космологии, является система, в которой 

Практические измерения и вычисления обычно выполняются в единицах СИ, но преобразования к геометрической системе единиц, как правило, довольно просты.
Определение[править | править код]
В геометрических единицах каждый временной интервал интерпретируется как расстояние, пройденное светом в течение данного временного интервала. То есть одна секунда интерпретируется как одна световая секунда, поэтому время имеет геометрические единицы длины. Это размерно согласуется с представлением о том, что в соответствии с кинематическими законами специальной теории относительности интервалы времени и расстояния в пространстве находятся в равном положении.
Энергия и импульс интерпретируются как компоненты вектора четырёхимпульса, а масса – это длина этого вектора, поэтому в геометрических единицах все они должны иметь размерность длины. Мы можем преобразовать массу, выраженную в килограммах, в эквивалентную массу, выраженную в метрах, путём умножения на коэффициент преобразования G/c2. Например, масса Солнца 

Небольшая численная величина коэффициентов преобразования из системы СИ в геометрическую систему единиц отражает тот факт, что релятивистские эффекты становятся заметными только тогда, когда рассматриваются большие массы или высокие скорости.
Преобразования[править | править код]
Ниже перечислены все коэффициенты преобразования, которые полезны для преобразования между всеми комбинациями базовых единиц СИ, а если это невозможно, то между ними и их уникальными элементами, потому что ампер – это безразмерное отношение двух длин, таких как [C/s], а кандела (1/683 [W / sr]) – это безразмерное отношение двух безразмерных отношений, таких как отношение двух объёмов [kg⋅m2/s3] = [W] и отношение двух областей [m2/m2] = [sr], в то время как моль является только безразмерным числом Авогадро сущностей, таких как атомы или частицы:
| m | kg | s | C | K | |
|---|---|---|---|---|---|
| m | 1 | c2/G [kg/m] | 1/c [s/m] | c2/(G/(4πε0))1/2 [C/m] | c4/(GkB) [K/m] |
| kg | G/c2 [m/kg] | 1 | G/c3 [s/kg] | (G 4πε0)1/2 [C/kg] | c2/kB [K/kg] |
| s | c [m/s] | c3/G [kg/s] | 1 | c3/(G/(4πε0))1/2 [C/s] | c5/(GkB) [K/s] |
| C | (G/(4πε0))1/2/c2 [m/C] | 1/(G 4πε0)1/2 [kg/C] | (G/(4πε0))1/2/c3 [s/C] | 1 | c2/(kB(G 4πε0)1/2) [K/C] |
| K | GkB/c4 [m/K] | kB/c2 [kg/K] | GkB/c5 [s/K] | kB(G 4πε0)1/2/c2 [C/K] | 1 |
Геометрические единицы[править | править код]
Компоненты “тензоров кривизны”, таких как тензор Эйнштейна, имеют в геометрических единицах размеры секционной кривизны. Так же рассматриваются и компоненты тензора энергии-импульса. Поэтому уравнения поля Эйнштейна в этих единицах измерения непротиворечивы.
Кривизна траектории является обратной величиной вектора кривизны кривой, поэтому в геометрических единицах она имеет размерность обратной длины. Кривизна траектории измеряет скорость, с которой негеодезическая кривая изгибается в пространстве-времени, и если мы интерпретируем временную кривую как мировую линию некоторого наблюдателя, то её кривизну траектории можно интерпретировать как величину ускорения, испытываемого этим наблюдателем. Физические величины, которые могут быть идентифицированы с кривизной траектории, включают компоненты тензора электромагнитного поля.
Любая скорость может быть интерпретирована как наклон кривой; в геометрических единицах наклоны, очевидно, являются безразмерными отношениями. Физические величины. которые можно отождествить с безразмерными отношениями, включают компоненты четырёхвектора электромагнитного потенциала и четырёхвектора электромагнитного тока.
Физические величины, такие как масса и электрический заряд, которые можно отождествить с величиной времениподобного вектора, имеют геометрическое измерение “длины”. Физические величины, такие как угловой момент, который можно отождествить с величиной бивектора, имеют геометрическую размерность “площадь”.
Вот таблица, в которой собраны некоторые важные физические величины в соответствии с их размерами в геометризованных единицах измерения. Они перечислены вместе с соответствующим коэффициентом пересчёта для единиц СИ.
| Величина | Размерность СИ | Геометрическая размерность | Множитель перевода |
|---|---|---|---|
| Длина | [L] | [L] | 1 |
| Время | [T] | [L] | c |
| Масса | [M] | [L] | G c-2 |
| Скорость | [L T-1] | 1 | c-1 |
| Угловая скорость | [T-1] | [L-1] | c-1 |
| Ускорение | [L T-2] | [L-1] | c-2 |
| Энергия | [M L2 T-2] | [L] | G c-4 |
| Плотность энергии | [M L-1 T-2] | [L-2] | G c-4 |
| Момент импульса | [M L2 T-1] | [L2] | G c-3 |
| Сила | [M L T-2] | 1 | G c-4 |
| Мощность | [M L2 T-3] | 1 | G c-5 |
| Давление | [M L-1 T-2] | [L-2] | G c-4 |
| Плотность | [M L-3] | [L-2] | G c-2 |
| Электрический заряд | [I T] | [L] | G1/2 c-2 (4πε0)-1/2 |
| Электрический потенциал | [M L2 T-3 I-1] | 1 | G1/2 c-2 (4πε0)1/2 |
| Электрическое поле | [M L T-3 I-1] | [L-1] | G1/2 c-2 (4πε0)1/2 |
| Магнитное поле | [M T?2 I?1] | [L-1] | G1/2 c-1 (4πε0)1/2 |
| Потенциал | [M L T-2 I-1] | 1 | G1/2 c?1 (4πε0)1/2 |
Эта таблица может быть дополнена путём включения температуры, как указано выше, а также дальнейших производных физических величин, таких как различные моменты.
Ссылки[править | править код]
- Robert Wald. General Relativity. — Chicago: University of Chicago Press, 1984. — ISBN 0-226-87033-2. See Appendix F
Внешние ссылки[править | править код]
- Conversion factors for energy equivalents