Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 13 сентября 2022 года; проверки требуют 3 правки.
У этого термина существуют и другие значения, см. Ампер (значения).
Ампе́р (русское обозначение: А; международное: A) — единица измерения силы электрического тока в Международной системе единиц (СИ), одна из семи основных единиц СИ. В амперах измеряется также магнитодвижущая сила и разность магнитных потенциалов (устаревшее наименование — ампер-виток)[1]: магнитодвижущая сила 1 ампер (ампер-виток) — это такая магнитодвижущая сила, которую создаёт замкнутый контур, по которому протекает ток, равный 1 амперу. Кроме системы СИ, ампер является единицей силы тока и относится к числу основных единиц в системе единиц МКСА.
Определение[править | править код]
16 ноября 2018 года на XXVI Генеральной конференции мер и весов было принято новое определение ампера, основанное на использовании численного значения элементарного электрического заряда. Формулировка, вступившая в силу 20 мая 2019 года, гласит[2][3]:
Ампер, обозначение А (A), есть единица электрического тока в SI. Он определяется путем принятия фиксированного числового значения элементарного заряда e равным 1,602176634 × 10−19 при выражении в единице Кл, что соответствует А с, где секунда определяется через


История[править | править код]
Происхождение[править | править код]
Единица измерения, предложенная на 1-м Международном конгрессе электриков[5] (1881 г., Париж) и принятая на Международном электрическом конгрессе (1893 г., Чикаго)[6], названа в честь французского физика Андре Ампера. Она была первоначально определена как одна десятая единицы тока системы СГСМ (эта единица, известная в настоящее время как абампер или био, определяла ток, создающий силу в 2 дины на сантиметр длины между двумя тонкими проводниками на расстоянии в 1 см)[7].
Международный ампер[править | править код]
В 1893 году было принято определение единицы измерения силы тока как тока, необходимого для электрохимического осаждения 1,118 миллиграммов серебра в секунду из раствора нитрата серебра[5]. Предполагалось, что величина единицы при этом не изменится, однако оказалось, что она изменилась на 0,015 %. Эта единица стала известна как международный ампер.
Определение 1948 года[править | править код]
Определение ампера, предложенное Международным комитетом мер и весов в 1946 году и принятое IX Генеральной конференцией по мерам и весам (ГКМВ) в октябре 1948 года, гласит[8][9][10]:
Ампер — сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 метр один от другого, вызвал бы на каждом участке проводника длиной 1 метр силу взаимодействия, равную 2⋅10−7 ньютона.
Иллюстрация к определению ампера 1948 года
Таким образом, фактически было возвращено изначальное определение.
Из этого определения ампера следовало, что магнитная постоянная 





После того, как в 1983 году было изменено определение метра (с 1960 года оно было привязано к длине волны определённого излучения атома криптона-86, а в 1983 стало определяться как расстояние, которое свет проходит за определённое время) и стало фиксированным (то есть точно определённым) значение скорости света c, фиксированным стало в результате и значение электрической постоянной ε0, поскольку ε0μ0 по определению равно 1/c2 [6]:
Ф/м ≈ 8,85418781762039 × 10−12 Ф·м−1.
Однако определение ампера, принятое в 1948 году, оказалось трудным для реализации, и в качестве практической реализации эталона ампера с 1980-х годов стали использоваться квантовые приборы, которые привязывали с помощью закона Ома ампер к вольту и ому (1 А = 1 В / 1 Ом), а те, в свою очередь, реализовывались с помощью эффекта Джозефсона и квантового эффекта Холла как определённые зависимости от постоянной Планка h и элементарного заряда e. Поэтому фиксация численных значений постоянной Планка (требуемая в первую очередь для переопределения килограмма) и элементарного заряда позволила ввести новое определение ампера, привязанное к значениям фундаментальных констант[6].
Определение 2019 года[править | править код]
В 2018 году на 26-й ГКМВ было принято и на следующий год вступило в силу нынешнее определение ампера (при этом старое определение ампера, действовавшее с 1948 года, отменено). Величина ампера не изменилась при смене определения. Однако изменение определения привело к тому, что указанные выше выражения для магнитной и электрической постоянных μ0 и ε0 перестали быть точными, а стали выполняться лишь численно (но с огромной точностью) и подлежат экспериментальному измерению. Относительная стандартная неопределённость μ0 и ε0 равна относительной стандартной неопределённости величины α (постоянной тонкой структуры), а именно 2,3 × 10−10 на момент принятия резолюции 2018 года[11].
Кратные и дольные единицы[править | править код]
В соответствии с полным официальным описанием СИ, содержащемся в действующей редакции Брошюры СИ (фр. Brochure SI, англ. The SI Brochure), опубликованной Международным бюро мер и весов (МБМВ), десятичные кратные и дольные единицы ампера образуются с помощью стандартных приставок СИ[9][12]. «Положение о единицах величин, допускаемых к применению в Российской Федерации», принятое Правительством Российской Федерации, предусматривает использование в России тех же приставок[13].
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 101 А | декаампер | даА | daA | 10−1 А | дециампер | дА | dA |
| 102 А | гектоампер | гА | hA | 10−2 А | сантиампер | сА | cA |
| 103 А | килоампер | кА | kA | 10−3 А | миллиампер | мА | mA |
| 106 А | мегаампер | МА | MA | 10−6 А | микроампер | мкА | µA |
| 109 А | гигаампер | ГА | GA | 10−9 А | наноампер | нА | nA |
| 1012 А | тераампер | ТА | TA | 10−12 А | пикоампер | пА | pA |
| 1015 А | петаампер | ПА | PA | 10−15 А | фемтоампер | фА | fA |
| 1018 А | эксаампер | ЭА | EA | 10−18 А | аттоампер | аА | aA |
| 1021 А | зеттаампер | ЗА | ZA | 10−21 А | зептоампер | зА | zA |
| 1024 А | иоттаампер | ИА | YA | 10−24 А | иоктоампер | иА | yA |
| 1027 А | роннаампер | РА | RA | 10−27 А | ронтоампер | рА | rA |
| 1030 А | кветтаампер | КвА | QA | 10−30 А | квектоампер | квА | qA |
| рекомендовано к применению применять не рекомендуется |
Связь с другими единицами СИ[править | править код]
Если сила тока в проводнике равна 1 амперу, то за одну секунду через поперечное сечение проходит заряд, равный 1 кулону[14].
Разность потенциалов в 1 вольт на концах проводника с электрическим сопротивлением 1 ом создаёт в нём ток 1 ампер.
Если конденсатор ёмкостью в 1 фарад заряжать током 1 ампер, то напряжение на обкладках будет возрастать на 1 вольт каждую секунду.
Если изменять ток со скоростью 1 ампер в секунду в проводнике, имеющем индуктивность 1 генри, в нём создаётся ЭДС индукции, равная одному вольту.
См. также[править | править код]
- Закон Ома
- Электричество
- Закон Ампера
Примечания[править | править код]
- ↑ Магнитодвижущая сила // Большая советская энциклопедия
- ↑ Le Système international d’unités (SI) / The International System of Units (SI). — BIPM, 2019. — P. 20, 132. — ISBN 978-92-822-2272-0.
- ↑ Брошюра СИ, 2019, с. 16, 84.
- ↑ ampere (A). www.npl.co.uk. Дата обращения: 21 мая 2019. Архивировано 20 января 2021 года.
- ↑ 1 2 History of the ampere, Sizes, 1 April 2014, <http://www.sizes.com/units/ampHist.htm>. Проверено 29 января 2017. Архивная копия от 20 октября 2016 на Wayback Machine
- ↑ 1 2 3 Брошюра СИ, 2019, с. 92—93.
- ↑ Kowalski, L, A short history of the SI units in electricity, Montclair, <http://alpha.montclair.edu/~kowalskiL/SI/SI_PAGE.HTML> Архивная копия от 29 апреля 2009 на Wayback Machine
- ↑ Брошюра СИ, 2019, с. 48.
- ↑ 1 2 The SI brochure Архивная копия от 26 апреля 2006 на Wayback Machine Описание СИ на сайте Международного бюро мер и весов.
- ↑ Положение о единицах величин, допускаемых к применению в Российской Федерации. Основные единицы Международной системы единиц (СИ). Федеральный информационный фонд по обеспечению единства измерений. Росстандарт. Дата обращения: 28 февраля 2018. Архивировано из оригинала 18 сентября 2017 года.
- ↑ Брошюра СИ, 2019, с. 82—84.
- ↑ Брошюра СИ, 2019, с. 27.
- ↑ Положение о единицах величин, допускаемых к применению в Российской Федерации. Дата обращения: 28 декабря 2014. Архивировано из оригинала 5 марта 2016 года.
- ↑ Bodanis, David (2005), Electric Universe, New York: Three Rivers Press, ISBN 978-0-307-33598-2
Литература[править | править код]
- Краткий словарь физических терминов / Сост. А. И. Болсун, рец. М. А. Ельяшевич. — Мн.: Вышэйшая школа, 1979. — С. 23—24. — 416 с. — 30 000 экз.
- Международная система единиц (SI) : Брошюра СИ. — Изд. 9-е. — Росстандарт, 2019. — 100 с.
Ссылки[править | править код]
- The NIST Reference on Constants, Units, and Uncertainty // physics.nist.gov
- NIST Definition of ampere and μ0 // physics.nist.gov
- Tutorial video explaining amperes and current // afrotechmods.com
From Wikipedia, the free encyclopedia
| ampere | |
|---|---|

Demonstration model of a moving iron ammeter. As the current through the coil increases, the plunger is drawn further into the coil and the pointer deflects to the right. |
|
| General information | |
| Unit system | SI |
| Unit of | electric current |
| Symbol | A |
| Named after | André-Marie Ampère |
The ampere (, ;[1][2][3] symbol: A),[4] often shortened to amp,[5] is the unit of electric current in the International System of Units (SI). One ampere is equal to 1 coulomb, or 6.241509074×1018 electrons worth of charge, moving past a point in a second.[6][7][8] It is named after French mathematician and physicist André-Marie Ampère (1775–1836), considered the father of electromagnetism along with Danish physicist Hans Christian Ørsted.
As of the 2019 redefinition of the SI base units, the ampere is defined by fixing the elementary charge e to be exactly 1.602176634×10−19 C (coulomb),[6][9] which means an ampere is an electrical current equivalent to 1019 elementary charges moving every 1.602176634 seconds or 6.241509074×1018 elementary charges moving in a second. Prior to the redefinition the ampere was defined as the current that would need to be passed through 2 parallel wires 1 metre apart to produce a magnetic force of 2×10−7 newtons per metre.
The earlier CGS system had two definitions of current, one essentially the same as the SI’s and the other using Coulomb’s law as a fundamental relationship, with the unit of charge defined by measuring the force between two charged metal plates. The ampere was then defined as one coulomb of charge per second.[10] In SI, the unit of charge, the coulomb, is defined as the charge carried by one ampere during one second.
History[edit]
The ampere is named for French physicist and mathematician André-Marie Ampère (1775–1836), who studied electromagnetism and laid the foundation of electrodynamics. In recognition of Ampère’s contributions to the creation of modern electrical science, an international convention, signed at the 1881 International Exposition of Electricity, established the ampere as a standard unit of electrical measurement for electric current.
The ampere was originally defined as one tenth of the unit of electric current in the centimetre–gram–second system of units. That unit, now known as the abampere, was defined as the amount of current that generates a force of two dynes per centimetre of length between two wires one centimetre apart.[11] The size of the unit was chosen so that the units derived from it in the MKSA system would be conveniently sized.
The “international ampere” was an early realization of the ampere, defined as the current that would deposit 0.001118 grams of silver per second from a silver nitrate solution.[12] Later, more accurate measurements revealed that this current is 0.99985 A.
Since power is defined as the product of current and voltage, the ampere can alternatively be expressed in terms of the other units using the relationship I = P/V, and thus 1 A = 1 W/V. Current can be measured by a multimeter, a device that can measure electrical voltage, current, and resistance.
Former definition in the SI[edit]
Until 2019, the SI defined the ampere as follows:
The ampere is that constant current which, if maintained in two straight parallel conductors of infinite length, of negligible circular cross-section, and placed one metre apart in vacuum, would produce between these conductors a force equal to 2×10−7 newtons per metre of length.[13]: 113 [14]
Ampère’s force law[15][16] states that there is an attractive or repulsive force between two parallel wires carrying an electric current. This force is used in the formal definition of the ampere.
The SI unit of charge, the coulomb, was then defined as “the quantity of electricity carried in 1 second by a current of 1 ampere”.[13]: 144 Conversely, a current of one ampere is one coulomb of charge going past a given point per second:
In general, charge Q was determined by steady current I flowing for a time t as Q = It.
This definition of the ampere was most accurately realised using a Kibble balance, but in practice the unit was maintained via Ohm’s law from the units of electromotive force and resistance, the volt and the ohm, since the latter two could be tied to physical phenomena that are relatively easy to reproduce, the Josephson effect and the quantum Hall effect, respectively.[17]
Techniques to establish the realisation of an ampere had a relative uncertainty of approximately a few parts in 107, and involved realisations of the watt, the ohm and the volt.[17]
Present definition[edit]
The 2019 redefinition of the SI base units defined the ampere by taking the fixed numerical value of the elementary charge e to be 1.602 176 634 × 10−19 when expressed in the unit C, which is equal to A⋅s, where the second is defined in terms of ∆νCs, the unperturbed ground state hyperfine transition frequency of the caesium-133 atom.[18]
The SI unit of charge, the coulomb, “is the quantity of electricity carried in 1 second by a current of 1 ampere”.[19] Conversely, a current of one ampere is one coulomb of charge going past a given point per second:
In general, charge Q is determined by steady current I flowing for a time t as Q = I t.
Constant, instantaneous and average current are expressed in amperes (as in “the charging current is 1.2 A”) and the charge accumulated (or passed through a circuit) over a period of time is expressed in coulombs (as in “the battery charge is 30000 C“). The relation of the ampere (C/s) to the coulomb is the same as that of the watt (J/s) to the joule.
Units derived from the ampere[edit]
The international system of units (SI) is based on 7 SI base units the second, metre, kilogram, kelvin, ampere, mole, and candela representing 7 fundamental types of physical quantity, or “dimensions”, (time, length, mass, temperature, electrical current, amount of substance, and luminous intensity respectively) with all other SI units being defined using these. These SI derived units can either be given special names e.g. watt, volt, lux, etc. or defined in terms of others, e.g. metre per second. The units with special names derived from the ampere are:
| Quantity | Unit | Symbol | Meaning | In SI base units |
|---|---|---|---|---|
| Electric charge | coulomb | C | ampere second | A⋅s |
| Electric potential difference | volt | V | joule per coulomb | kg⋅m2⋅s−3⋅A−1 |
| Electrical resistance | ohm | Ω | volt per ampere | kg⋅m2⋅s−3⋅A−2 |
| Electrical conductance | siemens | S | ampere per volt or inverse ohm | s3⋅A2⋅kg−1⋅m−2 |
| Electrical inductance | henry | H | ohm second | kg⋅m2⋅s−2⋅A−2 |
| Electrical capacitance | farad | F | coulomb per volt | s4⋅A2⋅kg−1⋅m−2 |
| Magnetic flux | weber | Wb | volt second | kg⋅m2⋅s−2⋅A−1 |
| Magnetic flux density | tesla | T | weber per square metre | kg⋅s−2⋅A−1 |
There are also some SI units that are frequently used in the context of electrical engineering and electrical appliances, but can be defined independently of the ampere, notably the hertz, joule, watt, candela, lumen, and lux.
SI prefixes[edit]
Like other SI units, the ampere can be modified by adding a prefix that multiplies it by a power of 10.
| Submultiples | Multiples | ||||
|---|---|---|---|---|---|
| Value | SI symbol | Name | Value | SI symbol | Name |
| 10−1 A | dA | deciampere | 101 A | daA | decaampere |
| 10−2 A | cA | centiampere | 102 A | hA | hectoampere |
| 10−3 A | mA | milliampere | 103 A | kA | kiloampere |
| 10−6 A | µA | microampere | 106 A | MA | megaampere |
| 10−9 A | nA | nanoampere | 109 A | GA | gigaampere |
| 10−12 A | pA | picoampere | 1012 A | TA | teraampere |
| 10−15 A | fA | femtoampere | 1015 A | PA | petaampere |
| 10−18 A | aA | attoampere | 1018 A | EA | exaampere |
| 10−21 A | zA | zeptoampere | 1021 A | ZA | zettaampere |
| 10−24 A | yA | yoctoampere | 1024 A | YA | yottaampere |
| 10−27 A | rA | rontoampere | 1027 A | RA | ronnaampere |
| 10−30 A | qA | quectoampere | 1030 A | QA | quettaampere |
See also[edit]
- Ammeter
- Ampacity (current-carrying capacity)
- Electric current
- Electric shock
- Hydraulic analogy
- Magnetic constant
- Orders of magnitude (current)
References[edit]
- ^ Jones, Daniel (2011). Roach, Peter; Setter, Jane; Esling, John (eds.). Cambridge English Pronouncing Dictionary (18th ed.). Cambridge University Press. ISBN 978-0-521-15255-6.
- ^ Wells, John C. (2008). Longman Pronunciation Dictionary (3rd ed.). Longman. ISBN 978-1-4058-8118-0.
- ^ “ampere”. Merriam-Webster Dictionary. Retrieved 29 September 2020.
- ^ “2. SI base units”, SI brochure (8th ed.), BIPM, archived from the original on 7 October 2014, retrieved 19 November 2011
- ^ SI supports only the use of symbols and deprecates the use of abbreviations for units.“Bureau International des Poids et Mesures” (PDF). 2006. p. 130. Archived from the original (PDF) on 14 August 2017. Retrieved 21 November 2011.
- ^ a b BIPM (20 May 2019). “Mise en pratique for the definition of the ampere in the SI”. BIPM. Retrieved 18 February 2022.
- ^ “2.1. Unit of electric current (ampere)”, SI brochure (8th ed.), BIPM, archived from the original on 3 February 2012, retrieved 19 November 2011
- ^ Base unit definitions: Ampere Archived 25 April 2017 at the Wayback Machine Physics.nist.gov. Retrieved on 28 September 2010.
- ^ Draft Resolution A “On the revision of the International System of units (SI)” to be submitted to the CGPM at its 26th meeting (2018) (PDF), archived from the original (PDF) on 29 April 2018, retrieved 28 October 2018
- ^ Bodanis, David (2005), Electric Universe, New York: Three Rivers Press, ISBN 978-0-307-33598-2
- ^ Kowalski, L (1986), “A short history of the SI units in electricity”, The Physics Teacher, Montclair, 24 (2): 97–99, Bibcode:1986PhTea..24…97K, doi:10.1119/1.2341955, archived from the original on 14 February 2002
- ^ History of the ampere, Sizes, 1 April 2014, archived from the original on 20 October 2016, retrieved 29 January 2017
- ^ a b International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), ISBN 92-822-2213-6, archived (PDF) from the original on 4 June 2021, retrieved 16 December 2021
- ^ Monk, Paul MS (2004), Physical Chemistry: Understanding our Chemical World, John Wiley & Sons, ISBN 0-471-49180-2, archived from the original on 2 January 2014
- ^ Serway, Raymond A; Jewett, JW (2006). Serway’s principles of physics: a calculus based text (Fourth ed.). Belmont, CA: Thompson Brooks/Cole. p. 746. ISBN 0-53449143-X. Archived from the original on 21 June 2013.
- ^ Beyond the Kilogram: Redefining the International System of Units, US: National Institute of Standards and Technology, 2006, archived from the original on 21 March 2008, retrieved 3 December 2008.
- ^ a b “Appendix 2: Practical realisation of unit definitions: Electrical quantities”, SI brochure, BIPM, archived from the original on 14 April 2013.
- ^ “ampere (A)”. www.npl.co.uk. Retrieved 21 May 2019.
- ^ The International System of Units (SI) (PDF) (8th ed.), Bureau International des Poids et Mesures, 2006, p. 144, archived (PDF) from the original on 5 November 2013.
External links[edit]
- The NIST Reference on Constants, Units, and Uncertainty
- NIST Definition of ampere and μ0
Содержание:
- Определение и формула силы Ампера
- Закон Ампера
- Силы, действующие на проводники с током в магнитном поле
- Единицы измерения силы Ампера
- Примеры решения задач
Определение и формула силы Ампера
Определение
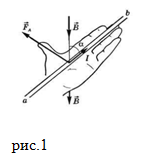
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. Ее обозначения:
$bar{F}, bar{F}_A$ . Сила Ампера векторная величина. Ее направление определяет
правило левой руки: следует расположить ладонь левой руки так, чтобы силовые линии магнитного поля входили в нее.
Вытянутые четыре пальца указывали направление силы тока. В таком случае отогнутый на
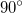
Закон Ампера
Элементарная сила Ампера
($dbar{F}_A$) определена законом (или формулой) Ампера:
$$d bar{F}_{A}=I d bar{l} times bar{B}(1)$$
где I – сила тока,
$d bar{l}$ – малый элемент длины проводника – это вектор, равный
по модулю длине проводника, направленный в таком же направлении как вектор плотности тока,
$bar{B}$ – индукция магнитного поля, в которое помещен проводник с током.
Иначе эту формулу для силы Ампера записывают как:
$$d bar{F}_{A}=bar{j} times bar{B} d V(2)$$
где $bar{j}$ – вектор плотности тока, dV – элемент объема проводника.
Модуль силы Ампера находят в соответствии с выражением:
$$d F=I cdot B cdot d l cdot sin alpha(3)$$
где $alpha$ – угол между векторами магнитной индукции и направление течения тока. Из выражения (3) очевидно, что
сила Ампера максимальна в случае перпендикулярности линий магнитной индукции поля по отношению к проводнику с током.
Силы, действующие на проводники с током в магнитном поле
Из закона Ампера следует, что на проводник с током, равным I, действует сила равная:
$$bar{F}_{A}=I int_{l} d bar{l} times bar{B}(4)$$
где $bar{B}$ магнитная индукция, рассматриваемая в пределах малого кусочка проводника dl.
Интегрирование в формуле (4) проводят по всей длине проводника (l). Из выражения (4) следует, что на замкнутый контур с током I,
в однородном магнитном поле действует сила Ампера равная $bar{F}_{A}=0(H)$
Сила Ампера, которая действует на элемент (dl) прямого проводника с током I1, помещённый в магнитное поле, которое
создает другой прямой проводник, параллельный первому с током I2, равна по модулю:
$$d F=frac{mu_{0}}{2 pi} frac{I_{1} I_{2}}{d} d l(5)$$
где d – расстояние между проводниками, $mu_{0}=4 pi cdot 10^{7}$ Гн/м(или Н/А2 ) – магнитная постоянная.
Проводники с токами одного направления притягиваются. Если направления токов в проводниках различны, то они отталкиваются.
Для рассмотренных выше параллельных проводников бесконечной длины сила Амперана единицу длины может быть вычислена по формуле:
$$frac{F}{l}=frac{mu_{0}}{2 pi} frac{I_{1} I_{2}}{d}$$
Формулу (6) в системе СИ применяют для получения количественного значения магнитной постоянной.
Единицы измерения силы Ампера
Основной единицей измерения силы Ампер (как и любой другой силы) в системе СИ является: [FA]=H
В СГС: [FA]=дин
Примеры решения задач
Пример
Задание. Прямой проводник длины l с током I находится в однородном магнитном поле B. На проводник
действует сила F. Каков угол между направлением течения тока и вектором магнитной индукции?
Решение. На проводник с током, находящийся в магнитном поле действует сила Ампера, модуль которой для
прямолинейного проводника с током расположенном в однородном поле можно представить как:
$$F=F_{A}=I B operatorname{lsin} alpha$$
где $alpha$ – искомый угол. Следовательно:
$$alpha=arcsin left(frac{F}{I B l}right)$$
Ответ. $alpha=arcsin left(frac{F}{I B l}right)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
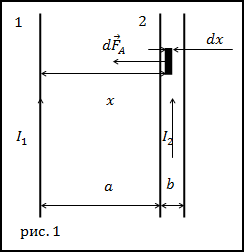
Задание. Два тонких, длинных проводника с токами лежат в одной плоскости на расстоянии d друг от друга.
Ширина правого проводника равна a. По проводникам текут токи I1 и I2 (рис.1). Какова, сила Ампера, действующая
на проводники в расчете на единицу длины?
Решение. За основу решения задачи примем формулу элементарной силы Ампера:
$$d bar{F}_{A}=I d bar{l} times bar{B}(2.1)$$
Будем считать, что проводник с током I1 создает магнитное поле, а другой проводник в нем находится.Станем искать силу
Ампера, действующую на проводник с током I2. Выделим в проводнике (2) маленький элемент dx (рис.1), который находится
на расстоянии x от первого проводника. Магнитное поле, которое создает проводник 1 (магнитное поле бесконечного прямолинейного проводника с
током) в точке нахождения элементаdxпо теореме о циркуляции можно найти как:
$$B cdot 2 pi x=mu_{0} I_{1} rightarrow B=frac{mu_{0} I_{1}}{2 pi x}$$
Вектор магнитной индукции в точке нахождения элемента dx направлен перпендикулярно плоскости
рисунка, следовательно, модуль элементарной силы Ампера, действующий на него можно представить как:
$$B cdot 2 pi x=mu_{0} I_{1} rightarrow B=frac{mu_{0} I_{1}}{2 pi x}$$
где ток, который течет в элементе проводника dx, выразим как:
$$B cdot 2 pi x=mu_{0} I_{1} rightarrow B=frac{mu_{0} I_{1}}{2 pi x}$$
Тогда выражение для dFA, учитывая (2.2) и (2.4) запишем как:
$$B cdot 2 pi x=mu_{0} I_{1} rightarrow B=frac{mu_{0} I_{1}}{2 pi x}$$
где из рис.1 видно, что $a leq x leq a+b$, по условию задачи силу следует
найти на единицу длины, значит $0 leq l leq 1$ . Для нахождения суммарной силы Ампера, действующей на проводник (2) возьмем двойной интеграл от выражения (2.5):
$$F_{A}=int_{a}^{a+b} int_{0}^{1} frac{mu_{0} I_{1}}{2 pi x} cdot frac{I_{2}}{b} d x d l=int_{a}^{a+b} frac{mu_{0} I_{1}}{2 pi x} cdot frac{I_{2}}{b} d x=frac{mu_{0} I_{1}}{2 pi} cdot frac{I_{2}}{b} ln left|frac{a+b}{a}right|$$
Проводники действуют друг на друга с силами равными по модулю и так как токи направлены одинаково, то они притягиваются.
Ответ. $F_{A}=frac{mu_{0} I_{1}}{2 pi} cdot frac{I_{2}}{b} ln left|frac{a+b}{a}right|$
Читать дальше: Формула силы выталкивания.
Содержание
- Что такое амперы и миллиамперы
- Методика измерений
- Физическая величина
- Методика измерений
- Как правильно измерять электрический ток в амперах
- Как обозначаются амперы, миллиамперы и микроамперы
- Сколько Ватт в 1 Ампере?
- Что измеряется в амперах
- Способы перевода величины тока
- Как правильно измерять электрический ток в амперах
- Как переводить миллиамперы в амперы и наоборот
- Параметры замыкающих герконов стандартного и промежуточного типов
- Формула для перевода А в мА
Что такое амперы и миллиамперы
Ампер – это единица измерения силы тока, физическая величина, равная отношению между величиной заряда и интервалом времени его прохождения через любую поверхность или объект; одна из 7 основных единиц Международной системы единиц (СИ).
Амперметр – это прибор, измеряющий в амперах.
Дополнительная информация! Ампер был принят в качестве единицы измерения в 1881 году на 1-м Международном конгрессе электриков, проходившем в Париже, и был назван в честь французского физика, математика и химика Андре-Мари Ампера.
Андре Ампер
В соответствии с поправками 2021 года Международный комитет мер и весов дает следующее определение ампера:
«Величина ампера фиксируется путем определения числового значения элементарного заряда и равна 1,602 176 634 × 10 ^ -19, выраженная в кулонах.»
Эмблема Международного комитета мер и весов
Миллиампер – это дробное значение, которое, согласно его префиксу, равно одной тысячной ампера, или 10 ^ -3. Его также часто пишут как «мампер» – это своего рода среднее обозначение между его обозначением (мА) и именем.
1 микроампер эквивалентен 10 ^ -6 А.
Важно! Регистрация как «milliA» не рекомендуется; при использовании обозначения единицы измерения лучше сокращать префикс, которым она используется.
Таблица префиксов и их значение
Методика измерений
Как отмечалось ранее, для измерения тока используются амперметры, мультиметры и тестеры. Наибольшую точность измерений обеспечивает первый из них. Они измеряют только один размер и одну шкалу. И это не очень удобно. В свою очередь, мультиметры и тестеры позволяют измерять практически все электрические величины, а не только в определенном диапазоне. Кроме того, в этих устройствах есть возможность изменять единицы измерения. Например, прибор показывает, что интервал превышен. В этом случае необходимо перевести миллиамперы в амперы и за счет этого узнать нужное значение. Главный недостаток тестеров и мультиметров в том, что их погрешность, в отличие от амперметров, намного больше. Однако на практике они часто используются, так как это позволяет легко и просто найти неисправность и устранить ее. Еще один важный нюанс, связанный с этими приборами: если раньше было необходимо разорвать цепь, то теперь есть тестеры и мультиметры, позволяющие измерять силу тока бесконтактным способом, то есть без подключения. Это решение все чаще применяется на практике.
Физическая величина
Ампер – это единица измерения силы тока. Его значение можно определить, произведя прямые измерения мультиметром, тестером или амперметром (прямой метод). Сила тока измеряется только при последовательном подключении измерительного прибора к электрической цепи. Во втором случае его значение можно узнать путем расчетов (косвенный метод). Если вы знаете напряжение, приложенное к участку цепи, а также его сопротивление, просто разделите первое на второе, и мы получим требуемое значение. На практике усилители используются нечасто – это большое значение. Следовательно, необходимо использовать больше единиц: микро (10-6) и милли (10-3). Но для выполнения электрических расчетов необходимо преобразовать их в основные единицы измерения (например, миллиампер в ампер). Рассмотрим следующий пример. Напряжение на участке цепи U = 6 В, сопротивление R = 100 Ом. Действующую на него силу тока I определяем по закону Ома:
I = U / R, (1)
где это находится:
- U – напряжение на участке цепи, В;
- R – сопротивление того же сечения, Ом;
- I – текущая сила, действующая на него, A.
В результате вычислений получаем I = U / R = 6/100 = 0,06 А. Это не очень удобное число для восприятия. Поэтому он пересчитывается в нескольких единицах измерения. В этом случае удобно выражать это значение в миллиамперах. Для этого полученное значение 0,06 А умножаем на 1000 и получаем 60 мА. Вы также можете сделать обратное преобразование – из миллиампер в амперы. Для этого достаточно 60 мА разделить на 1000 и мы получим те же 0,06 А. Из этого пересчета видно, сколько миллиампер в амперах – 1000. Поэтому делим или умножаем на это число. Если используется префикс «микро», чтобы перейти от одной единицы измерения к другой, умножьте или разделите на 1 000 000.
Методика измерений
Как отмечалось ранее, для измерения тока используются амперметры, мультиметры и тестеры. Наибольшую точность измерений обеспечивает первый из них. Они измеряют только один размер и одну шкалу. И это не очень удобно. В свою очередь, мультиметры и тестеры позволяют измерять практически все электрические величины, а не только в определенном диапазоне. Кроме того, в этих устройствах есть возможность изменять единицы измерения. Например, прибор показывает, что интервал превышен. В этом случае необходимо перевести миллиамперы в амперы и за счет этого узнать нужное значение. Главный недостаток тестеров и мультиметров в том, что их погрешность, в отличие от амперметров, намного больше. Однако на практике они часто используются, так как это позволяет легко и просто найти неисправность и устранить ее. Еще один важный нюанс, связанный с этими приборами: если раньше было необходимо разорвать цепь, то теперь есть тестеры и мультиметры, позволяющие измерять силу тока бесконтактным способом, то есть без подключения. Это решение все чаще применяется на практике.
Как правильно измерять электрический ток в амперах
Следует уточнить, что измерение тока – это измерение его основных характеристик (силы и напряжения). Чаще всего в лабораторных или школьных условиях силу тока измеряют на проводнике или во всей электрической цепи. Для этого используется специальный прибор – амперметр. Что на схемах правильно обозначено кружком с латинской буквой «А» внутри.
При подключении амперметра необходимо соблюдать следующие правила:
- Подключайтесь к электрической цепи только последовательно с участком цепи, на котором вы хотите измерить ток. Другими словами, до или после участка схемы для измерений.
- Обязательно обратите внимание на «признаки» тока в цепи. Провод с «плюсом» от блока питания подключаем к «плюсу» амперметра, а «минус» – к «минусу».
- Старайтесь не превышать значение на шкале измерений, потому что в этом случае прибор может не работать. Если амперметр с двумя шкалами, используйте тот, предел которого превышает допустимое значение.
Схема правильного подключения амперметра в электрическую схему
При измерении сопротивления рекомендуется учитывать внутреннее сопротивление самого амперметра, которое на нем указано. Но в школе ими пренебрегают.
Дополнительная информация! Для измерений можно использовать мультиметр – прибор, сочетающий в себе функции измерения силы, мощности и других параметров тока. Для этого используются все те же правила включения в схему амперметра.
Как обозначаются амперы, миллиамперы и микроамперы
Правильные обозначения: ампер – А, миллиампер – мА, микроампер – мкА.
Эта физическая величина названа по фамилии ученого, поэтому его запись всегда будет содержать заглавную букву A в русском обозначении и заглавную латинскую букву A в международном обозначении.
Примечание! Не путайте МА и МА, особенно при решении задач. В первом случае указывается мегаампер (10 ^ 6 А), а во втором миллиампер (10 ^ -3 А), что в миллиард раз меньше мегаампера.
Написание долей и кратных единиц, включая миллиампер и микроампер, будет выполняться в соответствии с правилами написания единиц и префиксов, установленными вышеупомянутой Международной системой измерений (СИ).
- Префикс пишется вместе с названием или обозначением агрегата.
- недопустимо использование двух и более приставок подряд (например, микромиллиампер).
- В большинстве случаев принято выбирать префикс таким образом, чтобы перед ним стояло число от 0,1 до 1000.
Дополнительная информация! Приставка милли переводится с латыни (тысяча) как «тысяча». Приставка «микро» имеет древнегреческие корни (μικρός) и переводится как «маленький».
Сколько Ватт в 1 Ампере?
Понятие напряжения также важно при определении мощности цепи. Это электродвижущая сила, которая перемещает электроны. Измеряется в вольтах. У большинства устройств есть эта функция в документации.
Чтобы определить мощность при токе в один ампер, нужно знать сетевое напряжение. Итак, для розетки на 220 вольт получится: P = 1 * 220 = 220 Вт. Формула для расчета: P = I * U, где I – ток, а U – напряжение. В трехфазной сети необходимо учитывать поправочный коэффициент, который отражает процент эффективности работы. В большинстве случаев он составляет от 0,67 до 0,95.
Что измеряется в амперах
Основной физической величиной, измеряемой в амперах, является сила тока (обозначаемая в формулах буквой «I»). Как упоминалось ранее в определении ампера, он равен отношению количества заряда, прошедшего через проводник за определенное время, и самого времени прохождения.
Магнитодвижущая сила (физическая величина, модуль которой показывает способность создавать магнитные потоки с использованием электрических токов) и разность магнитных потенциалов (скалярная величина, которая характеризует энергетическую характеристику электростатического поля в данной точке) также измеряются в амперах… Часто на практике можно встретить использование термина «ампер-виток» для обозначения этих значений. Но официально это считается устаревшей терминологией.
Способы перевода величины тока
Для современных энергоемких бытовых приборов вполне прилично работают токи в несколько ампер и более, и пользоваться этой единицей измерения несложно. К самым дешевым устройствам относятся:
- Компьютер;
- Ноутбук;
- Обычные смартфоны и сотовые телефоны;
- MP3-плееры, приставки;
- LCD – осветительное оборудование;
- LCD – видеоустройства (мониторы, телевизоры);
- Таблетки;
- Электронные книги;
- Навигаторы;
- Видеомагнитофоны.
Типичные токи потребления этих устройств составляют от десятков до сотен миллиампер. Чтобы правильно преобразовать амперы в миллиамперы, помните, что префикс «милли» означает одну тысячную от базовой единицы. Вы можете использовать 10 -3 или 0,001 в качестве числового коэффициента. Использование такой кратной или дробной единицы вполне допустимо и узаконено национальным законодательством в виде ГОСТ 8.417-2002 «Межгосударственный стандарт. Единица количества».
Сокращенное обозначение приставки «милли» в русской версии – «м», в международной – «м». Поэтому совершенно ясно, что 1000 миллиампер равны 1 ампер.
Как правильно измерять электрический ток в амперах
Следует уточнить, что измерение тока – это измерение его основных характеристик (силы и напряжения). Чаще всего в лабораторных или школьных условиях силу тока измеряют на проводнике или во всей электрической цепи. Для этого используется специальный прибор – амперметр. Что на схемах правильно обозначено кружком с латинской буквой «А» внутри.
При подключении амперметра необходимо соблюдать следующие правила:
- Подключайтесь к электрической цепи только последовательно с участком цепи, на котором вы хотите измерить ток. Другими словами, до или после участка схемы для измерений.
- Обязательно обратите внимание на «признаки» тока в цепи. Провод с «плюсом» от блока питания подключаем к «плюсу» амперметра, а «минус» – к «минусу».
- Старайтесь не превышать значение на шкале измерений, потому что в этом случае прибор может не работать. Если амперметр с двумя шкалами, используйте тот, предел которого превышает допустимое значение.
Схема правильного подключения амперметра в электрическую схему
При измерении сопротивления рекомендуется учитывать внутреннее сопротивление самого амперметра, которое на нем указано. Но в школе ими пренебрегают.
Дополнительная информация! Для измерений можно использовать мультиметр – прибор, сочетающий в себе функции измерения силы, мощности и других параметров тока. Для этого используются все те же правила включения в схему амперметра.
Как переводить миллиамперы в амперы и наоборот
Преобразовывая значения из одной величины в другую, вы должны уметь работать со степенью и стандартной формой числа в физике. Будет легче переводить, если вы знаете соответствие между степенями и префиксами. Рекомендуется освоить.
Чтобы преобразовать миллиамперы в амперы, разделите доступное числовое значение на 1000 или умножьте на 10 ^ -3 при работе со стандартным дисплеем. А для обратного перевода вы должны либо умножить на 1000, либо умножить значение на 10 ^ 3.
Пример: сколько ампер в 500 миллиампер?
Миллиампер в 1000 раз меньше, чем ампер, поэтому разделите его на 1000; 500/1000 = 0,5. Получается 0,5 А.
Конвертер
1 мкА = 10 ^ -6 А = 0,0000001 А. Один микроампер меньше одного ампер на миллион раз. Чтобы преобразовать первое значение во второе, вам нужно будет разделить на 1000000 или умножить на 10 ^ -6 A.
Чтобы преобразовать микроампер в миллиампер, нужно учесть, что 1 мА = 1000 мкА. Для преобразования значений в первом алгоритме будут использоваться те же шаги в миллиамперах и амперах.
Электричество – обширная тема в физике, для ее усвоения необходимо разбираться во многих процессах и, самое главное, в основной единице, которая его характеризует – ампер. А для правильного перевода значений необходимо знать принятые префиксы в СИ и математике.
Параметры замыкающих герконов стандартного и промежуточного типов
| Название геркон | КЭМ-1 | КЭМ-6 | MK-36701 | МКА-27101 |
| Тип геркона | стандарт | стандарт | средний | средний |
| Действующая магнитодвижущая сила, А | 55… 110 | 38… 50 | 50… 80 | 30… 60 |
| Время отклика, мс | 3 | 2 | 2 | 1.5 |
| Максимальная коммутируемая мощность, Вт | тридцать | 12 | 21 год | 12 |
| Максимальное коммутируемое напряжение, В | 220 | 150 | 100 | 110 |
| Максимальный коммутируемый ток, А | 1 | 0,25 | 0,35 | 0,35 |
| Электрическое сопротивление, В | 500 | 500 | — | 500 |
| Сопротивление электрических контактов, Ом | 0,08 | 0,1 | 0,07 | 0,12 |
| Максимальная частота коммутации, Гц | 100 | ветры | 50 | 100 |
| Температура окружающей среды, ° С | -60… + 125 | -60… + 125 | -60… + 100 | -60… + 100 |
| Вибрационные нагрузки, частотный диапазон, Гц | 1… 600 | 1… 50 | 1… 600 | 1… 600 |
| Вибрационные нагрузки, максимальное ускорение, м / с2 | 98 | 98 | 98 | 98 |
| Диаметр цилиндра, общая длина, мм | 50/80 | 36 / 63,5 | 36 / 63,5 | 27 / 45,6 |
Формула для перевода А в мА
IMA = IA 1000
Ток I в миллиамперах (мА) равен току I в амперах (А), умноженному на 1000.
Для мастера, домашнего любителя и всех, кому интересно электричество и как оно работает – я расскажу про то, как понять и посчитать Вольты, Амперы и Киловатты – это полезно и нужно знать всем!
Электрический ток и его «три лица» – как это быстро понять
Электрический ток, если не погружаться в физику, это просто течение энергии по проводам. Поэтому, говоря о токе, лучше всего иметь в виду, что это поток энергии. Какие у этого потока свойства?
Сила тока – на самом деле это никакая не «сила», а просто количество электрического заряда. Чем больше заряда прошло через провод за 1 секунду, тем больше там ампер.
Напряжение – количество энергии, «закачанной» в единицу заряда. 1 Ампер на 100 Вольтах перенесёт в сто раз больше энергии, чем 1 Ампер на 1 Вольте и, соответственно, выполнит в 100 раз больше полезной работы.
Ну а мощность это количество энергии, прошедшей через провод за 1 секунду и найти её проще простого, нужно силу тока (количество единиц заряда) умножить на напряжение (количество энергии в единице заряда). Как видите, всё просто – если разобраться в вопросе не по учебникам, а «по факту». Теперь поговорим про то, как посчитать трёхфазную мощность – там немного сложнее, но тоже элементарно, если не усложнять.
Три фазы – в чём хитрость?
Трёхфазная линия это не просто три независимые фазы, проложенные совместно: каждая из этих фаз взаимодействует как с нулём, так и с другими двумя фазами. Но вам не нужно ломать над этим голову: просто запомните, что мощность трёхфазного тока равна мощностям каждой отдельной фазы, сложенным вместе.
Например, если по каждой фазе проходит 10 Ампер, то мощность на одной фазе получится 10 х 230 = 2300 Ватт, а на трёх фазах – 2300 Вт х 3 = 6900 Вт. Всё просто. Есть формулы, где берётся не 230, а 380 Вольт и дополнительно умножается на 1,73 (корень из 3), но в итоге получается то же самое – поэтому усложнять незачем.
Амперы из Киловатт – просто!
Само собой, чтобы посчитать не мощность из ампер, а наоборот – нужно мощность разделить на напряжение. Например, чтобы узнать, сколько ампер потребляет электрочайник на 2 кВт, нужно его мощность 2000 Вт разделить на напряжение сети 230 Вольт – 2000/230 = 8,7 Ампера. Так вы поймёте, какой провод подойдёт для питания чайника – не меньше 1,5 квадрат по меди.
Спасибо, что дочитали – если в первого раза не вся информация уложилась у вас в голове – не стесняйтесь перечитать заново – это нормально и обязательно вам пригодится! Ставьте лайк и подписывайтесь!