Как найти эдс амплитуды

Для определения амплитуды ЭДС источника, запитывающего последовательный контур, нужно воспользоваться формулой для напряжения на конденсаторе при резонансе:

Uc = U0 / (2Q),

где Uc – амплитуда напряжения на емкости, U0 – амплитуда ЭДС источника, Q – добротность контура.

Добротность контура можно найти по формуле:

Q = XL / R,

где XL – индуктивность катушки, равная ее реактивному сопротивлению на резонансной частоте, R – суммарное сопротивление контура, включающее характеристическое сопротивление и сопротивление потерь.

Индуктивность катушки можно выразить через ее реактивное сопротивление на резонансной частоте по формуле:

XL = Q * R.

Таким образом, имеем систему уравнений:

XL = Q * R
Q = XL / R
Uc = U0 / (2Q)

Подставляем известные значения:

R = 100 Ом
Rp = 1 Ом
Uc = 5 В

XL = (R – Rp) = 99 Ом
Q = XL / R = 0.99
U0 = 2Q * Uc = 9.9 В

Таким образом, амплитуда ЭДС источника, запитывающего последовательный контур, равна 9.9 В.

3.1 Основные величины, характеризующие синусоидальные ток, напряжение и эдс

Этими основными
величинами являются:

• мгновенное
  значение;

• амплитудное
  значение;

• начальная фаза;

• действующее
  значение;

• среднее значение;

• комплекс
  действующего или амплитудного значения
  и др.

3.1.1
Мгновенное значение.
Мгновенное значение величины а
показывает
закон ее изменения и записывается в
виде:

(3.1)

где
–
амплитуда (максимальное значение)
величины;

–
угловая частота,
рад/с;

_t
–
текущее значение времени, с;

–начальная фаза.

Мгновенные
значения тока i,
напряжения
и
или
ЭДС е
записываются
в
виде:

(3.2)

(3.3)

(3.4)

Аргумент
синуса

называется
фазой.
Угол


равен
фазе в начальный
момент времени t
=
0 и поэтому называется начальной
фазой.

Угловая
частота


связана
с периодом T
и частотой f
=1/T

формулами:

или

(3.5)

Частота
f,
равная числу колебаний в 1с, измеряется
в герцах (Гц). При f
=50
Гц имеем
=
314 рад/с.

С учетом (3.5) формула
(3.1) может иметь вид:

(3.6)

На
рисунке 3.1 изображены графики синусоидальных
токов одинаковой
частоты, но с различными амплитудами и
начальными фазами:

По
оси абсцисс отложено время t
и
величина,
пропорциональнаявремени
и измеряемая в радианах.

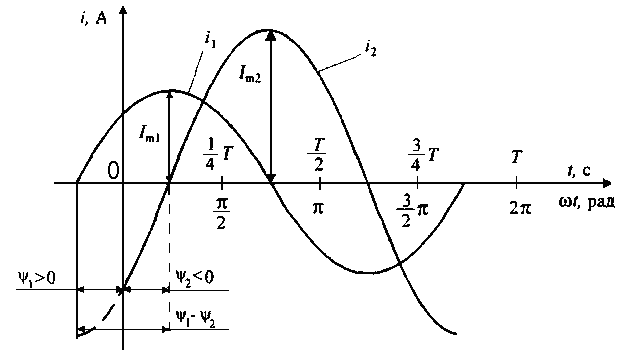
Рис.
3.1. График синусоидальных токов одинаковой
частоты, но

с
различными амплитудами и начальными
фазами

Начальный
фазный угол отсчитывается от начала
синусоиды, т.е. от момента перехода
синусоиды от отрицательных к положительным
значениям
до момента времени t
=
0 (начало
координат). При
начало
синусоиды сдвинуто
влево, а
при–
вправо
от
начала координат.

Если
у нескольких синусоидальных функций,
изменяющихся с одинаковой частотой,
начала синусоид не совпадают, то говорят,
что они сдвинуты
друг относительно друга по фазе.

Сдвиг
фаз измеряется их разностью, которая
равна разности начальных
фаз. На рисунке 3.1,
т.е. ток i₁
опережает по фазе ток i₂
на
угол

или, что то же самое, ток
i₂
отстает
по фазе от тока
i₁
на
угол

.

Если
у синусоидальных функций одной частоты
одинаковые начальные
фазы, то говорят, что они совпадают
по фазе; если
разность их фаз равна
то говорят, что онипротивоположны
по фазе (в
противофазе). И
если разность их фаз равна

то говорят, что они находятся
в квадратуре.

Наибольшее
распространение в электротехнике
получил синусоидальный ток частотой
50 Гц, которая принята за стандартную. В
США, например, стандартной
является частота
f
=
60
Гц.

Диапазон
частот, применяемых на практике
синусоидальных токов и напряжений,
очень широк: от долей герца, например,
в геологоразведке, до десятков
тысяч мегагерц (МГц) в радиолокации.

Синусоидальные
токи и напряжения низких частот (до
нескольких килогерц) получают с помощью
синхронных
генераторов, в
которых используется
принцип получения синусоидального
напряжения путем вращения
витка с постоянной угловой скоростью
в однородном магнитном поле.
Этот принцип основан на явлении
электромагнитной индукции, открытом в
1831 году М. Фарадеем. Синусоидальные токи
и напряжения высоких
частот (ВЧ) получают с помощью ламповых
или полупроводниковых
генераторов.

Источники
синусоидальной ЭДС (источники
синусоидального напряжения)
показывают на схемах с помощью условных
обозначений (рис.
3.2,а, б) или только указывают напряжение
между зажимами источника
(рис. 3.2,в), т.к. в большинстве случаев
принимают источники идеальными
и ввиду равенства нулю их внутреннего
сопротивления имеем e
= u,
Ė = Ů
и
т.д.

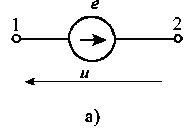
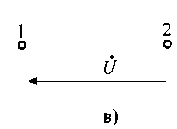
Рис.
3.2. Условные обозначения идеальных
источников ЭДС

3.1.2
Действующее и среднее значения
синусоидальных токов и напряжений.
Согласно закону Джоуля–Ленца, тепловая
энергия Q,
выделяемая
в резисторе с сопротивлением R
при
протекании по нему постоянного тока
I₀
в течение промежутка времени t,
равна:

(3.7)

Для
синусоидального тока формулу (3.7) можно
применить лишь для определения
тепловой энергии dQ,
выделившейся в резисторе с сопротивлением
R
за
бесконечно малый промежуток времени
dt,
в течение которого силу тока
_i
можно
считать не изменяющейся:

(3.8)

За
период времени Т
выделившаяся энергия равна:

(3.9)

Пусть

,
тогда:

.

Введем
величину

,
называемуюдействующим
значением синусоидального
тока, и,
подставив ее в последнее выражение,
получим:

(3.10)

Сопоставив
формулу (3.10), полученную для синусоидального
тока, с
формулой (3.7), справедливой для постоянного
тока, делаем вывод: Действующее
значение синусоидального тока равно
такому значению постоянного
тока, который за один период выделяет
в том же резисторе такое
же количество тепла, как и синусоидальный
ток.

Аналогично
существуют понятия действующих значений
синусоидальных
напряжений и ЭДС:

и

(3.11)

Из формул (3.9) и
(3.10) получаем:

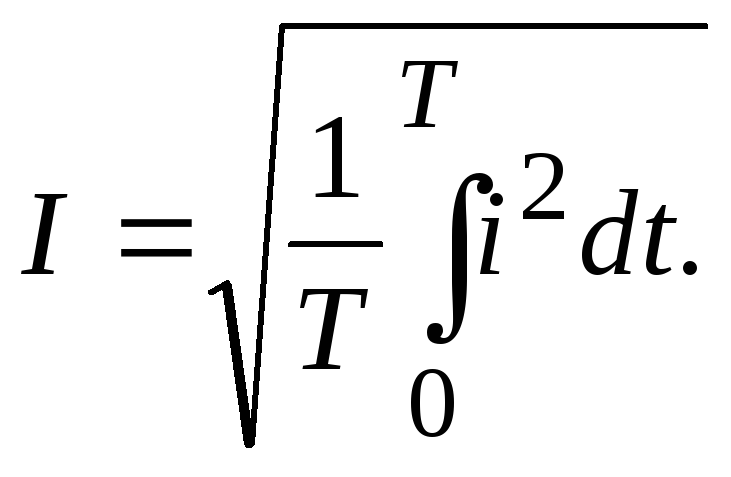(3.12)

В
силу (3.12) действующее значение
синусоидального тока часто называют
среднеквадратичным
или эффективным
значениями.

Действующие
значения токов и напряжений показывают
большинство электроизмерительных
приборов (амперметров, вольтметров).

В
действующих значениях указываются
номинальные токи и напряжения в паспортах
различных электроприборов и устройств.

Под
средним
значением
синусоидального тока понимают его
среднее значение
за полупериод:

(3.13)

т.е.
среднее значение синусоидального тока
составляет

от
амплитудного
значения. Аналогично,

3.1.3
Изображение синусоидальных токов,
напряжений и ЭДС комплексными
числами и векторами.
Синусоидально изменяющийся ток i
изображается комплексным числом:

(3.14)

Принято
изображение тока находить для момента
времени t
=
0:

(3.15)

Величину

называют
комплексной
амплитудой тока
или комплексом
амплитуды тока.

Под
комплексом действующего значения тока
или
под комплексом тока
понимают
частное от деления комплексной амплитуды
тока на
:

(3.16)

Под
комплексами напряжения и ЭДС понимают
подобные выражения

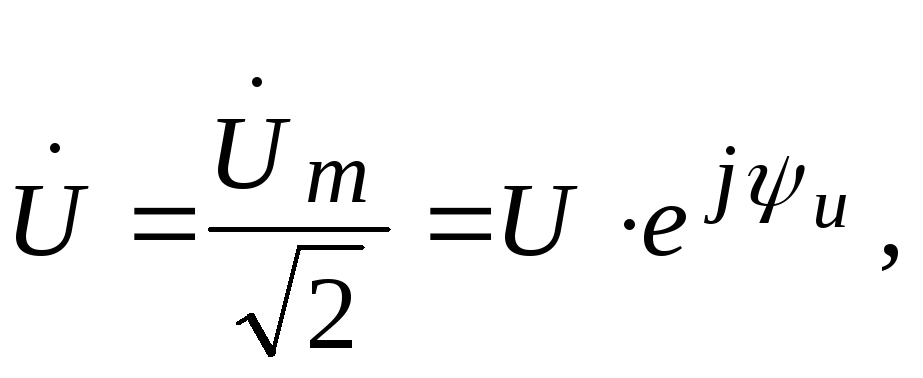
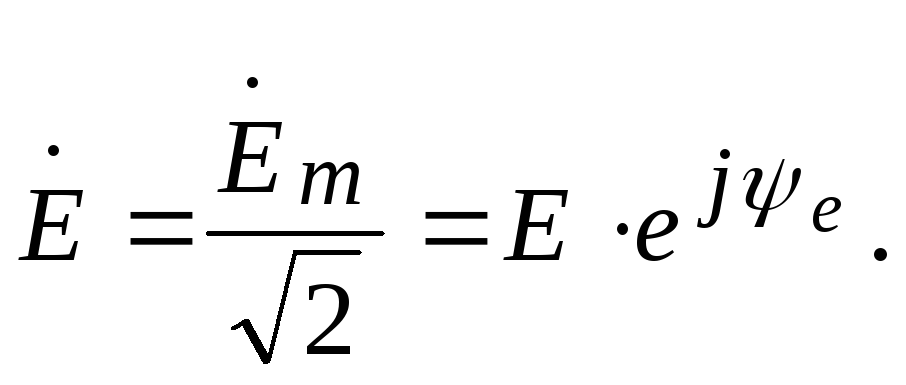
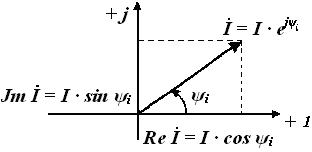
Рис.
3.3. Изображение синусоидального тока
на комплексной плоскости
вектором

Комплексы
тока, напряжения и ЭДС изображаются
также на комплексной
плоскости векторами. Например, на рисунке
3.3 изображен вектор
.
При этом угол


отсчитывается
от оси +1
против
часовой стрелки, если

.
Из рисунка 3.3 следует, что комплекс тока


(так же, как комплекс
напряжения и ЭДС) можно представить

а)
вектором

;

б)
комплексным числом в показательной,
алгебраической и тригонометрической
формах:

(3.17)

Пример
3.1
Ток

.
Записать выражение для комплексной
амплитуды этого тока.

Решение.
В
данном случае


Следовательно,

Пример
3.2
Комплексная
амплитуда тока
.
Записать выражение
для мгновенного значения этого тока.

Решение.
Для
перехода от комплексной амплитуды к
мгновенному значению
надо умножить

на


и
взять коэффициент при мнимой части
от полученного произведения:

Пример
3.3 Записать
выражение комплекса действующего
значения тока для примера 3.1.

Решение.

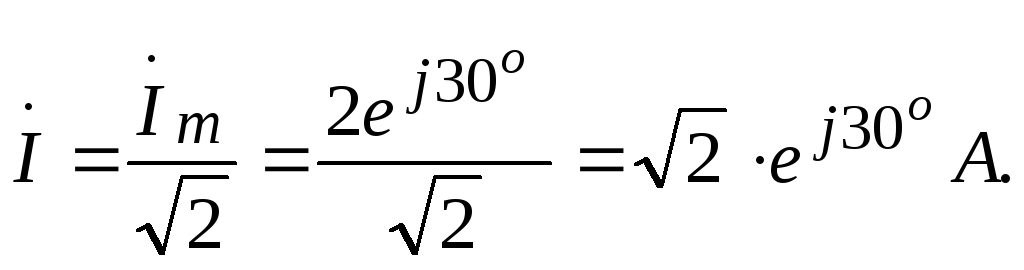
Соседние файлы в предмете Теоретические основы электротехники

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

  02.05.20141.14 Mб47Примеры решения задач – Линейные цепи. Автоматизированный метод рассчета.mcd

• #

Ранее мы познакомились с постоянным электрическим током — направленным движением зарядов, для которого сила тока постоянна. В случае, если значение силы тока непостоянно, тогда ток будем называть переменным.

Для школьной физики переменный ток рассматривается в двух, в общем-то, похожих случаях:

• вынужденные колебания (на вход цепи подаётся внешняя разность потенциалов/ток, которые изменяются гармонически).
• колебания в LC (состоящем из катушек индуктивности и конденсаторов) или LCR (состоящем их катушек индуктивности, конденсаторов и сопротивлений) контурах.

Рассмотрение свободных колебаний в случае переменного тока аналогично постоянному. Точно так же существует закон Ома для цепи переменного тока, рассчитываются мощности и энергии (работы) для такого случая.

Для школы характерно описание переменного тока через гармонические законы. Переменными параметрами в цепи могут быть ЭДС (), напряжение на элементе (), сила тока (), заряд конденсатора (). Рассмотрим ЭДС источника гармонический колебаний:

(1)

• где

Аналогичным образом можно ввести колебания напряжения  на элементе:

(2)

• где

Таким же образом вводится и колебание силы тока:

(3)

• где

И, аналогично, заряд на конденсаторе:

(4)

• где

Важно: нужно помнить, что тригонометрически можно превратить синус в косинус:

(5)

• где
  • — новая начальная фаза колебания.

Вывод: таким образом, рассмотрение переменного тока в случае формульных задач, связанных с соотношениями (1) — (4), касается анализа сомножителей и слагаемых, входящих в само соотношение.

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.