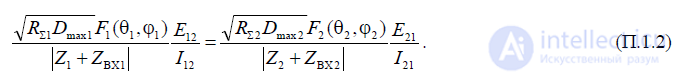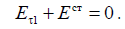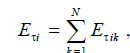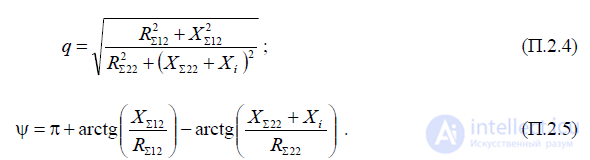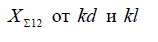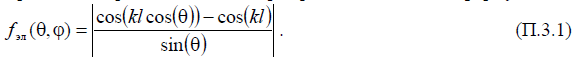Как найти эдс антенны

Процесс приема заключается в преобразовании
радиоволн, принятых антенной, в
направляемые волны фидерного тракта,
поступающие затем на вход приемника.
Следует подчеркнуть, что как бы тщательно
не конструировались антенна, фидерный
тракт и приемное устройство, падающая
на антенну мощность не может полностью
поступить в приемник, поскольку часть
ее рассеивается в окружающем пространстве.
Способ отбора энергии от антенны в
приемник зависит от ее конструктивных
особенностей и диапазона частот. Он
может быть электрическим, если фидер
включен в разрыв проводника с протекающим
по нему электрическим током (например,
вибраторные антенны); магнитным, если
используются щели; и электромагнитным
– при использовании волноводов.

Эквивалентная
схема приемной антенны приведена на
рис. 5.6. На схеме: Z_А=R_А
+ iX_А
– внутреннее сопротивление антенны;
Z_ПР
– сопротивление

Рис. 5.6 Эквивалентная схема цепи приемной
антенны

приемника.
Сопротивление R_А
характеризует
принятую антенной активную мощность и
мощность суммарных потерь в антенне, а
мнимая часть (X_А
) связана с реактивной мощностью.
Внутреннее сопротивление антенны
определяется только ее конструкцией.
По отношению к приемнику антенна является
генератором с сопротивлением Z_А
и ЭДС
,
которая определяется напряженностью
поля и поляризацией падающей волны в
месте расположения приемной антенны.
Комплексная амплитуда тока в цепи равна

(5.25)

Отсюда
видно, что при фиксированной ЭДС мощность,
выделяемая в приемнике, будет зависеть
как от сопротивления антенны, так и от
сопротивления приемника.

ЭДС,
возбуждаемая в приемной антенне, через
напряженность электрического поля Е
действующей
на антенну волны определяется по формуле
Неймана

,
(5.26)

где

– угол
между плоскостями поляризации приемной
антенны и передающей (или пришедшей
волны).

Максимальное значение эдс достигается при условии

(5.27)

т.е.
когда плоскости поляризации приемной
антенны и пришедшей волны совпадают и
антенна максимумом ДН сориентирована
в направлении прихода волны. С учетом
(5.24) для линейных антенн вместо (5.26)
можно также записать

.
(5.28)

На основании
принципа взаимности можно показать,
что основные параметры антенны в
передающем режиме также характеризуют
антенну и в режиме приема. Для одной и
той же антенны справедливо следующее:

• нормированные
  диаграммы направленности в режиме
  приема и передачи одинаковы;

• входное
  сопротивление в режиме передачи равно
  ее внутреннему сопротивлению в режиме
  приема Z_вх=Z_А;

• эффективная
  длина антенны в режиме приема равна
  эффективной длине антенны в режиме
  передачи.

Так
как КНД, КПД, КУ и другие параметры
антенны однозначно определяются через
перечисленные выше характеристики, то
они также одинаковы при работе антенны
в режимах приема и передачи. Однако у
приемной антенны есть и свои специфические
параметры. Один из них называется шумовой
температурой Т_А,
а другой –
эффективной площадью приемной антенны
S_эф
(,
).

Эффективная
площадь

Эффективная
площадь
антенны
S_эф(,)
– это параметр, имеющий размерность
площади и связывающий между собой
величину радиальной составляющей
вектора Пойнтинга приходящей волны и
мощность
Р_ПР,
выделяемую в согласованной нагрузке
(приемнике) антенны,

.
(5.29)

Эффективная площадь антенны через
диаграмму направленности зависит от
направления приема и угла между
плоскостями поляризации приходящей
волны и приемной антенны. Эта зависимость
выражается формулой

,
(5.30)

где
S_эф
– значение в
направлении максимума диаграммы
направленности и при условии согласования
по поляризации (
= 0). При
проектировании антенн полезна формула,
связывающая S_эф
и КНД в
направлении максимума диаграммы
направленности,

.
(5.31)

На
основании этих формул можно дать такое
определение: S_эф
– это поверхность
фронта плоской электромагнитной волны,
с которой антенна «собирает» и передает
в согласованную нагрузку принимаемую
мощность с направления максимума ДН и
при полном совпадении поляризации
падающей волны и приемной антенны и
при отсутствии в антенне потерь. Иногда
в S_эф

включают
потери и тогда правую часть (5.31) необходимо
умножить на КПД.

Для
апертурных антенн эффективная площадь
связана с размерами раскрыва и не
превышает геометрической площади
раскрыва.

Для
линейных антенн эффективная площадь
вводится формально и пропорциональна
квадрату эффективной длины антенны

,
(5.32)

где
w
– волновое
сопротивление среды.

Для апертурных антенн вводят также
коэффициент использования поверхности
апертуры (КИП)

,
(5.33)

где
S
– геометрическая
площадь раскрыва.

Коэффициент
использования поверхности зависит от
амплитудно-фазового распределения поля
в апертуре антенны и обычно меньше
единицы. Только для синфазного
равно-амплитудного распределения 
= 1.

Шумовая
температура

Шумы
в диапазоне СВЧ могут создаваться как
техногенными источниками, так и
переотражениями от поверхности земли
и окружающих предметов, а также источниками
внеземного происхождения. Это –
прежде всего радиоизлучение Солнца,
других звезд и галактик. Абсолютный
уровень этих помех, как правило, очень
мал. Поэтому имеет смысл увеличивать
чувствительность приемника, снижая
уровень его собственных шумов.
Чувствительность СВЧ приемника может
быть доведена до 10^–18
… 10^–20
Вт.
При столь высокой чувствительности
заметную роль начинают играть помехи,
вызванные тепловым движением электронов
в АФУ, или внутренний шум АФУ.

Поскольку
как внутренние, так и внешние шумы по
своему воздействию эквивалентны, принято
их суммарное действие оценивать с
помощью единого параметра, называемого
шумовой температурой антенны T_A
и выражаемого
в градусах Кельвина (К).
Шумовая температура приписывается
внутреннему сопротивлению антенны R_A
и позволяет
подводимую к согласованному с ней
приемнику мощность шумов P_ША
в некоторой
полосе частот f
оценивать по формуле

где

–
постоянная Больцмана.

Тем
самым мы осуществляем замену всех шумов
тепловыми шумами внутреннего сопротивления
антенны.

Шумовую
температуру антенны T_A
можно представить
в виде

,
(5.34)

где
Т_АТ
–
температура
за счет флуктуационных тепловых шумов,

Т_А
–
температура
шумового излучения внешних источников.

Для
Т_АТ
известна простая формула

,
(5.35)

где
Т₀
–
температура
окружающей среды в градусах Кельвина.

Таким
образом, шумовая температура антенны
Т_АТ
зависит от КПД антенно-фидерного
тракта, температуры окружающей среды
и не зависят от характеристик излучения
антенны. С ростом КПД эти шумы уменьшаются.

Для

известно выражение

,
(5.36)

где

–
яркостная температура источников шумов,
не связанных с антенной.

Заметный
вклад в Т_Я
могут вносить
источники внеземного происхождения.
Их вклад для различных геофизических
условий (географических координат точек
на поверхности Земли, времен года и
суток, состояния солнечной активности)
определяется радиоастрономическими
методами. Для уменьшения
,
уменьшают потери в антенне, снижают
уровень задних и боковых лепестков ДН.

Энергетические соотношения в цепи
приемной антенны

На
низких частотах антенны с фидерным
трактом соединяются посредством
электрического контакта. Приемники
имеют высокое входное сопротивление,
а сопротивление антенны обычно мало.
Поэтому чувствительность АФУ определяется
минимально необходимым значением
амплитуды напряженности электрического
поля E_min
в пункте
приема, а приемника – минимальным
напряжением U_min
на
его входе. Протяженность фидерного
тракта по сравнению с длиной волны мала,
поэтому можно считать, что приемник
непосредственно соединен с антенной.
Тогда

.
(5.37)

Из
этой формулы следует, что на низких
частотах для увеличения напряжения U
на входе
приемника необходимо антенну сориентировать
максимумом ДН в направлении прихода
волны и совместить их плоскости
поляризации. Тогда
.
Для дальнейшего повышенияU
на
входе приемника необходимо в антенне
реализовывать синфазное равноамплитудное
распределение тока и увеличивать ее
геометрическую длину. Согласование
антенны с приемником и потери в ней
можно не учитывать.

В
диапазоне СВЧ в связи с особенностями
антенн и фидерных трактов регистрируемой
величиной является принимаемая мощность,
а не напряжение. Как и на низких частотах,
для увеличения поступающей на вход
приемника мощности необходимо антенну
сориентировать максимумом ДН в направлении
прихода волны и совместить их плоскости
поляризации.

Сначала
рассмотрим случай, когда приемник
подключен непосредственно к антенне,
т.е. фидер учитывать не будем. Принимаемая
приемником мощность равна

(5.38)

или с учетом (5.25)

.
(5.39)

Если
антенна согласована с приемником (R_ПР=R_А
, X_ПР=
–X_А)
и не имеет потерь (R_А=R_
),
то величину

(5.40)

называют
максимальной мощностью, поступающей
на вход приемника. При работе в
несогласованном режиме, подставив
(5.40) в (5.39), получим

.
(5.41)

Отношение

(5.42)

Сразу хочу сказать, что здесь никакой воды про теория приемных антенн, и только нужная информация. Для того чтобы лучше понимать что такое
теория приемных антенн, Приемная антенна , настоятельно рекомендую прочитать все из категории Устройства СВЧ и антенны.

Приемная антенна преобразует энергию радиоволн в энергии токов высокой частоты.

Она является, таким образом, маломощным генератором переменного тока,

нагрузкой которогослужит входное сопротивление приемника.

При рассмотрении приемной антеннынас будут интересовать следующие вопросы:

• каковы будут величины ЭДС и тока в приемной антенне при заданной напряженности полярадиоволн, падающих на антенну;
• как зависят эти величины от направления прихода и поляризации падающей на антенну волны;
• какова величина сопротивления приемной антенны,играющего роль внутреннего сопротивления генератора;
• какова величина мощности, отдаваемой приемной антенной приемнику.

Исследование приемной антенны можно производить двумя различными методами. Первый из них состоит в

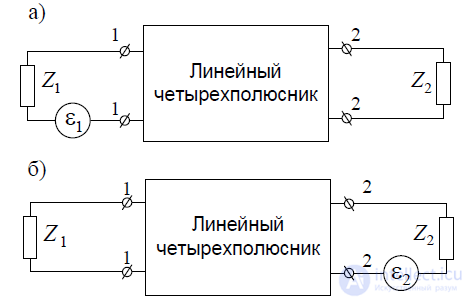
непосредственном анализе воздействия приходящей волны на приемнуюантенну (рис. П.1.1).

В частности, в случае проволочной антенны поступают следующим образом. Антенну мысленно разбивают

на элементарные вибраторы и находят ЭДС, наводимую вкаждом элементарном вибраторе. Суммируя эти

ЭДС по всем элементам антенны, определяют ЭДС на клеммах ее. Зная ЭДС, можно определить ток на входе приемникаи другие параметры приемной антенны.

Рис. П.1.1 — Симметричныйвибратор в поле действия плоскойволны

Поле, создающее ЭДС на элементарном излучателе d z определяется соотношение

Элементарная ЭДС .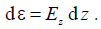

В общем случае для произвольной антенны этот метод оказывается весьма сложным. Поэтому, как правило, пользуются вторым методом, основанным на применении известного из теориипассивных линейных четырехполюсников принципа взаимности. Принцип взаимности позволяет определить свойства и параметры приемной антенны, если известны свойства и параметры этойже антенны при работе ее в качестве передающей. Справедливость принципа взаимности для антенн была доказана в 1927 г. М. П. Свешниковой. На основе этого принципа М. С. Нейманом в1935 г. была разработана
теория приемных антенн .

Теорема взаимности. Рассмотрим две произвольные и произвольно ориентированные в пространстве антенны А1 и А2 (рис. П.1.2). Промежуточная среда считается линейной(характеристики ее не зависят от величины напряженности поля) и изотропной.

Следовательно, исключаются случаи распространения радиоволн в ионосфере или какой-нибудь другойанизотропной среде (например, в феррите).

Рис. П.1.2 — Взаимное расположение передающейи приемной антенн Как было доказано М. П. Свешниковой,

систему из двух антенн можно рассматривать каклинейный пассивный четырехполюсник с зажимами 1—1 и 2—12.

Рис. П.1.3 — Модели линейных четырехполюсников

Рассмотрим токи на входе и выходе такого четырехполюсника для двух случаев. Первый случай, когда А1 — передающая антенна; А2 — приемная (рис. П.1.3, а). На входе и выходевключены дополнительные сопротивления Z1 и Z2, которые можно рассматривать как внутреннее сопротивление источника ЭДС и сопротивление нагрузки (входное сопротивление приемника)соответственно. Пусть в этом случае при ЭДС 1 ток на выходе четырехполюсника (ток в нагрузке) будет I21. Второй случай, когда А2 — передающая антенна; А1 — приемная (рис. П.1.3, б).Величину ЭДС в этом случае положим равной 2 и ток на входныхзажимах приемнойантенныбудет составлять I112.

Принцип взаимности утверждает, что для амплитуд токов и ЭДС имеем

Это соотношение и будет использовано далее для нахождения амплитуд тока и ЭДС в приемной антенне.

Дальнейшее рассмотрение проводится для антенн с линейной поляризацией поля. Считаем известными параметры обеих антенн в режиме передачи

Так как мы хотим найти ток в приемной антенне в зависимости от величины поля, падающего на антенну, то необходимо выразить ЭДС 1 и 2 через параметры антенны при работе их напередачу и поля, создаваемые этими антеннами. Полагаем, что антенны находятсявдальней зоне друготносительно друга. Расстояние между ними — r .

Амплитуда поля, возбуждаемого антенной А1 возле антенны А2

Соберем все, что относится к антенне А1, влево, а к антенне А2 — вправо, тогда получим

Левая часть выражения (П.1.2) зависит лишь от параметров первой антенны. Величина

E12 зависит, конечно, от параметров второй антенны, но отношение E12 к вызванному ею же току в первой антенне I12

зависит лишь от параметров первой антенны.

Таким образом, в (П.1.2)слева и справа стоят две независимые величины. Левая часть зависит от параметров первой антенны,

правая — от параметров второй антенны. Это дает основание заключить,

что каждая из этихвеличин порознь равна одной и той же постоянной, которую мы обозначимбуквой N.

Таким образом, для произвольной антенны

Полученное соотношение (П.1.3), по существу, и содержит в себе искомые связи между параметрами антенны в двух режимах.

Для амплитуды тока приемной антеннывобщем случае получим

— угол между плоскостями поляризации приемной антенны и приходящей волны. Заметим, что плоскостью поляризацииприемной антенны называется плоскость поляризации поля, излучаемого этой антенной в режимепередачи. Соотношение (П.1.3) показывает, что приемную антенну можнорассматривать как генераторс ЭДС

и внутренним сопротивлением, равным входному сопротивлению этой антенны в режиме передачи.

Если внутреннее сопротивление этого генератора назвать входным сопротивлением антенны в режиме приема, то ZBX в режиме приема и передачи совпадают.

Диаграмма направленности приемной антенны — зависимость амплитуды ЭДС (или тока) в приемной антенне от углов и , характеризующих направление прихода плоскойэлектромагнитной волны, при постоянной величине напряженности поля в месте приема . Об этом говорит сайт https://intellect.icu . Нормированные ДН антенн в режиме приема и передачи совпадают. Фазовые ДН антенны в обоихрежимах также совпадают. Заметим, что совпадение параметров антенны в

режиме передачи и приема имеет место при условии, что приемник и передатчик подключаются к антенне одинаковым образом.

Можно показать, что мощность отдаваемая приемной антенной в нагрузку будет составлять

— коэффициент усиления приемной антенны.

Как видно из (П.1.6), чембольше направленность антенны,

тем большую мощность она извлекает из поля. В выражении (П.1.6) первый множитель представляет собой плотность потока

2

мощности 5 в точке приема. Второй множитель 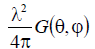имеет размерность площади и

4 называется эффективной или действующей площадью антенны SФ . Тогда значение коэффициента усиления приемной антенны можноопределить по формуле

где — геометрическая площадь антенны;  — коэффициент использования поверхности.

Эффективная площадь представляет собою такую площадку, которая, будучи умноженной на плотность потока мощности приходящей волны, дает мощность, отдаваемую антеннойсогласованной нагрузке при условии, что поляризации антенны и падающей волны совпадают

Соотношение (П.1.7) является одним из важнейших в теории антенн. Оно связывает эффективную площадь — параметр, удобный в режиме приема, с коэффициентом усиления

— параметром, использование которого естественно в режиме передачи. Соотношение (П.1.7) пригодно для антеннылюбой конструкции безвсяких ограничений.

Обычно наряду с (П.1.7) используют и другоесоотношение 4SФ

Для большинства антенн УКВ-диапазона потери малы, т. е. . При этом значения SФ , определенные согласно(П.1.7) и (П.1.8), практически совпадают. Совпадают и соответствующиезначения КИП.

Определения.

Коэффициент направленного действия приемной антенны в направлении , называется отношение мощности, поступающей на вход приемника при приеме с направления, к среднему, при приеме по всем направлениям, значению мощности, поступающей на вход приемника.

Коэффициент направленного действия приемной антенны называется отношение мощности, поступающей на вход приемника при приеме на данной антенне, к мощности,поступающей на вход приемника при приеме на ненаправленной антенне. При этом предполагается, что данная антенна и ненаправленная антенна согласованы с приемником и обе антенныимеютКПДравный единице.

Коэффициентом усиления приемной антенны называется отношение мощности, поступающей на вход приемника при приеме на данной антенне, к мощности, поступающей на входприемника при приеме на ненаправленной антенне. При этом предполагается, что данная антенна и ненаправленная антенна согласованы с приемником и что ненаправленная антенна имеетКПД, равный единице.

Приложение 2. Методнаводимых ЭДС

Метод наведенных ЭДС был предложен Бриллуеном и Д. А. Рожанским разработан И. Г. Кляцкиным, А. А. Пистолькорсом, В. В. Татариновым и др. Этот метод может быть развит иприменительно к щелевым вибраторам (метод, наведенных МДС).

Метод наведенных ЭДС и вытекающие из него соотношения широко известны и изложены во многих монографиях. Сущность метода наведенных ЭДС заключается в следующем. Пустьимеем электрический вибратор, к которому приложена некоторая ЭДС. Под влиянием этой ЭДС в вибраторе возникает ток. Ток распределяется таким образом, что на поверхности вибраторавыполняются граничные условия, а именно условия равенства нулю тангенциальной составляющей вектора Е. Мощность излучения симметричного вибратора определяется выражением

Рассмотрим систему излучателей (рис. П.2.1).

Рис. П.2.1 — Модельвзаимного размещенияизлучателей

Граничное условие для первого излучателя

При наличии N излучающих элементов касательная составляющая для i-го элемента определяется по формуле

где Eik — тангенциальная составляющая вблизи i-го элемента, обусловленная полем k-го

элемента. После преобразований получим для мощности излучения следующее выражение

Тогда сопротивление излучения i-го элемента будет определятьсяпо формуле

Интеграл можно определить как некоторое вносимое сопротивление, тогда результирующая формуладля сопротивления излучения i-го элемента имеетвид

Сопротивление излучения i-го элемента определяется, как сумма произведений

отношения токов k-го элемента к рассматриваемому i-му элементу на вносимое
сопротивление

Полное сопротивление излучения для системы излучателей имеет вид

Рассмотрим пример двухэлементной антенной решетки (рис. П.2.2).

Рис. П.2.2 — Система двухактивных излучателей: а) модельвзаимного размещения излучателей; б) эквивалентная схема

Для эквивалентной схемы, приведенной на рис. П.2.2, б, тока на первом и втором излучателях будут определятьсяв ыражениями:

Рассмотрим систему двух излучателей, один из которых активный, а другой — пассивный инагруженна некоторое сопротивление (рис. П.2.3)

а) б) Рис. П.2.3 — Система двух излучателей: а) модельвзаимного размещенияизлучателей; б) эквивалентная схема Определить амплитуды ифазы токов в вибраторах системы излучателей, представленных на рис. П.2.3, а можно на основании эквивалентной схемы, изображенной на рисунке П.2.3,б, где введеныследующие обозначения:  — возбуждающая ЭДС; Z ,

a 11

Z , Z , Z — собственные и взаимные сопротивления излучения активного и

22 12 21

пассивного вибраторов; Zí — сопротивление нагрузки. В общем случае , а для

исследуемой антенны также 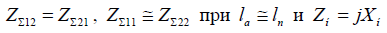. Тогда отношение

амплитуд и разность фаз токов в пассивном и активном вибраторах можно вычислить по следующим формулам:

Амплитуда и фаза тока в пассивном вибраторе определяются его расстоянием до активного вибратора и настройкой, которая осуществляется изменением длины плеча вибратора.

Результирующие значения для активной и реактивной составляющей сопротивления излучения активного и пассивного излучателей определяются формулами:

Коэффициента направленного действия D можно вычислить по следующему выражению

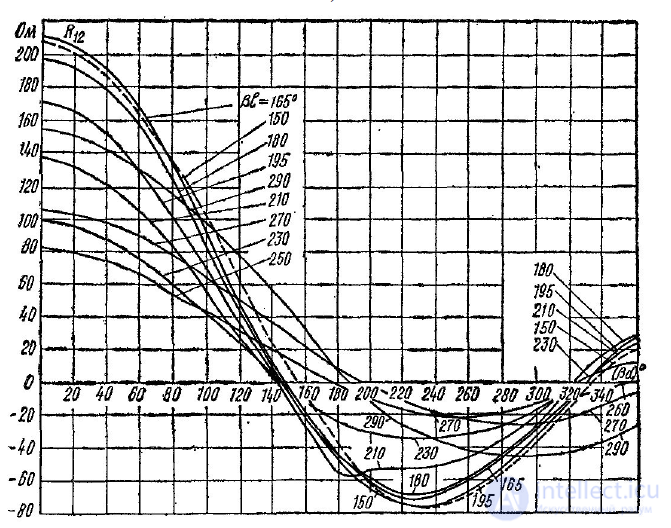
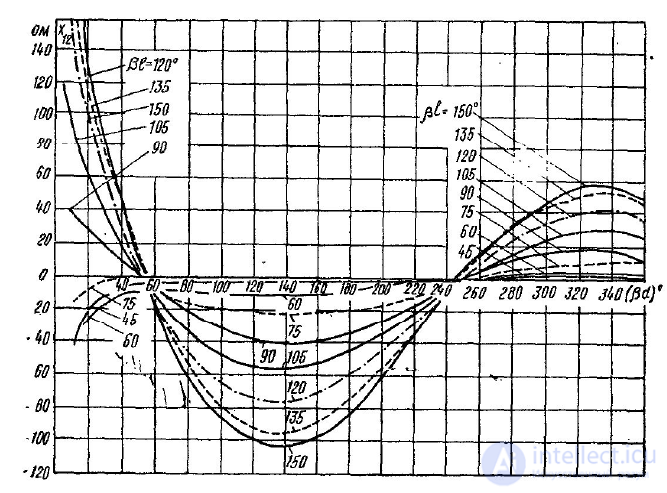
Для определения R12 и Х12 можно использовать графики, приведенные на рис. П.2.4,

П.2.10.

а)

б) Рис. П.2.4 — Зависимость

а)

б)

Рис. П.2.5 — Зависимость

Приложение 3. Анализ диаграммы направленности двухэлементной решетки симметричных вибраторов

Рассмотрим двухэлементную решетку симметричных вибраторов, расположенных на оси ОY, как показано на рис. П.3.1. Пусть 1-йи 2-й излучатели расположены вдоль оси ОY. Системаотсчета угловтакже указана на рис. П.3.1.

Рис. П.3.1 — Схема размещенияизлучателей в решетке

Рассмотрим двухэлементную решетку излучателей, расположенных параллельно вдоль оси ОY, тогда согласно теореме умножения результирующая диаграмма направленности будет определяться выражениями:

В случае размещения излучателей параллельно оси OZ (рис. П.3.1), результирующая диаграмма направленности двухэлементной решетки будет определяться выражениями:

В случае размещения излучателей параллельно оси OХ (рис. П.3.1), результирующая диаграмма направленности двухэлементной решетки будет определяться выражениями:

В качестве примера рассмотрим случай размещения излучателей параллельно оси OZ. В проекции на плоскость YOZ схемаразмещения будет выглядеть, как показано на рис. П.3.2.

Рис. П.3.2 — Проекция решетки излучателей на плоскость YOZ

На входы соответствующих симметричных вибраторов подводятся токи и

.

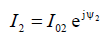
Поле излучения каждого из симметричных вибраторов, представленных на рис. П.3.2, характеризуется диаграммой направленности, которая

рассчитывается по формуле

Надо отметить, что при размещении излучателей в плоскости YOХ диаграмма направленности в указанной на рис. П.3.2 системе отсчета углов определяется поформуле

Рассмотрим несколько примеров для двух излучателей, размещенных, как показано на рис. П.3.2, когда на их входыподаютсяразличные по фазетоки.



Пусть тогда множитель решетки, диаграмма

направленности одного элемента и результирующая диаграмма направленности в плоскости YOZ будет выглядеть, как показано на рис. П.3.3, а.

Пусть 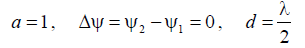тогда множитель решетки, диаграмма

направленности одного элемента и результирующая диаграмма направленности в плоскости YOZ будет выглядеть, как показано на рис. П.3.3, б.

Пусть тогда множитель решетки, диаграмма направленности одного элемента и результирующая диаграмма направленности в плоскости YOZ будет выглядеть,какпоказанона рис. П.3.3, в.

в) Рис. П.3.3 — Диаграмма направленности двухэлементной решетки симметричных вибраторов



Пусть 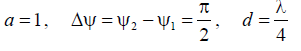тогда множитель решетки, диаграмма

направленности одного элемента и результирующая диаграмма направленности в плоскости YOZ будет выглядеть, какпоказанона рис. П.3.4, а.



Пусть a 1, 2 1  , d  тогда множитель решетки, диаграмма

22 направленности одного элемента и результирующая диаграмма направленности в плоскости YOZ будетвыглядеть, как показано на рис. П.3.4, б.



Пусть a 1, 2 1  , d  тогда множитель решетки, диаграмма

2 направленности одного элемента и результирующая диаграмма направленности в плоскости YOZ будетвыглядеть, как показано на рис. П.3.4, в.

в) Рис. П.3.4 — Диаграмма направленности двухэлементной решеткисимметричных вибраторов



Пусть a 1, 2 1 , d  тогда множитель решетки, диаграмма

4 направленности одного элемента и результирующая диаграмма направленности в плоскости YOZ будет выглядеть, какпоказанона рис. П.3.5, а.



Пусть a 1,   , d  тогда множитель решетки, диаграмма

21 2

направленности одного элемента и результирующая диаграмма направленности в плоскости YOZ будет выглядеть, какпоказанона рис. П.3.5, б.

Пусть a 1, 2 1 , d  тогда множитель решетки, диаграмма направленности одного элемента и результирующая диаграмма направленности в плоскости YOZ будетвыглядеть, какпоказанона рис. П.3.5, в.

в) Рис. П.3.5 — Диаграмма направленности двухэлементной решетки симметричных вибраторов

Таким образом, видно, что при 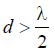диаграмма направленности антенной решетки

характеризуется наличием дифракционных максимумов. При антенная решетка характеризуется ненаправленным излучением.

Наибольшая направленность

излучения обеспечивается для случая , когда диаграмма направленности двухэлементной решетки имеет форму кардиоиды.

Статью про теория приемных антенн я написал специально для тебя. Если ты хотел бы внести свой вклад в развии теории и практики,
ты можешь написать коммент или статью отправив на мою почту в разделе контакты.
Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое теория приемных антенн, Приемная антенна
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Устройства СВЧ и антенны

Ответы на вопросы для самопроверки пишите в комментариях,
мы проверим, или же задавайте свой вопрос по данной теме.

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)