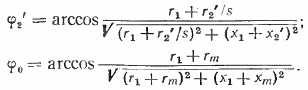Как найти эдс асинхронного двигателя

ПРАКТИЧЕСКАЯ РАБОТА №6

«Расчет ЭДС и токов асинхронных
двигателей»

ЦЕЛЬ РАБОТЫ: рассчитать значение скольжения, ЭДС асинхронного двигателя
и величину протекающих в нем  токов.   

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ:

В соответствии с принципом обратимости элек­трических
машин асинхронные машины могут работать как в двигательном, так и в генератор­ном
режимах. Кроме того, возможен еще и режим электромагнитного торможения
противовключением. 

Двигательный режим. При включении обмотки статора в сеть трех­фазного тока возникает
вращающееся магнитное поле, которое, сцепляясь с короткозамкнутой обмот­кой
ротора, наводит в ней ЭДС. При этом в стерж­нях обмотки ротора появляются токи.
В результате взаимодействия этих токов с вращаю­щимся магнитным полем на роторе
возникают элек­тромагнитные силы. Совокупность этих сил создает
электромагнитный вращающий момент, под дейст­вием которого ротор асинхронного
двигателя при­ходит во вращение с частотой n₂ < n₁ в сторону вра­щения поля статора. Если вал асинхронного
двигателя механически соединить с валом какого-либо исполнительного механизма
ИМ (станка, подъ­емного крана и т. п.), то вращающий момент двига­теля М,
преодолев противодействующий (нагрузоч­ный) момент М_нагр,
исполнительного механизма, приведет механизм во вращение. Следовательно,
электрическая мощность Р₁, поступающая в двига­тель из сети, в
основной своей части преобразуется в механическую мощность Р₁ и передается исполни­тельному
механизму ИМ.

   Весьма важным параметром асинхронной ма­шины
является скольжение — величина, характери­зующая разность частот вращения
ротора и вра­щающегося поля статора:

S = (n₁ – n₂)/ n₁                   (формула 6.1)

Скольжение выражают в долях единицы либо в
процентах. В последнем случае величину, получен­ную по (6.1), следует умножить
на 100.

С увеличением нагрузочного момента на валу
асинхронного двигателя частота вращения ротора n₂ умень­шается. Следовательно, скольжение асинхронного двигателя зави­сит
от механической нагрузки на валу двигателя и может изме­няться в диапазоне 0
< s ≤ 1.

Скольжение, соответствующее номинальной
нагрузке двигателя, называют номинальным скольжением s_hom. Для асинхронных
дви­гателей общего назначения s_hom
= 18%,
при этом для двигателей большой мощности s_ном = 1%, а для двигателей малой мощности s_ном = 8%.

Формула для опре­деления асинхронной частоты вращения
(об/мин):

n₂ = n₁(1-s).                           (формула 
6.2)

Пример 6.1. Трехфазный
асинхронный двигатель с числом полюсов 2р = 4 работает от сети с
частотой тока f₁ = 50 Гц.
Определить частоту вращения двигателя при номинальной нагрузке, если скольжение
при этом составляет 6%.

Решение.
Синхронная частота вращения по (6.9) n₁ = f₁ 60/ р = 50 • 60/4 = 1500 об/мин.

Номинальная частота вращения по (6.2): n_ном = n₁(1 – s_ном ) = 1500(1 – 0,06) = 1412 об/мин.

Генераторный режим. Если обмотку статора включить в сеть, а ротор асинхронной машины
посредством приводного дви­гателя ПД (двигатель внутреннего сгорания, турбина и
т. п.),  яв­ляющегося источником механической энергии, вращать в направ­лении
вращения магнитного поля статора с частотой n₂ > n₁, то направление движения ротора относительно поля
статора изме­нится на обратное (по сравнению с двигательным режимом работы пой
машины), так как ротор будет обгонять поле статора. При этом скольжение станет
отрицательным, а ЭДС, наведенная в обмотке ротора, изменит свое направление.
Электромагнитный момент на роторе М также изменит свое направление, т. е. будет
направлен встречно вращающемуся магнитному полю статора и станет тормозящим по
отношению к вращающемуся моменту приводного двигателя М₁. В этом
случае механическая мощность приводного двигателя в основной своей части будет
преобразована в электрическую активную мощность Р₂ перемен­ного
тока. Особенность работы асинхронного генератора состоит в том, что вращающееся
магнитное поле в нем создается реактивной мощностью Q
трехфазной сети, в которую включен генератор и да он отдает вырабатываемую
активную мощность Р₂. Следовательно,
для работы асинхронного генератора необходим источник переменного тока, при
подключении к которому происходит возбуждение генератора.

Скольжение асинхронной машины в генераторном
режиме может изменяться в диапазоне       – ∞ < s <
0, т. е. оно может прини­мать любые отрицательные значения.

Наибольшее практическое применение получил
двигательный режим асинхронной машины, т. е. чаще используют асинхронные
двигатели, которые составля­ют основу современного электропривода, выгодно
отличаясь от других электродвигателей простотой конструкции и высокой на­дежностью.

Магнитодвижущая сила обмотки статора созда­ет магнитный поток, который замыкается через эле­менты магнитной
системы машины. Магнитную систему асинхронной машины называют неявнополюсной,
так как она не имеет явно выра­женных магнитных полюсов. Количество магнитных
полюсов в неявнополюсной магнитной системе определяется числом полюсов в
обмотке, возбуждающей магнитное поле, в данном случае в обмотке статора.
Магнитная система маши­ны, состоящая из сердечников статора и ротора, представляет
собой разветвленную симметричную магнитную цепь.

Значение МДС на пару полюсов позволяет определить
намагничиваю­щий ток (основную гармонику) обмотки статора:

I_1μ =                                    (формула
6.3)

Исходным параметром при расчете магнитной
цепи асин­хронного двигателя является максимальная магнитная индукция в
воздушном зазоре В_δ. Величину В_δ  принимают по
рекомендуемым значениям в зависимости от наружного диаметра сердечника статора D_1нар и числа полюсов 2р.

Магнитная индукция В_δ определяет
магнитную нагрузку двигателя: при слишком малом В_δ магнитная система
двигателя недогружена, а поэтому габаритные размеры двигателя получаются
неоправданно большими; если же задаться чрезмерно большим течением В_δ,
то резко возрастут магнитные напряжения на участ­ках магнитной системы,
особенно в зубцовых слоях статора и ротopa, в результате
возрастет намагничивающий ток статора I_1μ  снизится КПД двигателя.

Расчет магнитной цепи асинхронного
двигателя. Расчет магнитной цепи электрической машины
состоит в ос­новном в определении магнитных напряжений для всех ее участ­ков.
Магнитное напряжение F_x для любого участка
магнитной це­пи равно произведению напряженности поля на этом участке Н_х
на его длину l_Х.

Участки магнитной цепи различаются
конфигурацией, разме­рами и материалом. Наибольшее магнитное напряжение в
воздуш­ном зазоре δ. Напряженность магнитного поля в воздушном зазоре

H_δ = B_δ/
μ₀, где μ₀ = 4π/ 10^-7  Гн/м. Расчетная длина
зазора l_δ = δk_δ
, где k_δ, — коэффициент воздушного зазора,
учитывающий увеличение магнитного сопротивления зазора, вызванное зубчато­стью
поверхностей статора и ротора, ограничивающих воздушный зазор в асинхронном
двигателе (k_δ > 1). Учитывая это, получим вы­ражение
магнитного напряжения воздушного зазора (А):

F_δ
= 0,8 B_δ δ k_δ 10³.                    (формула
6.4)

где δ — значение
одностороннего воздушного зазора, мм.

Обычно магнитное напряжение двух воздушных
зазоров, вхо­дящих в расчетную часть магнитной цепи асинхронного двигателя,
составляет — 85% от суммарной МДС на пару полю­сов . Из
этого следует, насколько значительно влияние вели­чины воздушного зазора  δ на свойства двигателя. С увеличением δ МДС  значительно возрастает, что ведет к
увеличению намаг­ничивающего тока статора I_1μ, а, следовательно, ведет к росту потерь и снижению КПД двигателя. И
наоборот, с уменьше­нием δ  уменьшается , что ведет к росту КПД, т. е. двигатель
становится более экономичным в эксплуатации. Однако при слишком малых зазорах δ усложняется изготовление двигателя (он становится менее
технологичным), так как требует более высокой точности при обработке деталей и
сборке двигателя. При этом снижается надежность двигателя – возрастает
вероятность возникновения не­равномерности зазора и, как следствие, вероятность
задевания ро­тора о статор.

Пример 6.2. Воздушный зазор трехфазного асинхронного двигателя δ = 0,5 мм, максимальное
значение магнитной индукции В_δ  = 0,9 Тл. Обмотка
статора              четырехполюсная, число последовательно соединенных витков
в обмотке одной фазы ω₁ = 130, обмоточный коэффициент k_об1 = 0,91. Определить значение намагничивающего
тока обмотки статора I_1μ, если коэффициент
воздушного зазора      k_δ = 1,38, а коэффициент
магнитного насыщения k_μ = 1,4.

Решение.

Магнитное напряжение воздушного зазора по (6
.4)

F_δ = 0,8 В_δ
δ k_δ • 10³ = 0,8 • 0,9 • 0,5 • 1,38 •
10³ = 497 A.

Так как коэффициент магнитного насыщения k_μ = _ном / (2F_δ), то МДС обмотки статора в режиме х.х. на пару полюсов _ном = 2F_δ  k_μ =2 • 497 • 1,4 = 1392 А.

Намагничивающий ток статора по (6.3)

I_1μ = p _ном
/ (0,9 m₁ ω₁ k_об1) = 2 • 1392 / (0,9 • 3 • 130 • 0,91) = 8,7 A

Если воздушный зазор данного двигателя
увеличить на 20%, т. е. принять δ = 0,6 мм (при прочих
неизменных условиях), то намагничивающий ток статора станет равным  I_1μ = 10,4 А, т. е. он возрастет
пропорционально увеличению воз­душного зазора.

Электродвижущие силы, наводимые в обмотке
ротора. Асинхронный двигатель аналогичен трансформатору,
у которо­го вторичная обмотка (обмотка ротора) вращается. При этом вра­щающийся
магнитный поток сцепляется не только с обмоткой ста­тора, где индуцирует ЭДС Е_и но и с обмоткой вращающегося рото­ра, где индуцирует ЭДС.  В
процессе работы асинхронного двигателя ротор вращается в сто­рону вращения поля
статора с частотой n₂.
Поэтому частота вра­щения поля статора относительно ротора равна разности
частот вращения (n₁ – n₂). Основной магнитный поток Ф, обгоняя
ротор с частотой вращения  n_s = (n₁ – n₂), индуцирует в обмотке ротора ЭДС

Е₂
= 4,44 f₂ Ф ω₂ к_об2                         (формула
6.5)

где f₂— частота ЭДС Е_2s в роторе,
Гц; ω₂ — число последовательно соединенных витков одной фазы обмотки
ротора; k_o62 —
обмоточный коэффициент обмотки ротора.

Частота ЭДС (тока) в обмотке вращающегося
ротора пропор­циональна частоте вращения магнитного поля относительно ротора n_s = n₁ – n₂, называемой частотой скольжения:

f₂ = pn_s
/ 60 = p(n₁ – n₂) / 60,

или

f₂ = =  =
f₁s       (формула 6.6)

т. е. частота ЭДС (тока) ротора
пропорциональна скольжению. Для асинхронных двигателей общепромышленного
назначения эта частота обычно невелика и при f₁ = 50 Гц не превышает нескольких герц, так при s =
5%  частота f₂ = 50 0,05 = 2,5 Гц.  

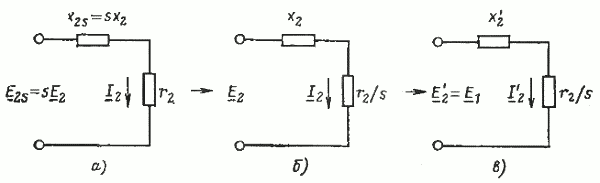
E_2s =
4,44 f₁ s Ф ω₂ k_об2
= E₂ s.         (формула 6.7)

Здесь Е₂ –  ЭДС, наведенная в
обмотке ротора при скольжении s = 1, т. е. при неподвижном
роторе, В.

Уравнения МДС и токов асинхронного
двигателя. МДС обмоток статора и ротора на один полюс
в режиме на­груженного двигателя

                                            
F₁ = 0,45 m₁ I₁ ω₁ k_об1/ P

       F₂
= 0,45 m₂ I₂ ω₂ k_об2/
P            (формула 6.8)

где m₂ — число фаз в обмотке
ротора; k_o62 —
обмоточный коэффи­циент обмотки ротора.

С подключением нагрузки в фазах обмотки
статора появляются токи I_А,
I_B, I_C.  При этом
трехфазная обмотка ста­тора создает вращаю­щееся магнитное поле. Частота вращения
этого поля равна частоте вра­щения ротора генерато­ра (об/мин):

n₁ = f₁60/p.         
(формула 6.9)

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:

1.   
Решить задачу №1. В табл. 6.1 приведены данные
следующих параметров трехфазного асинхронного двигателя с короткозамкнутым
ротором: основной магнитный поток ф, число последовательно соединенных витков  в обмотке статора,
номинальное скольжение , ЭДС, индуцируемая в
обмотке ротора при его неподвижном состоянии , и ЭДС ротора при его
вращении с номинальным скольжением E_2s, частота этой ЭДС f₂ при частоте вращения ротора n_ном. Частота тока в питающей сети 50 Гц. Требуется определить значения
параметров, не указанные в таблице в каждом из вариантов.

Таблица 6.1.

Параметр	Варианты
1	2	3	4	5	6	7	8	9	10
Ф, Вб	0,028	0,032	0,048	−	0,025	−	−	0,028	0,028	−
Kоб1	0,95	0,96	0,96	0,98	0,98	0,96	0,95	0,95	0,98	0,98
1, витков	18	−	24	16	−	24	18	−	36	18
Sном	0,04	−	0,05	0,04	−	0,05	−	−	−	−
2p	4	6	2	4	−	8	4	8	−	4
E1ф, В	−	210	−	98	110	200	−	120	−	100
E2,В	−	−	−	−	−	−	−	−	−	−
E2s,В	−	−	−	−	−	−	0,13	−	−	−
f2, Гц	−	−	−	−	−	−	2,5	3,2	−	2,5
nном, об/мин	−	970	−	−	2920	−	−	−	1470	−

2.   
Решить задачу №2. В табл.6.2. приведены значения
следующих параметров трехфазного асинхронного двигателя: односторонний
воздушный зазор между статором и ротором δ, число полюсов 2Ƥ, число
пазов , максимальное значение
магнитной индукции в воздушном зазоре , число витков в одной
катушке обмотки статора (все катушки фазной обмотки
соединены последовательно), обмоточный коэффициент обмотки
статора для основной гармоники , коэффициент магнитного
насыщения , коэффициент воздушного
зазора , Необходимо определить
величину намагничивающего тока статора при заданном воздушном
зазоре.

                                                                                                                                              
Таблица 6.2.

Параметры	Варианты
1	2	3	4	5	6	7	8	9	10
δ,мм	0,6	0,4	0,8	0,5	0,7	0,3	0,4	0,7	0,5	0,6
2Ƥ	6	4	8	6	6	2	4	6	4	8
Число пазов	24	24	48	36	60	18	36	48	32	54
,Тл	0,9	0,8	0,9	1,0	0,7	0,8	0,8	1,0	0,7	0,9
Число витков	8	7	6	8	5	4	5	5	6	4
	0,91	0,95	0,92	0,94	0,96	0,92	0,92	0,94	0,93	0,92
	1,37	1,35	1,38	1,40	1,35	1,40	1,34	1,37	1,35	1,38
	1,30	1,35	1,36	1,38	1,34	1,37	1,35	1,36	1,34	1,38

       
Решение:

–         
Определить величину магнитного напряжения
воздушного зазора.

–         
Определить значение МДС обмотки статора на пару
полюсов в режиме холостого хода номинальном подведении напряжении.

–         
Определить число последовательно соединенных витков
фазной обмотки статора.

–           
Определить величину намагничивающего тока статора.                   

3. Решить задачу №3. Трехфазный
асинхронный двигатель с фазным ро­тором имеет данные, приведенные в табл. 6.3.
максимальное значе­ние магнитной индукции в воздушном зазоре В_δ,
диаметр расточки статора D_1, длина
сердечника статора l₁,
равная 0,81D₁,
число полю­сов в обмотках статора и ротора 2р,
число последовательно соеди­ненных витков в фазных обмотках статора ω₁
и ротора ω₂,
обмоточные коэффициенты для основной гармоники статора к_об1
и ротора к_об2
принять равными к_об1
= к_иб2
= 0,93. Требуется определить фаз­ные значения ЭДС в обмотке статора Е₁
 и в обмотке фазного ротора при неподвижном его состоянии Е₂
и вращающемся со скольжени­ем s,
частоту тока в неподвижном и вращающемся роторе.
Частота тока в питающей сети f
= 50 Гц.

Таблица 6.3.

Параметр	Варианты
1	2	3	4	5	6	7	8	9	10
Вδ , Тл	1,5	1,35	1,50	1,40	1,45	1,50	1,38	1,45	1,50	1,38
D1, мм	180	160	228	235	160	300	280	320	360	290
l1, мм	141	130	180	190	130	250	250	270	300	250
2 р	4	4	4	6	4	4	6	4	8	6
ω1	48	18	24	32	48	36	32	36	12	24
ω2	8	4	6	10	16	12	16	18	8	12
s, %	8	12	10	6	5	12	8	10	6	8

Решение:

–         
Определить полюсное деление.

–         
Определить величину основного магнитного
потока.

–         
Определить ЭДС фазной обмотки статора.

–         
Определить ЭДС в обмотке неподвижного
ротора.

–         
Определить ЭДС во вращающемся роторе при
скольжении 8 %.

–         
Определить частоту тока во вращающемся
роторе при скольжении 8
%.

–         
 

4.
Решить задачу №4. Трехфазный асинхронный двигатель с
короткозамкнутым ротором серии 4А имеет технические данные, приведенные в табл.
6.4. Определить высоту оси вращения h, число полюсов 2p, скольжение при номинальной нагрузке s_ном, момент на валу М_ном, начальный пусковой М_n и максимальный  момент, потребляемую
двигателем из сети активную мощность Р_1ном,
суммарные потери при номинальной нагрузки ∑Р, номинальный и пусковой токи I_1ном и I_n в
питающей сети при соединении обмоток статора «звездой» и «треугольником».

 Таблица 6.4.

№ В	Тип двигателя	Pном, кВт	n2ном, об/мин	nном, %					U1,В
1	4A100S2У3	4,0	2880	86,5	0,89	7,5	2,0	2,5	220/380
2	4A160S2У3	15,0	2945	88,0	0,91	7,0	1,4	2,2	220/380
3	4A200М2У3	37,0	2945	90,0	0,89	7,5	1,4	2,5	380/660
4	4A112М2У3	5,5	1445	85,5	0,85	7,0	2,0	2,2	220/380
5	4A132М2У3	11,0	1460	87,5	0,87	7,5	2,2	3,0	220/380
6	4A180М2У3	30,0	1470	91,0	0,89	6,5	1,4	2,3	380/660
7	4A200М6У3	22,0	475	90,0	0,90	6,5	1,3	2,4	220/380
8	4A280М6У3	90,0	985	92,5	0,89	5,5	1,4	2,2	380/660
9	4A315М8У3	110	740	93,0	0,85	6,5	1,2	2,3	380/660
10	4A355М10У3	110	590	93,0	0,83	6,0	1,0	1,8	380/660

Решение:

–         
В обозначении типоразмера двигателя цифры, стоящие
после обозначения серии  4А, указывают на высоту оси вращения (мм).

–         
Следующая далее цифра указывает на число плюсов 2p.

–         
Определить синхронную частоту вращения  при частоте переменного
тока 50 Гц.

–         
Определить скольжение при номинальной нагрузке  =/.

–         
Определить момент на валу двигателя (полезный
момент двигателя) при номинальной нагрузке  = 9,55/.

–         
Определить начальный пусковой момент. =().

–         
Определить максимальный (критический)момент
двигателя по его перегрузочной способности..

–    
Определить номинальный ток в фазной обмотке
статора.

–         
Определить потребляемую двигателем из сети активную
мощность в режиме номинальной нагрузки..

–         
Определить суммарные потери двигателя при номинальной
нагрузке

–    
=

–         
Определить линейный ток статора: при соединении
обмоток статора «звездой» =.

–         
При соединении обмоток статора «треугольником» .

5.       
Решить задачу №5. Трехфазный асинхронный
двигатель с фазным ро­тором имеет эффективное число витков в фазных обмотках
статора  и ротора , ЭДС фазной обмотки статора
= 0,95, ЭДС фазной обмотки
неподвижного ротора  , а вращающегося со
скольжением s, равно . Используя приведенные в
табл. 6.5. значения параметров, определить неуказанные значения, если
напряжение питания двигателя = 220/380 B.

Таблица 6.5. 

Параметр	Варианты
1	2	3	4	5	6	7	8	9	10
	18	24	—	32	—	36	—	24	—	48
	12	—	18	—	12	—	18	—	16	—
, B	—	—	—	—	—	—	—	—	—	—
, B	—	93	—	105	—	104	—	98	—	110
, B	—	5,58	6,5	5,25	5,8	—	4,0	5,8	4,6	—
s	0,05	—	0,04	—	0,07	0,05	0,03	—	0,05	0,04

6.     
Оформить отчет по практической работе.

7.     
Ответить на контрольные вопросы.

8.     
Сделать вывод о проделанной работе.

КОНТРОЛЬНЫЕ
ВОПРОСЫ:

1.     
Что такое скольжение асинхронной машины?

2.       
Какие режимы работы синхронной машины
существуют?

3.       
Каков диапазон изменения скольжения
асинхронной машины в различных режимах ее работы?

4.       
Что такое номинальное скольжение?

5.       
С какой целью обмотку статора асинхронного
генератора подключают к сети трехфазного тока?

6.       
Какова цель расчета магнитной цепи
асинхронной машины?

7.       
Как влияет выбор значения магнитной индукции
в воздушном зазоре на свойства асинхронного двигателя?

8.       
В чем сходство трансформатора и асинхронного
двигателя?

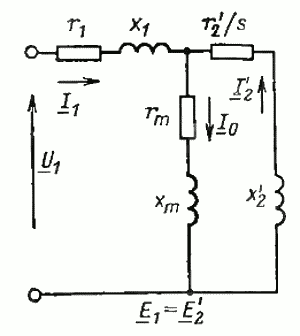
Основные уравнения асинхронной машины.

Векторная диаграмма асинхронного
двигателя.

Используя принципы построения векторной
диаграммы для трансформатора, построим
ее для асинхронного двигателя.

Вначале во втором основном уравнении
величину r2′ представим в виде:

,

что математически не противоречит друг
другу.

Тогда само уравнение можно переписать:

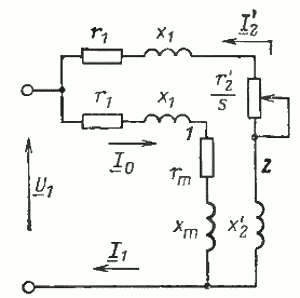
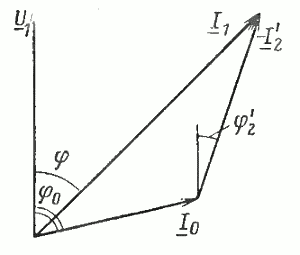
Используя три основных уравнения
двигателя, построим векторную диаграмму,
которая, будет несколько напоминать
диаграмму трансформатора (рис. 5.7.1).

Вторичное напряжение определяется
вектором:

,

иначе говоря, асинхронный двигатель в
электрическом отношении работает как
трансформатор при активной нагрузке.

Мощность, отдаваемая вторичной обмоткой
данного трансформатора

,

представляет собой полную механическую
мощность, развиваемую двигателем.

Электромагнитный момент асинхронного
двигателя.

Вращающий момент в асинхронном двигателе
создается взаимодействием тока ротора
с магнитным полем машины. Вращающий
момент математически можно выразить
через электромагнитную мощность машины:

,

где w1=2pn1/60 – угловая частота вращения
поля.

В свою очередь, n1=f160/Р, тогда

.

Подставим в формулу M1 выражение Рэм=Рэ2/S
и, разделив на 9,81, получим:

,

Отсюда следует, что момент двигателя
пропорционален электрическим потерям
в роторе. Подставим в последнюю формулу
значение тока I2’:

,

получим

,

где U1 – фазное напряжение обмотки статора.

Механические характеристики асинхронного
двигателя.

В последнем выражении для M1 единственным
переменным параметром является скольжение
S. Зависимость М=f(S) получило название
механической характеристики двигателя
(рис. 5.11.1).

В момент пуска двигателя, когда n2=0,
скольжение S=1, тогда:
.

Под действием момента Mn ротор придет
во вращение. В дальнейшем скольжение
будет уменьшаться, а вращающий момент
увеличиваться. При скольжении Sкр он
достигает максимального значения Mmax..
Величина критического скольжения

.

Тогда, подставив его значение в формулу
для М, получим:

.

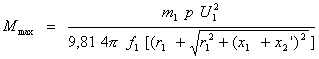
Дальнейший разгон двигателя будет
сопровождаться уменьшением скольжения
и, вместе с тем уменьшением вращающего
момента. Равновесие наступит, когда
величине вращающего момента будет
противостоять тормозной момент, вызванный
нагрузкой.

При номинальной нагрузке будут номинальный
вращающий момент Мн и номинальное
скольжение Sн.

Отношение максимального момента к
номинальному называется перегрузочной
способностью двигателя.

.

Обычно она составляет величину от 1,7 до
2,5.

Отношение пускового момента к номинальному
называется кратностью пускового момента

.

Эта величина может быть меньше единицы
(например, 0,8) и больше ее (до 1,2). При
меньшей кратности двигатель следует
включать в работу без нагрузки, и лишь
после разгона подается нагрузка.
Двигатель с кратностью Кп.м.>1 можно
включать в сеть с полной нагрузкой.

Регулирование частоты вращения
асинхронного двигателя.

Регулирование частоты вращения
асинхронного двигателя определяется
формулой:

.

Здесь возможны три различных способа
реализации:

Первый заключается в изменении частоты
тока f, подаваемого в обмотки двигателя.
Этот способ позволяет осуществлять
плавное регулирование частоты вращения
двигателя. Регуляторы частоты тока пока
еще очень дороги, поэтому они мало
применяются.

Второй способ связан с изменением пар
полюсов p на статоре.

Укладывая на статоре несколько обмоток,
рассчитанных на различные числа пар
полюсов (р=1,2,3,4), можно обеспечить
различные частоты вращения магнитного
поля (соответственно: 3000, 1500, 1000, 750
об/мин). Подключение к сети необходимой
обмотки производится специальным
переключателем.

Этот способ регулирования ступенчатый,
но в ряде металлообрабатывающих станков
он нашел самое широкое применение
(например, для привода продольно-строгального
станка при рабочем и обратном ходе).

Третий способ регулирования частоты
вращения возможен лишь для двигателей
с фазным ротором. Здесь изменение
скольжения S достигается введением в
цепь ротора регулировочных сопротивлений.
Такие схемы широко используются на
грузоподъемных кранах.

Области применения и устройство машин
постоянного тока.

Машины постоянного тока используют в
качестве генераторов и двигателей.

Электрическая энергия постоянного
тока, вырабатываемая генераторами,
служит для питания двигателей постоянного
тока, электролитических ванн,
электромагнитов различного назначения,
аппаратуры управления и контроля и т.
д. В настоящее время генераторы постоянного
тока во многих установках заменяют
полупроводниковыми преобразователями
переменного тока в постоянный.

Двигатели постоянного тока применяют
на транспорте для привода некоторых
металлорежущих станков, прокатных
станов, подъемно-транспортных машин,
экскаваторов и т. д. Одной из главнейших
причин применения двигателей постоянного
тока вместо наиболее широко распространенных
асинхронных двигателей (см. гл. 10) является
возможность плавного регулирования
частоты вращения в широком диапазоне
и получения желаемых механических
характеристик n(М).

Рис. 9 1. Устройство (а) и якорь (б) машины
постоянного тока

Генераторы и двигатели постоянного
тока устроены одинаково. Неподвижная
часть машины, называемая статором (рис.
9.1, а), состоит из массивного стального
корпуса 1, к которому прикреплены главные
полюсы 2 и дополнительные полюсы 6. Исходя
из технологических и других соображений
главные полюсы изготовляют чаще из
отдельных стальных листов; иногда их
изготовляют сплошными. Из отдельных
листов либо сплошными изготовляют и
дополнительные полюсы. Перечисленные
детали статора являются также и деталями
его магнитопровода. На главных полюсах
размещают катушки одной или нескольких
обмоток возбуждения 3, на дополнительных
полюсах — катушки 7 обмотки дополнительных
полюсов.

В подшипниковых щитах, прикрепленных
с торцевых сторон к корпусу, расположены
подшипники, несущие вал 4 вращающейся
части машины, называемой якорем (рис.
9.1, а и б). На валу закреплен цилиндрический
сердечник якоря 5, который для уменьшения
потерь мощности от перемагничивания и
вихревых токов набирают из стальных
листов. В пазах, расположенных по
поверхности якоря, уложена обмотка
якоря 8. Так же, как обмотку возбуждения
и обмотку дополнительных полюсов, ее
изготовляют из медного изолированного
провода. Выводы от обмотки якоря
присоединяют к расположенному на валу
коллектору 9. Последний представляет
собой цилиндр, состоящий из медных
пластин, изолированных друг от друга и
от вала. К коллектору с помощью пружин
прижимаются графитные, угольно-графитные
или металлографитные щетки 10. Щетки
расположены в специальных щеткодержателях.

Обмотка возбуждения машины питается
постоянным током и служит для создания
основного магнитного поля, показанного
на рис 9.1, а условно с помощью двух линий
магнитной индукции, изображенных
пунктиром.

Главные полюсы имеют полюсные наконечники
11, служащие для получения по большей
части окружности якоря одного и того
же воздушного зазора между сердечником
якоря и главными полюсами. Это необходимо
для получения на большей части окружности
якоря одной и той же магнитной индукции,
а в проводниках обмотки якоря — постоянной
по значению ЭДС. Дополнительные полюсы
предназначены для уменьшения искрения
под щетками .

С помощью коллектора и щеток вращающаяся
обмотка якоря соединяется с внешней
электрической цепью. О других важных
назначениях коллектора и щеток будет
говориться в.

На рис. 9.1, а показана машина постоянного
тока с двумя главными полюсами. В
зависимости от мощности и напряжения
машины могут иметь и большее число
полюсов. При этом соответственно
увеличиваются число комплектов щеток
и дополнительных полюсов. Крепление
машины к фундаменту, специальным салазкам
или металлоконструкции осуществляется
с помощью лап 12. Корпус некоторых машин
снабжается для крепления специальными
фланцами.

Принцип действия машин постоянного
тока.

Принцип действия генератора. Допустим,
что якорь машины (см. рис. 9.5) вращается
с помощью какого-то двигателя в
направлении, указанном стрелкой. Если
щетки генератора соединить с каким-либо
приемником r, то под действием ЭДС
генератора в обмотке якоря и приемника
появится ток, приемник начнет потреблять
электрическую энергию, а машина будет
ее отдавать, т. е. будет работать в
качестве генератора. Естественно, что
электрическая энергия, вырабатываемая
генератором, преобразуется из механической
энергии двигателя, вращающего якорь
генератора.

Направление тока в проводниках обмотки
якоря генератора совпадает, конечно, с
направлением ЭДС проводников и при
вращении якоря изменяется. Однако с
помощью коллектора изменяющийся по
направлению ток проводников преобразуется
в неизменные по направлению токи
параллельных ветвей iпар и ток внешней
цепи iя, называемый током якоря. Согласно
первому закону Кирхгофа для рассматриваемого
генератора iя = 2iпар. Машины постоянного
тока могут иметь число параллельных
ветвей больше двух. Обозначив в общем
случае число параллельных ветвей 2а,
получим

(9.3)

iя = 2аiпар .

Если воспользоваться правилом левой
руки, нетрудно установить, что генератор
развивает электромагнитный момент,
направленный против направления
вращения, т. е. является тормозящим.

Изменение полярности щеток и, следовательно,
направлений ЭДС, напряжения и тока во
внешней цепи генератора возможно
произвести одним из двух способов:

1) изменением направления магнитного
поля главных полюсов, что осуществляется
изменением направления тока обмотки
возбуждения, располагаемой на главных
полюсах;

2) изменением направления вращения
якоря генератора с помощью приводного
двигателя.

Обычно используется первый способ.

Принцип действия двигателя. Предположим,
что якорь той же машины (см. рис. 9.5)
неподвижен. Если от источника постоянного
тока подвести к якорю двигателя
напряжение, например указанной на рис.
9.5 полярности, то во внешней цепи и в
обмотке якоря возникнут токи, направление
которых будет противоположным указанным
на рисунке. С помощью правила левой руки
можно установить, что на якорь будет
действовать вращающий электромагнитный
момент и якорь начнет вращаться против
часовой стрелки. При вращении в обмотке
якоря возникнет ЭДС, которая согласно
правилу правой руки будет направлена,
как указано на рис. 9.5, т. е. против тока
двигателя. Противоположные направления
тока и ЭДС говорят о том, что в машине
происходит преобразование электрической
энергии в механическую. Двигатель
разгонится до такой частоты вращения,
при которой его момент станет равным
моменту, обусловленному нагрузкой.

Говоря о принципе действия двигателя,
нельзя не остановиться на назначении
коллектора в этом случае. Коллектор
необходим для того, чтобы неизменный
по направлению ток внешней цепи
преобразовывать в изменяющийся по
направлению ток в проводниках обмотки
якоря при его вращении. Только благодаря
коллектору ток всех проводников,
находящихся под одним полюсом, имеет
одно и то же направление. Вследствие
этого остается неизменным и направление
вращающего момента, развиваемого
двигателем.

Для изменения направления вращения
двигателя необходимо изменить направление
развиваемого им вращающего момента.
Это можно сделать одним из двух способов:

изменением полярности напряжения,
подводимого к якорю двигателя и,
следовательно, направления тока якоря;

изменением направления магнитного
потока главных полюсов.

Обычно используется первый способ.

Рассмотрев принципы действия генератора
и двигателя, можно сделать вывод о том,
что машины постоянного тока обратимы.
Это значит, что при определенных условиях
генераторы могут работать в качестве
двигателей и наоборот. Возможность
двигателей работать в качестве генераторов
и. следовательно, развивать тормозящий
момент широко используется на практике
.

Обмотки якоря.

Типы обмоток. В настоящее время в основном
применяют якоря барабанного типа, в
которых проводники обмотка укладывают
в два слоя в пазы, расположенные на
наружной поверхности якоря (рис. 8.13, а).
Для того чтобы ЭДС, индуцированные в
двух сторонах каждого витка, складывались,
стороны его следует располагать под
полюсами противоположной полярности
(рис. 8.13,б). В этом случае в каждом витке
индуцируется ЭДС, в два раза большая,
чем в одном проводнике. Следовательно,
как и в обмотках переменного тока,
основной шаг обмотки должен быть примерно
равен полюсному делению τ.

Рис. 8.13. Схемы расположения проводников
обмотки на якоре барабанного типа (а и
б) и схема двухслойной обмотки 7 (в) 1. 2,
3, …. 8, 1′, 2′, 3’…………. 8’— проводники,
образующие обмотку

Обмотки барабанного якоря подразделяют
на две основные группы: петлевые
(параллельные) и волновые (последовательные).
В машинах большой мощности применяют
также «лягушачью» (параллельно-последовательную)
обмотку, в которой сочетаются элементы
петлевой и волновой обмоток. Основной
частью каждой обмотки является секция,
состоящая из одного или нескольких
последовательно включенных витков;
концы секции присоединяют к двум
коллекторным пластинам. Число секций
S равно числу коллекторных пластин К.
Все секции обмотки обычно имеют одинаковое
количество витков.

На схемах обмоток секции для простоты
всегда изображают одновитковыми. При
двухслойной обмотке стороны секции,
расположенные в верхнем слое, изображают
сплошными линиями, а в нижнем слое —
штриховыми (рис. 8.13, в). Шаг секции y1 (его
называют также основным или первым
частичным шагом обмотки) должен быть
приблизительно равен полюсному делению
τ. При. y1 = τ шаг называют диаметральным;
при y1 < τ — укороченным; при y1 > τ —
удлиненным.

Эдс машин постоянного тока.

Как было показано ранее, ЭДС проводника
обмотки якоря определяется по формуле
епр = Blv.

При вращении якоря ЭДС епр изменяется
в соответствии с графиком, приведенным
на рис. 9.2, б. Среднее значение ЭДС
проводника епр,ср при его перемещении
в пределах полюсного деления можно
определить через среднее значение
магнитной индукции (см. рис. 9,2 б):

епр,ср = Bcplv.

Если обмотка якоря имеет N проводников
и 2а параллельных ветвей, то число
последовательно соединенных проводников
в каждой параллельной ветви будет N/2a.
Тогда среднее значение ЭДС машины

(9,4)Е = BcplN/2а

Среднее значение магнитной индукции

(9,5)Bcp =Ф/πDяl/2p

где Ф — магнитный поток одного полюса,
Вб; Dя — диаметр якоря, м; 2р — число
полюсов машины.

Величина πDяl/2p в (9.5) представляет собой
поверхность сердечника якоря, приходящуюся
на один полюс.Линейную скорость
проводников v можно определить по формуле

(9,6)v =πDяn/60

где n— частота вращения якоря, об/мин.

После замены в (9.4) магнитной индукции
Вср и скорости v согласно (9.5) и (9.6) получим

(9.7)Е =p/а*N/60*Фn = kеФn,

где kе =p/а*N/60- коэффициент ЭДС, зависящий
от конструк тивных особенностей машины.

Как видно, ЭДС прямо пропорциональна
произведению магнитного потока на
частоту вращения. По формуле (9.7)
можно определять как ЭДС генераторов,
так и ЭДС двигателей.

Электромагнитный момент машин
постоянного тока.

Электромагнитная сила в ньютонах,
действующая на проводник обмотки якоря,
определяется соотношением

Fпр = BlIпр = BlIя /2a,

где Iпр — ток проводника, равный току
параллельной ветви, А; Iя — ток якоря,
А.

При вращении якоря сила, действующая
на проводник, изменяется.

Среднее значение силы можно определить
через среднее значение магнитной
индукции:

Fпр, ср = BcplIя/2a.

Средний электромагнитный момент, Н•м,
действующий на якорь,

(9.8)Mcp = Fпр, ср*Dя/2* N= Bcpl*lя/2a*Dя/2*N.

После замены в (9.8) магнитной индукции
Вср согласно (9.5) получим

(9.9)Mэм =р/а*N/2π*ФIя = kMФIя,

где kM =р/а*N/2π- коэффициент момента,
зависящий от конструктивных особенностей
машины.

Как видно, момент электромагнитный
прямо пропорционален произведению
магнитного потока на ток якоря. По
формуле (9.9) можно определять как момент
генераторов, так и момент двигателей.

Если момент выражен в ньютоно-метрах,
то между коэффициентами kе и kM существует
следующее соотношение:

kе /kM ≈ 0,105.

Электромагнитный момент Мэм, вызванный
взаимодействием магнитного потока и
тока якоря и определяемый по формуле
(9.9), отличается от момента М, развиваемого
машиной на валу, вследствие трения в
подшипниках, вращающегося якоря о воздух
и вентиляционных потерь. Так как указанные
два момента отличаются незначительно,
будем в дальнейшем считать их равными
и обозначать М.

Магнитное поле машины. Реакция якоря.

Режим холостого хода. Магнитный поток
при холостом ходе в машине создается
только МДС Fв обмотки возбуждения. В
этом случае магнитный поток Фв при
симметричном воздушном зазоре между
якорем и сердечником главного полюса
распределяется симметрично относительно
продольной оси машины (рис. 8.21).

Зависимость магнитного потока возбуждения
Фв от МДС Fв (магнитная характеристика
— рис. 8.22) для машин постоянного тока
подобна магнитной характеристике для
синхронных машин. Однако при проектировании
машин постоянного тока допускают большие
индукции на участках магнитной цепи (в
зубцах, якоре, станине и полюсах), чем в
синхронных машинах, вследствие чего
для них коэффициент насыщения kнас =
F/Fδ = ab/ac = 1,2 ÷ 2. Расчет магнитной цепи
машины постоянного тока производят так
же, как и для машин переменного тока
(см. § 3.7).

Реакция якоря. При работе машины под
нагрузкой по обмотке якоря проходит
ток, вследствие чего возникает МДС
якоря. Воздействие МДС якоря на магнитное
поле машины называют реакцией якоря.
Для упрощения анализа явления реакции
якоря будем пренебрегать насыщением
магнитной цепи машины и считать, что
МДС Fв обмотки возбуждения и МДС Faq
обмотки якоря расходуются на преодоление
магнитными потоками воздушного зазора.
В этом случае вместо указанных МДС можно
рассматривать соответствующие потоки:
возбуждения Фв и реакции якоря Фaq .

Рис. 8.21. Магнитное поле машины постоянного
тока в режиме холостого хода: 1 — полюс;

2 — обмотка возбуждения;

3 — якорь;

4 — корпус (станина)

Рис. 8.22. Магнитная характеристика машины
постоянного тока (а) и график для
определения размагничивающего действия
поперечного поля реакции якоря (б)

Рис. 8.23. Характер магнитного поля машины
постоянного тока,:

создаваемые обмоткой возбуждения (а),
обмоткой якоря (б)и результирующего
поля (в)

При холостом ходе магнитный поток
возбуждения направлен по продольной
оси машины (рис. 8.23, а). При работе под
нагрузкой магнитный поток Фaq , созданный
МДС якоря Faq , в двухполюсной машине при
установке щеток на геометрической
нейтрали направлен по поперечной оси
машины (см. рис. 8.23,б), поэтому магнитное
поле якоря называют поперечным. В
результате действия реакции якоря
симметричное распределение магнитного
поля машины относительно оси главных
полюсов искажается и результирующее
поле оказывается смещенным к одному из
краев каждого главного полюса (см. рис.
8.23, в). При этом физическая нейтраль О’
—О’ (линия, соединяющая точки окружности
якоря, в которых индукция равна нулю)
смещается относительно геометрической
нейтрали О — О на некоторый угол β. В
генераторах (обозначение Г на рис. 8.23,
в) физическая нейтраль смещается по
направлению вращения якоря; в двигателях
(обозначение Д) — против направления
вращения.

Чтобы построить кривую Врез = f(х)
распределения результирующей индукции
вдоль окружности якоря, применим метод
суперпозиции. Его можно использовать,
если пренебречь насыщением магнитной
цепи машины и считать, что МДС Fв и Faq
расходуются на компенсацию разности
магнитных потенциалов в воздушном
зазоре. Так как обмотка возбуждения
является сосредоточенной, то кривая
распределения создаваемой ею МДС F’в
=f(x) имеет форму прямоугольника, где F’в
= 0,5Fв — МДС, приходящаяся на один воздушный
зазор. В этом случае кривая индукции Вв
= f(x) имеет форму криволинейной трапеции
(рис. 8.24, а).

Коммутация машин постоянного тока.

Под коммутацией в машинах постоянного
тока понимают процесс переключения
секций обмотки якоря из одной параллельной
ветви в другую, сопровождающийся
изменением направления тока в секциях.
Направления и значения тока коммутируемой
(переключаемой) секции в различных ее
положениях относительно неподвижной
щетки показаны на рис. 9.10.

В результате изменения тока в коммутирующей
секции возникает ЭДС самоиндукции eL.

Для увеличения механической прочности
щеток их ширину выбирают обычно больше
ширины коллекторной пластины. Вследствие
этого щеткой замыкаются накоротко и
одновременно коммутируются несколько
секций. Последнее вызывает в каждой
секции ЭДС взаимной индукции еM. Кроме
того, в секции возникает ЭДС еv, вызываемая
вращением секции в магнитном поле
поперечной реакции якоря.

Сумма перечисленных ЭДС невелика.
Однако, поскольку секция замкнута щеткой
накоротко, это приводит к заметному
дополнительному току в замкнутом контуре
секции, в результате чего плотность
тока под щеткой становится неодинаковой.
Под сбегающим краем щетки плотность
тока возрастает, что приводит к искрению
под щеткой, особенно интенсивному в
момент размыкания секции. Если не принять
специальных мер для улучшения условий
коммутации (уменьшения искрения под
щетками), то наиболее ответственная
часть машины — коллектор — через
непродолжительное время выйдет из
строя.

Рис. 9.10. К пояснению явления коммутации

Способы улучшения коммутации.

Рис. 9.11. Полярность главных и дополнительных
полюсов

Для улучшения коммутации машины мощностью
1 кВт и более снабжаются дополнительными
полюсами (рис. 9.11). В машинах с дополнительными
полюсами щетки устанавливают на
геометрической нейтрали. С помощью
дополнительных полюсов в зоне коммутации
создается магнитное поле, в результате
чего в коммутируемых секциях индуктируется
ЭДС, компенсирующая ЭДС eL, eM и ev. Так как
ЭДС eL, eM и ev зависят от тока якоря, то для
их компенсации при различных нагрузках
обмотку дополнительных полюсов включают
последовательно с якорем. Вследствие
насыщения дополнительных полюсов при
перегрузках машины условия коммутации
ухудшаются и под щетками появляется
недопустимое искрение. Наибольший
допустимый ток машин постоянного тока
определяется условиями коммутации и
лежит для различных машин в пределах
(2 ÷ 3) Iном , где Iном — номинальный ток
машины.

Так как ЭДС ev возникает вследствие
вращения якоря в магнитном поле реакции
якоря, то для ее уничтожения с помощью
МДС дополнительных полюсов должно быть
создано магнитное поле, от вращения в
котором возникла бы ЭДС, направленная
против ev. Учитывая характер изменения
результирующего магнитного поля при
нагрузке генератора и двигателя с
указанными направлениями их вращения
(см. рис. 9.8, в), следует сказать: полярность
дополнительного полюса генератора
должна быть такой же, как последующего
за ним по направлению вращения главного
полюса (рис. 9.11); полярность дополнительного
полюса двигателя должна быть такой же,
как предшествующего ему по направлению
вращения главного полюса. Выбирая
соответствующее значение МДС обмотки
дополнительных полюсов, можно
скомпенсировать также ЭДС eL и еM.

Двигатели постоянного тока. Способы
возбуждения.

Свойства и характеристики двигателей
постоянного тока существенно зависят
от того, как меняется магнитный поток
двигателей при изменении их механической
нагрузки. Характер изменения магнитного
потока зависит в свою очередь от числа
и способа включения обмоток возбуждения,
т. е. от способа возбуждения двигателей.
В зависимости от способа возбуждения
различают:

двигатели независимого возбуждения;

двигатели параллельного возбуждения
(ранее шунтовые);

двигатели последовательного возбуждения
(ранее сериесные);

двигатели смешанного возбуждения (ранее
компаундные).

Двигатели независимого возбуждения
находят применение, когда обмотки якоря
и возбуждения должны получать питание
от различных источников постоянного
тока. Это может быть в случае использования
двигателей значительной мощности,
обмотку якоря которых изготовляют
обычно на более высокое напряжение, чем
обмотку возбуждения. Кроме того,
раздельное питание обмоток якоря и
возбуждения применяется для расширения
диапазона регулирования частоты вращения
и улучшения качества переходных процессов
пуска, торможения и реверса двигателей.

При изложении материала сначала будут
рассмотрены свойства и характеристики
двигателей параллельного, последовательного
и смешанного возбуждения, получающих
питание от источника (от сети) с неизменным
напряжением, а далее, в конце § 9.18,—
свойства и характеристики двигателя
независимого возбуждения, обмотка якоря
которого питается от источника с
изменяемым напряжением.

Для более четкого представления о том,
чем отличаются двигатели параллельного,
последовательного и смешанного
возбуждения, будем рассматривать их
совместно, предполагая для удобства
сравнения, что различные двигатели
имеют одинаковое номинальные данные
(в частности, номинальные магнитные
потоки Фном, токи якоря Iя,ном , моменты
Мном и частоты вращения nном).

Рис. 9.22. Схема включения двигателя
смешанного возбуждения

На рис. 9.22 приведена схема включения
двигателя смешанного возбуждения.
Магнитное поле двигателя возбуждается
двумя обмотками: обмоткой параллельного
возбуждения Ш1 — Ш2 и обмоткой
последовательного возбуждения C1 — C2.
В двигательном режиме работы обмотки
включены согласно. Как и у генераторов,
обмотки параллельного и последовательного
возбуждения существенно отличаются в
конструктивном отношении (см. § 9.7).

Имея схему включения двигателя смешанного
возбуждения (рис. 9.22), нетрудно представить
себе схемы включения двух других
двигателей. Исключив мысленно обмотку
C1 — C2, получим схему включения двигателя
параллельного возбуждения; исключив
цепь обмотки Ш1 — Ш2, получим схему
включения двигателя последовательного
возбуждения.

В цепь якоря двигателей включают реостат
r, служащий для пуска двигателей. Им же
пользуются иногда для регулирования
частоты вращения. Реостат rр включают
в цепи двигателей параллельного или
смешанного возбуждения лишь в том
случае, если необходимо регулировать
частоту вращения путем изменения
магнитного потока.

Направления токов якоря Iя , возбуждения
Iв , тока I, потребляемого из сети (рис.
9.22), магнитного потока Ф, ЭДС Е, момента
М и частоты вращения и двигателя зависят
от полярности напряжений на выводах
обмоток якоря и возбуждения, а также от
того, в двигательном или каком-либо из
тормозных режимов работает электродвигатель.

Двигательным называется режим, при
котором направление частоты вращения
и якоря определяется направлением
действия момента М двигателя. При
установившемся движении момент М
двигателя уравновешивается статическим
моментом Мс, возникающим на валу двигателя
под действием производственной машины.
В двигательном режиме работы статический
режим Мс является тормозящим и направлен
против направления частоты вращения
n. Тормозные режимы рассматриваются в
§ 9.19.

Пуск двигателя постоянного тока.

На практике замечено, что ток, потребляемый
обмоткой статора в первый момент пуска
двигателя, очень большой. В ряде случаев
он превышает номинальный ток в 6 – 10 раз.

Такой нагрузки может не выдержать не
только питающая сеть, но и сама обмотка
статора. Поэтому для пуска крупных
асинхронных двигателей применяют
специальные устройства, снижающие
пусковой ток. На рис. 5.13.1. показаны схемы
пуска мощных двигателей с помощью
реакторов и автотрансформатора.

Принцип ограничения тока заключается
в том, что к статорной обмотке двигателя
на период пуска подводится пониженное
напряжение. После разгона его дополнительные
устройства от двигателя отключаются.

Иногда для снижения напряжения,
подаваемого в обмотки статора, изменяют
схему переключения обмоток. Например,
асинхронный двигатель нормально работает
по схеме “треугольник”. Если на
период пуска его обмотки включить
“звездой”, то на каждую фазу придется
напряжение в раз меньшее.

Двигатели с фазным ротором пускаются
в работу с помощью дополнительных
сопротивлений. Вводя дополнительные
сопротивления в цепь ротора, добиваются
ограничения пускового тока.

В начальный момент пуска в ход якорь
двигателя неподвижен и противо-эдс
равна нулю (Е = 0). При непосредственном
включении двигателя в сеть в обмотке
якоря будет протекать чрезмерно большой
ток Iпуск = U/Rя. Поэтому непосредственное
включение в сеть допускается только
для двигателей очень малой мощности, у
которых падение напряжения в якоре
представляет относительно большую
величину и броски тока не столь велики.

В машинах постоянного тока большой
мощности падение напряжения в обмотке
якоря при полной нагрузке составляет
несколько процентов от номинального
напряжения, т. е. IRя = (0,02 0,1)U.

Следовательно, пусковой ток в случае
включения двигателя в сеть с номинальным
напряжением во много раз превышает
номинальный.

Для ограничения пускового тока используют
пусковые реостаты, включаемые
последовательно с якорем двигателя при
пуске в ход.

Пусковые реостаты представляют собой
проволочные сопротивления, рассчитываемые
на кратковременный режим работы, и
выполняются ступенчатыми, что дает
возможность изменять ток в якоре
двигателя в процессе пуска его в ход.

Схема двигателя параллельного возбуждения
с пусковым реостатом показана на изо,
а.

Пусковой реостат этого двигателя имеет
три зажима, обозначаемые

буквами Л, Я, Ш.

Зажим Л соединен с движком реостата и
подключается к одному из полюсов
рубильника (к линии). Зажим Я соединяется
с сопротивлением реостата и подключается
к зажиму якоря. Зажим Ш соединен с
металлической шиной, помещенной на
реостате (шунт).

Движок реостата скользит по шине так,
что между ними имеется непрерывный
контакт. К зажиму Ш через регулировочное
сопротивление Rр присоединяется обмотка
возбуждения. Вторые зажимы якоря и
обмотки возбуждения соединены между
собой перемычкой и подключены ко второму
полюсу рубильника, включающего двигатель
в сеть.

При пуске в ход включается рубильник
и движок реостата переводится на контакт
1, так что последовательно с якорем
соединено полное сопротивление пускового
реостата ПР, которое выбирается таким,
чтобы наибольший ток при пуске в ход
Imах не превышал номинальный ток более
чем в 1,7—2,5 раза, т.е.

Rп = U/Imax – Rя.

При включении двигателя в сеть по
обмотке возбуждения также проходит
ток, возбуждающий магнитный поток. В
результате взаимодействия тока в якоре
с магнитным полем полюсов создается
пусковой момент.

Если пусковой момент окажется больше
тормозного момента на валу двигателя
(Мпуск > Мт), то якорь машины придет во
вращение

.Схема (а) и характеристики (б) двигателя
параллельного возбуждения

Под действием инерции частота вращения
не может претерпевать мгновенных
изменений и будет постепенно увеличиваться.
Вместе с ней возрастает противо-эдс и
ток в якоре начнет уменьшаться, что
вызывает уменьшение вращающего момента
двигателя.

В рабочем режиме сопротивление пускового
реостата должно быть полностью выведено,
так как оно рассчитано на кратковременный
режим работы и при длительном прохождении
тока выйдет из строя.

Когда ток в якоре уменьшится до небольшого
значения Imin, движок пускового реостата
переводится на контакт 2. При этом
сопротивление пускового реостата
уменьшится на одну ступень, что увеличит
ток.

Сопротивление всех ступеней пускового
реостата выбирают так, чтобы при переводе
движка реостата с одного контакта на
другой ток в якоре изменялся от Imin до
Imax.

С увеличением тока в якоре возрастает
вращающий момент, вследствие чего
частота вращения вновь увеличивается.
С увеличением частоты вращения якоря
возрастает противо-эдс, что вызовет
уменьшение тока в якоре.

Когда ток в якоре достигает вновь
наименьшего значения, движок реостата
переводится на контакт 3.

Таким образом, сопротивление пускового
реостата постепенно (ступенями)
уменьшается, пока оно полностью не будет
выведено (движок реостата на контакте
5), и в рабочем режиме ток и частота
вращения якоря принимают установившиеся
значения, соответствующие тормозному
моменту на валу двигателя.

Наименьший ток при пуске в ход зависит
от режима работы двигателя.

Если двигатель пускается при полной
нагрузке, то Imin = 1.1Iн.

При пуске двигателя без нагрузки или
при малых нагрузках этот ток может быть
меньше номинального тока двигателя.

Число ступеней пускового реостата
зависит от разности Imax – Imin, причем чем
меньше разность этих токов, тем больше
число ступеней. Обычно пусковые реостаты
имеют от 2 до 7 ступеней. При пуске
двигателя в ход регулировочное
сопротивление Rv в цепи возбуждения
должно быть полностью выведено, т. е.
ток возбуждения должен быть наибольшим,
что дает возможность уменьшить пусковой
ток.

Для пуска двигателя необходимо создать
пусковой момент, больший тормозного
момента на валу.

Так как Mпуск = KIпускФ, то для уменьшения
пускового тока надо увеличить магнитный
поток, т. е. увеличить ток в обмотке
возбуждения.

Металлическая шина пускового реостата
соединена с зажимом 1. Это необходимо
для того, чтобы при отключении двигателя
от сети не было разрыва цепи обмотки
возбуждения, имеющей значительную
индуктивность.

При отключении двигателя движок
пускового реостата переводится на
холостой контакт 0 и рубильник отключается.
При этом обмотка возбуждения будет
замкнута на сопротивление пускового
реостата и якоря, что дает возможность
избежать перенапряжений и дугообразования.

Скоростные и механические характеристики
двигателя постоянного тока.

Скоростные характеристики дают
зависимость скорости вращения п от
полезной мощности Р2 на валу двигателя
в случае, если напряжение U сети и
сопротивление rв регулировочного
реостата цепи возбуждения остаются
неизменными, т. е. n=f(P2), при U=const и rв =
const.

Рис. 3. Скоростные характеристики

С возрастанием тока якоря при увеличении
механической нагрузки двигателя
параллельного возбуждения одновременно
увеличивается падения напряжения в
якоре и появляется реакция якоря, которая
обычно действует размагничивающим
образом. Первая причина стремится
уменьшить скорость вращения двигателя,
вторая — увеличить. Действие падения
напряжения в якоре обычно оказывает
большее влияние. Поэтому скоростная
характеристика двигателя параллельного
возбуждения имеет слегка падающий
характер (кривая 1, рис. 3).

В двигателе последовательного возбуждения
ток якоря является током возбуждения.
В результате скоростная характеристика
двигателя с последовательным возбуждением
имеет характер, близкий к гиперболическому.
При увеличении нагрузки по мере насыщения
магнитной цепи характеристика приобретает
более прямолинейный характер (кривая
3 на рис. 3).

В компаундном двигателе при согласном
включении обмоток скоростная характеристика
занимает промежуточное положение между
характеристиками двигателя параллельного
и последовательного возбуждения (кривая
2).

Важнейшей характеристикой двигателя
является механическая n(M). Она показывает,
как зависит частота вращения двигателя
от развиваемого момента. Если к обмоткам
двигателя подведены номинальные
напряжения и отсутствуют дополнительные
резисторы в его цепях, то двигатель
имеет механическую характеристику,
называемую естественной. На естественной
характеристике находится точка,
соответствующая номинальным данным
двигателя (Мн, Ря и т.д.). Если же напряжение
на обмотке якоря меньше номинального,
либо Iв < Iвн, то двигатель будет иметь
различные искусственные механические
характеристики. На этих характеристиках
двигатель работает при пуске, торможении,
реверсе и регулировании частоты вращения.

Преобразовав выражение (3) относительно
частоты вращения, получим уравнение
электромеханической характеристики
n(Iя):

(7)

После замены в уравнении (7) тока Iя
согласно формуле (1), получим уравнение
механической характеристики n(М):

(8)

При Ф = соnst, электромеханическая n(Iя) и
механическая n(М) характеристики двигателя
параллельного возбуждения представляют
собой прямые линии. Так как за счет
реакции якоря магнитный поток немного
изменяется, то характеристики в
действительности несколько отличаются
от прямых.

При работе вхолостую (М = 0) двигатель
имеет частоту вращения холостого хода,
определяемую первым членом уравнения
(8). С увеличением нагрузки n уменьшается.
Как следует из уравнения (8), это объясняется
наличием сопротивления якоря rя.

Поскольку rя не велико, частота вращения
двигателя при увеличении момента
изменяется мало, и двигатель имеет
жесткую естественную механическую
характеристику (рис.6, характеристика
1).

Из уравнения (8) следует, что регулировать
частоту вращения при заданной постоянной
нагрузке (М = const) можно тремя способами:

а) изменением сопротивления цепи якоря;

б) изменением магнитного потока двигателя;

в) изменением напряжения на зажимах
якоря.

Рис. 6 Механические характеристики

Для регулирования частоты вращения
первым способом в цепь якоря. должно
быть включено добавочное сопротивление
rд. Тогда сопротивление в уравнении (8)
необходимо заменить на rя + rд.

Как следует из уравнения (8), частота
вращения n связана с сопротивлением
цепи якоря rя + rд при постоянной нагрузке
(М = const) линейной зависимостью, т.е. при
увеличении сопротивления частота
вращения уменьшается. Разным сопротивлениям
rд соответствуют различные искусственные
механические характеристики, одна из
которых приведена на рис.2 (характеристика
2). С помощью характеристики 2 при заданном
моменте М1 можно получить частоту
вращения n2.

Изменение частоты вращения вторым
способом осуществляется с помощью
регулируемого источника напряжения
UD2. Изменяя его напряжение регулятором
R2, можно изменить ток возбуждения IВ и
тем самым магнитный поток двигателя.
Как видно из уравнения (8), при постоянной
нагрузке (М = соnst) частота вращения
находится в сложной зависимости от
магнитного потока Ф. Анализ уравнения
(8) показывает, что в некотором диапазоне
изменения магнитного потока Ф уменьшение
последнего приводит к увеличению частоты
вращения. Именно этот диапазон изменения
потока используют при регулировании
частоты вращения.

Каждому значению магнитного потока
соответствует искусственная механическая
характеристика двигателя, одна из
которых приведена на рис.2 (характеристика
4). С помощью характеристики 4 при моменте
М1 можно получить частоту вращения n4.

Чтобы регулировать частоту вращения
изменением напряжения на зажимах якоря,
необходимо иметь относительно мощный
регулируемый источник напряжения.
Каждому значению напряжения соответствует
искусственная механическая характеристика
двигателя, одна из которых приведена
на рис.2(характеристика 3). С помощью
характеристики 3 при заданном моменте
М1 можно получить частоту вращения n3.

ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ

1.1. ОБЩИЕ СВЕДЕНИЯ И КЛАССИФИКАЦИЯ

Усилителем называют такое устройство,
в котором по средством сигнала малой
мощности (входная величина) управляют
сравнительно большой мощностью (выходная
величина). При этом выходная величина
является функцией входного сигнала и
усиле ние происходит за счет энергии
внешнего источника.

По виду управляемой энергии усилители
можно разделить на электрические,
пневматические, гидрав лические,
механические.

Электрические усилители в свою очередь
подразделяются на электронные,
тиратронные, транзисторные, магнитные,
сег-нетоэлектрические и электромашинные.
Первые пять являются статическими, а
электромашинные — вращающимися
усилителями.

В электромашинных усилителях выходная
(управляемая) элек трическая мощность
создается за счет механической мощности
при водного двигателя.

Электромашинные усилители (ЭМУ)
представляют собой кол лекторную машину
постоянного тока.

В зависимости от способа возбуждения
электромашинные уси лители подразделяются
на усилители продольного поля и усили
тели поперечного поля.

К усилителям продольного поля, в которых
основной поток воз буждения направлен
по продольной оси машины, относятся:

1) независимый ЭМУ,

2) ЭМУ с самовозбуждением,

двухмашинные усилители,

4) двухколлекторный ЭМУ,

5)двух- и трехступенчатые ЭМУ продольного
поля

К усилителям поперечного поля, в которых
основной поток воз буждения направлен
по поперечной оси машины, относятся:

1 )ЭМУ с диаметральным шагом обмотки
якоря,

2) ЭМУ с полудиаметральным шагом обмотки
якоря,

ЭМУ с разделенной магнитной системой.

Чем меньше мощность управления
электромашинного усилителя, тем меньше
вес и габариты аппаратуры управления.
Поэтому

основной характеристикой является
коэффициент усиления. Различают
коэффициенты усиления по мощности, току
и напряжению.

Коэффициент усиления ЭМУ по мощности
kp есть отношение мощности на выходе
РВых к мощности на входе Рвх при
установившемся режиме работы:

Коэффициент усилен

Коэффициент усиления по напряжению

где UВЫХ — напряжение выходной цепи; —
напряжение входной цепи.

Из сказанного следует, что

Коэффициент усиления п о току kt — это
отношение тока выход ной цепи /вых
усилителя к току входной цепи /вх:

Электромашинные усилители могут иметь
достаточно высокий коэффициент усиления
по мощности (103-М05).

Не менее важным для усилителя является
его быстродействие, характеризуемое
постоянными времени его цепей.

Постоянная времени определяется
величиной энергии магнит ного поля,
изменяющегося в процессе регулирования.
Для элект рической цепи постоянная
времени

где L — индуктивность цепи;

ΣR — активное сопротивление цепи. В
электромашинных усилителях постоянная
времени T= 0,02÷0,2 сек.

От ЭМУ стремятся получить большой
коэффициент усиления по мощности и
большое быстродействие, т. е. по возможности
мень шие постоянные времени. Так как
постоянная времени ЭМУ про порциональна
коэффициенту усиления по мощности ЭМУ,
то для удобства сравнения различных
усилителей вводят коэффициент добротности
&д, представляющий собой отношение
коэффициента по мощносте к сумме
постоянных времени ступеней усиления:

B системах автоматического регулирования
ЭМУ применяются в качестве усилителей
мощности и работают в основном при пере
ходных режимах, в процессе которых
возникаютзначительные пере грузки по
току. Поэтому одним из требований к ЭМУ
является хорошая перегрузочная
способность.

К числу важнейших требований, предъявляемых
к ЭМУ, от носятся надежность в работе и
стабильность характеристик.

ЭМУ, используемые на самолетах и
транспортных установках, должны обладать
минимальными габаритами и весом.

В радиоэлектронной промышленности
наибольшее распростра нение получили
независимый ЭМУ, ЭМУ с самовозбуждением
и ЭМУ поперечного поля с диаметральным
шагом. Далее рассмот рены эти типы
усилителей.

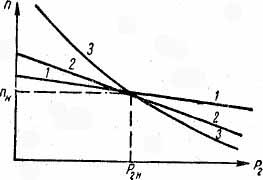
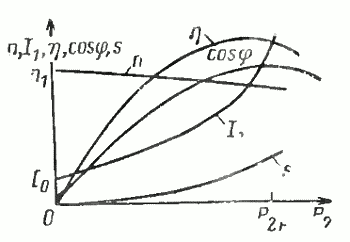
 Рабочие характеристики асинхронного двигателя – зависимости потребляемого тока I₁ и мощности Р₁, КПД, cos φ и скольжения s от полезной механической мощности P₂. Эти характеристики определяются при постоянном напряжении U₁ и частоте f₁ сети.

Рабочие характеристики асинхронного двигателя могут быть получены экспериментально (опытным путем) и рассчитаны с помощью схемы замещения.

Ниже приводится расчет рабочих характеристик асинхронного двигателя по схеме замещения.

По обмотке статора асинхронной машины протекает многофазная система токов, обычно трехфазная, которая создает в воздушном зазоре машины вращающееся магнитное поле (магнитный поток Ф).

 Вращающееся магнитное поле в свою очередь индуктирует (наводит) в проводниках обмотки ротора ЭДС, под действием которой в замкнутой накоротко обмотке ротора протекает ток I₂. Этот ток, взаимодействуя с магнитным потоком Ф, создает механическую силу, стремящуюся привести ротор во вращение в сторону вращения магнитного поля.

Определим, с какой частотой вращения магнитное поле машины пересекает проводники ротора. Эта частота равна, об/мин:

             (9)

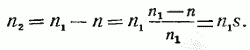
Определим частоту ЭДС f₂, которая наводится магнитным полем асинхронной машины в проводниках ротора, Гц:

f₂=р n₂/60.            (10)

Если учесть, что n₂=n₁s [см. формулу (9)], то можно записать

       (11)

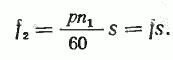
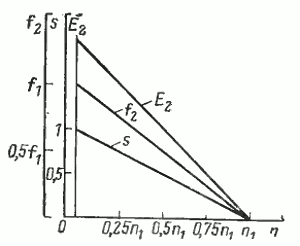
Из формулы (11) видно, что если ротор машины неподвижен (n=0, s=l), то частота ЭДС, наводимой в роторе, равна частоте сети. По мере увеличения частоты вращения ротора ЭДС понижается и при синхронной частоте будет равна нулю. На рис. 13 показаны изменения скольжения, частоты и ЭДС в роторе в зависимости от частоты вращения ротора.

Рис. 13. Зависимость скольжения s, частоты f₂ и ЭДС, наводимой в роторе, E2 от частоты вращения асинхронного двигателя n

Из закона электромагнитной индукции следует, что при гармоническом изменении магнитного поля наводимая в обмотке ЭДС равна:

E=4,44fwk_обФ_max,             (12)

где f — электрическая частота, Гц; w — число последовательно соединенных витков фазы; k_об — обмоточный коэффициент; Ф_max — максимальное значение рабочего потока, сцепленного с обмоткой, Вб.

Знание частоты f₂ в роторе дает возможность определить ЭДС ротора Е₂ при произвольной частоте вращения (скольжении), В, в виде

E₂=4,44f₂w2k_об2Ф_max,           (13)

где w₂ — число последовательно  соединенных витков обмотки ротора; k_об2 — обмоточный   коэффициент   ротора.

Подстановка f₂  из формулы (11) дает, В,

E_2s=4,44f s w₂k_об2Ф_max=sE₂,     (   14)

где Е₂ — ЭДС, наводимая в неподвижной обмотке ротора потоком Ф_max, В.

Осветим теперь важный для анализа работы асинхронных двигателей вопрос о зависимости вращающегося магнитного потока двигателя от режима работы машины. Для этого, чтобы представить себе эту зависимость, определим вначале, какую ЭДС Е₁ наводит этот поток в каждой фазе обмотки статора, В:

E₁=4,44fw₁k_об1Ф_max,     (15)

где w₁ — число витков одной фазы статора; k_об1 —обмоточный коэффициент обмотки статора.

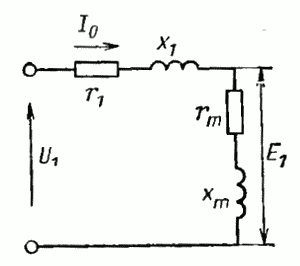
Напряжение U₁, приложенное к статору, уравновешивается ЭДС E₁ и падением напряжения I₁z₁ на внутреннем сопротивлении z₁=r₁+jx₁ обмотки статора (х₁— индуктивное сопротивление обмотки, определяемое потоком рассеяния) . При изменении нагрузки двигателя от нуля (холостой ход) до номинальной падение напряжения составляет 5—10 % приложенного. Таким образом, с достаточной для качественного анализа точностью можно полагать, что напряжение U₁ полностью компенсируется ЭДС Е1 т. е. .

U₁≈E₁         (16)

Учитывая формулу (15), нетрудно заключить, что ЭДС и вращающийся магнитный поток двигателя зависят от приложенного к двигателю напряжения. При постоянном напряжении поток Фmах остается приблизительно постоянным независимо от изменения нагрузки двигателя.

Рассмотрим вначале явления, происходящие в машине с заторможенным ротором и замкнутой накоротко обмоткой ротора. Асинхронный двигатель в этом режиме подобен трансформатору с короткозамкнутой вторичной обмоткой. Отличие состоит в том, что вторичная магнитная цепь отделена от первичной воздушным зазором, первичная обмотка (статора) и вторичная обмотка (ротора) равномерно распределены по окружности, а магнитное поле вращающееся.

Как видно из формулы (14) и рис. 13, ЭДС, наводимая в обмотке ротора, когда он неподвижен, является максимальной. В силу этого и ток, проходящий по обмоткам статора и ротора, также будет наибольшим. Этот режим называется режимом короткого замыкания (КЗ). Ток статора в этом режиме называется током короткого замыкания и превышает его номинальный ток в 4—7 раз. Асинхронный двигатель в таких условиях нельзя длительно оставлять под полным напряжением из-за перегрева обмоток, который может привести к аварии.

Для определения тока короткого замыкания двигателя делают опыт КЗ. Этот опыт заключается в том, что к двигателю с заторможенным (неподвижным) ротором подводят пониженное напряжение, регулируя которое, устанавливают номинальный ток. Напряжение, подводимое к двигателю в опыте КЗ, оказывается малым (15— 20%) по сравнению с номинальным. На базе этого опыта можно в безопасных для двигателя условиях определить величину тока короткого замыкания /к при номинальном напряжении, А:

       (17)

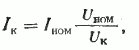
где U_ном — номинальное напряжение, В; U_к — напряжение в опыте КЗ при номинальном токе, В; I_ном — номинальный ток, А.

Замеряя в этом опыте по ваттметру мощность короткого замыкания Р_к, подводимую к одной фазе двигателя,  находят также  коэффициент  мощности в режиме  КЗ

      (18)

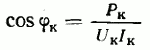
и эквивалентное активное сопротивление статора и ротора двигателя гк в режиме КЗ на одну фазу, Ом,

r_к=P_к/I_ном2              (19) 

Это эквивалентное активное сопротивление равно сумме активного сопротивления статора и приведенного активного сопротивления ротора. Понятие о приведенном активном и реактивном сопротивлении ротора будет дано ниже.

Определив угол φк по значению cosφк из формулы (18), легко найти и эквивалентное реактивное сопротивление двигателя в режиме короткого замыкания, Ом:

х_к=r_кctgφ_к (20)

Индуктивное сопротивление хк равно сумме индуктивного сопротивления статора и приведенного индуктивного сопротивления ротора.

Поскольку частота вращения ротора двигателя в этом режиме равна нулю, его механическая мощность также равна нулю. Потери в стали во время опыта короткого замыкания очень малы, так как мал вращающийся магнитный поток. Поэтому мощность Р_к, которая подводится к машине, почти вся идет на нагрев проводников обмоток статора и ротора. То же самое можно сказать о режиме КЗ при полном напряжении.

Теперь представим себе, что обмотка ротора разомкнута, а обмотка статора включена в сеть. Ток по роторной обмотке при этом не проходит и асинхронный двигатель подобен трансформатору, но уже в режиме холостого хода (XX). Так как ток в проводниках ротора отсутствует, то механическая сила не возникает и ротор остается неподвижным.

По обмотке статора при этом проходит ток холостого хода I₀, который создает магнитодвижущую силу (МДС), необходимую для создания магнитного потока Ф_max. Поскольку в магнитной цепи асинхронного двигателя имеется зазор, то для создания магнитного потока требуется относительно больший ток, чем в трансформаторе. В двигателях большой и средней мощности ток XX составляет 25—35, а в двигателях малой мощности — 35—60% номинального тока.

Наводимая в неподвижном роторе ЭДС может быть определена по формуле (14), если учесть, что скольжение в этом режиме равно 1. Отношение ЭДС в обмотке статора к ЭДС в обмотке ротора называется коэффициентом трансформации ЭДС и может быть определено по формуле

           (21)

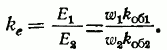
Мощность, потребляемая двигателем в режиме XX при неподвижном роторе, расходуется на потери в проводниках статора двигателя, потери на перемагничивание и вихревые токи в стали статора и в стали ротора.

Важно заметить, что режим XX при неподвижном роторе очень близок к режиму, который возникает, когда  асинхронный двигатель не выполняет полезной работы и вращается на холостом ходу. В этом случае частота вращения ротора двигателя почти равна синхронной, а  скольжение примерно равно нулю [см. формулы (4), (9) и рис. 13]. Электродвижущая сила в роторе будет близкой к нулю, и, следовательно, подобно режиму XX при неподвижном роторе практически равен  нулю ток в роторе. При холостом ходе вращающегося двигателя ток в обмотке статора, как и в случае холостого хода неподвижного двигателя, определяется в основном МДС, необходимой для создания магнитного потока Ф_max.

При вращении ротора в двигателе появляются потери, которых нет в случае неподвижного ротора; это механические потери на трение и вентиляционные. Однако когда частота вращения ротора примерно равна синхронной, исчезают потери в стали ротора двигателя, поскольку магнитное поле теперь очень медленно перемещается относительно ротора и его сталь почти не перемагничивается. Таким образом, потери и, следовательно, мощность в двух режимах холостого хода оказываются близкими.

Асинхронная машина в режиме холостого хода может быть представлена схемой замещения, показанной на рис. 14. Для определения параметров и характеристик двигателя помимо опыта КЗ выполняют опыт XX, во время которого замеряют ток обмотки статора I₀ (А) и потребляемую мощность Р₀ (Вт). Это позволяет определить сопротивления в схеме замещения двигателя на холостом ходу, а также коэффициент мощности XX:

cosφ₀=P₀/(UI₀).            (22)

Рис. 14. Схема замещения первичной цепи (статора)   асинхронного  двигателя,  работающего  в режиме холостого хода

Перейдем теперь к рассмотрению общего случая режима нагрузки, когда ротор вращается с частотой, меньшей частоты XX. Определим, какой ток будет проходить по обмотке ротора во всем диапазоне рабочих режимов. Наводимая вращающимся магнитным потоком ЭДС в обмотке ротора зависит при постоянном напряжении только от скольжения и может быть найдена по (14). Ток ротора будет, очевидно, зависеть от ЭДС, наводимой в роторе, и сопротивления обмотки ротора, при этом полное сопротивление цепи в случае переменного тока определяется не только активным сопротивлением проводников обмотки, но и ее индуктивным сопротивлением. Индуктивное сопротивление обмотки ротора изменяется так же, как и ЭДС ротора E_2s, Ом:

x_2s=2πf₂L₂=s2πf₁L₂ =sx₂,      (23)

где L₂ — индуктивность обмотки ротора, Гн; х₂— индуктивное сопротивление рассеяния обмотки неподвижного ротора при s=l, Ом.

Теперь, используя закон Ома для цепей переменного тока, найдем ток ротора, А:

      (24)

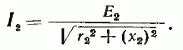
Учитывая (14) и (23), формулу (24) можно записать иначе:

           (25)

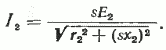
Таким образом, можно видеть, что при скольжении, равном нулю или близком к нему (это соответствует синхронной или близкой к синхронной частоте вращения ротора), ток ротора равен нулю или очень мал. Это совпадает с тем, что было сказано выше относительно режима XX при вращающемся роторе. По мере уменьшения частоты вращения двигателя, т. е. при увеличении скольжения, ток возрастает за счет увеличения ЭДС ротора, однако рост тока ограничивается увеличением индуктивного сопротивления ротора.

Если разделить числитель и знаменатель выражения (25) для тока ротора I₂ на s, то получим следующую формулу:

           (26)

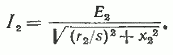
Из этого следует, что если мы примем, что ротор неподвижен, а его активное сопротивление меняется обратно пропорционально скольжению, то по его обмотке будет проходить точно такой же ток, как и при вращающемся роторе. Удобство такого преобразования состоит в том, что оно позволяет вместо вращающегося ротора (вращающаяся вторичная электрическая цепь) рассматривать неподвижный ротор (неподвижная вторичная цепь).

Однако изучение процессов, происходящих в асинхронной машине, и расчет ее характеристик можно сделать более удобными, если заменить реальную обмотку ротора эквивалентной с числом витков в фазе и числом фаз, равным им у первичной обмотки (обмотки статора), т. е. вместо обмотки ротора с числом фаз m₂, числом витков в фазе w₂ и обмоточным коэффициентом k_об2 будем полагать, что обмотка ротора имеет число фаз ти число витков в фазе w₁ и обмоточный коэффициент k_об1. Эта замена называется приведением обмотки ротора к обмотке статора. Нетрудно видеть, что магнитный поток Ф в этом случае будет наводить в эквивалентной (приведенной) обмотке ротора ЭДС, равную ЭДС обмотки статора E₂‘=E₁ (штрихом будем обозначать приведенные величины).

Замена обмотки ротора не должна привести к изменению потребляемой мощности, потерь, магнитодвижущей силы и фазы тока обмотки. Из этого условия определяются приведенные величины тока, активного и индуктивного сопротивлений обмотки ротора .

В соответствии с (13) имеем, В

           (27)

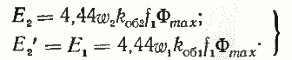
Из формул (27) вытекает отношение между ЭДС приведенной и реальной обмоток заторможенного ротора, которое называется коэффициентом трансформации ЭДС или напряжений. Он равен:

          (28)

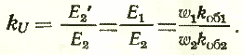
Из условия неизменности магнитодвижущих сил F₂‘ =F₂ следует, что

   

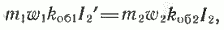
откуда вытекает отношение между токами, которое называется коэффициентом трансформации токов. Он равен:

          (29)

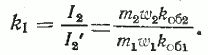
Из условия неизменности потерь в обмотке ротора при приведении следует, что

   

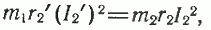
откуда

           (30)

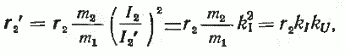
или r₂‘=k_rr₂,

где k_r=k_Ik_U — коэффициент приведения сопротивлений.

Из условия неизменности фазы тока обмотки ротора следует

           (31)

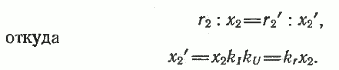
Процесс приведения цепи ротора показан на рис. 15. От схемы замещения обмотки вращающегося ротора (рис. 15,а) переходим к схеме замещения неподвижного ротора (рис. 15,б), а затем приводим обмотку ротора к обмотке статора (рис. 15, в).

Рис. 15. Схемы замещения: а — обмотки вращающегося ротора; б — неподвижного ротора; в — обмотки ротора, приведенной к обмотке статора

Поскольку теперь ЭДС Е₁ первичной обмотки равна ЭДС Е₂‘ вторичной обмотки, мы можем соединить электрически соответствующие точки схемы замещения обмотки статора и ротора. В результате получим схему замещения асинхронного двигателя, показанную на рис. 16. Здесь активное сопротивление r_m отражает наличие потерь в стали двигателя. Для двигателей средней и большой мощности удобнее пользоваться упрощенной схемой замещения, приведенной на рис. 17.

Рис. 16. Т-образная схема замещения  асинхронного двигателя

Рис. 17. Упрощенная Г-образная схема замещения  асинхронного двигателя

Используя последнюю схему, легко найти токи и ЭДС в обмотках, подводимую и полезную мощность, а также мощность потерь при любой частоте вращения двигателя. Для этого следует лишь найти скольжение, соответствующее заданной частоте n, по формуле (4)
и вычислить сопротивление r₂‘/s в схеме по рис. 17. После этого нетрудно найти ток намагничивания I₀ и приведенный ток I₂‘ в роторной цепи, А:

              (32)

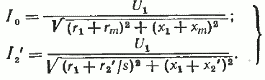
Это дает возможность вычислить электрические потери в обмотке статора трехфазного двигателя (m₁=3), Вт:

               (33)

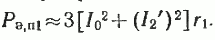
Электрические потери в обмотке ротора (Вт) можно найти, предварительно рассчитав по (30) приведенное сопротивление ротора r₂‘  (Ом):

              (34)

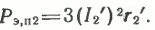
Суммарная активная мощность, передаваемая со статора на ротор, как видно из схемы (рис. 17), будет равна, Вт:

               (35)

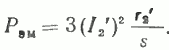
Эта мощность передается на ротор электромагнитным путем и поэтому называется электромагнитной мощностью.

Если из электромагнитной мощности вычесть мощность электрических потерь в обмотке ротора, то получим полную механическую мощность двигателя, Вт:

               (36)

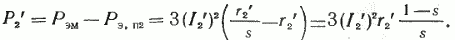
Полная механическая мощность расходуется на вращение приводного механизма (полезная механическая мощность) и на покрытие механических Р_мх.п и добавочных Р_д.п потерь самого двигателя. Поэтому полезная механическая мощность Р₂ будет равна, Вт:

               (37)

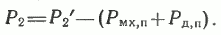
Коэффициент полезного действия двигателя по определению равен отношению отдаваемой (полезной механической) мощности к потребляемой (активной электрической) мощности. Разность между этими мощностями составляют потери в двигателе, равные, Вт:

 

где P_м.п=m₁I₀2r_m — магнитные потери или потери в стали. Таким образом, КПД двигателя равен:

              (38)

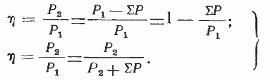
Использование первого или второго выражения для КПД определяется тем, какая из мощностей — P₁ или Р₂— известна. На практике наиболее часто применяется первое выражение (38).

Используя схему замещения, можно определить также ток, потребляемый двигателем из сети, т. е. ток статора, который равен сумме двух токов. Первый из них — это ток XX, который протекает по цепи 1 (рис. 17) и не изменяется при изменении частоты вращения ротора, второй — ток ротора I₂‘, который определяется по (32). Складывая геометрически эти два тока, можно получить ток статорной обмотки. Такое геометрическое сложение показано на рис. 18. Углы φ₂‘, φ₀, необходимые для построения, можно найти с помощью схемы замещения (см. рис. 17):

Таким образом, знание параметров схемы замещения (r₁, x₁, r₂‘, х₂‘, rm, хm) и приложенного напряжения U₁ (напряжение сети) позволяет с помощью приведенных выше формул определить полезную мощность, токи, потери, КПД, коэффициент мощности двигателя при различных скольжениях (частоте вращения).

Рис. 18. Диаграмма токов асинхронного двигателя  

Зависимости потребляемого тока I₁ и мощности Р₁, КПД, cosφ и скольжения s от полезной механической мощности P₂ носят название рабочих характеристик двигателя. Эти характеристики определяются при постоянном напряжении U₁ и частоте f₁ сети. Пример рабочих характеристик приведен на рис. 19.

Рис. 19. Рабочие характеристики асинхронного двигателя 

Рассмотрим рабочие характеристики асинхронного двигателя. При холостом ходе (полезная мощность Р₂—0) скольжение s также равно нулю (частота вращения ротора n практически равна синхронной), сопротивление r₂/’s равно бесконечности (см. рис. 17) и ток I₂‘==0. По обмотке статора протекает ток холостого хода I₀. Коэффициент полезного действия η равен нулю, так как равна нулю полезная мощность Р₂, а коэффициент мощности равен коэффициенту мощности для тока холостого хода (cosφ₁=cosφ₀).

При увеличении нагрузки частота вращения ротора уменьшается и увеличивается скольжение s. За счет увеличения s уменьшается сопротивление цепи 2 (см. рис. 17) и увеличивается ток ротора, а следовательно, и ток статоpa. Поскольку увеличивается полезная мощность, растет, КПД двигателя, а также коэффициент мощности.

Обычно номинальная мощность на валу двигателя достигается уже при небольшом понижении частоты вращения ротора и вся область рабочих режимов находится в диапазоне скольжений от 0 до 2—5%.

Поэтому скоростная характеристика n=f(P₂) у асинхронного двигателя имеет небольшой наклон к оси абсцисс. Характеристики такого вида принято называть жесткими. Соответственно характеристика s=f(P₂) имеет слабый подъем при возрастании нагрузки. В асинхронном двигателе частота вращения ротора меньше частоты вращения поля, за счет чего обеспечивается наведение ЭДС, а также создание тока 1% в обмотке ротора и вращающего электромагнитного момента, под действием которого ротор приходит во вращение.

Характеристика cosφ=f(P₂) лежит в области значений, меньших 1, так как асинхронный двигатель всегда потребляет ток I₀, почти не зависящий от нагрузки в диапазоне мощностей от Р₀ до Р₂≈Р_ном. При XX обычно  φ₀<0,2, т. е. он содержит большую реактивную составляющую. При увеличении нагрузки cosφ быстро возрастает и достигает максимального значения при мощности Р₂≈Р_2ном. При увеличении нагрузки выше номинальной cosφ  несколько снижается.

Коэффициент полезного действия достигает своего максимального значения при Р₂≈ (0,6÷0,8)Р_2ном и снижается при дальнейшем росте нагрузки. Поскольку двигатель обычно работает при переменной нагрузке, изменяющейся в пределах (0,6—1)Р_2ном, то КПД в этом диапазоне изменения нагрузки должен быть достаточно высок.

Макеты страниц