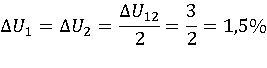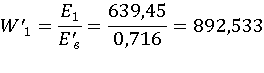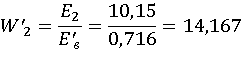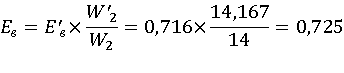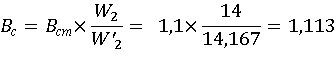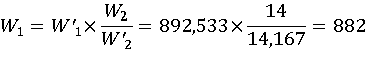ЭДС и МДС обмоток машин переменного тока
ЭДС. ЭДС катушки. При вращении магнитного поля относительно проводников обмотки в ней наводится ЭДС с частотой
fpn . 60
Обычно требуется, чтобы ЭДС была практически синусоидальна. Особенно это относится к генераторам, так как при несинусоидальной ЭДС появляются высшие гармоники ЭДС и тока, оказывающие вредное влияние на генератор и большинство приемников, вызывая в них увеличение потерь. Кроме того, токи высших гармоник способствуют возникновению перенапряжений на различных участках линии передачи и создают помехи в близлежащих линиях связи.
Форма кривой ЭДС в значительной мере зависит от формы кривой распределения магнитного поля на полюсном делении. Получить идеальное синусоидальное распределение этого поля практически невозможно. Улучшение кривой ЭДС достигается за счет правильного выбора схемы обмотки, для чего она выполняется распределенной с
|
укороченным шагом. |
|
|
Электродвижущая сила, ин- |
|
|
B x |
дуктируемая в фазе обмотки ма- |
|
шины переменного тока, может |
|
|
быть найдена как сумма ЭДС всех |
|
|
катушек, включенных в эту фазу, |
|
|
x |
поэтому определим сначала ЭДС |
одной катушки. Катушка состоит из витков, которые размещаются
|
Рис. 1.18. К определению ЭДС одного |
в одних и тех же пазах, поэтому |
|
|
проводника полюсное деление) |
||
|
можно считать, что все витки в |
||
магнитном поле будут находиться в одинаковых условиях. Виток образуется последовательным соединением двух проводников, расположенных в разных пазах на расстоянии y друг от друга.
При вращении магнитного поля относительно проводника в нем индуцируется ЭДС, мгновенное значение которой определяется по формуле:
ex B xlV .
При постоянной скорости V и неизменной активной длине l

проводника эта ЭДС пропорциональна нормальной составляющей индукции B x (рис. 1.18) в том месте окружности якоря, где в данный
момент находится рассматриваемый проводник. Кривая изменения ЭДС проводника во времени будет повторять форму кривой распределения индукции на протяжении двух полюсных делений машины.
В общем случае кривая распределения индукции имеет несинусоидальный характер. Ее можно разложить в гармонический ряд. Так как кривая индукции симметрична относительно оси абсцисс и оси полюсов, то при разложении в ней будут только нечетные гармоники (рис. 1.19), амплитуды которых уменьшаются с увеличением их порядка . Гармоники кривой поля называются пространственными, так как распределение индукций этих гармоник является функцией пространственных координат и от времени не зависит.
Характерной особенностью пространственных гармоник являет-
ся увеличение числа их полюсов и соответственно уменьшение полюсного деления пропорционально их порядку.
Магнитное поле каждой гармоники будет индуцировать ЭДС в обмотке. От поля 1-й (основной) гармоники в проводнике индуцируется ЭДС:
en1 Em n 1 sin t
|
амплитуда которой |
|||||||
|
Emn1 B m1lV , (1.5) |
|||||||
|
где B m1 – амплитуда индукции |
|||||||
|
Тл; l – активная длина проводника |
|||||||
|
При расчете ЭДС удобно |
|||||||
|
нии. Для 1-й гармоники |
|||||||
|
Ф В |
l |
2 |
, |
(1.6) |
|||
|
ср1 |
В т1 l |
||||||
|
где Bcp – среднее значение индукции; |
– полюсное деление, , |
D – |
|||||
|
диаметр якоря. |
|||||||
|
Так как для синусоиды B |
2 |
В |
, то из (1.6) получим |
||||
|
ср1 |
т1 |

|
B |
Ф1 |
. |
(1.7) |
||||
|
m1 |
2 l |
||||||
|
Подставляя (1.7) в (1.5) и учитывая, что |
|||||||
|
V |
Dn |
2p n |
2 f , |
||||
|
60 |
60 |
получаем
Emn1 fФ .
Для анализа обмоток и оценки некоторых их свойств удобно использовать векторные диаграммы. При построении диаграмм первую гармоническую ЭДС проводника будем изображать в виде временного вектора. Период изменения ЭДС проводника будет соответствовать перемещению магнитного поля относительно этого проводника на два полюсных деления. Это в угловом измерении соответствует 2 рад, или 360°. За 1 оборот якоря ЭДС в проводнике изменится на p перио-
дов, т.е. на 360° p . Таким образом, окружность, соответствующая
геометрическому углу 360°, в электрическом отношении соответствует углу 360° p. Этот угол называется электрическим.
Следовательно, один геометрический радиан (или градус) равен p «электрическим» радианам или p «электрическим» градусам.
Так как проводники, расположенные в соседних пазах, имеют
пространственный сдвиг 360 , то их ЭДС не будут совпадать по
Z
фазе. Электрический угол сдвига векторов ЭДС проводников, лежащих в соседних пазах, равен:
эл 360p p .
Z
Если витки катушки образованы из проводников, расположенных в пазах, отстоящих друг от друга на расстоянии полюсного деления y (рис. 1.20, а), то ЭДС этих проводников будут сдвинуты по фазе на угол 180° (рис. 1.20, б).

пК
ККy
N S
yп
НН
H
Рис. 1.20. К определению ЭДС одного витка
Поскольку проводники, образуя виток, соединяются встречно (конец K одногопроводника соединяется сконцом K другогопроводника), тоЭДС витка Eв будетравна геометрическойразностиЭДС проводников
(рис. 1.20, б). Как следует из векторной диаграммы, геометрическая разность ЭДС проводников равна их арифметической сумме. При укороченном шаге обмотки (y ) векторы ЭДС проводников будут сдвинуты по фазе на угол 180 , а поэтому их геометрическая разность будет меньше арифметической суммы ЭДС проводников. Действующее значение электродвижущей силы витка при y можно найти по векторной диа-
граммена рис. 1.20, вкак
Eв1 2Esin 4.44f 1Ky1 ,
2
где Ку sin – коэффициент укорочения, который учитывает
уменьшение ЭДС при укорочении шага обмотки. Электродвижущая сила катушки, содержащей Wк витков
|
Eк1 WкEв1 4,44f 1WкKy1. |
(1.8) |
ЭДС. ЭДС катушечной группы. Катушечная группа состоит из q одинаковых катушек, расположенных в соседних пазах (рис. 1.21).

Из-за пространственного сдвига катушек их ЭДС будут сдвинуты относительно друг друга по фазе на угол эл.
Все секции катушечной группы соединены между собой последовательно, и суммарная ЭДС группы будет равна геометрической сумме ЭДС отдельных секций, как показано на рис. 1.22.
Геометрическая сумма ЭДС катушечной группы Eq будет меньше
арифметической суммы ЭДС катушек qEк . Отношение Eq Kр qEк1
называется коэффициентом распределения обмотки и характеризует уменьшение ЭДС катушечной группы вследствие распределения обмотки на каждом полюсном делении по q пазам. Коэффициент Kр
можно определить с помощью векторной диаграммы на рис. 1.22. Рассматривая векторы Eк как часть многоугольника, вписанного в окружность с радиусом R , получаем
|
q |
эл |
||||||||||
|
sin |
|||||||||||
|
Eq1 |
2 |
||||||||||
|
Кр1 |
. |
||||||||||
|
qE |
к1 |
эл |
|||||||||
|
qsin |
|||||||||||
|
2 |
|||||||||||
Зная коэффициент распределения обмотки и учитывая формулу (1.8), находим ЭДС катушечной группы:

|
Eq1 qEк1Kр1 4.44f Ф1Wк1qKу1Kp1. |
(1.9) |
ЭДС. ЭДС фазы. Двухслойная обмотка фазы состоит из p ка-
тушечных групп, а однослойная – из p групп. Катушечные группы могут быть соединены последовательно или параллельно. Все катушечные группы состоят из p катушек с числом витков Wк . Если об-
мотка фазы состоит из a параллельных ветвей, то общее число последовательно соединенных витков фазы, равно:
для двухслойной обмотки
W 2pqWк ,
a
для однослойной обмотки
W pqWк . a
Тогда с учётом формул (1.8) и(1.9) ЭДС фазы обмотки от поля 1-ой гармоники
|
E1 4.44f WKy1Kp1Ф . |
(110) |
ЭДС. Улучшение формы кривой ЭДС. В обмотке фазы кроме ЭДС 1-ой гармоники будут индуцироваться ЭДС от высших гармоник магнитного поля. Электродвижущая сила от высших гармоник определяется по формуле
|
E |
. f WKy Kp Ф , |
(1.11) |
|
где f f – частота ЭДС |
– ой гармоники; |
– магнитный поток |
|
-ой гармоники, Ky , Kp |
– коэффициенты укорочения и распреде- |
|
|
ления для -ой гармоники. |
Число полюсов для -ой гармоники в раз больше, чем для 1- ой. Поэтому электрические углы сдвига между ЭДС для высших гармоник будут в раз больше, чем для 1-ой. С учетом этого

|
sinq |
эл |
||||||
|
2 |
|||||||
|
Kу sin |
; |
Kр |
. |
||||
|
2 |
|||||||
|
qsin |
эл |
||||||
|
2 |
Определяя по формулам (1.10) и (1.11) ЭДС для 1-й – Е , 3-й –
Е , 5-ой – E и т.д. гармоник, можем найти действующее значение результирующей ЭДС фазы:
Е 
Уменьшению амплитуды высших гармонических ЭДС и за счет этого приближению кривой результирующей ЭДС фазы к синусоидальной способствуют укорочение шага обмотки и распределение ее по пазам.
При укорочении шага обмотки форма кривой результирующей ЭДС улучшается вследствие того, что происходит более резкое уменьшение ЭДС высших гармоник, индуцируемых в секции, по сравнению с ЭДС 1-ой (основной) гармоники. Численно это учитывается посредством коэффициента укорочения для каждой гармоники. При укороче-
|
нии шага на |
1 |
часть полюс- |
|
ного деления в кривой ЭДС полностью исчезает -ая гармоника. В этом можно убедиться, рассмотрев рис. 1.23, на котором изображена катушка. Ширина ее равна полюсному делению. При y проводни-
ки витка будут располагаться под разноименными полюсами 5-ой гармоники и индуцируемые ими ЭДС в контуре витка будут суммироваться.
Если произвести укорочение шага обмотки на / , то стороны витка окажутся под полюсами одинаковой полярности и индуцируемые ими ЭДС проводников витка взаимно компенсируются. Вследствие это-

го в кривой результирующей ЭДС витка будет полностью отсутствовать 5-ая гармоника. Приэтом также уменьшатся иЭДС других гармоник.
При выборе шага обмотки следует стремиться к тому, чтобы уничтожить полностью или значительно ослабить ЭДС тех гармоник, которые наиболее сильно проявлены в магнитном поле.
Пространственные гармоники магнитного поля резко уменьшаются с увеличением их порядка, поэтому наиболее сильно будут проявляться 3, 5 и 7-ая гармоники. Третью гармонику в линейной ЭДС обычно уничтожают соединением трехфазной обмотки в звезду. Для ослабления 5-ой и 7-ой гармоник шаг обмотки выбирают в пределах от
y 4 до y 6 . 5 7
При увеличении числа пазов на полюс и фазу q также происходит
улучшение формы кривой результирующей ЭДС фазы, так как при этом сильно уменьшаются коэффициенты распределения, а, следовательно, и ЭДС гармоник. Это объясняется тем, чтоЭДС катушеккатушечных групп для -x гармоник будут сдвинуты относительно друг друга на угол, в раз больший, чем для 1-ой гармоники, вследствие чего их геометрическая сумма уменьшается. Значения коэффициента распределения трехфазных обмотокприведены в табл. 1.1.
Таблица 1.1
|
Порядок |
Коэффициент распределения Кр |
трехфазной |
|||||
|
обмотки с фазной зоной 60° при различных q |
|||||||
|
гармоник |
|||||||
|
q 2 |
q 3 |
q 4 |
q 5 |
q 6 |
|||
|
1 |
0,966 |
0,960 |
0,958 |
0,957 |
0,957 |
||
|
3 |
0,707 |
0,667 |
0,654 |
0,646 |
0,644 |
||
|
5 |
0,259 |
0,217 |
0,205 |
0,200 |
0,197 |
||
|
7 |
0,259 |
0,177 |
0,158 |
0,149 |
0,145 |
||
|
9 |
0,707 |
0,333 |
0,270 |
0,247 |
0,236 |
||
|
11 |
0,966 |
0,177 |
0,126 |
0,110 |
0,102 |
||
|
13 |
0,966 |
0,217 |
0,126 |
0,102 |
0,092 |
||
|
15 |
0,707 |
0,667 |
0,270 |
0,200 |
0,172 |
Кривая результирующей ЭДС обмотки с большим q ближе к

синусоиде. Однако следует иметь в виду, что с возрастанием q маши-
на становится дороже из-за относительного увеличения объема изоляции и удорожания работ по выполнению обмотки. Обычно q выбира-
|
ется равным 2–6. |
|||
|
Искажение кривой ЭДС вызыва- |
|||
|
ется |
также |
пульсациями магнитного |
B |
|
поля |
вследствие зубчатого строения |
B 1 |
|
|
статора и ротора (рис.1.24, 1.25, а). |
|||
|
Наличие пазов и зубцов на статоре и |
|||
|
роторе приводит к перераспределе- |
|||
|
нию потока в воздушном зазоре |
|||
|
вдоль полюсного деления . В тех |
|||
|
местах, где зубец располагается под |
|||
|
зубцом, индукция увеличивается, а в |
|||
|
тех местах, где под зубцом распола- |
|||
|
гается паз или под пазом паз – ин- |
|||
|
дукция уменьшается. В результате |
|||
|
этого кривая распределения индукции |
1 |
||
|
приобретает |
пилообразный характер |
||
|
(рис. 1.24, 1.25, б), а в магнитном поле |
Рис. 1.24. Искажение кривой |
||
|
появляются |
гармоники, называемые |
||
|
зубцовыми. |
Порядок этих гармоник |
индукции вследствие зубчатости |
|
зависит от числа зубцов. |
статора |
|
Зубцовые гармоники поля индуцируют в обмотках ЭДС, которые |
|
|
вызывают токи, ухудшающие характеристики машины. |
|
|
Для уменьшения зубцовых гармоник в кривой ЭДС применяют |
скос пазов или скос полюсов. Если скос выполняется на статоре, то он производится на одно зубцовое деление ротора, а если на роторе – на одно зубцовое деление статора.
При скосе пазов можно полностью уничтожить зубцовые гармоники в ЭДС. Физически это можно объяснить тем, что у зубцовых гармоник магнитное поле под зубцом и пазом имеет противоположную полярность, вследствие чего в отдельных участках проводника, расположенного в скошенном пазу противоположного магнитопровода, индуцируются одинаковые по значению, но противоположные по направлению ЭДС (рис. 1.25, в), а их сумма равна нулю.
При скосе пазов будет происходить уменьшение ЭДС 1-ой гармоники, что необходимо учитывать при расчете.

Рис. 1.25. Влияние скоса пазов на ЭДС в проводнике, лежащем в этом пазу:
а– пазы; б – зубцовая гармоника магнитного поля;
в– проводник в скошенном пазу
При скосе пазов каждый проводник, лежащий в пазу, по своей длине в магнитном поле находится в разных условиях, вследствие чего ЭДС отдельных его участков будут сдвинуты по фазе и должны складываться геометрически. Уменьшение ЭДС проводника в результате геометрического сложения учитывается коэффициентом скоса.
Примем, что скос равен bск , или в угловом измерении
с bск . Заменим проводник, лежащий в скошенном пазу, очень
большим (в пределе бесконечно большим) числом прямых проводников очень малой длины (рис. 1.26, а). Геометрическая сумма ЭДС этих малых проводников будет равна хорде окружности с радиусом R , а их арифметическая сумма – длине дуги, на которую опираются стороны угла с (рис. 1.26, б). Коэффициент скоса, равный отношению геомет-
рической суммы ЭДС к арифметической, будет равен: для 1-ой гармоники
|
c |
c |
||||||||||
|
2Rsin |
2sin |
||||||||||
|
2 |
2 |
||||||||||
|
Кск1 |
, |
||||||||||
|
R c |
c |
||||||||||
для -той гармоники
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
напряжение
вторичных обмоток.
При
расчете трансформатора на минимум стоимости обмотку с наименьшим диаметром
провода выгодно располагать на стержне первой, так как это дает экономию в
затратах. Из этого можно сделать вывод, что обмотки располагаются в
порядке 1-2-3, так как ток первого трансформатора является наименьшим.
Разобравшись с расположение обмоток, вычисляем ЭДС по формулам:
( 2.2)
где –
падение напряжения на обмотках трансформатора в процентах от номинальных
значений напряжений соответствующих обмоток, %;
–
напряжение обмоток.
Для нахождения ЭДС рассчитываем напряжение на обмотках, которые вычисляются
по формулам:
(2.3)
где –
падение напряжения на вторичных обмотках трансформатора при номинальной
нагрузке;
– падение
напряжения на обмотках трансформатора в процентах от номинальных значений
напряжений соответствующих обмоток, %;
Подставляем
найденные значения в формулу для вычисления ЭДС и получаем, что:
(2.2)
Далее находим ЭДС одного витка по нижеизложенной формуле:
(2.4)
где f- частота, данная в таблице «Исходных
данных»;
– предварительное значение магнитной индукции;
– поперечное сечение стержня сердечника трансформатора
определенное по формуле (1.7);
– коэффициент заполнения магтитопровода, которое дано в табл.
1.4.
Определяем число витков соответствующих обмоток трансформатора:
(2.5)
где – ЭДС
одного витка, найденного по формуле;
,
,
–
вычисленное ЭДС, .
Округляется число витков обмотки низшего напряжения до ближайшего целого
числа:
Пересчитываем ЭДС витка, величины индукции в стержне и числа витков, в
других обмотках подставив округленное число витка низшего напряжения:
(2.6)
где –
действительные значения ЭДС одного витка магнитной индукции в стержне и числа
витков в обмотках трансформатора;
– ЭДС
одного витка;
,
,
– число
витков соответствующих обмоток трансформатора;
округленное
число витков обмотки низшего напряжения.
Найденные витки в обмотках трансформатора округляем до ближайшего целого
числа:
3РАСЧЕТ ПОТЕРЬ В СТАЛИ И ТОКА НАМАГНИЧЕВАНИЯ
ТРАНСФОРМАТОРА
Находим
потери в стали сердечника трансформатор по формуле:
.
(3.1)
где
–
удельные потери в сердечнике;
–
масса стали;
–
коэффициент увеличения потерь, в сердечнике выбираемый из табл. 3.1, нужно
уменьшить в 1,2 раза, потому что нами рассматривается большой сердечник;
–
удельные потери в материале зависит от:
· магнитной
индукции: ;
·
марки стали: 3415;
·
толщины листа: ;
· частоты
сети: f=400 Гц и выбирается из табл. 3.2, где
Вт/кг.
Находим
массу стали трансформатора по формуле:
(3.2)
где =
7,8 · 10-6 – удельный вес стали, кг/мм3;
-поперечное сечение стержня сердечника трансформатора;
-коэффициент заполнения магтитопровода;
–
длина средней магнитной линии в сердечнике трансформатора, которая определяется
по формулам, приведенным в табл. 3.3.
Нами
рассматривается стержневой ленточный двухкатушечный трансформатор, поэтому длина
средней магнитной линии вычисляется по формуле:
(3.3)
где h – высота окна сердечника;
с -ширина окна сердечника;
а – ширина стержня.
Найдя
длину средней магнитной линии, можем определить массу стали трансформатора по
формуле (3.2):
(3.2)
Подставляем
вычисленную длину средней магнитной линии и удельную потерь в сердечнике и находим
потери в стали сердечника трансформатора:
.
(3.1)
Вычисляем
активную составляющую тока холостого хода:
(3.3)
где –
потери в стали сердечника, найденные по формуле (3.1);
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
Основная формула трансформаторной ЭДС
Возьмем катушку с ферромагнитным сердечником и вынесем отдельным элементом омическое сопротивление обмотки как это показано на рисунке 1.
Рисунок 1. Катушка индуктивности с ферромагнитным сердечником
При подаче переменного напряжения ec в катушке, cогласно закону электромагнитной индукции, возникает ЭДС самоиндукции еL.
Потоком рассеяния пренебрегаем. Приложенное к катушке напряжение и наведённая ЭДС уравновешиваются. По второму закону Кирхгофа для входной цепи можно записать:
где Rобм — активное сопротивление обмотки.
Поскольку , то падением напряжения на омическом сопротивлении пренебрегаем, тогда . Если напряжение сети гармоническое, , то:
Найдем из этой формулы магнитный поток. Для этого перенесем количество витков в обмотке в левую часть, а магнитный поток Ф в правую:
Теперь возьмем неопределённый интеграл от правой и левой частей:
Так как магнитопровод считаем линейным, то в цепи протекает только гармонический ток и нет постоянного магнита или постоянной составляющей магнитного потока, то постоянная интегрирования . Тогда дробь перед синусом является амплитудой магнитного потока
откуда выразим амплитуду входной ЭДС
Его действующее значение равно
Выражение (9) называют основной формулой трансформаторной ЭДС, которая справедлива только для гармонического напряжения. При негармоническом напряжении её видоизменяют и вводят так называемый коэффициент формы, равный отношению действующего значения к среднему:
Найдем коэффициент формы для гармонического сигнала, при этом среднее значение находим на интервале от 0 до π/2
Тогда коэффициент формы равен 
Если сигнал является последовательностью прямоугольных импульсов одинаковой длительности (меандр), то амплитудное, действующее и среднее значения за половину периода равны между собой и его . Можно найти коэффициент формы и для других сигналов. Основная формула трансформаторной ЭДС будет справедлива.
Построим векторную диаграмму катушки с ферромагнитным сердечником. При синусоидальном напряжении на зажимах катушки её магнитный поток тоже синусоидальный и отстаёт по фазе от напряжения на угол π/2 как показано на рисунке 2.
Рисунок 2. Векторная диаграмма катушки с магнитным сердечником без потерь
В катушке без потерь намагничивающий ток — реактивный ток (Ip) совпадает по фазе с магнитным потоком Фm. Если в сердечнике есть потери (), то угол — это угол потерь на перемагничивание сердечника. Активная составляющая тока Iа характеризует потери в магнитопроводе.
Рисунок 3. Векторная диаграмма катушки с магнитным сердечником с потерями
Понравился материал? Поделись с друзьями!
Вместе со статьей «Основная формула трансформаторной ЭДС» читают:
Источник
Задачи на тему «Трансформатор» с решением
Трансформатор – устройство для изменения напряжения или тока. В сегодняшней статье рассмотрим несколько простых задач на расчет трансформаторов.
Подписывайтесь на нас в телеграме, чтобы не пропустить ничего важного. А если хотите получить скидку – загляните на наш второй канал с акциями и бонусами для клиентов.
Задачи на расчет трансформаторов
Задача на трансформатор №1
Определите напряжение на концах первичной обмотки трансформатора,имеющей N1=2000 витков, если напряжение на концах вторичной обмотки, содержащей N2=5000 витков, равно 50 В. Активными сопротивлениями обмоток трансформатора можно пренебречь.
Применим форулу для коэффициента трансформации:
Из данной формулы следует, что:
Подставим значения и вычислим:
Ответ: 20 В.
Задача на трансформатор №2
Первичная обмотка трансформатора находится под напряжением 220 В, по ней проходит ток 0,5 А. На вторичной обмотке напряжение составляет 9,5 В, а сила тока равна 11 А. Определите коэффициент полезного действия трансформатора.
Формула для коэффициента полезного действия трансформатора:
Здесь P=UI – мощность тока в обмотке.
Возьмем данные из условия и применим указанную формулу:
η = U 2 I 2 U 1 I 1 · 100 % η = 9 , 5 · 11 220 · 0 , 5 · 100 % = 95 %
Задача на трансформатор №3
Напряжение на первичной обмотке понижающего трансформатора 220 В, мощность 44 Вт. Определите силу тока во вторичной обмотке, если отношения числа витков обмоток равно 5. Потерями энергии можно пренебречь
Напряжение на вторичной обмотке будет равно:
U 2 = U 1 k U 2 = 220 5 = 44 В
Если считать, что потерь энергии нет, то мощность во вторичной обмотке будет такая же, как и в первичной:
I 2 = P 2 U 2 = 44 В т 44 В = 1 А
При решении задач не забывайте проверять размерности величин!
Задача на трансформатор №4
Понижающий трансформатор включен в сеть с напряжением 1000 В и потребляет от сети мощность, равную 400 Вт. Каков КПД трансформатора, если во вторичной обмотке течет ток 3,8 А, а коэффициент трансформации равен 10?
Сначала определим напряжение на вторичной обмотке трансформатора:
U 2 = U 1 k = 1000 10 = 100 В
Запишем формулу для КПД трансформатора и рассчитаем:
η = P 2 P 1 · 100 % = U 2 I 2 P 1 · 100 % η = 100 · 3 , 8 400 · 100 % = 95 %
Задача на трансформатор №5
Вторичная обмотка трансформатора, имеющая 95 витков, пронизывается магнитным потоком, изменяющимся со временем через один виток по закону Ф = 0 , 01 sin 100 π t . Напишите формулу, выражающую зависимость ЭДС во вторичной обмотке от времени.
По закону электромагнитной индукции:
Продифференцируем магнитный поток по времени:
d Ф d t = d ( 0 , 01 sin 100 π t ) d t = 0 , 01 · 100 π · cos 100 π t = πcos 100 πt
Подставим результат в формулу для ЭДС:
От минуса в данном выражении можно избавиться с помощью формул тригонометрии. Сделаем это и запишем окончательный результат:
ε = N π sin ( 100 π t — π 2 ) = 95 π sin ( 100 π t — π 2 )
Ответ: 95 π sin ( 100 π t — π 2 )
Вопросы на тему «Трансформаторы»
Вопрос 1. Что такое трансформатор?
Ответ. Трансформатор – статическое устройство, имеющее две или более связанные обмотки на магнитопроводе. Трансформатор предназначен для преобразования одной величины напряжения и тока в другое без изменения частоты посредством электромагнитной индукции.
Основное назначение трансформаторов: изменять напряжение переменного тока.
Вопрос 2. Где используются трансформаторы?
Ответ. Трансформатор – очень распространенное устройство в электронике и электротехнике. Трансформаторы используются:
- В сетях передачи электроэнергии.
- В радиоэлектронных приборах (услилители низкой частоты и т.д.)
- В источниках электропитания практически всех бытовых приборов.
Вопрос 3. Какие бывают трансформаторы?
Ответ. Трансформаторы делятся на:
- силовые;
- сварочные;
- измерительные;
- импульсные;
- разделительные;
- согласующие и т.д.
Помимо этого трансформаторы разделяют по числу фаз: однофазные, двухфазные, трехфазные и многофазные.
Вопрос 4. Из чего состоит простейший трансформатор?
Ответ. Основными элементами любого трансформатора являются изолированные обмотки, намотанные на сердечник.
Вопрос 5. Когда изобрели трансформатор?
Ответ. Прообразом трансформатора считается индукционная катушка француза Г. Румкорфа, представленная в 1848-м. В 1876 году русский электротехник П. Н. Яблочков запатентовал трансформатор переменного тока с разомкнутым сердечником. Затем английские братья Гопкинсон, а также румыны К. Циперановский и О. Блати доработали устройство, добавив замкнутый магнитопровод. В таком виде конструкция трансформатора остается актуальной и по сей день.
В основе работы трансформатора лежит явление электромагнитной индукции, открытое Майклом Фарадеем.
Проблемы с учебой? Обращайтесь в сервис помощи студентам в любое время!
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Источник
Как правильно провести расчет трансформаторов разных видов, формулы и примеры
Сложные многофункциональные устройства, способные преобразовывать электроэнергию из одной величины в другую, на языке электротехники, называют трансформаторами. Для создания такого оборудования, в зависимости от конкретных величин преобразования, применяется специальный расчет. Как правильно проводить расчет трансформаторов, знать в нем основные параметры и формулы, правильно их использовать, уметь пользоваться упрощенной системой проектирования трансформаторов распространенных энерговеличин и становится целью содержания этой статьи.
Принцип работы
Любая энергосистема, установка, особенно в сети трехфазного (3ф) тока и напряжения просто не могла и не может обойтись без такого функционального устройства, как трансформатор. В высоковольтных сетях он производит повышение напряжения, получая его непосредственного из недр генератора и направляя в высоковольтные линии электропередач. На том конце линий тоже стоят трансформаторы высокого напряжения, которые уже производят процесс понижения его величины для подачи на объекты, которыми являются обычные потребители.
Трансформаторы тока в тех же мощных электроустановках производят преобразования первоначальной токовой величины в номинальные его значения, допустимые для питания контрольных и измерительных приборов, защит, учетных систем и прочих энергетических элементов.
В бытовых нуждах, однофазного тока и напряжения широко используют различные трансформаторы, которые преобразуя электрические величины обеспечивают питанием многие бытовые приборы, являются источником различного освещения, питают системы электроники и мультимедиа. В целом, без таких преобразователей в электричестве никуда.
Конструкция
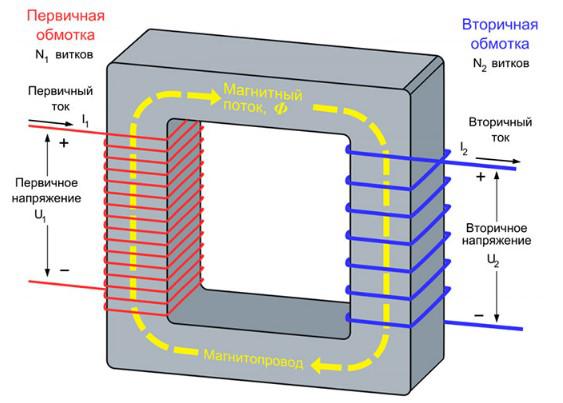
На примере простейшего однофазного трансформатора возможно подробно рассмотреть его основные конструктивные элементы и узнать основы принципа его работы. Конструктивно такой трансформатор состоит из трех главных элементов:
- Первичная обмотка – катушка с изолированными проводниками, намотанная в определенном порядке, выводы которой являются принимающим определенную величину электроэнергии. Проводники первичной обмотки передают электроэнергию дальше, для проведения ее трансформации;
- Магнитопровод или сердечник – выполненный из специальной шихтованной (слоенной) электротехнической стали, различной конструкции и формы. На его части с одной и другой стороны наматываются проводники обмоток и именно в нем происходит бесконтактное явление трансформации величины электроэнергии;
- Вторичная обмотка – изолированные проводники, с намоткой на вторую часть сердечника в определенном количестве, с конкретной толщиной. Выводы вторичных проводников передают выходную величину энергии к потребителю или другому энерго устройству, в цепь которого был установлен преобразователь.
Особенности
Принцип работы любого трансформатора основан на явлении электромагнитной индукции, в замкнутом контуре магнитопровода, сквозь намотанные на него проводники первичной и вторичной обмотки. Подключенная к сети переменного тока первичная обмотка создает в замкнутом контуре магнитное поле с движущимся по кольцу магнитопровода магнитным потоком. Его движение проходит, через обе намотки обмоток и согласно закону индукции, создает в них электродвижущую силу (ЭДС).
Величина ЭДС напрямую зависит от количества витков в обмотках, сечения проводников и отличительными особенностями между первичной и вторичной обмотками. ЭДС, в системе трансформатора, это и есть выходное напряжение на выводах преобразователя. Чтобы ее величина стала меньше входного сигнала – количество витков вторичной обмотки должно быть меньше первичной катушки трансформатора.
Проектирование функций устройств преобразования, точное определение способности преобразования электровеличины – мощности трансформатора, количества витков обмоток, формы их намотки, выбор материала магнитопровода, его форма и размеры как раз и определяется в процессе расчета трансформатора.
Формулы расчета силового трансформатора
В силовой энерго установки при проектировании модели и типа трансформатора применяются основные формулы расчета его главных параметров и конструктивных величин. Как выполнить в некоторых подробностях стоит разобрать ниже.
Мощность вторичной обмотки
В зависимости от того, в какой сети (однофазной или трехфазной) участвует трансформатор, какой по типу трансформации – повышающей или понижающей, будет являться его вторичная обмотка, а так же при наличии конкретных данных указанных величин возможно произвести расчет мощности вторичной обмотки, согласно известной формулы электротехники.
Формула 1. Мощность вторичной обмотки трансформатора:
P2 – величина электрической мощности вторичной обмотки, единицы измерения – Вт;
U2 – напряжение сети вторичной обмотки, на выходе трансформатора, единицы измерения – В;
I2 – ток вторичной обмотки, возникшей на выходе трансформатора, и предназначенный для питания подключенного к нему потребителя и другого энергоустройства.
Общая мощность
Для силовых трансформаторов, особенно повышающего типа, всегда стоит учитывать потери, возникающие в проводниках обмоток, стали магнитопровода, которые влияют на коэффициент полезного действия устройства. Поданная мощность на первичную обмотку трансформатора, за счет электрических потерь в устройстве преобразователя всегда будет больше ее вторичного выходного сигнала. Отсюда КПД силового трансформатора будет равен 0,8-0,85 от ее величины.
При расчете общей мощности трансформатора потери и оставшееся полезное действие на выходе электроагрегата стоит учитывать в виде произведения полученной мощности вторичной обмотки P2 и КПД устройства.
Формула 2. Полная мощность с учетом КПД:
Это будет более реальная величина мощности выходной обмотки трансформатора. Остальные параметры в расчетных формулах будут зависеть от количества витков первичной и вторичной обмоток, их сечения, материала проводников. Строение, материал и форма сердечников в свою очередь тоже имеет немаловажное значение в проведении точных и верных расчетов силовых трансформаторов.
Понятие полной мощности трансформатора так же включает в себя более широкое понятие мощностных характеристик в зависимости от типа устройства. Если трансформатор имеет несколько вторичных обмоток, то его полная мощность (Sполн.) будет равна сумме активных мощностей этих обмоток (P2.1+P2.2+….+P2.N), умноженных на коэффициент мощности (Км).
Формула 3. Полная мощность с коэффициентом мощности:
В любом случае в ее расчет всегда закладывают величины активной мощности – энергии, которая продуктивно потратится на питание электро потребителей или других электро систем в составе установки, а так же реактивную составляющую мощности, выраженную в простейших расчетах в виде КПД трансформатора, а боле детальных формулах представляющих собой коэффициент мощности. Так в общей мощности участвуют активная и реактивные составляющие трансформатора, единицы измерения ее представлены в вольтамперном произведении – ВА.
Это значение реактивной составляющей является справочным табличным значением в зависимости от трансформатора, строения, сечения и материала его сердечника.
Сечение сердечника
Строение сердечника в любом трансформаторе в зависимости от его назначения имеет несколько основных видовых особенностей. Магнитопроводы преобразователей электро энергетических величин всегда выполняются из прессованных (шихтованных) железных или стальных пластин. Отказ в применении монолитного сердечника в трансформаторе, выбор в пользу пластинчато-прессованного его строения связан, с уменьшением потерь выходных величин трансформатора, уменьшением вихревых токов в магнитопроводе, а значит повышением его КПД.
От того, где преимущественно будет использован трансформатор, применяют три основных конструктивных формы строения его сердечника:
- броневые – на Рис. 1 модели «1» и «4»;
- стержневые – на Рис. 1 модели «2» и «5»;
- кольцевые. – на Рис. 1 модели «3» и «6»;
Методы изготовления каждого из них в зависимости от детальных форм и различий выполняют производственными процессами типа штамповки или навивания стальной проволоки.
Рисунок 1. Типы сердечников и параметры расчета сечения магнитопровода
На Рис. 1 подробно представлены формы каждого из строений сердечника, обозначены два параметра (A и B), измеряемые в сантиметрах, посредством которых производят расчет сечение конкретного магнитопровода.
Формула 4. Площадь сечения сердечника трансформатора:
Единицы измерения – сантиметры в квадрате см 2
Произведением этих двух величин можно получить значение сечения магнитопровода, которое будет крайне необходимо для проведения остальных расчетов трансформатора.
Количество витков
Первоначальный этап расчета трансформатора электроэнергии. От значения зависят величины трансформации энергии оборудования, а также изменения выходных номиналов на клеммах вторичных обмоток.
Вычисления количества витков в намотке первичной и вторичной обмотки тесно связаны с предыдущем понятием – сечения магнитопровода. Производится по двум формулам: начальной и конечной. В состав расчета начальной формулы входит выяснения расчетного значения витков обмоток трансформаторов на единицу напряжения, равную 1В. Формула в составе имеет справочный коэффициент сердечника.
Формула 5. Количество витков в обмотке на 1В:
N1v – количество витков обмотки на единицу напряжения равную 1 В;
K – технический коэффициент формы магнитопровода: для Ш-образного сердечника значение принято – 60; П-образного из пластин – 50; кольцевого – 40.
S – сечение сердечника, полученного из расчета, выполненного ранее и описанного выше.
Конечная формула расчета сводится к применению следующей формулы, из которой можно получить значение количества витков в полном объеме.
Формула 6. Количество витков обмоток трансформаторов:
Wv -значение количества витков в обмотке;
N – количество витков на 1В полученное в начальной формуле;
U – величина напряжения обмотки без нагрузки (на холостом ходу).
После применения подобного расчета количества витков в обмотках, особенно в проектировании трансформаторов минимальной мощности, применяют 5% компенсационный коэффициент падений напряжения на обмотках. Тем самым расчетные значения увеличивают на 5% от их расчетной величины.
Выбор пластин для сердечника
Зависимость применения различных материалов самих магнитопроводов, их форм, конструкции и производству пластин сердечника трансформаторов, строится на уменьшении потерь различного рода в результате преобразовательных процессов работы устройства, уменьшении значения вихревых токов на сердечнике, по средствам увеличения электрического сопротивления сердечника.
Для производства, создания сердечников силовых трансформаторов применяются разнообразные типы электротехнической стали. Из нее производят пластины, которые после изолировании между собой производят сборку определенных форм магнитопровода. Самые распространенные виды сердечников выполняются из:
- Ш-образных стальных пластин – тип сердечника трансформатора, выполненного по технологии штамповки пластин между собой, предварительно качественно изолировав их друг от друга. Имеют два отличия соединения стержней с ярмом сердечника. Могут собираться встык или вперемешку. По форме пластины такого рода напоминают букву «Ш», от которой и получили свое название.
- П – образных пластин – так же штампованный тип сердечника, по форме напоминающий букву «П». Несколько мене распространен в производстве магнитопровода, так как имеет хуже магнитные характеристики.
- «Торро» или кольцевая форма – сердечник выполнен не штамповкой, а навиванием стальной проволоки. По магнитным характеристикам имеют самые лучшие показатели, но на практике не смогли получить широкого распространения в связи с сложным процессом их производства и включения в состав трансформатора, как готового устройства.
Оценивая при расчете параметры напряжения, тока, мощности в значениях активной и реактивной энергии, выяснив количество витков обмотки и сечение магнитопровода стоит обратится к детальному выбору пластин сердечника и его оптимальной формы в конкретике расчетного проекта конкретного преобразователя.
Определение толщины набора сердечника
Один из окончательных расчетов геометрии сердечника, который выполняется в большинстве случаев, обращаясь к справочной технической литературе, где указаны табличные значения геометрии шаблонных форматов сердечников разного вида пластин и их материала.
Формулы расчета этого параметра существуют, исходят из показателей диаметра стержня магнитопровода, толщины листа пластин при их сборке, специальных коэффициентов заполнения в зависимости от толщины листа и прочих технически сложных параметров.
Формула 7. Площадь сечения Ш-образного сердечника:
S ш – значение площади сечение Ш-образного магнитопровода;
Полная мощность трансформатора, если имеет место двух катушечный тип устройства рассчитывается по Формуле 2, если вторичных обмоток много – рассчитывается по Формуле 3.
А уже после возможно определить значение толщины пластин сердечника по формуле.
Формула 8. Толщина пластин Ш-образного сердечника:
Tш – толщина пластин сердечника, мм;
S ш – площадь сечения Ш-образного сердечника, см 2 ;
A – ширина среднего лепестка Ш-образного сердечника, мм.
Для сборки в заводских условиях подобные расчеты имеют автоматизированный характер, если значения необходимы радиолюбителям или начинающим электронщикам – проще обратится к стандартным базовым шаблонам того или иного сердечника. Получить такие параметры из справочника возможно, зная значение диаметр стержня сердечника.
Как рассчитать габаритную мощность
Окончательный геометрический параметр трансформатора зависит от комплекса всех ранее рассчитанных величин магнитопровода, добавляя к ним электромагнитные справочные значения, а также значения проводников первичной и вторичной обмоток, их сечения, материал и остальное.
Существует вариант определения мощности, на которую максимально рассчитан трансформаторный материал сердечника, его сталь, по величине сечения магнитопровода. Такой вариант расчета мощности магнитопровода является крайне наглядным. Ошибки в нем могут составлять до 50%. Поэтому лучше, воспользовавшись несколькими основными геометрическими величинами и справочными данными произвести расчет геометрической мощности по формуле.
Формула 9. Габаритная мощность трансформатора:
Pгеом. – величина геометрической мощности для понижающего или повышающего типа трансформатора;
B – справочное значение и параметр индукции, наводящейся в конкретном магнитопроводе, измеряется в Тесла;
S – сечение магнитопровода, расчет которой по Формуле 4;
1,69 – постоянный поправочный коэффициент из технических справочников.
Зная параметры геометрии проектируемого трансформатора, используя приведенную формулу достаточно легко рассчитать геометрическую мощность трансформаторного изделия, с целью понимания его максимальных значений и возможностей в размерном эквиваленте.
Главный фактор в расчете параметра мощности геометрии трансформатора – превышение ее расчетной величины над значением электрической мощности.
Этот электромеханический параметр очень важный при дальнейшем определении параметров проводников в обмотках. Зная геометрическую мощность проекта преобразователя, уже точно нельзя будет ошибиться с диаметром проводника в расчетах обмоточных данных устройства.
Правильный расчет по сечению сердечника
Из электротехнических научных опытов, практики работы с трансформаторами известно, что стержневые сердечники в преобразователях энергии целиком носят обе обмотки на стержнях конструкций магнитопроводов, броневые конструкции лишь частично охватываются намоткой первичных и вторичных проводников катушек, и наиболее равномерное распределение, а значит и самые лучшие магнитные свойства устройства имеют кольцевые сердечники энергоагрегатов преобразования энергии, но они в связи со многими сложными пунктами своего строения, а главное тяжести сборки все меньше и меньше участвуют в реальной работе.
Электротехническая сталь тонкими пластинами, изолированными между друг другом различными диэлектриками образуют строение наиболее популярных сердечников стержневого и броневого типа. Площадь поперечного сечения для таких сердечников оказывает громадное влияние на электрическую мощность трансформатора.
Рассматривая стандартный Ш-образный магнитопровод, зная, что сечение его сердечника рассчитывается по Формула 4, и не имея других электрических параметров, таких как допустимый ток первичной или вторичной обмотки, напряжение на обоих выводах, вполне точно и правильно возможно вычислить электрическую мощность устройства.
Формула 10. Расчет электрической мощности по сечению сердечника:
Pтр-р – электрическая мощность расчетного сердечника, Вт;
S – площадь сечения магнитопровода оборудования, см 2 .
Зависимость двух мощностей в расчетном проекте преобразователя энергии видно из формулы достаточно наглядно.
Учет площади сечения сердечника к тому же еще необходим для недопущения попадания стали магнитопровода в большую зону магнитного насыщения. Неправильный расчет площади может привезти именно к этому. Создать режим трансформатора от микроволновки, но обеспечения кратковременного режима работы. А это значит получение режима перегрузки в работе, износ, потери на выходе вторичной обмотки.
Окончательный показатель, оценивающий важность верного расчета площади сечения сердечника, называется коэффициентом заполняемости окна сердечника проводниковой медью первичной и вторичных обмоток. Если сравнивать по этому параметру кольцевой трансформатор с броневым или стержневым – значения конечно же сильно будут разница в пользу тороидального трансформатора, но для двух последних этот коэффициент как раз можно улучшить вышеприведенным расчетом.
Как определить число витков обмотки
В Формула 5 и Формула 6 приведены расчетные способы в начальной и конечной технологии, для математического определения необходимого количества витков на вторичной обмотке трансформатора.
Первичная намотка проводников оборудования тоже имеет определенное количество витков в своем номинале. Чем больше витков на этой обмотке – тем больше электрическое сопротивление ввода, а значит меньше нагрев. Определить количество витков обоих обмоток в процессе проекта расчета трансформатора возможно по отношению следующих равенств.
Формула 11. Расчет количества витков первичной обмотки:
N1, N2 – количество витков намотки первичной и вторичной катушек трансформатора;
U1, U2 – номинальные напряжение обмоток трансформатора.
Из такого равенства отношений, особенно, когда уже успешно посчитано количество витков вторичной обмотки, используя математику, можно вывести формулу расчета витков обмотки на вводе трансформатора.
Формула 12. Количество витков в намотке первичной обмотки:
Если проект имеет не только теоретическое обоснование, но и практическую составляющую в виде реального трансформатора, то с помощью медного проводника в изоляции (если позволяет конструкция устройства) и мультиметра возможно измерениями получить это же значение витков трансформатора на вводной обмотке, отталкиваясь от количества витков на 1В, и разматывая старую или наматывая новую первичную обмотку.
Упрощенный расчет 220/36 Вольт
Всю теорию легко показывать и пояснять на практическом примере ведения расчета трансформаторного устройства.
Итак, в качестве примера поставлена следующая задача: необходимо рассчитать самый простой понижающий трансформатор двухкатушечного типа с номинальным значением напряжений 220/36В.
Трансформатор будет использоваться в качестве источника слаботочного освещения мощностью 75Вт, напряжения 36В:
1 этап
По Формуле 1 известно, что электрическая мощность вторичной цепи: P2 = 75Вт;
Отсюда, воспользовавшись справочником по трансформаторам возьмем значение КПД, исходя из значения до 100 Вт, которое равно 0,8;
Следовательно, можем определить электрическую мощность P1 вводной обмотки трансформатора по формуле.
Формула 13. Расчет мощности первичной обмотки:
2 этап
Теперь рассмотрим электромеханические характеристики, исходя из того, что сердечник расчетного трансформатора имеет Ш-образную форму. На его поверхности с двух сторон будут располагаться первичная и вторичные обмотки оборудования.
Поэтому расчет площади сечения магнитопровода Sсерд. необходимы в обязательном порядке. Ее значение имеет квадратичную зависимость от мощности первичной обмотки , исходя из принципа работы трансформатора, как электротехнического устройства.
Формула 14. Расчет площади сечения исходя из мощности первичной обмотки:
Sсерд. = 1,2 х = 1,2 х 9,7 = 11.63 см 2
3 этап
Следующий шаг так же направлен на просчет параметров первичной обмотки – количество витков в ней на единицу напряжения 1В по Формуле 5:
На единицу напряжения количество витков получено. Используя его значение по Формула 6 найдем значение витков на вводной обмотке оборудования преобразования всего:
Wv1 = 5.16 x 220 = 1135 витков – первичная обмотка посчитана по количеству витков, аналогичные действия проведем для вторички, используя тоже количество витков на 1В и Формуле 6:
Wv2 = 5.16 x 36 = 186 витков – намотка вторичной обмотки по виткам тоже стала известна.
4 этап
Номинальные токи нагрузки трансформатора тоже необходимо узнать, чтобы провести проверку трансформатора согласно методике испытаний. Исходя из Форм. 1 можно вывести формулу токового значения.
Формула 15. Расчет номинального тока обмоток трансформатора:
I1, I2 – номинальные токи трансформаторных обмоток;
P1, P2 – электрические мощности ввода и вывода устройства;
U1, U2 – номинальные напряжения первичной и вторичной стороны трансформатора.
5 этап
Новые параметр, которые не рассматривался ранее – это диаметр проводника обмоток трансформатора (зависит от номинального тока на каждой обмотке).
Формула 16. Расчет диаметра проводника обмоток трансформатора:
D1, D2 – диаметр проводника первичной и вторичной обмоток;
I1, I2 – номинальные токи обмоток первичной и вторичной намотки;
0,8 – постоянный поправочный коэффициент расчетов диаметров.
Для проводников первичной и для проводника вторичной обмоток:
6 этап
В электротехнике кабельно-проводниковая продукция всегда представлена в значения площади поперечного сечения жилы, а значит, чтобы не возникало проблем с реальным подбором проводника требуется перевести полученные диаметры в площадь поперечного сечения с помощью электронных конвекторов по Формуле 17. Перевод из диаметра в сечение провода:
Отсюда для каждого из диаметров получаем:
- SКПП1= (0,5) 2 * 0.8 = 0,2 мм 2 – провод для первичной обмотки;
- SКПП2= (1,15) 2 * 0.8 = 1,0 мм 2 – провод для вторичной обмотки.
Далее получив все расчетные значения по трансформатору из примера, приступают к практической части намотки витков с обеих сторон одновременно, коммутации их выводов и другим работам.
Как рассчитать Ш-образный трансформатор
Универсальность конструкции Ш-образного магнитопровода позволяет одинаково эффективно использовать, закладывать форму сердечника в проекты расчета, как импульсных– современных трансформаторов, участвующих в процессах обеспечения питания электронной бытовой и мультимедийной техники, так и проводить серьезные проектные расчеты силовых трансформаторов напряжения, находящийся в составе высоковольтных подстанций, основного и аварийного питания значительного количества потребителей (в случае двух трансформаторной структуры энергоснабжения).
Расчеты Ш-образного трансформатора по своим характеристикам ничем особенным не может отличаться от основных пунктов упрощенного или детального расчета преобразователей энергии. Для него могут использоваться формулы нахождения параметрических величин или применяться расчеты онлайн автоматизации проектов. Второй метод несколько универсален и быстротечен, в том плане, что для его использования достаточно знать исходную геометрию и номинальные значения выходных величин, что авто программа расчетов смогла предоставить необходимые значения для оборудования.
Единственным нюансом для Ш-образного магнитопровода может быть расчет номинальной мощности вторичных обмоток, если у него она не одна, тогда расчет мощности можно выполнить по Формуле 3. И расчет толщины набора сердечника будет зависеть от расчетов и данных Ш-образного магнитопровода по Формула 8
В остальном в зависимости от параметров можно применять все вышеуказанные формулы, исходя из конкретных электрических величин Ш-образного сердечника.
Определение параметров ТТ
Измерительный преобразователь тока, в основном принципе своей работы имеет некоторые важные отличительные особенности по сравнению с силовыми трансформаторами питания электропотребителей или трансформаторов напряжения.
Отличия заключаются в токовой величине его вторичной обмотки. Ток «вторички» ТТ независим от нагрузки цепей в ней, и имеет сопротивление, которое всегда соответствует количеству витков первичной обмотки с минимальным значением по величине в сравнении с сопротивлением силовых цепей первичного подключения.
Рисунок 2. Принципиальная схема трансформатора тока.
К тому же протекающий ток I2 через цепь вторичной обмотки имеет постоянное направление, при помощи которого производится размагничивание сердечника данного устройства. I1 обозначено направление тока первичной обмотки ТТ.
В связи с условием что верхний конец первичной обмотки находится там же, где и верхний конец первичной обмотки, учитывая из физики равенства магнитных потоков его обмоток можно составить определенный алгоритм расчета такого оборудования преобразования тока с учетом нюансов изделия:
- Определяется номинальное напряжение первичного обмотки ТТ – величина выбор которой производится из стандартных паспортных значений таблиц и измеряется в киловольтах: 0,66/ 3/6/10/15/20/24/ 27/ 35/ 110/ 150/ 220/ 330/ 750.
- Второй важный параметр токового устройство – определение номинального тока первичной обмотки – учитывая перегрузочные способности, данная величина рассчитывается большей или равной (> =) номинального тока первичной цепи электроустановки. Его токовый ряд первичной обмотки выбирается из ГОСТ значений: 1, 5, 10, 15, 20, 30, 40, 50, 75, 80, 100, 150, 200, 300, 400, 500, 600, 750, 800, 1000, 1200, 1500, 1600, 2000, 3000, 4000, 5000, 6000, 8000, 10000, 12000, 14000, 16000, 18000, 20000, 25000, 28000, 30000, 32000, 35000, 40000. Измеряется в амперах и кило амперах. В случае выбора ТТ на пусковое, генераторное оборудование к его номинальному току прибавляется 10% значение и от полученной суммы выбирается первичный ток ТТ.
- Ведут проверки преобразователя по термической и электродинамической стойкости согласно формулам из паспортных формуляров проверок.
- Выбирается и проверяется ТТ по мощности вторичных нагрузок – учитывая формулу 18:
Sном2 – номинальная мощность вторичной обмотки;
Sнагр2 – мощность вторичной нагрузки, где будет установлен ТТ.
Кроме основных параметров выбора ТТ – это измерительное оборудование, учитывая значение номинала класса точности выбирается для питания и защиты цепей РЗиА, а так же преобразователи с завышенным коэффициентом трансформации и повышенным классом точности подбирают для питания токовых обмоток энергоучета.
Трансформаторы тока подключаются по каждому изделию на каждую фазу для включения в состав защитных, измерительных или учетных цепей.
Важное для расчета ТТ должно выполняться равенство по форм. 19:
I1, I2 – значения токов первичной и вторичной обмотки;
N1, N2 – количество витков в обмотках ТТ.
Отсюда для вычисления количество витков в обмотке вторичного подключения определяется его токовое значение, совместно с основными понятиями магнитных характеристик:
- Lind – значения индуктивности ТТ;
- XLreac – сопротивления реактивной мощности ТТ;
- Rc – сопротивления нагрузки вторичной цепи.
Вычисления значений по формулам достаточно трудоемкий факт работы, поэтому в большинстве случаев, чтобы получить понимание выбора определенного трансформатора тока пользуются или целиком справочно-паспортными значениями их выбора или калькуляторами расчета параметров устройств.
Сердечники трансформаторов могут изготавливаться из ферромагнитных материалов или пластин Ш-образной формы электротехнической стали. Возможны кольцевые магнитопроводы из ленточно-проволочных материалов производства.
Особенности расчета сетевого трансформатора
Трансформаторы типа сетевой являют собой преобразователи напряжения, участвующие в цепях питания различных маломощных, относительно электроустановок силовых трансформаторов, энергопотребителей, приборов и устройств автоматики, контроля, телемеханики. Они очень популярны и широко распространены в мире подобного оборудования.
В связи с этим их выбор должен обладать определенными критериями по мимо основных номинальных электрических величин:
- номинальные токи первичной и вторичной обмотки;
- номинальные напряжения первичной и вторичной обмотки;
- мощности первичной и вторичной обмотки;
- полной мощности трансформатора;
Их выбор может варьироваться от отличий параметров конструкции и их различных типов. Главные из которых выделено рассматриваются ниже.
Выбор магнитопровода
Этот центральный элемент устройства обладает сразу несколькими характеристиками выбора.
Прежде всего, в зависимости от места установки и сферы применения сердечник трансформатора должен отвечать параметрам прочности, износостойкости, электрической прочности, экономичности.
Технология изготовления
Следующий параметр выбора зависит от его электромагнитных свойств. Технология изготовления делит магнитопроводы на два типа:
- Пластинчатые – выполненные из пластин электротехнической стали, изолированных и спрессованных между собой в определенные формы, габаритные размеры.
- Ленточные – выполнение из навивки стальной проволоки (менее распространены).
Формы серденичков
Каждый из двух видов в свою очередь подразделяется на формы и конструктивные различия стержней, окон для намотки проводников обмоток, диаметры которых зависят от электрических параметров оборудования. Формы сердечников бывают:
- Стержневые – в пластинчатом исполнении производятся из пластин П-образной формы одинаковой ширины. Имеют одно окно с определенным размером прохода намотки обмоток. Замыкаются прямоугольными пластинами.
- Броневые – Ш-образные пластины собираются в двух оконный магнитопровод, который замыкается прямоугольными пластинами из стали. Набираются переплетом для уменьшения магнитного сопротивления в местах стыка. С целью уменьшения вихревых токов производятся методом прессования.
Что касается таких же форм ленточных сердечников – набираются прямоугольной формы с разрезами вдоль и поперек. Для уменьшения магнитного сопротивления их сердечники подвергаются шлифовки.
Существуют еще кольцевые формы сердечников, которые обладают отличными магнитными свойствами в работе, но трудоемки в своем изготовлении. Некоторое время их производили в виде трансформаторов для питания освещения, но в настоящее время используют редко.
Самыми популярными в зависимости от токовых и мощностных характеристик выступают Ш-образные и П-образные сердечники при изготовлении сетевых трансформаторов. Для вторичных цепей много катушечного характера используют стержневой тип сердечников. Броневое исполнение содержит на каждой стороне только по одной катушке, что является его ограничительным фактором применения.
Варианты размещения катушек
С учетом конструктивных исполнений магнитопровода, электромагнитных характеристик устройства, его механики, следует различать несколько основных типов размещения обмоток:
- прямоугольный провод класс «Цилиндр – 1-2слоя» – преимущества – имеет хорошее охлаждение при эксплуатации, простота изготовления. К недостаткам относится малая прочность;
- прямоугольный провод класс «Цилиндр – многослой» – достоинства имеет в отличных магнитных свойствах системы, простоте изготовления. Минусы вида обмотки в плохом охлаждении в момент работы;
- круглый провод класс «Цилиндр – многослой» – плюсы варианта в простоте изготовления, минусы в плохой теплоотдаче, возможности перегрева;
- прямоугольный провод класс «Винтовая на 1-2 или многоход» – достоинства состоят в высокой прочности отличной изоляции, хорошем охлаждении. Минус в дороговизне при производстве;
- прямоугольный провод класс «Непрерывный» – механическая и электрическая прочность, хорошее охлаждение придают этому варианту положительных характеристик, но неудобство при обслуживании относят к недостаткам;
- алюминиевая фольга класс «Катушечный многослой или цилиндр» – достоинства в механической прочности, магнитных свойствах. Минус в сложности изготовления.
Так же есть катушки в виде дискового формата. Соединяемые между собой. В целом тип катушки и форма обмотки выбирается от электрических параметров необходимых в конкретном применении с учетом экономичной стороны и технологий.
Краткая справка о материалах магнитопровода
Для изготовления сердечников трансформаторов в обязательном порядке отбирают материалы, имеющие высокую магнитную проницаемость, малую площадь петли гистерезиса, минимальные энергетические потери при возникновении в них вихревых токов.
Сталь низкоуглеродистого состава – основа для производства сердечников. Мощные трансформаторы, которые имеют сложные структуры магнитопроводов, в генераторных системах и подобных им имеют сердечники, изготовленные из малоуглеродистых стальных материалов.
Для эксплуатации в высокочастотных режимах работы преобразователей энергии, их сердечник выполняют из ферритов или подобных им композитов (прессованные порошки с свойствами магнитной мягкости по типу магнетитов или карбонильного железа). Такие системы связывают с диэлектрической структурой в виде эпоксидных смол. В итоге получается собрание мелкозернистого порошка ферромагнитного (вещества в твердом состоянии, кристаллах, обладающих свойством намагниченности) состава, изолированного друг друга токопроводящей смолой.
Распространенная технология сердечников связана с набором отдельных пластин в пакетную стальную структуру с малым содержанием углерода
Исходные данные
Для выполнения проектных расчетов силовых агрегатов преобразования энергии, сетевых трансформаторов напряжения, импульсных энергетических преобразователей необходимо иметь часть справочно-табличных данных, исходя из составов материалов проводов обмоток, изоляции, стали сердечников, таких как:
- Величина максимальной индуктивности – для точного расчета габаритной мощности.
- Значение плотности тока – аналогичное участие справочного значения в расчете размерной мощности изделия.
- Коэффициенты мощности конкретного устройства – для расчета мощностного параметра.
- Сопротивления материалов сердечников и значение в проводниках обмоток для возможности расчета полной мощности.
Необходимы номинально-заданные параметры оборудования исходя из конкретного применения, нагрузки, которая будет использоваться в расчетном преобразователи:
- габаритные размеры сердечника и материалы из чего он изготовлен, тип и форма – размеры окна магнитопровода по длине и ширине особенно важны, т.к. связаны с площадью сечения магнитопровода, от которой идут дальнейшие расчеты;
- номинальные токи обмоток первичной и вторичной стороны устройства;
- номинальные напряжения в сети со стороны первичной и вторичной обмотки;
- значение и функционал трансформатора, на который направлен расчет;
- мощность по активной составляющей (первичной или вторичной обмотки)
- количество обмоток со стороны нагрузок;
- прочие детали или возможные подробности по изделию и функционалу его применения.
На основании исходных данных номинального и справочного характера вполне реально произвести ручной расчет трансформатора согласно формулам или воспользоваться автоматизированным сервисам в сети Интернет.
Как посчитать магнитопровод
В совокупности справочных и расчетных материалов, параметрических значений расчета трансформатора достаточно несложно произвести расчет его магнитопровода.
1 шаг
Расчету подвергается произведение площади сечения стержня Sст на площадь сердечника Sсер согласно равенству форм. 20:
Sст x Sсер = Pгаб x 10 2 / (2,22F х B х j x КПД x Nster x Kc x Km), где:
- Pгаб – габаритная мощность рассчитываемого трансформатора;
- F – частота переменного тока 50Гц
- B – максимальная индукция трансформатора, Тл;
- J – значение плотности тока А/м 2 ;
- КПД – базовый коэффициент полезного действия устройства;
- Nster– Число стержней сердечника;
- Kc – коэффициент заполнения сечения сердечника магнитной сталью;
- Km – коэффициент заполнения окна стержня магнитной сталью;
Частично данные берутся из исходных номинальных значений оборудования, но большая часть вытекает из технической справочной литературы и табличных параметров и величин согласно указанному сердечнику изделия. В них входят: индукция, КПД оборудования, плотность тока, А/м 2 , коэффициенты заполнения сердечника и его окна.
2 шаг
Следующий шаг в расчете предполагает получение значения толщины сечения сердечника по Формуле 8, опубликованной в обзоре выше.
3 шаг
Последним шагом для расчета магнитопровода необходимо посчитать еще одно равенство значений узнав ширину ленты сердечника по форм. 21:
- Bline – ширина ленты сердечника для расчета, мм;
- Sст x Sсер -площади сечения стержня и самого сердечника, см 2 ;
- A x С x H – размеры сторон сердечника, мм.
После чего, имея на руках три основных параметра магнитопровода с помощью литературы подбора, методом сравнительного анализа полученного значения с ближайшим стандартом производится выбор марки, размеров и всех данных магнитопровода трансформатора.
Определение параметров обмоток
Параметрические составляющие в обмотках в расчете ручных формул начинаются с определения ЭДС одного витка обмотки Е по формуле 22:
Е = 4,44 x F x В х Sст x Kc x 10 -4 , где
- F -частота переменного тока, ГЦ;
- В – максимум индукции, ТЛ;
- Sст –площадь сечения стержня;
- Kc– – коэффициент заполнения стержня.
Следующим расчетным показателем требуется получить падения напряжения на каждой обмотке трансформатора по формуле 23:
А от падения напряжения рассчитываются количество витков первичной и вторичной обмотки по новым формулам.
Формула 24. Расчет количества витков на основе падения напряжения:
Получив количество витков возможно узнать диаметры проводников (форм. 25):
Обычно при этом расчет обмоток завершается по проектному трансформатору, однако в его содержании возможно еще высчитывать средние длины витка обмоток, длины витков каждой обмотки и их массы. Допустимо вывести расчет и массы магнитопровода, для более детальных и точных вычислений.
Мощность потерь
Их зависимость просматривается от воздействия силы магнитного поля на сердечник. Деление по виду потерь сердечника происходит в двух формациях:
- Статические потери Pstat – перемагничивание магнитопровода. Они прямо пропорциональны длине петли магнитного потока Sпетли, частоте переменного тока F и весу магнитопровода G:
Еще их называют потерями на гистерезисе. При уменьшении толщины ленты начинает рост таких потерь, аналогично при росте петли, частоты сети или весу сердечника.
- Динамические потери – потери, которые происходят при возникновении в сердечники вихревых токов.
Постоянный ток имеет нулевую частоту петли гистерезиса, как только частота начинает расти – идет возникновение динамических потерь в сердечнике.
Особенности расчета автотрансформатора
Автотрансформатор – преобразователь напряжений, имеющий в отличии от обычного трансформатора, единую и единственную обмотку с одним или несколькими промежуточными выводами.
Рисунок 3. Внешний вид автотрансформатора.
Если коэффициент трансформации нагруженного электротехнического устройства малого значения – автотрансформатор становится более экономически выгодным обычного преобразователя напряжения, т.к. расход медного провода его катушки заметно меньше, чем у двух обмоточного обычного трансформатора.
Рисунок 4. Принципиальная схема автотрансформатора.
В общей точке обмотки судя по схеме на Рисунок 4 обмотки устройства протекает ток с определенным значением дельты:
Важно! Вход и Выход изделия напрямую связаны. Это означает опасность и запрет в проведении защитного заземления схемы, в которую включен нагруженный автотрансформатор.
Устройство автотрансформатора в нагруженном состоянии или в режиме холостого хода имеет дополнительную обмотку, без какой-либо связи с основной. И как только значение мощности дополнительной катушки больше мощности основной обмотки – экономическая и выгода автотрансформатора падает с критической скоростью.
Для расчета мощности во вторичной обмотке устройства представляет собой сумму двух значений:
- Ppreborn – преобразовательная мощность, величина проходящая в зону вторичной обмотки по средствам магнитной связи;
- Pprox– проходящая мощность во вторичную обмотку посредством электрической связи
- Uii, I – напряжение, ток автотрансформатора.
Расчет автотрансформатора похож систему расчета силового преобразователя напряжения с одной поправкой – магнитопровод автотрансформатора рассчитывается на единицу значения преобразовательной мощности:
Pa – мощность автотрансформатора, общая, Вт;
коэффициент трансформации оборудования.
Автотрансформаторы, как бы парадоксальны их свойства и устройства не были, в однофазных и трехфазных сетях низковольтного и высоковольтного напряжения достаточно популярны за счет своих характеристик и возможности изменять выходную электрическую величину, низкой стоимости и коэффициентом полезного действия около 99%.
Мощные автотрансформаторы, начиная с напряжения 110 кВ используются в регулировочных ступенчатых узлах распределительных установок.
Слабые устройства, небольшой мощности, внешнего вида, как на Рисунок 3 стали очень популярны в научно-исследовательских организациях, как стендовое оборудование, позволяющее проводить многие тесты. Это касается и учебных заведениях. В них используются лабораторные автотрансформаторы (ЛАТР) для проведения работ и испытаний с целью обучения молодых специалистов.
Как посчитать пленочный трансформатор
Инновация в разработках сверхпроводников, в области криоэлектроники представлена в виде криогенного устройства на сверхпроводниках. Схематически его основные элементы представлены ниже на Рисунке 5 Это и есть – пленочный трансформатор магнитного потока.
Рисунок 5. Схематика пленочного трансформатора.
Квадратообразный обруч с активной полоской, изолирующей пленку, помещается между активной полосой трансформатора магнитного потока и магниточувствительным элементом.
С помощью преобразовательного устройства на сверхпроводниках происходит повышение умножение трансформатора магнитного потока.
Сверхпроводниковый трансформатор магнитного потока – пленочный трансформатор – устройство разработанная в научно-исследовательских институтах, имеет определенные свойства и преимущества:
- увеличение чувствительности датчиков;
- расширение динамического диапазона;
- увеличение помехозащищенности.
Пленочные трансформаторы сверхпроводимости нашли широкое применение в медицине в магнита-резонансных установках, позволяющих снять информацию сразу по всему организму и телу человека.
Рисунок 6. Схематика пленочного трансформатора с движением потока.
Однородность магнитного поля в активной полосе трансформатора увеличивается как показано на Рис. 7.
Рисунок 7. Схемы активных пластин.
Концентрация магнитного поля имеет определенный темп увеличения эффективности, рассчитываемый по формуле:
Наконец-то на последней схематике приведен эскиз активной полосы и приведены ее основные параметры для расчета:
В настоящее время на сверхпроводниках реализованы лишь пленочные трансформаторы способные увеличивая магнитный поток воздействовать на магниточувствительным элемент для проведения определенной работы. Если сверхпроводимость войдет в нашу жизнь для любого материала изменится не только конкретный преобразователь энергии, но и весь человеческий мир.
Обзор онлайн сервисов
Произвести расчеты трансформаторов любого типа, их составных частей или комплектующих помимо технических справок и таблиц, научной литературы в настоящее время довольно много качественных онлайн сервисов расчет электротехнических параметров или оборудования по конкретному запросу.
Если брать расчет трансформаторов – онлайн площадки в богатом остатке предлагают различные онлайн калькуляторы, расчетам которых вполне можно доверять.
Они не требуют никаких сложных значений или данных – достаточно иметь несколько основных исходных параметров электрических величин и знания геометрии оборудования.
Несколько вариантов онлайн площадок расчета трансформаторов предлагается в обзоре статьи на справедливую оценку и тестирование любым радиолюбителем или бывалым специалистом электронщиком:
- Интересная программа онлайн доступа и расчета с возможностью провести расчет как по стержневому виду, так и броневому виду сердечника, что увеличивает функционал и улучшает поддержку: Калькулятор расчета трансформатора №1.
- Помощь в расчете «Пуш-Пулл» трансформатора – простота и умение наращивать мощность являются основными преимуществами трансформаторов «Push-Pull», что в переводе с английского языка означает – двухтактный – трансформатор напряжения использующий импульсный трансформатор и становится трансформатор с двунаправленным возбуждением. Расчет такого устройства по формулам в ручном режиме может занять весомую часть времени. Помочь в этом может автоматизация расчета программой «ExcellentIT».
- Любые расчеты преобразователей электрической энергии, блоков питания, сложных устройств, которые так хочется собрать многими радиолюбителями и электронщиками-самоучками, но не хватает технической базы и формул, теперь возможно производить с помощью «Сборника Расчетных программ».
Но не стоит автоматизированные, онлайн сервисы делать панацеей в расчетах и проектировании преобразующих, питающих энергоустройств и систем электроники. Нужно помнить, что любая автоматика или компьютеризация без человека – оператора не стоит и не может ничего.
Примеры расчета
Для получения практических навыков расчета преобразователей напряжения упрощенными формулами в ручном режиме произведем:
Расчет силового трансформатора, который должен запитывать N-оборудование
Условия и исходные данные для расчета
- Тип оборудования: трансформатор напряжения силовой;
- Напряжение обмотки ВН: 660В;
- Ток обмотки ВН: 60mA;
- Напряжение обмотки НН: 12В;
- Ток обмотки НН: 6А;
- Тип сердечника: П-образный / коэффициентом количества витков на 1В = 50;
- Размеры окна сердечника: А = 10 см, И = 3 см.
Расчет силового трансформатора пошагово
- Т.к. обмотки ВН и НН в единственном экземпляре определить общую мощность трансформатора можно по формуле:
Pобщ = (660 * 0,06) + (12 * 6) = 39,6 + 72 = 111,6 Вт;
- Следующий шаг определение мощности первичной цепи обмотки по формуле:
P1 = 1,25 * Pобщ;
P1 = 1,25 * 111,6 = 139,5 Вт;
- Третий шаг определить площадь сечения сердечника из формулы:
- Определение количества витков на 1В и номинальный ток первичной обмотки можно:
- Остается найти число витков и диаметр проводников для первичной и вторичной обмотки:
- N1 = N1v * Uнн = 4,2 * 220 = 924 витков;
- D1 = 0,8 * = 0,8 * = 0,8 * 0,79 = 0,63 mm;
- N2 = N1v * Uвн = 4,2 * 660 = 2772 витка;
- D2 = 0,8 * = 0,8 * = 0,8 * 0,24 = 0,2 mm;
- С учетом того, что в исходных данных у нас есть размеры окна сердечника найдем ее площадь поперечного сечения, через который проверим войдут ли проводники в заданную площадь:
Sser = A * В = 10 * 3 = 30 см 2 = 3000 мм 2
Зная параметры диаметра проводников на каждой обмотке, можно вычислить опытную площадь проводников, которая должна быть меньше расчетной окна сердечника.
Этот расчет является защитным и проверочным предохранителем от ненужной траты сил и материалов по заранее ошибочным расчетным данным:
- S1 Первичная: 0,8 * D1 * N1 = 0,8 * 0,63 * 924 = 465 мм 2 ;
- S2 Вторичная: 0,8 * D2 * N2 = 0,8 * 0,2 * 2772 = 444 мм 2 ;
- Sser> (S1 + S2) – Необходимое условие
«Что и требовалось доказать»
3000> (444 + 465) – условие правильности расчета выполняется.
Остальные расчеты трансформаторов напряжения проводятся примерно в таком же формате, что и пример выше. Если позволяется – используют калькуляторы расчета в сети интернет.
Оборудование преобразования других величин электрической энергии проверяется расчетными методами по своим правилам и формулам или в тех же сервисах компьютерных программ.
Источник
- Подробности
- Обновлено 03.07.2018 17:37
- Просмотров: 1894
Задачи по физике – это просто!
Не забываем, что решать задачи надо всегда в системе СИ!
А теперь к задачам!
Элементарные задачи из курса школьной физики на вычисление ЭДС индукции.
Задача 1
За время 5 мс в соленоиде, содержащем 500 витков провода, магнитный поток равномерно убывает от 7 мВб до 3 мВб.
Найдите ЭДС индукции в соленоиде.
Задача 2
Какой магнитный поток пронизывает каждый виток катушки, имеющей 1000 витков, если при равномерном исчезновении магнитного поля в течение 0,1 с в катушке индуцируется ЭДС равная 10 В ?
Задача 3
Виток проводника площадью 2 см2 расположен перпендикулярно вектору магнитной индукции.
Чему равна ЭДС индукции в витке, если за время 0,05 секунд магнитная индукция равномерно убывает с 0,5 Тл до 0,1 Тл?
Задача 4
В однородном
магнитном поле перпендикулярно к направлению вектора индукции , модуль которого 0,1 Тл, движется провод длиной 2 метра со скоростью 5 м/с, перпендикулярной проводнику.
Какая ЭДС индуцируется в этом проводнике?
Задача 5
Перпендикулярно вектору магнитной индукции перемещается проводник длиной 1,8 метра со скоростью 6 м/c. ЭДС индукции равна 1,44 В.
Найти магнитную индукцию магнитного поля.
Задача 6
Самолет имеет размах крыльев 15 метров. Горизонтальная скорость полета равна720 км/час.
Определить разность потенциалов, возникающих между концами крыльев. Вертикальная составляющая магнитной индукции (перпендикулярно поверхности Земли) равна 50 мкТл.
Задача 7
Магнитный поток через контур проводника сопротивлением 0,03 Ом за 2 секунды изменился на 0,012 Вб.
Найдите силу тока в проводнике если изменение потока происходило равномерно.
Задача 8
В однородном магнитном поле находится плоский виток площадью 10 см2, расположенный перпендикулярно вектору магнитной индукции.
Какой ток течет по витку, если поле будет убывать с постоянной скоростью 0,5 Тл/с?
Задача 9
Сопротивление замкнутого контура равно 0,5 Ом. При перемещении кольца в магнитном поле магнитный поток через кольцо изменился на 5×10-3 Вб.
Какой за это время прошел заряд через поперечное сечение проводника?
ЭДС индукции, возникающая при равномерном вращении многовитковой рамки в однородном магнитном поле
Теорема физики (формула) и словесная формулировка математической записи: (varepsilon = – NBSomega sin (omega t))
При равномерном вращении многовитковой рамки с одинаковыми площадями витков в однородном магнитном поле в каждом витке этой рамки возникает ЭДС индукции, так что суммарная ЭДС численно равна произведению числа витков рамки N, индукции магнитного поля В, площади одного витка рамки S, угловой скорости вращения рамки ω и синуса угла поворота рамки, отсчитанного от положения, когда нормаль рамки параллельна линиям индукции.
Доказательство теоремы. Вывод формулы: рассмотрим случай, когда в начальный момент времени плоскость контура перпендикулярна силовым линиям поля и рамка вращается вокруг оси, перпендикулярной линиям поля и проходящей через середины противоположных сторон рамки.
Докажем теорему для одного витка, а затем результат необходимо будет умножить на N, поскольку в каждом витке по закону электромагнитной индукции Фарадея будет возникать одинаковая ЭДС (все витки будут находиться в одинаковых условиях возникновения ЭДС).
Итак, по закону Фарадея для одного витка (varepsilon = – frac{{Delta Phi }}{{Delta t}}.)
По условию рамка вращается равномерно, угловая скорость рамки w = const, угол a зависит от времени по линейному закону a = wt, следовательно: по определению магнитного потока Ф=BScosa= BScos(wt). Здесь B – магнитная индукция, S – площадь витка. Подставляя значения потока в закон Фарадея, получим
(varepsilon = – frac{{Delta Phi }}{{Delta t}} = – frac{{BS{rm{cos}}left( {omega {t_2}} right) – BS{rm{cos}}left( {omega {t_1}} right)}}{{{t_2} – {t_1}}})
Когда на уроке математике вы пройдете тему «Производные», вы докажете, что, если разность t2–t1 достаточно мала, то (frac{{{rm{cos}}omega {t_2} – {rm{cos}}omega {t_1}}}{{{t_2} – {t_1}}} = {rm{sin}}omega t). Заменяя последнее соотношение, получим искомую формулу (varepsilon = – {rm B}Somega sin (omega t)). Такая ЭДС индукции возникает в каждом витке. Суммарная ЭДС будет равна: (varepsilon = – NBSomega sin (omega t){rm{ }}). Теорема доказана.
Условия выполнения: выполняется для короткой и плотно намотанной многовитковой рамки. Все витки должны быть плоскими, иметь одинаковые площади и одинаковые углы между своими нормалями и линиями магнитной индукции.