Содержание:
- Определение и формула ЭДС
- Закон Ома для произвольного участка цепи
- Единицы измерения
- Примеры решения задач
Для поддержания электрического тока в проводнике длительное время, необходимо чтобы от конца проводника, имеющего меньший потенциал
(учтем, что носители тока предполагаются положительными зарядами) постоянно убирались доставляемые током заряды, при этом к концу с
большим потенциалом заряды постоянно подводились. То есть следует обеспечить круговорот зарядов. В этом круговороте заряды должны
перемещаться по замкнутому пути. Движение носителей тока при этом реализуется при помощи сил неэлектростатического происхождения.
Такие силы именуются сторонними. Получается, что для поддержания тока нужны сторонние силы, которые действуют на всем протяжении цепи
или на отдельных участках цепи.
Определение и формула ЭДС
Определение
Скалярная физическая величина, которая равна работе сторонних сил по перемещению единичного положительного заряда, называется
электродвижущей силой (ЭДС), действующей в цепи или на участке цепи. ЭДС обозначается
$varepsilon$ . Математически определение ЭДС запишем как:
$$varepsilon=frac{A}{q}(1)$$
где A – работа сторонних сил, q – заряд, над которым производится работа.
Электродвижущая сила источника численно равна разности потенциалов на концах элемента, если он разомкнут, что дает возможность измерить ЭДС по напряжению.
ЭДС, которая действует в замкнутой цепи, может бытьопределена как циркуляция вектора напряжённости сторонних сил:
$$varepsilon=oint_{L} bar{E}^{*} d bar{l}(2)$$
где $bar{E}^{*}$ – напряженность поля сторонних сил. Если напряженность поля сторонних
сил не равна нулю только в части цепи, например, на отрезке 1-2, тогда интегрирование в выражении (2) можно вести только по
данному участку. Соответственно, ЭДС, действующая на участке цепи 1-2 определяется как:
$$varepsilon=int_{1}^{2} bar{E}^{*} d bar{l}(3)$$
Формула (2) дает самое общее определение ЭДС, которое можно использовать для любых случаев.
Закон Ома для произвольного участка цепи
Участок цепи, на котором действуют сторонние силы, называют неоднородным. Для него выполняется равенство:
$$U_{12}=varphi_{1}-varphi_{2}+varepsilon_{12}(4)$$
где U12=IR21 – падение напряжения (или напряжение) на участке цепи 1-2 (I-сила тока);
$varphi_{1}-varphi_{2}$ – разность потенциалов концов участка;
$varepsilon_12$ – электродвижущая сила, которую содержит участок цепи.
$varepsilon_12$ равна алгебраической сумме ЭДС всех источников, которые находятся на данном участке.
Следует учитывать, что ЭДС может быть положительной и отрицательной. ЭДС называют положительной, если она увеличивает потенциал в
направлении тока (ток течет от минуса к плюсу источника).
Единицы измерения
Размерность ЭДС совпадает с размерностью потенциала. Основной единицей измерения ЭДС в системе СИ является: [$varepsilon$]=В
1В=1Дж/1Кл
Примеры решения задач
Пример
Задание. Электродвижущая сила элемента равна 10 В. Он создает в цепи силу тока равную 0,4 А.
Какова работа, которую совершают сторонние силы за 1 мин?
Решение. В качество основы для решения задачи используем формулу для вычисления ЭДС:
$$varepsilon=frac{A}{q}(1.1)$$
Заряд, который проходит в рассматриваемой цепи за 1 мин. можно найти как:
$$q=I Delta t(1.2)$$
Выразим из (1.1) работу, используем (1.2) для вычисления заряда, получим:
$$A=varepsilon I Delta t$$
Переведем время, данной в условиях задачи в секунды ($Delta t$ мин=60 с), проведем вычисления:
$A=10 cdot 0,4 cdot 60=240$ (Дж)
Ответ. A=240 Дж

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
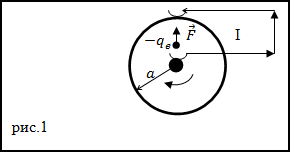
Задание. Металлический диск, имеющий радиус a, вращается с угловой скоростью
$omega$, включен в электрическую цепь при
помощи скользящих контактов, которые касаются оси диска и его окружности (рис.1). Какой будет ЭДС, которая появится между осью
диска и его наружным краем?
Решение. В условиях, которые описаны в задаче, на каждый электрон проводника действует центробежная сила (F)
которая является сторонней. Вследствие ее действия, в диске возникает ЭДС и между осью диска и его наружным краем появляется напряжение.
Формулу для вычисления центробежной силы запишем как:
$$F=m r omega^{2}(2.1)$$
где m – масса электрона, r – расстояние от оси диска.Fдействует на заряженную частицу (электрон), следовательноучитывая (2.1), имеем:
$$E^{*}=frac{F}{q}=frac{m r omega^{2}}{q}$$
где q – заряд электрона.
В соответствии с формулой, определяющей ЭДС участка цепи, получаем:
$$varepsilon=int_{1}^{2} bar{E} d bar{l}=int_{0}^{a} E^{*} d r=int_{0}^{a} frac{m r omega^{2}}{q} d r=frac{m r omega^{2} a^{2}}{2 q}$$
Ответ. $varepsilon=frac{m r omega^{2} a^{2}}{2 q}$
Читать дальше: Формулы по физике.
Возьмем два участка цепи a–bи c–d (см.
рис. 1) и составим для них уравнения в комплексной форме с учетом указанных на
рис. 1 положительных направлений напряжений
и токов.


Объединяя оба случая, получим
 |
(1) |
или для постоянного тока
| (2) |
Формулы (1) и (2) являются аналитическим выражением закона Ома для участка
цепи с источником ЭДС, согласно которому ток на участке цепи с источником
ЭДС равен алгебраической сумме напряжения на зажимах участка цепи и ЭДС, деленной
на сопротивление участка. В случае переменного тока все указанные величины суть
комплексы. При этом ЭДС и напряжение берут со знаком “+”, если их направление
совпадает с выбранным направлением тока, и со знаком “-”, если их направление
противоположно направлению тока.
Основы символического метода расчета цепей
синусоидального тока
Расчет цепей переменного синусоидального тока может производиться не только
путем построения векторных диаграмм, но и аналитически – путем операций с комплексами,
символически изображающими синусоидальные ЭДС, напряжения и токи. Достоинством
векторных диаграмм является их наглядность, недостатком – малая точность графических
построений. Применение символического метода позволяет производить расчеты цепей
с большой степенью точности.
Символический метод расчета цепей синусоидального тока основан на законах Кирхгофа
и законе Ома в комплексной форме.
Уравнения, выражающие законы Кирхгофа в комплексной форме, имеют совершенно
такой же вид, как и соответствующие уравнения для цепей постоянного тока. Только
токи, ЭДС, напряжения и сопротивления входят в уравнение в виде комплексных
величин.
1.
Первый закон Кирхгофа в комплексной форме:
| (3) |
2.
Второй закон Кирхгофа в комплексной форме:
| (4) |
или применительно к схемам замещения с источниками
ЭДС
| (5) |
3.
Соответственно матричная запись законов Кирхгофа в комплексной
форме имеет вид:
§
первый закон Кирхгофа:
| . |
(6) |
§
второй закон Кирхгофа
| (7) |
Пример.
Дано:
Рис. 2
Решение:
1.
.
2.

3.
.
4.
Принимая начальную фазу напряжения за нуль, запишем:
.
Тогда

5.
Поскольку ток распределяется обратно пропорционально сопротивлению
ветвей (это вытекает из закона Ома), то

6.
.
7.
Аналогичный результат можно получить, составив для данной схемы
уравнения по законам Кирхгофа в комплексной форме
или после подстановки численных значений параметров
схемы
Специальные методы расчета
Режим работы любой цепи полностью характеризуется уравнениями, составленными
на основании законов Кирхгофа. При этом необходимо составить и решить систему
с n неизвестными, что может оказаться
весьма трудоемкой задачей при большом числе n ветвей схемы. Однако, число уравнений, подлежащих решению, может
быть сокращено, если воспользоваться специальными методами расчета, к
которым относятся методы контурных токов и узловых потенциалов.
Метод контурных токов
Идея метода контурных токов: уравнения составляются только по второму закону
Кирхгофа, но не для действительных, а для воображаемых токов, циркулирующих
по замкнутым контурам, т.е. в случае выбора главных контуров равных токам ветвей
связи. Число уравнений равно числу независимых контуров, т.е. числу ветвей связи
графа . Первый закон Кирхгофа выполняется автоматически.
Контуры можно выбирать произвольно, лишь бы их число было равно и чтобы каждый новый контур содержал хотя
бы одну ветвь, не входящую в предыдущие. Такие контуры называются независимыми.
Их выбор облегчает использование топологических понятий дерева и ветвей связи.
Направления истинных и контурных токов выбираются произвольно. Выбор положительных
направлений перед началом расчета может не определять действительные направления
токов в цепи. Если в результате расчета какой-либо из токов, как и при использовании
уравнений по законам Кирхгофа, получится со знаком “-”, это означает, что его
истинное направление противоположно.
Пусть имеем схему по рис. 3.
Выразим токи ветвей через контурные токи:
;
;
;
;
.
Обойдя контур aeda, по второму закону Кирхгофа
имеем
.
Поскольку ,
то
.
Таким образом, получили уравнение для первого контура относительно контурных
токов. Аналогично можно составить уравнения для второго, третьего и четвертого
контуров:

совместно с первым решить их относительно контурных токов и затем по уравнениям,
связывающим контурные токи и токи ветвей, найти последние.
Однако данная система уравнений может быть составлена формальным путем:

При составлении уравнений необходимо помнить следующее:
– сумма сопротивлений, входящих в
i–й контур;
– сумма сопротивлений, общих для i–го и k–го контуров, причем
;
члены на главной диагонали всегда пишутся со знаком “+”;
знак “+” перед остальными членами ставится в случае, если через общее сопротивление
i–й и k–
й контурные токи проходят в одном направлении, в противном случае ставится знак
“-”;
если i–й и k– й контуры не имеют общих сопротивлений, то ;
в правой части уравнений записывается алгебраическая сумма ЭДС, входящих в
контур: со знаком “+”, если направление ЭДС совпадает с выбранным направлением
контурного тока, и “-”, если не совпадает.
В нашем случае, для первого уравнения системы, имеем:
Следует обратить внимание на то, что, поскольку , коэффициенты контурных уравнений всегда
симметричны относительно главной диагонали.
Если в цепи содержатся помимо источников ЭДС источники тока, то они учитываются
в левых частях уравнений как известные контурные токи: k– й контурный ток, проходящий через ветвь с k–
м источником тока равен этому току .
Метод узловых потенциалов
Данный метод вытекает из первого закона Кирхгофа.
В качестве неизвестных принимаются потенциалы узлов, по найденным значениям
которых с помощью закона Ома для участка цепи с источником ЭДС затем находят
токи в ветвях. Поскольку потенциал – величина относительная, потенциал одного
из узлов (любого) принимается равным нулю. Таким образом, число неизвестных
потенциалов, а следовательно, и число уравнений равно , т.е. числу ветвей дерева
.
Пусть имеем схему по рис. 4, в которой примем
.
Допустим, что и
известны. Тогда значения токов на основании
закона Ома для участка цепи с источником ЭДС

Запишем уравнение по первому закону Кирхгофа для
узла а:
и подставим значения входящих
в него токов, определенных выше:
.
Сгруппировав соответствующие члены, получим:
.
Аналогично можно записать для узла b:
.
Как и по методу контурных токов, система уравнений
по методу узловых потенциалов может быть составлена формальным путем. При этом
необходимо руководствоваться следующими правилами:
1. В
левой части i–го
уравнения записывается со знаком “+”потенциал i–го узла, для которого составляется данное
i–е уравнение, умноженный на сумму проводимостей ветвей, присоединенных к данному i–му узлу, и со знаком “-”потенциал
соседних узлов, каждый из которых умножен
на сумму проводимостей ветвей, присоединенных к i–му
и k–му узлам.
Из сказанного следует, что все члены
, стоящие на главной диагонали в левой части
системы уравнений, записываются со знаком “+”, а все остальные – со знаком “-”,
причем . Последнее равенство по аналогии с методом
контурных токов обеспечивает симметрию коэффициентов уравнений относительно
главной диагонали.
2. В
правой части i–го
уравнения записывается так называемый узловой ток , равный сумме произведений ЭДС ветвей, подходящих
к i–му узлу, и проводимостей этих ветвей. При этом член суммы записывается
со знаком “+”, если соответствующая ЭДС направлена к i–му узлу, в противном случае ставится знак “-”. Если в подходящих
к i–му узлу ветвях содержатся источники тока,
то знаки токов источников токов, входящих в узловой ток простыми слагаемыми,
определяются аналогично.
В заключение отметим,
что выбор того или иного из рассмотренных методов определяется тем, что следует
найти, а также тем, какой из них обеспечивает меньший порядок системы уравнений.
При расчете токов при одинаковом числе уравнений предпочтительнее использовать
метод контурных токов, так как он не требует дополнительных вычислений с использованием
закона Ома. Метод узловых потенциалов очень удобен при расчетах многофазных
цепей, но не удобен при расчете цепей со взаимной индуктивностью.
Литература
1.
Основы теории
цепей: Учеб.для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е
изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2.
Бессонов Л.А. Теоретические основы электротехники: Электрические
цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных
специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с
.
Контрольные вопросы и задачи
1. В
ветви на рис. 1
. Определить ток
.
Ответ: .
2. В
чем заключается сущность символического метода расчета цепей синусоидального
тока?
3. В
чем состоит сущность метода контурных токов?
4. В
чем состоит сущность метода узловых потенциалов?
5.
В цепи на рис. 5 ;
;
;
. Методом контурных токов определить комплексы
действующих значений токов ветвей.
Ответ: ;
;
.
6. В
цепи на рис. 6
. Рассчитать токи в ветвях, используя метод
узловых потенциалов.
Ответ: ;
;
;
;
;
;
.

Закон Ома назван в честь своего открывателя это ученый Георг Симон Ом. Свои эксперименты в области электричества он начал вдохновляясь опытами Фурье. Ом проводил свои опыты с различными материалами и изучение их электропроводности. Так была разработана знаменитая формула, которая стала краеугольной в современной физике, которая вошла в школьные учебники: I=U/R. Сила тока пропорциональна величине напряжения и имеет обратную пропорциональность сопротивлению.
В статье подробно разобраны области теории и практического применения принципов закона Ома в современной электротехнике. В качестве дополнения, в материале содержатся два обучающих видеоролика и один научный материал на тему статьи.
Закон Ома
Закон Ома показывает отношения между напряжением (U), током (I) и сопротивлением (R). Записано это может быть тремя разными способами:
U = I × R
или
I = V/R
или
R = V/I
Где:
- V – напряжение в вольтах (В);
- I – сила тока в амперах (А);
- R – сопротивление в омах (Ом);
Для большинства схем амперы – слишком большие величины, а омы – слишком маленькие. Поэтому в формулу можно подставлять миллиамперы и килоомы. Если силу тока подставлять в миллиамперах (мА), то сопротивление обязательно должно быть в килоомах (кОм) и наоборот. Напряжение – всегда в вольтах.
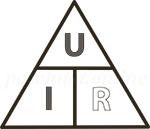
Чтобы проще запомнить три разные версии определения Закона Ома, можно воспользоваться «VIR-треугольником».
- Если надо вычислить напряжение, закрываем пальцем V. У нас остаются I и R. Они на одном уровне, значит между ними ставим знак умножения. Получается: V = I × R .
- Если вычисляем ток, закрываем пальцем I. У нас остаётся V над R. Значит напряжение делится на сопротивление: I = V/R .
- Аналогичным образом поступаем при вычислении сопротивления. Закрываем R. Остаётся V над I. Значит: R = V/I .
Закон Ома, определение: Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. Есть также частный случай – Закон Ома для участка цепи – сила тока в участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению этого участка.
Закон Ома для цепи
Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).
Итак, закон Ома для рассматриваемого участка цепи имеет вид:
φ1-φ2=I*R, где
- I – ток, протекающий по участку цепи.
- R – сопротивление этого участка.
- φ1-φ2 – разность потенциалов между точками 1-2.
Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).
В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:
- U1=I*R1
- U2=I*R2
- Un=I*Rn
- U=I*(R1+R2+…+Rn
Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:
U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn
Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:
Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
Для полной цепи
Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Для переменного тока
Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).
Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.
Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.
Для замкнутой цепи
На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.
Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.
Формула для расчета падения напряжения на индуктивном сопротивлении:
U = I ⋅ ωL
Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).
Формула для расчета падения напряжения на емкостном сопротивлении:
U = I / ω ⋅ С
С – емкость реактивного сопротивления.
Эти две формулы – частные случаи закона Ома для переменных цепей.
Полный же будет выглядеть следующем образом:
I = U / Z
Здесь Z – полное сопротивление переменной цепи известное как импеданс.
Сфера применения
Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:
- Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
- В сверхпроводниках;
- Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
- В вакуумных и газовых радиолампах;
- В диодах и транзисторах.
Последовательное и параллельное включение элементов
Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.
Цепь последовательно включенных резистивных элементов
Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:
- I = I1= I2 ;
- U = U1+ U2 ;
- R = R1+ R2
Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.
При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.
Цепь параллельно включенных резистивных элементов
На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:
- I = I1+ I2 … ;
- U = U1= U2 … ;
- 1 / R = 1 / R1+ 1 / R2 + …
Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.
Друзья, не забывайте подписываться на обновления блога, ведь чем больше читателей подписано на обновления, тем больше я понимаю что делаю что-то важное и полезное и это чертовски мотивирует на новые статьи и материалы.
-
Напряжение на участке цепи.
Под
напряжением на некотором участке
электрической цепи понимают разность
потенциалов между крайними точками
этого участка.
На
рис. 13 изображен участок цепи, на котором
есть резистор сопротивлением
и нет ЭДС. Крайние точки этого участка
обозначены буквами a
и b.
Пусть ток течет от точки a
к точке b.
Рис.
13. Участок электрической цепи
На
участке без ЭДС ток течет от более
высокого потенциала к более низкому.
Следовательно, потенциал
точки
a
выше потенциала
точки b
на величину, равную произведению тока
на сопротивление :
.
В
соответствии с определением, напряжение
между точками a
и b
.
(8)
Другими
словами, напряжение на резисторе равно
произведению тока, протекающего по
резистору, на величину сопротивления
этого резистора.
В
электротехнике разность потенциалов
на концах резистора принято называть
либо «напряжением на резисторе», либо
«падением напряжения». В литературе
встречаются оба этих определения.
Рассмотрим
теперь вопрос о напряжении на участке
цепи, содержащем не только резистор, но
и источник ЭДС.
На
рис. 14 а
и б
показаны участки некоторых цепей, по
которым протекает ток ..
Найдем напряжение между точками a
и c
для этих участков.
а)
б)
Рис.
14. Участки электрической цепи
По
определению
.
(9)
Выразим
потенциал точки a
через потенциал точки c.
При перемещении от точки c
к точке b
(рис. 14,а)
идем встречно ЭДС ,
поэтому потенциал точки b
оказывается меньше, чем потенциал точки
c
на величину ЭДС ,
т.е.
.
(10)
На
рис. 14,б
при перемещении от точки c
к точке b
идем согласно ЭДС
и потому потенциал точки b
оказывается больше, чем потенциал точки
c
на величину ЭДС ,
т.е.
.
(11)
Ранее
говорилось, что на участке цепи без ЭДС
ток течет от более высокого потенциала
к более низкому. Поэтому в обеих схемах
рис. 14 потенциал точки a
выше, чем потенциал точки b
на величину падения напряжения на
резисторе сопротивлением :
. (12)
Таким
образом, для рис. 14,а
имеем
,
или
.
(13)
И
для рис. 14, б
имеем
,
или
.
(14)
Положительное
направление напряжения указывают на
схемах стрелкой. Стрелка должна быть
направлена от первой буквы индекса ко
второй. Так, положительное направление
напряжения
изобразится
стрелкой, направленной от a
к c.
Из
самого определения напряжения следует
также, что .
Поэтому .
Другими словами, изменение чередования
индексов равносильно изменению знака
этого напряжения. Из изложенного ясно,
что напряжение может быть и положительной,
и отрицательной величиной.
-
Закон Ома для участка цепи, не содержащего эдс.
Закон
Ома устанавливает связь между током и
напряжением на некотором участке цепи.
Так, применительно к участку цепи,
изображенному на рис. 13 имеем
или
.
(15)
-
Закон Ома для участка цепи, содержащего эдс.
Закон
Ома для участка цепи, содержащего ЭДС,
позволяет найти ток этого участка по
известной разности потенциалов на
концах этого участка и имеющейся на
этом участке ЭДС .
Так из уравнения (13) имеем для схемы рис.
14, а
.
(16)
Аналогично
из уравнения (14) для схемы рис. 14, б
следует
.
(17)
Уравнения
(16) и (17) выражают собой закон Ома для
участка цепи, содержащего ЭДС, для разных
случаев включения ЭДС .
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Закон Ома
- Главная
- /
- Физика
- /
- Закон Ома
Чтобы посчитать Закон Ома воспользуйтесь нашим очень удобным онлайн калькулятором:
Закон Ома для участка цепи
Закон Ома для участка цепи гласит, что сила тока (I) на участке электрической цепи прямо пропорциональна напряжению (U) на концах участка цепи и обратно пропорциональна его сопротивлению (R).
Онлайн калькулятор
Найти силу тока
Напряжение: U =В
Сопротивление: R =Ом
Сила тока: I =
0
А
Формула
I = U/R
Пример
Если напряжение на концах участка цепи U = 12 В, а его электрическое сопротивление R = 2 Ом, то:
Сила тока на этом участке I = 12/2= 6 А
Найти напряжение
Сила тока: I =A
Сопротивление: R =Ом
Напряжение: U =
0
В
Формула
U = I ⋅ R
Пример
Если сила тока на участке цепи I = 6 А, а электрическое сопротивление этого участка R = 2 Ом, то:
Напряжение на этом участке U = 6⋅2 = 12 В
Найти сопротивление
Напряжение: U =В
Сила тока: I =A
Сопротивление: R =
0
Ом
Формула
R = U/I
Пример
Если напряжение на концах участка цепи U = 12 В, а сила тока на участке цепи I = 6 А, то:
Электрическое сопротивление на этом участке R = 12/6 = 2 Ом
Закон Ома для полной цепи
Закон Ома для полной цепи гласит, что сила тока в цепи пропорциональна действующей в цепи электродвижущей силе (ЭДС) и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.
Онлайн калькулятор
Найти силу тока
ЭДС: ε =В
Сопротивление всех внешних элементов цепи: R =Ом
Внутреннее сопротивление источника напряжения: r =Ом
Сила тока: I =
0
А
Формула
I = ε/R+r
Пример
Если ЭДС источника напряжения ε = 12 В, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:
Сила тока I = 12/4+2 = 2 А
Найти ЭДС
Сила тока: I =А
Сопротивление всех внешних элементов цепи: R =Ом
Внутреннее сопротивление источника напряжения: r =Ом
ЭДС: ε =
0
В
Формула
ε = I ⋅ (R+r)
Пример
Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:
ЭДС ε = 2 ⋅ (4+2) = 12 В
Найти внутреннее сопротивление источника напряжения
Сила тока: I =А
ЭДС: ε =В
Сопротивление всех внешних элементов цепи: R =Ом
Внутреннее сопротивление источника напряжения: r =
0
Ом
Формула
r = ε/I – R
Пример
Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а ЭДС источника напряжения ε = 12 В, то:
Внутреннее сопротивление источника напряжения r = 12/2 – 4 = 2 Ом
Найти сопротивление всех внешних элементов цепи
Сила тока: I =А
ЭДС: ε =В
Внутреннее сопротивление источника напряжения: r =Ом
Сопротивление всех внешних элементов цепи: R =
0
Ом
Формула
R = ε/I – r
Пример
Если сила тока в цепи I = 2A, внутреннее сопротивление источника напряжения r = 2 Ом, а ЭДС источника напряжения ε = 12 В, то:
Сопротивление всех внешних элементов цепи: R = 12/2 – 2 = 4 Ом