
Электрическая цепь может содержать несколько источников или приемников электроэнергии. Такие цепи называются сложными, для расчетов основных величин в таких цепях применяют специальные методы.
На рисунке 1 приведена схема с двумя источниками ЭДС: E1 и E2. Источники имеют внутренние сопротивления r1 и r2. Нагрузка условно обозначена резистором с сопротивлением R. Так как в цепи отсутствуют разветвления, то ток во всех ветвях будет одинаков и равен I

Для расчета сложных электрических цепей наряду с законом Ома применяются два закона Кирхгофа.
Одним из наиболее простых способов расчета цепи с двумя источниками ЭДС является метод наложения токов. Данный метод основан на аддитивном свойстве токов, согласно которому ток в цепи равен алгебраической сумме токов, создаваемых каждым источником питания независимо друг от друга. Это правило применимо для расчета любой линейной цепи (то есть цепи, в которой сопротивления всех участков постоянны).
Пусть в электрической цепи действует только один источник ЭДС E1, тогда ток в цепи будет равен

Теперь положим обратную ситуацию: в электрической цепи действует только один источник ЭДС E2, а источник E1 присутствует, но не производит ток. Тогда ток в цепи будет равен

Два источника ЭДС в цепи направлены встречно, следовательно, суммарный ток I будет равен разности токов I1 и I2

Из свойства аддитивности токов можно сделать немаловажный вывод: если ЭДС E1 и E2 имеют встречное направление, и равны, то ток в цепи будет равен нулю
I = I1 — I2 = 0.
Если значения E1 и E2 различны, то в цепи возникает ток, направление которого совпадает с током, создаваемой «большим» ЭДС. Иными словами, если E1 > E2, то направление тока совпадает с ЭДС E1, если E1 < E2, то направление тока будет противоположным. На рисунке 1 выбранное направление тока соответствует первой ситуации (E1 > E2).
Электродвижущая сила E2, направленная в противоположную току I сторону, называется встречной или противо-ЭДС.
Рассмотрим процессы и запишем основные зависимости, которые соответствуют каждому из участков цепи.
На участке ab имеется сопротивление источника ЭДС r1, а действие самого источника совпадает с направлением тока I. Следовательно указанный источник работает в режиме генератора (источника энергии). Таким образом, ЭДС источника равна сумме напряжения на его выводах и внутреннего падения напряжения
E1 = Uab + Ur1 = Uab + I ⋅ r1.
Согласно записанному выше выражению,
![]()
Иными словами, напряжение на выводах источника, отдающего энергию в цепь, равно разности ЭДС источника и внутреннего падения напряжения.
Согласно закону Ома, на участке bc падение напряжения равно
Ubc = I ⋅ R.
Кроме того, следует отметить, что на участке bc электрическая энергия преобразуется в тепловую, при этом происходит выделение мощности, равной
Pbc = I2 ⋅ R.
На последнем рассматриваемом участке ca источник ЭДС E2 действует против направления тока I. Источник имеет сопротивление r2. На данном участке имеется потеря мощности (нагрев), равная r2 ⋅ I2. Кроме того, источник ЭДС создает собственную мощность E2⋅ I, направленную на преодоление сил встречной ЭДС. Получается, что источник с противо-ЭДС работает в цепи как потребитель (приемник).
Мощность, выделяемая на участке ca равна
Pca = E2 ⋅ I + r2 ⋅ I2.
Cледовательно, напряжение на этом участке равно

На основании записанного выше выражения можно сделать вывод, что напряжение на вывод источника, работающего в режиме противо-ЭДС равно сумме самого ЭДС и внутреннего падения напряжения на нем.
#1. Чему равно напряжение на выводах источника, отдающего энергию в цепь?
Разности ЭДС источника и внутреннего падения напряжения.
Сумме ЭДС источника и внутреннего падения напряжения.
Произведению ЭДС источника и внутреннего падения напряжения.
![]()

#2. Дано: ЭДС E1 = 20 В, E2 = 20000 мВ имеют встречное направление, найдите ток в цепи. R1 = 10 Ом, R2 = 2 Ом, R = 0.5 Ом.
I = 0 A
I = 10 А.
I = 2 А

Так как Е2 = 20000 мВ = 20 В = E1, следовательно:
I = 0 А.
Результат
Отлично!
Попытайтесь снова(
§ 17. Последовательное и параллельное соединение источников
При последовательном соединении источников общая ЭДС равна алгебраической сумме ЭДС отдельных источников, общее внутреннее сопротивление равно сумме внутренних сопротивлений отдельных источников. Для определения знака ЭДС каждого источника нужно выбрать положительное направление движения на участке с этим источником. ЭДС источника берётся со знаком `«+»`, если направление действия ЭДС совпадает с выбранным направлением. В противном случае ставится знак `«-»`.
При параллельном соединении источников с одинаковыми ЭДС и возможно различными внутренними сопротивлениями общая ЭДС (ЭДС батареи) равна ЭДС одного источника. Внутреннее сопротивление батареи рассчитывается как при параллельном соединении проводников с сопротивлениями, равными внутренним сопротивлениям источников.
При параллельном соединении источников с различными ЭДС выражение для ЭДС батареи усложняется и здесь не приводится.
В схеме на рис. 17.1 $$ {mathcal{E}}_{1}=12$$ В, $$ {mathcal{E}}_{2}=3$$ В, $$ {r}_{1}=1$$ Ом, $$ {r}_{2}=2$$ Ом, $$ R=6$$ Ом.
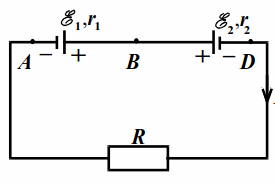 |
| Рис. 17.1 |
Найти напряжения на зажимах источников, т. е. разность потенциалов $$ {varphi }_{A}-{varphi }_{B}$$ и $$ {varphi }_{B}-{varphi }_{D}$$.
ЭДС батареи последовательно соединённых источников:
$$ mathcal{E}={mathcal{E}}_{1}-{mathcal{E}}_{2}=9$$ B.
Причём, полярность батареи совпадает с полярностью источника $$ {mathcal{E}}_{1}$$ т. к. $$ {mathcal{E}}_{1}>{mathcal{E}}_{2}$$.
Ток по закону Ома для замкнутой цепи $$ I=mathcal{E}/(R+{r}_{1}+{r}_{2})=1$$ A. По закону Ома для участков цепи `AB` и `BD`:
$$ {varphi }_{A}-{varphi }_{B}+{mathcal{E}}_{1}=I{r}_{1,}$$, $$ {varphi }_{B}-{varphi }_{D}-{mathcal{E}}_{2}=I{r}_{2}$$.
Отсюда $$ {varphi }_{A}-{varphi }_{B}=I{r}_{1}-{mathcal{E}}_{1}=-11$$ B, $$ {varphi }_{B}-{varphi }_{D}=I{r}_{2}+{mathcal{E}}_{2}=5$$ B.
Найти ток через резистор с сопротивлением $$ R$$ в схеме на рис. 17.2.
Между точками `A` и `B` имеем параллельное соединение источников. На рис. 17.3 показана эквивалентная схема, для которой $$ {mathcal{E}}_{1}=mathcal{E}$$, $$ {r}_{1}=r·2r/left(r+2rright)=2r/3$$. Общая ЭДС и внутреннее сопротивление последовательно соединённых источников с ЭДС $$ 3mathcal{E}$$ и $$ {mathcal{E}}_{1}$$:
$$ {mathcal{E}}_{0}=3mathcal{E}-{mathcal{E}}_{1}=3mathcal{E}-mathcal{E}=2mathcal{E}$$,
$$ {r}_{0}=3r+{r}_{1}=3r+2r/3=11r/3$$.
Ток $$ I={displaystyle frac{{mathcal{E}}_{0}}{R+{r}_{0}}}={displaystyle frac{6mathcal{E}}{3R+11r}}$$.
В этом случае эквивалентная ЭДС будет
равна:
|
|
(14) |
где r1иr2– внутренние сопротивления двух
неизвестных источников. Эти
сопротивления следует измерить для
каждого источника отдельно, собрав
простую схему из последовательно
соединенных источника тока, реохорда
н амперметра. Используя значенияx,
иx2,
полученные в разделе I, и измеренные
значенияr1иr2, по
формуле (14) следует рассчитать искомое
значение ЭДС.
КОНТРОЛЬНЫЕ
ВОПРОСЫ
-
В чем суть метода
компенсации? Зарисовать схему цепи. -
Что называется
ЭДС? -
Какие преимущества
имеет метод компенсации по сравнению
с другими методами измерения ЭДС? -
Как устроен гальванический элемент?
-
Что называется напряжением?
-
В каких единицах измеряются ЭДС и
напряжение в международной системе
единиц? -
Сформулировать закон Ома для замкнутой
цепи, участка цепи, содержащего ЭДС, и
участка цепи, не содержащего ЭДС.
СПИСОК ЛИТЕРАТУРЫ
-
Калашников
С. Г.
Электричество,— М., 1964. -
Савельев
И. В. Курс общей физики.—М., 1989.—Т. II. -
Детлаф
А. А., Яворский
Б. М., Милковская
Л. Б. Kуpc
физики.—М.: Высш. шк. 1988.—Т. 2. -
Руководство к
лабораторным занятиям по физике/Под
ред. Гольдина Л. Л.—М., 1964. -
Методические
указания к лабораторным работам по
физике Работы № 60-63.—M.,
МИИТ. 1976. -
Методические
указания к вводным занятиям в физическом
практикуме. Расчет погрешностей в
лабораторных работах физического
практикума. Под редакцией проф. Ф.
П. Денисова,—М.,—Изд. МГУ ПС (МИИТ).—
1995.
23
Работа 18 законы разветвленных цепей постоянного тока
Цель работы.Измерение силы тока в
узле разветвленной цепи. Определение
ЭДС источников тока и разности потенциалов
с использованием обобщенного закона
Ома.
Введение
Для характеристики электрического тока
в электрических цепях используют понятие
силы тока и плотности тока. Сила
стационарного электрического тока есть
алгебраическая величина, равная
заряду, протекающему через некоторую
поверхность, в единицу времени. Если
за время dtчерез поверхность
проводника переносится зарядdq,то
|
|
За положительное направление тока
принято направление движения положительных
зарядов. Плотность тока – векторная
величина, численно равная силе тока,
протекающего через единичную площадку,
перпендикулярную скорости движения
зарядов:
|
|
где dl—сила тока,
протекающего через площадкуdS1.
Вектор плотности тока совпадает по
направлению с вектором скорости
положительно заряженных частиц. Связь
силы тока и плотности тока может быть
записана в виде интеграла по поверхностиS, через которую течет
ток:
|
|
То есть сила тока равняется потоку
плотности тока через поверхность S.Здесь- угол, образованный вектором плотности
тока и нормалью к элементу поверхностиds
В зависимости от величины сила тока может иметь положительный
или отрицательный знак.
24
 Одним
Одним
из элементов разветвленной цепи является
узел – место соединения трех и более
проводников (рис. 1).
Поскольку в цепях постоянного тока
нигде не происходит накапливания
электрического заряда, а также его
возникновения или уничтожения (закон
сохранения заряда), то заряд, приходящий
в единицу времени к узлу, равен заряду,
уходящему за это же время от узла. Из
этого следует первое правило
Кирхгофадля цепей постоянного тока:
алгебраическая сумма сил токов,
сходящихся в узле, равна нулю:
![]()
При составлении уравнений с использованием
этого правила токи, текущие к узлу,
считают положительными, а токи, текущие
от узла – отрицательными.
Свободные носители заряда в проводнике
(электроны, ионы) при движении испытывают
сопротивление. В металле, например,
электроны взаимодействуют с ионами
кристаллической решетки и теряют
свою энергию. Поэтому ток в проводнике
поддерживается только при условии
непрерывного действия на электроны
ускоряющего электрического ноля.
Между плотностью тока и напряженностью
электрического поля в каждой точке
проводника существует зависимость:
|
|
(1) |
где
удельная
электропроводность вещества.
Эту формулу
называютзаконом Ома в дифференциальной
форме.Рассмотрим этот закон подробнее.
Существование напряженности
электрического поля указывает на
изменение потенциала вдоль проводника.
Следовательно, условием существования
электрического тока на участке цепи
является наличие разности потенциалов
на концах этого участка.
Один из источников создания электрического
поля внутри проводника – избыточный
положительный или отрицательный заряд,
накапливающийся в некоторых участках
проводника. Но этoполе,
имеющее электростатическое
25
происхождение, одно не может поддерживать
в цепи постоянный электрический ток,
т.к. электростатические силы способствуют
сближению разноименных
зарядов и выравниванию потенциала
проводника. Для поддержания постоянного
тока в цепи, в ней на некоторых участках
должны существовать силы неэлектростатиче
ского происхождения. Эти силы поддерживают
такое распределение зарядов в
проводниках, которое создает внутри
них поле с напряженностью, не равной
нулю. При этом на некоторых участках
цепи силы неэлектростатического
происхождения заставляют свободные
носители зарядов двигаться против
поля, вызванного электростатическими
силами.
Силы неэлектростатического происхождения
называют сторонними. Они могут быть
обусловлены химическими процессами,
диффузией носителей зарядов в неоднородной
среде или через границу двух разнородных
веществ, явлением электромагнитной
индукции и т. д. С учетом всех сил,
действующих на заряды, формулу (1)
записывают в более общем виде:
|
|
(2) |
Иными словами, в уравнении (1)
|
|
здесь
![]() – напряженность поля сторонних сил, т.
– напряженность поля сторонних сил, т.
е. сила неэлектростатического
происхождения, действующая на пробный
единичный положительный заряд,
![]() –
–
напряженность поля кулоновских сил.
Сторонние силы в практике удобно
характеризовать не напряженностью, а
работой, которую они совершают при
переносе единичного положительного
заряда. Эта работа называется
электродвижущей силой (ЭДС), обозначается
буквой и может быть выражена в виде интеграла,
начало и конец которого обозначен
соответственно 1 и 2:
|
|
(3) |
где dl – элемент
проводника с током.
26
На основании равенства (2) запишем
интеграл для участка 1-2:
|
|
(4) |
где
![]() – удельное сопротивление проводника.
– удельное сопротивление проводника.
Предположим,
что ток течет по прямолинейному
однородному проводнику и на участке
1-2 постоянен. Вынесем
за знак интегралов в правой части
уравнения. Разделим последнее равенство
на .
В правой части полученного равенства
первое слагаемое есть разность потенциалов
на концах участка 1-2:
|
|
(5) |
а второе—ЭДС на
этом участке:
|
|
(6) |
Подставим уравнения (5) и (6) в уравнение
(4) н учтем, что вектор
![]() совпадает по направлению с
совпадает по направлению с
![]() .Учитывая, что поперечное сечение
.Учитывая, что поперечное сечение
проводникаS1перпендикулярно этим векторам, уравнение
(4) примет вид:
|
|
(7) |
здесь
|
|
(8) |
а I – сила постоянного
тока, и получим:
|
|
(9) |
27
Здесь
![]() – сопротивление участка 1-2.
– сопротивление участка 1-2.
Тогда (9) примет вид:
|
|
(10) |
Полученное
уравнение носит название
закона Ома для участка цепи, содержащего
ЭДС.
Иногда его записывают
в виде:
|
|
(11) |
и
Рис. 1
называют обобщенным
законом Ома.
При записи этого уравнения применяется
правило знаков которое утверждает, что,
если направление токов совпадает–
с направлением обхода участка цепи 1—2,
ток в уравнении (11) считается положительным.
Если в направлении обхода участка от
точки 1 к точке 2 потенциал источника
повышается, то ЭДС берется с плюсом,
в противном случае— с минусом.
Соседние файлы в папке 14 16 17. 18
- #
- #
- #
09.06.2015288.28 Кб2617.ARJ
Рассмотрим электрическую цепь, в которой включены два источника ЭДС, например, два аккумулятора.

На рисунке изображена электрическая цепь с двумя источниками ЭДС.
По общефизическому принципу наложения ток в такой цепи равен алгебраической сумме токов, создаваемых в ней каждой из ЭДС, действующих отдельно друг от друга при неизменных сопротивлениях всех участков цепи.
Рассмотрим случай, когда имеем два источника эдс с внутренним сопротивлением r01 + r02. Положим сначала, что в цепи действует только источник с ЭДС E1. В этом случае получается простейшая цепь, и ток
I1 = E1 / r01 + r02 + r
будет направлен ту же сторону, что и ЭДС Е1. Затем находим ток, который возникнет, если будет действовать ЭДС Е2;
I2 = E2 / r01 + r02 + r
Этот ток будет совпадать по направлению с Е2.
Результирующий ток в цепи при совместном действии E1 и E2 при одинаковом их направлении равен сумме токов I1 и I2,
I = I1 + I2 = E1 + E2 / r01 + r02 + r
При встречном направлении E1 и E2 общий ток будет равен разности токов I1 и I2, т. е.
I = I1 — I2 = E1 — E2 / r01 + r02 + r
В последнем случае электрический ток возникает при условии, если E1 не равен E2 И будет направлен в сторону действия большей э. д. с. Пусть E1 больше E2, В таком случае ток в цепи будет совпадать по направлению с E1 и окажется направленным навстречу E2 (направление тока для этого случая показано на рисунке выше).
Электродвижущая сила, направленная противоположно току, называется встречной или противоэлектродвижущей силой.
Преобразуя формулу I = I1 — I2 = E1 — E2 / r01 + r02 + r, находим:
E1 — E2 = Ir01 + Ir02 + Ir
откуда следует, что
E1 = E2 + Ir01 + Ir02 + Ir
Источник с ЭДС E1 развивает полную мощность
Р’ = E1I
и отдает во внешний для него участок цепи мощность
P1 = P’ — P01 = E1I — I2r01
так как работает в режиме генератора.
Напряжение на зажимах (БА) источника, работающего в генераторном режиме,
U БА = E1 — Ir01 = E2 + Ir02 + Ir
Произведение Ir есть напряжение U БВ между точками Б и В электрической цепи на зажимах сопротивления r.
Мощность этого участка
Р = I2r.
Сумма E2 + Ir02 выражает напряжение U БА между точками В и А, т. е. на зажимах источника со встречной ЭДС. Таким образом,
U БА = E2 + Ir02,
а мощность
Р2 = E2I + I2r02 = Р» + Р02
где
Р» = E2I.
По закону сохранения энергии
P1 = P + Р2.
В участке ВА, где действует встречная э. д. с. E2, электрические силы преодолевают химические или механические силы, и происходит преобразование электрической энергии не только в тепловую, но также в химическую или механическую в зависимости от устройства источника с э. д. с. E2 (аккумулятор, который в этом случае заряжается, или машина постоянного тока, которая в этом случае работает в режиме электродвигателя).
Таким образом, источник с э. д. с. E2 является потребителем электрической энергии.
Итак, в общем случае источник э. д. с. может работать генератором или потребителем электрической энергии, а напряжение на его зажимах соответственно будет:
U = Е + (-) Ir0.
Начало лекции 28 ЭДС источника. Соединения проводников и источников.
Проводники в электрических цепях тоже могут соединяться последовательно и параллельно.
1. При последовательном соединении проводников
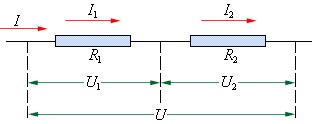
1. Сила тока во всех проводниках одинакова:
I1 = I2 = I
2. Общее напряжение U на обоих проводниках равно сумме напряжений U1 и U2 на каждом проводнике:
U = U1 + U2
3. По закону Ома, напряжения U1 и U2 на проводниках равны U1 = IR1, U2 = IR2 а общее напряжение U = IR где R – электрическое сопротивление всей цепи, тогда IR = IR1 + IR2.Отсюда следует
R = R1 + R2
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
2. При параллельном соединении проводников
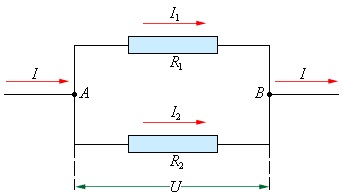
1. Напряжения U1 и U2 на обоих проводниках одинаковы
U1 = U2 = U
2. Сумма токов I1 + I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
I = I1 + I2
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt + I2Δt. Следовательно, I = I1 + I2.
3. Записывая на основании закона Ома
![]()
![]()
![]()
где R – электрическое сопротивление всей цепи, получим
![]() или
или ![]()
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рисунке приведен пример такой сложной цепи и указана последовательность вычислений. Сопротивления всех проводников указаны в омах (Ом).
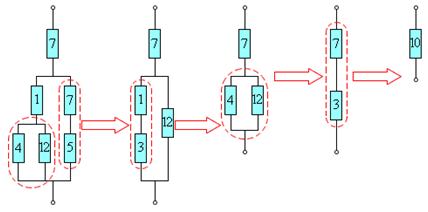
На пракутике одного источника тока в цепи бывает недостаточно, и тогда источники тока тоже соединяют между собой для питания цепи. Соединение источников в батарею может быть последовательным и параллельным.
При последовательном соединении два соседних источника соединяются разноименными полюсами.
Т.е., для последовательного соединения аккумуляторов, к ″плюсу″ электрической схемы подключают положительную клемму первого аккумулятора. К его отрицательной клемме подключают положительную клемму второго аккумулятора и т.д. Отрицательную клемму последнего аккумулятора подключают к ″минусу″ электрической схемы.
Получившаяся при последовательном соединении аккумуляторная батарея имеет ту же емкость, что и у одиночного аккумулятора, а напряжение такой аккумуляторной батареи равно сумме напряжений входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые напряжения, то напряжение батареи равно напряжению одного аккумулятора, умноженному на количество аккумуляторов в аккумуляторной батарее.
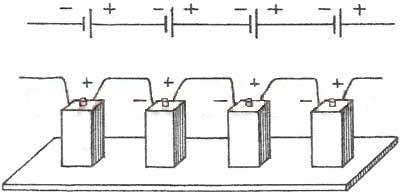
1. ЭДС батареи равна сумме ЭДС отдельных источников ε= ε1 + ε2 + ε3
2. Общее сопротивление батареи источников равно сумме внутренних сопротивлений отдельных источников rбатареи= r1 + r2 + r3
Если в батарею соединены n одинаковых источников, то ЭДС батареи ε= nε1, а сопротивление rбатареи= nr1
3. Сила тока в такой цепи по закону Ома ![]()
При параллельном соединении соединяют между собой все положительные и все отрицательные полюсы двух или n источников.
Т.е., при параллельном соединении, аккумуляторы соединяют так, чтобы положительные клеммы всех аккумуляторов были подключены к одной точке электрической схемы (″плюсу″), а отрицательные клеммы всех аккумуляторов были подключены к другой точке схемы (″минусу″).
Параллельно соединяют только источники с одинаковой ЭДС. Получившаяся при параллельном соединении аккумуляторная батарея имеет то же напряжение, что и у одиночного аккумулятора, а емкость такой аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые емкости, то емкость аккумуляторной батареи равна емкости одного аккумулятора, умноженной на количество аккумуляторов в батарее.
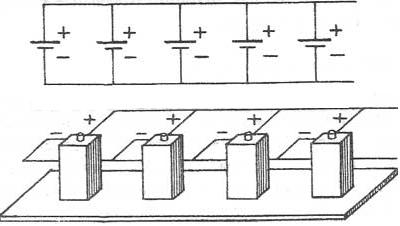
1. ЭДС батареи одинаковых источников равна ЭДС одного источника. ε= ε1= ε2 = ε3
2. Сопротивление батареи меньше, чем сопротивление одного источника rбатареи= r1/n
3. Сила тока в такой цепи по закону Ома ![]()
Электрическая энергия, накопленная в аккумуляторной батарее равна сумме энергий отдельных аккумуляторов (произведению энергий отдельных аккумуляторов, если аккумуляторы одинаковые), независимо от того, как соединены аккумуляторы – параллельно или последовательно.
Внутреннее сопротивление аккумуляторов, изготовленных по одной технологии, примерно обратно пропорционально емкости аккумулятора. Поэтому т.к.при параллельном соединении емкость аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов, т.е увеличивается, то внутреннее сопротивление уменьшается.
