Электромагнитная индукция
-
Темы кодификатора ЕГЭ: явление электромагнитной индукции, магнитный поток, закон электромагнитной индукции Фарадея, правило Ленца.
-
Магнитный поток
-
ЭДС индукции
-
Закон электромагнитной индукции Фарадея
-
Правило Ленца
-
Взаимодействие магнита с контуром
-
Закон Фарадея + Правило Ленца = Снятие модуля
-
Вихревое электрическое поле
-
ЭДС индукции в движущемся проводнике
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: явление электромагнитной индукции, магнитный поток, закон электромагнитной индукции Фарадея, правило Ленца.
Опыт Эрстеда показал, что электрический ток создаёт в окружающем пространстве магнитное поле. Майкл Фарадей пришёл к мысли, что может существовать и обратный эффект: магнитное поле, в свою очередь, порождает электрический ток.
Иными словами, пусть в магнитном поле находится замкнутый проводник; не будет ли в этом проводнике возникать электрический ток под действием магнитного поля?
Через десять лет поисков и экспериментов Фарадею наконец удалось этот эффект обнаружить. В 1831 году он поставил следующие опыты.
1. На одну и ту же деревянную основу были намотаны две катушки; витки второй катушки были проложены между витками первой и изолированы. Выводы первой катушки подключались к источнику тока, выводы второй катушки — к гальванометру (гальванометр — чувствительный прибор для измерения малых токов). Таким образом, получались два контура: «источник тока — первая катушка» и «вторая катушка — гальванометр».
Электрического контакта между контурами не было, только лишь магнитное поле первой катушки пронизывало вторую катушку.
При замыкании цепи первой катушки гальванометр регистрировал короткий и слабый импульс тока во второй катушке.
Когда по первой катушке протекал постоянный ток, никакого тока во второй катушке не возникало.
При размыкании цепи первой катушки снова возникал короткий и слабый импульс тока во второй катушке, но на сей раз в обратном направлении по сравнению с током при замыкании цепи.
Вывод.
Меняющееся во времени магнитное поле первой катушки порождает (или, как говорят, индуцирует) электрический ток во второй катушке. Этот ток называется индукционным током.
Если магнитное поле первой катушки увеличивается (в момент нарастания тока при замыкании цепи), то индукционный ток во второй катушке течёт в одном направлении.
Если магнитное поле первой катушки уменьшается (в момент убывания тока при размыкании цепи), то индукционный ток во второй катушке течёт в другом направлении.
Если магнитное поле первой катушки не меняется (постоянный ток через неё), то индукционного тока во второй катушке нет.
Обнаруженное явление Фарадей назвал электромагнитной индукцией (т. е. «наведение электричества магнетизмом»).
2. Для подтверждения догадки о том, что индукционный ток порождается переменным магнитным полем, Фарадей перемещал катушки друг относительно друга. Цепь первой катушки всё время оставалась замкнутой, по ней протекал постоянный ток, но за счёт перемещения (сближения или удаления) вторая катушка оказывалась в переменном магнитном поле первой катушки.
Гальванометр снова фиксировал ток во второй катушке. Индукционный ток имел одно направление при сближении катушек, и другое — при их удалении. При этом сила индукционного тока была тем больше, чем быстрее перемещались катушки.
3. Первая катушка была заменена постоянным магнитом. При внесении магнита внутрь второй катушки возникал индукционный ток. При выдвигании магнита снова появлялся ток, но в другом направлении. И опять-таки сила индукционного тока была тем больше, чем быстрее двигался магнит.
Эти и последующие опыты показали, что индукционный ток в проводящем контуре возникает во всех тех случаях, когда меняется «количество линий» магнитного поля, пронизывающих контур. Сила индукционного тока оказывается тем больше, чем быстрее меняется это количество линий. Направление тока будет одним при увеличении количества линий сквозь контур, и другим — при их уменьшении.
Замечательно, что для величины силы тока в данном контуре важна лишь скорость изменения количества линий. Что конкретно при этом происходит, роли не играет — меняется ли само поле, пронизывающее неподвижный контур, или же контур перемещается из области с одной густотой линий в область с другой густотой.
Такова суть закона электромагнитной индукции. Но, чтобы написать формулу и производить расчёты, нужно чётко формализовать расплывчатое понятие «количество линий поля сквозь контур».
к оглавлению ▴
Магнитный поток
Понятие магнитного потока как раз и является характеристикой количества линий магнитного поля, пронизывающих контур.
Для простоты мы ограничиваемся случаем однородного магнитного поля. Рассмотрим контур площади , находящийся в магнитном поле с индукцией
.
Пусть сначала магнитное поле перпендикулярно плоскости контура (рис. 1).

Рис. 1.
В этом случае магнитный поток определяется очень просто — как произведение индукции магнитного поля на площадь контура:
(1)
Теперь рассмотрим общий случай, когда вектор образует угол
с нормалью к плоскости контура (рис. 2).

Рис. 2.
Мы видим, что теперь сквозь контур «протекает» лишь перпендикулярная составляющая вектора магнитной индукции
(а та составляющая, которая параллельна контуру, не «течёт» сквозь него). Поэтому, согласно формуле (1), имеем
. Но
, поэтому
(2)
Это и есть общее определение магнитного потока в случае однородного магнитного поля. Обратите внимание, что если вектор параллелен плоскости контура (то есть
), то магнитный поток становится равным нулю.
А как определить магнитный поток, если поле не является однородным? Укажем лишь идею. Поверхность контура разбивается на очень большое число очень маленьких площадок, в пределах которых поле можно считать однородным. Для каждой площадки вычисляем свой маленький магнитный поток по формуле (2), а затем все эти магнитные потоки суммируем.
Единицей измерения магнитного потока является вебер (Вб). Как видим,
Вб = Тл · м = В · с. (3)
Почему же магнитный поток характеризует «количество линий» магнитного поля, пронизывающих контур? Очень просто. «Количество линий» определяется их густотой (а значит, величиной — ведь чем больше индукция, тем гуще линии) и «эффективной» площадью, пронизываемой полем (а это есть не что иное, как
). Но множители
и
как раз и образуют магнитный поток!
Теперь мы можем дать более чёткое определение явления электромагнитной индукции, открытого Фарадеем.
Электромагнитная индукция — это явление возникновения электрического тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего контур.
к оглавлению ▴
ЭДС индукции
Каков механизм возникновения индукционного тока? Это мы обсудим позже. Пока ясно одно: при изменении магнитного потока, проходящего через контур, на свободные заряды в контуре действуют некоторые силы — сторонние силы, вызывающие движение зарядов.
Как мы знаем, работа сторонних сил по перемещению единичного положительного заряда вокруг контура называется электродвижущей силой (ЭДС): . В нашем случае, когда меняется магнитный поток сквозь контур, соответствующая ЭДС называется ЭДС индукции и обозначается
.
Итак, ЭДС индукции — это работа сторонних сил, возникающих при изменении магнитного потока через контур, по перемещению единичного положительного заряда вокруг контура.
Природу сторонних сил, возникающих в данном случае в контуре, мы скоро выясним.
к оглавлению ▴
Закон электромагнитной индукции Фарадея
Сила индукционного тока в опытах Фарадея оказывалась тем больше, чем быстрее менялся магнитный поток через контур.
Если за малое время изменение магнитного потока равно
, то скорость изменения магнитного потока — это дробь
(или, что тоже самое, производная
магнитного потока по времени).
Опыты показали, что сила индукционного тока прямо пропорциональна модулю скорости изменения магнитного потока:
Модуль поставлен для того, чтобы не связываться пока с отрицательными величинами (ведь при убывании магнитного потока будет ). Впоследствии мы это модуль снимем.
Из закона Ома для полной цепи мы в то же время имеем: . Поэтому ЭДС индукции прямо пропорциональна скорости изменения магнитного потока:
(4)
ЭДС измеряется в вольтах. Но и скорость изменения магнитного потока также измеряется в вольтах! Действительно, из (3) мы видим, что Вб/с = В. Стало быть, единицы измерения обеих частей пропорциональности (4) совпадают, поэтому коэффициент пропорциональности — величина безразмерная. В системе СИ она полагается равной единице, и мы получаем:
(5)
Это и есть закон электромагнитной индукции или закон Фарадея. Дадим его словесную формулировку.
Закон электромагнитной индукции Фарадея. При изменении магнитного потока, пронизывающего контур, в этом контуре возникает ЭДС индукции, равная модулю скорости изменения магнитного потока.
к оглавлению ▴
Правило Ленца
Магнитный поток, изменение которого приводит к появлению индукционного тока в контуре, мы будем называть внешним магнитным потоком. А само магнитное поле, которое создаёт этот магнитный поток, мы будем называть внешним магнитным полем.
Зачем нам эти термины? Дело в том, что индукционный ток, возникающий в контуре, создаёт своё собственное магнитное поле, которое по принципу суперпозиции складывается с внешним магнитным полем.
Соответственно, наряду с внешним магнитным потоком через контур будет проходить собственный магнитный поток, создаваемый магнитным полем индукционного тока.
Оказывается, эти два магнитных потока — собственный и внешний — связаны между собой строго определённым образом.
Правило Ленца . Индукционный ток всегда имеет такое направление, что собственный магнитный поток препятствует изменению внешнего магнитного потока .
Правило Ленца позволяет находить направление индукционного тока в любой ситуации.
Рассмотрим некоторые примеры применения правила Ленца.
Предположим, что контур пронизывается магнитным полем, которое возрастает со временем (рис. (3)). Например, мы приближаем снизу к контуру магнит, северный полюс которого направлен в данном случае вверх, к контуру.
Магнитный поток через контур увеличивается. Индукционный ток будет иметь такое направление, чтобы создаваемый им магнитный поток препятствовал увеличению внешнего магнитного потока. Для этого магнитное поле, создаваемое индукционным током, должно быть направлено против внешнего магнитного поля.
Индукционный ток течёт против часовой стрелки, если смотреть со стороны создаваемого им магнитного поля. В данном случае ток будет направлен по часовой стрелке, если смотреть сверху, со стороны внешнего магнитного поля, как и показано на (рис. (3)).

Рис. 3. Магнитный поток возрастает
Теперь предположим, что магнитное поле, пронизывающее контур, уменьшается со временем (рис. 4). Например, мы удаляем магнит вниз от контура, а северный полюс магнита направлен на контур.

Рис. 4. Магнитный поток убывает
Магнитный поток через контур уменьшается. Индукционный ток будет иметь такое направление, чтобы его собственный магнитный поток поддерживал внешний магнитный поток, препятствуя его убыванию. Для этого магнитное поле индукционного тока должно быть направлено в ту же сторону , что и внешнее магнитное поле.
В этом случае индукционный ток потечёт против часовой стрелки, если смотреть сверху, со стороны обоих магнитных полей.
к оглавлению ▴
Взаимодействие магнита с контуром
Итак, приближение или удаление магнита приводит к появлению в контуре индукционного тока, направление которого определяется правилом Ленца. Но ведь магнитное поле действует на ток! Появится сила Ампера, действующая на контур со стороны поля магнита. Куда будет направлена эта сила?
Если вы хотите хорошо разобраться в правиле Ленца и в определении направления силы Ампера, попробуйте ответить на данный вопрос самостоятельно. Это не очень простое упражнение и отличная задача для С1 на ЕГЭ. Рассмотрите четыре возможных случая.
1. Магнит приближаем к контуру, северный полюс направлен на контур.
2. Магнит удаляем от контура, северный полюс направлен на контур.
3. Магнит приближаем к контуру, южный полюс направлен на контур.
4. Магнит удаляем от контура, южный полюс направлен на контур.
Не забывайте, что поле магнита не однородно: линии поля расходятся от северного полюса и сходятся к южному. Это очень существенно для определения результирующей силы Ампера. Результат получается следующий.
Если приближать магнит, то контур отталкивается от магнита. Если удалять магнит, то контур притягивается к магниту. Таким образом, если контур подвешен на нити, то он всегда будет отклоняться в сторону движения магнита, словно следуя за ним. Расположение полюсов магнита при этом роли не играет .
Уж во всяком случае вы должны запомнить этот факт — вдруг такой вопрос попадётся в части А1
Результат этот можно объяснить и из совершенно общих соображений — при помощи закона сохранения энергии.
Допустим, мы приближаем магнит к контуру. В контуре появляется индукционный ток. Но для создания тока надо совершить работу! Кто её совершает? В конечном счёте — мы, перемещая магнит. Мы совершаем положительную механическую работу, которая преобразуется в положительную работу возникающих в контуре сторонних сил, создающих индукционный ток.
Итак, наша работа по перемещению магнита должна быть положительна . Это значит, что мы, приближая магнит, должны преодолевать силу взаимодействия магнита с контуром, которая, стало быть, является силой отталкивания .
Теперь удаляем магнит. Повторите, пожалуйста, эти рассуждения и убедитесь, что между магнитом и контуром должна возникнуть сила притяжения.
к оглавлению ▴
Закон Фарадея + Правило Ленца = Снятие модуля
Выше мы обещали снять модуль в законе Фарадея (5). Правило Ленца позволяет это сделать. Но сначала нам нужно будет договориться о знаке ЭДС индукции — ведь без модуля, стоящего в правой части (5), величина ЭДС может получаться как положительной, так и отрицательной.
Прежде всего, фиксируется одно из двух возможных направлений обхода контура. Это направление объявляется положительным . Противоположное направление обхода контура называется, соответственно, отрицательным . Какое именно направление обхода мы берём в качестве положительного, роли не играет — важно лишь сделать этот выбор.
Магнитный поток через контур считается положительным , если магнитное поле, пронизывающее контур, направлено туда, глядя откуда обход контура в положительном направлении совершается против часовой стрелки. Если же с конца вектора магнитной индукции положительное направление обхода видится по часовой стрелке, то магнитный поток считается отрицательным
.
ЭДС индукции считается положительной , если индукционный ток течёт в положительном направлении. В этом случае направление сторонних сил, возникающих в контуре при изменении магнитного потока через него, совпадает с положительным направлением обхода контура.
Наоборот, ЭДС индукции считается отрицательной , если индукционный ток течёт в отрицательном направлении. Сторонние силы в данном случае также будут действовать вдоль отрицательного направления обхода контура.
Итак, пусть контур находится в магнитном поле . Фиксируем направление положительного обхода контура. Предположим, что магнитное поле направлено туда, глядя откуда положительный обход совершается против часовой стрелки. Тогда магнитный поток положителен:
.
Предположим, далее, что магнитный поток увеличивается . Согласно правилу Ленца индукционный ток потечёт в отрицательном направлении (рис. 5).

Рис. 5. Магнитный поток возрастает
Стало быть, в данном случае имеем . Знак ЭДС индукции оказался противоположен знаку скорости изменения магнитного потока. Проверим это в другой ситуации.
А именно, предположим теперь, что магнитный поток убывает . По правилу Ленца индукционный ток потечёт в положительном направлении. Стало быть,
(рис. 6).

Рис. 6. Магнитный поток возрастает
Таков в действительности общий факт: при нашей договорённости о знаках правило Ленца всегда приводит к тому, что знак ЭДС индукции противоположен знаку скорости изменения магнитного потока :
(6)
Тем самым ликвидирован знак модуля в законе электромагнитной индукции Фарадея.
к оглавлению ▴
Вихревое электрическое поле
Рассмотрим неподвижный контур, находящийся в переменном магнитном поле. Каков же механизм возникновения индукционного тока в контуре? А именно, какие силы вызывают движение свободных зарядов, какова природа этих сторонних сил?
Пытаясь ответить на эти вопросы, великий английский физик Максвелл открыл фундаментальное свойство природы: меняющееся во времени магнитное поле порождает поле электрическое . Именно это электрическое поле и действует на свободные заряды, вызывая индукционный ток.
Линии возникающего электрического поля оказываются замкнутыми, в связи с чем оно было названо вихревым электрическим полем . Линии вихревого электрического поля идут вокруг линий магнитного поля и направлены следующим образом.
Пусть магнитное поле увеличивается. Если в нём находится проводящий контур, то индукционный ток потечёт в соответствии с правилом Ленца — по часовой стрелке, если смотреть с конца вектора . Значит, туда же направлена и сила, действующая со стороны вихревого электрического поля на положительные свободные заряды контура; значит, именно туда направлен вектор напряжённости вихревого электрического поля.
Итак, линии напряжённости вихревого электрического поля направлены в данном случае по часовой стрелке (смотрим с конца вектора , (рис. 7).

Рис. 7. Вихревое электрическое поле при увеличении магнитного поля
Наоборот, если магнитное поле убывает, то линии напряжённости вихревого электрического поля направлены против часовой стрелки (рис. 8).

Рис. 8. Вихревое электрическое поле при уменьшении магнитного поля
Теперь мы можем глубже понять явление электромагнитной индукции. Суть его состоит именно в том, что переменное магнитное поле порождает вихревое электрическое поле. Данный эффект не зависит от того, присутствует ли в магнитном поле замкнутый проводящий контур или нет; с помощью контура мы лишь обнаруживаем это явление, наблюдая индукционный ток.
Вихревое электрическое поле по некоторым свойствам отличается от уже известных нам электрических полей: электростатического поля и стационарного поля зарядов, образующих постоянный ток.
1. Линии вихревого поля замкнуты, тогда как линии электростатического и стационарного полей начинаются на положительных зарядах и оканчиваются на отрицательных.
2. Вихревое поле непотенциально: его работа перемещению заряда по замкнутому контуру не равна нулю. Иначе вихревое поле не могло бы создавать электрический ток! В то же время, как мы знаем, электростатическое и стационарное поля являются потенциальными.
Итак, ЭДС индукции в неподвижном контуре — это работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура .
Пусть, например, контур является кольцом радиуса и пронизывается однородным переменным магнитным полем. Тогда напряжённость
вихревого электрического поля одинакова во всех точках кольца. Работа
силы
, с которой вихревое поле действует на заряд
, равна:
Следовательно, для ЭДС индукции получаем:
к оглавлению ▴
ЭДС индукции в движущемся проводнике
Если проводник перемещается в постоянном магнитном поле, то в нём также появляется ЭДС индукции. Однако причиной теперь служит не вихревое электрическое поле (оно не возникает — ведь магнитное поле постоянно), а действие силы Лоренца на свободные заряды проводника.
Рассмотрим ситуацию, которая часто встречается в задачах. В горизонтальной плоскости расположены параллельные рельсы, расстояние между которыми равно . Рельсы находятся в вертикальном однородном магнитном поле
. По рельсам движется тонкий проводящий стержень
со скоростью
; он всё время остаётся перпендикулярным рельсам (рис. 9).

Рис. 9. Движение проводника в магнитном поле
Возьмём внутри стержня положительный свободный заряд . Вследствие движения этого заряда вместе со стержнем со скоростью
на заряд будет действовать сила Лоренца:
Направлена эта сила вдоль оси стержня, как показано на рисунке (убедитесь в этом сами — не забывайте правило часовой стрелки или левой руки!).
Сила Лоренца играет в данном случае роль сторонней силы: она приводит в движение свободные заряды стержня. При перемещении заряда
от точки
к точке
наша сторонняя сила совершит работу:
(Длину стержня мы также считаем равной .) Стало быть, ЭДС индукции в стержне окажется равной:
(7)
Таким образом, стержень аналогичен источнику тока с положительной клеммой
и отрицательной клеммой
. Внутри стержня за счёт действия сторонней силы Лоренца происходит разделение зарядов: положительные заряды двигаются к точке
, отрицательные — к точке
.
Допустим сначала,что рельсы непроводят ток.Тогда движение зарядов в стержне постепенно прекратится. Ведь по мере накопления положительных зарядов на торце и отрицательных зарядов на торце
будет возрастать кулоновская сила, с которой положительный свободный заряд
отталкивается от
и притягивается к
— и в какой-то момент эта кулоновская сила уравновесит силу Лоренца. Между концами стержня установится разность потенциалов, равная ЭДС индукции (7).
Теперь предположим, что рельсы и перемычка являются проводящими. Тогда в цепи возникнет индукционный ток; он пойдёт в направлении
(от «плюса источника»
к «минусу» N). Предположим, что сопротивление стержня равно
(это аналог внутреннего сопротивления источника тока), а сопротивление участка
равно
(сопротивление внешней цепи). Тогда сила индукционного тока найдётся по закону Ома для полной цепи:
Замечательно, что выражение (7) для ЭДС индукции можно получить также с помощью закона Фарадея. Сделаем это.
За время наш стержень
проходит путь
и занимает положение
(рис. 9). Площадь контура возрастает на величину площади прямоугольника
:
Магнитный поток через контур увеличивается. Приращение магнитного потока равно:
Скорость изменения магнитного потока положительна и равна ЭДС индукции:
Мы получили тот же самый результат, что и в (7). Направление индукционного тока, заметим, подчиняется правилу Ленца. Действительно, раз ток течёт в направлении , то его магнитное поле направлено противоположно внешнему полю
и, стало быть, препятствует возрастанию магнитного потока через контур.
На этом примере мы видим, что в ситуациях, когда проводник движется в магнитном поле, можно действовать двояко: либо с привлечением силы Лоренца как сторонней силы, либо с помощью закона Фарадея. Результаты будут получаться одинаковые.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Электромагнитная индукция» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
07.05.2023
Комментарии
Опубликовано 9 января, 2012 – 12:21 пользователем В. Грабцевич
Ei = −ΔФ / Δt,
где ΔФ = BΔS.
Рассмотрите изменение площади за t = T, только учтите направление создаваемых Ei.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 10 января, 2012 – 19:18 пользователем Иваг
то есть получается, что ΔS = ωL2/2 − ω(L/9)2/2 ?
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 11 января, 2012 – 10:52 пользователем Иваг
Да, то есть должно быть (8/9) L, а не L. Глупо ошибся.)
Спасибо большое!
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 12 января, 2012 – 15:19 пользователем Smoke
Иваг, выложите, пожалуйста, Ваше полное решение задачи. Интересно увидеть.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 12 января, 2012 – 19:56 пользователем Иваг
Ei = −?Ф / ?t,
где ?Ф = B?S.
?S = ? (8/9L)2/2 − ? (L/9)2 / 2 = 64?L2 / 81 − ?L2 / 81 = 63?L2 / 81,
?S = 0,0504 м2,
Ei = B?S / 2 = 0,0252 В.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 13 января, 2012 – 21:20 пользователем Smoke
Тогда помогите решить, пожалуйста. Все было бы просто, если б ось проходила через конец стержня.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Магнитный поток наглядно истолковывается как число линий магнитной индукции, пронизывающих поверхность площадью S. Поэтому скорость изменения этого числа есть не что иное, как скорость изменения магнитного потока.
Если за малое время ∆t магнитный поток поменялся на ∆Ф, то скорость изменения магнитного потока равна ΔΦΔt. Поэтому утверждение, которое вытекает непосредственно из опыта, можно сформулировать так:
Сила индукционного тока пропорциональная скорости изменения магнитного потока через поверхность, ограниченную контуром:
Ii~ΔΦΔt
Известно, что в цепи появляется электрический ток в том случае, когда на свободные заряды проводника действуют сторонние силы. Работу этих сил при перемещении единичного положительного заряда вдоль замкнутого контура называют электродвижущей силой. Следовательно, при изменении магнитного потока через поверхность, ограниченную контуров, появляются сторонние силы, действие которых характеризуется ЭДС, называемой ЭДС индукции. Обозначают ее как εi.
Согласно закону Ома для замкнутой цепи:
Ii=εiR
Сопротивление проводника не зависит от изменения магнитного потока. Следовательно, сила индукционного тока пропорциональна скорости изменения магнитного потока только потому, что ЭДС индукции тоже пропорциональна этой скорости изменения потока.
Закон электромагнитной индукции
ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром.
εi=∣∣∣ΔΦΔt∣∣∣
Закон электромагнитной индукции формулируется именно для ЭДС, а не для силы тока. При такой формулировке закон выражает сущность явления, не зависящую от свойств проводников, в которых возникает индукционный ток.
Определение знака ЭДС индукции
На рисунке изображен замкнутый контур. Будем считать положительным направление обхода контура против часовой стрелки. Нормаль →n к контуру образует правый винт с направлением обхода.
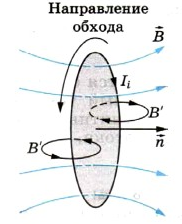
Пусть магнитная индукция →B внешнего магнитного поля направлена вдоль нормали к контуру и возрастает со временем. Тогда Φ>0 и ΔΦΔt>0. Согласно правилу Ленца индукционный ток создает магнитный поток Φ‘<0. Линии магнитной индукции B’ магнитного поля индукционного тока изображены черным цветом. Следовательно, индукционный ток Ii согласно правилу буравчика направлен по часовой стрелке (против направления положительного обхода) и ЭДС индукции отрицательна. Поэтому в законе электромагнитной индукции должен стоять знак «–», указывающий на то, что εi и ΔΦΔt имеют разные знаки:
εi=−ΔΦΔt
Пример №1. Магнитный поток через контур проводника сопротивлением 3∙10–2 Ом за 2 с изменился на 1,2∙10–2 Вб. Найдите силу тока в проводнике, если изменение потока происходило равномерно.
Известно, что:
Ii=εiR
εi=∣∣∣ΔΦΔt∣∣∣
Следовательно:
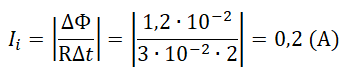
ЭДС индукции в движущихся проводниках
Электроны в неподвижном проводнике приводятся в движение электрическим полем, и это поле порождается переменным магнитным полем. Следовательно, изменяясь во времени, магнитное поле порождает электрическое поле. Но если проводник движется в постоянном во времени магнитном поле, то ЭДС индукции в проводнике обусловлена не вихревым электрическим полем, которое в этом случае не может возникнуть, а другой причиной.
При движении проводника его свободные заряды движутся вместе с ним. Поэтому на заряды со стороны магнитного поля действует сила Лоренца. Она и вызывает перемещение зарядов внутри проводника. ЭДС индукции, следовательно, имеет магнитное происхождение.
Вычислим ЭДС индукции, возникающую в проводнике, движущемся в однородном магнитном поле (см. рисунок). Пусть сторона контура MN длиной l скользит с постоянной скоростью →v вдоль сторон NC и MD, оставаясь все это время параллельной стороне CD. Вектор магнитной индукции →B однородного поля перпендикулярен проводнику и составляет угол α с направлением его скорости.
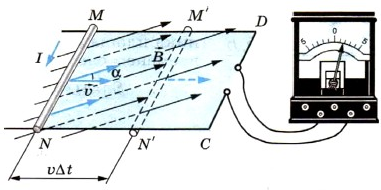
Сила, с которой магнитное поле действует на движущуюся заряженную частицу, равна по модулю:
FL=|q|vBsinα
Направлена эта сила вдоль проводника MN. Работа силы Лоренца на пути l положительна и составляет:
A=FLl=|q|vBlsinα
Внимание!
Формула выше определяет неполную работу силы Лоренца. Кроме силы Лоренца имеется составляющая силы Лоренца, направленная против скорости проводника →v. Такая составляющая тормозит проводник и совершает отрицательную работу. В результате полная работа силы Лоренца оказывается равной нулю.
Электродвижущая сила индукции в проводнике MN равна по определению отношению работы по перемещению заряда q к этому заряду:
εi=A|q|=vBlsinα
Эта формула справедлива для любого проводника длиной l, движущегося со скоростью →v в однородном магнитном поле.
В других проводниках контура ЭДС равна нулю, так как проводники неподвижны. Следовательно, ЭДС во всем контуре MNCD равна εi и остается неизменной, если скорость движения →v постоянна. Электрический ток при этом будет увеличиваться, так как при смещении проводника MN вправо уменьшается общее сопротивление контура.
С другой стороны, ЭДС индукции можно вычислить с помощью закона электромагнитной индукции. Магнитный поток через контур MNCD равен:
Φ=BScos(90°−α)=BSsinα
угол 90°−α представляет собой угол между векторами →B и нормалью →n к поверхности контура, а S — площадь контура MNCD. Если считать, что в начальный момент времени t=0 проводник MN находится на расстоянии NC от проводника CD, то при перемещении проводника площадь S изменяется со временем следующим образом:
S=l(NC−vt)
За время ∆t площадь контура меняется на ΔS=−lvΔt. Знак «минус» указывает на то, что она уменьшается. Изменение магнитного потока за это время равно:
ΔΦ=−BvlΔtsinα
Следовательно:
εi=−ΔΦΔt=Bvlsinα
Если весь контур MNCD движется в однородном магнитном поле, сохраняя свою ориентацию по отношению к вектору →B, то ЭДС индукции в контуре будет равна нулю, так как поток Φ через поверхность, ограниченную контуром, не меняется. Объяснить это можно так. При движении контура в проводниках MN и CD возникают силы, действующие на электроны в направлениях от N к M и от C к D. Суммарная работа этих сил при обходе контура по часовой стрелке или против нее равна нулю.
Пример №2. Проводник длиной 50 см движется в однородном магнитном поле со скоростью 4 м/с перпендикулярно силовым линиям. Найдите разность потенциалов, возникающую на концах проводника, если вектор магнитной индукции 8 мТл.
50 см = 0,5 м
8 мТл = 8∙10–3 Тл
Так как проводник движется перпендикулярно силовым линиям, то угол α равен 90 градусам, а синус прямого угла равен единице. Поэтому:
εi=Bvlsinα=8·10−3·4·0,5·1=16·10−3 (В)
Задание EF17754
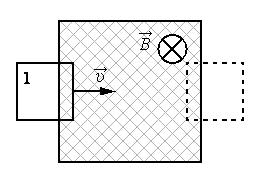 В заштрихованной области на рисунке действует однородное магнитное поле, направленное перпендикулярно плоскости рисунка, В = 0,1 Тл. Проволочную квадратную рамку сопротивлением R=10Ом и стороной l=10см перемещают в плоскости рисунка поступательно со скоростью υ=1м/с. Чему равен индукционный ток в рамке в состоянии 1?
В заштрихованной области на рисунке действует однородное магнитное поле, направленное перпендикулярно плоскости рисунка, В = 0,1 Тл. Проволочную квадратную рамку сопротивлением R=10Ом и стороной l=10см перемещают в плоскости рисунка поступательно со скоростью υ=1м/с. Чему равен индукционный ток в рамке в состоянии 1?
Ответ:
а) 1 мА
б) 5 мА
в) 10 мА
г) 20 мА
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать формулу для определения величины индукционного тока.
3.Записать закон электромагнитной индукции для движущихся проводников.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решения
Запишем исходные данные:
• Модуль вектора магнитной индукции однородного магнитного поля: B = 0,1 Тл.
• Сопротивление внутри квадратной проволочной рамки: R = 10 Ом.
• Сторона рамки: l = 10 см.
• Скорость перемещения рамки: v = 1 м/с.
10 см = 0,1 м
Индукционный ток, возникающий в рамке, определяется по формуле:
Ii=εiR
Закон электромагнитной индукции для движущихся проводников:
εi=vBlsinα
Отсюда индукционный ток равен:
Ii=vBlsinαR
На рисунке вектор магнитной индукции направлен в сторону от наблюдателя. Следовательно, угол между направлением движения рамки и вектором магнитной индукции равен 90 градусам. А синус прямого угла равен единице. Тогда:
Ii=vBlsin90°R=1·0,1·0,1·110=0,001 (А)=1 (мА)
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17970
При вращении в однородном магнитном поле плоскости металлического кольца из тонкой проволоки вокруг оси, перпендикулярной линиям поля, максимальная сила индукционного тока, возникающего в кольце, равна I1. Чему будет равна максимальная сила индукционного тока I2 в этом кольце при уменьшении скорости вращения кольца в 2 раза?
Ответ:
а) I2 = 2I1
б) I2 = I1
в) I2 = 0,5I1
г) I2 = 4I1
Алгоритм решения
1.Записать закон электромагнитной индукции.
2.Установить зависимость между величиной индукционного тока и скоростью вращения рамки.
3.Определить, как изменится величина индукционного тока в кольце при уменьшении скорости ее вращения.
Решение
Запишем формулу закона электромагнитной индукции:
εi=∣∣∣ΔΦΔt∣∣∣
Известно, что отношение изменения магнитного потока ко времени его изменения — это величина, характеризующая скорость этого изменения. Если кольцо в однородном магнитном поле вращать медленнее, то и магнитный поток начнет менять медленнее. Так как ЭДС индукции прямо пропорционально зависит от скорости изменения магнитного потока, то при уменьшении скорости вращения кольца в 2 раза она также уменьшится вдвое.
Также известно, что индукционный ток в рамке определяется формулой:
Ii=εiR
Видно, что индукционный ток и ЭДС индукции — прямо пропорциональные величины. Следовательно, при уменьшении ЭДС индукции вдвое сила индукционного тока тоже уменьшится в 2 раза. Отсюда следует, что I2 = 0,5I1.
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18860
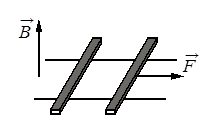 По горизонтально расположенным шероховатым рельсам с пренебрежимо малым сопротивлением могут скользить два одинаковых стержня массой m = 100 г и сопротивлением R = 0,1 Ом каждый. Расстояние между рельсами l = 10 см, а коэффициент трения между стержнями и рельсами μ = 0,1 Рельсы со стержнями находятся в однородном вертикальном магнитном поле с индукцией B = 1 Тл (см. рисунок). Под действием горизонтальной силы, действующей на первый стержень вдоль рельс, оба стержня движутся поступательно равномерно с разными скоростями. Какова скорость движения первого стержня относительно второго? Самоиндукцией контура пренебречь. Ответ записать в системе СИ.
По горизонтально расположенным шероховатым рельсам с пренебрежимо малым сопротивлением могут скользить два одинаковых стержня массой m = 100 г и сопротивлением R = 0,1 Ом каждый. Расстояние между рельсами l = 10 см, а коэффициент трения между стержнями и рельсами μ = 0,1 Рельсы со стержнями находятся в однородном вертикальном магнитном поле с индукцией B = 1 Тл (см. рисунок). Под действием горизонтальной силы, действующей на первый стержень вдоль рельс, оба стержня движутся поступательно равномерно с разными скоростями. Какова скорость движения первого стержня относительно второго? Самоиндукцией контура пренебречь. Ответ записать в системе СИ.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать закон электромагнитной индукции для двигающихся стержней.
3.Выполнить решение задачи в общем виде.
4.Подставить неизвестные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса стержней: m1=m2=m=100 г.
• Сопротивление стержней: R1=R2=R=0,1 Ом.
• Расстояние между рельсами: l = 10 см.
• Коэффициент трения между стержнями и рельсами: μ = 0,1.
• Модуль вектора магнитной индукции магнитного поля: B = 1 Тл.
• Угол между вектором магнитной индукцией и вектором скорости стержней: α = 90 градусов (синус прямого угла равен «1»).
100 г = 0,1 кг
10 см = 0,1 м
Когда под действием некой силы начинается двигаться первый стержень, магнитный поток, пронизывающий контур, образованные проводящими рельсами и двумя стержнями, меняется. Это приводит к возникновению в этом контуре электродвижущей силы, которую можно определить с помощью закона электромагнитной индукции для двигающихся стержней:
εi=vBlsinα
Причем v — это разность скоростей стержней (v2 – v1), которая характеризует скорость изменения площади проводящего контура.
Индукционный ток, возникающей в этом контуре, можно выразить, используя закон Ома:
εi=IRк
где Rк — сопротивление контура. Так как стержни соединяются последовательно, и их сопротивления равны R, а сопротивление рельсов ничтожно мало, сопротивление контура равно:
Rк=2R
Отсюда закон Ома принимает вид:
εi=2IR
Тогда ток в контуре равен:
I=εi2R=vBlsinα2R
С одной стороны на стержни действует сила Ампера, с другой — сила трения, возникающего между ними и рельсами. Так как стержни движутся равномерно, равнодействующая сил, приложенных к ним, равна нулю. Следовательно, сила трения и сила Ампера компенсируют друг друга (их модули равны):
Fтр=FА
μmg=BIlsinα
Подставим сюда выражение, полученное для силы тока в контуре:
μmg=BvBlsinα2Rlsinα=vB2l2sin2α2R
Отсюда скорость равна:
v=2μmgRB2l2sin2α
Так как синус угла равен «1»:
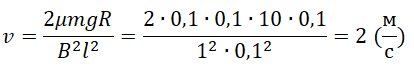
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5.6k
На прошлом уроке мы с вами ввели
в рассмотрение понятие магнитного потока (или потока вектора магнитной
индукции). Напомним, что так называют скалярную физическую величину,
равную произведению модуля индукции магнитного поля, площади поверхности,
ограниченной контуром, и косинуса угла между направлениями нормали к этой
поверхности и магнитной индукции:
А ещё мы с вами познакомились с некоторыми опытами Майкла Фарадея, позволившие ему открыть одно из
уникальных явлений современного мира — явление электромагнитной индукции.
Давайте с вами вспомним, что это явление заключается в том, что при всяком
изменении магнитного потока, пронизывающего замкнутый проводящий контур, в этом
контуре возникает индукционный ток, существующий в течение всего времени
изменения магнитного потока.
Но у нас с вами остался ещё
один важный и нерешённый вопрос: какого же направление возникающего
индукционного тока? Этим вопросом задавались многие учёные, среди которых был и
петербургский академик Эмилий Христианович Ленц. В 1833 году после серии
исследований явления электромагнитной индукции ему удалось сформулировать
правило для определения направления индукционного тока — правило Ленца.
Согласно этому правилу, возникающий в замкнутом проводящем контуре индукционный
ток имеет такое направление, что созданный им магнитный поток через
поверхность, ограниченную контуром, противодействует изменению магнитного
потока, которым вызывается этот индукционный ток.
Правило Ленца можно проиллюстрировать
на таком опыте. Возьмём два лёгких алюминиевых кольца, находящихся на острие
подставки. Одно кольцо, как видно, сплошное. Другое же кольцо имеет небольшой разрез.
Теперь возьмём постоянный магнит попробуем приблизить его к разрезанному кольцу.
Как видим, разрезанное кольцо никак не реагирует на магнит. Это говорит нам о
том, что индукционный ток в этом кольце не возникает.
А теперь попробуем приблизить
магнит к сплошному кольцу. Как видим, оно отталкивается от магнита, подобно
тому, как отталкиваются два одноимённых полюса магнита. И действительно, когда
мы пытаемся внести магнит в кольцо, то в последнем возникает индукционный ток,
который порождает в собственное магнитное поле. По правилу Ленца это поле имеет
такое направление, что его линии индукции направлены противоположно линиям
индукции внешнего поля магнита. Иными словами, кольцо и магнит оказываются
обращёнными друг к другу одноименными полюсами.
Продолжим наши опыты. Но
теперь, придерживая коромысло рукой, внесём магнит в сплошное кольцо. Отпустив
коромысло, попробуем вытянуть магнит — кольцо следует за магнитом, подобно
тому, как притягиваются два разноимённых полюса магнита. Объясним и этот
случай. Когда мы пытаемся убрать магнит из кольца (то есть уменьшаем магнитный
поток), то в кольце вновь возникает индукционный ток, но уже другого
направления. Этот ток также порождает собственное магнитное поле. Однако линии
индукции этого поля теперь направлены так же, как и линии индукции внешнего поля
магнита. Иными словами, кольцо и магнит оказываются обращёнными друг к другу разноимёнными
полюсами.
В более сжатой форме правило
Ленца можно сформулировать следующим образом: индукционный ток всегда
направлен так, что его действие противоположно действию причины, вызвавшей этот
ток.
Индукционный ток, как и всякий
ток, обладает энергией. Следовательно, получая индукционный ток, мы тем самым
получаем электрическую энергию. Согласно закону сохранения и превращения
энергии, последняя может быть получена только за счёт эквивалентного количества
энергии какого-нибудь другого вида.
Когда мы приближаем, например,
к катушке магнит, то возникающий в ней индукционный ток своим магнитным полем
отталкивает магнит. Двигая магнит, мы преодолеваем эти силы отталкивания, то
есть совершаем работу, в результате чего механическая энергия и превращается в
энергию индукционного тока.
При выдвигании магнита из
катушки совершается работа по преодолению силы притяжения катушки. Механическая
энергия здесь также превращается в энергию индукционного тока. Таким образом,
закон Ленца находится в полном соответствии с законом сохранения и превращения
энергии.
Для того, чтобы определить
направление индукционного тока по правилу Ленца, необходимо выполнить несколько
нехитрых операций:
1) необходимо выяснить, как
направлены линии магнитной индукции внешнего магнитного поля%
2) установить, увеличивается
или уменьшается магнитный поток через поверхность, ограниченную проводящим
контуром;
3) определить направление
линий индукции магнитного поля индукционного тока. Для этого необходимо
руководствоваться следующим: если изменение магнитного потока является
величиной отрицательной, то направления индукций внешнего магнитного поля и
магнитного поля индукционного тока совпадают, в противном случае эти направления
противоположны.
4) узнав направление линий
индукции магнитного поля индукционного тока, воспользоваться правилом буравчика
для определения направления индукционного тока.
Открыв явление
электромагнитной индукции, Фарадей буквально за полтора месяца установил все его
существенные закономерности. Ему стала понятна сущность явления, которое
сыграло такую важную, без преувеличения, роль для всего человечества: во всех проведённых
опытах индукционный ток в проводящем контуре возникал только в результате
изменения магнитного потока через поверхность, ограниченную этим контуром.
Как вы уже знаете, для
существования тока в замкнутой электрической цепи необходимо, чтобы на
свободные заряженные частицы действовали сторонние силы, то есть в цепи должен
быть источник ЭДС. Вы, наверное, догадались, что в опытах Фарадея источником
этих самых сторонних сил был изменяющийся магнитный поток, который и создавал в
цепи электродвижущую силу. Эту ЭДС мы с вами будем называть электродвижущей
силой индукции или, сокращённо, ЭДС индукцией.
Заметим, что для явления
электромагнитной индукции именно ЭДС индукции является характерной величиной, а
не индукционный ток, так как он зависит от сопротивления контура. Например, в
двух одинаковых по размерам и форме проводниках при одинаковых условиях ЭДС
индукции будет одинакова, а индукционный ток будет меньше в том проводнике, сопротивление
которого больше.
Теперь, введя понятие ЭДС
индукции мы можем дать более строгое определение явления электромагнитной
индукции. Итак, явление возникновения ЭДС индукции в контуре, который
либо покоится в изменяющемся во времени магнитном поле, либо движется в
постоянном магнитном поле так, что магнитный поток через поверхность,
ограниченную контуром, меняется, называют электромагнитной индукцией.
В 1873 году ещё один
выдающийся английский физик Джеймс Клерк Максвелл, занялся анализом результатов
опытов Фарадея. В частности, он заметил одно очень важное обстоятельство: чем
быстрее меняется магнитный поток, пронизывающий контур, тем больший индукционный
ток идёт по проводнику и, следовательно, тем большая ЭДС индукции в нём
возникает:
Однако из закона Ома для замкнутой
цепи следует, что сила индукционного тока должна быть прямо пропорциональна ЭДС
индукции и обратно пропорциональна сопротивлению проводника:
А так как сопротивление
проводника не зависит от изменения магнитного потока, то выражение для силы
индукционного тока будет справедливо только тогда, когда ЭДС индукции
пропорциональна скорости изменения магнитного потока
Чтобы обеспечить строгое
равенство в записанном выражении, необходимо учесть направление индукционного
тока. Как мы уже с вами выяснили, по правилу Ленца при увеличении магнитного
потока ЭДС индукции отрицательная и, наоборот, при уменьшении магнитного потока
ЭДС индукции положительная. Тогда можно записать, что ЭДС электромагнитной
индукции в контуре равна скорости изменения магнитного потока через
поверхность, ограниченную контуром, взятой с противоположным знаком:
В
этом и состоит математическая суть закона электромагнитной индукции,
установленного Джеймсом Максвеллом и названного в честь Майкла Фарадея законом
электромагнитной индукции Фарадея.
Для
закрепления нового материала, давайте с вами решим такую задачу. И условие
первой из них такое: в однородном магнитном поле, индукция которого равна 500
мТл, вращается стержень длиной 1 м с постоянной угловой скоростью 20 рад/с.
Определите ЭДС индукцию, возникающую в стержне, если ось вращения проходит
через конец стержня параллельно линиям магнитной индукции.
В заключении урока отметим, что
наибольшего значения индукционные токи достигают в массивных проводниках. Такие
токи принято называть токами Фуко́ по имени исследовавшего их французского
физика Поль-Мишеля Фуко. Как правило, эти токи используются для нагревания
проводников, например, в индукционных печах, современных индукционных плитах и
так далее. Однако существует много устройств, в которых возникновение токов
Фуко́ приводит к бесполезным, а порой и нежелательным потерям энергии на
выделение тепла. Поэтому, например, в электродвигателях, генераторах, и
трансформаторах железные сердечники выполняются не из сплошного металла,
состоящие из отдельных пластин, изолированных друг от друга.
Рассмотрим движущийся в однородном магнитном поле проводник. В нём на каждый заряд действует сила Лоренца. Под её действием внутри проводника начинают двигаться свободные заряды, из-за чего появляется электродвижущая сила. Эта сила имеет магнитное происхождение и является сторонней.
Если в однородном магнитном поле находится контур, состоящий из рамки и движущегося по ней проводника (скорость проводника постоянна и равна (V)) (рис. (1)), то сила Лоренца, которая действует на каждую частицу в движущемся проводнике, равна:
(boxed{vec{F}_л=qvec{V}times vec{B}}). ((1))

Рис. (1). Физическая модель движения проводника в магнитном поле
Формула ((1)) описывает силу, которая действует на положительный заряд. Она направлена вдоль проводника, а её работа по перемещению заряда между концами этого проводника равна:
(A_{ст}=F_л l=q V B l sinalpha), ((2))
где (l) — это длина движущегося проводника, а (alpha) — это угол между вектором индукции магнитного поля и вектором скорости проводника.
Из формулы ((2)) следует формула для ЭДС:
(boxed{E_i=frac{A_{ст}}{q}= V B lsinalpha}). ((3))
Эту же формулу можно получить из другого типа рассуждений. Рассмотрим этот же эксперимент, однако положим, что движущийся проводник и рамка создают замкнутый контур с некоторой площадью (S). За некоторое время (Delta t ) площадь изменится на:
(Delta S= – V l Delta t), ((4))
где знак «(-)» указывает на уменьшение площади.
Как следствие, изменится магнитный поток через рассматриваемый контур:
(Delta Phi=- B V l Delta t sin alpha). ((5))
По закону электромагнитной индукции величина возникающей ЭДС может быть определена как:
(E_i=-frac{Delta Phi}{Delta t}=B V l sin alpha). ((6))
Источники:
Рис. 1. Физическая модель движения проводника в магнитном поле. © ЯКласс.
