Как найти эдс источника по графику – Сайт, где вы сможете решить свои вопросы

ЭДС. Закон Ома для полной цепи

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
Сторонняя сила
Закон Ома для полной цепи
КПД электрической цепи
Закон Ома для неоднородного участка

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.

До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.

Как мы знаем, положительный заряд $q$ :

• уходит во внешнюю цепь с положительной клеммы источника;

• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;

• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.

Теперь нашему положительному заряду $q$ нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила $vec{F_E}$ , направленная против движения заряда (т.е. против направления тока).

к оглавлению ▴

Сторонняя сила

Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).

Рис. 1. Сторонняя сила

Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила $vec{F_{CT}}$ не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.

Обозначим через $A_{CT}$ работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы $A_{CT}$ называется также работой источника тока.

Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда $q$ вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, $A_{CT}$ — это также работа сторонней силы по перемещению заряда по всей цепи.

Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.

Опыт показывает, что работа $A_{CT}$ прямо пропорциональна перемещаемому заряду $q$ . Поэтому отношение $A_{CT}/q$ уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается $mathcal E$ :

$mathcal E = frac{displaystyle A_{CT}}{displaystyle q vphantom{1^a}}.$ (1)

Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.

Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.

к оглавлению ▴

Закон Ома для полной цепи

Любой источник тока обладает своим сопротивлением $r$ , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.

Пусть источник тока с ЭДС, равной $mathcal E$ , и внутренним сопротивлением $r$ подключён к резистору $R$ (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).

Рис. 2. Полная цепь

Наша задача — найти силу тока $I$ в цепи и напряжение $U$ на резисторе $R$ .

За время $t$ по цепи проходит заряд $q = It$ . Согласно формуле (1) источник тока совершает при этом работу:

$A_{CT} = Eq = EIt.$ (2)

Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях $R$ и $r$ . Данное количество теплоты определяется законом Джоуля–Ленца:

$Q = I^2Rt + I^2rt = I^2(R + r)t.$ (3)

Итак, $A_{CT} = Q$ , и мы приравниваем правые части формул (2) и (3):

$mathcal E It = I^2(R + r)t.$

После сокращения на $It$ получаем:

$mathcal E = I(R + r).$

Вот мы и нашли ток в цепи:

$I = frac{displaystyle mathcal E}{displaystyle R + r vphantom{1^a}}.$ (4)

Формула (4) называется законом Ома для полной цепи.

Если соединить клеммы источника проводом пренебрежимо малого сопротивления $(R = 0)$ , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:

$I_{K3} = frac{displaystyle mathcal E}{displaystyle r vphantom{1^a}}.$

Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.

Зная силу тока (формула (4)), мы можем найти напряжение на резисторе $R$ с помощью закона Ома для участка цепи:

$U = IR = frac{displaystyle mathcal E R}{displaystyle R + r vphantom{1^a}}.$ (5)

Это напряжение является разностью потенциалов между точками $a$ и $b$ (рис. 2). Потенциал точки $a$ равен потенциалу положительной клеммы источника; потенциал точки $b$ равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.

Мы видим из формулы (5), что в реальной цепи будет $Utextless mathcal E$ — ведь $mathcal E$ умножается на дробь, меньшую единицы. Но есть два случая, когда $U = mathcal E$ .

1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При $r = 0$ формула (5) даёт $U = mathcal E$ .

2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: $R = infty$ . Тогда величина $R + r$ неотличима от $R$ , и формула (5) снова даёт нам $U = mathcal E$ .

Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.

к оглавлению ▴

КПД электрической цепи

Нетрудно понять, почему резистор $R$ называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.

Количество теплоты, выделяющееся на полезной нагрузке $R$ за время $t$ , обозначим $Q_{polezn}$ .

Если сила тока в цепи равна $I$ , то

$Q_{polezn} = I^2Rt.$

Некоторое количество теплоты выделяется также на источнике тока:

$Q_{ist} = I^2rt.$

Полное количество теплоты, которое выделяется в цепи, равно:

$Q_{poln} = Q_{polezn} + Q_{ist} = I^2Rt + I^2rt = I^2(R + r)t.$

КПД электрической цепи — это отношение полезного тепла к полному:

$eta = frac{displaystyle Q_{polezn}}{displaystyle Q_{poln} vphantom{1^a}} = frac{displaystyle I^2Rt}{displaystyle I^2(R+r)t vphantom{1^a}} = frac{displaystyle R}{displaystyle R+r vphantom{1^a}}.$

КПД цепи равен единице лишь в том случае, если источник тока идеальный $(r = 0)$ .

к оглавлению ▴

Закон Ома для неоднородного участка

Простой закон Ома $U = IR$ справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.

Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.

На рис. 3 показан неоднородный участок, содержащий резистор $R$ и источник тока. ЭДС источника равна $mathcal E$ , его внутреннее сопротивление считаем равным нулю (если внутреннее сопротивление источника равно $r$ , можно просто заменить резистор $R$ на резистор $R + r$ ).

Рис. 3. ЭДС «помогает» току: $varphi_a - varphi_b + mathcal E = IR$

Сила тока на участке равна $I$ , ток течёт от точки $a$ к точке $b$ . Этот ток не обязательно вызван одним лишь источником $mathcal E$ . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток $I$ является результатом совокупного действия всех источников, имеющихся в цепи.

Пусть потенциалы точек $a$ и $b$ равны соответственно $varphi_a$ и $varphi_b$ . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.

Напряжение на нашем участке равно: $U = varphi_a - varphi_b$ . За время $t$ через участок проходит заряд $q = It$ , при этом стационарное электрическое поле совершает работу:

$A_{POL} = Uq = UIt.$

Кроме того, положительную работу совершает источник тока (ведь заряд $q$ прошёл сквозь него!):

$A_{CT} = mathcal Eq = mathcal EIt.$

Сила тока постоянна, поэтому суммарная работа по продвижению заряда $q$ , совершаемая на участке стационарным электрическим полем и сторонними силами источника, целиком превращается в тепло: $A_{POL} + A_{CT} = Q$ .

Подставляем сюда выражения для $A_{POL}$ , $A_{CT}$ и закон Джоуля–Ленца:

$UIt + mathcal EIt = I^2Rt.$

Сокращая на $It$ , получаем закон Ома для неоднородного участка цепи:

$U + mathcal E = IR,$ (6)

или, что то же самое:

$varphi a - varphi b + mathcal E = IR.$ (7)

Обратите внимание: перед $mathcal E$ стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд $q$ от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки $a$ к точке $b$ .

Отметим два следствия выведенных формул (6) и (7).

1. Если участок однородный, то $mathcal E = 0$ . Тогда из формулы (6) получаем $U = IR$ — закон Ома для однородного участка цепи.

2. Предположим, что источник тока обладает внутренним сопротивлением $r$ . Это, как мы уже упоминали, равносильно замене $R$ на $R + r$ :

$varphi_a - varphi_b + mathcal E = I(R + r).$

Теперь замкнём наш участок, соединив точки $a$ и $b$ . Получим рассмотренную выше полную цепь. При этом окажется, что $varphi_a = varphi_b,$ и предыдущая формула превратится в закон Ома для полной цепи:

$mathcal E = I(R + r).$

Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.

Может быть и другой случай подключения, когда источник $mathcal E$ «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от $a$ к $b$ , направлен против действия сторонних сил источника.

Рис. 4. ЭДС «мешает» току: $varphi_a - varphi_b - mathcal E = IR$

Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против $mathcal E$ . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!

Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:

$A_{CT} = mathcal E q = mathcal EIt.$

Тогда закон Ома для неоднородного участка примет вид:

$varphi_a - varphi_b - mathcal E = IR,$ (8)

или:

$U - mathcal E = IR,$

где по-прежнему $U = varphi_a - varphi_b$ — напряжение на участке.

Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:

$varphi_a - varphi_b pm mathcal E = IR.$

Ток при этом течёт от точки $a$ к точке $b$ . Если направление тока совпадает с направлением сторонних сил, то перед $mathcal E$ ставится «плюс»; если же эти направления противоположны, то ставится «минус».

Повторим основные понятия и определения по теме «Закон Ома».

Напомним, что напряжение измеряется в вольтах.

Сила тока измеряется в амперах.

Сопротивление измеряется в омах. Эта единица измерения названа в честь Георга Симона Ома, открывшего взаимосвязь между напряжением, сопротивлением цепи и силой тока в этой цепи.

Основные определения, которые мы используем в решении задач:

Источник тока – это устройство, способное создавать необходимую для существования тока разность потенциалов.

Можно сказать, что источник тока действует, как насос. Он «качает» электроны по проводникам, как водяной насос воду по трубам. Эту аналогию можно продолжить. При этом источник тока совершает работу, за счёт химических реакций, происходящих внутри него.

Если эту работу разделить на переносимый источником заряд q (суммарный заряд всех проходящих через источник электронов), то мы получим величину, которую называют электродвижущей силой или сокращённо ЭДС.

Измеряется эта ЭДС, как и разность потенциалов, в вольтах и имеет примерно тот же смысл.

По определению, сила тока равна отношению суммарного заряда электронов, проходящих через сечение проводника, ко времени прохождения. Измеряется сила тока в амперах (А).

Свойство проводника препятствовать прохождению по нему тока характеризуется величиной, которую назвали электрическим сопротивлением – R. Проходя через проводник, электрический ток нагревает его.

Сопротивление измеряют в омах (Ом).

Сам источник тока тоже обладает сопротивлением. Такое сопротивление принято называть внутренним сопротивлением источника r (Ом).

Именно немецкому учёному Георгу Ому удалось установить, от чего может зависеть электрическое сопротивление проводника. Проведя многочисленные эксперименты, Ом сделал следующие выводы:

Сопротивление проводника тем больше, чем больше его длина.
Сопротивление проводника тем больше, чем меньше его толщина или площадь поперечного сечения.

Кроме того, Ом выяснил, что каждый материал обладает своим электрическим сопротивлением. Величина, которая показывает, каким сопротивлением будет обладать проводник единичной длины и единичной площади сечения из данного материала, называется удельным электрическим сопротивлением: (Ом*мм²/м). Эта величина справочная. Таким образом, получается, что электрическое сопротивление проводника равно:

Рассмотрим задачи ЕГЭ по теме «Закон Ома» для полной цепи.

Задача 1. На рисунке приведён график зависимости напряжения на концах железного провода площадью поперечного сечения 0,05 мм² от силы тока в нём. Чему равна длина провода? Ответ дайте в метрах. Удельное сопротивление железа 0,1 Ом*мм²/м.

Решение:

Из закона Ома для проводника или участка цепи без источника следует:

$displaystyle I=frac{U}{R};$

$displaystyle R=frac{U}{I}.$

По графику: при $U=60 B, I=3 B.$

Из формулы сопротивления выражаем и находим длину проводника:

Ответ: 10.

Задача 2. Через поперечное сечение проводников за 8 с прошло 10²⁰ электронов. Какова сила тока в проводнике? Ответ дайте в амперах.

Решение:

По определению силы тока:

$displaystyle I=frac{q}{t}.$

Заряд всех электронов: $q=Ncdot e,$ где е — модуль заряда электрона, $e=1,6cdot 10^{-19}$ Кл.

Тогда $displaystyle I=frac{Ncdot e}{t}=frac{10^{20}cdot 1,6cdot 10^{-19}}{8}=2 A.$

Ответ: 2.

Задача 3. Идеальный амперметр и три резистора общим сопротивлением 66 Ом включены последовательно в электрическую цепь, содержащую источник с ЭДС равной 5 В, и внутренним сопротивлением r=4 Ом. Каковы показания амперметра? (Ответ дайте в амперах, округлив до сотых.)

Решение:

По закону Ома для полной цепи:

Тогда $displaystyle I=frac{5}{66+4}=0,07 A.$

Ответ: 0,07.

Задача 4. ЭДС источника тока равна 1,5 В. Определите сопротивление внешней цепи, при котором сила тока будет равна 0,6 А, если сила тока при коротком замыкании равна 2,5 А. Ответ дайте в Ом, округлив до десятых.

Решение:

Сила тока короткого замыкания определяется следующим образом:

Отсюда выражаем и находим внутреннее сопротивление источника:

При внешнем сопротивлении, не равном нулю, сила тока в цепи определяется законом Ома для полной цепи:

Отсюда выражаем сопротивление резистора и находим его:

Ответ: 1,9.

Задача 5. На рисунке изображена схема электрической цепи, состоящей из источника постоянного напряжения с ЭДС 5 В и пренебрежимо малым внутренним сопротивлением, ключа, резистора с сопротивлением 2 Ом и соединительных проводов. Ключ замыкают. Какой заряд протечет через резистор за 10 минут? Ответ дайте в кулонах.

Решение:

Выражаем время в секундах: t = 10 минут = 600 с.

Определяем силу тока по закону Ома для полной цепи:

Внутреннее сопротивление пренебрежимо мало, поэтому r = 0.

По определению силы тока:

$displaystyle I=frac{q}{t}.$

Отсюда $q=Icdot t=2,5cdot 600=1500$ Кл.

Ответ: 1500.

Если вам нравятся наши материалы – записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «ЭДС. Закон Ома для полной цепи» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Лабораторная работа № 05

Тема: Определение ЭДС и внутреннего сопротивления источника тока графическим методом.

Цель работы: изучить измерения ЭДС, внутреннего сопротивления и тока короткого замыкания источника тока, основанный на анализе графика зависимости напряжения на выходе источника от силы тока в цепи.

Оборудование:

гальванический элемент;
амперметр;
вольтметр;
резистор R₁;
переменный резистор;
ключ;
зажимы;
металлический планшет;
соединительные провода.

Теоретическая часть

Из закона Ома для полной цепи следует, что напряжение на выходе источника тока зависит прямо пропорционально от силы тока в цепи:
так как I = E/(R + r), то IR + Ir = Е, но IR = U, откуда U + Iг = Е или U = Е – Iг.

Если построить график зависимости U от I, то по его точкам пересечения с осями координат можно определить Е, I_к.з.– силу тока короткого замыкания (ток, который потечет в цепи источника, когда внешнее сопротивление R станет равным нулю).

ЭДС определяют по точке пересечения графика с осью напряжений. Эта точка графика соответствует состоянию цепи, при котором ток в ней отсутствует и, следовательно, U = Е.

Силу тока короткого замыкания определяют по точке пересечения графика с осью токов. В этом случае внешнее сопротивление R = 0 и, следовательно, напряжение на выходе источника U = 0.

Внутреннее сопротивление источника находят по тангенсу угла наклона графика относительно оси токов. (Сравните формулу U = Е – Iг с математической функцией вида y = ax + b и вспомните смысл коэффициента при x).

Указания к работе

1. Исходя из перечня оборудования, рекомендованного для выполнения работы, составьте схему установки для исследования зависимости напряжения на выходе источника тока от силы тока в цепи.

2. Для записи результатов измерений подготовьте таблицу:

U, В	знач	знач	знач	знач	знач
I, А

3. После проверки схемы преподавателем соберите электрическую цепь. Ползунок переменного резистора установите в положение, при котором сопротивление цепи, подключенной к источнику тока, будет максимальным.

4. Определите значение силы тока в цепи и напряжение на зажимах источника при максимальной величине сопротивления переменного резистора. Данные измерений занесите в таблицу.

5. Повторите несколько раз измерения силы тока и напряжения, уменьшая всякий раз величину переменного сопротивления так, чтобы напряжение на зажимах источника уменьшалось на 0,1В. Измерения прекратите, когда сила тока в цепи достигнет значения в 1А.

6. Нанесите полученные в эксперименте точки на график. Напряжение откладывайте по вертикальной оси, а силу тока – по горизонтальной. Проведите по точкам прямую линию.

7. Продолжите график до пересечения с осями координат и определите величины Е и I_к.з..

8. Измерьте ЭДС источника, подключив вольтметр к его выводам при разомкнутой внешней цепи. Сопоставьте значения ЭДС, полученные двумя способами, и укажите причину возможного расхождения результатов.

9. Определите внутреннее сопротивление источника тока. Для этого вычислите тангенс угла наклона построенного графика к оси токов. Так как тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, то практически это можно сделать, найдя отношение Е /I_к.з..

Источник

ИССЛЕДОВАНИЕ
ЗАКОНОВ ПОСТОЯННОГО ТОКА

Цель
работы: исследование зависимости
величины U_R
(падения напряжения
на внешнем сопротивлении цепи) от
величины силы тока; определение ЭДС
и внутреннего сопротивления источника;
изучение зависимости между Р, полной
мощностью всей цепи; P_R,
мощностью внешней части цепи; Р_r,
мощностью внутри источника, КПД
источника и внешним сопротивлением R
.

Приборы
и оборудование: установка для изучения
законов постоянного тока.

Теоретические
сведения

Работа по переносу
электрического заряда определяется по
формуле

Так
как величина заряда q=It,
то работа электрического тока на участке
цепи

A
= UIt.

Для
однородного участка цепи U=IR,
т.е.

A
= I²Rt
=

Так
как мощность
тоP=IU;
для однородного участка цепи

(1)

где
P_R
– мощность, выделяемая во внешней части
цепи, обладающей сопротивлением R.

Учитывая закон
Ома для замкнутой цепи

получим выражение

.
(2)

Взяв
производную
и приравняв ее к нулю, найдем, чтоP_R
будет иметь максимальное значение при
R=r,
т.е.
когда внешнее сопротивление цепи равно
внутреннему сопротивлению источника.
В замкнутой цепи работу совершают
только сторонние силы. По
определению ЭДС

Полная мощность
всей замкнутой цепи

Учитывая закон
Ома для замкнутой цепи, получим выражение

(3)

Коэффициент
полезного действия источника тока
рассчитывается по формуле

(4)

Для
исследования законов постоянного тока
применяется установка, схема которой
изображена на рис. 1
– источник тока;mA
– миллиамперметр для измерения
тока; V
– вольтметр для измерения напряжения
на внешнем резисторе;
–
магазин резисторов, при помощи которого
можно устанавливать необходимое
сопротивление).

По закону Ома для
замкнутой цепи

(5)

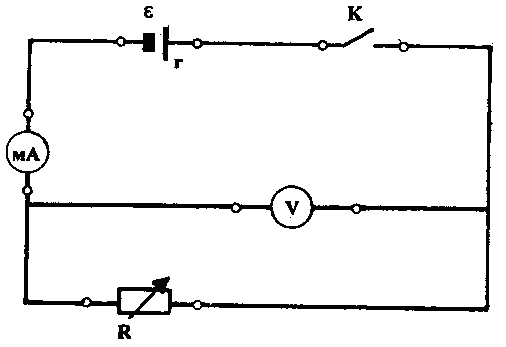
Рис. 1

График
зависимости U_R(I),
см. рис. 2, есть прямая линия, отсекающая
на оси U_R
значение, равное ЭДС источника ε, а на
оси I-значение,
равное силе тока короткого замыкания

Внутреннее
сопротивление источника –

Мощность внешней
части цепи (полезная мощность) –

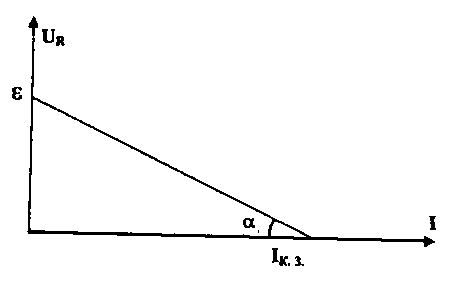
Рис. 2

Графиком
зависимости P_R(R),
см. рис. Заявляется кривая линия, имеющая
экстремальную точку при R=r
и асимптотически приближающаяся к оси
сопротивления R:

→0
при R→0;

при R=0

Полная
мощность равна

Графиком
зависимости Р(R)
является
гипербола (рис. 4):

При
R→0

При
R→∞

Р→0.

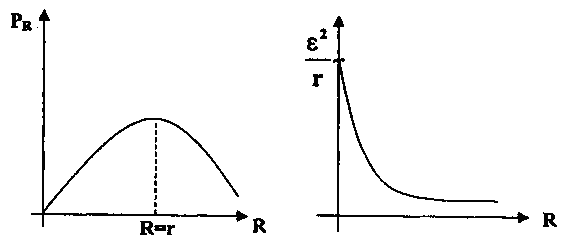
Рис.
3 Рис. 4

Коэффициент
полезного действия источника тока
определяется по формуле (4)

и
имеет график, асимптотически приближающийся
к горизонтальной прямой
;
приR→∞

→1(рис.
5).

Рис.5

Порядок выполнения
работы

Собрать рабочую
схему (рис. 1) на тренаже и показать ее
преподавателю.
Получив допуск,
подойти к готовой установке и замкнуть
цепь ключом К.

На
магазине резисторов установить
сопротивления R,
равные 10, 20, 30 Ом
и т.д. Выбрать 30 точек,
записывая при этом показания
миллиамперметра и
вольтметра
в таблицу.

Таблица

R	I

По
данным таблицы построить график
зависимости
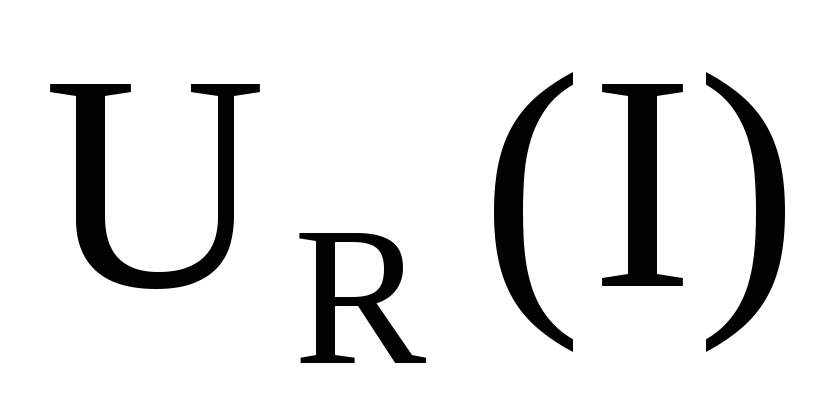так, чтобы числоэкстремальных
точек, лежащих ниже и выше этой прямой,
было одинаково.
Разброс точек происходит
из-за случайных явлений, сопровождающих
процесс
измерения.
По
графику определить ЭДС источника ε и
внутреннее сопротивление г, учитывая,
что
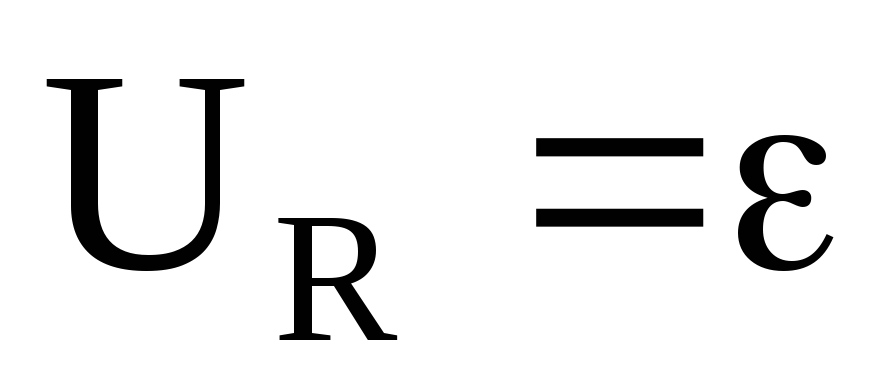приI=0,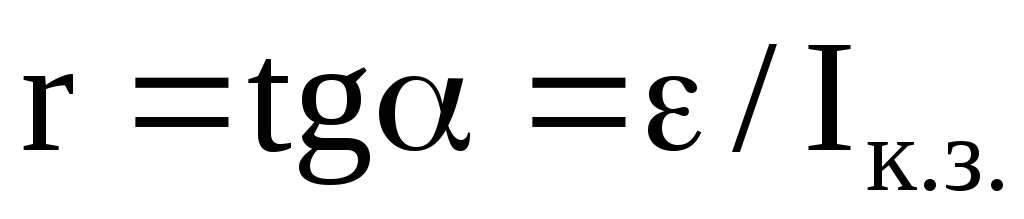

Провести
дополнительные измерения I
и

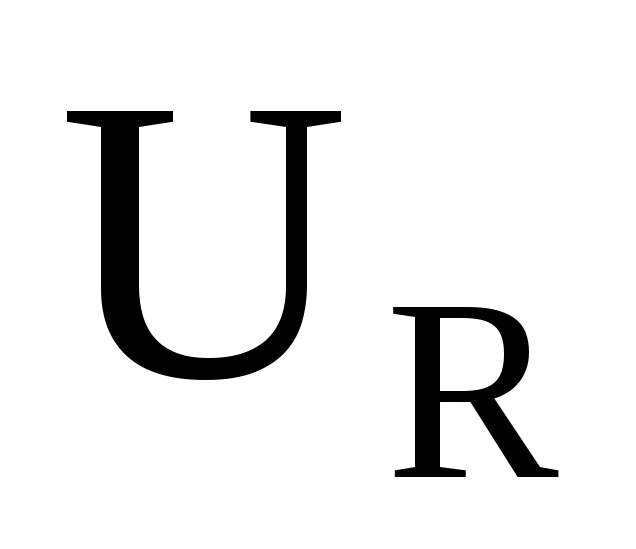
при
R=r
и в окрестности этой
точки через 2
Ома.
Заполнить нее
графы таблицы по расчетным формулам,
указанным в ней.
По
данным таблицы построить графики
зависимостей P(R),
P_R(Р),
P_r(R)
По
данным таблицы построить графики
зависимости
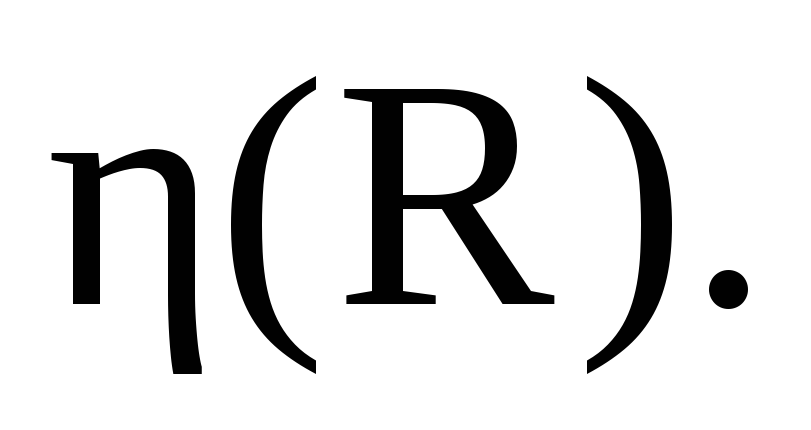
Сравнить
полученные экспериментальные кривые
с теоретическими
кривыми.

Контрольные вопросы

Дать понятие
мощности тока и назвать единицы ее
измерения.
Какие виды мощности
вы знаете? Дать их краткую характеристику.
От чего зависит
КПД источника тока?
По
графику (рис. 6) определить зависимость
U_R(I),
ЭДС источника
,
силу
тока короткого замыкания;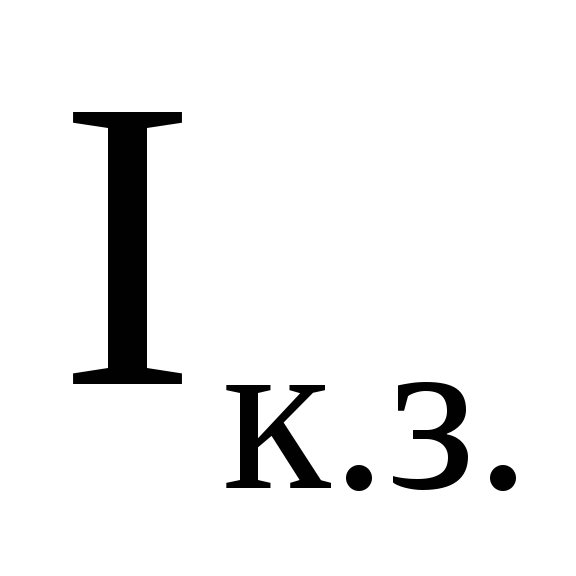
внутреннее сопротивление источника
г, силутока
и падение напряжения, при которых
мощность, выделяемая на внешнем
резисторе,
будет максимальной.

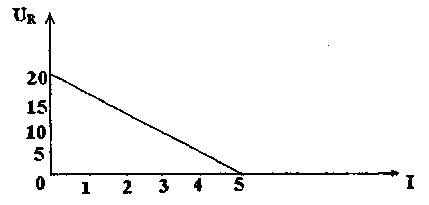
Рис. 6

5. На
координатной плоскости изображены 3
графика (рис. 7). Указать, какой из них
соответствует графикам зависимости:
P_r(R
) – полезной мощности от внешнего
сопротивления, P(R
) – полной мощности от внешнего
сопротивления,

КПД
источника от внешнего сопротивления.

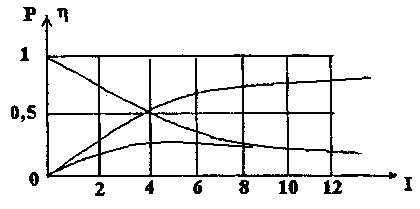
Рис. 7

Определить
по этим графикам ЭДС источника ε,
внутреннее сопротивление источника r
и записать аналитическое выражение
зависимостей P(R),
P_R(R
),

6. Как
изменятся графики зависимостей P_R(R),
U_R(I),
P_R(I),
если внутреннее сопротивление источника
увеличится вдвое? Почему лампочка в 3,5
В не горит
при подключении ее к батарее «Крона» –
источнику питания для транзисторных
приемников (ЭДС источника равна 9В)?

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Как найти ЭДС и внутреннее сопротивление источника, зная напряжение и силу тока?

Саня Дальнобойщик

Знаток

(371),
на голосовании

3 года назад

Нужно построить график зависимости напряжения от силы тока в цепи, а затем из графика с учётом закона U = ɛ – Ir найти ɛ и r источника. Первый график я построил, а вот как потом определите по графику путем его экстраполяции ( продолжения ) до пересечения с осью координат U значение ЭДС, а с осью координат I – ток « короткого замыкания» Iкз. Как это все показать на графике?

Голосование за лучший ответ

Источник

При изменении сопротивления внешней цепи изменяются и сила тока I, и напряжение U на источнике тока. Определите ЭДС источника тока и его внутреннее сопротивление по приведенному на рисунке графику зависимости U(I).

Спрятать решение

Решение.

Из графика при силе тока I_1=1А напряжение равно U_1=5В, при силе тока I_2=3А напряжение равно U_2=3В. Запишем закон Ома для полной цепи для каждого случая: