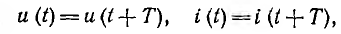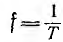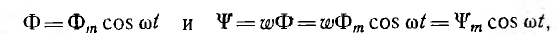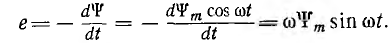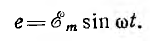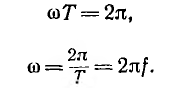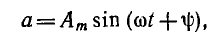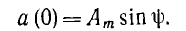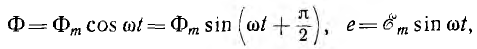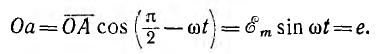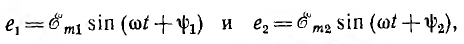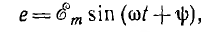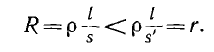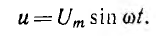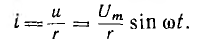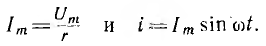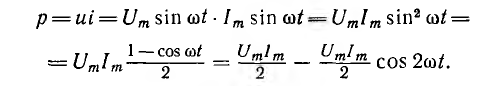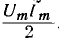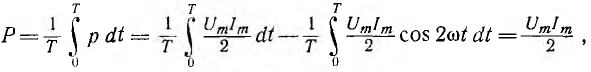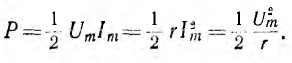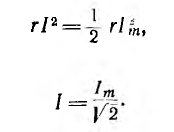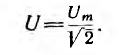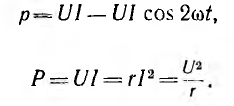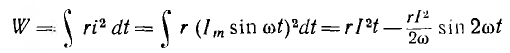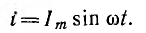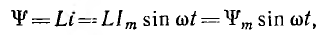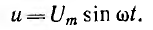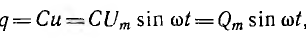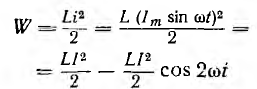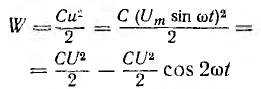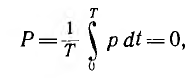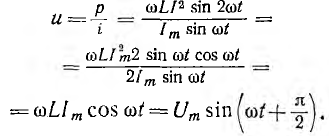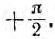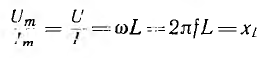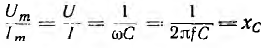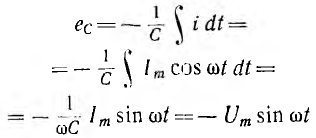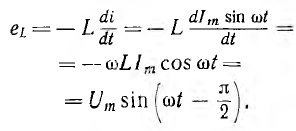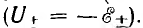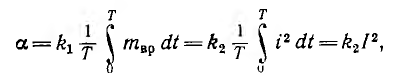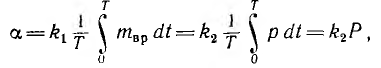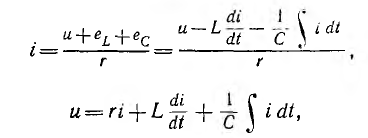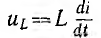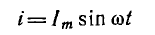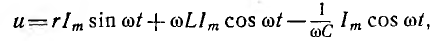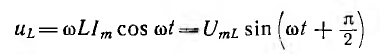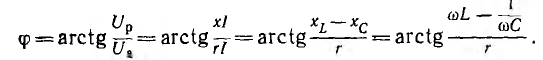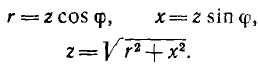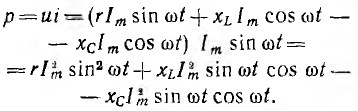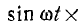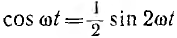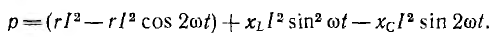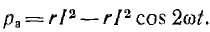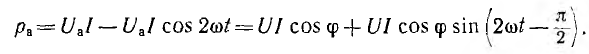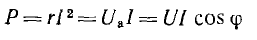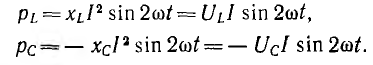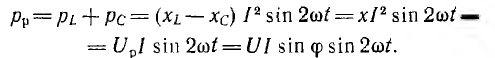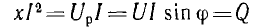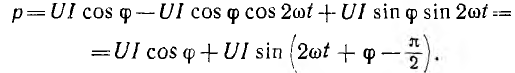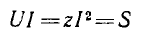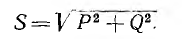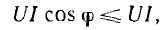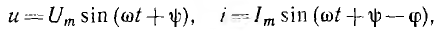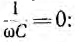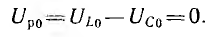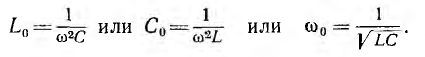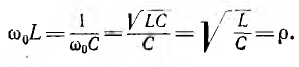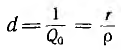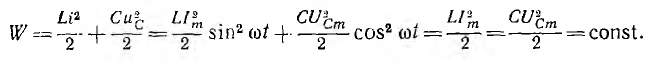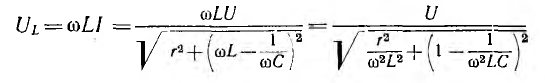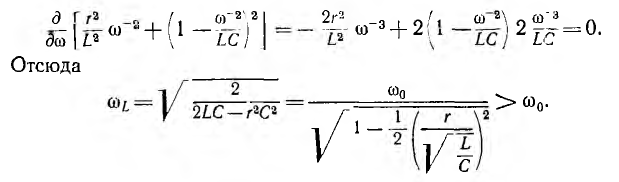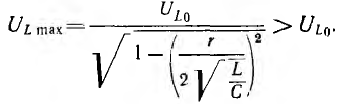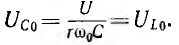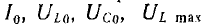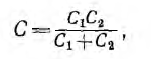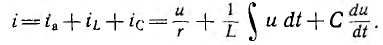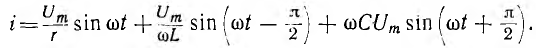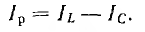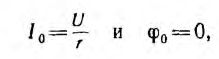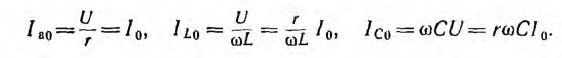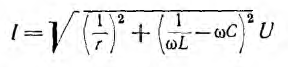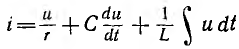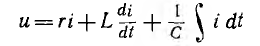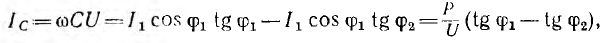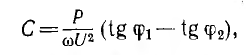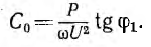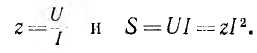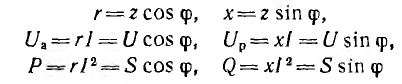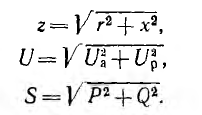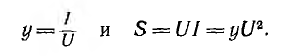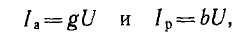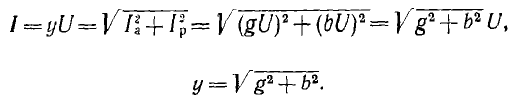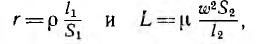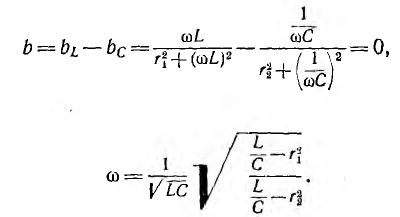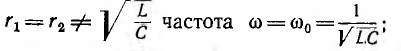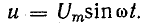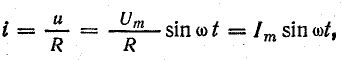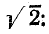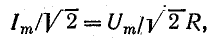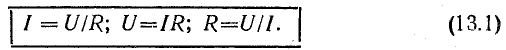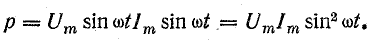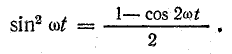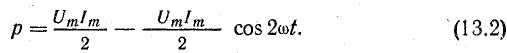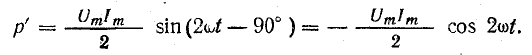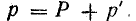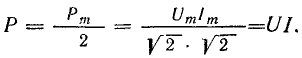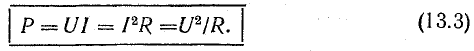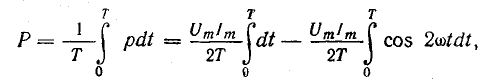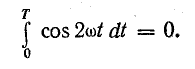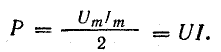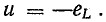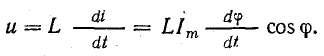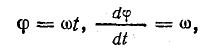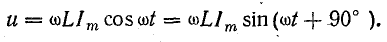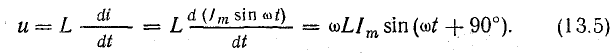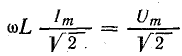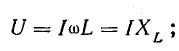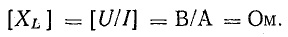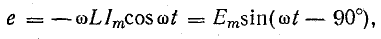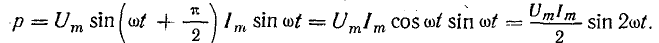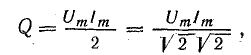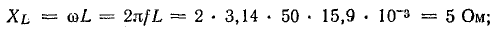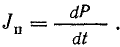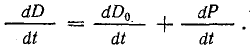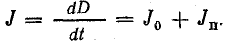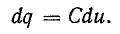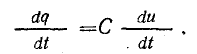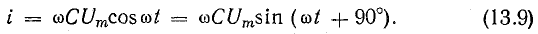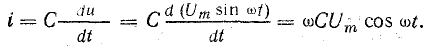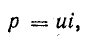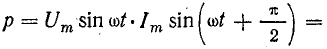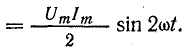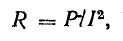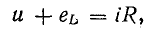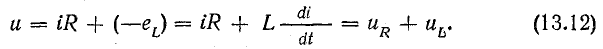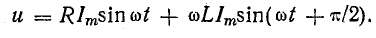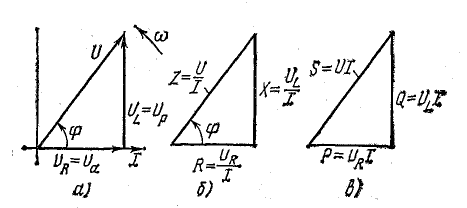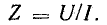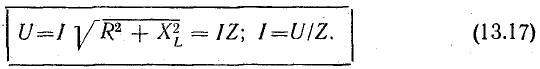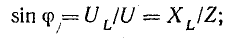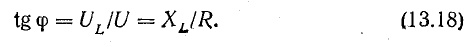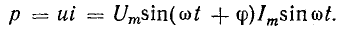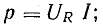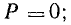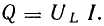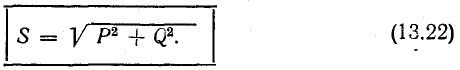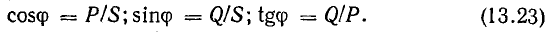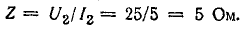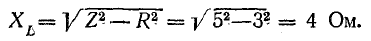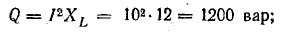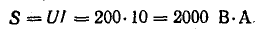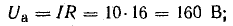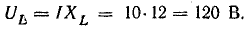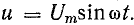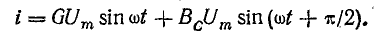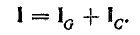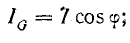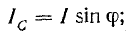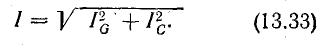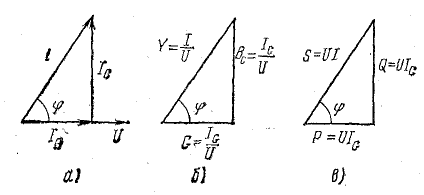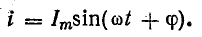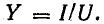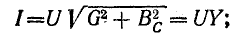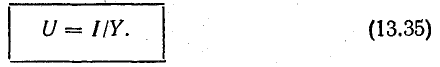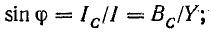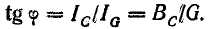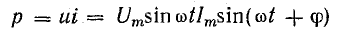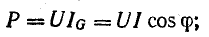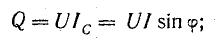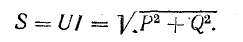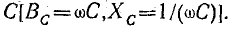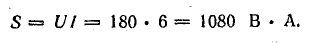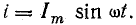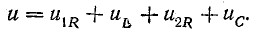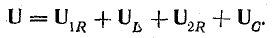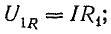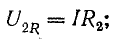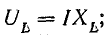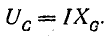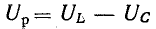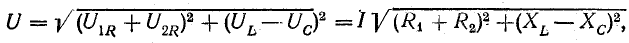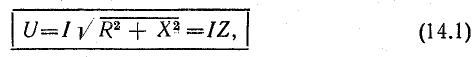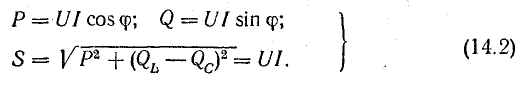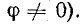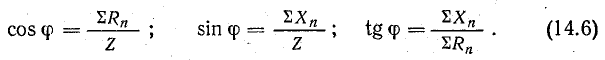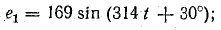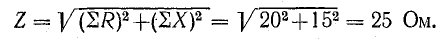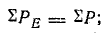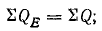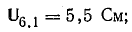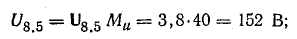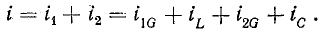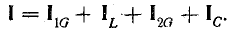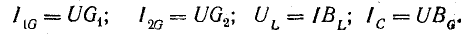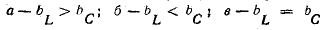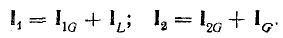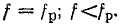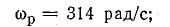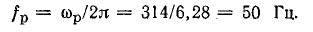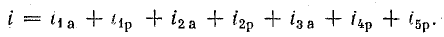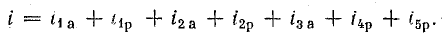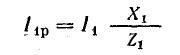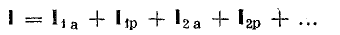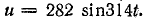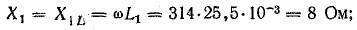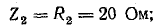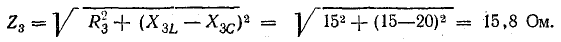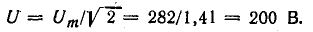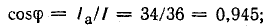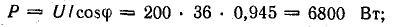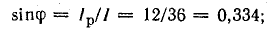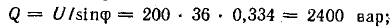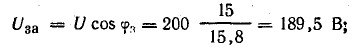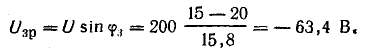Получение, передача и распределение
электрической энергии осуществляются
в основном с помощью устройств и
сооружений переменного тока. Для
этого применяют генераторы, трансформаторы,
линии передачи и распределительные
сети переменного тока. Широко используют
приемники электрической энергии,
работающие на переменном токе.
Переменным током называют любой
изменяющийся с течением времени
электрический ток.
Переменным синусоидальным током
называют изменяющийся по закону
синуса (косинуса) с течением времени
электрический ток.
В электротехнике чаще всего приходится
иметь дело с переменным током, величина
которого изменяется по периодическому
синусоидальному закону. В некоторых
случаях ток изменяется по периодическому
несинусоидальному закону
В линейных электрических
цепях переменный синусоидальныйток возникает под действием
ЭДС такой же формы. Дляизучения
электрических устройств и цепейпеременного тока необходимо
прежде рассмотреть способы получения
синусоидальной ЭДС и основные понятия,
относящиеся к величинам, которые
изменяются по синусоидальному закону.
3.1. Получение синусоидальной эдс
Переменным током (ЭДС) в электрических
цепях называется такой ток (ЭДС), который
изменяет свое значение и направление
во времени.
В электротехнике в основном приходится
иметь дело с током, величина которого
изменяется по синусоидальному закону.
Для получения ЭДС синусоидальной формы
генератор переменного тока
промышленного типа имеет определенные
конструктивные особенности.
Рис. 3.1
Синусоидально изменяющуюся
величину ЭДС со временем можно получить,
вращая с постоянной скоростью в
однородном магнитном поле проводник
в виде прямоугольной рамки. При движении
проводника в магнитном поле в нем
возбуждается ЭДС индукции
e=Bυlsina
(3.1)
При вращении витка в
магнитном поле с постоянной скоростью
изменяется угол между направлением
индукции магнитного поля и нормалью к
плоскости рамки
α = ωt,
где ω
– угловая скорость.
Наибольшее значение ЭДС достигается
при угле
α = ωt
= 90°:
ЕМ
=Bυl.
(3.2)
Синусоидальное изменение
ЭДС достигается путем равномерного
изменения угла, под которым виток
пересекает линии магнитной индукции.
Таким образом,
е = ЕМ
sinα
= ЕМ
sin
ωt
(3.3)
Аналогично запишутся
формулы переменного напряжения и тока:
и =
UМ
sin
ωt, i
= IМ
sin
ωt
3.2. Характеристики синусоидальных величин
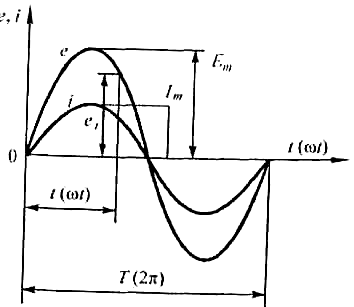
Синусоидально изменяющиеся ЭДС,
напряжение и ток характеризуются
следующими величинами: мгновенным
значением, амплитудой, периодом,
частотой, фазой (сдвигом фаз) (рис.
3.2). Мгновенное значение
ЭДС, напряжения и силы тока – значение
этих величин в любой момент времени.
Мгновенные значения обозначаются
строчными буквами е,
и, i.
Амплитуда
– это наибольшие
значения, которые принимает ЭДС,
напряжение и сила тока. Амплитудные
значения обозначаются прописными
буквами Еm
, Um
, Im
.
Период Т
– промежуток времени,
в течение которого ЭДС, напряжение
и ток совершают полное колебание и
принимают
прежнее по величине и знаку значение.
Рис.3.2
Графики изменения переменного тока и
ЭДС.
Частота
f
(число периодов в
секунду) – величина, обратная периоду:f
=
(3.4)
Единица частоты – герц (Гц). Стандартная
промышленная частота 50 Гц. В США и
Японии-60 Гц. В некоторых областях
промышленности находят применение
другие частоты.
Угловая частота ω
есть величина, равная числу периодов
за 2п секунд.
Так как в течение периода α = 2π, то ω
=
,
т. е.
ω =
(3.5)
Размерность угловой частоты
– град/с или рад/с.ω
=
или ω
= 2π f
Фаза
– угловое значение
аргумента синусоидальной ЭДС, напряжения,
тока, определяющее мгновенное значение
этих величин. При α
= ωt = 0 мгновенные
значения е, и и
i
будут равны нулю.
Если фаза имеет выражение (ωt
+ ψ),
то при t
= 0 фаза не равна нулю
и мгновенное значение е
будет равнo
е = Еm
sin(ωt
+ ψ),а фаза ψ
называется начальной фазой.
Таким образом, в общем виде уравнение
ЭДС может быть записано так:
е = Еm
sin(ωt
+ ψ)
(3.6)
где α =
(ωt
+ ψ)
– угол, называемый
фазой. Аналогично запишутся выражения
для переменного напряжения и тока.
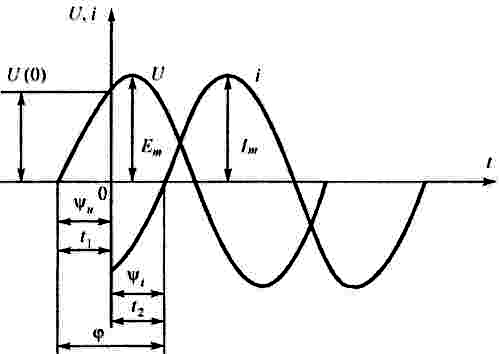
Две синусоидальные величины,
имеющие разные начальные фазы, называются
сдвинутыми по фазе (рис. 3.3). Угол сдвига
фаз φ = ψu
+ ψi
Та величина, в которой
начало периода, или положительная
амплитуда достигается раньше, чем у
другой, считается опережающей по фазе,
а та, у которой те же значения достигаются
позже – отстающей по фазе.
Изображенные на рис. 3.2
синусоидальные величины называют
совпадающими по фазе. Если угол
сдвига составляет π,
то говорят, что они
находятся в противофазе. Сдвиг по фазе
можно установить и на графике. Для этого
достаточно выбрать две ближайшие
точки, соответствующие положительным
амплитудам величин, и установить
разность фазовых углов.
Действующая и средняя
величины переменного тока. Переменный
ток, как и постоянный, оказывает тепловое,
механическое, магнитное и химическое
действие. В формулы расчета теплового,
механического, магнитного и химического
действия переменного тока подставляют
действующее значение переменного тока.
Действующим значением переменного
тока называется постоянный ток,
который за время одного периода оказывает
такое тепловое (механическое и др.)
действие, как и данный переменный ток.
Действующее значение для данного
переменного тока есть величина постоянная
и равна амплитудному значению,
деленному на
,
т. е.IД
=
Для доказательства этого
рассмотрим тепловое действие тока.
Тепловое действие постоянного тока
определяется по закону Джоуля -Ленца:
Q
= I2
RT
(3.7)
где Т-
время, равное одному
периоду.Такое же
количество теплоты в данном проводнике
за это время выделится и при переменном
токе i
= 1тsinωt.
Тогда формула (3.7)
для переменного тока примет вид:Q
= IД2
RT,
(3.8)
где IД
– действующее значение переменного
тока. Из формулы (3.8) можно записать
I
Д2 R=Р
(5.9)
где Р –
средняя мощность
переменного тока за период. Мгновенная
мощность синусоидального тока равнаp
= i2R
=Iт2
sin2
ωt
·R
=Iт2·R
= Iт2·−Iт2
(3.10)
Как видно из формулы (3.10),
мгновенная мощность переменного тока
выражается двумя слагаемыми. Первое
слагаемое является величиной постоянной
и от времени не зависит, а второе −
изменяется по синусоидальному закону
и в сумме за период равно нулю.
Следовательно, средняя мощность
переменного тока за период может быть
выражена формулой
р =
Iт2·(3.11)
Из равенств (3.9) и (3.11) можно записать:
I
Д2 R
=
Iт2·,
т. е. IД
=илиIД
= 0,707 · Iт,
т. к.
≈1,41
Все определения и соотношения действующего
значения переменного тока справедливы
и для переменного напряжения, и для
ЭДС.
Все амперметры и вольтметры
при измерении переменного тока и
напряжения показывают их действующие
значения, так как принцип работы их
основан на механическом или тепловом
действии тока.Пусть
при включении в сеть сопротивления R
= 40 Ом амперметр
показал ток 5,5 А. Действующее напряжение
в сети U
= R
· I
= 40 Ом • 5,5А = 220 В,
а амплитудное Um
= 220В • 1,41 =310,2 В.
При изучении электрических
машин, выпрямительных устройств
пользуются средним значением ЭДС,
силы тока и напряжения. Средним значением
переменного тока,
напряжения и ЭДС называется среднее
арифметическое из всех мгновенных
значений за полупериод.
Для
синусоидального тока IСР== 0,637 ·Iт
Изображение синусоидальных величин
вращающимся вектором.
Прирасчете
электрических цепей переменного тока
пользуются простым и наглядным
способом графического изображения
синусоидальных величин при помощи
вращающихся векторов.Пусть
напряжение задано уравнением и
= Um
sin(ωt
+ ψ)
Проведем две
перпендикулярные оси, затем из точки
пересечения осей вектор длиной U
в выбранном масштабе
(рис/3.4).
Направление вектора выбирается
таким, чтобы с горизонтальной осью он
составлял угол ψ,
т. е. равный начальной
фазе. Проекция этого вектора на ось
ординат определяет мгновенные
значения напряжения u(0)
= Um
sin
ψt
Рис. 3.4.
. Выражение переменного синусоидального
напряжения через проекцию радиуса-вектора
на ось у.
Вращаем вектор U
против часовой стрелки
с угловой скоростью ω.
Положение радиуса-вектора в любой
момент времени определяется углом (ωt
+ ψ). Для
произвольного значения времени t
мгновенное значение напряжения
определяется проекцией вектора U
на вертикальную ось
в этот момент времени. Например, для t
= t1,
u(t1)
= Um
sin(ωt1
+ ψ),
т. е. мы имеем уравнение
такого вида, как и заданное. Это дает
нам возможность изобразить напряжение
вращающимся вектором, нанесенном
на чертеж в начальном положении.Вращая вектор Um
против часовой
стрелки, построим в прямоугольной
системе координат график изменения
проекции его на вертикальную ось за
один период. Соединив полученные точки,
получим график синусоидальной функции,
соответствующий заданному уравнению.Совокупность векторов,
изображающих на одном чертеже несколько
синусоидальных величин одинаковой
частоты, называется векторной диаграммой.
Достоинством векторных диаграмм
является простота и наглядность.
Сложение и вычитание синусоидальных
величин осуществляется по правилам
сложения и вычитания векторов.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
11.02.201626.11 Mб2404_006 Кудрявцев – Шрифт.djvu
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ранее мы познакомились с постоянным электрическим током — направленным движением зарядов, для которого сила тока постоянна. В случае, если значение силы тока непостоянно, тогда ток будем называть переменным.
Для школьной физики переменный ток рассматривается в двух, в общем-то, похожих случаях:
- вынужденные колебания (на вход цепи подаётся внешняя разность потенциалов/ток, которые изменяются гармонически).
- колебания в LC (состоящем из катушек индуктивности и конденсаторов) или LCR (состоящем их катушек индуктивности, конденсаторов и сопротивлений) контурах.
Рассмотрение свободных колебаний в случае переменного тока аналогично постоянному. Точно так же существует закон Ома для цепи переменного тока, рассчитываются мощности и энергии (работы) для такого случая.
Для школы характерно описание переменного тока через гармонические законы. Переменными параметрами в цепи могут быть ЭДС (), напряжение на элементе (
), сила тока (
), заряд конденсатора (
). Рассмотрим ЭДС источника гармонический колебаний:
(1)
- где
Аналогичным образом можно ввести колебания напряжения на элементе:
(2)
- где
Таким же образом вводится и колебание силы тока:
(3)
- где
И, аналогично, заряд на конденсаторе:
(4)
- где
Важно: нужно помнить, что тригонометрически можно превратить синус в косинус:
(5)
- где
— новая начальная фаза колебания.
Вывод: таким образом, рассмотрение переменного тока в случае формульных задач, связанных с соотношениями (1) — (4), касается анализа сомножителей и слагаемых, входящих в само соотношение.
Электродвижущая сила или сокращено ЭДС – это способность источника тока ил по-другому питающий элемент, создавать в электрической цепи разность потенциалов. Элементами питания являются аккумуляторы или батареи. Это скалярная физическая величина, равная работе сторонних сил для перемещения одного заряда с положительной величиной. В данной статье будут рассмотрены теоритические вопросы ЭДС, как она образуется, а также для чего она может быть использована на практике и где используются, а главное как рассчитать ее.
Что такое ЭДС: объяснение простыми словами
Под ЭДС понимается удельная работа сторонних сил по перемещению единичного заряда в контуре электрической цепи. Это понятие в электричестве предполагает множество физических толкований, относящихся к различным областям технических знаний. В электротехнике — это удельная работа сторонних сил, появляющаяся в индуктивных обмотках при наведении в них переменного поля. В химии она означает разность потенциалов, возникающее при электролизе, а также при реакциях, сопровождающихся разделением электрических зарядов.
В физике она соответствует электродвижущей силе, создаваемой на концах электрической термопары, например. Чтобы объяснить суть ЭДС простыми словами – потребуется рассмотреть каждый из вариантов ее трактовки. Прежде чем перейти к основной части статьи отметим, что ЭДС и напряжение очень близкие по смыслу понятия, но всё же несколько отличаются. Если сказать кратко, то ЭДС — на источнике питания без нагрузки, а когда к нему подключают нагрузку — это уже напряжение. Потому что количество вольт на ИП под нагрузкой почти всегда несколько меньше, чем без неё. Это связано с наличием внутреннего сопротивления таких источников питания, как трансформаторы и гальванические элементы.
Дополнительный материал по теме: Простыми словами о преобразователях напряжения.
Электродвижущая сила (эдс), физическая величина, характеризующая действие сторонних (непотенциальных) сил в источниках постоянного или переменного тока; в замкнутом проводящем контуре равна работе этих сил по перемещению единичного положительного заряда вдоль контура. Если через Eстр обозначить напряжённость поля сторонних сил, то эдс в замкнутом контуре (L) равна , где dl — элемент длины контура. Потенциальные силы электростатического (или стационарного) поля не могут поддерживать постоянный ток в цепи, т. к. работа этих сил на замкнутом пути равна нулю. Прохождение же тока по проводникам сопровождается выделением энергии — нагреванием проводников.
Сторонние силы приводят в движение заряженные частицы внутри источников тока: генераторов, гальванических элементов, аккумуляторов и т. д. Происхождение сторонних сил может быть различным. В генераторах сторонние силы — это силы со стороны вихревого электрического поля, возникающего при изменении магнитного поля со временем, или Лоренца сила, действующая со стороны магнитного поля на электроны в движущемся проводнике; в гальванических элементах и аккумуляторах — это химические силы и т. д. Эдс определяет силу тока в цепи при заданном её сопротивлении (см. Ома закон). Измеряется эдс, как и напряжение, в вольтах.

Природа ЭДС
Причина возникновения ЭДС в разных источниках тока разная. По природе возникновения различают следующие типы:
- Химическая ЭДС. Возникает в батарейках и аккумуляторах вследствие химических реакций.
- Термо ЭДС. Возникает, когда находящиеся при разных температурах контакты разнородных проводников соединены.
- ЭДС индукции. Возникает в генераторе при помещении вращающегося проводника в магнитное поле. ЭДС будет наводиться в проводнике, когда проводник пересекает силовые линии постоянного магнитного поля или когда магнитное поле изменяется по величине.
- Фотоэлектрическая ЭДС. Возникновению этой ЭДС способствует явление внешнего или внутреннего фотоэффекта.
- Пьезоэлектрическая ЭДС. ЭДС возникает при растяжении или сдавливании веществ.
Электромагнитная индукция (самоиндукция)
Начнем с электромагнитной индукции. Это явление описывает закон электромагнитной индукции Фарадея. Физический смысл этого явления состоит в способности электромагнитного поля наводить ЭДС в находящемся рядом проводнике. При этом или поле должно изменяться, например, по величине и направлению векторов, или перемещаться относительно проводника, или должен двигаться проводник относительно этого поля. На концах проводника в этом случае возникает разность потенциалов.
Опыт демонстрирует появление ЭДС в катушке при воздействии изменяющегося магнитного поля постоянного магнита. Есть и другое похожее по смыслу явление — взаимоиндукция. Оно заключается в том, что изменение направления и силы тока одной катушки индуцирует ЭДС на выводах расположенной рядом катушки, широко применяется в различных областях техники, включая электрику и электронику. Оно лежит в основе работы трансформаторов, где магнитный поток одной обмотки наводит ток и напряжение во второй.
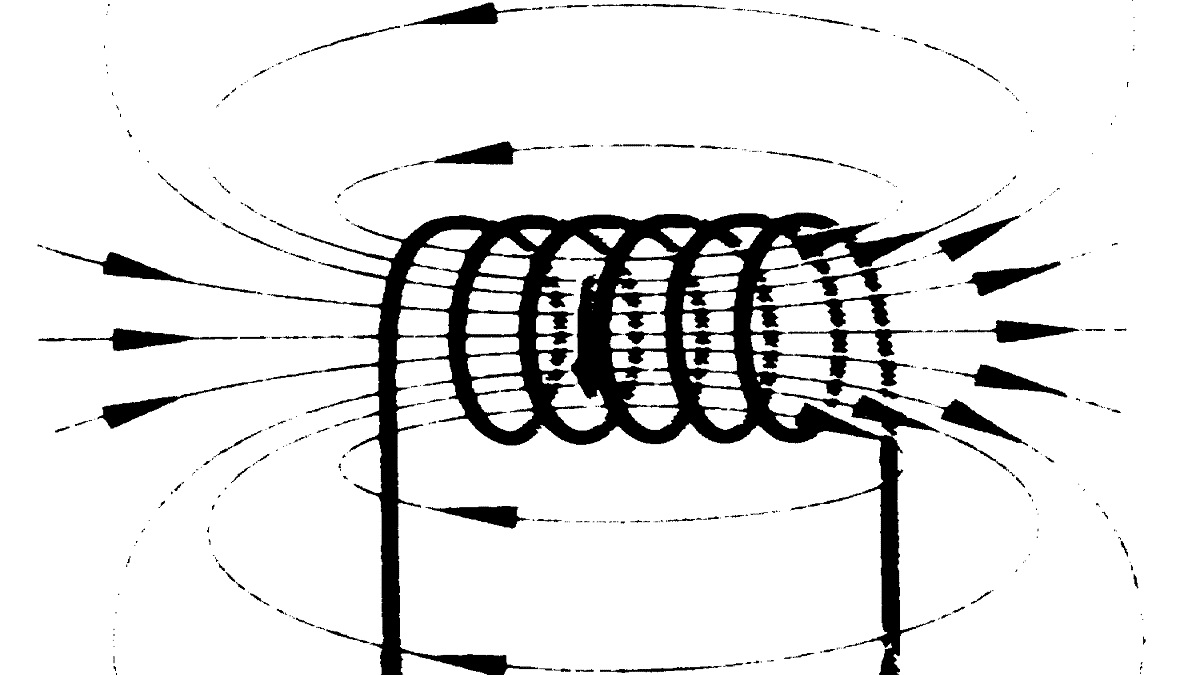
В электрике физический эффект под названием ЭДС используется при изготовлении специальных преобразователей переменного тока, обеспечивающих получение нужных значений действующих величин (тока и напряжения). Благодаря явлениям индукции и самоиндукции инженерам удалось разработать множество электротехнических устройств: от обычной катушки индуктивности (дросселя) и вплоть до трансформатора. Понятие взаимоиндукции касается только переменного тока, при протекании которого в контуре или проводнике меняется магнитный поток.
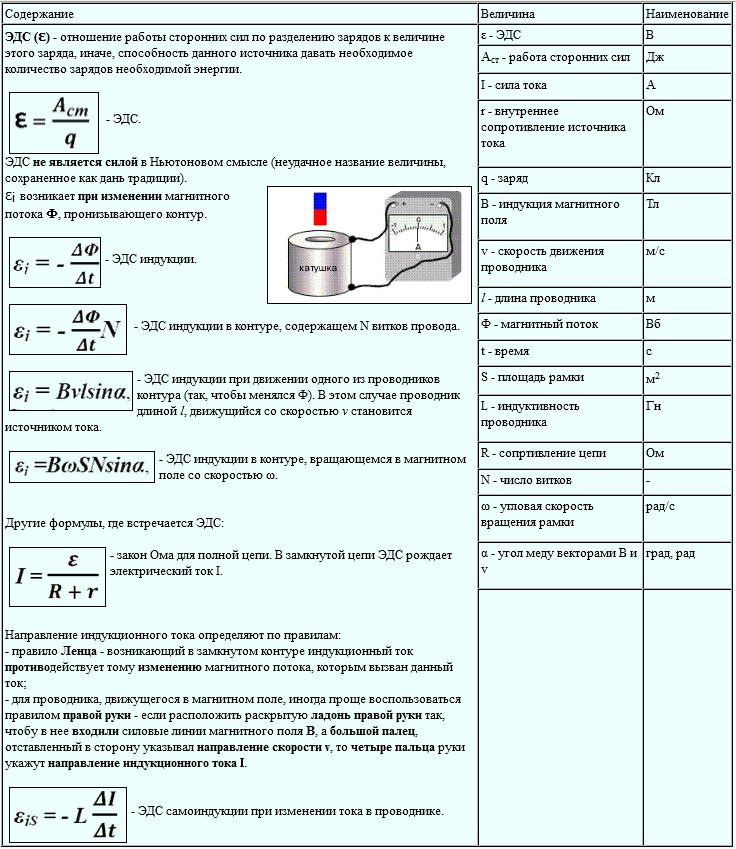
ЭДС в быту и единицы измерения
Другие примеры встречаются в практической жизни любого рядового человека. Под эту категорию попадают такие привычные вещи, как малогабаритные батарейки, а также другие миниатюрные элементы питания. В этом случае рабочая ЭДС формируется за счет химических процессов, протекающих внутри источников постоянного напряжения. Когда оно возникает на клеммах (полюсах) батареи вследствие внутренних изменений – элемент полностью готов к работе. Со временем величина ЭДС несколько снижается, а внутреннее сопротивление заметно возрастает.
В результате если вы измеряете напряжение на не подключенной ни к чему пальчиковой батарейке вы видите нормальные для неё 1.5В (или около того), но когда к батарейке подключается нагрузка, допустим, вы установили её в какой-то прибор — он не работает. Почему? Потому что если предположить, что у вольтметра внутреннее сопротивление во много раз выше, чем внутреннее сопротивлении батарейки — то вы измеряли её ЭДС. Когда батарейка начала отдавать ток в нагрузке на её выводах стало не 1.5В, а, допустим, 1.2В — прибору недостаточно ни напряжения, ни тока для нормальной работы.
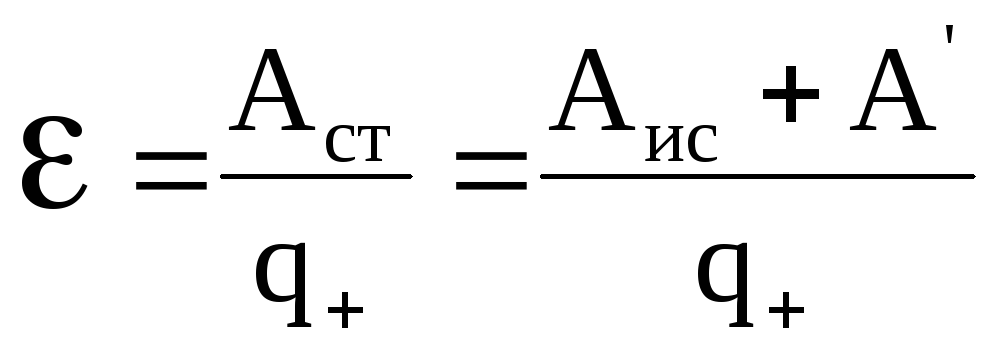
Как раз вот эти 0.3 В и упали на внутреннем сопротивлении гальванического элемента. Если батарейка совсем старая и её электроды разрушены, то на клеммах батареи может не быть вообще никакой электродвижущей силы или напряжения — т.е. ноль. Совсем небольшая по величине электродвижущая сила наводится и в рамках антенны приемника, которая усиливается затем специальными каскадами, и мы получаем наш телевизионный, радио и даже Wi-Fi сигнал.
Материал по теме: Выбираем цифро-аналоговый преобразователь.
Как образуется ЭДС
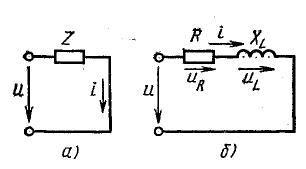
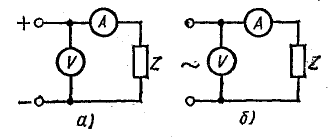
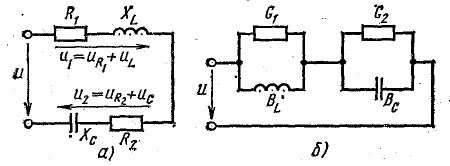
Идеальный источник ЭДС – генератор, внутреннее сопротивление которого равно нулю, а напряжение на его зажимах не зависит от нагрузки. Мощность идеального источника ЭДС бесконечна. Реальный источник ЭДС, в отличие от идеального, содержит внутреннее сопротивление Ri и его напряжение зависит от нагрузки (рис. 1., б), а мощность источника конечна. Электрическая схема реального генератора ЭДС представляет собой последовательное соединение идеального генератора ЭДС Е и его внутреннего сопротивления Ri.
На практике для того чтобы приблизить режим работы реального генератора ЭДС к режиму работы идеального, внутреннее сопротивление реального генератора Ri стараются делать как можно меньше, а сопротивление нагрузки Rн необходимо подключать величиной не менее чем в 10 раз большей величины внутреннего сопротивления генератора, т.е. необходимо выполнять условие: Rн >> Ri
Для того чтобы выходное напряжение реального генератора ЭДС не зависело от нагрузки, его стабилизируют применением специальных электронных схем стабилизации напряжения. Поскольку внутреннее сопротивление реального генератора ЭДС не может быть выполнено бесконечно малым, его минимизируют и выполняют стандартным для возможности согласованного подключения к нему потребителей энергии. В радиотехнике величины стандартного выходного сопротивления генераторов ЭДС составляют 50 Ом (промышленный стандарт) и 75 Ом (бытовой стандарт).
Например, все телевизионные приемники имеют входное сопротивление 75 Ом и подключены к антеннам коаксиальным кабелем именно такого волнового сопротивления. Для приближения к идеальным генераторам ЭДС источники питающего напряжения, используемые во всей промышленной и бытовой радиоэлектронной аппаратуре, выполняют с применением специальных электронных схем стабилизации выходного напряжения, которые позволяют выдерживать практически неизменное выходное напряжение источника питания в заданном диапазоне токов, потребляемых от источника ЭДС (иногда его называют источником напряжения).
На электрических схемах источники ЭДС изображаются так: Е — источник постоянной ЭДС, е(t) – источник гармонической (переменной) ЭДС в форме функции времени. Электродвижущая сила Е батареи последовательно соединенных одинаковых элементов равна электродвижущей силе одного элемента Е, умноженной на число элементов n батареи: Е = nЕ.
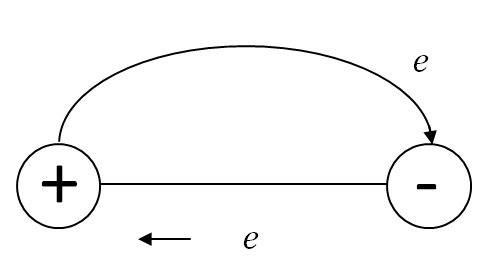
Электродвижущая сила (ЭДС) источника энергии
Для поддержания электрического тока в проводнике требуется внешний источник энергии, создающий все время разность потенциалов между концами этого проводника. Такие источники энергии получили название источников электрической энергии (или источников тока). Источники электрической энергии обладают определенной электродвижущей силой (сокращенно ЭДС), которая создает и длительное время поддерживает разность потенциалов между концами проводника.
Инженер по специальности “Программное обеспечение вычислительной техники и автоматизированных систем”, МИФИ, 2005–2010 гг.
Задать вопрос
Иногда говорят, что ЭДС создает электрический ток в цепи. Нужно помнить об условности такого определения, так как выше мы уже установили, что причина возникновения и существования электрического тока — электрическое поле.
Источник электрической энергии производит определенную работу, перемещая электрические заряды по всей замкнутой цепи. За единицу измерения электродвижущей силы принят вольт (сокращенно вольт обозначается буквой В или V — «вэ» латинское). ЭДС источника электрической энергии равна одному вольту, если при перемещении одного кулона электричества по всей замкнутой, цепи источник электрической энергии совершает работу, равную одному джоулю:
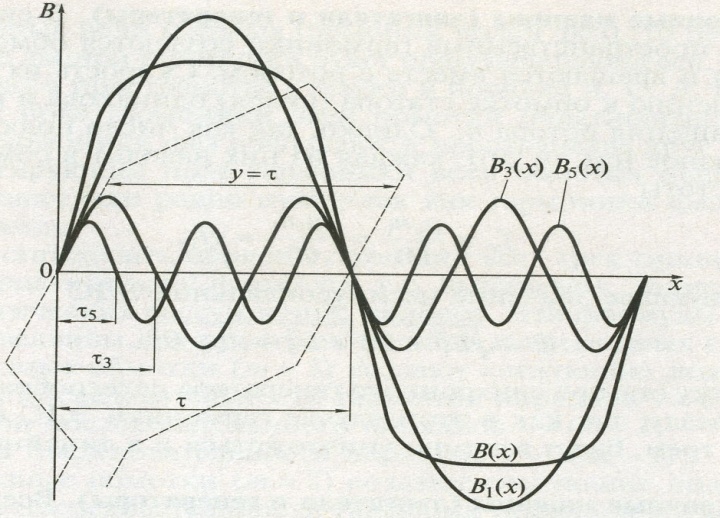
В практике для измерения ЭДС используются как более крупные, так и более мелкие единицы, а именно:
- 1 киловольт (кВ, kV), равный 1000 В;
- 1 милливольт (мВ, mV), равный одной тысячной доле вольта (10-3 В),
- 1 микровольт (мкВ, μV), равный одной миллионной доле вольта (10-6 В).
Очевидно, что 1 кВ = 1000 В; 1 В = 1000 мВ = 1 000 000 мкВ; 1 мВ= 1000 мкВ.
В настоящее, время существует несколько видов источников электрической энергии. Впервые в качестве источника электрической энергии была использована гальваническая батарея, состоящая из нескольких цинковых и медных кружков, между которыми была проложена кожа, смоченная в подкисленной воде. В гальванической батарее химическая энергия превращалась в электрическую (подробнее об этом будет рассказано в главе XVI). Свое название гальваническая батарея получила по имени итальянского физиолога Луиджи Гальвани (1737—1798), одного из основателей учения об электричестве.
Многочисленные опыты по усовершенствованию и практическому использованию гальванических батарей были проведены русским ученым Василием Владимировичем Петровым. Еще в начале прошлого века он создал самую большую в мире гальваническую батарею и использовал ее для ряда блестящих опытов. Источники электрической энергии, работающие по принципу преобразования химической энергии в электрическую, называются химическими источниками электрической энергии.
Полезно знать: Как рассчитать мощность электрического тока.
Другим основным источником электрической энергий, получившим широкое применение в электротехнике и радиотехнике, является генератор. В генераторах механическая энергия преобразуется в электрическую. У химических источников электрической энергии и у генераторов электродвижущая сила проявляется одинаково, создавая на зажимах источника разность потенциалов и поддерживая ее длительное время.
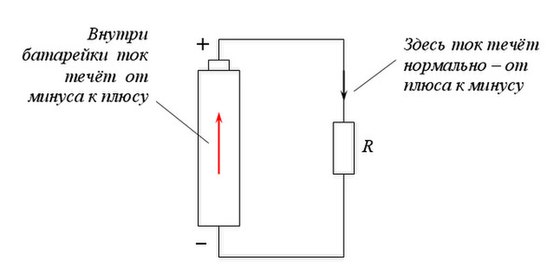
[stextbox id=’info’]Эти зажимы называются полюсами источника электрической энергии. Один полюс источника электрической энергии имеет положительный потенциал (недостаток электронов), обозначается знаком плюс ( + ) и называется положительным полюсом. [/stextbox]
Другой полюс имеет отрицательный потенциал (избыток электронов), обозначается знаком минус (—) и называется отрицательным полюсом. От источников электрической энергии электрическая энергия передается по проводам к ее потребителям (электрические лампы, электродвигатели, электрические дуги, электронагревательные приборы и т. д.).
Примеры решения задач
К каждой позиции первого столбца подберите соответствующую позицию второго:
Решение: Электродвижущая сила гальванического элемента есть величина, численно равная работе сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому.
Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории перемещения зарядов.
ЭДС определяется по формуле:
Сила тока определяется по формуле:
Сопротивление определяется по формуле:
Разность потенциалов определяется по формуле:
Правильный ответ:
Что такое электродвижущая сила?
Это отношение работы сторонних сил при перемещении заряда по замкнутому контуру к абсолютной величине этого заряда.
Что такое электрическая цепь?
Набор устройств, которые соединены проводниками, предназначенный для протекания тока.
Как звучит закон Ома для полной цепи?
Сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.
Заключение
Инженер по специальности “Программное обеспечение вычислительной техники и автоматизированных систем”, МИФИ, 2005–2010 гг.
Задать вопрос
Если в проводнике создать электрическое поле и не поддерживать это поле, то перемещение носителей тока приведет к тому, что поле внутри проводника исчезнет, и ток прекратится. Для того чтобы поддерживать ток в цепи достаточно долго, необходимо осуществить движение зарядов по замкнутой траектории, то есть сделать линии постоянного тока замкнутыми. Следовательно, в замкнутой цепи должны быть участки, на которых носители заряда будут двигаться против сил электростатического поля, то есть от точек с меньшим потенциалом к точкам с большим потенциалом. Это возможно лишь при наличии неэлектрических сил, называемых сторонними силами. Сторонними силами являются силы любой природы, кроме кулоновских.
Дополнительную информацию о предмете статьи можно узнать из файла «Электродвижущая сила в цепях электрического тока». А также в нашей группе ВК публикуются интересные материалы, с которыми вы можете познакомиться первыми. Для этого приглашаем читателей подписаться и вступить в группу.
В завершение хочу выразить благодарность источникам, откуда почерпнут материал для подготовки статьи:
www.booksite.ru
www.scsiexplorer.com.ua
www.samelectrik.ru
www.electricalschool.info
www.sxemotehnika.ru
www.zaochnik.ru
www.ido.tsu.ru
Предыдущая
ТеорияЧто такое термопара: об устройстве простыми словами
Следующая
ТеорияЧто такое заземление простыми словами
Содержание:
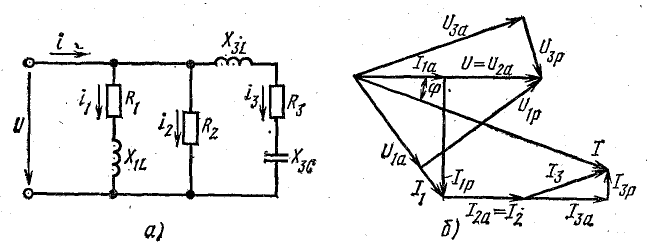
Цепи переменного тока:
Основное применение в электротехнике и радиотехнике имеют переменные напряжения и токи, являющиеся периодическими функциями времени. Мгновенные значения периодических напряжений u и токов i повторяются через промежуток времени Т, называемый периодом:
где t — время; число периодов в единицу времени
Электротехника сильных токов использует в основном низкие частоты. Промышленной частотой в СССР и Европе является 50 гц, в Америке 60 гц, в некоторых областях техники применяют частоты в сотни герц и выше. Техника проводной и радиосвязи использует широкий диапазон частот от долей герц до 1012 гц. Постоянные э.д. с. и токи можно рассматривать как частный случай переменных, частота которых равна нулю (f — 0).
Простейшими и широко применяемыми в электротехнических и радиотехнических устройствах являются периодические напряжения и токи, изменяющиеся по закону синуса. Для случая синусоидального закона изменения функций разработаны простые методы расчета цепей, подобные методам расчета цепей постоянного тока. Если закон изменения периодического напряжения u (t) или i (t) отличен от синусоиды, эти функции могут быть разложены в ряд Фурье, т. е. представлены в виде суммы синусоид, что позволит при расчетах линейных цепей применить метод наложения и свести расчеты к синусоидальным функциям.
Что такое цепь постоянного тока
Цепью постоянного тока называется такая цепь, в которой ЭДС, токи и напряжения остаются постоянными по величине и не зависят от времени.
Цепи делятся на два больших класса:
- линейные;
- нелинейные.
Электрические цепи, содержащие только элементы с линейными вольтамперными характеристиками, называются линейными цепями.
Генератор синусоидального напряжения
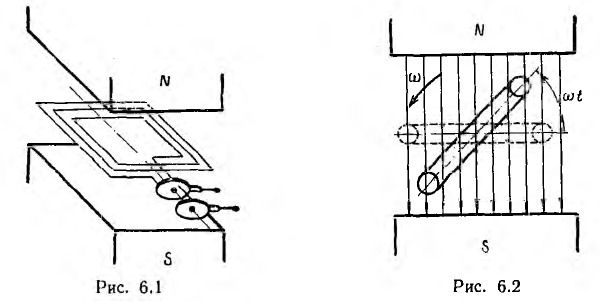
Для получения синусоидальных переменных токов в линейных цепях э. д. с. также должны изменяться по синусоиде. Простейшим генератором синусоидальной э. д. с. может служить прямоугольная катушка, вращающаяся с постоянной угловой скоростью в однородном магнитном поле вокруг оси, перпендикулярной к направлению линий магнитной индукции (рис. 6.1). При этом пронизывающий катушку магнитный поток изменяется, и в ней по закону электромагнитной индукции индуктируется э. д. с. Цепь нагрузки подключается к генератору с помощью щеток, наложенных на два кольца, соединенных с катушкой.
Пусть в начальный момент времени t=О плоскость катушки будет перпендикулярна магнитным линиям (пунктир на рис. 6.2). Тогда магнитный поток, пронизывающий катушку, будет иметь максимальное (амплитудное) значение Фm. Если угловая скорость вращения катушки с числом витков w равна ω, то в момент времени t катушка окажется повернутой на угол ωt, и мгновенные значения ее потока и потокосцепления будут равны
где 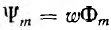
Тогда мгновенное значение э. д. с. катушки
Величина 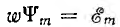
э. д. с., которое она получает, когда sinωt становится равным единице.
Следовательно,
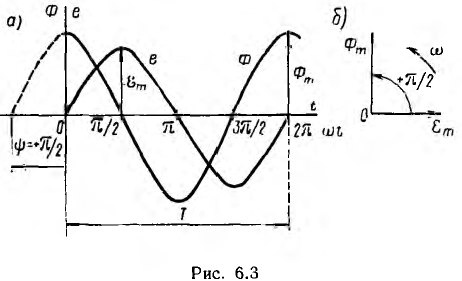
Временные диаграммы
Временная диаграмма магнитного потока и электродвижущей силы катушки показана на рис. 6.3, а. Максимальная э. д. с. индуктируется в моменты, когда поток, пронизывающий катушку, равен нулю, так как тогда скорость изменения потока достигает наибольшего значения. Э д. с. равна нулю в моменты, когда поток получает максимальное значение, так как при этом поток не меняет своей величины.
Как видно из рис. 6.3, а,
откуда
Величина ω, пропорциональная частоте f и равная в данном случае угловой скорости вращения катушки, называется угловой частотой.
Общее выражение для синусоидальной функции времени имеет вид:
где а — мгновенное значение функции; Аm — ее максимальное значение (амплитуда); ω— угловая частота; угол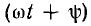
Так, для рассмотренного источника синусоидальной э. д. с.
начальная фаза потока равна + π/2 , э. д. с. — нулю, т. е. магнитный поток и э. д. с. сдвинуты по фазе на π/2.
На временной диаграмме, как видно из рис. 6.3, а, положительная начальная фаза откладывается от начала координат влево, т. е. в сторону отрицательных значений ωt, а отрицательную начальную фазу следует откладывать в сторону положительных значений ωt.
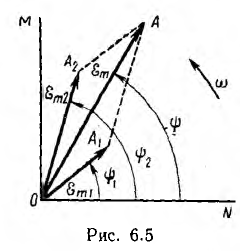
Векторные диаграммы
Расчеты в цепях с синусоидальными напряжениями и токами весьма упрощаются, если вместо синусоид оперировать с их изображениями — вращающимися векторами.
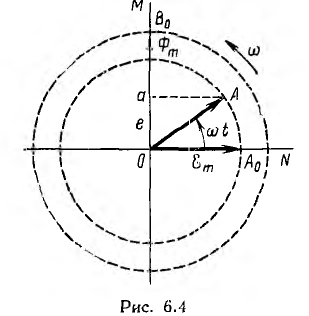
Пусть NOM является прямоугольной системой осей координат и пусть положительные углы откладываются против направления вращения стрелки часов (рис. 6.4). Если нужно найти, например, мгновенные значения синусоиды э. д. с. 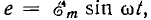
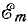
для этого момента времени будет равно проекции Оа вектора ОА на ось ОМ:
Проекция вектора ОА на ось ОМ для начального момента времени
будет равна нулю, для момента времени, когда вектор повернется на угол π/2, проекция будет равна 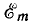
Таким же образом можно находить мгновенные значения потока 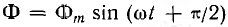
времени вектор ОВ0, изображающий в выбранном масштабе максимальное значение потока Фm, необходимо направить по оси ОМ, так как он должен образовать с осью ON угол + π/2, равный начальной фазе потока.
Таким образом, можно условиться изображать синусоидальную функцию вектором, длина которого определяется максимальным ее значением, а направление — ее начальной фазой, при этом положительная начальная фаза откладывается от горизонтальной оси в сторону вращения векторов. В результате получается векторная диаграмма, показанная для рассмотренного примера потока и э. д. с. на рис. 6.3, б.
Векторы, изображающие синусоидальные функции времени, имеют совсем другой смысл, чем векторы, изображающие, например, силы в механике. Вектор силы дает ее величину и направление в пространстве, вектор, изображающий синусоиду, является вращающимся вектором, дающим своей проекцией на неподвижную ось мгновенное значение синусоиды. Такой вектор чертится в начальном своем положении, которое дает начальную фазу синусоиды, но, конечно, не направление изображаемой величины впространстве. Подобным вектором можно изображать любую синусоидально изменяющуюся величину, в том числе скалярную — э. д. с., тон, поток и т. п.
Векторные диаграммы особенно удобны при сложении или вычитании синусоид одинаковой частоты. Как известно, результатом будет также синусоида той же частоты. При сложении нескольких синусоид нужно складывать их мгновенные значения, т. е. проекции векторов, изображающих эти синусоиды, но так как сумма проекций векторов на какую-либо ось равна проекции геометрической суммы этих векторов на ту же ось, то эга геометрическая сумма и будет вектором, изображающим результирующую синусоиду. Длина вектора даст амплитуду результирующей синусоиды, угол с горизонтальной осью — ее начальную фазу.
Так, например, для двух синусоид (рис. 6.5)
изображаемых векторами 0А1 и 0А2, вектор ОА, изображающий суммарную синусоиду
будет геометрической суммой векторов OA1 и ОА2. Он имеет величину 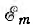
Аналогично, путем геометрического вычитания, может быть найден вектор, изображающий результирующую синусоиду разности двух синусоид. Следовательно, алгебраическому суммированию синусоид, т.е. суммированию их мгновенных значений, соответствуют геометрические действия над изображающими их векторами.
Особенности цепей переменного тока
Для цепей переменного тока справедливы законы Ома, Кирхгофа и Джоуля — Ленца применительно к мгновенным значениям напряжений, токов и мощностей для одного и того же момента времени. Однако в отличие от пассивной цепи постоянного тока, в которой ток определяется приложенным к ней напряжением и ее сопротивлением, в пассивной цепи переменного тока возникают внутренние переменные э. д. с. самоиндукции и э. д. с. емкости, которые должны, быть учтены, кроме приложенного напряжения, при составлении уравнений по основным законам.
Так же, как и в цепях постоянного тока, при составлении уравнений по этим законам для цепей переменного тока необходимо задаться условным положительным направлением напряжений и токов, хотя действительные их направления периодически меняются. По аналогии с цепями постоянного тока удобно принять, что положительные направления напряжения и тока всей цепи и каждого из ее элементов — резистора, катушки индуктивности и конденсатора — совпадают. Тогда мгновенная мощность р = ui всей цепи и каждого из ее элементов будет положительной, когда действительные направления их напряжения и тока совпадают, т. е. когда цепь или ее элементы являются потребителями энергии, что принято характеризовать положительной мощностью.
Выбранные положительные направления для мгновенных значений напряжений и токов сохраняются при переходе к векторам— сумме (разности) мгновенных значений соответствует геометрическая сумма (разность) изображающих их векторов.
Физические и энергетические процессы на участках цепи с сопротивлением, с индуктивностью, с емкостью весьма различны, поэтому предварительно они рассматриваются раздельно до изучения цепей с их сочетанием.
Цепь с сопротивлением
Постоянный ток распределяется по всему сечению проводника равномерно, т. е. во всех точках его сечения плотность тока одинакова.
Плотность переменного тока возрастает от оси проводника к его поверхности. Это явление называется поверхностным эффектом, рассматриваемым в ч. IV. Приближенно можно считать, что переменный ток в проводнике использует только часть s’ его сечения s. Следовательно, сопротивление R постоянному току, называемое обычно омическим, будет меньше сопротивления r переменному току:
Сопротивление г получило название активного сопротивления проводника.
Поверхностный эффект проявляется тем сильней, чем больше частота, сечение, удельная проводимость и магнитная проницаемость проводника. При промышленной частоте (50 гц) и тонких медных или алюминиевых проводах поверхностным эффектом можно пренебречь и считать активное сопротивление равным омическому.
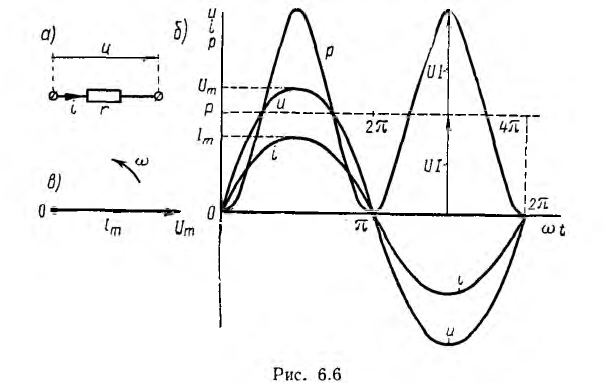
Пусть к активному сопротивлению (рис. 6.6, а) приложено синусоидальное напряжение
По закону Ома ток
Ток получает максимальное значение 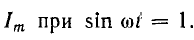
Следовательно, в цепи с сопротивлением r напряжение и ток совпадают по фазе (рис. 6.6, 6.) На векторной диаграмме вектор напряжении совпадает по направлению с вектором тока (рис. 6.6, в). Максимальные значения напряжения и тока также подчинены закону Ома.
Мгновенная мощность р равна произведению мгновенных значений напряжения и тока:
Как видно из этого выражения, мгновенная мощность имеет постоянную составляющую 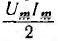
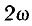
Кривая мощности также изображена на рис. 6.6, б. Мощность равна нулю при u = 0 и i = 0, всегда положительна и получает максимальное значение в те моменты, когда напряжение и ток также максимальны.
Среднее значение мощности за период — средняя мощность
т. e. равна постоянной составляющей мгновенной мощности.
Пользуясь зависимостью между максимальными значениями напряжения и тока, выражение для средней мощности можно переписать следующим образом:
Обычно величина переменного тока характеризуется действующим значением. Так называется значение постоянного тока I, которое дает ту же мощность Р в том же сопротивлении r:
следовательно,
Аналогично, действующее значение напряжения
Следовательно, мгновенная мощность
средняя мощность
Энергия, поглощаемая активным сопротивлением,
непрерывно растет. Эта энергия поставляется источником, питающим цепь.
Цепь с индуктивностью и цепь с емкостью
Цепь с индуктивностью и цепь с емкостью являются накопителями энергии соответственно электрического и магнитного поля. Чтобы подчеркнуть эту аналогию, цепь с индуктивностью и цепь с емкостью
рассматриваются одновременно. Величины, определяющие процессы в них, — ток в цепи с индуктивностью и напряжение на цепи с емкостью — задаются с одинаковой фазой.
Пусть ток цепи с индуктивностью L (рис. 6.7, а)
Тогда потокосцепление
т. e. совпадает по фазе с током.
Пусть напряжение цепи с емкостью С (рис. 6.7, б)
Тогда заряд
т. e. совпадает по фазе с напряжением.
Временная диаграмма этих и далее вычисляемых величин изображена на рис. 6.7, в, причем обозначения кривых показаны соответственно слева и справа.
Энергия, запасаемая в электрическом поле,
пульсирует с двойной частотой 2ω около среднего значения 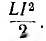
Энергия, запасаемая в магнитном поле,
пульсирует с двойной частотой 2ω около среднего значенияя 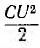
Мгновенная мощность, равная производной энергии по времени,
также изменяется с двойной частотой, будучи положительной, когда энергия поступает в приемник, и отрицательной, когда приемник возвращает энергию источнику.
Средняя мощность
т. е. процесс колебаний энергии между источником и приемником не сопровождается потерями. Максимальное значение мощности
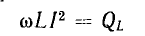
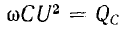
В системе СИ эти мощности измеряются в реактивных вольтамперах (вар).
Мгновенное значение напряжения
Векторная диаграмма цепи с L показана на рис. 6.7, а. Следовательно, в цепи с L ток отстает от напряжения пофазе на угол 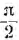
Максимальное значение напряжения
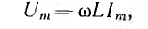
Мгновенное значение тока
Векторная диаграмма цепи с С показана на рис. 6.7, б. Следовательно, в цепи с С ток опережает напряжение по фазе на угол 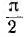
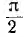
Максимальное значение тока
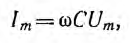
играют роль сопротивления применительно к максимальным и действующим значениям напряжения и тока. Они называются индуктивным сопротивлением емкостным сопротивлением и в системе единиц СИ измеряются в омах.
Емкостное сопротивление обратно пропорционально емкости и частоте; при постоянном напряжении оно равно бесконечности.
В цепи с емкостью величина
может быть названа э. д. с. емкости. Она равна и противоположна по фазе напряжению цепи.
Индуктивное сопротивление прямо пропорционально индуктивности и частоте; при постоянном токе оно равно нулю.
В цепи с индуктивностью возникает э. д. с. самоиндукции
Она равна и противоположна по фазе напряжению цепи.
Отсюда видно, что применять индуктивное или емкостное сопротивления в соотношениях между мгновенными напряжениями и токами нельзя, так как
Соотношения u = —е, полученные в предположении их одинакового положительного направления, аналогичны соотношениям для напряжения U и э. д. с. 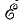
Итак, соотношения в цепи с индуктивностью и в цепи с емкостью аналогичны. От зависимостей в одной цепи к зависимостям в другой можно перейти, заменяя соответствующие величины по табл. 6.1.
Таблица 6.1
| Цепь с индуктивностью | L | ψ | u | i | ω | t | W | p |
| Цепь с емкостью | C | q | i | u | ω | t | W | p |
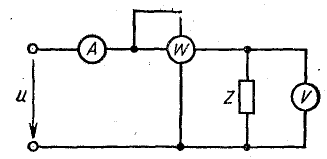
Измерения в цепях переменного тока
Для измерения переменного тока и напряжения могут быть применены амперметры и вольтметры электромагнитной и электродинамической систем, рассмотренные. При включении такого aмперметра в цепь переменного тока его мгновенный момент вращения mвр будет пропорционален квадрату мгновенного значения тока i, подвижная же часть прибора, очевидно, даст отклонение, пропорциональное среднему значению этого момента:
т. е. прибор измерит действующее значение тока. Аналогично, вольтметры этих двух систем измеряют действующее значение напряжения.
Для измерения мгновенных значений переменных токов и напряжений применяется осциллограф, основным элементом которого является вибратор — прибор магнитоэлектрической системы, подвижной частью которой является легкая петелька; ее момент вращения и угол отклонения пропорциональны измеряемой величине. Вместо стрелки на подвижной части укреплено зеркальце, отражающее луч света на движущуюся фотопленку, на которой записывается временная диаграмма тока или напряжения.
Для измерения средней мощности в цепях переменного тока применим ваттметр электродинамической системы. Как следует из , его мгновенный момент вращения mвр будет пропорционален мгновенной мощности р = ui. Тогда отклонение подвижней части пропорционально ее среднему значению:
т. е. средней мощности.
Для получения положительного отклонения ваттметр следует включать по схеме рис. 2.9. В цепях только с индуктивностью и с емкостью ваттметр, очевидно, должен дать нулевое показание.
Анализ и расчет простых цепей переменного тока
Основной особенностью цепей переменного тока (по сравнению с цепями постоянного тока) является наличие в них реактивных элементов – емкостей и индуктивностей . Реактивные элементы, не рассеивая мощность электромагнитных колебаний, изменяют разность фаз между колебаниями электрического тока и напряжения на участке цепи. Вследствие этого амплитудные значения напряжения и силы тока достигаются не одновременно. При расчете электрической цепи переменного тока необходимо учитывать эту особенность, т.е. учитывать фазовые отношения между колебаниями токов и напряжений.
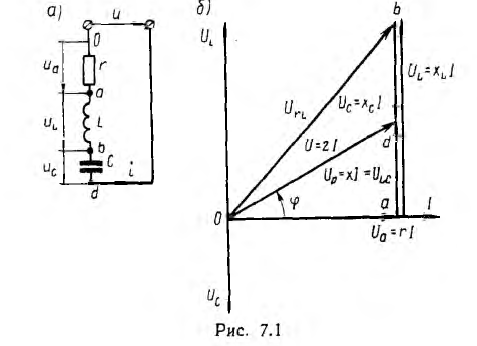
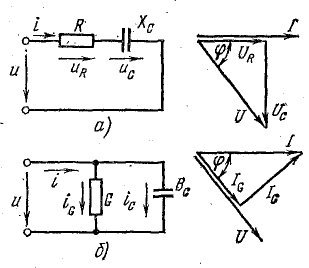
Цепь с последовательным соединением участков с сопротивлением, с индуктивностью и с емкостью
По закону Ома мгновенное значение тока в цепи с последовательно
включенными активным сопротивлением r, индуктивностью L и емкостью С (рис. 7.1, а) зависит не только от приложенного напряжения и, но и от возникающих в цепи э. д. с. индуктивности eL и э. д.с. емкости ес–
отсюда
т. е. приложенное напряжение распадается на три напряжения, из которых первое Ua=ri преодолевает активное сопротивление цепи, второе
уравновешивает противоположную ему по знаку э. д. с. индуктивности eL и третье 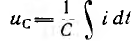
Задавшись током цепи
и подставив это выражение тока в уравнение напряжений:
можно видеть, что отдельные составляющие напряжения представляют собой синусоиды и, следовательно, суммарное напряжение также будет синусоидой, вектор которой равен геометрической сумме векторов составляющих синусоид.
Это построение сделано на рис. 7.1, б для векторов, равных по величине действующим значениям. Вектор активного напряжения UB=rl совпадает по фазе с вектором тока I. Индуктивное напряжение
опережает ток на 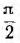
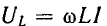
и его вектор 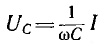
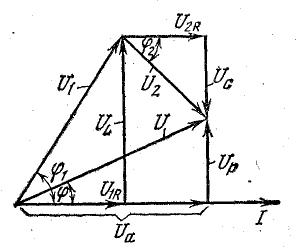
При ее построении векторы напряжений на участках цепи откладывались в той же последовательности, в какой эти участки включены в цепь рис. 7.1, а. Поэтому отдельным точкам векторной диаграммы (0, a, b, d) соответствуют одноименные точки цепи. Такая диаграмма может быть названа топографической. Она позволяет сразу найти векторы напряжений между любыми точками цепи, соединив их прямой линией. На рис. 7.1, б показаны векторы напряжений UrL и ULC на участках rL и LC.
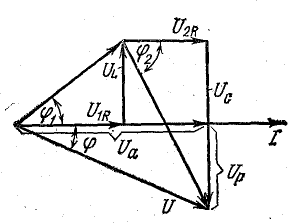
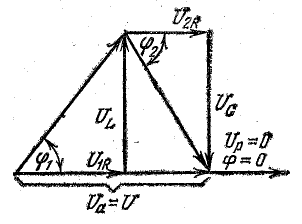
В результате сложения векторов получается прямоугольный треугольник напряжений с гипотенузой, равной полному напряжению U, катетом, равным активному напряжению UB и катетом Up = UL — Uc; напряжение Up называется реактивным. На диаграмме рис. 7.1, б преобладает индуктивное напряжение (UL > Uс) и поэтому реактивное напряжение совпадает по фазе с индуктивным.
Из треугольника напряжений видно, что
Сопротивление 
играет роль сопротивления и называется полным сопротивлением.
В системе единиц СИ z также измеряется в омах.
Следовательно,
Полученные выражения могут рассматриваться как аналог закона Ома для переменного тока. Необходимо подчеркнуть, что закон Ома в таком виде справедлив только для максимальных и действующих значений переменного тока и напряжения. Для мгновенных значений но в таком виде неприменим; написать 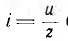
Здесь полезно сопоставить различные выражения закона Ома для этой цепи. Для мгновенных значений
для векторов, очевидно, можно было бы написать:
где 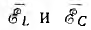
Отсюда видно, что физически существующие э. д. с. индуктивности и емкости, входящие в выражения (7.1) и (7.2), в выражении (7.3) формально учитываются через реактивные сопротивления xL и хс.
Вектор тока сдвинут по фазе относительно вектора напряжения на острый угол 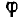
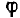
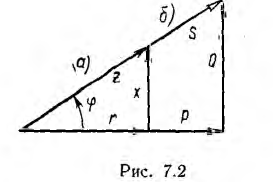
Если разделить все стороны треугольника напряжений на общий множитель I, получится подобный ему треугольник сопротивлений с гипотенузой z и
катетами r и х (рис. 7.2, а), откуда
Мгновенная мощность цепи равна произведению мгновенных значений напряжения и тока:
После подстановки значений 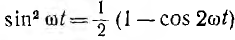
выражение для мгновенной мощности получает вид
Первый член правой части есть мгновенная мощность активного сопротивления
После подстановки соотношений из треугольника напряжений
Эта мощность (рис. 7.3, a) имеет постоянную составляющую
переменную — синусоиду двойной частоты с такой же амплитудой.
Величина Р является, очевидно, средней мощностью за период. Она называется активной мощностью. В системе СИ мгновенная и активная мощности измеряются в ваттах (вт).
Второй и третий член дают мгновенную мощность индуктивности и емкости (см. рис. 7.3, а):
Эти мощности изменяются по синусоидам двойной частоты противоположным по фазе, т. е. когда индуктивность отдает энергию, емкость ее получает, и наоборот. Среднее значение pL и рс равно нулю. В сумме они дают мгновенную мощность реактивных участков цепи:
Амплитуда синусоиды этой мощности
называется реактивной мощностью. В системе СИ реактивная мощность измеряется в реактивных вольт-амперах (вар).
Теперь выражение для мгновенной мощности всей цепи может быть
преобразовано:
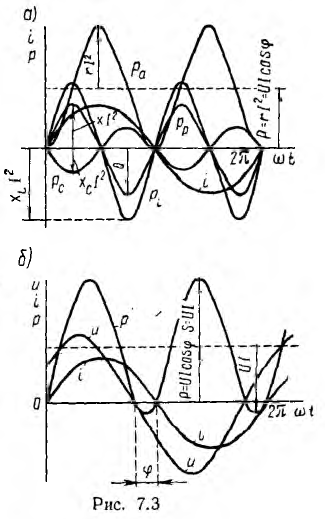
Таким образом, мгновенная мощность р всей цепи имеет постоянную составляющую UI cos ф и переменную составляющую — синусоиду с амплитудой UI (рис. 7.3, б); р равно нулю когда u = 0 или i = 0.
Так как амплитуда переменной части UI больше постоянной составля
ющей UI cosϕ, мощность в определенные промежутки времени становится отрицательной. Когда мощность положительна, цепь получает энергию от источника; когда мощность отрицательна, цепь отдает энергию источнику. Очевидно, возврат энергии источнику получается за счет энергии поля того из реактивных участков цепи, мощность которого больше (для рис. 7.3, б за счет индуктивности). Отдавая запасенную в своем поле энергию, индуктивность снабжает энергией емкость, отдает часть своей энергии безвозвратно активному сопротивлению, а остаток возвращает источнику. Промежутки времени, в течение которых мощность положительна, больше, чем те, при которых мощность отрицательна.
Амплитуда переменной части мгновенной мощности всей цепи
называется полной мощностью и измеряется в системе СИ в вольт-амперах (ва).
Если умножить все стороны треугольника сопротивлений на общий множитель I2, получается подобный ему прямоугольный треугольник мощностей (см. рис. 7.2, б) с углом у вершины, равным ϕ, гипотенузой, равной полной мощности 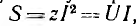
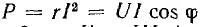
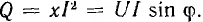
Полная мощность S является характерной величиной для всякой электрической установки, любой электрической машины, аппарата, линии передачи и т. п. Сечение их проводов рассчитывается на ток I таким образом, чтобы провода не перегревались от выделяемого в них тепла. Изоляция рассчитывается на напряжение U; сердечник и н. с. обмотки электромагнитных механизмов рассчитываются на магнитный поток, который также пропорционален напряжению (см., например, формулу для 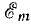
так как 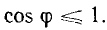
В общем случае напряжение и и ток i цепи записываются так:
где ψ — начальная фаза напряжения;
ϕ — разность фаз напряжения и тока.
Если в рассмотренной цепи 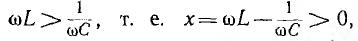
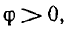
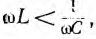
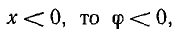
Для цепи с последовательным соединением сопротивления r и индуктивности L аналог закона Ома и сдвиг по фазе могут быть получены
Аналогично, для цепи с последовательным соединением сопротивления r и емкости С, положив 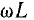
Резонанс напряжений
В электрических цепях, содержащих индуктивности и емкости, возможно явление резонанса, при котором напряжение и ток цепи совпадают по фазе. В цепи с последовательным соединением сопротивления, индуктивности и емкости (см. рис. 7.1, а) будет резонанс напряжений, когда
так как в этом случае ток и разность фаз напряжения и тока
Напряжения на участках цепи при резонансе
т. е. активное напряжение равно полному, а индуктивное напряжение — емкостному напряжению, так как индуктивное сопротивление xL равно емкостному хс. Если
При резонансе, ограниченный лишь активным сопротивлением, при малом r также может получить большое значение.
На рис. 7.4 показана векторная диаграмма для случая резонанса. Как видно из этой диаграммы и приведенных соотношений, при резонансе цепь, несмотря на наличие в ней индуктивности и емкости, ведет себя как активное сопротивление. Ток совпадает по фазе с напряжением и получает наибольшее значение. Реактивное напряжение
Так как условием резонанса является равенство 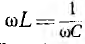
Индуктивное и емкостное сопротивления при резонансе
Величина р называется характеристическим сопротивлением цепи, а ее отношение к активному сопротивлению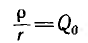
называется затуханием цепи. Чем меньше r, а следовательно, и d, тем при резонансе больше активная (средняя) мощность
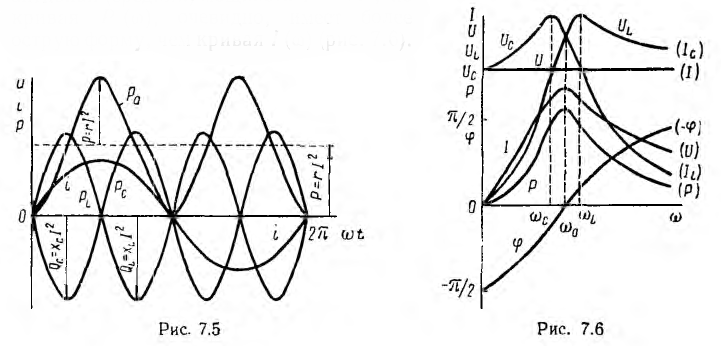
Мгновенные мощности индуктивности и емкости при резонансе равны по величине и обратны по знаку (рис. 7.5):
Индуктивная QL = xLP2 и емкостная Qc = ХсР2 мощности также равны друг другу. Следовательно, при резонансе мгновенная мощность рр и реактивная мощность Q всей цепи будут
Этого следовало ожидать, так как при резонансе, как показано, цепь ведет себя как активное сопротивление.
Максимальное значение энергии индуктивности
т. е. равно максимальному значению энергии емкости. Тогда, если
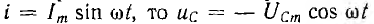
Отсюда видно, что при резонансе суммарная энергия, запасенная реактивными элементами цепи, постоянна и равна максимальной энергии индуктивности, равной, в свою очередь, максимальной энергии емкости. Колебания энергии индуктивности и емкости противоположны по фазе и в цепи происходит полный обмен энергиями между ними.
Источник не участвует в этом обмене и доставляет лишь энергию активному сопротивлению цепи.
Таким образом, при резонансе происходит взаимная компенсация индуктивных и емкостных сопротивлений, напряжений и мощностей.
Далее рассмотрен режим, когда напряжение на зажимах цепи постоянно, а частота изменяется от 0 до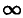
Ток I = 0 при ω = 0 и ω = 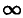
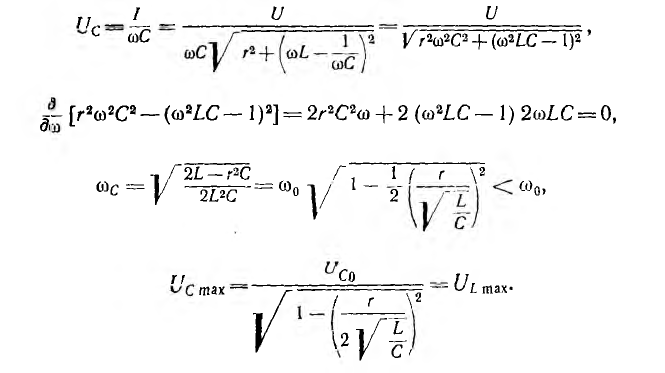
Аналогично изменяется активное напряжение Uа = rl и активная (средняя) мощность Р = rI2, но кривая Р (ω), очевидно, имеет более острую форму, чем кривая I(ω) (рис. 7.6). Индуктивное напряжение UL = 0 при ω = 0. При ω =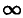
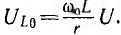
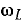
проще исследовать подрадикальное выражение на минимум, взяв его
производную по ω и приравняв нулю:
Значение ULmax получится после подстановки значения 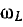
Емкостное напряжение Uc = U при ω=0, U=0 при ω= 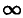
Определение частоты 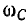
Таким образом, наибольшие значения напряжений на индуктивности и емкости равны между собой.
Графики зависимостей 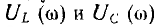
При увеличении активного сопротивления r цепи
и Ucmax уменьшаются, а частоты ωL и ωс удаляются от резонансной частоты
ω0; при 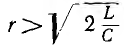
Кривые на рис. 7.6 называются резонансными кривыми или частотными характеристиками цепи.
Явление резонанса имеет широкое применение в радиотехнике.
Например, в ряде устройств используется зависимость режима работы
цепи с последовательным соединением L и С от частоты и повышение тока этой цепи при резонансе.
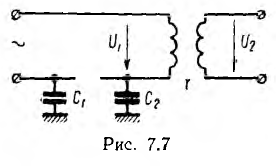
В электротехнике резонанс напряжений часто является аварийным режимом; так при обрыве линии передачи, питающей отключенный со вторичной стороны трансформатор Т (рис. 7.7), может наступить резонанс между емкостью
(С1 и С2 — емкости на землю двух участков линии передачи) и индуктивностью L первичной обмотки трансформатора, что вызовет недопустимое для изоляции и безопасности установки повышение напряжения U1 в первичной и, следовательно, U2 во вторичной обмотках трансформатора.
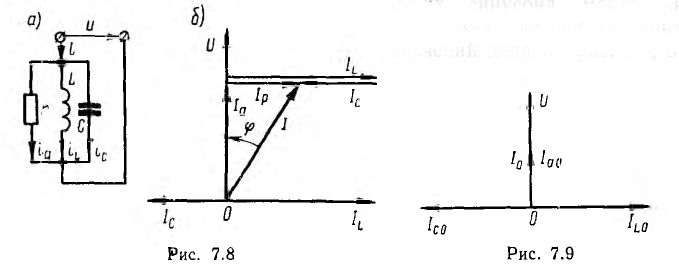
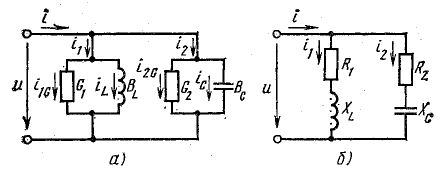
Цепь с параллельным соединением участков с сопротивлением, с индуктивностью и с емкостью. Резонанс токов
Основные соотношения:
При параллельном соединении сопротивления r, индуктивности L и емкости С (рис. 7.8, а) мгновенное значение тока i всей цепи, согласно первому закону Кирхгофа, равно алгебраической сумме мгновенных значений токов отдельных приемников:
После подстановки в это выражение напряжения 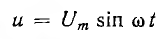
Следовательно, ток всей цепи также будет синусоидой, вектор которой может быть найден как геометрическая сумма векторов слагающих синусоид. Векторная диаграмма для действующих значений дана на рис. 7.8, б.
Активный ток 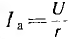
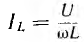
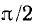
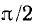
Тогда действующее значение тока всей цепи а разность фаз напряжения и тока
а разность фаз напряжения и тока
Резонанс токов наступит при
т. е. при условии, аналогичном условию резонанса напряжений.
Тогда
т. е. цепь будет вести себя как активное сопротивление.
Токи ветвей цепи при резонансе:
Векторная диаграмма для случая резонанса изображена на рис. 7.9.
Так как векторы 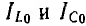
При 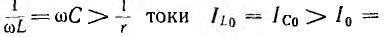
емкости будут больше тока всей цепи, равного току в активном сопротивлении.
Энергетическая сторона процесса здесь такая же, как и при резонансе напряжений: суммарная энергия, запасенная в полях цепи, постоянна и равна максимальной энергии емкости, равной в свою очередь максимальной индуктивности. Колебания энергии емкости и индуктивности противоположны по фазе, и в цепи происходит полный обмен энергиями между ними. Источник не участвует в этом обмене, он доставляет лишь энергию активному сопротивлению.
Если в рассматриваемой цепи поддерживать неизменным напряжение U и увеличивать частоту ω, активный ток 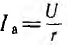
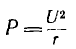
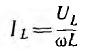
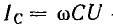
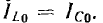
Ток всей цепи
получает при резонансе, когда 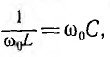
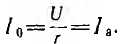

В высокочастотных генераторах, усилителях и других радиотехнических устройствах используется зависимость режимов работы от частоты в цепи с параллельным соединением L и С и повышение напряжения этой цепи при резонансе токов.
Дуальные цепи
При сравнении уравнения, написанного для цепи с параллельным соединением r, L и С (см. рис. 7.8, а) на основе первого закона Кирхгофа,
с уравнением для цепи с последовательным соединением r, L и С (см. рис. 7.1, а), написанного на основе второго закона Кирхгофа,
видно, что оба уравнения имеют в качестве независимой переменной время t и совершенно аналогичны, причем одно получается из другого при взаимной замене схемы и величин по табл. 7.1.
Таблица 7.1
| Парaллельное соединение | i | u | 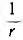 |
L | C |
| Последовательное соединение | u | i | r | C | L |
Две цепи, в которых напряжения первой цепи ведут себя, как токи второй и, наоборот, токи первой ведут себя, как напряжения второй, называются дуальными. Цепь с L и цепь с С, как видно, дуальны. Дуальными являются также цепи с последовательным и параллельным соединениями r, L и С, и все выводы, сделанные для последовательной схемы, можно перенести на параллельную, если заменить величины так, как указано в приведенной таблице. Взаимная замена напряжения и тока должна, очевидно, производиться
и для их действующих значений U и I, а частота ш для обеих схем должна быть одинакова.
Так, например, результаты исследования последовательной схемы при U = const и ω = var, изображенные на рис. 7.6, могут быть целиком перенесены на параллельную схему, работающую при I = const и ω= var, причем кривая, изображающая изменение тока I цепи, будет изображать кривую изменения напряжения U, кривая UL — кривую Iс и кривая Uc — кривую IL. Зависимость активной (средней) мощности 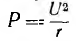

справа в скобках). Дуальными будут и векторные диаграммы, что можно видеть, например, из сравнения рис. 7.1, б и 7.3, б.
Общему выражению для емкостного напряжения последовательной схемы будет соответствовать общее выражение для индуктивного тока параллельной схемы:
выражению для максимумов напряжений UL и Uc будет соответствовать выражение для максимумов токов Iс и IL:
выражению для частоты 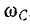
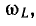
Совершенно аналогичны между собой и режимы работы параллельной цепи при ω = var и U = const (см. рис. 7.10) и последовательной — при ω = var и 1=const, если произвести указанную замену величин (обозначения кривых даны справа в скобках). Интересно отметить,что при неизменном токе напряжение U последовательной цепи при резонансе, когда 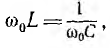
Повышение коэффициента мощности
Схема, в которой возможен резонанс токов, используется в электротехнике для повышения коэффициента мощности. Обычно приемники электрической энергии имеют активно-индуктивный характер, т. е. работают со сдвигом фаз 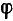
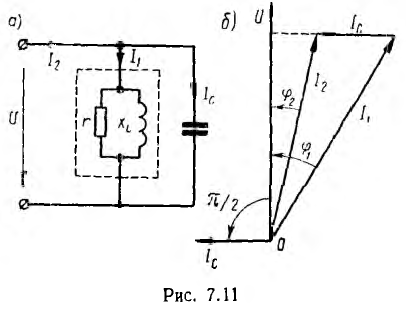
Источник энергии, питающий такой приемник, а также линия передачи должны быть рассчитаны на полную мощность S = UI, превышающую среднюю мощность приемника Р = UI cosϕ. Для меньшения полной мощности источника и линии передачи путем повышения коэффициента мощности часто применяется параллельное пюдключение к приемнику батареи конденсаторов, т. е. схема, в которой возможен резонанс токов.
На рис. 7.11, б показана векторная диаграмма этой цепи. Здесь r1 — ток нагрузки, ϕ1 — фазный сдвиг, / с — ток батареи конденсаторов, который при пренебрежении потерями в них опережает напряжение U по фазе на угол 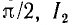
где Р — средняя мощность приемника.
Отсюда
при ϕ2 = 0 емкость
Элементарные методы расчета простых цепей переменного тока
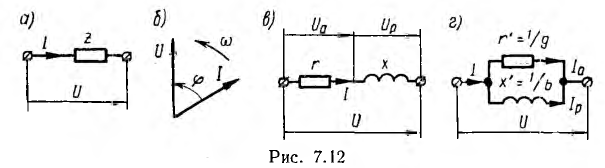
Эквивалентные схемы:
При расчете цепи любой приемник может быть заменен эквивалентной схемой с сосредоточенными параметрами, имеющей равные ток и фазный сдвиг при том же напряжении и той же частоте. Если приемник (рис. 7.12, а) при напряжении U и частоте f потребляет ток I с фазным сдвигом 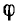
Первой простейшей эквивалентной схемой является последовательное соединение активного г и реактивного х сопротивлени, (рис. 7.12, в для случая преобладания индуктивного сопротивления)
Тогда активные и реактивные сопротивления, напряжения и мощности этой эквивалентной схемы соответственно равны:
и могут быть представлены катетами подобных прямоугольных треугольников, гипотенузы которых равны полным величинам:
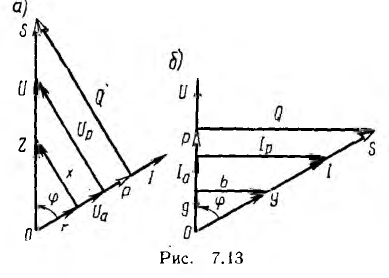
Треугольники сопротивлений, напряжений и мощностей изображены на рис. 7.13, а.
Второй простейшей эквивалентной схемой того же приемника является параллельное соединение активного r’ и реактивного x’ сопротивлений (рис. 7.12, г), не равных r и х эквивалентной ей последовательной схемы. Параллельную схему удобней характеризовать проводимостями: активной 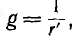
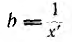
Токи ветвей параллельной эквивалентной схемы, называемые активным и реактивным:
изображены на векторной диаграмме рис. 7.13, б. Так как они сдвинуты между собой по фазе на угол π/2, полный ток
откуда
На рис. 7.13, б прямоугольный треугольник токов совмещен стреугольником проводимостей, а также с треугольником мощностей, гипотенуза которого равна полной мощности S, а катеты —активной и реактивной мощностям:
Все эти треугольники имеют у вершины угол 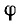
Сопротивления и проводимости часто называют параметрами приемников. Это определение полностью справедливо для и у, величины же r, х и g, b правильней называть параметрам и эквивалентных схем.
Так как последовательная и параллельная схемы эквивалентны между собой, активные, реактивные и полные мощности их должны быть также между собой равны:
Отсюда могут быть получены переходные формулы зт сопротивлений последовательной схемы к проводимостям параллельной схемы:
Аналогичным образом могут быть получены переходные формулы от проводимостей параллельной схемы к сопротивлениям последовательной:
Таким образом, обратными друг другу являются только полные сопротивление г и проводимость у, активные и реактивные сопротивления и проводимости находятся в более сложной зависимости.
При анализе поведения какого-либо приемника при переменной частоте необходимо заменять его эквивалентной схемой, близкой физической сущности этого приемника, т. е. схемой, в которой сопротивления, индуктивности и емкости ее элементов могут быть приняты пастояинными. Так, в некотором диапазоне частот можно пренебречь поверхностным эффектом, и, например, для кольцевого соленоида считать сопротивление r и индуктивность L независящими от частоты, определяя их по формулам:
где l1 и l2 — соответственно длины провода обмотки и сердечника, S1, и S2 — их сечения. Пренебрегая током через межвитковые емкости соленоида, что допустимо только при низких частотах, следует представить соленоид в виде последовательной эквивалентной схемы постоянными параметрами r и L (см. рис. 7.12, в). Тогда при постоянном токе (ω = 0) соленоид и его эквивалентная схема будут иметь сопротивление r, а с ростом частоты ω его сопротивление z = 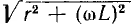
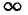
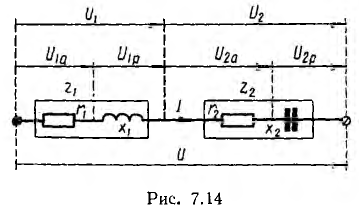
Цепи с последовательным и параллельным соединением приемников
При последовательном соединении нескольких приемников каждый из них удобно заменить эквивалентной схемой, состоящей из последовательного соединения активного г и реактивного х сопротивлений.
Ток всех приемников такой цепи одинаков, а мгновенное значение напряжения, согласие второму закону Кирхгофа, равно алгебраической сумме мгновенных значений напряжений отдельных приемников. При переходе к векторам алгебраическая сумма заменяется геометрической.
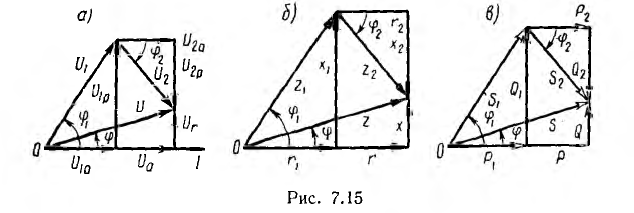
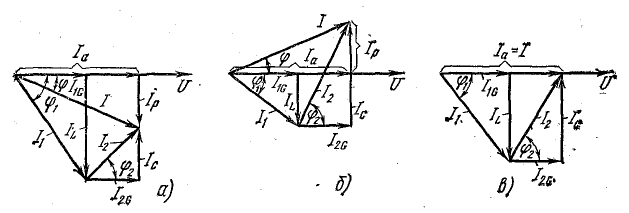
В качестве примера на рис. 7.15, а показана векторная диаграмма для цепи рис. 7.14, состоящей из последовательного соединения двух приемников —одного с индуктивным характером нагрузки и другого с емкостным. Векторы напряжения приемников и всей цени разлагаются на составляющие: активные Uа — по вектору тока и реактивные Uр — перпендикулярно вектору тока. Если разделить все напряжения (стороны треугольников напряжений: 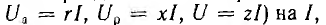
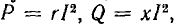
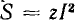
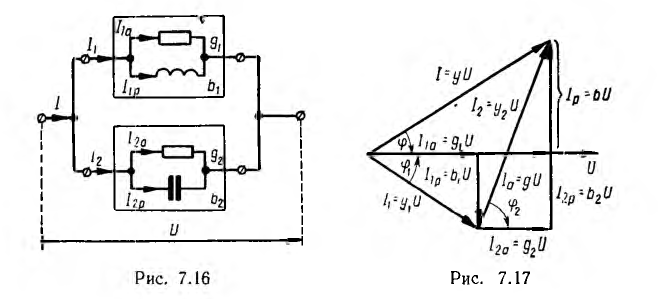
При параллельном соединении нескольких приемников каждый из них удобно заменить эквивалентной схемой, состоящей из параллельного соединения активной g и реактивной b проводимостей. Напряжение всех приемников такой цепи одинаково, а мгновенное значение тока цепи, согласно первому закону Кирхгофа, равно алгебраической сумме мгновенных значений токов отдельных приемников. При пере ходе к векторам алгебраическая сумма заменяется геометрической.
В качестве примера на рис. 7.17 дана векторная диаграмма для цепи, состоящей из параллельного соединения приемника с индуктивным характером нагрузки и приемника с емкостной нагрузкой (рис. 7.16). Векторы тока приемников и всей цепи разлагаются на составляющие:
активные Iа по вектору напряжения U и реактивные Iр — перпендикулярно вектору напряжения. Если разделить все токи (стороны треугольников токов: 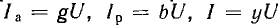
Из многоугольников рис. 7.15 и 7.17 видно, что при последовательном соединении складываются сопротивления, напряжения и мощности, а при параллельном — проводимости, токи и тоже мощности. Активные величины складываются арифметически, реактивные — алгебраически, а полные — геометрически.
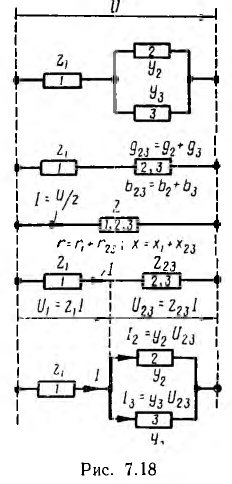
Расчет цепей со смешанным соединением приемников методами преобразования и пропорционального пересчета
При смешанном (параллельно-последовательном) соединении приемников с заданными параметрами, питаемых одним источником энергии, токи, напряжения и мощности ветвей цепи могут быть определены аналитически методом преобразования, заключающимся в постепенной замене сложной цепи более простой, ей эквивалентной. Ход решения подобной задачи показан на рис. 7.18.
Группа приемников, соединенных параллельно, заменяется одним, активная проводимость которого равна арифметической сумме активных проводимостей приемников, а реактивная—алгебраической сумме реактивных. Группа приемников, соединенных последовательно, заменяется одним, активное сопротивление которого равно арифметической сумме активных сопротивлений отдельных приемников, а реактивное — алгебраической сумме. После замены всей цени одним приемником определяется ток при заданном напряжении или напряжение при заданном токе и сдвиг фаз между ними. Затем схема разворачивается в первоначальную цепь с постепенным определением напряжений, токов и фазных сдвигов в отдельных приемниках.
В процессе решения этой задачи несколько раз приходится при менять переходные формулы от сопротивлений к проводимостях и от проводимостей к сопротивлениям.
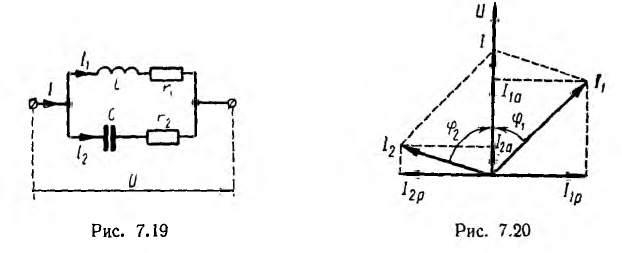
В качестве примера далее решается важная для электротехники задача определения частоты ω, при которой в схеме рис. 7.19 наступит резонанс токов, т. е. напряжение и ток всей цепи будут совпадать по фазе. Для этого, очевидно, реактивная проводимость всей цепи должна быть равна нулю:
откуда
Таким образом, в общем случае, когда 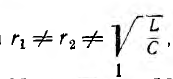
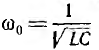
Так как в общем случае токи ветвей сдвинуты по фазе не на π/2, их мгновенные мощности, изменяющиеся с двойной частотой, будут сдвинуты по фазе на угол, отличный от π, т. е. они не находятся в противофазе. Это значит, что в общем случае резонанса полного обмена энергиями между индуктивной и емкостной ветвями не происходит.
Интересно отметить частные случаи:
1) при
2) при 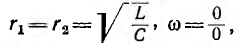
3) при 
Расчет подобных цепей может быть произведен также графоаналитически — методом пропорционального пересчета. Он основан на том, что в линейной цепи токи пропорциональны напряжениям, следовательно, векторная диаграмма напряжений и токов, рассчитанная или построенная для одного значения питающего цепь напряжения, сохранит свой вид при изменении этого напряжения, и лишь масштабы для напряжения и тока изменятся во столько же раз.
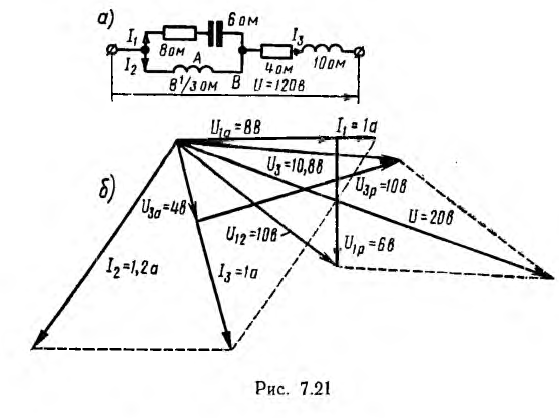
Например, для цепи рис. 7.21, а, решая задачу графоаналитически, целесообразно строить векторную диаграмму, задавшись током первой ветви l1, = 1а. Затем последовательно вычисляются и в выбранном масштабе наносятся на диаграмму векторы в соответствии со своей фазой, после чего они складываются графически (рис. 7.21, б):
Таким образом, напряжение всей цепи оказалось равным 20 б вместо заданных 120 в. Следовательно, векторная диаграмма рис. 7.21, б остается действительной и для заданного напряжения, если увеличить масштабы для напряжений и токов в 120/20 = 6 раз.
Элементы и параметры электрических цепей переменного тока
Все реальные электротехнические устройства обладают электрическим сопротивлением R, индуктивностью L и емкостью С, которые являются параметрами электрической цепи переменного тока. Однако влияние каждого из параметров на ток в цепи различно, поэтому в некоторых случаях из расчетной схемы исключаются те, влияние которых незначительно.
Таким образом схема электрической цепи переменного тока характеризуется одним из указанных параметров R, L, C или комбинацией их при различных способах соединения элементов.
Цепь с активным сопротивлением
Электрические лампы накаливания, печи сопротивления, бытовые нагревательные приборы, реостаты и другие приемники, где электрическая энергия преобразуется в тепловую, на схемах замещения обычно представлены только сопротивлением R.
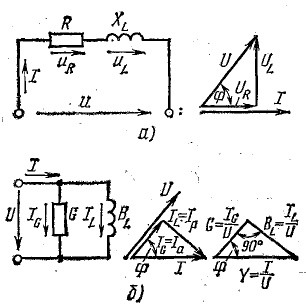
Для схемы, изображенной на рис. 13.1, а, заданы сопротивление R и напряжение, изменяющееся по закону
Требуется определить ток и мощность цепи.
Рис. 13.1. К вопросу о цепи с активным сопротивлением
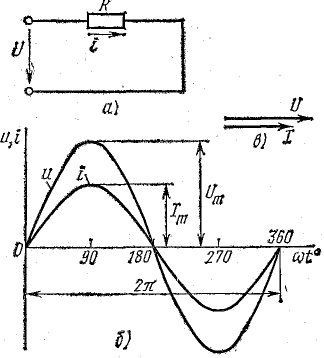
Рис. 13.2. График мгновенной мощности в цепи с активным сопротивлением
Ток в цепи
Выражение для мгновенного тока найдем по закону Ома:
где 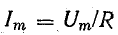
Из уравнений напряжения и тока видно, что начальные фазы обеих кривых одинаковы, т. е. напряжение и ток в цепи с сопротивлением R совпадают по фазе. Это показано на графиках и векторной диаграмме (рис. 13.1, б, в).
Действующий ток найдем, разделив амплитуду на
отсюда
Формулы (13.1) выражают закон Ома для цепи переменного тока с сопротивлением R. Внешне они ничем не отличаются от формулы (2.6) для цепи постоянного тока, если переменные напряжение и ток выражены действующими величинами.
Мгновенная мощность
При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока:
Из тригонометрии найдем
Учитывая это, запишем
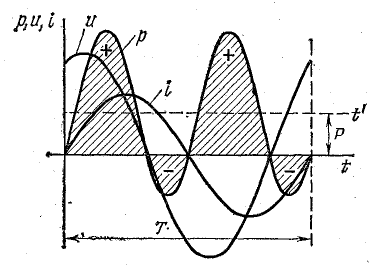
Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени t. Зависимость мощности от времени — периодическая кривая (рис. 13.2).
Если ось времени t поднять по чертежу на величину р = Рm/2 = UmIm/2, то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:
Таким образом, в первоначальной системе координат мгновенная мощность равна сумме постоянной величины 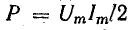
Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпадению по фазе напряжения и тока.
Постоянство знака мощности говорит о том, что направление потока электрической энергии остается в течение периода неизменным, в данном случае от сети (от источника энергии) в приемник с сопротивлением R, где электрическая энергия необратимо преобразуется в другой вид энергии. В этом случае электрическая энергия называется активной.
Если R — сопротивление проводника, то в соответствии с законом Ленца — Джоуля электрическая энергия в нем преобразуется в тепло.
Активная мощность
Скорость преобразования электрической энергии в другой вид энергии за конечный промежуток времени, значительно больший периода изменения тока, характеризуется средней мощностью. Она равна средней мощности за период, которую называют активной.
Активная мощность — среднее арифметическое мгновенной мощности за период.
Для рассматриваемой цепи активную мощность Р нетрудно определить из графика рис. 13.2.
Средняя величина мощности равна высоте прямоугольника с основанием Т, равновеликого площади, ограниченной кривой р(t) и осью абсцисс (на рисунке заштриховано).
Равенство площадей РТ = Sр выполняется, если высоту прямоугольника взять равной половине наибольшей мгновенной мощности Рm.
В этом случае часть площади Sр, находящаяся выше прямоугольника, точно укладывается в оставшуюся незаштрихованной его часть:
Активная мощность цепи с сопротивлением равна произведению действующих величин напряжения и тока:
С математической точки зрения активная мощность является постоянной составляющей в уравнении мгновенной мощности р(t) [см. выражение (13.2)].
Среднюю мощность за период можно найти интегрированием уравнения (13.2) в пределах периода:
Поэтому
Сопротивление R, определяемое из формулы (13.3) отношением активной мощности цепи к квадрату действующего тока, называется активным электрическим сопротивлением.
Цепь с индуктивностью
Исследуемая далее цепь, содержащая только индуктивность, является искусственной, так как катушки, линии электропередачи и другие устройства кроме индуктивности L имеют и активное сопротивление.
Однако рассмотрение идеальной катушки (при R = 0) необходимо для уяснения физических процессов в реальных цепях.
Рис. 13.4. К вопросу о цепи с индуктивностью
Это тем более важно, что в отдельных случаях активным сопротивлением и емкостью можно пренебречь из-за их малости. Например, ненагруженный трансформатор в схеме замещения в ряде случаев может быть представлен только своей индуктивностью.
Допустим, что для цепи (рис. 13.4, а) известны индуктивность L и ток, изменяющийся по закону
Требуется определить напряжение и мощность цепи.
Индуктивное напряжение
Переменный ток в катушке вызывает э. д. с. самоиндукции. При отсутствии активного сопротивления приложенное к катушке напряжение уравновешивается только э. д. с. самоиндукции, поэтому в соответствии со вторым законом Кирхгофа в любой момент времени
Э. д. с. самоиндукции пропорциональна скорости изменения тока [см. формулу (10.10)]
а напряжение
Уравнение приложенного напряжения можно найти, рассматривая векторную диаграмму на рис. 13.5, где ток изображен вектором Im, который предполагается вращающимся с угловой скоростью, равной угловой частоте ω. В начальном положении (при t = 0) вектор Im направлен по горизонтальной оси вправо. Это соответствует уравнению тока (13.4), если мгновенные величины i определять проекцией вращающегося вектора Im на вертикальную ось.
Рис. 13.5. Векторная диаграмма цепи с индуктивностью
Рассмотрим промежуточные положения вектора Im, отстоящие от начального на угол 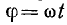
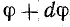
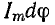
Уравнение напряжения
Но
поэтому
Это уравнение можно получить, дифференцируя уравнение тока:
Индуктивное сопротивление
Действующая величина напряжения определяется из уравнения (13.5), где 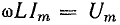
Разделив это выражение на 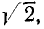
Отсюда
Коэффициент пропорциональности между действующими величинами напряжения и тока, равный произведению индуктивности и угловой частоты ωL, обозначают XL и называют реактивным сопротивлением индуктивности или индуктивным сопротивление е м.
Индуктивное сопротивление выражается в омах:
Действующая величина тока в цепи с индуктивностью равна отношению действующей величины напряжения к индуктивному сопротивлению.
Формула (13.6) похожа на формулу Ома. Это позволяет ток в цепи с индуктивностью определять так же, как ток в цепи с активным сопротивлением. Но нужно помнить, что индуктивное сопротивление с физической точки зрения ничего общего с обычным сопротивлением не имеет. Понятие об индуктивном сопротивлении, введенное для облегчения расчета, заменяет в расчете фактическое влияние э. д. с. самоиндукции на ток в цени, т. е. отражает инерционные свойства электрической цепи.
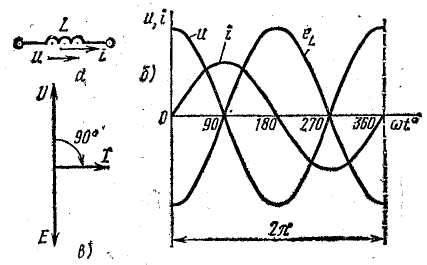
Векторная диаграмма цепи
Сопоставление уравнений тока (13.4) и напряжения (13.5) показывает, что в цепи с индуктивностью ток отстает от напряжения по фазе на четверть периода, или в угловой мере на π/2. Это видно также на рис. 13.5. Мгновенное напряжение выражается отрезком о-d в масштабе, отличающемся от масштаба тока в ωL раз. Перенесем этот отрезок на вертикальную ось (отрезок о-d’), где откладываются мгновенные величины тока. Этому мгновенному напряжению и соответствует вектор Um, опережающий вектор Im по ходу вращения на угол 90°. Э.д.с. самоиндукции, направленная против приложенного напряжения, имеет уравнение
а на рис. 13.5 изображена вектором Еm, отстающим от вектора тока Im на 90°. На рис. 13.4 это показано отдельно на графике и векторной диаграмме (на векторной диаграмме отложены действующие величины).
Мгновенная и реактивная мощности
Мгновенная мощность 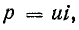
График изменения мощности (рис. 13.6) представляет собой синусоиду двойной частоты с амплитудой
или
Наибольшая величина мощности в цепи с индуктивностью равна произведению действующих напряжения и тока.
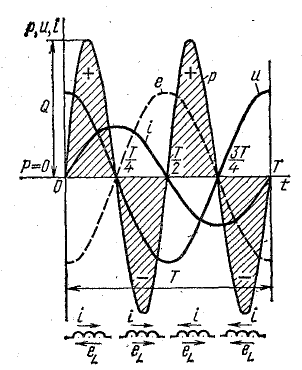
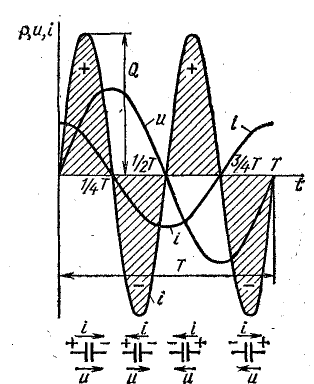
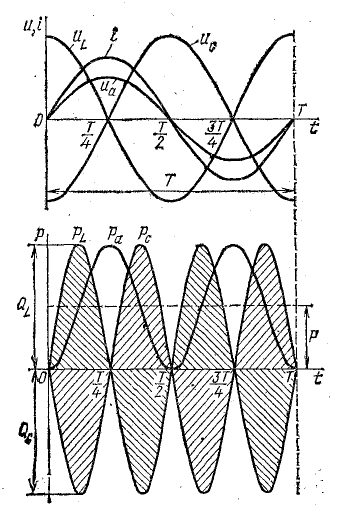
Для выяснения физического смысла энергетических процессов обратим еще раз внимание на график мощности. Из него видно, что мгновенная мощность в течение периода четыре раза меняет знак (в моменты времени Т/4; Т/2; 3/4Т; Т). Изменение знака мощности означает, что направление потока энергии меняется.
Рис. 13.6. График мгновенной мощности в цепи с индуктивностью
В первую четверть периода, когда ток в цепи увеличивается, энергия накапливается в магнитном поле катушки за счет энергии источника. Катушка в это время является приемником энергии, ток направлен против э. д. с. самоиндукции. Во вторую четверть периода, когда ток уменьшается, энергия возвращается в сеть (источнику).
Направления э. д. с. самоиндукции и тока в катушке совпадают — катушка является источником энергии. В следующую половину периода процесс повторяется. Нетрудно заметить, что количество энергии, накапливаемой в катушке за одну четверть периода (заштрихованная площадь «+»), точно равно количеству энергии, возвращаемой обратно в следующую четверть периода (заштрихованная площадь «—»).
Средняя (активная) мощность за период в цепи с индуктивностью равна нулю (Р = 0), так как в цепи с индуктивностью преобразования электрической энергии в другие виды энергии (тепловую, механическую) не происходит.
Скорость накопления и убыли энергии магнитного поля меняется по гармоническому закону. Амплитуда кривой мгновенной мощности Q является характеристикой этого процесса и называется реактивной мощностью.
Единицу мощности в этом случае называют вар — вольт-ампер реактивный — в отличие от единицы активной мощности — ватта.
Задача 13.4.
Катушка имеет индуктивность L = 15,9 мГн, активное сопротивление R = 0. Начертить график зависимости индуктивного сопротивления и тока в катушке от частоты приложенного напряжения, если действующее напряжение U = 100 В остается неизменным.
Решение. Нужно задаться несколькими величинами частоты, определить соответствующие индуктивные сопротивления, а затем величины тока.
Для частоты f = 50 Гц
По результатам расчета для других частот (f = 0,25, 100, 500, 1000, 10 000 Гц) постройте в прямоугольной системе координат графики согласно условию задачи.
Цепь с емкостью
В конденсаторе с идеальным диэлектриком предполагается полное отсутствие тока проводимости и потерь энергии. Изменение напряжения между обкладками конденсатора сопровождается электрическим током смешения, величина которого зависит от емкости С. При напряжении на конденсаторе (рис. 13.7, а) 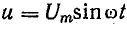
Рис. 13.7, К вопросу о цепи с емкостью
Электрический ток смещения
Внешнее электрическое поле вызывает поляризацию диэлектрика.
При всяком изменении электрического поля изменяется поляризованность диэлектрика, причем связанные заряженные частицы, входящие в состав атомов и молекул вещества, перемещаются, образуя электрический ток.
Явление движения связанных заряженных частиц в диэлектрике при изменении поляризации диэлектрика называют электрическим током поляризации.
Ток поляризации, согласно формуле (2.2),
где σ —плотность электрического смещения заряда; отсюда
где 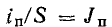
Учитывая формулу (7.20), найдем, что плотность тока поляризации равна скорости изменения поляризованности:
При изменении электрического поля меняется не только вектор поляризации Р, но и вектор электрического смещения в вакууме D0.Из выражений (7.22) и (7.24) следует
Второе слагаемое в правой части этого уравнения есть плотность тока поляризации, связанного с движением заряженных частиц диэлектрика. Первое слагаемое также имеет размерность плотности тока, но характеризует физический процесс в самом электрическом поле при его изменении во времени.
Величину 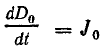
Введение понятия о токе смещения позволяет рассматривать электрическую цепь с конденсатором непрерывной: на участках из проводников имеется ток проводимости, а в диэлектрике — равный ему ток смещения.
Ток в цепи с емкостью
Заряд конденсатора пропорционален напряжению между его обкладками [см. формулу (7.28)], поэтому изменение напряжения сопровождается изменением заряда:
Скорость изменения заряда пропорциональна скорости изменения напряжения:
Но скорость изменения заряда равна электрическому току [см. формулу (2.2)]:
При этом во внешнем по отношению к конденсатору участке цепи происходит движение электронов (ток проводимости) через источник. Одновременно при увеличении напряжения совершается поляризация диэлектрика в конденсаторе и возникает ток смещения. При уменьшении напряжения диэлектрик деполяризуется.
Таким образом, ток в цепи с конденсатором пропорционален скорости изменения напряжения на его обкладках.
Уравнение (13.8) по форме подобно уравнению (13.5). Поэтому характер изменения тока при синусоидальном напряжении можно проследить на векторной диаграмме аналогично тому, как это сделано при рассмотрении цепи с индуктивностью (см. рис. 13.5), отнеся рассуждения к скорости изменения напряжения.
На диаграмме векторы тока и напряжения следует поменять местами . В связи с этим уравнение тока для цепи с емкостью можно записать аналогично уравнению для напряжения в цепи с индуктивностью:
Уравнение тока можно получить, дифференцируя уравнение напряжения:
Емкостное сопротивление
Величина 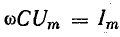
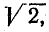
Величину 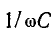
Действующий ток в цепи с емкостью равен отношению действующего напряжения к емкостному сопротивлению.
Формула (13.10) по форме совпадает с формулой Ома. Однако емкостное сопротивление физически ничего общего с обычным сопротивлением R не имеет.
Понятие о емкостном сопротивлении, введенное для облегчения расчетов, отражает в расчете противодействие заряженного конденсатора току в цепи.
Сопоставление уравнений напряжения и тока показывает, что в цепи с емкостью напряжение отстает от тока по фазе на четверть периода, или в угловой мере на π/2. На рис. 13.7, б, в это показано на графике и векторной диаграмме.
Мощность в цепи
Построение графика мгновенной мощности (рис. 13.8) выполняется точно так же, как и для цепи с индуктивностью, если иметь в виду, что мгновенная мощность выражается таким же произведением:
или
Рис. 13.8. График мгновенной мощности в цепи с емкостью
Из графика видно, что мгновенная мощность, как и в цепи с индуктивностью, четыре раза в течение периода меняет знак. В первую четверть периода, когда напряжение на конденсаторе увеличивается, энергия накапливается в электрическом поле конденсатора за счет работы источника. Конденсатор в это время заряжается, т. е. является приемником энергии: направления тока и приложенного напряжения совпадают. Во вторую четверть периода, когда напряжение уменьшается, энергия в том же количестве возвращается в сеть (к источнику), ток в цепи направлен против напряжения сети, т. е. конденсатор является источником энергии (разряжается).
Проведя рассуждения, аналогичные тем, какие были вделаны для цепи с индуктивностью, найдем, что активная мощность в цепи с емкостью равна нулю (Р = 0), а реактивная мощность равна произведению действующих величин напряжения и тока:
Таким образом, в цепи с емкостью, так же как и в цепи с индуктивностью, преобразования электрической энергии в другие виды энергии (тепловую, механическую) не происходит.
Задача 13.7. Конденсатор имеет емкость С = 637 мкФ. Начертить график зависимости емкостного сопротивления и тока в конденсаторе от частоты приложенного напряжения, действующее значение которого U = 100 В остается неизменным.
Решение. Для решения задачи нужно задаться несколькими значениями частоты. Определить соответствующие величины емкостного сопротивления, а затем тока.
Для частоты 50 Гц
По результатам расчета для других частот (f = 0,25, 100, 500, 1000, 10 000 Гц) постройте и прямоугольной системе координат графики согласно условию задачи.
Цепь с реальной катушкой индуктивности
Реальная катушка отличается от идеальной тем, что переменный ток в ней сопровождается не только изменением энергии в магнитном поле, но и преобразованием электрической энергии в другой вид. В частности, в проводе катушки электрическая энергия преобразуется в тепло в соответствии с законом Ленца — Джоуля.
Ранее было выяснено, что в цепи переменного тока процесс преобразования электрической энергии в другой вид характеризуется активной мощностью цепи Р , а изменение энергии в магнитном поле — реактивной мощностью Q .
В реальной катушке имеют место оба процесса, т. е. ее активная и реактивная мощности отличны от нуля. Поэтому в схеме замещения реальная катушка должна быть представлена активным и реактивным элементами.
Деление реальной катушки на два элемента искусственно, так как конструктивно оба элемента неразделимы. Однако такой же схемой замещения можно представить реальную цепь из двух конструктивно не совмещенных элементов, один из которых характеризуется только активной мощностью Р(Q = 0), а другой — реактивной (индуктивной) мощностью Q (Р = 0).
Схема замещения катушки с последовательным соединением элементов
В схеме с последовательным соединением элементов реальная катушка характеризуется активным сопротивлением R и индуктивностью L.
Активное сопротивление определяется величиной мощности потерь
а индуктивность — конструкцией катушки. Предположим, что ток в катушке (рис. 13.9, а) выражается уравнением 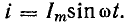
Рис. 13.9. Схема замещения реальной катушки индуктивности (цепь R, L)
При переменном токе в катушке возникает э. д. с. самоиндукции еL, поэтому ток зависит от действия приложенного напряжения и э. д. с. еL. Уравнение электрического равновесия цепи, составленное по второму закону Кирхгофа, имеет вид
или
Приложенное к катушке напряжение состоит из двух слагаемых, одно из которых uR равно падению напряжения в активном сопротивлении, а другое 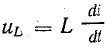
В соответствии с этим катушку в схеме замещения можно представить активным и индуктивным сопротивлениями, соединенными последовательно (рис. 13.9, б).
Дополнительно заметим, что оба слагаемых в правой части равенства (13.12) являются синусоидальными функциями времени. Согласно выводам, полученным, uR совпадает по фазе с током, а uL опережает ток на 90°.
Поэтому
Векторная диаграмма напряжений. Полное сопротивление катушки
Несовпадение по фазе слагаемых в выражении (13.12) затрудняет определение амплитуды и действующей величины приложенного к цепи напряжения U. Поэтому воспользуемся векторным способом сложения синусоидальных величин. Амплитуды составляющих общего напряжения
а действующие величины
Вектор общего напряжения
Для того чтобы найти величину вектора U, построим векторную диаграмму (рис. 13.10, а), предварительно выбрав масштабы тока Мi и напряжения Мu.
За исходный вектор диаграммы принимаем вектор тока I. Направление этого вектора совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза заданного тока ψi = 0). Как и ранее, эту ось удобно (но не обязательно) направить по горизонтали.
Вектор UR по направлению совпадает с вектором тока I, а вектор UL направлен перпендикулярно вектору I с положительным углом.
Из диаграммы видно, что вектор тока I общего напряжения U отражает вектор тока I на угол φ > 0, но <90°, а по величине равен гипотенузе прямоугольного треугольника, катетами которого являются векторы падений напряжения в активном и индуктивном сопротивлениях UR и UL:
Рис. 13.10. Векторная диаграмма цепи, треугольники сопротивлений и мощностей
Проекция вектора напряжения U на направление вектора тока называется активной составляющей вектора напряжения и обозначается Ua. Для катушки по схеме рис. 13.9 при Uа = UR
Проекция вектора напряжения U на направление, перпендикулярное вектору тока, называется реактивной составляющей вектора напряжения и обозначается Uр. Для катушки Up = UL
При токе 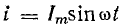
Стороны треугольника напряжений, выраженные в единицах напряжения, разделим на ток I. Получим подобный треугольник сопротивлений (рис. 13.10, б), катетами которого являются активное 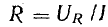
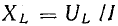
Отношение действующего напряжения к действующему току данной цепи называется полным сопротивлением цепи. Стороны треугольника сопротивлений нельзя считать векторами, так как сопротивления не являются функциями времени.
Из треугольника сопротивлений следует
Понятие о полном сопротивлении цепи Z позволяет выразить связь между действующими величинами напряжения и тока формулой, подобной формуле Ома (2.6):
Из треугольников напряжений и сопротивлений определяются
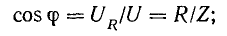
Мощность катушки
Мгновенная мощность катушки
Из графика мгновенной мощности (рис. 13.11) видно, что в течение периода мощность четыре раза меняет знак; следовательно, направление потока энергии и в данном случае в течение периода меняется. Относительно некоторой оси t’, сдвинутой параллельно оси t на величину Р, график мгновенной мощности является синусоидальной функцией двойной частоты.
При положительном значении мощности энергия переходит от источника в приемник, а при отрицательном — наоборот. Нетрудно заметить, что количество энергии, поступившей в приемник (положительная площадь), больше возвращенной обратно (отрицательная площадь).
Рис. 13.11. График мгновенной мощности цепи
Следовательно, в цепи с активным сопротивлением и индуктивностью часть энергии, поступающей от генератора, необратимо превращается в другой вид энергии, но некоторая часть возвращается обратно. Этот процесс повторяется в каждый период тока, поэтому в цепи наряду с непрерывным превращением электрической энергии в другой вид энергии (активная энергия) часть ее совершает колебания между источником и приемником (реактивная энергия).
Скорость необратимого процесса преобразования энергии оценивается средней мощностью за период, или активной мощностью Р, скорость обменного процесса характеризуется реактивной мощностью Q.
На основании выводов, в активном сопротивлении 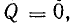
Активная мощность всей цепи равна активной мощности в сопротивлении R, а реактивная — реактивной мощности в индуктивном сопротивлении ХL . Подставляя значения 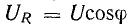
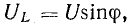
Кроме активной и реактивной мощностей пользуются понятием полной мощности S, которая определяется произведением действующих величин напряжения и тока цепи:
Величину полной мощности можно получить из выражения (13.22), которое легко доказать на основании формул (13.19) и (13.20):
Мощности S, Р, Q графически можно выразить сторонами прямоугольного треугольника (см. рис. 13.10, в). Треугольник мощностей получается из треугольника напряжений, если стороны последнего, выраженные в единицах напряжения, умножить на ток.
Из треугольника мощностей можно определить
Полная мощность имеет ту же размерность, что Р и Q, но для различия единицу полной мощности называют вольт-ампер (В • А).
Активная мощность Р меньше или равна полной мощности цепи. Отношение активной мощности цепи к ее полной мощности 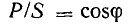
Назначение приемников электрической энергии — преобразование ее в другие виды энергии. Поэтому колебания энергии в цепи не только бесполезны, но и вредны, так как при этом в приемнике не совершается полного преобразования электрической энергии в работу или тепло, а в соединительных проводах она теряется.
Схема замещения катушки с параллельным соединением элементов
Для реальной катушки можно составить и другую расчетную схему — с параллельным соединением двух ветвей: с активной G и индуктивной ВL проводимостями. На рис. 13.12, б эта схема показана в сравнении со схемой последовательного соединения активного и индуктивного сопротивлений (рис. 13.12, а), рассмотренной ранее.
Покажем, что схемы рис. 13.12, а, б эквивалентны в том смысле, что при одинаковом напряжении сохраняются неизменными ток в неразветвленной части цепи, активная и реактивная мощности.
Вектор тока I можно разложить на две взаимно перпендикулярные составляющие и в соответствии со схемой и векторной диаграммой на рис. 13.12, б выразить векторным равенством
Рис. 13.12. Варианты схемы замещения катушки индуктивности
Для схемы параллельного соединения активного и индуктивного элементов общим является приложенное напряжение, а токи разные: IG — ток в ветви с активной проводимостью, по фазе совпадает с напряжением; IL — ток в ветви с индуктивной проводимостью, по фазе отстает от напряжения на угол 90°.
Вектор тока I и его составляющие IG и ILобразуют прямоугольный треугольник, поэтому
Составляющая тока в активном элементе
Проекция вектора тока I на направление напряжения называется активной составляющей вектора тока и обозначается Iа. Для катушки по схеме на рис. 13.12,
Составляющая тока в реактивном элементе
Проекция вектора тока I на направление, перпендикулярное вектору напряжения, называется реактивной составляющей вектора тока и обозначается Iр. Для катушки Iр = IL .
Стороны треугольника токов, выраженные в единицах тока, можно разделить на напряжение U и получить подобный треугольник проводимостей, катетами которого являются активная 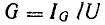
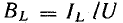
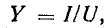
Из треугольника проводимостей и с учетом ранее полученных выражений из треугольника сопротивлений получим
Кроме того,
Задача 13.10.
Для определения параметров катушки R и L ее включили сначала в цепь постоянного тока, а затем в цепь переменного тока с частотой f = 50 Гц по схемам рис. 13.13, а, б.
При постоянном токе I1 = 4 А вольтметр показал U1 = 12 В, а при переменном I2 = 5А — U2 = 25 В. Определить активное сопротивление и индуктивность катушки и при переменном токе активную, реактивную и полную мощности. Построить векторную диаграмму и треугольник сопротивлений.
Решение. При постоянном токе э. д. с. самоиндукции в катушке не возникает. Поэтому индуктивное сопротивление ХL = 0. Ток определяется приложенным напряжением и активным сопротивлением.
По формуле Ома,
При переменном токе отношение напряжения к току даст величину полного сопротивления
Рис. 13.13. к задаче 13.10
Рис. 13.14. К задачам 13.12, 13.13
Индуктивное сопротивление
Индуктивность
При разборе решения данной задачи на отдельном листе миллиметровой бумаги рекомендуется построить векторную диаграмму цепи и треугольники сопротивлений и мощностей, предварительно определив необходимые величины.
Задача 13.12.
В цепи переменного тока с активным сопротивлением и индуктивностью (рис. 13.14) при частоте f = 100 Гц измерительные приборы показывают: амперметр — 10 А, вольтметр — 200 В, ваттметр — 1600 Вт. Определить параметры схем замещения цепи с последовательным (R, XL) и параллельным (G, ВL) соединением элементов; реактивную и полную мощности цепи. Построить векторные диаграммы применительно к обеим схемам замещения.
Решение (для схемы замещения с последовательным соединением элементов).
Сопротивления:
активное
полное
индуктивное
Мощности цепи:
реактивная
полная
Для построения векторной диаграммы дополнительно определим активную и реактивную составляющие напряжения:
Векторная диаграмма показана на рис. 13.10, а.
Цепь с реальным конденсатором
При переменном напряжении на реальном конденсаторе кроме тока смещения имеются небольшие токи проводимости через толщу диэлектрика (объемный ток) и по поверхности (поверхностный ток). Токи проводимости и поляризацию диэлектрика сопровождают потери энергии.
Таким образом, в реальном конденсаторе наряду с изменением энергии электрического поля (это характеризует реактивная мощность Q) из-за несовершенства диэлектрика идет необратимый процесс преобразования электрической энергии в тепло, скорость которого выражается активной мощностью Р. Поэтому в схеме замещения реальный конденсатор должен быть представлен активным и реактивным элементами.
Деление реального конденсатора на два элемента — это расчетный прием, так как конструктивно их выделить нельзя. Однако такую же схему замещения имеет реальная цепь из двух элементов, один из которых характеризуется только активной мощностью Р (Q = 0), другой — реактивной (емкостной) мощностью Q(Р = 0).
Схема замещения конденсатора с параллельным соединением элементов
Реальный конденсатор (с потерями) можно представить эквивалентной схемой параллельного соединения активной G и емкостной Вс проводимостей (рис. 13.15), причем активная проводимость определяется мощностью потерь в конденсаторе 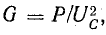
Предположим, что проводимости G и Вс для такой цепи известны, а напряжение имеет уравнение
Требуется определить токи в цепи и мощность.
Исследование цепи с активным сопротивлением и цепи с емкостью показало, что при синусоидальном напряжении токи в них также синусоидальны.
Рис. 13.15. Схема замещения реального конденсатора
При параллельном соединении ветвей G и Вс , согласно первому закону Кирхгофа, общий ток i равен сумме токов в ветвях с активной и емкостной проводимостями:
Учитывая, что ток iG совпадает по фазе с напряжением, а ток ic опережает напряжение на четверть периода, уравнение общего тока можно записать в следующем виде:
Так как
то
Векторная диаграмма токов
Для определения действующей величины общего тока I методом векторного сложения построим векторную диаграмму согласно уравнению
Действующие величины составляющих тока:
Первым на векторной диаграмме изображается вектор напряжения U (рис. 13.16, а), его направление совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза напряжения 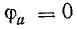
Вектор IG совпадает по направлению с вектором U, а вектор Iс направлен перпендикулярно вектору U с положительным углом.
Из векторной диаграммы видно, что вектор общего напряжения отстает от вектора общего тока на угол φ, величина которого больше нуля, но меньше 90′.
Вектор I является гипотенузой прямоугольного треугольника, катеты которого — составляющие его векторы IG и IC:
Рис. 13.16. Треугольники токов, проводимостей, мощностей
Рис. 13.17. График мгновенной мощности цепи
При напряжении 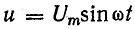
Треугольник проводимостей
Стороны треугольников токов, выраженные в единицах тока, разделим на напряжение U. Получим подобный треугольник проводимостей (рис. 13.16, б), катетами которого являются активная 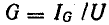
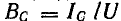
Из треугольника проводимостей
Связь между действующими величинами напряжения и тока выражается формулами
Из треугольников токов и проводимостей определяют величины
Мощность
Выражение мгновенной мощности реального конденсатора
совпадает с выражением мгновенной мощности катушки.
Рассуждения, аналогичные тем, которые сделаны при рассмотрении графика мгновенной мощности катушки (см. рис.13. 11), можно провести и для реального конденсатора на основе графика рис. 13.17.
Величины активной, реактивной и полной мощностей выражаются теми же формулами, какие были получены для катушки [см. (13.19)— (13.22)].
Это нетрудно показать, если стороны треугольника токов, выраженные в единицах тока, умножить на напряжение U.
В результате умножения получится подобный треугольник мощностей (рис. 13.16, в), катетами которого являются мощности:
активная
реактивная
полная
Схема замещения конденсатора с последовательным соединением элементов
Реальный конденсатор, так же как и катушка, на расчетной схеме может быть представлен последовательным соединением двух участков: с активным R и емкостным Хс сопротивлениями.
На рис. 13.18, а такая схема показана в сравнении со схемой параллельного соединения активной и емкостной проводимостей (рис.13.18, б). Все выводы и формулы, полученные для катушки, остаются в силе и для конденсатора при условии замены индуктивного сопротивления емкостным.
Рис. 13.18. Варианты схемы замещения реального конденсатора
Конденсаторы, применяемые на практике, имеют относительно малые потери энергии. Поэтому в схемах замещения они представлены чаще всего только реактивной частью, т. е. емкостью
Участки цепи, где последовательно соединены отдельные элементы — резистор R и конденсатор С, имеют такую схему замещения, как показано на рис. 13.18, а.
Задача 13.13.
В цепи переменного тока с активным сопротивлением и емкостью (см. рис. 13.14) при частоте f = 100 Гц измерительные приборы показывают. амперметр — 6 А, вольтметр — 180 В, ваттметр — 360 Вт. Определите параметры схем замещения цепи с параллельным (G, ВL) и последовательным (R, ХC) соединением элементов: реактивную и полную мощности цепи. Постройте векторные диаграммы применительно к обеим схемам замещения.
Решение (для схемы замещения с параллельным соединением элементов). Проводимости:
активная
полная
емкостная
Мощности цепи
реактивная
полная
Для построения векторной диаграммы дополнительно определим активную и реактивную составляющие тока:
Векторная диаграмма показана на рис. 13.16, а.
Решить задачу для схемы с последовательным соединением элементов.
Расчет электрических цепей переменного тока с помощью векторных диаграмм
В данной главе будут рассмотрены электрические цепи переменного тока, содержащие три параметра R, L, С при последовательном, параллельном соединении резисторов, катушек и конденсаторов.
Расчет таких цепей можно вести на основе векторных диаграмм, из которых получаются расчетные формулы.
Последовательное соединение катушки и конденсатора
При последовательном соединении катушки и конденсатора на расчетной схеме каждый из этих элементов электрической цепи может быть представлен активным и реактивным сопротивлениями или активной и реактивной проводимостями.
Для расчета более простой является схема рис. 14.1, а, где элементы соединены последовательно, а в схеме рис. 14.1, б они соединены смешанно.
Рис. 14.1. Схемы замещения катушки и конденсатора при последовательном соединении
Предположим известными параметры катушки R1, L и конденсатора R2С; ток в цепи
Требуется определить напряжение на участках цепи и мощность.
Векторная диаграмма и полное сопротивление цепи
Мгновенную величину общего напряжения можно представить суммой мгновенных напряжений на отдельных элементах схемы:
Имея в виду несовпадение по фазе активных и реактивных напряжений, общее напряжение получим векторным сложением:
Для построения векторной диаграммы находим:
В зависимости от соотношения величин реактивных сопротивлений индуктивности и емкости можно отметить три случая.
1. 
Векторная сумма напряжений 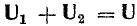
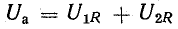
Рис. 14.2. Векторная диаграмма при ХL > ХC
Рис. 14.3. Векторная диаграмма при ХL < X
Векторы реактивных составляющих напряжения направлены по одной прямой в противоположные стороны, поэтому им придают разные знаки: реактивное напряжение индуктивности считают положительным, а напряжение емкости — отрицательным:
При одинаковом токе во всех элементах цепи 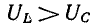
или
где 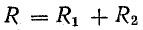
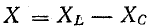
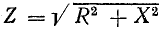
Эти сопротивления графически можно изобразить сторонами прямоугольного треугольника сопротивлений, который получают уже известным способом из треугольника напряжений.
Полное сопротивление цепи Z является коэффициентом пропорциональности между действующими величинами тока и общего напряжения цепи:
Из треугольников напряжения и сопротивлений определяют следующие величины:
Угол сдвига по фазе между напряжением и током в цепи положительный (φ > 0) (фазовые углы отсчитываются от вектора тока).
2. 
Реактивное сопротивление цепи носит емкостный характер. Расчетные формулы для первого случая остаются без изменения и для второго случая.
Рис. 14.4. Векторная диаграмма при XL = XC
3. 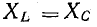
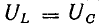
Угол φ сдвига фаз между током и общим напряжением равен нулю.
Ток в цепи и общее напряжение связаны формулой
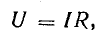
В случае ХL = ХC в цепи имеет место явление резонанса напряжений.
Энергетический процесс в цепи
Из треугольника напряжений легко получить треугольник мощностей, из которого следуют уже известные формулы:
Реактивные мощности входят в расчеты также с разными знаками: индуктивная мощность положительна, а емкостная — отрицательна.
В соответствии с этим знак реактивной мощности всей цепи может быть тем или другим, что следует и из формул (14.2).
При φ > 0 Q > 0; при φ < 0 Q < 0.
Активная мощность положительна при любом угле, так как
Полная мощность также всегда положительна.
На основании формул (14.2) можно сделать вывод, что в рассматриваемой цепи совершается преобразование электрической энергии 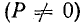
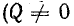
14.5. Графики u, i, p при XL = XC
Энергетические процессы в данном случае сложнее, чем в ранее рассмотренных простых цепях. Усложнение объясняется тем, что наряду с обменом энергией между генератором и приемником совершается обмен энергией внутри приемника, между катушкой и конденсатором.
Особенности энергетического процесса в цепи с последовательным соединением катушки и конденсаторов отражены на рис. 14.5, где показаны графики мгновенной мощности отдельных элементов и цепи в целом при
Катушка и конденсатор в течение полупериода накапливают равные количества энергии. Однако в первую четверть периода, когда ток увеличивается, а напряжение на конденсаторе уменьшается, энергия накапливается в магнитном поле катушки и уменьшается в электрическом поле конденсатора, причем скорость изменения энергии (мощность) в любой момент времени одинакова. Это дает основание считать, что обмен энергией происходит только в приемнике между катушками и конденсатором.
Для преобразования электрической энергии в другой вид приемник получает ее от генератора со средней скоростью (мощностью) Р.
Задача 14.1.
Конденсатор емкостью С = 3,4 мкФ и катушка с активным сопротивлением R = 50 Ом и индуктивностью L = 29,8 мГн подключены последовательно к генератору с напряжением U = 200 В (рис. 14.6). Определить ток, активную, реактивную и полную мощности катушки, конденсатора и всей цепи при неизменном напряжении генератора и трех значениях частоты: 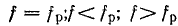
Решение. Для примера далее приведен расчет при частоте f = 250 Гц.
Реактивное сопротивление индуктивности
Рис. 14.6. К задаче 14.1
Реактивное сопротивление емкости
Полное сопротивление
Ток в цепи
Угол сдвига фаз между током и напряжением
Активная мощность
Реактивная мощность индуктивности
Реактивная мощность емкости
Реактивная мощность цепи
Сделать аналогичный подсчет для частот: f = fр; f < fр; f > fр.
Расчет неразветвленных цепей переменного тока
Порядок расчета, установленный для цепи при последовательном соединении катушки и конденсатора, можно применить и для цепи, содержащей произвольное число катушек и конденсаторов, соединенных последовательно.
На рис. 14.7, а для примера дана схема неразветвленной цепи, состоящей из пяти участков: конденсатора (R1, Х1) и катушки (R2, Х2), представленных активными и реактивными сопротивлениями; резистора R3; идеальных конденсатора Х4 и катушки Х5.
Рис. 14.7. Расчетная схема неразветвленной цепи и ее векторная диаграмма
Предположим, что кроме сопротивлений известен ток в цепи i = Imsinωt.
Требуется найти напряжения на участках, общее напряжение в цепи и мощность.
Векторная диаграмма
Выберем условно-положительное направление тока i, как указано на схеме. Для мгновенных величин в соответствии со вторым законом Кирхгофа уравнение напряжений
Переходя к действующим величинам напряжений, нужно написать векторную сумму:
Численно векторы напряжений определяются произведением тока и сопротивления соответствующего участка.
На рис. 14.7, б построена векторная диаграмма, соответствующая этому уравнению. За исходный, как обычно при расчете неразветвленных цепей, принят вектор тока, а затем проведены векторы падения напряжения на каждом участке схемы, причем направления их относительно вектора тока выбраны в соответствии с характером сопротивления участков.
При построении диаграммы напряжений начальной точкой выбрана точка 6, совпадающая с началом вектора тока I. Из этой точки проведен вектор U5р реактивного напряжения индуктивности (по фазе опережает ток на 90°) между точками 5 и 6 цепи. Из конца его проведен вектор U4р реактивного напряжения емкости (по фазе отстает от тока на 90°) между точками 4 и 5 цепи. Затем отложен вектор U3a активного напряжения на резисторе (совпадает по фазе с током) между точками 3 и 4 цепи и т. д., если следовать по цепи против направления тока. Точки векторной диаграммы, где сходятся начало следующего вектора с концом предыдущего, обозначены теми же номерами, какими на схеме обозначены точки, отделяющие один элемент от другого.
При таком, построении напряжение между любыми двумя точками цепи можно найти по величине и фазе, проведя вектор на диаграмме между точками с теми же номерами. Например, напряжение U5.2 между точками 5 и 2 выражается вектором, проведенным из точки 2 в точку 5 (вектор U5.2 направлен в обратную сторону); напряжение U3.1 между точками 3 и 1 выражается вектором, проведенным из точки 1 в точку 3.
Векторная диаграмма, построенная в соответствии с чередованием элементов цепи, называется топографической, так как точки, отделяющие векторы друг от друга, соответствуют точкам, разделяющим элементы схемы.
Расчетные формулы
Из векторной диаграммы видно, что все активные составляющие векторов напряжений направлены одинаково — параллельно вектору тока, поэтому векторное сложение их можно заменить арифметическим и найти активную составляющую напряжения цепи:
Реактивные составляющие векторов напряжений перпендикулярны вектору тока, причем индуктивные напряжения направлены в одну сторону, а емкостные — в другую. Поэтому реактивная составляющая напряжения цепи Uр определяется их алгебраической суммой, в которой индуктивные напряжения считаются положительными, а емкостные — отрицательными:
Векторы активного, реактивного и полного напряжений цепи образуют прямоугольный треугольник, из которого следует
Подставив падения напряжения, выраженные через ток и соответствующие сопротивления, получим:
Таким образом снова получена знакомая уже формула, связывающая ток, напряжение и полное сопротивление цепи [ср. (14.4) и (14.1)].
В этой формуле 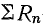
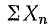
В общем случае полное сопротивление цепи определяется как гипотенуза прямоугольного треугольника, катетами которого являются выраженные в определенном масштабе активное и реактивное сопротивления всей цепи. Из треугольника сопротивлений следует:
От треугольника напряжений можно перейти также к треугольнику мощностей и получить уже известные формулы для определения мощностей в цепи:
Вместе с тем активную мощность цепи можно представить как арифметическую сумму активных мощностей в элементах с активным сопротивлением. Реактивная мощность цепи равна алгебраической сумме мощностей реактивных элементов.
В этой сумме мощность индуктивных элементов считается положительной, а емкостных — отрицательной:
Формулы (14.2)—(14.7) являются общими; из них можно получить конкретное выражение для любой неразветвленной цепи.
Задача 14.3.
Определить ток и составить баланс мощностей для цепи, схема которой изображена на рис. 14.8. Построить топографическую диаграмму и по ней определить напряжение U8.5 между точками 8 и 5 и U6.1 между точками 6 и 1.
Дано:
Рис. 14.8. К задаче 14.3
Решение. Согласно второму закону Кирхгофа, составим уравнение напряжений в векторной форме, предварительно выбрав условно-положительные направления э. д. с. и тока в схеме (их целесообразно выбрать одинаковыми независимо от того, в каком режиме работает источник э. д. с., так как фазовый угол сдвига, полученный в результате расчета, укажет истинный режим его работы):
или
Общее активное сопротивление
Общее реактивное сопротивление
Как видно, общее реактивное сопротивление имеет емкостный характер. Полное сопротивление цепи
Действующие величины э. д. с.:
Для определения действующей величины суммы двух э. д. с. ( Е1 + Е2) построим векторную диаграмму (рис. 14.9, а) (рекомендуется построить на отдельном листе миллиметровой бумаги в масштабе Ми = 40 В/см).
Измерение вектора Е показывает, что величина суммарной э. д. с. Е = 200 В. Э. д. с. можно найти, учитывая, что ее составляющие взаимно перпендикулярны. В этом случае
Ток
Напряжения на отдельных участках схемы:
Для построения векторной топографической диаграммы (рис. 14.9, б) выберите масштабы Мi = 2 А/см; Ми = 40 В/см (рекомендуется построить на отдельном листе миллиметровой бумаги).
Рис. 14.9. К задаче 14.3
По векторной диаграмме найдены углы сдвига фаз между током и э. д. с. Е1 и Е2: φ1 = –90°, φ2 = 0.
Мощности участков приемника:
Мощности источников:
Баланс мощностей:
1280 = 192 + 576 + 512 = 1280;
— 960 = — 640— 960 + 384 + 256 = — 960.
Реактивные мощности емкостного характера Q2С, Q1С и Q1E и отрицательны, так как между векторами напряжений и токов, определяющими их, углы отрицательны.
Для определения напряжений U8.5 и U6.1, проведем векторы между соответствующими точками топографической диаграммы. Вектор направляется к точке, стоящей первой в обозначении напряжения. Например, вектор U8.5 направлен в точку 8 из точки 5. Измерение векторов U8.5 и U6.1 дает:
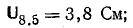
Параллельное соединение катушки и конденсатора
Для рассмотрения параллельного соединения катушки и конденсатора представим их на схеме активными и реактивными проводимостями (рис. 14.11, а).
Рис. 14.11. Схемы замещения катушки и конденсатора при параллельном соединении
На схеме рис. 14.11, б те же катушки и конденсатор представлены активными и реактивными сопротивлениями. Первая схема имеет некоторое преимущество, так как в ней все элементы соединены параллельно, а в другой они соединены смешанно.
Считая известными параметры катушки G1, ВL и конденсатора G2, Вс, а также напряжение 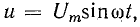
Векторная диаграмма цепи. Полная проводимость цепи
Согласно первому закону Кирхгофа, мгновенная величина общего тока равна сумме мгновенных токов отдельных ветвей:
Имея в виду несовпадение по фазе активных и реактивных токов, величину общего тока найдем векторным сложением:
Для построения векторной диаграммы находим:
В зависимости от соотношения величин реактивных проводимостей ветвей с индуктивностью и емкостью можно отметить три случая.
Рис. 14.12. Векторные диаграммы:
1. 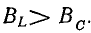
Векторная сумма токов 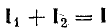
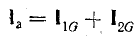
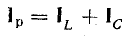
Векторы активных составляющих токов направлены в одну сторону, поэтому их численные значения складываются. Векторы реактивных составляющих токов направлены перпендикулярно вектору напряжения в противоположные стороны, поэтому им даются разные знаки: индуктивные токи считаются положительными, а емкостные — отрицательными. При одинаковом напряжении на всех элементах цепи 
или
где 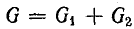
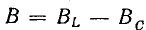
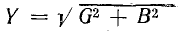
Эти три проводимости графически можно изобразить сторонами прямоугольного треугольника проводимостей, который получается уже известным способом из треугольника токов.
Полная проводимость цепи У является коэффициентом пропорциональности между действующими величинами общего тока и напряжения цепи:
Из треугольников токов и проводимостей определяются величины:
Угол сдвига по фазе между напряжением и общим током в цепи положительный (φ > 0) (фазовые углы отсчитываются от вектора тока).
2. 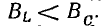
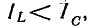
Реактивная проводимость цепи имеет емкостный характер. Расчетные формулы, полученные для случая 1, действительны и для этого случая.
3. 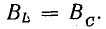

Общий ток в цепи и напряжение связаны формулой
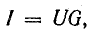
В случае 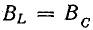
Энергетический процесс в цепи
Из векторной диаграммы токов легко получить треугольник мощностей, из которого следуют те же формулы (14.2), которые были получены для последовательного соединения катушки и конденсатора.
Реактивные мощности индуктивности и емкости входят в расчет с разными знаками: реактивная мощность индуктивности положительна, а реактивная мощность емкости отрицательна. В соответствии с этим знак реактивной мощности всей цепи может быть тем или другим, что следует из формул (14.2).
Если φ > 0, то Q > 0; при φ < 0 Q < 0.
Активная мощность положительна при любом значении угла. Полная мощность тоже всегда положительна.
В рассматриваемой цепи активная мощность имеет определенную величину 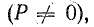
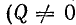
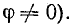
Задача 14.5.
В цепи, схема которой изображена на рис. 14.13, определить ток, активную, реактивную и полную мощность катушки, конденсатора и всей цепи при неизменном напряжении U = 200 В и частоте источника f = 100 Гц. Параметры цепи: R1 = 10 Ом, L = 55,2 мГн, С = 138 мкФ, R2 = 0.
Рис. 14.13. К задаче 14.5
Решение. При частоте f = 100 Гц индуктивное сопротивление первой ветви
Проводимости:
активная
реактивная
Полная проводимость катушки
Проводимости второй ветви:
активная
реактивная
Полная проводимость цепи
Токи:
в неразветвленной части цепи
в конденсаторе
в катушке
Коэффициент мощности цепи
Реактивные мощности:
катушки
конденсатора
цепи
Активная мощность цепи
Полные мощности:
катушки
конденсатора
цепи
Задача 14.6.
Для схемы рис. 14.13 по данным условия задачи 14.5 найти резонансную частоту fр. Выполнить расчет цепи в порядке, изложенном при решении задачи 14.4, для двух значений частоты источника:
Решение. При резонансе 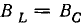
Решая относительно резонансной частоты, можно получить формулу
Учитывая, что R2 = 0, и подставляя другие данные, получим:
Далее расчет цепи по условию задачи выполните самостоятельно.
Расчет цепей с параллельным соединением ветвей
Расчет электрической цепи, рассмотренный в предыдущем параграфе, можно распространить на цепи, содержащие произвольное число приемников, соединенных параллельно.
Рис. 14.14. Расчетная схема разветвленной цепи с двумя узлами и ее векторная диаграмма
На рис. 14.14, а параллельно соединены те же элементы цепи, были рассмотрены при последовательном соединении (см. рис. 14.7, а). Предположим, что для этой цепи известны напряжение 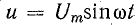
Векторная диаграмма
Для мгновенных величин в соответствии с первым законом Кирхгофа уравнение токов
Представляя ток в каждой ветви суммой активной и реактивной составляющих, получим
Для действующих токов нужно написать векторное уравнение
Численные значения векторов токов определяются произведением напряжения и проводимости соответствующей ветви.
На рис. 14.14, б построена векторная диаграмма, соответствующая этому уравнению. За исходный вектор принят, как обычно при расчете цепей с параллельным соединением ветвей, вектор напряжения U, а затем нанесены векторы тока в каждой ветви, причем направления их относительно вектора напряжения выбраны в соответствии с характером проводимости ветвей. Начальной точкой при построении диаграммы токов выбрана точка, совпадающая с началом вектора напряжения . Из этой точки проведен вектор I1а активного тока ветви I-I (по фазе совпадает с напряжением), а из конца его проведен вектор I1p реактивного тока той же ветви (опережает напряжение на 90°). Эти два вектора являются составляющими вектора I1 тока первой ветви. Далее в том же порядке отложены векторы токов других ветвей. Следует обратить внимание на то, что проводимость ветви 3-3 активная, поэтому реактивная составляющая тока в этой ветви равна нулю. В ветвях 4-4 и 5-5 проводимости реактивные, поэтому в составе этих токов нет активных составляющих.
Расчетные формулы
Из векторной диаграммы видно, что все активные составляющие векторов тока направлены одинаково — параллельно вектору напряжения, поэтому векторное сложение их можно заменить арифметическими найти активную составляющую общего тока:
Реактивные составляющие векторов токов перпендикулярны вектору напряжения, причем индуктивные токи направлены в одну сторону, а емкостные — в другую. Поэтому реактивная составляющая общего тока в цепи определяется их алгебраической суммой, в которой индуктивные токи считаются положительными, а емкостные — отрицательными:
Векторы активного, реактивного и полного тока всей цепи образуют прямоугольный треугольник, из которого следует
Подставив величины токов в ветвях, выраженные через напряжение и соответствующие проводимости, получим
где 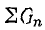
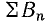
Таким образом получена знакомая уже формула (14.12), связывающая напряжение, ток и проводимость цепи [ср. (14.12) и (14.8)].
Следует обратить внимание на возможные ошибки при определении полной проводимости цепи по известным проводимостям отдельных ветвей: нельзя складывать арифметически проводимости ветвей, если токи в них не совпадают по фазе.
Полную проводимость цепи в общем случае определяют как гипотенузу прямоугольного треугольника, катетами которого являются выраженные в определенном масштабе активная и реактивная проводимости всей цепи:
От треугольника токов можно перейти также к треугольнику мощностей и для определения мощности получить известные уже формулы
Активную мощность цепи можно представить как арифметическую сумму активных мощностей ветвей.
Реактивная мощность цепи равна алгебраической сумме мощностей ветвей. В этом случае индуктивная мощность берется положительной, а емкостная — отрицательной:
Расчет цепи без определения проводимостей ветвей
Расчет электрической цепи при параллельном соединении ветвей можно выполнить без предварительного определения активных и реактивных проводимостей, т. е. представляя элементы цепи в схеме замещения их активными и реактивными сопротивлениями (рис. 14.15, а).
Определяют токи в ветвях по формуле (14.4):
где Z1, Z2 и т. д. — полные сопротивления ветвей.
Полное сопротивление ветви, в которую входят несколько элементов, соединенных последовательно, определяют по формуле (14.5).
Рис. 14.15. Схема электрической цепи и ее векторная диаграмма
Для построения векторной диаграммы токов (рис. 14.15, б) можно определить активную и реактивную составляющие тока каждой ветви по формулам
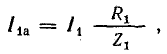
и т. д. для всех ветрей.
В этом случае отпадает необходимость определения углов φ1, φ2 и построения их на чертеже.
Ток в неразветвленной части цепи
Общий ток и мощность цепи определяются далее в том же порядке, какой был показан ранее [см. формулы (14.10), (14.15), (14.16)].
Задача 14.7.
Определить ток в неразветвленной части цепи (рис. 14.16, а), активную, реактивную и полную мощности всей цепи. Построить векторную диаграмму токов и напряжений. Дано: R1 = 6 Ом, L1 = 25,5 мГн, R2 = 20 Ом, R2 = 15 Ом; L3 = 47,9 мГн, С3 = 159 мкФ, и
Решение. Реактивные сопротивления ветвей:
Полные сопротивления ветвей:
Рис. 14.16. к задаче 14.7
Действующее, напряжение
Токи в ветвях:
Составляющие токов ветвей:
активные
реактивные
Общий ток:
активный
реактивный
в неразветвленной части цепи
Активные мощности:
ветвей
всей цепи
Реактивные мощности:
ветвей
всей цепи
Полная мощность цепи
Проверка правильности подсчета мощности:
Для построения векторной диаграммы дополнительно определим активные и реактивные напряжения ветвей:
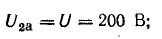
Векторная диаграмма показана на рис. 14.16, б.
- Символический метод расчета цепей
- Четырехполюсники
- Линейные диаграммы
- Круговые диаграммы
- Энергия в электрических цепях
- Линейные электрические цепи
- Нелинейные электрические цепи
- Магнитные цепи и их расчёт
-
Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.
-
Условие квазистационарности
-
Резистор в цепи переменного тока
-
Конденсатор в цепи переменного тока
-
Катушка в цепи переменного тока
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.
Переменный ток — это вынужденные электромагнитные колебания, вызываемые в электрической цепи источником переменного (чаще всего синусоидального) напряжения.
Переменный ток присутствует всюду. Он течёт по проводам наших квартир, в промышленных электросетях, в высоковольтных линиях электропередач. И если вам нужен постоянный ток, чтобы зарядить аккумулятор телефона или ноутбука, вы используете специальный адаптер, выпрямляющий переменный ток из розетки.
Почему переменный ток распространён так широко? Оказывается, он прост в получении и идеально приспособлен для передачи электроэнергии на большие расстояния. Подробнее об этом мы поговорим в листке, посвящённом производству, передаче и потреблению электрической энергии.
А сейчас мы рассмотрим простейшие цепи переменного тока. Будем подключать к источнику переменного напряжения поочерёдно: резистор сопротивлением , конденсатор ёмкости
и катушку индуктивности
. Изучив поведение этих элементов, мы в следующем листке «Переменный ток. 2» подключим их одновременно и исследуем прохождение переменного тока через колебательный контур, обладающий сопротивлением.
Напряжение на клеммах источника меняется по закону:
(1)
Как видим, напряжение может быть положительным и отрицательным. Каков смысл знака напряжения?
Всегда подразумевается, что выбрано положительное направление обхода контура. Напряжение считается положительным, если электрическое поле зарядов, образующих ток, имеет положительное направление. В противном случае напряжение считается отрицательным.
Начальная фаза напряжения не играет никакой роли, поскольку мы рассматриваем процессы, установившиеся во времени. При желании вместо синуса в выражении (1) можно было бы взять косинус — принципиально от этого ничего не изменится.
Текущее значение напряжения в момент времени
называется мгновенным значением напряжения.
к оглавлению ▴
Условие квазистационарности
В случае переменного тока возникает один тонкий момент. Предположим, что цепь состоит из нескольких последовательно соединённых элементов.
Если напряжение источника меняется по синусоидальному закону, то сила тока не успевает мгновенно принимать одно и то же значение во всей цепи — на передачу взаимодействий между заряженными частицами вдоль цепи требуется некоторое время.
Между тем, как и в случае постоянного тока, нам хотелось бы считать силу тока одинаковой во всех элементах цепи. К счастью, во многих практически важных случаях мы действительно имеем на это право.
Возьмём, к примеру, переменное напряжение частоты Гц (это промышленный стандарт России и многих других стран). Период колебаний напряжения:
с.
Взаимодействие между зарядами передаётся со скоростью света: м/с. За время, равное периоду колебаний, это взаимодействие распространится на расстояние:
м
км.
Поэтому в тех случаях, когда длина цепи на несколько порядков меньше данного расстояния, мы можем пренебречь временем распространения взаимодействия и считать, что сила тока мгновенно принимает одно и то же значение во всей цепи.
Теперь рассмотрим общий случай, когда напряжение колеблется с циклической частотой . Период колебаний равен
, и за это время взаимодействие между зарядами передаётся на расстояние
. Пусть
— длина цепи. Мы можем пренебречь временем распространения взаимодействия, если
много меньше
:
(2)
Неравенство (2) называется условием квазистационарности. При выполнении этого условия можно считать, что сила тока в цепи мгновенно принимает одно и то же значение во всей цепи. Такой ток называется квазистационарным.
В дальнейшем мы подразумеваем, что переменный ток меняется достаточно медленно и его можно считать квазистационарным. Поэтому сила тока во всех последовательно включённых элементах цепи будет принимать одинаковое значение — своё в каждый момент времени. Оно называется мгновенным значением силы тока.
к оглавлению ▴
Резистор в цепи переменного тока
Простейшая цепь переменного тока получится, если к источнику переменного напряжения подключить обычный резистор (мы полагаем, разумеется, что индуктивность этого резистора пренебрежимо мала, так что эффект самоиндукции можно не принимать во внимание)
, называемый также активным сопротивлением (рис. 1)
Рис. 1. Резистор в цепи переменного тока
Положительное направление обхода цепи выбираем против часовой стрелки, как показано на рисунке. Напомним, что сила тока считается положительной, если ток течёт в положительном направлении; в противном случае сила тока отрицательна.
Оказывается, мгновенные значения силы тока и напряжения связаны формулой, аналогичной закону Ома для постоянного тока:
Таким образом, сила тока в резисторе также меняется по закону синуса:
Амплитуда тока равна отношению амплитуды напряжения
к сопротивлению
:
Мы видим, что сила тока через резистор и напряжение на нём меняются «синхронно», точнее говоря — синфазно (рис. 2).
Рис. 2. Ток через резистор совпадает по фазе с напряжением
Фаза тока равна фазе напряжения, то есть сдвиг фаз между током и напряжением равен нулю.
к оглавлению ▴
Конденсатор в цепи переменного тока
Постоянный ток через конденсатор не течёт — для постоянного тока конденсатор является разрывом цепи. Однако переменному току конденсатор не помеха! Протекание переменного тока через конденсатор обеспечивается периодическим изменением заряда на его пластинах.
Рассмотрим конденсатор ёмкости , подключённый к источнику синусоидального напряжения (рис. 3). Активное сопротивление проводов, как всегда, считаем равным нулю. Положительное направление обхода цепи снова выбираем против часовой стрелки.
Рис. 3. Конденсатор в цепи переменного тока
Как и ранее, обозначим через заряд той пластины конденсатора, на которую течёт положительный ток — в данном случае это будет правая пластина. Тогда знак величины
совпадает со знаком напряжения
. Кроме того, как мы помним из предыдущего листка, при таком согласовании знака заряда и направления тока будет выполнено равенство
.
Напряжение на конденсаторе равно напряжению источника:
Отсюда
Дифференцируя это равенство по времени, находим силу тока через конденсатор:
(3)
Графики тока и напряжения представлены на рис. 4. Мы видим, что сила тока каждый раз достигает максимума на четверть периода раньше, чем напряжение. Это означает, что фаза силы тока на больше фазы напряжения (ток опережает по фазе напряжение на
).
Рис. 4. Ток через конденсатор опережает по фазе напряжение на
Найти сдвиг фаз между током и напряжением можно также с помощью формулы приведения:
Используя её, получим из (3):
И теперь мы чётко видим, что фаза тока больше фазы напряжения на .
Для амплитуды силы тока имеем:
Таким образом, амплитуда силы тока связана с амплитудой напряжения соотношением, аналогичным закону Ома:
где
Величина называется ёмкостным сопротивлением конденсатора. Чем больше ёмкостное сопротивление конденсатора, тем меньше амплитуда тока, протекающего через него, и наоборот.
Ёмкостное сопротивление обратно пропорционально циклической частоте колебаний напряжения (тока) и ёмкости конденсатора. Попробуем понять физическую причину такой зависимости.
1. Чем больше частота колебаний (при фиксированной ёмкости ), тем за меньшее время по цепи проходит заряд
; тем больше амплитуда силы тока и тем меньше ёмкостное сопротивление. При
ёмкостное сопротивление стремится к нулю:
. Это означает, что для тока высокой частоты конденсатор фактически является коротким замыканием цепи.
Наоборот, при уменьшении частоты ёмкостное сопротивление увеличивается, и при имеем
. Это неудивительно: случай
отвечает постоянному току, а конденсатор для постоянного тока представляет собой бесконечное сопротивление (разрыв цепи).
2. Чем больше ёмкость конденсатора (при фиксированной частоте), тем больший заряд проходит по цепи за то же время (за ту же четверть периода); тем больше амплитуда силы тока и тем меньше ёмкостное сопротивление.
Подчеркнём, что, в отличие от ситуации с резистором, мгновенные значения тока и напряжения в одни и те же моменты времени уже не будут удовлетворять соотношению, аналогичному закону Ома. Причина заключается в сдвиге фаз: напряжение меняется по закону синуса, а сила тока — по закону косинуса; эти функции не пропорциональны друг другу. Законом Ома связаны лишь амплитудные значения тока и напряжения.
к оглавлению ▴
Катушка в цепи переменного тока
Теперь подключим к нашему источнику переменного напряжения катушку индуктивности (рис. 5). Активное сопротивление катушки считается равным нулю.
Рис. 5. Катушка в цепи переменного тока
Казалось бы, при нулевом активном (или, как ещё говорят, омическом) сопротивлении через катушку должен потечь бесконечный ток. Однако катушка оказывает переменному току сопротивление иного рода.
Магнитное поле тока, меняющееся во времени, порождает в катушке вихревое электрическое поле , которое, оказывается, в точности уравновешивает кулоновское поле
движущихся зарядов:
(4)
Работа кулоновского поля по перемещению единичного положительного заряда по внешней цепи в положительном направлении — это как раз напряжение
. Аналогичная работа вихревого поля — это ЭДС индукции
.
Поэтому из (4) получаем:
(5)
Равенство (5) можно объяснить и с энергетической точки зрения. Допустим, что оно не выполняется. Тогда при перемещении заряда по цепи совершается ненулевая работа, которая должна превращаться в тепло. Но тепловая мощность равна нулю при нулевом омическом сопротивлении цепи. Возникшее противоречие показывает, что равенство (5) обязано выполняться.
Вспоминая закон Фарадея , переписываем соотношение (5):
откуда
(6)
Остаётся выяснить, какую функцию, меняющуюся по гармоническому закону, надо продифференцировать, чтобы получить правую часть выражения (6). Сообразить это нетрудно (продифференцируйте и проверьте!):
(7)
Мы получили выражение для силы тока через катушку. Графики тока и напряжения представлены на рис. 6.
Рис. 6. Ток через катушку отстаёт по фазе от напряжения на
Как видим, сила тока достигает каждого своего максимума на четверть периода позже, чем напряжение. Это означает, что сила тока отстаёт по фазе от напряжения на .
Определить сдвиг фаз можно и с помощью формулы приведения:
Получаем:
Непосредственно видим, что фаза силы тока меньше фазы напряжения на .
Амплитуда силы тока через катушку равна:
Это можно записать в виде, аналогичном закону Ома:
где
Величина называется индуктивным сопротивлением катушки. Это и есть то самое сопротивление, которое наша катушка оказывает переменному току (при нулевом омическом сопротивлении).
Индуктивное сопротивление катушки пропорционально её индуктивности и частоте колебаний. Обсудим физический смысл этой зависимости.
1. Чем больше индуктивность катушки, тем большая в ней возникает ЭДС индукции, противодействующая нарастанию тока; тем меньшего амплитудного значения достигнет сила тока. Это и означает, что будет больше.
2. Чем больше частота, тем быстрее меняется ток, тем больше скорость изменения магнитного поля в катушке, и тем большая возникает в ней ЭДС индукции, препятствующая возрастанию тока. При имеем
, т. е. высокочастотный ток практически не проходит через катушку.
Наоборот, при имеем
. Для постоянного тока катушка является коротким замыканием цепи.
И снова мы видим, что закону Ома подчиняются лишь амплитудные, но не мгновенные значения тока и напряжения. Причина та же — наличие сдвига фаз.
Резистор, конденсатор и катушка, рассмотренные пока что по отдельности, теперь соберутся вместе в колебательный контур, подключённый к источнику переменного напряжения. Читайте следующий листок — «Переменный ток. 2».
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Переменный ток. 1» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023