Начало лекции 28 ЭДС источника. Соединения проводников и источников.
Проводники в электрических цепях тоже могут соединяться последовательно и параллельно.
1. При последовательном соединении проводников
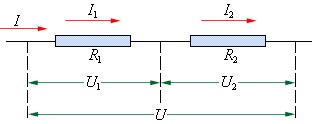
1. Сила тока во всех проводниках одинакова:
I1 = I2 = I
2. Общее напряжение U на обоих проводниках равно сумме напряжений U1 и U2 на каждом проводнике:
U = U1 + U2
3. По закону Ома, напряжения U1 и U2 на проводниках равны U1 = IR1, U2 = IR2 а общее напряжение U = IR где R – электрическое сопротивление всей цепи, тогда IR = IR1 + IR2.Отсюда следует
R = R1 + R2
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
2. При параллельном соединении проводников
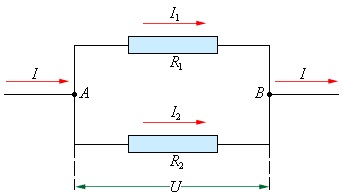
1. Напряжения U1 и U2 на обоих проводниках одинаковы
U1 = U2 = U
2. Сумма токов I1 + I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
I = I1 + I2
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt + I2Δt. Следовательно, I = I1 + I2.
3. Записывая на основании закона Ома
![]()
![]()
![]()
где R – электрическое сопротивление всей цепи, получим
![]() или
или ![]()
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
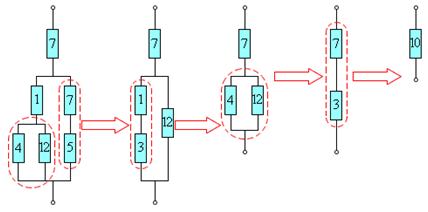
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рисунке приведен пример такой сложной цепи и указана последовательность вычислений. Сопротивления всех проводников указаны в омах (Ом).
На пракутике одного источника тока в цепи бывает недостаточно, и тогда источники тока тоже соединяют между собой для питания цепи. Соединение источников в батарею может быть последовательным и параллельным.
При последовательном соединении два соседних источника соединяются разноименными полюсами.
Т.е., для последовательного соединения аккумуляторов, к ″плюсу″ электрической схемы подключают положительную клемму первого аккумулятора. К его отрицательной клемме подключают положительную клемму второго аккумулятора и т.д. Отрицательную клемму последнего аккумулятора подключают к ″минусу″ электрической схемы.
Получившаяся при последовательном соединении аккумуляторная батарея имеет ту же емкость, что и у одиночного аккумулятора, а напряжение такой аккумуляторной батареи равно сумме напряжений входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые напряжения, то напряжение батареи равно напряжению одного аккумулятора, умноженному на количество аккумуляторов в аккумуляторной батарее.
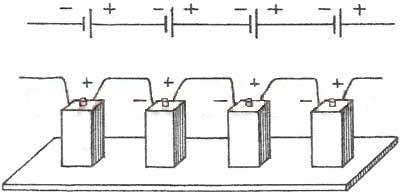
1. ЭДС батареи равна сумме ЭДС отдельных источников ε= ε1 + ε2 + ε3
2. Общее сопротивление батареи источников равно сумме внутренних сопротивлений отдельных источников rбатареи= r1 + r2 + r3
Если в батарею соединены n одинаковых источников, то ЭДС батареи ε= nε1, а сопротивление rбатареи= nr1
3. Сила тока в такой цепи по закону Ома ![]()
При параллельном соединении соединяют между собой все положительные и все отрицательные полюсы двух или n источников.
Т.е., при параллельном соединении, аккумуляторы соединяют так, чтобы положительные клеммы всех аккумуляторов были подключены к одной точке электрической схемы (″плюсу″), а отрицательные клеммы всех аккумуляторов были подключены к другой точке схемы (″минусу″).
Параллельно соединяют только источники с одинаковой ЭДС. Получившаяся при параллельном соединении аккумуляторная батарея имеет то же напряжение, что и у одиночного аккумулятора, а емкость такой аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые емкости, то емкость аккумуляторной батареи равна емкости одного аккумулятора, умноженной на количество аккумуляторов в батарее.
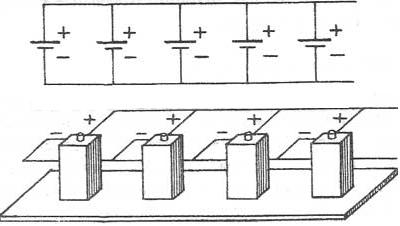
1. ЭДС батареи одинаковых источников равна ЭДС одного источника. ε= ε1= ε2 = ε3
2. Сопротивление батареи меньше, чем сопротивление одного источника rбатареи= r1/n
3. Сила тока в такой цепи по закону Ома ![]()
Электрическая энергия, накопленная в аккумуляторной батарее равна сумме энергий отдельных аккумуляторов (произведению энергий отдельных аккумуляторов, если аккумуляторы одинаковые), независимо от того, как соединены аккумуляторы – параллельно или последовательно.
Внутреннее сопротивление аккумуляторов, изготовленных по одной технологии, примерно обратно пропорционально емкости аккумулятора. Поэтому т.к.при параллельном соединении емкость аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов, т.е увеличивается, то внутреннее сопротивление уменьшается.
§ 17. Последовательное и параллельное соединение источников
При последовательном соединении источников общая ЭДС равна алгебраической сумме ЭДС отдельных источников, общее внутреннее сопротивление равно сумме внутренних сопротивлений отдельных источников. Для определения знака ЭДС каждого источника нужно выбрать положительное направление движения на участке с этим источником. ЭДС источника берётся со знаком `«+»`, если направление действия ЭДС совпадает с выбранным направлением. В противном случае ставится знак `«-»`.
При параллельном соединении источников с одинаковыми ЭДС и возможно различными внутренними сопротивлениями общая ЭДС (ЭДС батареи) равна ЭДС одного источника. Внутреннее сопротивление батареи рассчитывается как при параллельном соединении проводников с сопротивлениями, равными внутренним сопротивлениям источников.
При параллельном соединении источников с различными ЭДС выражение для ЭДС батареи усложняется и здесь не приводится.
В схеме на рис. 17.1 $$ {mathcal{E}}_{1}=12$$ В, $$ {mathcal{E}}_{2}=3$$ В, $$ {r}_{1}=1$$ Ом, $$ {r}_{2}=2$$ Ом, $$ R=6$$ Ом.
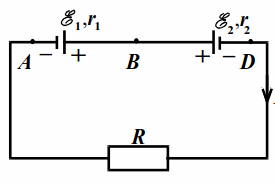 |
| Рис. 17.1 |
Найти напряжения на зажимах источников, т. е. разность потенциалов $$ {varphi }_{A}-{varphi }_{B}$$ и $$ {varphi }_{B}-{varphi }_{D}$$.
ЭДС батареи последовательно соединённых источников:
$$ mathcal{E}={mathcal{E}}_{1}-{mathcal{E}}_{2}=9$$ B.
Причём, полярность батареи совпадает с полярностью источника $$ {mathcal{E}}_{1}$$ т. к. $$ {mathcal{E}}_{1}>{mathcal{E}}_{2}$$.
Ток по закону Ома для замкнутой цепи $$ I=mathcal{E}/(R+{r}_{1}+{r}_{2})=1$$ A. По закону Ома для участков цепи `AB` и `BD`:
$$ {varphi }_{A}-{varphi }_{B}+{mathcal{E}}_{1}=I{r}_{1,}$$, $$ {varphi }_{B}-{varphi }_{D}-{mathcal{E}}_{2}=I{r}_{2}$$.
Отсюда $$ {varphi }_{A}-{varphi }_{B}=I{r}_{1}-{mathcal{E}}_{1}=-11$$ B, $$ {varphi }_{B}-{varphi }_{D}=I{r}_{2}+{mathcal{E}}_{2}=5$$ B.
Найти ток через резистор с сопротивлением $$ R$$ в схеме на рис. 17.2.
Между точками `A` и `B` имеем параллельное соединение источников. На рис. 17.3 показана эквивалентная схема, для которой $$ {mathcal{E}}_{1}=mathcal{E}$$, $$ {r}_{1}=r·2r/left(r+2rright)=2r/3$$. Общая ЭДС и внутреннее сопротивление последовательно соединённых источников с ЭДС $$ 3mathcal{E}$$ и $$ {mathcal{E}}_{1}$$:
$$ {mathcal{E}}_{0}=3mathcal{E}-{mathcal{E}}_{1}=3mathcal{E}-mathcal{E}=2mathcal{E}$$,
$$ {r}_{0}=3r+{r}_{1}=3r+2r/3=11r/3$$.
Ток $$ I={displaystyle frac{{mathcal{E}}_{0}}{R+{r}_{0}}}={displaystyle frac{6mathcal{E}}{3R+11r}}$$.
В случае последовательного соединения прохождение тока осуществляется только через один проводник. Параллельное соединение резисторов предполагает распределение электрического тока среди нескольких проводников. При добавлении еще одного резистора в электрическую цепь, ток будет частично проходить через разные резисторы.
Схемы последовательного и параллельного соединения
Если рассматривать соединение на примере громкоговорителя, то при последовательном соединении с усилителем мощности подключается только один динамик, поскольку прохождение тока осуществляется только через один проводник. Подключение второго громкоговорителя может быть выполнено разными способами.
При последовательном соединении по обоим устройствам будет протекать одинаковый ток. В этом случае общее сопротивление приборов представляет собой сумму отдельно взятых сопротивлений.
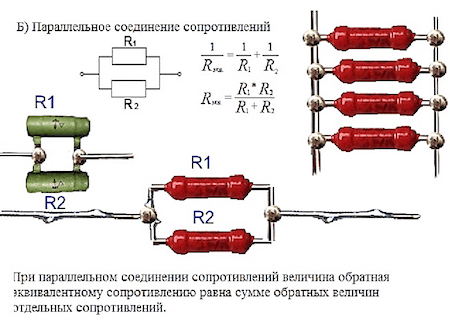
При параллельном соединении протекание тока будет происходить по двум направлениям. Здесь общее значение сопротивления в отличие от последовательного соединения, наоборот, будет уменьшаться. То есть, при параллельном соединении двух сопротивлений, их общее значение будет составлять половину каждого из них.
Если последовательное и параллельное соединение резисторов рассматривается с точки зрения радиоэлектроники, необходимо четко представлять себе, что представляет собой данный элемент и какова его роль в электронных схемах. Эта деталь является неотъемлемой частью многих устройств, благодаря такому свойству, как сопротивление электрическому току. Резисторы могут быть двух типов – постоянными и переменными, то есть подстроечными. При создании тех или иных электрических схем требуется резистор установленного номинала, которого в данный момент может не оказаться в наличии. Поэтому приходится использовать элементы с другими номинальными значениями, формула для каждого из которых подтверждает их физические свойства.
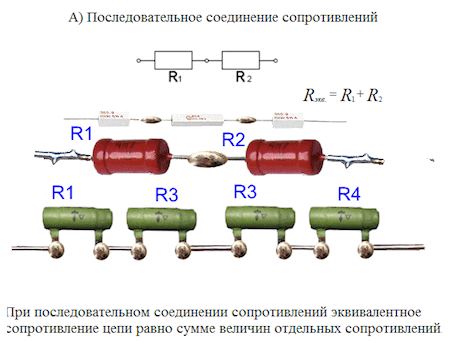
Последовательное соединение считается наиболее простым. Оно используется, когда необходимо увеличить общее сопротивление электрической цепи. В этом случае все сопротивления резисторов просто складываются и дают общую сумму. При параллельном соединении, наоборот, можно снизить результирующее сопротивление или увеличить мощность за счет нескольких подключенных резисторов.
Отличие параллельного и последовательного соединения
Последовательное и параллельное соединение резисторов отличаются между собой значениями напряжения. В каждой части параллельных контуров этот показатель будет одинаковым. Однако, при одном и том же напряжении, сила тока в контурах будет разной. Кроме того, сопротивление резисторов при параллельном соединении будет существенно отличаться от того же показателя при последовательном соединении.
В процессе использования последовательной схемы наблюдаются обратные явления. Сила тока в каждом сопротивлении будет одна и та же, а напряжение на каждом участке будет отличаться. Это связано с тем, что во время протекания тока, каждый резистор частично забирает приложенное напряжение. Из-за различного сопротивления резисторов, при последовательном соединении, напряжение в цепи может падать. Для того чтобы подтвердить данное явление, выполняется расчет сопротивления. Все падения напряжения в общей сумме равняются общему напряжению, которое было приложено. Для проведения вычислений используются формулы, с помощью которых можно получить наиболее точные результаты.
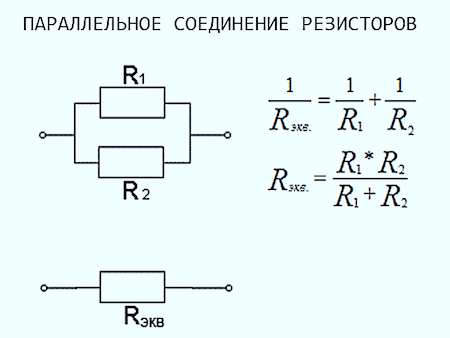
Таким образом, параллельное соединение резисторов, находящихся под одинаковым напряжением, не влияет на режим работы каждого из них. То есть, они совершенно не зависят друг от друга, и ток, проходящий по одному приемнику, не может существенно влиять на другие приемники.
Формула расчета параллельного соединения резисторов
Свои особенности имеет и ток при параллельном соединении резисторов. Попадая в первый узел соединения, он разделяется на столько частей, сколько имеется резисторов, подключенных параллельно. То есть, через сопротивление R1 будет протекать ток I1, а через R2 – ток I2. При попадании во второй узел, они вновь соединяются в один общий ток: I = I1 + I2.
Если какой-либо резистор вышел из строя, то остальные будут нормально функционировать. В этом заключается основное преимущество параллельного соединения. Особенно, это касается двигателей и электрических ламп, работающих от определенного номинального напряжения.
Расчет общего номинального сопротивления осуществляется с помощью формулы: R(общ)=1/(1/R1+1/R2+1/R3+1/R n), где R(общ) – является общим сопротивлением, а R1, R2, R3 и Rn – параллельно подключенными резисторами. Если выполняется параллельное соединение двух резисторов, при котором используется всего лишь два элемента, то в этом случае для расчетов используется следующая схема: R(общ)=R1хR2/R1+R2.
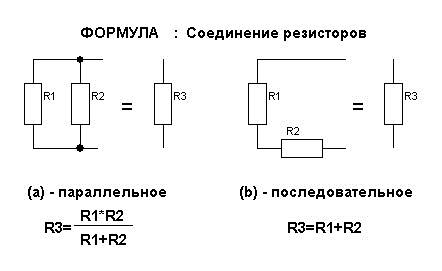
Очень часто в радиоэлектронике приходится пользоваться следующим правилом: если резисторы, подключенные параллельно, имеют один и тот же номинал, то итоговое сопротивление высчитывается путем деления номинала на число подключенных элементов. Такое параллельное соединение резисторов формула представляется следующим образом: R(общ)=R1n, где R(общ) представляет собой сопротивление, R – номинал параллельно подключенного резистора, n – число подключенных элементов.
Для того чтобы рассчитать параллельное соединение резисторов, следует учитывать, что итоговое сопротивление всех подключенных элементов будет всегда ниже, чем сопротивление резистора с самым низким номиналом. В качестве примера можно рассмотреть схему с тремя резисторами, сопротивления которых составляют 30, 100 и 150 Ом. При использовании основной формулы будет получен следующий результат: R(общ)=1/(1/30+1/100+1/150) =1/(0,03+0,01+0,007)=1/0,047=21,28Ом. Таким образом, три резистора, соединенные параллельно, с минимальным номиналом 30 Ом, в итоге дадут общее сопротивление электрической цепи 21,28 Ом.
Онлайн калькулятор
В случае больших объемов вычислений, расчет параллельного соединения резисторов выполняется с помощью онлайн-калькулятора.
Все разнообразие схем построено на двух типах соединения — параллельном и последовательном. Для разных соединений действуют разные законы, что и дает возможность создания устройств с различными характеристиками. Рассмотрим последовательное и параллельное соединение резисторов.
Содержание статьи
- 1 Что такое резистор и для чего он нужен
- 2 Последовательное соединение сопротивлений
- 2.1 Теоретическая часть
- 2.2 Примеры расчета
- 3 Параллельное соединение резисторов
- 3.1 Теория и законы параллельного соединения
- 3.2 Примеры расчета параллельного соединения сопротивлений
- 4 Смешанное соединение
- 5 Практическое применение параллельного и последовательного соединения резисторов
Что такое резистор и для чего он нужен
Резистор — это радиоэлемент, который увеличивает сопротивление цепи. Ставят его обычно для того, чтобы понизить/ограничить напряжение или ток. Есть сопротивления постоянные и переменные.
Например, светодиоды требуют небольшого тока, иначе перегревается и быстро выходит из строя. Чтобы ограничить ток, перед светодиодом поставьте сопротивление. Ток в цепи станет меньше.

Для чего нужны резисторы: для подстройки параметров питания
Постоянные сопротивления — это те, которые не меняют своего номинала в процессе работы. Если это и происходит, то считается выходом из строя.

Так выглядят переменные и постоянные резисторы
Переменные резисторы, наоборот, отличаются тем, что их сопротивление можно изменять. Они имеют бегунок или поворотную ручку, при помощи которых и изменяется номинал. На основе таких устройств делают регуляторы. Например, регулятор громкости, накала греющего элемента и т.д.
Последовательное соединение сопротивлений
Последовательное соединение характеризуется тем, что элементы идут друг за другом. Конец одного подключается к началу другого. При подключении полученной цепочки к источнику тока получается кольцо.

Лампы накаливания соединенные последовательно, можно рассматривать как сопротивления
Теоретическая часть
Последовательное соединение характерно тем, что через все элементы протекает ток одинаковой силы. То есть, если цепочка состоит из двух резисторов R1 и R2 (как на рисунке ниже), то ток протекающий через каждое из них и любую другую часть цепи будет одинаковой (I = I1 = I2).

Последовательно соединенные сопротивления. I1 — ток протекающий через резистор R1, I2 — ток протекающий через резистор R2
Суммарное сопротивление всей цепи последовательно соединенных резисторов считается как сумма сопротивлений всех ее элементов. То есть, номиналы складывают.
R = R1 + R2 — это и есть формула расчета сопротивления при последовательном соединении резисторов. Если элементов больше двух, будет просто больше слагаемых.
Еще одно свойство последовательного соединения — на каждом элементе напряжение отличается. Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.
Примеры расчета
Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:
- U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
- U2 = R2 * I = 800 Ом * 2А = 1600 В.
Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В.

Так понятнее, что такое последовательное соединение
Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток. R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом. Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2 А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В.
А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором — 1600 В. При этом напряжение источника питания — 4000 В.
Параллельное соединение резисторов
Параллельное соединение — это когда входы нескольких деталей соединяются в одной точке. Точно так же — в одну точку — соединяют их выходы.

Так выглядит параллельное соединение на схеме и в реальности
Теория и законы параллельного соединения
Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение. То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение.
U = U1 = U2 = U3.
Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.

Так выглядит параллельное соединение резисторов на схеме
Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле:
1/R = 1/R1 + 1/R + 1/R3+…
Такая форма хоть и понятна, но неудобна. Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно. Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.

Формулы расчета сопротивления при параллельном подключении двух и трех резисторов
Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала.
Примеры расчета параллельного соединения сопротивлений
Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.
- Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом.
- Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом.
Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.
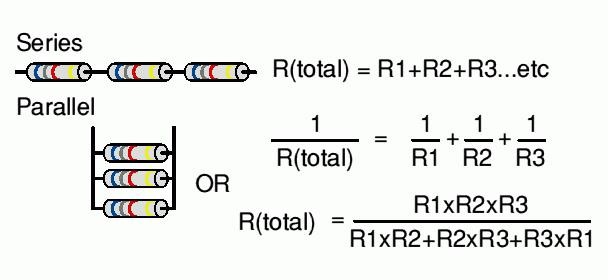
Как высчитывать сопротивление составных резисторов
Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом.

Еще один пример с лампочками
При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее. Но картина не отличается:
- Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом.
- Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом.
Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.
Смешанное соединение
Как быть, если в схеме есть и параллельное, и последовательное соединение резисторов? В таком случае считают общее сопротивление по участкам. Можно при этом перерисовывать схему, заменяя составные сопротивления на один «прямоугольник», но проставляя над ним высчитанный результат.

Пример расчета сопротивления при смешанном соединении резисторов. Рассматриваем исходную схему как совокупность параллельных и последовательных соединений
Шаг 1. Нашли общее сопротивление последовательно соединенных резисторов R3 и R4:
R3-4 = 3 кОм + 3 кОм = 6 кОм;
Шаг 2. Рассчитали сопротивление параллельно соединенных резисторов R2 и R3-4:
R2-4 = 3 кОм * 6 кОм / (3 кОм + 6 кОм) = 18 кОм/9 кОм = 2 кОм;
Шаг 3. Рассчитали общее сопротивление последовательно соединенных резисторов R1 и R2-4:
R1-4 = R1 + R2-4 = 1 кОм + 2 кОм = 3 кОм.
Практическое применение параллельного и последовательного соединения резисторов
Для чего практически можно использовать параллельное и последовательное соединение резисторов? Случается, что при ремонте электронной аппаратуры, не всегда в наличии сопротивление нужного номинала. Ехать в магазин за одним копеечным элементом — накладно. Вот тут и могут пригодиться составные резисторы. Просто надо последовательно или параллельно соединить их, подобрав требуемый номинал.

Последовательное и параллельное соединение резисторов применяют для подбора требуемого номинала. Контролировать точное значение получившегося сопротивления можно при помощи цифрового мультиметра
При соединении резисторов, их ножки первоначально скручивают. Какой стороной разворачивать сопротивление — неважно (в отличие от диодов, резисторы одинаково пропускают ток в обоих направлениях). На концах скрутку слегка обжимают плоскогубцами, затем пропаивают. Следите за тем, чтобы корпуса были друг от друга подальше — так они будут лучше охлаждаться при работе.

Метод эквивалентного преобразования электрических цепей
Сущность и цель преобразований
Цель преобразования электрических цепей состоит в упрощении схем путем эквивалентных преобразований, приводящих к уменьшению числа ветвей и узлов. Эквивалентные преобразования входят во все методы расчета в качестве первого шага в последовательностях расчета. Под эквивалентными преобразованиями мы будем понимать преобразования одной части схемы, при которых в остальной части величины токов и напряжений остаются неизменными, как и сама схема.
Расчет цепи при последовательном соединении элементов и закон Ома для ветви, содержащей ЭДС
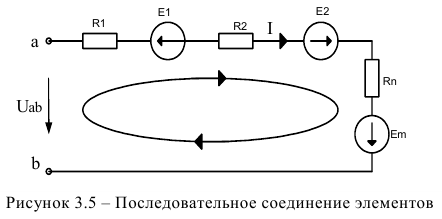
Рассмотрим электрическую цепь при последовательном соединении и ЭДС и резисторов, когда величина тока во всех элементах одинакова.
Все величины ЭДС и резисторов известны, как и напряжение на входе цепи. Необходимо упростить цепь до двух элементов (рисунок 3.6) и определить величину тока.
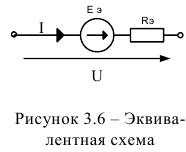
Для решения задачи выберем произвольное направление тока 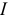 и обхода контура и на основании второго закона Кирхгофа составим уравнение:
и обхода контура и на основании второго закона Кирхгофа составим уравнение:
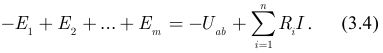
Учитывая, что ток 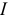 одинаковый во всех резисторах, выносим его за знак суммы и вводим обозначения:
одинаковый во всех резисторах, выносим его за знак суммы и вводим обозначения:
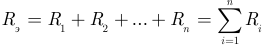 — эквивалентное сопротивление, определяемое в виде арифметической суммы всех последовательно соединенных сопротивлении;
— эквивалентное сопротивление, определяемое в виде арифметической суммы всех последовательно соединенных сопротивлении;
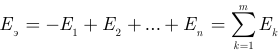 — эквивалентная ЭДС, определяемая как алгебраическая сумма ЭДС.
— эквивалентная ЭДС, определяемая как алгебраическая сумма ЭДС.
С учетом выполненных обозначений, уравнение приобретает вид:

Схема имеет вид (рисунок 3.6), а величина тока:

Расчет цепи при параллельном соединении элементов
Задана электрическая цепь, содержащая параллельно соединенные элементы, т.е. на всех элементах напряжения одинаковые (рисунок 3.7). Величины сопротивлений резисторов заданы 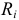 и токи источников тока
и токи источников тока 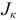 . Необходимо рассчитать ток
. Необходимо рассчитать ток 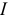 .
.
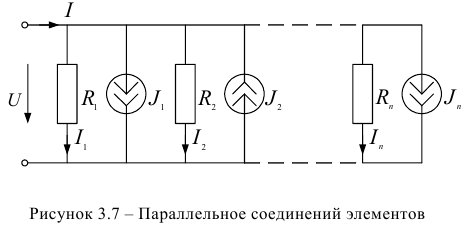
Решение задачи выполним на основании первого закона Кирхгофа, предварительно выбрав направления токов в ветвях, с резисторами от верхнего узла с большим потенциалом к нижнему с меньшим потенциалом:

В представленном уравнении все подтекающие токи взяты со знаком «+», а оттекающие — со знаком «-». Т.к. величина тока в любом резисторе может быть найдена по закону Ома:

то ток 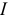 на входе цепи может быть вычислен по выражению:
на входе цепи может быть вычислен по выражению:
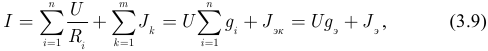
где 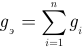 — эквивалентная проводимость всех ветвей с резисторами определяемая как арифметическая сумма проводимостей всех параллельно соединенных резисторов;
— эквивалентная проводимость всех ветвей с резисторами определяемая как арифметическая сумма проводимостей всех параллельно соединенных резисторов; 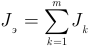 — ток эквивалентного источника тока, определяемый как алгебраическая сумма всех параллельно соединенных источников тока. Знак тока источника тока положителен, если он направлен от узла и отрицателен, если он направлен к узлу.
— ток эквивалентного источника тока, определяемый как алгебраическая сумма всех параллельно соединенных источников тока. Знак тока источника тока положителен, если он направлен от узла и отрицателен, если он направлен к узлу.
В соответствии с последним уравнением можно зарисовать эквивалентную схему замещения (рисунок 3.8).
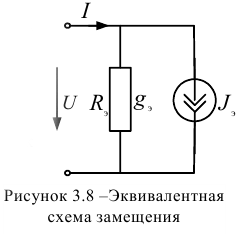
Расчет цепи при смешанном соединении элементов
Под смешанным соединением элементов понимают такие соединения, при которых цепь содержит одновременно последовательно соединенные элементы и параллельно соединенные элементы.
Задача 3.1.
Рассчитать эквивалентное сопротивление для схемы, представленной на рисунке 3.9, если:
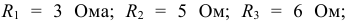
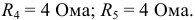
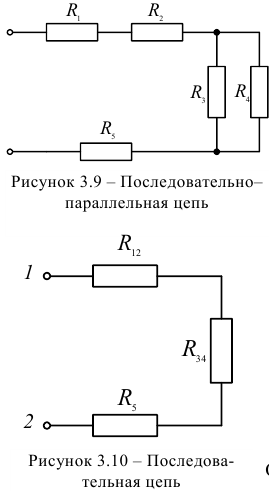
Решение:
На первом этапе объединим последовательно соединенные элементы 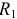 и
и 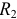 и параллельно соединенные элементы
и параллельно соединенные элементы 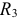 и
и 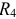 :
: 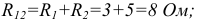
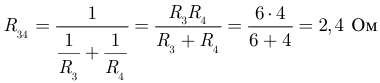
В результате получаем упрощенную схему (рисунок 3.10).
На втором этапе суммируем сопротивления 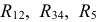 и получаем эквивалентное сопротивление всей схемы относительно входных зажимов 1 и 2:
и получаем эквивалентное сопротивление всей схемы относительно входных зажимов 1 и 2: 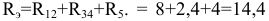 Ом.
Ом.
Задача 3.2.
Задана электрическая цепь (рисунок 3.11.). Для величин элементов: 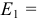
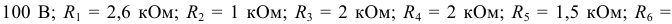
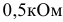 выполнить расчет величин токов в ветвях электрической цепи.
выполнить расчет величин токов в ветвях электрической цепи.
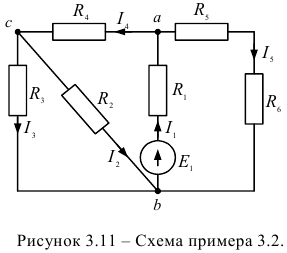
Решение:
Выбираем направления токов в ветвях электрической цепи с учетом направления ЭДС 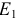 . На первом этапе объединяем резисторы
. На первом этапе объединяем резисторы 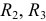 и
и 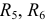 .
.
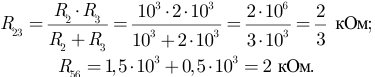
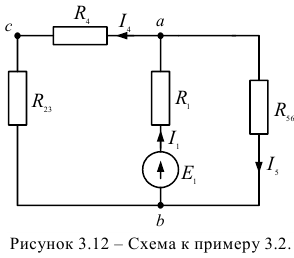
На рисунке 3.12 представлена упрощенная схема. Объединяем сопротивления ветвей, подключенных параллельно, к узлам 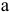 и
и 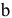 :
:
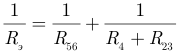
Следовательно:
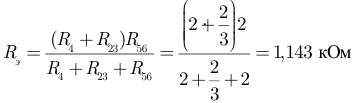
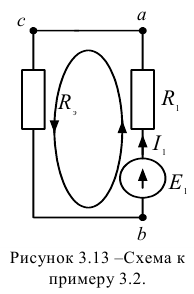
На рисунке 3.13 получена неразветвленная электрическая цепь.
Применяем второй закон Кирхгофа для замкнутого контура:
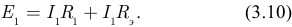
Решаем уравнение относительно тока 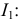
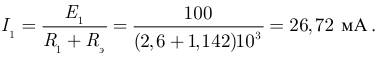
Вычисляем напряжение 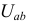 по закону Ома:
по закону Ома:
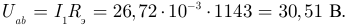
Тогда:
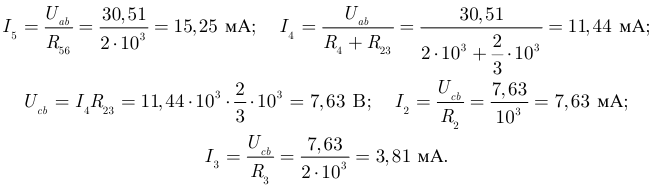
Выполним проверку вычислений по балансу мощностей:
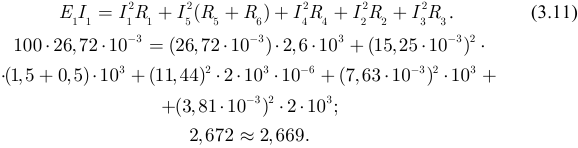
Задача 3.3.
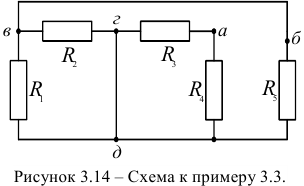
Пользуясь методом преобразования, рассчитать эквивалентное входное сопротивление электрической цепи (рисунок 3.14.) относительно точек 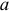 и
и 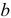 если величины элементов имеют значения:
если величины элементов имеют значения:
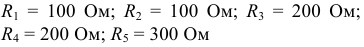
Решение:
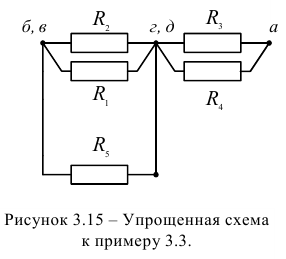
Так как схема содержит ветви без элементов, то узлы и точки с равными потенциалами можно объединить. Объединяем точку в и б и узел г с узлом д. Упрощенная схема представлена на рисунке 3.15. Рассчитаем эквивалентные сопротивления 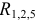 и
и 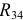 :
:
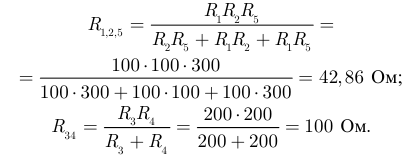
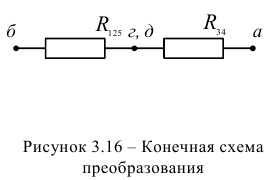
Эквивалентное сопротивление всей цепи относительно точек а и б, в соответствии с новой схемой (рисунок 3.16):
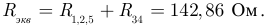
Эта страница взята со страницы задач по электротехнике:
Электротехника — решения задач и примеры выполнения заданий
Возможно эти страницы вам будут полезны:

