Содержание
Задание 15. На рисунке приведён график зависимости силы тока от времени в электрической цепи, индуктивность которой 1 мГн. Определите модуль ЭДС самоиндукции в интервале времени от 5 до 10 с.
Решение задачи
Запишем формулу ЭДС самоиндукции:
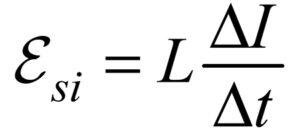
По графику определим изменение силы тока в интервале времени от 5 до 10 с. Подставляем числовые значения в формулу.
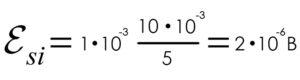
E si = 2 * 10-6 В = 2 мкВ.
Ответ к задаче
Ответ: 2 мкВ.
Просмотров: 8 315
Читайте также: Определите ЭДС источника, если при перемещении заряда 10 Кл сторонние силы совершают работу в 120 Дж
Печатать книгу
| Сайт: | Профильное обучение |
| Курс: | Физика. 10 класс |
| Книга: | § 33. Явление самоиндукции. Индуктивность. Энергия магнитного поля катушки с током |
| Напечатано:: | Гость |
| Дата: | Четверг, 25 Май 2023, 01:00 |
Оглавление
- Самоиндукция
- Наблюдение самоиндукции
- Энергия магнитного поля
- Примеры решения задач
- Упражнение 24
Фарадей опытным путём установил, что электромагнитная индукция проявляется во всех случаях изменения магнитного потока через поверхность, ограниченную контуром. Современник Фарадея американский физик Джозеф Генри (1797–1878) независимо от своего английского коллеги открыл некоторые из электромагнитных эффектов. В 1829 г. Генри обнаружил, что ЭДС индукции возникает в неподвижном контуре и в отсутствие изменения внешнего магнитного поля. Каков механизм возникновения ЭДС индукции в этом случае?
Самоиндукция. Если электрический ток, проходящий в замкнутом проводящем контуре, по каким-либо причинам изменяется, то изменяется и магнитное поле, создаваемое этим током. Это влечёт за собой изменение магнитного потока через поверхность, ограниченную контуром. Поскольку магнитный поток Ф пропорционален модулю магнитной индукции В поля, который, в свою очередь, пропорционален силе тока I в контуре, то
Коэффициенту пропорциональности между магнитным потоком Ф и силой тока I Томсон (лорд Кельвин) в 1853 г. предложил название «коэффициент самоиндукции»:
Коэффициент самоиндукции L часто называют индуктивностью контура. В СИ индуктивность измеряют в генри (Гн). Индуктивность контура равна 1 Гн, если при силе тока в контуре 1 А магнитный поток через поверхность, ограниченную этим контуром, равен 1 Вб. Индуктивность зависит от размеров и формы контура, а также от магнитных свойств среды, в которой находится этот контур.
Если электрический ток, проходящий в контуре, изменяется, то он создаёт изменяющийся магнитный поток, что приводит к появлению ЭДС индукции. Это явление назвали самоиндукцией.
Самоиндукция — явление возникновения ЭДС индукции в электрической цепи в результате изменения силы тока в этой же цепи.
Возникающую в этом случае ЭДС назвали электродвижущей силой самоиндукции. Согласно закону электромагнитной индукции,
Если индуктивность контура не изменяется во времени, т. е. L = const, то
Поскольку контур замкнут, ЭДС самоиндукции создаёт в нём ток самоиндукции. Силу тока самоиндукции можно определить по закону Ома 
где R — сопротивление контура. Согласно правилу Ленца, ток самоиндукции всегда направлен так, чтобы противодействовать изменению тока, создаваемого источником. При возрастании силы тока ток самоиндукции направлен против тока источника, а при уменьшении — направления тока источника и тока самоиндукции совпадают.
От теории к практике
Какой должна быть скорость изменения силы тока, чтобы в катушке с индуктивностью L = 0,20 Гн возникла ЭДС самоиндукции 
= 4,0 В?
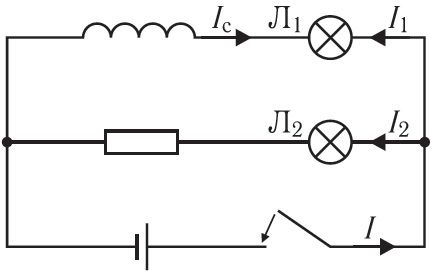
Наблюдение самоиндукции. Для наблюдения явления самоиндукции соберём электрическую цепь, состоящую из катушки с большой индуктивностью, резистора с электрическим сопротивлением, равным сопротивлению обмотки катушки, двух одинаковых лампочек, ключа и источника постоянного тока. Схема цепи представлена на рисунке 185. При замыкании ключа лампочка Л2 начинает светиться практически сразу, а лампочка Л1 — с заметным запаздыванием. При возрастании силы тока I1, созданного источником на участке, образованном катушкой и лампочкой Л1, ЭДС самоиндукции в катушке имеет такую полярность, что создаваемый ею ток самоиндукции Iс направлен навстречу току источника. В результате рост силы тока I1 источника замедляется, и сила тока I1 — |Iс| не сразу достигает своего максимального значения.
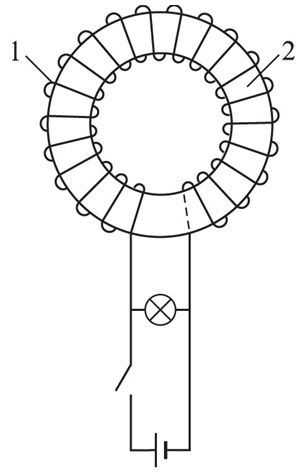
Явление самоиндукции можно наблюдать и при размыкании электрической цепи. Соберём цепь, состоящую из катушки с большим количеством витков 1, намотанных на железный сердечник 2, к зажимам которой подключена лампочка с большим электрическим сопротивлением по сравнению с сопротивлением обмотки катушки (рис. 185.1). В качестве источника тока возьмём источник, ЭДС которого 2 В. Лампочка подключена параллельно катушке. При размыкании ключа сохраняется замкнутой часть цепи, состоящая из уже последовательно соединённых катушки и лампочки.
Пока ключ замкнут, лампочка будет тускло светиться, так как отношение сил токов, проходящих через лампочку и катушку, обратно отношению их сопротивлений 
. Однако при размыкании ключа можно увидеть, что лампочка ярко вспыхивает. Почему это происходит? При размыкании цепи сила тока в катушке убывает, что приводит к возникновению ЭДС самоиндукции. Возникающий в цепи ток самоиндукции, согласно правилу Ленца, совпадает по направлению с током катушки, не позволяя ему резко уменьшать силу тока. Это и обеспечивает вспышку лампочки. Заметим, что явление самоиндукции имеет место в любых случаях изменения силы тока в цепи, содержащей индуктивность, или изменения самой индуктивности.
Энергия магнитного поля. Откуда берётся энергия, обеспечивающая вспышку лампочки? Это не энергия источника тока, так как он уже отсоединён. Вспышка лампочки происходит одновременно с уменьшением силы тока в катушке и создаваемого током магнитного поля. Можно предположить, что запасённая в катушке в процессе самоиндукции энергия магнитного поля превращается во внутреннюю энергию спирали лампочки и энергию её излучения.
При замыкании цепи, состоящей из источника тока с ЭДС 
, катушки с индуктивностью L и резистора, сопротивление которого R, сила тока в цепи начнёт возрастать и появится ЭДС самоиндукции 
.
Тогда в соответствии с законом Ома сила тока в цепи 
.
Значит, 
.
Умножив полученное равенство на IΔt, где Δt — достаточно малый промежуток времени, в течение которого сила тока I остаётся практически постоянной, найдём элементарную работу, совершаемую сторонними силами в источнике тока: 
.
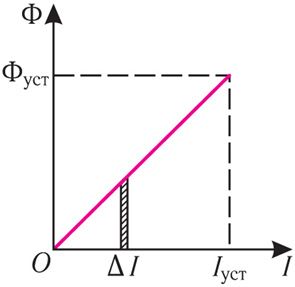
В процессе установления тока, когда сила тока I и магнитный поток Ф = LI возрастают, работа, совершаемая сторонними силами в источнике тока, превышает выделяющееся в резисторе количество теплоты. Элементарная дополнительная работа, совершаемая сторонними силами за промежуток времени Δt при преодолении ЭДС самоиндукции в процессе установления тока (рис. 185.2):
δAдоп = ФΔI.
Полная дополнительная работа Адоп, равная сумме элементарных дополнительных работ δAдоп в процессе установления тока, равна сумме площадей всех аналогичных столбиков, т. е. площади фигуры под графиком зависимости Ф = Ф(I) (см. рис. 185.2).
Эта работа превращается в энергию магнитного поля катушки, поэтому:
где L — индуктивность контура; I — сила тока.
От теории к практике
Какова индуктивность катушки, если при силе тока I = 2,0 А энергия магнитного поля катушки Wм = 1,2 Дж?
1. Что называют самоиндукцией?
2. В каких опытах можно наблюдать явление самоиндукции?
3. От чего зависит ЭДС самоиндукции?
4. Что называют индуктивностью? В каких единицах в СИ её измеряют?
5. Как вычислить энергию магнитного поля катушки с током?
6. Почему для создания электрического тока в цепи с катушкой индуктивности источник тока должен затратить энергию?
Примеры решения задач
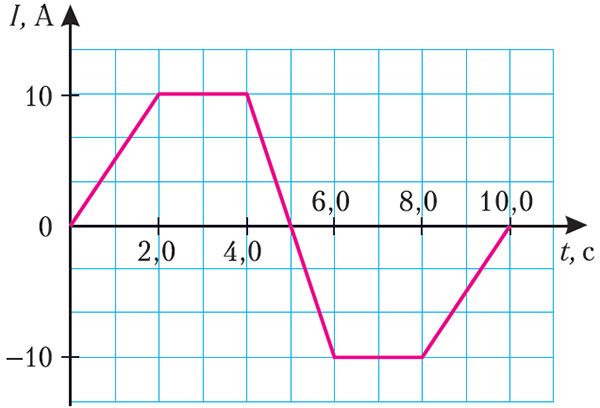
Пример 1. На рисунке 186 представлен график зависимости силы тока, проходящего по соленоиду, от времени. Определите максимальное значение модуля ЭДС самоиндукции в соленоиде, если его индуктивность L = 40 мГн.
Дано:
L = 40 мГн = 4,0 · 10–2 Гн
— ?
Решение: ЭДС самоиндукции . Анализируя график (рис. 186), можно сделать вывод, что сила тока, проходящего по соленоиду, изменяется на трёх участках:
1) от момента времени t1 = 0,0 с до момента времени t2 = 2,0 с сила тока изменяется на ΔI1 = 10 А за промежуток времени Δt1 = 2,0 с;
2) от момента времени t3 = 4,0 с до момента времени t4 = 6,0 с сила тока изменяется на ΔI2 = –20 А за промежуток времени Δt2 = 2,0 с;
3) от момента времени t5 = 8,0 с до момента времени t6 = 10,0 с сила тока изменяется на ΔI3 =10 А за промежуток времени Δt3 = 2,0 с.
Поскольку промежутки времени Δt1 = Δ t2 = Δ t3 = 2,0 с, то очевидно, что максимальное значение модуля скорости изменения силы тока, а следовательно, и максимальное значение модуля ЭДС самоиндукции, создаваемой в соленоиде, соответствует промежутку времени Δt2 = 2,0 с (от t3 = 4,0 с до t4 = 6,0 с):
Таким образом,
Ответ: = 0,40 В.
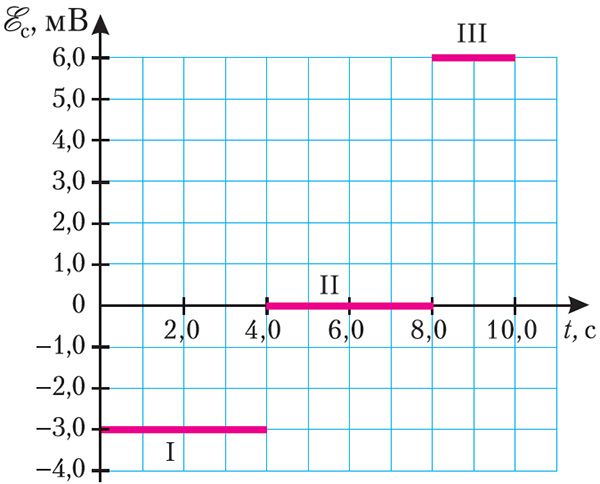
Пример 2. На рисунке 187 представлен график зависимости ЭДС самоиндукции, возникающей в катушке с индуктивностью L = 2,0 мГн, от времени. Определите изменения силы тока на участках I, II и III графика. Чему равна энергия магнитного поля в момент времени t = 4,0 с, если в начальный момент времени сила тока в катушке I = 0?
Дано:
L = 2,0 мГн = 2,0 · 10–3 Гн
t = 4,0 с
ΔII — ? ΔIII — ?
ΔIIII — ? Wм — ?
Решение: Анализируя график, можно сделать вывод, что на участке I ЭДС самоиндукции 
= –3,0 мВ, на участке III — 
= 6,0 мВ. Изменение силы тока на этих участках графика можно определить, воспользовавшись законом электромагнитной индукции для явления самоиндукции:
; 
.
; 
.
На участке II графика 
= 0, следовательно, сила тока не изменялась: ΔIII = 0.
В момент времени t = 4,0 с энергия магнитного поля катушки 
.
Следовательно,
.
Ответ: ΔII = 6,0 А; ΔIII = 0; ΔIIII = –6,0 А; Wм = 36 мДж.
Пример 3. За промежуток времени Δt = 9,50 мс сила тока в катушке индуктивности равномерно возросла от I1 = 1,60 А до I2 = 2,40 А. При этом в катушке возникала ЭДС самоиндукции = ‒14,0 В. Определите собственный магнитный поток в конце процесса нарастания тока и приращение энергии магнитного поля катушки.
Дано:
Δt = 9,50 мс = 9,50 · 10-3 с
I1 = 1,60 А
I2 = 2,40 А
= ‒14,0 В
Фс — ?
ΔWм — ?
Решение: При изменении в катушке силы тока от I1 до I2 возникает собственный магнитный поток Фс = LI2. Индуктивность L катушки можно определить из закона электромагнитной индукции для явления самоиндукции: 
. Следовательно,
. Тогда 
.
Приращение энергии магнитного поля катушки
Ответ: Фс = 399 мВб, ΔWм = 266 мДж.
Упражнение 24
1. Сила тока, проходящего по замкнутому проводящему контуру, I = 1,2 А. Магнитное поле этого тока создаёт магнитный поток Ф = 3,0 мВб через поверхность, ограниченную контуром. Определите индуктивность контура.
2. При равномерном изменении силы тока в катушке на ΔI = –4,0 А за промежуток времени Δt = 0,10 с в ней возникает ЭДС самоиндукции = 20 В. Определите индуктивность катушки.
3. Определите ЭДС самоиндукции, возникающую в катушке, индуктивность которой L = 1,2 Гн, при равномерном изменении силы тока от I1 = 2,0 А до I2 = 6,0 А за промежуток времени Δt = 0,60 с. Определите приращение энергии магнитного поля при заданном изменении силы тока.
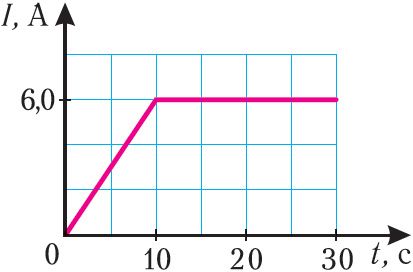
4. На рисунке 188 представлен график зависимости силы тока в катушке, индуктивность которой L = 10 мГн, от времени. Определите ЭДС самоиндукции через промежутки времени t1 = 10 с и t2 = 20 с от момента начала отсчёта времени.
5. Сила тока в катушке равномерно уменьшилась от I1 = 10 А до I2 = 5,0 А. При этом энергия магнитного поля изменилась на ΔWм = –3,0 Дж. Определите индуктивность катушки и первоначальное значение энергии магнитного поля.
6. Определите ЭДС самоиндукции, возникающую в катушке, индуктивность которой L = 0,12 Гн, при равномерном уменьшении силы тока от I1 = 8,0 А, если за промежуток времени t1 = 0,20 с энергия магнитного поля уменьшилась в α = 2,0 раза.
7. Энергия магнитного поля катушки с индуктивностью L1 = 0,5 Гн больше энергии магнитного поля катушки с индуктивностью L2 в α = 1,5 раза. Определите индуктивность второй катушки, если отношение собственного магнитного потока через поверхности, ограниченные витками второй катушки, к собственному магнитному потоку через поверхности, ограниченные витками первой катушки, 
.
Физика, 11 класс
Урок 6. Самоиндукция. Индуктивность
Перечень вопросов, рассматриваемых на уроке:
1) индуктивность, самоиндукция, ЭДС самоиндукции;
2) использование явления электромагнитной индукции, принцип действия электрогенератора и электродинамического микрофона;
3) аналогия между самоиндукцией и инертностью;
4) закон самоиндукции, границы его применимости;
5) ЭДС индукции в движущихся проводниках.
Глоссарий по теме
Самоиндукцией называют явление возникновения ЭДС индукции в самом проводнике, по которому идет переменный ток. Эта ЭДС называется ЭДС самоиндукции 
.
Величину L называют индуктивностью контура или его коэффициентом самоиндукции.
Индуктивность проводника равна 1 Гн, если в нём при равномерном изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В.
Энергия магнитного поля, созданного током, проходящим по участку цепи с индуктивностью L равна произведения индуктивности и квадрата силы тока деленная на два.
Магнитное поле, созданное электрическим током, обладает энергией, прямо пропорциональной квадрату силы тока.
Основная и дополнительная литература по теме урока:
Обязательная литература:
Мякишев Г.Я.,Буховцев Б.Б.,Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций. М.: Просвещение, 2014. – С. 47 – 52.
Рымкевич А.П. Сборник задач по физике. 10-11 класс. -М.: Дрофа, 2009. – С. 121 – 125.
Целых Д. Об измерении энергии магнитного поля //Квант. – 1998. – № 1. – С. 43-44.
Основное содержание урока
Самоиндукция – это явление возникновения электромагнитной индукции в проводнике при изменении силы тока, протекающего через проводник 
.
При самоиндукции проводящий контур выполняет двойную роль: переменный ток в проводнике вызывает появление магнитного потока через поверхность, ограниченную контуром. А так как магнитный поток изменяется со временем, то появляется ЭДС индукции 
.
По правилу Ленца, в момент нарастания тока напряженность вихревого электрического поля направлена против тока, препятствуя нарастанию тока. В момент уменьшения тока вихревое поле наоборот поддерживает его.
ЭДС самоиндукции E_si может быть больше ЭДС источника тока
.
Генератор – это устройство, преобразующее энергию того или иного вида в электрическую энергию.
Генератор состоит из подвижной части – ротора, и неподвижной части – статора.
Все генераторы состоят из магнита или электромагнита, создающего магнитное поле, и рамки (обмотки) в которой индуцируется ЭДС.
По закону электромагнитной индукции Фарадея, в условиях, когда проводник движется внутри магнитного поля, образуется эффект пересечения магнитных силовых линий. На заряды со стороны магнитного поля действует сила Лоренца и внутри проводника свободные заряды приходят в направленное движение, то есть индуцируется ЭДС (электродвижущая сила), которая имеет магнитное происхождение. Величина индуцированной электродвижущей силы проводника напрямую зависит от скорости изменения магнитного потока (от скорости вращения рамки), пронизывающий проводник. Генераторы вырабатывают переменный электрический ток.
Микрофон осуществляет превращение звуковых колебаний воздуха в колебания электрического тока. Его действие основано на явлении электромагнитной индукции.
В электродинамическом микрофоне мембрана механически жёстко соединена с катушкой, который находится в кольцевом зазоре постоянного магнита (аналогично динамикам). Линии магнитной индукции перпендикулярны виткам катушки.
Звуковая волна вызывает колебание мембраны и, соответственно, колебание звуковой катушки. Катушка движется в магнитном поле, в её витках индуцируется ток, и на концах катушки возникает переменная ЭДС индукции.
Это переменное напряжение вызывает колебание тока в цепи микрофона.
Самоиндукция является частным случаем электромагнитной индукции.
Самоиндукцию можно представить как своеобразный маховик или точнее – силу инерции. При действии на маховик внешней силы сначала сопротивляется этой силе, а при резком прекращении ее действия, когда уже маховик раскручен – еще какое-то время движется по инерции.
Явление самоиндукции используют в системах плавного включения электрических устройств, например, в осветительных приборах, цепях, содержащих трансформаторы, генераторы, электродвигатели, выключение тока проводят медленно, чтобы ЭДС самоиндукции не превысила ЭДС источника, и прибор не вышел из строя, выполняет очень важную роль в: электротехнике и радиотехнике. Индуктивность цепи оказывает существенное влияние на прохождение по цепи переменного электрического тока.
Магнитный поток 
пропорционален силе тока I:
где
– индуктивность контура, или его коэффициентом самоиндукции. Единицу индуктивности в СИ называют генри (обозначается 1 Гн). Индуктивность зависит от геометрических размеров проводника, его формы, и непосредственно не зависит от силы тока в проводнике. Кроме геометрии проводника, индуктивность зависит от магнитных свойств среды, в которой находится проводник.
Индуктивность одного проволочного витка меньше, чем у катушки (соленоида), состоящей из N таких же витков, так как магнитный поток катушки увеличивается в N раз.
если геометрические параметры проводника остаются неизменными и поток меняется только за счет изменения силы тока.
Электродвижущая сила самоиндукции 
прямо пропорциональна скорости изменения силы тока, протекающего сквозь проводник, взятого со знаком минус.
Источник тока, включенный в электрическую цепь, обладает запасом энергии. Источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, идет на образование магнитного поля.
Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока
Энергию магнитного поля можно выразить и через характеристики поля. Плотность энергии магнитного поля (то есть энергия единицы объёма) пропорциональна квадрату магнитной индукции: 
, подобно плотности энергии электрического поля пропорциональной квадрату напряженности электрического поля: 
Запас энергии магнитного поля катушки равен энергии, израсходованной источником тока на преодоление э. д. с. самоиндукции за весь тот промежуток времени, пока сила тока при замыкании цепи возрастала от нуля до некоторого значения. Часть работы ЭДС источника в катушке идет на нагревание ее проводов, а часть, равная э. д. с. самоиндукции, совершает работу против ЭДС самоиндукции.
При движении проводника длиной l в однородном магнитном поле на электроны проводника действует сила Лоренца 
.
Если концы проводника будут соединены через нагрузку друг с другом, то через проводник потечёт ток.
Сила Лоренца, совершает работу по перемещению зарядов по всей длине проводника l.
Возникающая за счет действия на заряды силы Лоренца ЭДС индукции имеет магнитное происхождение.
Электродвижущая сила индукции в проводнике равна отношению работы по перемещению заряда к этому заряду:
Эта формула справедлива для любого проводника длиной l, движущегося со скоростью v в однородном магнитном поле
Разбор тренировочных заданий
1. Катушка индуктивностью 2 Гн подключена к источнику тока так, как показано на рисунке. Сопротивление лампы равно 70 Ом, ЭДС источника 210 В.
Внутренним сопротивлением источника и сопротивлением проводов пренебречь. Выберите два верных утверждения о процессах, наблюдаемых в опыте.
1) Сила тока в цепи равна 3 А;
2) Энергия магнитного поля равна 18 Дж;
3) Ток через лампу сначала увеличивается, затем достигнув максимального значения не меняется;
4). Магнитный поток пронизывающий катушку сначала уменьшается, потом увеличивается.
Дано:
L=2 Гн
R=70 Ом
Ԑ=210В
r=0
Решение:
1) Согласно закону Ома для полной цепи
Утверждение 1 верно.
2) Энергия магнитного поля:
Утверждение 2 неверно.
3) Согласно явлению самоиндукции, ток в проводнике нарастает постепенно и не меняется, если в проводнике установится постоянный ток.
Утверждение 3 верно.
4) При увеличении тока магнитный поток пронизывающий катушку увеличивается, потом не изменяется.
Утверждение 4 неверно.
Правильные варианты: 1); 3).
2. На рисунке представлен график зависимости силы тока в катушке от времени. Индуктивность катушки равна 2,5 Гн. Найдите два правильных ответа:
1) модуль магнитного потока через катушку в интервале времени от 0 до 1 с равна 1,25 Вб;
2) модуль ЭДС самоиндукции в интервале времени от 1 до 5 с равна 0,625 В;
3) максимальное значение модуля ЭДС самоиндукции для данного графика равна 2,5 В;
4) энергия магнитного поля катушки за 2 секунды, начиная с момента времени t = 6 c равна 0,15625 Дж.
Дано:
L=2,5 Гн
Решение:
1) Модуль магнитного потока через катушку равен:
Утверждение 1 верно.
2) ЭДС самоиндукции согласно формуле равна:
Утверждение 2 неверно.
3) Согласно графику максимальное ЭДС самоиндукции будет на интервале от 5с до 6с.
Утверждение 3 верно.
4) Энергия магнитного поля катушки:
Утверждение 4 неверно.
Правильные варианты: 1); 3).
Явление электромагнитной индукции очень часто наблюдается в электротехнике. Взаимное влияние электрических и магнитных полей иногда приводит к интересным результатам. Самоиндукция – частный случай электромагнитной индукции.
Общеизвестно, что причиной порождения электрического тока является переменное магнитное поле. Именно этот принцип реализован в конструкциях современных генераторов. Природа самоиндукции также связана с электромагнетизмом, но это явление проявляется она по-другому.
Определение
Рассмотрим схему катушки, по обмоткам которой протекает электрический ток (рис. 1). Так как вокруг проводника, который находится под током, всегда существует связанное с ним магнитное поле, то силовые линии этого поля пронизывают плоскости витков. В результате такого взаимодействия соленоиды образуют собственное магнитное поле, магнитные линии которого замыкаются за его пределами.
Частным случаем катушки является замкнутый контур (один виток). В нём, как и в катушке, образуется собственное магнитное поле (см. рис. 2). Если ток постоянный, то в контуре никаких изменений не происходит.
Но при изменении параметров, например, в результате размыкания цепи, изменяется магнитный поток, создаваемый электрическим полем, что является причиной возникновения ЭДС индукции. Аналогичное изменение произойдёт и в случае замыкания цепи.
Изменение параметров магнитного поля вызывает появление вихревого электрического поля, что в свою очередь приводит к возбуждению индуктивной электродвижущей силы. Возникновение ЭДС индукции, в результате изменения ток в замкнутом контуре, называется самоиндукцией.
Магнитный поток, ограниченный поверхностью контура, меняется прямо пропорционально изменению тока, циркулирующего в нём.
Направление вектора ЭДС самоиндукции не совпадает с направлением тока в период его возрастания (при замыкании цепи), но он сонаправлен с ним в период убывания (разъединения цепи). Такое действие проявляется в замедлении появления тока в соленоиде при замыкания цепи, или в его задержке на какое-то время после разрыва цепи.
Описанное явление можно наблюдать на опыте с лампочками, одна из которых подключена последовательно с индуктивностью (см. рис. 3).
Как видно на рисунке слева, ток от источника питания, проходящий через лампочку 2, при замыкании контактов встретит сопротивление вихревых токов, поскольку они противоположно направлены. Поэтому зажигание этой лампочки произойдёт с задержкой.
На время включения лампочки 1 вихревые токи повлияют, но сила тока в её цепи уменьшится после зажигания лампы 2. При отключении цепи от источника питания произойдёт обратный процесс: лампочка в цепи индуктивности некоторое время будет медленно угасать, а вторая лампа потухнет сразу после разъединения контактов.
График на рисунке 4 красноречиво объясняет эффект задержки.
Обратите внимание на нелинейность изменения силы тока по времени.
Аналогичные процессы происходят в цепи, состоящей из одной катушки. На рисунке 5 изображена такая схема и график изменения силы тока.
Остаётся добавить, что скорость изменение величины ЭДС зависит от количества витков соленоида. Чем больше витков, тем больше влияние вихревых токов, на параметры цепи.
В случае с переменным током амплитуда ЭДС самоиндукции пропорциональна амплитуде синусоиды питания, её частоте и индуктивности катушки.
Синусоидальный ток, проходя через катушку индуктивности, сдвигается по фазе на величину π/2. Именно этот сдвиг является причиной отставания собственного тока катушки от тока, вырабатываемого источником питания.
Формулы
Собственный магнитный поток контура (Ф) связан прямо пропорциональной зависимостью с индуктивностью (L) этого контура и величиной тока в нём (i). Данная зависимость выражается формулой: Ф = L×i. Коэффициент пропорциональности L принято называть коэффициентом самоиндукции или же просто индуктивностью контура.
При этом индуктивность контура пребывает в зависимости от его геометрии, площади плоскости ограниченной витком и магнитной проницаемости окружающей среды. Но этот коэффициент не зависит от силы тока в контуре. Если же форма, линейные размеры и магнитная проницаемость не изменяются, то для определения величины индуктивной ЭДС применяется формула:
где Eсамоинд. – ЭДС самоиндукции, Δi – изменение силы тока за время Δt.
Индуктивность
Выше мы отметили, что индуктивность контура зависит от его геометрии и размеров, а также от магнитной проницаемости среды. Если речь идёт о катушке, то эти утверждения справедливы и для неё. На индуктивность катушки влияет её диаметр и количество витков. Индуктивность существенно повышается, если в катушку добавить ферромагнитный сердечник.
Магнитные поля отдельных витков катушки складываются. Если витков достаточно много, то ток, протекающий через катушку, образует вокруг неё сильное магнитное поле, реагирующее на изменения электрического поля. Индуктивность является той величиной, которая характеризует то, насколько сильно проводник, из которого состоят витки, противодействует электрическому току.
Чем больше индуктивность катушки и чем выше скорость прерывания её цепи, тем больший всплеск ЭДС произойдёт в цепи. При этом полярность вихревых токов на выводах катушки противоположна направлению тока источника питания.
Индуктивность (то есть коэффициент пропорциональности) является важной характеристикой катушек, дросселей и других контурных элементов. Этот параметр можно сравнить с ёмкостью конденсаторов. Тем более что действие катушки индуктивности и конденсатора в электрических цепях очень похожи. RL и RC цепочки часто используют для сглаживания всплесков напряжений в различных фильтрах.
Единицей измерения индуктивности в международной системе СИ является генри. Величина размеров в 1 Гн – это такая индуктивность, при которой ЭДС составляет 1 В, при скорости изменения тока на 1 А за секунду.
Индуктивность определяет количество энергии, выделяющейся в результате действия собственного магнитного поля при самоиндукции. Эту энергию легко рассчитать по формуле: Wм = LI2/2.
Собственная энергия катушки численно равна работе, которую необходимо выполнить источником питания при преодолении ЭДС самоиндукции.
Важно знать, что в результате резкого разрыва цепи с большой индуктивностью, энергия высвобождается в виде искры или даже с образованием дугового разряда.
Примеры использования на практике
Явление самоиндукции нашло широкое практическое применение. Автолюбители прекрасно знают, что такое катушка зажигания. Без неё карбюраторный двигатель не запустится.
Работает этот важный узел следующим образом:
- На катушку с большой индуктивностью подаётся бортовое напряжение 12 В.
- Электрическая цепь резко обрывается специальным прерывателем.
- Накопленная энергия самоиндукции поступает по высоковольтным проводам на свечу и образует на её электродах мощную искру.
- Искровой разряд зажигает топливную смесь, приводя в движение поршень.
В современных автомобилях разрыв цепи выполняет электроника, но суть от этого не меняется – для образования искры по-прежнему используется энергия самоиндукции.
Мы уже упоминали о сетевых фильтрах, в которых используется явление самоиндукции. RL цепочка реагирует на любое изменение параметров. При его возрастании она задерживает во времени пиковые скачки и заполняет собственными вихревыми токами провалы. Таким образом, происходит сглаживание напряжения в электрически цепях.
В блоках питания электронной аппаратуры таким же способом убирают:
- шумы:
- пульсации;
- нежелательные частоты.
Самоиндукция дросселей используется в люминесцентных лампах для розжига электродов. После срабатывания стартера происходит разрыв контактов, в результате чего в дросселе наводится ЭДС самоиндукции. Энергия дросселя разжигает дугу на электродах, и люминесцентная лампа начинает светиться.
Перечисленные примеры демонстрируют полезное применение самоиндукции. Однако, как это всегда бывает, индуктивная ЭДС может наносить вред. При разъединении контактов выключателей, нагрузкой которых являются цепи с большой индуктивностью, возможны дуговые разряды. Они разрушают контакты, замедляют время защиты и т.п. С целью снижения риска от негативных влияний самоиндукции автоматические выключатели оборудуют дугогасительными камерами.
В таких случаях приходится принимать меры для нейтрализации энергии ЭДС самоиндукции. Ещё большая потребность в рассеянии энергии самоиндукции возникает в полупроводниковых ключах, чувствительных к пробоям.
В промышленности и энергетике самоиндукция является серьёзной проблемой. При отключении нагруженных линий ЭДС самоиндукции может достигать опасных для жизни величин. Это требует дополнительных затрат на принятие мер предосторожности. В частности, необходимо устанавливать на линиях устройства, препятствующие молниеносному размыканию цепи.
