Силу переменного тока (напряжения) можно
охарактеризовать при помощи амплитуды.
Однако амплитудное значение тока
непросто измерить экспериментально.
Силу переменного тока удобно связать
с каким-либо действием, производимым
током, не зависящим от его направления.
Таковым является, например, тепловое
действие тока. Поворот стрелки амперметра,
измеряющего переменный ток, вызывается
удлинением нити, которая нагревается
при прохождении по ней тока.
Действующим
илиэффективнымзначением
переменного тока (напряжения) называется
такое значение постоянного тока, при
котором на активном сопротивлении
выделяется за период такое же количество
теплоты, как и при переменном токе.
Свяжем
эффективное значение тока с его
амплитудным значением. Для этого
рассчитаем количество теплоты, выделяемое
на активном сопротивлении переменным
током за время, равное периоду колебаний.
Напомним, что по закону Джоуля-Ленца
количество теплоты, выделяющееся на
участке цепи cсопротивлениемприпостоянномтоке
за время
,
определяется по формуле.
Переменный ток можно считать постоянным
только в течение очень малых промежутков
времени.
Поделим период колебанийна очень большое число малых промежутков
времени.
Количество теплоты,
выделяемое на сопротивленииза время
:
.
Общее количество теплоты, выделяемое
за период, найдется суммированием
теплот, выделяемых за отдельные малые
промежутки времени, или, другими словами,
интегрированием:
.
Сила тока в
цепи изменяется по синусоидальному
закону
,
тогда
.
Опуская
вычисления, связанные с интегрированием,
запишем окончательный результат
.
Если бы по
цепи шёл некоторый постоянный ток
,
то за время, равное,
выделилось бы тепло.
По определению постоянный ток,
оказывающий такое же тепловое действие,
что и переменный, будет равен эффективному
значению переменного тока.
Находим эффективное значение силы
тока, приравнивая теплоты, выделяемые
за период, в случаях постоянного и
переменного токов
(4.28)
Очевидно,
точно такое же соотношение связывает
эффективное и амплитудное значения
напряжения в цепи с синусоидальным
переменным током:
(4.29)
Например,
стандартное напряжение в сети 220 В –
это эффективное напряжение. По формуле
(4.29) легко посчитать, что амплитудное
значение напряжения в этом случае будет
равно 311 В.
4.4.5. Мощность в цепи переменного тока
Пусть на некотором участке цепи с
переменным током сдвиг фаз между током
и напряжением равен
,
т.е. сила тока и напряжение изменяются
по законам:
,
.
Тогда мгновенное
значение мощности, выделяемой на участке
цепи,
.
Мощность
изменяется со временем. Поэтому можно
говорить лишь о ее среднем значении.
Определим среднюю мощность, выделяемую
в течение достаточно длительного
промежутка времени (во много раз
превосходящего период колебаний):
.
С использованием
известной тригонометрической формулы
получим
.
Величину
усреднять не нужно, так как она не зависит
от времени, следовательно:
.
За длительное
время значение косинуса много раз
успевает измениться, принимая как
отрицательные, так и положительные
значения в пределах от (1)
до 1. Понятно, что среднее во времени
значение косинуса равно нулю
,
поэтому(4.30)
Выражая
амплитуды тока и напряжения через их
эффективные значения по формулам (4.28)
и (4.29), получим
. (4.31)
Мощность, выделяемая на участке цепи с
переменным током, зависит от эффективных
значений тока и напряжения и сдвига
фаз между током и напряжением. Например,
если участок цепи состоит из одного
только активного сопротивления, тои
.
Если участок цепи содержит только
индуктивность или только ёмкость, тои
.
Объяснить среднее нулевое значение
мощности, выделяемой на индуктивности
и ёмкости можно следующим образом.
Индуктивность и ёмкость лишь заимствуют
энергию у генератора, а затем возвращают
её обратно. Конденсатор заряжается, а
затем разряжается. Сила тока в катушке
увеличивается, затем снова спадает до
нуля и т. д. Именно по той причине, что
на индуктивном и ёмкостном сопротивлениях
средняя расходуемая генератором энергия
равна нулю, их назвали реактивными. На
активном же сопротивлении средняя
мощность отлична от нуля. Другими словами
провод с сопротивлением
при протекании по нему тока нагревается.
И энергия, выделяемая в виде тепла, назад
в генератор уже не возвращается.
Если участок цепи содержит несколько
элементов, то сдвига фаз
может быть иным. Например, в случае
участка цепи, изображенного на рис. 4.5,
сдвиг фаз между током и напряжением
определяется по формуле (4.27).
Пример 4.7.К генератору переменного
синусоидального тока подключён резистор
с сопротивлением.
Во сколько раз изменится средняя
мощность, расходуемая генератором, если
к резистору подключить катушку с
индуктивным сопротивлениема) последовательно, б) параллельно (рис.
4.10)? Активным сопротивлением катушки
пренебречь.
Решение.Когда к генератору подключено
одно только активное сопротивление,
расходуемая мощность
(см. формулу (4.30)).
Рассмотрим цепь на рис. 4.10, а. В примере
4.6 было определено амплитудное значение
силы тока генератора:
.
Из векторной диаграммы на рис. 4.11,а
определяем сдвиг фаз между током и
напряжением генератора
.
В результате средняя расходуемая
генератором мощность
.
Ответ: при
последовательном включении в цепь
индуктивности средняя мощность,
расходуемая генератором, уменьшится в
2 раза.
Рассмотрим цепь на рис. 4.10,б. В примере
4.6 было определено амплитудное значение
силы тока генератора
.
Из векторной диаграммы на рис. 4.11,б
определяем сдвиг фаз между током и
напряжением генератора
.
Тогда средняя
мощность, расходуемая генератором
.
Ответ: при
параллельном включении индуктивности
средняя мощность, расходуемая генератором,
не изменяется.
Соседние файлы в папке Методички_Общая физика
- #
- #
- #
- #
- #
- #
- #
- #
Виталий Викторович Карабут
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Определение 1
Эффективным (действующим) называют значение переменного тока равное величине эквивалентного постоянного тока, который при прохождении через такое же сопротивление, что и переменный ток выделяет на нем то же количество тепла за одинаковые промежутки времени.
Количественная связь амплитуд силы и напряжения переменного тока и эффективных значений
Количество тепла, которое выделяется переменным током на сопротивлении $R$ за малый промежуток времени $dt$, равно:
Тогда за один период переменный ток выделяет тепла ($W$):
Обозначим через $I_{ef}$ силу постоянного тока, который на сопротивлении $R$ выделяет такое же количество тепла ($W$), как и переменный ток $I$ за время равное периоду колебаний переменного тока ($T$). Тогда выразим $W$ через постоянный ток и приравняем выражение к правой части уравнения (2), имеем:
Выразим из уравнения (3) силу эквивалентного постоянного тока, получим:
Если сила тока изменяется по синусоидальному закону:
подставим выражение (5) для переменного тока в формулу (4), тогда величина постоянного тока выразится как:
Следовательно, выражение (6) может быть преобразовано к виду:
где $I_{ef}$ называют эффективным значением силы тока. Аналогично записывают выражения для эффективных (действующих) значений напряжений:
Применение действующих значений тока и напряжения
Когда в электротехнике говорят о силе переменного тока и напряжении, то имеют в виду их эффективные значения. В частности, вольтметры и амперметры градуируют обычно на эффективные значения. Следовательно, максимальное значение напряжения в цепи переменного тока примерно в 1,5 раза больше того, что показывает вольтметр. Этот факт следует учесть при расчете изоляторов, исследовании проблем безопасности.
Эффективные значения используют для характеристики формы сигнала переменного тока (напряжения). Так, вводят коэффициент амплитуды ($k_a$). равный:
«Эффективные значения тока и напряжения» 👇
и коэффициент формы ($k_f$):
где $I_{sr v}=frac{2}{pi }cdot I_m$ –средневыпрямленное значение силы тока.
Для синусоидального тока $k_a=sqrt{2}, k_f=frac{pi }{2sqrt{2}}=1,11.$
Пример 1
Задание: Напряжение, которое показал вольтметр равно $U=220 В$. Какова амплитуда напряжения?
Решение:
Как было сказано, вольтметры и амперметры обычно градуируют на действующие значения напряжения (силу тока), следовательно, прибор показывает в наших обозначениях $U_{ef}=220 В.$ В соответствии с известным соотношением:
[U_{ef}=frac{U_m}{sqrt{2}}left(1.1right)]
найдем амплитудное значение напряжения, как:
[U_m=sqrt{2}U_{ef}.]
Вычислим:
[U_mapprox 1,41cdot 220=310,2 left(Вright).]
Ответ: $U_mapprox 310,2 В.$
Пример 2
Задание: Как связана мощность переменного тока на сопротивлении $R$ и эффективные значения тока и напряжения?
Решение:
Среднее значение мощности переменного тока в цепи равно
[leftlangle Prightrangle =frac{A_T}{T}=frac{U_mI_mcosvarphi }{2}left(2.1right),]
где $cosvarphi $- коэффициент мощности, который показывает эффективность передачи мощности от источника тока к потребителю. С другой стороны средние мощности тока на отдельных элементах цепи $leftlangle P_{tC}rightrangle =0,leftlangle P_{tL}rightrangle =0,leftlangle P_{tR}rightrangle =frac{1}{2}{I^2}_mR,$ а результирующая мощность может быть найдена как сумма мощностей:
[leftlangle Prightrangle =leftlangle P_{tC}rightrangle +leftlangle P_{tL}rightrangle +leftlangle P_{tR}rightrangle left(2.2right).]
Следовательно, можно записать, что:
[leftlangle Prightrangle =P_{tR}=frac{1}{2}{I^2}_mR=frac{U_mI_mcos varphi}{2}left(2.3right),]
где $I_m $- амплитуда силы тока, $U_m$ — амплитуда внешнего напряжения, $varphi$ — разность фаз между силой тока и напряжением.
У постоянного тока мгновенная мощность совпадает со средней. Для $I_{ef}$=const можно положить $cosvarphi =1, $значит формулу (2.3) можно записать как:
[P=I_{ef}U left(2.4right),]
если вместо амплитудных значений ($U_m и I_m$) использовать их эффективные (действующие) значения:
[I_{ef}=frac{I_m}{sqrt{2}}, U_{ef}=frac{U_m}{sqrt{2}}left(2.5right).]
Следовательно, мощность тока можно записать как:
[P_{tR}=U_{ef}I_{ef}cos varphi left(2.6right),]
где $cos varphi$ — коэффициент мощности. В технике этот коэффициент делают как можно большим. При малом $cosvarphi $ для того, чтобы в цепи выделялась необходимая мощность нужно пропускать большой ток, что ведет к росту потерь в подводящих проводах.
Такую же мощность (как в выражении (2.3)) развивает постоянный ток, сила которого представлена в формуле (2.5).
Ответ: $P_{tR}=U_{ef}I_{ef}cosvarphi .$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Действующее (эффективное) значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.
В современной литературе чаще используется математическое определение этой величины — среднеквадратичное значение переменного тока. Иначе говоря, действующее значение переменного тока можно определить по формуле:
Действующее значение в типичных случаях[править | править код]
Приведены формулы для электрического тока. Аналогичным образом определяются действующие значения ЭДС и напряжения.
Синусоида[править | править код]
Для синусоидального тока:
где
— амплитудное значение тока.
Прямоугольная форма[править | править код]
Для тока, имеющего форму однополярного прямоугольного импульса, действующее значение тока зависит от скважности:
где
— коэффициент заполнения (величина, обратная скважности).
В частности, для тока, имеющего форму однополярного меандра (коэффициент заполнения 0,5):
Для тока, имеющего форму двухполярного меандра:
Треугольная форма[править | править код]
Для тока треугольной и пилообразной формы (независимо от того, меняется ли направление тока):
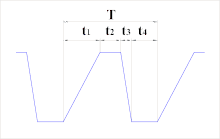
Трапециевидная форма[править | править код]
Для тока трапециевидной формы действующее значение можно определить разбив период на отрезки положительного фронта, действия максимального значения и отрицательного фронта:
где
— длительность положительного фронта;
— длительность действия максимального значения;
— длительность отрицательного фронта;
— длительность полного периода.
Дугообразная форма[править | править код]
Для тока имеющего форму дуги (половины окружности):
Дополнительные сведения[править | править код]
В англоязычной технической литературе для обозначения действующего значения употребляется термин effective value — эффективное значение. Также применяется аббревиатура RMS или rms — root mean square — среднеквадратичное (значение).
Электроизмерительные приборы (амперметры, вольтметры) для измерения в цепях переменного тока обычно градуируются так, чтобы их показания соответствовали действующему значению синусоидального тока или напряжения. При измерении несинусоидальных токов и напряжений приборы различных систем могут давать разные показания[1].
См. также[править | править код]
- Список параметров напряжения и силы электрического тока
Примечания[править | править код]
- ↑ 11.8. Показания приборов различных систем в цепях несинусоидального тока. StudFiles. Дата обращения: 16 февраля 2019.
Литература[править | править код]
- «Справочник по физике», Яворский Б. М., Детлаф А. А., изд. «Наука», 1979 г.1
- Курс физики. А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5
- «Теоретические основы электротехники», Л. А. Бессонов: Высш. шк., 1996. § 7.8 — § 7.10
Ссылки[править | править код]
- Действующие значения тока и напряжения
- Среднеквадратичное значение
Эффективные значения тока и напряжения
При вычислении работы и мощности нельзя пользоваться ни мгновенными, ни амплитудными значениями тока и напряжения. Переменный ток считают эквивалентным постоянному току такой же мощности, и таким образом определяют эффективные (действующие) значения напряжения и силы тока.
Эффективные значения тока и напряжения
Так как при постоянном сопротивлении мощность пропорциональна квадрату силы тока или напряжения
[ (Р sim I^{2} enspace и enspace Р sim V^{2}) ]
эффективное значение выражается через квадраты мгновенных значений.
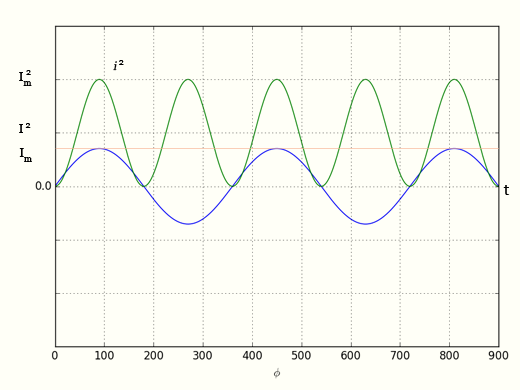
Возводя в квадрат синусоидальную функцию i(t), получаем периодическую кривую. Эффективное значение определяется средним по времени от этой функции:
[ I^{2} = average{i(t)^{2}} = frac{I^{2}_{m}}{2} ]
Если
| I | эффективная сила тока, | Ампер |
|---|---|---|
| Im | амплитуда силы тока, | Ампер |
| U | эффективное напряжение, | Вольт |
| Um | амплитуда напряжения, | Вольт |
то имеем
[ I = frac {I_{m}}{sqrt{2}}= 0.707I_{m} ]
после умножения на сопротивление получаем
[ U = frac {U_{m}}{sqrt{2}} = 0.707U_{m} ]
Эффективные значения силы тока и напряжения относятся к амплитуде (максимальному значению) как
[ frac{1}{sqrt{2}} ]
Эффективное значение тока и напряжения |
стр. 686 |
|---|
Классические измерения значений напряжения (тока) основаны на понятиях «среднее» и «эффективное». Для усреднения значения функции напряжения V во времени берётся чистая площадь функции, рассчитанная за определённый интервал времени, и делится на этот временно́й интервал:

Причём если значение напряжения (тока) является постоянной или периодической величиной, то его среднее значение не зависит от интервала, в течение которого производится измерение. С другой стороны, если функция напряжения (тока) растёт без ограничения во времени, среднее значение зависит от интервала измерения и не обязательно будет постоянным, то есть никакого среднего значения в данном случае не существует. К счастью, на практике в мире электротехники значения напряжений и токов не растут безгранично и, следовательно, имеют определимые средние значения. Это является следствием того факта, что источниками реального напряжения (тока), как правило, являются либо батареи с постоянными или медленно (экспоненциально) затухающими значениями токов/напряжений, либо генераторы, имеющие на выходе сигналы в виде ограниченных синусоидальных функций времени, либо сочетания перечисленного. Синусоидальные функции с постоянной амплитудой имеют чистое нулевое среднее значение за интервалы времени, кратные их периоду. Более того, их средние значения могут быть рассчитаны за бесконечное число интервалов, не равных периоду синусоиды. Эти средние значения также будут равны нулю. Но хотя среднее значение ограниченной синусоидальной функции равно нулю, её так называемое эффективное значение нулю не равно. В качестве примера приведём электрические водонагреватели, которые прекрасно работают, будучи запитанными от сети переменного тока с синусоидальным напряжением с нулевыми средними значениями.
Эффективное значение
Эффективное значение симметричных периодических функций напряжения (тока) от времени основано на понятии «нагревательная способность». Рассмотрим тестовую установку, показанную на рис. 1.
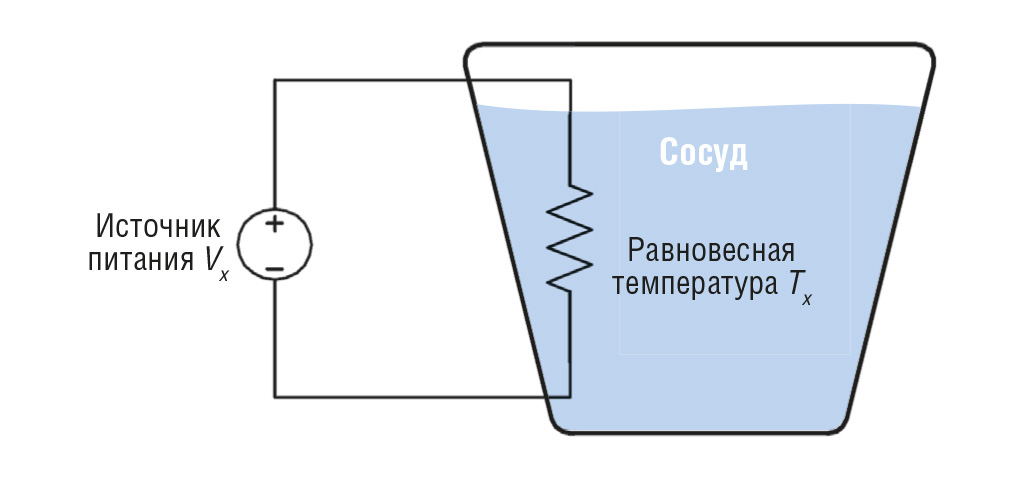
Сосуд на рисунке изолирован и заполнен некоторой стабильной жидкостью (например, трансформаторным маслом), способной достичь термодинамического равновесия. Если на внутренний нагреватель сосуда подать ток постоянного напряжения Vx, температура жидкости станет подниматься. В какой-то момент будет достигнуто состояние, при котором электрическая энергия, подаваемая на нагреватель в этом сосуде, будет равна потере энергии (тепла), и жидкость сосуда приобретёт равновесную температуру Tx градусов.
Заменим в этом экспериментальном сценарии источник постоянного напряжения Vx на источник с периодически изменяющимся во времени напряжением. Тогда через некоторое время Tfinal снова будет достигнуто тепловое равновесие. Если это условие равновесия устанавливает ту же температуру Tx, которая была достигнута ранее с приложенным напряжением постоянного тока Vx, то можно сказать, что эффективное значение этой изменяющейся во времени функции равно Vx.
Отсюда и определение эффективного значения, которое иллюстрирует формула (2):
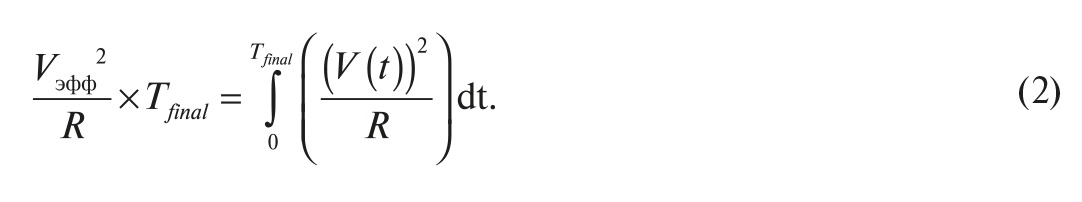
Здесь R – сопротивление. Если V(t) – периодическая функция времени с периодом Tp, а Tfinal – целое число, умноженное на период (n × Tp), то интеграл по Tfinal будет просто n-кратным интегралом по Tp. Результаты применения этих соображений приведены в формуле (3):

Формула (3) показывает, что эффективная эквивалентная теплопроизводительность ограниченной периодической функции напряжения (тока) может быть определена за один период. Это уравнение и есть представление действующего, или среднеквадратического значения электрического тока (Root Mean Square). Отсюда и происходит общеизвестная аббревиатура RMS.
Примеры использования формулы RMS
Прямое применение формулы (3) для распространённых случаев даёт следующие результаты.
.jpg)
Примечание. Приведённые примеры иллюстрируют, что среднеквадратическое значение определяется формой периодической функции. Для вычисления среднеквадратического значения часто ошибочно используется значение пика (гребня) функции напряжения (тока) во времени, делённое на 2. Этот метод может привести к ошибкам, и его определённо следует избегать.
Эффективные значения сложных функций
Чрезвычайно полезным для определения среднеквадратических значений фактом является то, что любая ограниченная во времени периодическая функция может быть выражена в виде суммы некоего постоянного значения и набора синусоид, представляющих гармонический спектр сложного колебания (преобразование Фурье).
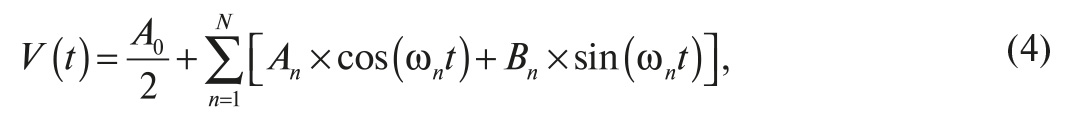
где t – текущее время; ωn=2π/T × n; T – длительность периода периодической функции; An, Bn – амплитудные коэффициенты Фурье; A0 – постоянная составляющая периодического сигнала.
Если этот ряд подставить в интегральное выражение формулы для RMS, получаем следующее:

где Fn – амплитуда n-й гармоники.
Практические соображения
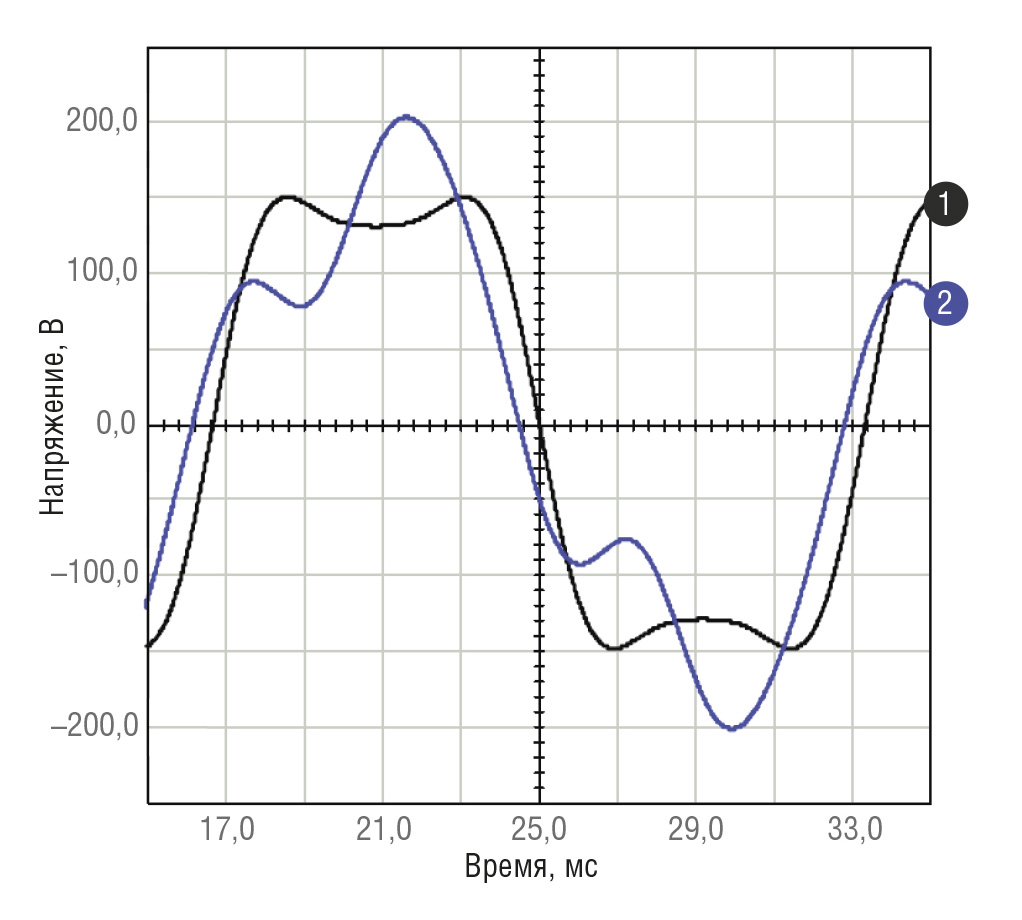
На рис. 2 показаны результирующие кривые, образованные сложением двух синусоид: одной с частотой 60 Гц и второй с частотой 180 Гц. Кривая 1 соответствует нулевому сдвигу фаз между синусоидами, а кривая 2 – сдвигу фаз 90°.
Кривая 1: V(t)=170×sin(377×t)+50×sin(1131×t).
Кривая 2: V(t)=170×sin(377×t)+50×cos(1131×t).
Форма результирующей кривой определяется гармониками фазы и частоты.
В промышленных электросетях часто присутствуют гармоники, влияющие на форму волны и её пиковые значения.
Например, кривая 2 типична для токов намагничивания в трансформаторах и двигателях при частоте 60 Гц. В недорогих устройствах для измерения среднеквадратических значений часто используются выпрямители, которые фиксируют пиковое значение, просто умножаемое затем на 0,707 и отображаемое как среднеквадратическое значение. Очевидно, что в некоторых случаях этот метод может дать ошибочные показания RMS. В этом примере использование формулы Vp/√2 явно даёт неверные результаты:
для кривой 1 получаем: 203 × 0,707 = 144 В, что не является истинным среднеквадратическим значением;
для кривой 2 получаем: 155 × 0,707 = 110 В, что также не является истинным среднеквадратическим значением.
Правильным среднеквадратическим значением для обеих этих составных функций будет следующее:
.jpg)
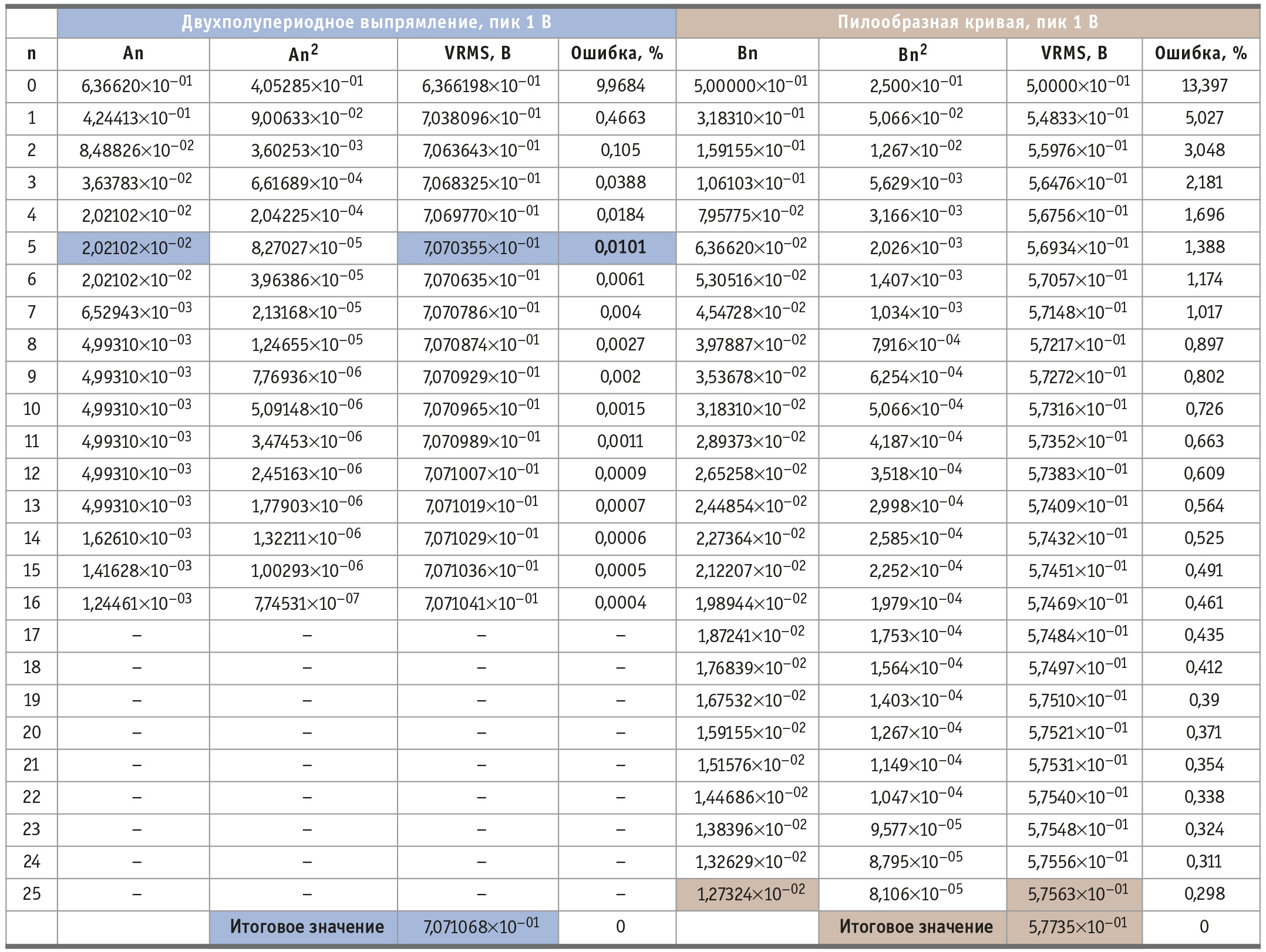
Таблица 1 иллюстрирует два примера вычислений RMS с использованием индивидуальных коэффициентов Фурье и формулы (5). Первым примером является выпрямленная двухполупериодным выпрямителем синусоида с пиком 1 В. Обратите внимание, что для функции двухполупериодного выпрямления измерительному устройству, необходимому для получения показаний RMS с погрешностью 0,01%, требуется полоса пропускания, захватывающая пятую гармонику, и разрешение 10 мВ.
Другой пример, проиллюстрированный таблицей 1, представляет собой пилообразную функцию напряжения 1 В.
В этом примере измерительному устройству, необходимому для получения показаний RMS с погрешностью 0,3%, требуется полоса пропускания, захватывающая двадцать пятую гармонику, и разрешение 10 мВ.
В целях иллюстрации предположим, что пульсации переменного тока на выходе выпрямителя могут быть аппроксимированы пилообразной функцией. В табл. 1 показано, что для измерения среднеквадратических пульсаций переменного тока с пиковыми значениями 10 мВ на выходе выпрямленной синусоиды частотой 20 кГц с погрешностью 0,3% измерительное устройство должно иметь полосу пропускания более 500 кГц и разрешение для фиксации уровней напряжения 40 дБ (100 мкВ). Этот пример ясно показывает, что на точность измерения истинного среднеквадратического значения чрезвычайно сильно влияют форма измеряемого сигнала, ширина полосы пропускания и разрешение.
Любое устройство измерения истинного среднеквадратического значения должно быть способно точно реализовать формулу (3). Тонкость этого утверждения состоит в том, что электронная реализация формулы (3) требует, чтобы устройство имело очень широкую полосу пропускания и было способно распознавать малые измеряемые величины.
Пик-коэффициент
Ещё одним показателем качества источника питания, часто используемым для описания периодической временно́й функции напряжения (тока), является пик-коэффициент, или пик-фактор (Crest Factor – CF). Это показатель, характеризующий способность источника питания питать нелинейную нагрузку, потребляющую импульсный ток. Пик-коэффициент для конкретной формы волны определяется как пиковое значение, делённое на среднеквадратическое значение:

Для ранее приведённых типовых случаев RMS можно вычислить и CF:
- Чистая синусоида: CF=√2
- Меандр: CF = 1.
- Несимметричная периодическая импульсная волна со спадами D: CF=1/√D
- Симметричная периодическая треугольная волна: CF=√3
- Выпрямленная двухполупериодным выпрямителем синусоида: CF=√2
- Выпрямленная однополупериодным выпрямителем синусоида: CF=2.
Для рис. 2 получаем:
кривая 1: CF = 1,62;
кривая 2: CF = 1,24.
Измерительные устройства Dataforth RMS

Итак, для качественных измерений среднеквадратических значений требуются измерительные приборы, которые точно реализуют уравнение среднеквадратического значения. Эти устройства должны иметь широкую полосу пропускания и хорошее разрешение для сигналов низкого уровня, что позволяет им поддерживать измерения при высоких значениях пик-коэффициентов. Компания Dataforth разработала два продукта, удовлетворяющих этим требованиям, – True RMS-модули ввода SCM5B33 (рис. 3) и DSCA33 (рис. 4). Оба этих продукта обеспечивают гальваническую изоляцию 1500 В между входом и выходом. SCM5B33 – это съёмный панельный модуль, а DSCA33 – устройство, предназначенное для монтажа на DIN-рейку. Каждый из них обеспечивает один канал входа переменного тока, значение которого преобразуется в истинное среднеквадратическое значение постоянного тока, фильтруется, гальванически развязывается, усиливается и преобразуется в выходной сигнал напряжения или тока.

Модуль SCM5B33
Модуль ввода SCM5B33 True RMS (рис. 5) обеспечивает один канал входа переменного тока, который преобразуется в стандартное выходное напряжение или ток процесса.
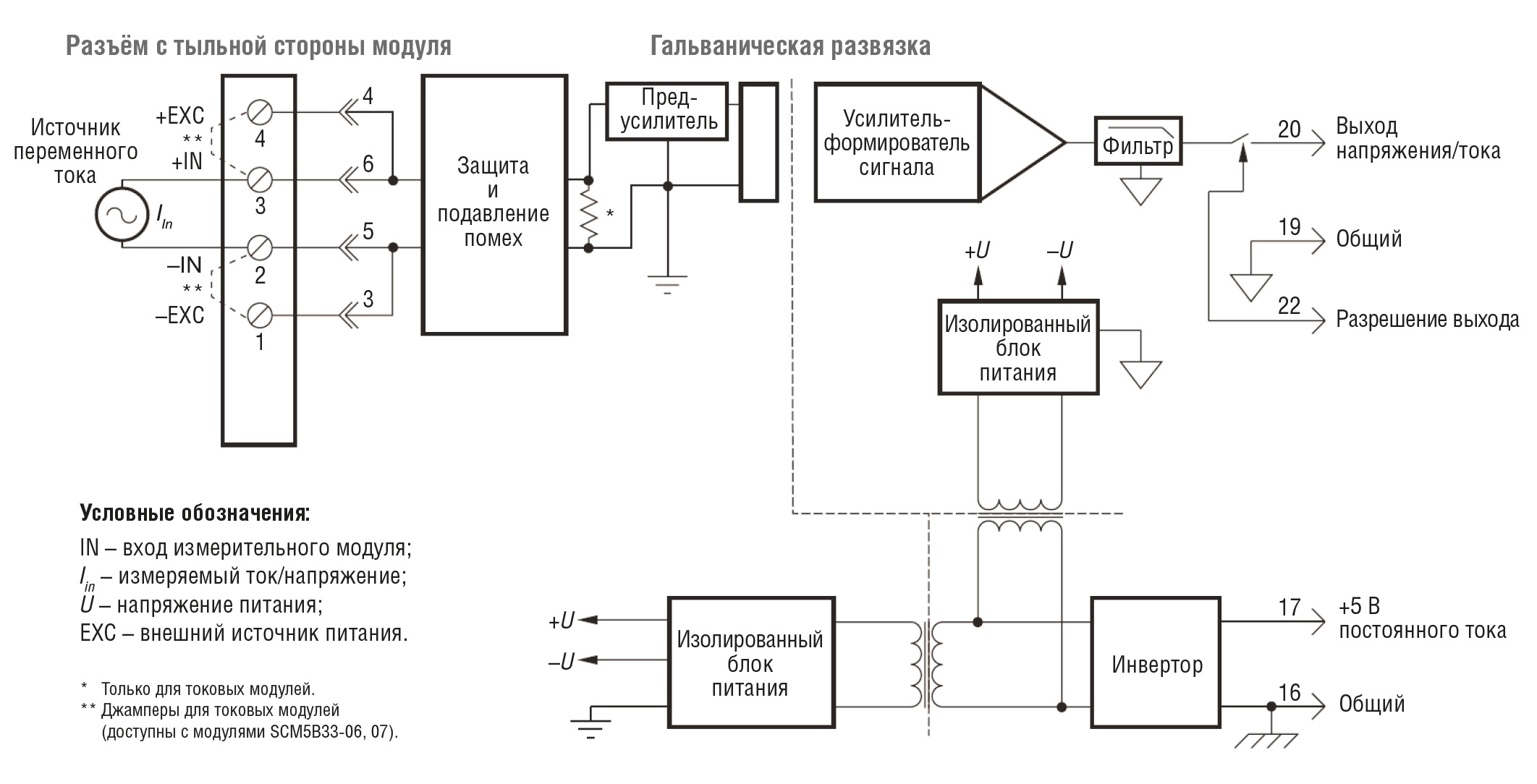
Модули SCM5B содержат полностью изолированную со стороны компьютера цепь, на которую может быть подано до ±50 В относительно общего провода (контакт 16). Эта полная изоляция означает, что для правильной работы выхода не требуется никакого соединения между общим входом/выходом и общим питанием. При желании выход модуля можно сделать включённым постоянно, просто подключив контакт разрешения чтения 22 к общему проводу ввода/вывода (контакт 19).
Входной сигнал напряжения или тока с полевой стороны обрабатывается предварительным усилителем и преобразователем среднеквадратических значений на полевой стороне изолирующего барьера. Преобразованный в постоянный ток сигнал затем гальванически развязывается запатентованной схемой и передаётся через трансформаторный изолирующий барьер, подавляющий передачу синфазных пиков и выбросов. Схема на стороне компьютера восстанавливает сигнал и преобразует его к стандартному выходному уровню. Модули питаются от +5 В постоянного тока ±5%.
Для моделей с токовым выходом требуется внешний источник питания с согласованным напряжением от 14 до 48 В постоянного тока. Подключение с последовательной нагрузкой осуществляется между контактом 20 (+) и контактом 19 (–).
Основные характеристики модуля
- Измерение напряжения RMS (0…300 В) или тока (0…5 А).
- Предназначен для стандартной работы с частотами от 45 до 1000 Гц (расширенный диапазон до 20 кГц).
- Совместим со стандартными трансформаторами тока и потенциальными трансформаторами.
- Отраслевые стандарты выхода: 0…1, 0…20, 4…20 мА, 0…5 или 0…10 В постоянного тока.
- Точность ±0,25%, калибруется на производстве.
- Гальваническая изоляция на основе трансформатора 1500 В (среднеквадратическое значение).
- Защита от перегрузки по входу до 480 В макс. (пиковый и постоянный ток) или 10 А RMS непрерывно.
- Сертификаты ANSI/IEEE C37.90.1-1989, CSA, FM.
Модуль DSCA33
Модуль ввода DSCA33 True RMS (рис. 6) по всем основным характеристикам идентичен SCM5B33. Отличие состоит в его конструктиве, оптимизированном для размещения на DIN-рейке.
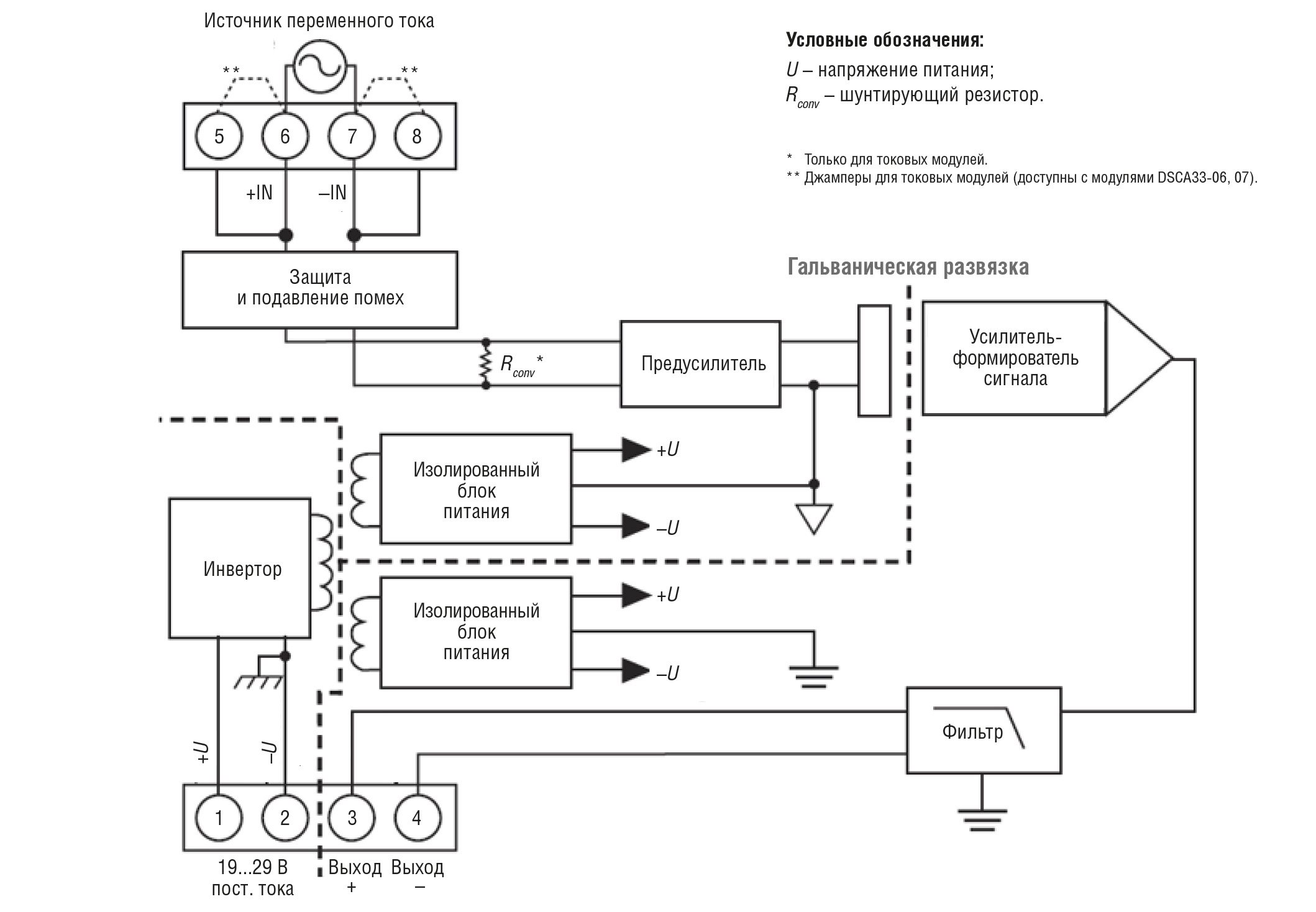
Модули DSCA33 обладают превосходной стабильностью во времени и не требуют повторной калибровки, однако в ситуациях, когда необходима точная настройка, это можно сделать вручную. Регулировки выполняются с помощью потенциометров, расположенных под этикеткой на передней панели, и не являются интерактивными.
Заключение
Итак, мы увидели, что измерить и рассчитать действующее значение тока или напряжения в условиях нестабильных показателей сетей реального производства не так-то просто: для этого требуется привлечение довольно сложного математического аппарата либо использование готовых качественных измерительных модулей из разряда рассмотренных в этой статье. Второе, разумеется, будет более практичным и простым решением. Что же касается надёжности и качества этих модулей Dataforth, то можно отметить их широкий диапазон рабочих температур –40…+80°C, малую погрешность измерений (класс точности 0,2), как для синусоидальных, так и для несинусоидальных токов, а также соответствие требованиям директивы 2014/34/EU (ATEX) для взрывозащищённого оборудования. ●
Статья подготовлена по материалам компании Dataforth
E-mail: textoed@gmail.com