Как найти эффективную оценку

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 апреля 2021 года; проверки требуют 4 правки.

Эффекти́вная оце́нка в математической статистике — наилучшая оценка в классе в среднеквадратичном смысле.^[1]

Определение[править | править код]

Оценка параметра называется эффективной оценкой в классе , если для любой другой оценки выполняется неравенство для любого .

Особую роль в математической статистике играют несмещенные оценки. Если несмещенная оценка является эффективной оценкой в классе несмещенных и дисперсия совпадает с оценкой в неравенстве Крамера-Рао, то такую статистику принято называть просто эффективной.

Единственность[править | править код]

Эффективная оценка в классе
, где — некоторая функция,
существует и единственна с точностью до значений на множестве , вероятность попасть в которое равна нулю ().

Асимптотическая эффективность[править | править код]

Некоторые оценки могут быть не самыми эффективными на малых выборках, однако могут обладать преимуществами на больших выборках. Обычно рассматриваются состоятельные оценки, дисперсия которых с увеличением объема выборки стремится к нулю. Поэтому сравнить такие оценки можно по скорости сходимости, то есть фактически по дисперсии (ковариационной матрицы) случайной величины (вектора) . В частности, асимптотически нормальная оценка

является асимптотически эффективной, если асимптотическая ковариационная матрица V минимальна в данном классе оценок.

См. также[править | править код]

• Статистическая оценка
• Неравенство Крамера — Рао

Примечания[править | править код]

Содержание:

Оценки и методы их получения:

Приближенные значения параметров, входящих в законы распределения, определяемые каким-либо способом по выборкам, называются оценками или статистиками. Оценки бывают точечными и интервальными. Точечные оцен­ки представляются одним числом, интервальные – двумя числами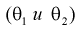

Метод моментов

Пусть генеральная случайная величина X имеет плотность распределения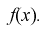

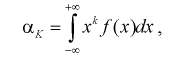                                   (8.1)

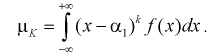                              (8.2)

По выборке 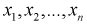 определяем выборочные начальные и центральные моменты:

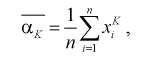                (8.3)

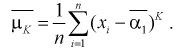           (8.4 )

Метод моментов состоит в том, что генеральные моменты (8.1, 8.2), в которые входят оцениваемые параметры, приблизительно приравниваются к со­ответствующим выборочным моментам (8.3), (8.4). Составляется система уравнений:
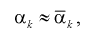                             (8.5)
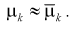                                (8.6)

Решая систему (8.5), (8.6), находим оцениваемые параметры.
Особо важную роль играет 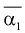 – выборочный начальный момент 1-го по­ рядка, он называется выборочным средним и обозначается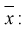

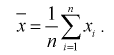    (8.7)

Следующим по важности выборочным моментом является выборочный центральный момент 2-го порядка 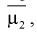 который называется выборочной дисперсией и обозначается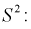
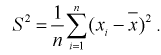                                    (8.8)

Наиболее часто используются две формулы метода моментов.
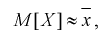                                        (8.9)

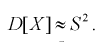         (8.10)

Сформулируем метод моментов в общем виде.
 

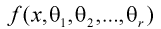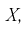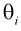Пусть плотность распределения случайной величины  где  – неизвестные параметры. Чтобы найти оценки  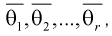выражаем первые  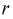начальных или центральных моментов случайной величины X через параметры  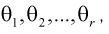затем генеральные моменты аппроксимируем соответствующими выборочными. В результате имеем систему из  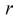уравнений с 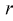неизвестными, откуда и получаем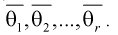
 

Пример:

Пусть генеральная случайная величина X имеет показательный закон распределения с плотностью 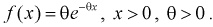 По выборке  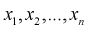методом моментов найти оценку параметра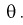

 1. Определяем 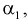 используя (8.1): 

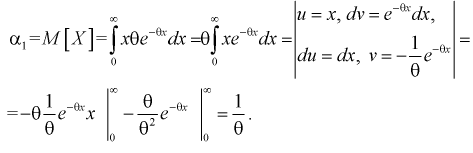
2. По (8.3) или (8.7) находим выборочный начальный момент 1-го поряд­ка или 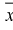 и составляем выражение вида (8.5) или (8.9):

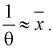
3. Заменяя в п. 2 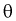 на оценку  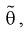составим уравнение: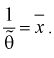

4. Откуда определим оценку параметра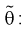

 

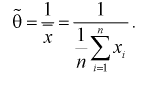
Метод наибольшего правдоподобия

Этот метод предложен математиком Фишером в 1912 г.
 

Пусть 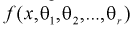 – плотность распределения генеральной случайной величины X, где  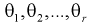– неизвестные параметры. Согласно методу, наилучшими оценками  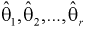параметров  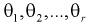являются такие, для которых функция правдоподобия L принимает наибольшее значение.

Для непрерывной случайной величины

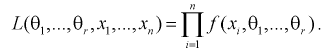   (8.11)

Для дискретной случайной величины

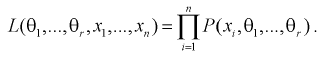                  (8.12)
Здесь 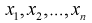– выборка из генеральной случайной величины X.
Априорные выборочные значения 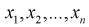 – являются независимыми случайными величинами, закон распределения которых совпадает с законом распределения генеральной случайной величины X. Тогда правую часть (8.11) на основании теоремы умножения законов распределений (см. раздел 3.5) можно рассматривать как плотность распределения вероятности 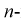мерного вектора  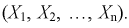Согласно методу, для наилучших оценок  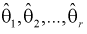случайный вектор  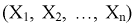будет иметь наибольшую плотность распределения. То есть надо найти такие оценки  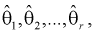для которых функция правдоподобия L – максимальна. Для этого составляют и решают такую систему уравнений:
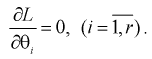                                   (8.13)

Так как функция и ее логарифм достигают экстремума в одной точке, то часто для упрощения решения задачи используют логарифмическую функцию правдоподобия. В случае логарифмической функции правдоподобия составляется система следующих уравнений:
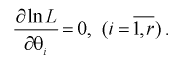                            (8.14)
 

Пример:

Пусть генеральная случайная величина X имеет показательный закон распределения с плотностью 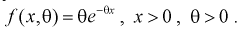 По выборке 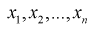методом наибольшего правдоподобия найти оценку параметра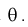

 1. Так как нам необходимо оценить один параметр 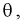 то надо составить и решить одно уравнение. Найдем функцию правдоподобия, используя (8.11):

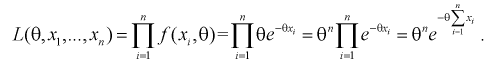
2. Составим логарифмическую функцию правдоподобия:

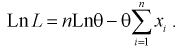
3. Для определения максимума логарифмической функции правдоподо­бия составляем и решаем следующее уравнение:

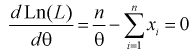
Откуда оценка 0 параметра 0 определяется так:

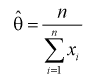
При сравнение это выражение с оценкой 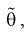 полученной по методу моментов (см. раздел 8.1), мы понимаем, что они одинаковы. Методы, рассмотренные нами, как видим, абсолютно разные. Это свидетельствует о их достоверности.

Свойства оценок

Пусть 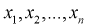 – выборка из генеральной совокупности. Обозначим оценку параметра  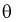через 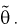 Ранее мы показали, что эта оценка определяется с помощью различных методов по полученной выборке , т. е. являляется функцией от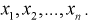

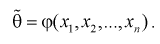
Так как любая выборка типа 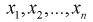– случайна, то и выборочные функции  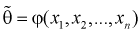– тоже являются случайными. Следовательно, она тоже имеет свои характеристики.
 

1. Оценка 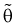 называется несмещенной, если ее математическое ожида­ние совпадает с самим оцениваемым параметром:

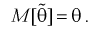
В противном случае оценка называется смещенной.

 

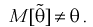
Полную погрешность 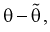 возникшую от замены 0 на 0, можно пред­ставить так:

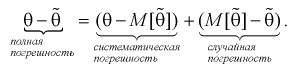
Таким образом, если оценка несмещенная, то систематическая погреш­ность равна нулю, т. е.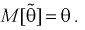

Наиболее опасна систематическая ошибка, если она заранее неизвестна или среднее квадратичное отклонение не очень большое. Среднее значение случайной ошибки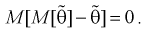

Мы уже отмечали, что 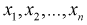– независимые случайные величины, имеющие тот же закон распределения, что и  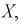генеральная случайная величина, в частности, выборочное математическое ожидание и дисперсия имеет те же числовые характеристики, т. е. справедливы тождества:

                                   (*)

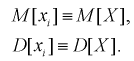Проверим смещенность оценки математического ожидания выборочной средней 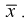 Используя обычные свойства математического ожидания, найдем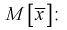

 

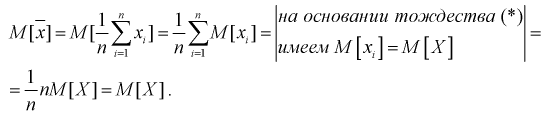
Обозначим 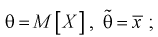 видим, что 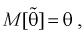значит, выборочное среднее  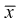является несмещенной оценкой математического ожидания.

Проверим смещенность оценки дисперсии выборочной дисперсией 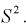 Найдем математическое ожидание от выборочной дисперсии:

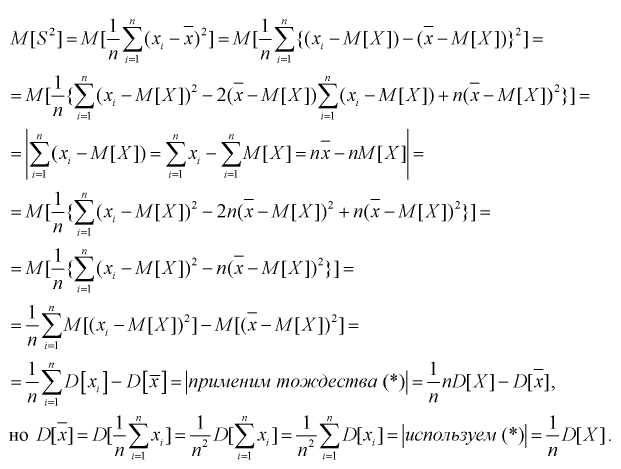
То есть дисперсия выборочной средней в 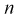 раз меньше дисперсии генеральной случайной величины. Тогда

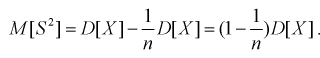
Обозначим 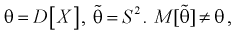 значит, выборочная дисперсия  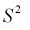является смещенной оценкой дисперсии. Можно отметить, что выборочная дисперсия  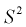является асимптотически несмещенной оценкой, т. к. при  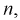стремящемся к бесконечности, смещение стремится к нулю.

При решении практических задач часто используется несмещенная оцен­ка дисперсии – это модифицированная выборочная дисперсия:

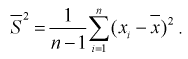
Найдем математическое ожидание от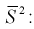

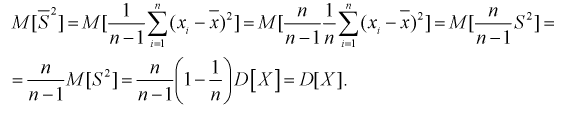
Обозначим 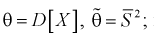 как видим,  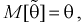значит, оценка  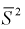уже несмещенная. При малых  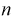этой формулой пользоваться лучше (при и > 30 оценки совпадают). На практике используют еще одну несмещенную оценку дисперсии – когда известно математическое ожидание:

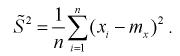
Найдем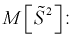 

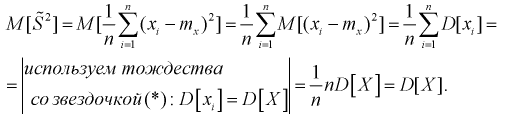
Обозначим 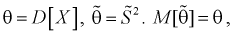 значит, оценка  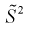несмещенная.
 

2. Оценка 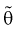 параметра  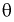называется состоятельной, если она сходит­ся по вероятности к параметру 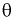, т. е. если  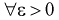выполняется:

                            

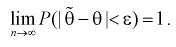
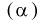
Условие 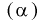на практике проверить трудно. Поэтому для проверки состоятельности оценок применяют более простые условия:

а)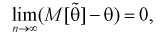

б)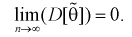

Как видим, оценка 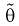 будет состоятельной, если при  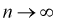смещение устраняется и дисперсия оценки стремится к нулю.
 

Пример:

Проверим состоятельность оценки математического ожидания выборочной средней 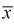. Ранее мы показали, что  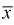является несмещенной оценкой математического ожидания, т. е. условие а) выполняется и без вычисления предела. Проверим условие б), найдем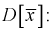 

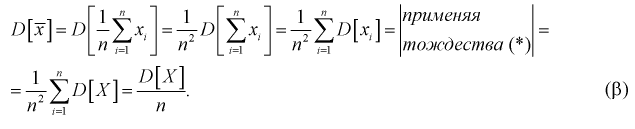
Видим, что при 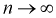 предел  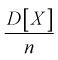будет стремиться к нулю, значит условие б) выполняется. Следовательно,  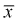является состоятельной оценкой математического ожидания.

3. Несмещенная оценка 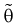 параметра  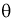называется эффективной, если она имеет наименьшую дисперсию среди всех оценок при одном и том же объеме выборки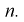
Для определения наименьшей дисперсии эффективной оценки 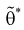 параметра  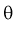применяется формула Рао-Крамера:

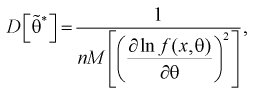                   (8.15)

где 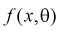 – плотность распределения генеральной случайной величины X.
Отметим, если оценка 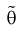 смещенная, то малость ее дисперсии еще не говорит о ее эффективности. Например, если в качестве оценки  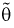взять любую постоянную величину с, то ее дисперсия будет равна нулю, а ошибка может быть какой угодно большой.
 

Пример:

Задана нормальная случайная величина 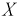 с плотностью распределения

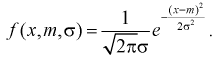
Проверим эффективность оценки математического ожидания выборочной средней .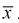

Найдем дисперсию эффективной оценки параметра 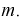 Обозначим эффективную оценку 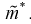Чтобы воспользоваться формулой Рао-Крамера (8.15), вычислим

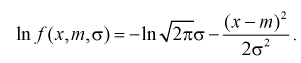
Найдем производную:

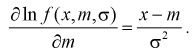
Подставим полученное выражение в (8.15): 

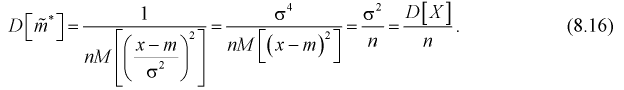
Ранее мы показали, что такую же дисперсию имеет 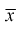 (см. формулу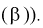
Видим, что правые части формул (8.16) и 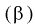 совпадают, следовательно, выборочное среднее  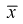является эффективной оценкой параметра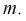

Отметим, что оценки, полученные методом наибольшего правдоподобия, являются состоятельными. Если существуют эффективная оценка, то метод наибольшего правдоподобия позволяет найти ее, но не всегда оценки, полученные этим методом, являются несмещенными.

Эффективность оценок. Неравенство Рао-Фреше-Крамера

Для
одних и тех же параметров распределения
существует бесконечно много различных
несмещенных и состоятельных оценок.
Поэтому важной задачей является сравнение
их между собой и поиск наилучшей среди
них. Естественным критерием такого
поиска является дисперсия, как мера
разброса значений случайной величины
вокруг его среднего значения, и наилучшей
оценкой является оценка с минимальной
дисперсией.
Однако для смещенной оценки дисперсия
служит мерой близости не к оцениваемому
параметру ,
а к математическому ожиданию этой же
оценки

.
Поэтому естественно искать наилучшие
оценки с наименьшей дисперсией только
среди несмещенных оценок.

Получая
ту или иную оценку, мы должны иметь
возможность определить, обладает ли
она минимальной дисперсией из всех
возможных, или нет. С этой целью вводится
понятие эффективности оценки и
используется неравенство Рао-Фреше-Крамера.

Информацией
Фишера
о неизвестном
параметре ,
содержащейся в одном из независимых
наблюдений случайной величины ,
называется величина

,

где
в качестве

берется либо плотность в точке x
(для непрерывных случайных величин),
либо вероятность принять значение x
(для дискретных случайных величин).
Говорят, что величина

определяет количество информации
Фишера.

Теорема
Рао-Фреше-Крамера).

Пусть задана
несмещенная оценка

,
построенная по выборке
х₁,x₂,…,x_n,
а функция плотности f(x,)
удовлетворяет следующим условиям
регулярности:

1) область G_n={x:
f(x,)>0}
не зависит от параметра ;

2) в тождествах

и

допустимо
дифференцирование по 
под знаком интеграла;

3) информация
Фишера I()
конечна и положительна.

Тогда выполняется
неравенство (Рао-Фреше-Крамера):

.

Доказательство.
Пусть

–
несмещенная оценка параметра ,
т.е.

,

где
Х = (х₁,x₂,…,x_n)
и f(X,)
– плотность распределения, так что

.

Дифференцируя по

равенства (7.4.1) и (7.4.2), получим

и
.

Умножим второе
равенство на 
и вычтем его из первого

По условию на
множестве G_n
плотность f(X,)
> 0, поэтому можно записать, что

.

Подставим полученное
выражение в равенство (7.4.3) и используя
неравенство Коши-Буняковского находим

или

Учитывая независимость
и одинаковый закон распределения
наблюдений x₁,x₂,…,x_n,
можно записать, что

Подставляя это
выражение в последнее неравенство,
окончательно получаем утверждение
теоремы D


.

Замечание 1.
Теорема верна и в дискретном случае,
если в условии 2) заменить интегралы на
суммы (по всем возможным значениям
случайной величины).

Замечание 2.
Если оценка

является
линейной функцией выборочного среднего,
т.е.

,
то первое тождество из условия 2)
эквивалентно более простому:

.

Замечание 3.
Информацию Фишера можно также представить
в виде:

и

.

Обозначим правую
часть неравенства Рао-Фреше-Крамера
через _n=1/nI().
Эта величина является нижней гранью
всех возможных дисперсий оценок.

Эффективностью
несмещенной оценки

называется
отношение
минимально возможного значения дисперсии
оценки в классе всех несмещенных оценок
параметра 
к дисперсии рассматриваемой оценки:

.

Из определения
следует, что эффективность любой
несмещенной оценки удовлетворяет
неравенству 0
1,
и чем ближе она к единице, тем лучше
оценка.

Несмещенная оценка



называется
эффективной,
если


=1.

Асимптотической
эффективностью
оценки
называется предел

,
если он существует. Оценку называют
асимптотически
эффективной,
если


=1.

Кроме того, для
асимптотически нормальных оценок
понятие асимптотической эффективности
иногда трактуется более широко. А именно,
для асимптотически нормальной оценки

при n,
полагают

.

Задача
Доказать,
что выборочное среднее является
эффективной оценкой математического
ожидания нормального распределения,
когда дисперсия известна.

Решение.
Выпишем функцию плотности для нормального
распределения:

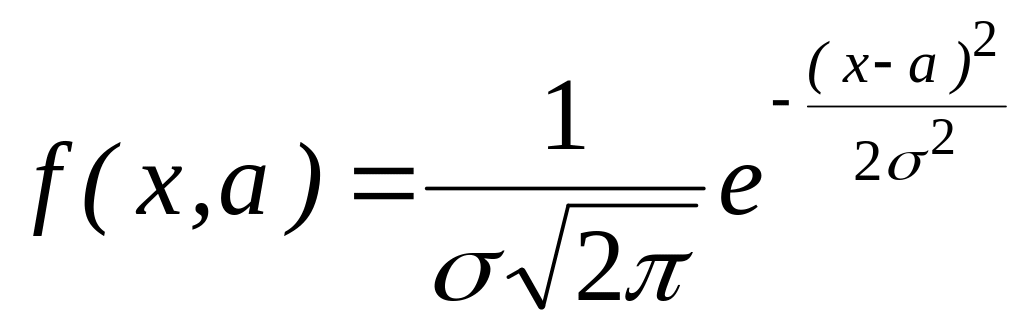
Прологарифмировав
ее, получим:

,
при этом производная будет равна

Отсюда
найдем информацию Фишера:

Получаем
значение

.
С другой стороны,

,
так что

.

Таким образом,
оценка является эффективной. Из
доказанного следует, что чем больше
дисперсия нормальной случайной величины,
тем меньше информации о значении
математического ожидания этой величины
заключено в одном наблюдении.

Задача.
Доказать, что относительная частота
успеха в качестве оценки неизвестной
вероятности θ в схеме Бернулли является
эффективной оценкой.

Решение.
Оценкой неизвестной вероятности является
относительная частота успеха

,
где х_i
– успех (1) или неудача (0) в i-ом
испытании. Эта оценка несмещенная, так
как

Дисперсия оценки имеет вид

.

Найдем информацию
Фишера, причем в данном случае наблюдаемая
величина принимает всего два значения:
0 и 1 с вероятностями P(0;)=1
и Р(1;)=.

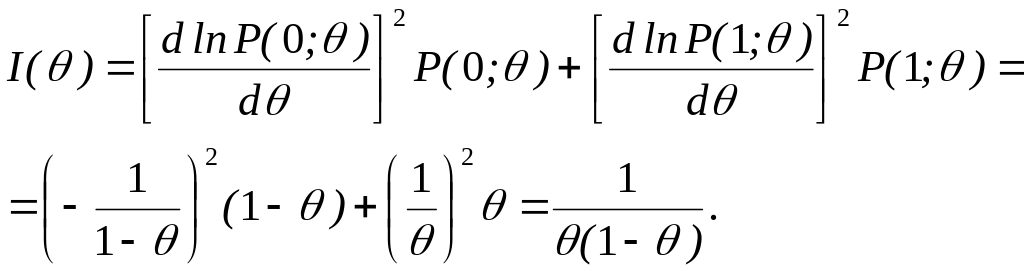
Таким образом,

.

Задача.
Пусть выборка x₁,
x₂,
…, x_n
произведена из генеральной совокупности
с равномерным распределением на отрезке
[0, ].
Проверить на эффективность оценку

для неизвестного параметра .

Решение.
Функция
распределения F_max(x)
максимума x_max
задается
формулой:

на
отрезке 0х.
Отсюда получаем

.

Значит,
оценка

несмещенная. Найдем дисперсию этой
оценки:

Видно, что дисперсия
оценки

при n
убывает как

.
Такая оценка оказалась лучше эффективной,
поскольку дисперсия эффективной оценки
имеет порядок убывания только

.
Разгадка парадокса в том, что для данного
семейства распределений не выполнены
условия теоремы Рао-Фреше-Крамера. А
именно, область значений случайной
величины зависит от параметра .
Подобные оценки называют сверхэффективными.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Материал из MachineLearning.

Перейти к: навигация, поиск

Постановка задачи

Задача статистического оценивания неизвестных параметров – одна из двух основных (наряду с задачей проверки статистических гипотез) задач математической статистики.

Предположим, что имеется параметрическое семейство распределений вероятностей (для простоты будем рассматривать распределение случайных величин и случай одного параметра). Здесь – числовой параметр, значение которого неизвестно. Требуется оценить его по имеющейся выборке значений, порожденной данным распределением.

Различают два основных типа оценок: точечные оценки и доверительные интервалы.

Точечное оценивание

Точечное оценивание – это вид статистического оценивания, при котором значение неизвестного параметра приближается отдельным числом. То есть необходимо указать функцию от выборки (статистику)

,

значение которой будет рассматриваться в качестве приближения к неизвестному истинному значению .

К общим методам построения точечных оценок параметров относятся: метод максимального правдоподобия, метод моментов, метод квантилей.

Ниже приводятся некоторые свойства, которыми могут обладать или не обладать точечные оценки.

Состоятельность

Одно из самых очевидных требований к точечной оценке заключается в том, чтобы можно было ожидать достаточно хорошего приближения к истинному значению параметра при достаточно больших значениях объема выборки . Это означает, что оценка должна сходиться к истинному значению при . Это свойство оценки и называется состоятельностью. Поскольку речь идет о случайных величинах, для которых имеются разные виды сходимости, то и данное свойство может быть точно сформулировано по-разному:

Когда употребляют просто термин состоятельность, то обычно имеется в виду слабая состоятельность, т.е. сходимость по вероятности.

Условие состоятельности является практически обязательным для всех используемых на практике оценок. Несостоятельные оценки используются крайне редко.

Несмещенность и асимптотическая несмещенность

Оценка параметра называется несмещенной, если ее математическое ожидание равно истинному значению оцениваемого параметра:

.

Более слабым условием является асимптотическая несмещенность, которая означает, что математическое ожидание оценки сходится к истинному значению параметра с ростом объема выборки:

.

Несмещенность является рекомендуемым свойством оценок. Однако не следует слишком переоценивать его значимость. Чаще всего несмещенные оценки параметров существуют и тогда стараются рассматривать только их. Однако могут быть такие статистические задачи, в которых несмещенных оценок не существует. Наиболее известным примером является следующий: рассмотрим распределение Пуассона с параметром и поставим задачу оценки параметра . Можно доказать, что для этой задачи не существует несмещенной оценки.

Сравнение оценок и эффективность

Для сравнения между собой различных оценок одного и того же параметра применяют следующий метод: выбирают некоторую функцию риска, которая измеряет отклонение оценки от истинного значения параметра, и лучшей считают ту, для которой эта функция принимает меньшее значение.

Чаще всего в качестве функции риска рассматривают математическое ожидание квадрата отклонения оценки от истинного значения

Для несмещенных оценок это есть просто дисперсия .

Существует нижняя граница на данную функцию риска, называемая неравенство Крамера-Рао.

(Несмещенные) оценки, для которых достигается эта нижняя граница (т.е. имеющие минимально возможную дисперсию), называются эффективными. Однако существование эффективной оценки есть довольно сильное требование на задачу, которое имеет место далеко не всегда.

Более слабым является условие асимптотической эффективности, которое означает, что отношение дисперсии несмещенной оценки к нижней границе Крамера-Рао стремится к единице при .

Заметим, что при достаточно широких предположениях относительно исследуемого распределения, метод максимального правдоподобия дает асимптотически эффективную оценку параметра, а если существует эффективная оценка – тогда он дает эффективную оценку.

Достаточные статистики

Статистика назвается достаточной для параметра , если условное распределение выборки при условии того, что , не зависит от параметра для всех .

Важность понятия достаточной статистики обуславливается следующим утверждением. Если – достаточная статистика, а – несмещенная оценка параметра , тогда условное математическое ожидание является также несмещенной оценкой параметра , причем ее дисперсия меньше или равна дисперсии исходной оценки .

Напомним, что условное математическое ожидание есть случайная величина, являющаяся функцией от . Таким образом, в классе несмещенных оценок достаточно рассматривать только такие, которые являются функциями от достаточной статистики (при условии, что такая существует для данной задачи).

(Несмещенная) эффективная оценка параметра всегда является достаточной статистикой.

Можно сказать, что достаточная статистика содержит в себе всю информацию об оцениваемом параметре, которая содержится в выборке .

Доверительные интервалы

Другим типом оценок статистических параметров являются доверительные интервалы.

Доверительный интервал – это случайный интервал, построенный по выборке (верхняя и нижняя границы этого интервала должны быть статистиками), который содержит (накрывает) истинное значение параметра с вероятностью, не меньшей заданного значения.

Доверительные интервалы используются, когда нам нужны надежные границы, в которые попадает значение оцениваемого параметра.

Часто вместе с точечной оценкой параметра строят доверительный интервал, середина которого равна этой оценке. Его ширина является наглядной характеристикой того, насколько точна может быть данная точечная оценка.

Иногда бывает наоборот: естественным образом строится некоторый доверительный интервал, а в качестве точечной оценки параметра рассматривают его середину.

Подробнее см. статью доверительный интервал.

Литература

1. Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006. — 816 с.

1. Гарольд Крамер. Математические методы статистики. — М.: Гос. изд-во иностр. лит-ры, 1948. — 631 с.

1. под ред. В.С. Королюка. Справочник по теории вероятностей и математической статистике. — Киев: Наукова думка, 1978. — 582 с.

Ссылки

• Статистическое оценивание(Яндекс.Словари)
• Точечная оценка (Википедия)
• Point estimation (Wikipedia)
• Estimator (Wikipedia)

Понятия «наилучшего» статистического оценщика

В статистике эффективным оценщиком является Оценщик, который оценивает интересующее количество некоторым «наилучшим возможным» способом. Понятие «наилучшего из возможных» основывается на выборе конкретной функции потерь – функции, которая количественно определяет относительную степень нежелательности ошибок оценки разной величины. Чаще всего выбирается функция потерь квадратичная, что дает среднеквадратичную ошибку критерий оптимальности.

Содержание

• 1 Эффективность по конечной выборке
  • 1.1 Пример
• 2 Относительная эффективность
• 3 Асимптотическая эффективность
• 4 См. Также
• 5 Ссылки
• 6 Дополнительная литература

Эффективность конечной выборки

Предположим {P θ | θ ∈ Θ} – это параметрическая модель, а X = (X 1,…, X n) – данные, выбранные из этой модели. Пусть T = T (X) будет оценкой для параметра θ. Если эта оценка несмещена (то есть E [T] = θ), то неравенство Крамера – Рао утверждает, что дисперсия этой оценки ограничена ниже:

Var ⁡ [T] ≥ I θ – 1, { displaystyle operatorname {Var} [, T ,] geq { mathcal {I}} _ { theta} ^ {- 1},}

где I θ { displaystyle scriptstyle { mathcal {I}} _ { theta}}– информационная матрица Фишера модель в точке θ. Обычно дисперсия измеряет степень разброса случайной величины вокруг ее среднего значения. Таким образом, оценщики с небольшими отклонениями более концентрированы, они более точно оценивают параметры. Мы говорим, что оценка является эффективной оценкой с конечной выборкой (в классе несмещенных оценок), если она достигает нижней границы в неравенстве Крамера – Рао, приведенном выше, для всех θ ∈ Θ. Эффективные оценщики всегда несмещенные оценщики с минимальной дисперсией. Однако обратное неверно: существуют задачи точечной оценки, для которых несмещенная оценка с минимальной дисперсией неэффективна.

Исторически эффективность конечной выборки была ранним критерием оптимальности. Однако этот критерий имеет некоторые ограничения:

• Эффективные оценки на основе конечной выборки крайне редки. Фактически, было доказано, что эффективное оценивание возможно только в экспоненциальном семействе и только для естественных параметров этого семейства.
• Это понятие эффективности иногда ограничивается классом объективные оценщики. (Часто это не так.) Поскольку нет веских теоретических причин требовать, чтобы оценки были беспристрастными, это ограничение неудобно. Фактически, если мы используем среднеквадратичную ошибку в качестве критерия выбора, многие смещенные оценки будут немного превосходить «лучшие» несмещенные. Например, в многомерной статистике для измерения три или более несмещенная оценка, выборочное среднее, является недопустимым : независимо от результата, его эффективность хуже, чем, например, оценка Джеймса – Стейна.
• Эффективность конечной выборки основана на дисперсии как критерии, по которому оцениваются оценки. Более общий подход заключается в использовании функций потерь, отличных от квадратичных, и в этом случае эффективность конечной выборки больше не может быть сформулирована.

Пример

Среди моделей, встречающихся на практике эффективные оценки существуют для: среднего μ нормального распределения (но не дисперсии σ), параметра λ распределения Пуассона, вероятности p в биномиальном или мультиномиальное распределение.

Рассмотрим модель нормального распределения с неизвестным средним, но известной дисперсией: {P θ = N (θ, σ) | θ ∈ R }. Данные состоят из n независимых и одинаково распределенных наблюдений из этой модели: X = (x 1,…, x n). Мы оцениваем параметр θ, используя выборочное среднее всех наблюдений:

T (X) = 1 n i = 1 n x i. { displaystyle T (X) = { frac {1} {n}} sum _ {i = 1} ^ {n} x_ {i} .}

Эта оценка имеет среднее значение θ и дисперсию σ / n, которое равно обратной величине информации Фишера из выборки. Таким образом, выборочное среднее – это эффективная оценка конечной выборки для среднего нормального распределения.

Относительная эффективность

Если T 1 { displaystyle T_ {1}}и T 2 { displaystyle T_ {2}}являются оценками для параметра θ { displaystyle theta}, тогда T 1 { displaystyle T_ {1}}считается доминировать T 2 { displaystyle T_ {2}}, если:

1. его среднеквадратичная ошибка (MSE) меньше хотя бы для некоторого значения из θ { displaystyle theta}
2. MSE не превышает MSE T 2 { displaystyle T_ {2}}для любого значения θ.

Формально, T 1 { displaystyle T_ {1}}доминирует T 2 { displaystyle T_ {2}}, если

E [(T 1 – θ) 2] ≤ E [(T 2 – θ) 2] { displaystyle mathrm {E} left [(T_ {1} – theta) ^ {2} right] leq mathrm {E} left [(T_ {2} – theta) ^ {2} right]}

выполняется для всех θ { displaystyle theta}, где где-то выполняется строгое неравенство.

Относительная эффективность определяется как

e (T 1, T 2) = E [(T 2 – θ) 2] E [(T 1 – θ) 2] { displaystyle e (T_ {1}, T_ {2}) = { frac { mathrm {E} left [(T_ {2} – theta) ^ {2} right]} { mathrm {E} left [(T_ {1} – theta) ^ {2} right]}}}

Хотя e { displaystyle e}, как правило, является функцией θ { displaystyle theta}, во многих случаях зависимость выпадает; если это так, то e { displaystyle e}больше единицы означает, что T 1 { displaystyle T_ {1}}предпочтительнее, независимо от того, истинное значение θ { displaystyle theta}.

Асимптотическая эффективность

Для некоторых оценок они могут достигать эффективности асимптотически и поэтому называются асимптотически эффективные оценки. Это может иметь место для некоторых оценок максимального правдоподобия или любых оценок, которые асимптотически достигают равенства границы Крамера – Рао.

См. Также

• Байесовская оценка
• Согласованная оценка
• Оценка Ходжеса
• Оптимальные инструменты

Ссылки

Дополнительная литература

• Lehmann, EL ; Казелла, Г. (1998). Теория точечного оценивания (2-е изд.). Springer. ISBN 0-387-98502-6 .
• ; при содействии Р. Хамбёкера (1994). Параметрическая статистическая теория. Берлин: Вальтер де Грюйтер. ISBN 3-11-013863-8. MR 1291393.