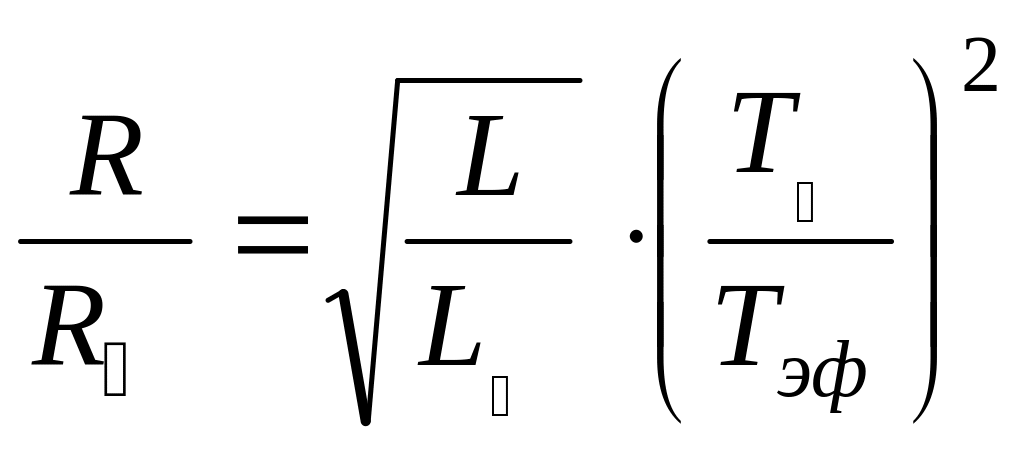Как найти эффективную температуру звезды

Эффекти́вная температу́ра ${displaystyle T_{E}}$ — параметр, характеризующий светимость (полную мощность излучения) небесного тела (или другого объекта), то есть это температура абсолютно чёрного тела с размерами, равными размерам небесного тела и излучающего такое же количество энергии в единицу времени^[1].

В соответствии с законом Стефана — Больцмана светимость сферического абсолютно чёрного тела с радиусом , то есть площадью излучающей поверхности ${displaystyle 4pi R^{2}}$ :

$L=4pi R^{2}sigma T_{E}^{4}$

Где sigma — это постоянная Стефана-Больцмана, равная 5,67⋅10^-8 Вт/(м² К⁴).

Таким образом, эффективная температура объекта равна температуре абсолютно чёрного тела, с единицы поверхности которого в единицу времени излучается энергия ${displaystyle L/4pi R^{2}}$ .

В случае небесных тел, окружённых атмосферами, эффективная температура определяется температурой внешнего излучающего слоя атмосферы с оптической толщиной : в случае звёзд — фотосферой, в случае планет — верхними слоями атмосфер. И в случае небесных тел с собственными источниками энергии (звёзды), и в случае небесных тел, получающих энергию от центрального светила (внутренние планеты, атмосферы которых содержат парниковые газы), эффективная температура ниже температуры недр звёзд или поверхностей планет.

Эффективная температура Земли[править | править код]

Земля освещена Солнцем с одной стороны, поэтому величина падающего потока излучения равна:
$J_{0}=pi R^{2}varepsilon$ , где — солнечная постоянная. Вследствие того, что Земля отражает часть излучения, с учётом среднего по всему спектру альбедо Земли поток энергии, поглощённой планетой будет равен:
$J_{1}=pi R^{2}varepsilon (1-a)$ , где — геометрическое альбедо Земли.
В равновесии поток поглощённой энергии равен потоку излучаемой (выражающейся из закона Стефана-Больцмана), поэтому получаем равенство

${displaystyle pi R^{2}varepsilon (1-a)=4pi R^{2}sigma T_{E}^{4},}$

откуда следует, что

${displaystyle T_{E}={sqrt[{4}]{frac {varepsilon (1-a)}{4sigma }}},}$

где sigma — постоянная Стефана-Больцмана, равная 5,67⋅10^-8 Вт/(м² К⁴).

Откуда численное значение эффективной температуры Земли равно 249 К, или −24 °C.

Реальное значение средней температуры земной поверхности выше указанного благодаря парниковому эффекту. Спектральный максимум солнечного излучения, соответствующий 5500 К, лежит в видимой области, для которой земная атмосфера прозрачна. А спектральный максимум теплового излучения земной поверхности лежит в инфракрасной области. Это инфракрасное излучение поглощается парниковыми газами земной атмосферы и переизлучается со спектральным максимумом, соответствующим температуре воздуха на этих высотах. Так что —24° — это эффективная температура земной атмосферы, как она видна из космоса.

См. также[править | править код]

Парниковый эффект
Яркостная температура

Примечания[править | править код]

↑ Бычков К. В. Эффективная температура // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1999. — Т. 5: Стробоскопические приборы — Яркость. — С. 645—646. — 692 с. — 20 000 экз. — ISBN 5-85270-101-7.

Ссылки[править | править код]

Archie E. Roy, David Clarke. Astronomy. — CRC Press, 2003. — ISBN 978-0-7503-0917-2.
Earth Fact Sheet. nssdc.gsfc.nasa.gov. Дата обращения: 8 мая 2018. Архивировано 30 октября 2010 года.

Источник

From Wikipedia, the free encyclopedia

The effective temperature or effective radiative emission temperature of a body such as a star or planet is the temperature of a black body that would emit the same total amount of electromagnetic radiation.^[1]^[2] Effective temperature is often used as an estimate of a body’s surface temperature when the body’s emissivity curve (as a function of wavelength) is not known.

When the star’s or planet’s net emissivity in the relevant wavelength band is less than unity (less than that of a black body), the actual temperature of the body will be higher than the effective temperature. The net emissivity may be low due to surface or atmospheric properties, including greenhouse effect.

Star[edit]

The effective temperature of the Sun (5777 kelvins) is the temperature a black body of the same size must have to yield the same total emissive power.

The effective temperature of a star is the temperature of a black body with the same luminosity per surface area (F_Bol) as the star and is defined according to the Stefan–Boltzmann law F_Bol = σT_eff⁴. Notice that the total (bolometric) luminosity of a star is then L = 4πR²σT_eff⁴, where R is the stellar radius.^[3] The definition of the stellar radius is obviously not straightforward. More rigorously the effective temperature corresponds to the temperature at the radius that is defined by a certain value of the Rosseland optical depth (usually 1) within the stellar atmosphere.^[4]^[5] The effective temperature and the bolometric luminosity are the two fundamental physical parameters needed to place a star on the Hertzsprung–Russell diagram. Both effective temperature and bolometric luminosity depend on the chemical composition of a star.

The effective temperature of the Sun is around 5,780 K.^[6]^[7]
The nominal value defined by the International Astronomical Union for use as a unit of measure of temperature is 5,772±0.8 K.^[8]
Stars have a decreasing temperature gradient, going from their central core up to the atmosphere. The “core temperature” of the Sun—the temperature at the centre of the Sun where nuclear reactions take place—is estimated to be 15,000,000 K.

The color index of a star indicates its temperature from the very cool—by stellar standards—red M stars that radiate heavily in the infrared to the very hot blue O stars that radiate largely in the ultraviolet. Various colour-effective temperature relations exist in the literature. There relations also have smaller dependencies on other stellar parameters, such as the stellar metallicity and surface gravity.^[9] The effective temperature of a star indicates the amount of heat that the star radiates per unit of surface area. From the hottest surfaces to the coolest is the sequence of stellar classifications known as O, B, A, F, G, K, M.

A red star could be a tiny red dwarf, a star of feeble energy production and a small surface or a bloated giant or even supergiant star such as Antares or Betelgeuse, either of which generates far greater energy but passes it through a surface so large that the star radiates little per unit of surface area. A star near the middle of the spectrum, such as the modest Sun or the giant Capella radiates more energy per unit of surface area than the feeble red dwarf stars or the bloated supergiants, but much less than such a white or blue star as Vega or Rigel.

Planet[edit]

Blackbody temperature[edit]

To find the effective (blackbody) temperature of a planet, it can be calculated by equating the power received by the planet to the known power emitted by a blackbody of temperature T.

Take the case of a planet at a distance D from the star, of luminosity L.

Assuming the star radiates isotropically and that the planet is a long way from the star, the power absorbed by the planet is given by treating the planet as a disc of radius r, which intercepts some of the power which is spread over the surface of a sphere of radius D (the distance of the planet from the star). The calculation assumes the planet reflects some of the incoming radiation by incorporating a parameter called the albedo (a). An albedo of 1 means that all the radiation is reflected, an albedo of 0 means all of it is absorbed. The expression for absorbed power is then:

${displaystyle P_{rm {abs}}={frac {Lr^{2}(1-a)}{4D^{2}}}}$

The next assumption we can make is that the entire planet is at the same temperature T, and that the planet radiates as a blackbody. The Stefan–Boltzmann law gives an expression for the power radiated by the planet:

$P_{{{rm {rad}}}}=4pi r^{2}sigma T^{4}$

Equating these two expressions and rearranging gives an expression for the effective temperature:

${displaystyle T={sqrt[{4}]{frac {L(1-a)}{16pi sigma D^{2}}}}}$

Where sigma is the Stefan–Boltzmann constant. Note that the planet’s radius has cancelled out of the final expression.

The effective temperature for Jupiter from this calculation is 88 K and 51 Pegasi b (Bellerophon) is 1,258 K.^{[citation needed]} A better estimate of effective temperature for some planets, such as Jupiter, would need to include the internal heating as a power input. The actual temperature depends on albedo and atmosphere effects. The actual temperature from spectroscopic analysis for HD 209458 b (Osiris) is 1,130 K, but the effective temperature is 1,359 K.^{[citation needed]} The internal heating within Jupiter raises the effective temperature to about 152 K.^{[citation needed]}

Surface temperature of a planet[edit]

The surface temperature of a planet can be estimated by modifying the effective-temperature calculation to account for emissivity and temperature variation.

The area of the planet that absorbs the power from the star is A_abs which is some fraction of the total surface area A_total = 4πr², where r is the radius of the planet. This area intercepts some of the power which is spread over the surface of a sphere of radius D. We also allow the planet to reflect some of the incoming radiation by incorporating a parameter a called the albedo. An albedo of 1 means that all the radiation is reflected, an albedo of 0 means all of it is absorbed. The expression for absorbed power is then:

$P_{{{rm {abs}}}}={frac {LA_{{{rm {abs}}}}(1-a)}{4pi D^{2}}}$

The next assumption we can make is that although the entire planet is not at the same temperature, it will radiate as if it had a temperature T over an area A_rad which is again some fraction of the total area of the planet. There is also a factor ε, which is the emissivity and represents atmospheric effects. ε ranges from 1 to 0 with 1 meaning the planet is a perfect blackbody and emits all the incident power. The Stefan–Boltzmann law gives an expression for the power radiated by the planet:

$P_{{{rm {rad}}}}=A_{{{rm {rad}}}}varepsilon sigma T^{4}$

Equating these two expressions and rearranging gives an expression for the surface temperature:

${displaystyle T={sqrt[{4}]{{frac {A_{rm {abs}}}{A_{rm {rad}}}}{frac {L(1-a)}{4pi sigma varepsilon D^{2}}}}}}$

Note the ratio of the two areas. Common assumptions for this ratio are 1/4 for a rapidly rotating body and 1/2 for a slowly rotating body, or a tidally locked body on the sunlit side. This ratio would be 1 for the subsolar point, the point on the planet directly below the sun and gives the maximum temperature of the planet — a factor of √2 (1.414) greater than the effective temperature of a rapidly rotating planet.^[10]

Also note here that this equation does not take into account any effects from internal heating of the planet, which can arise directly from sources such as radioactive decay and also be produced from frictions resulting from tidal forces.

Earth effective temperature[edit]

The Earth has an albedo of about 0.306.^[11] The emissivity is dependent on the type of surface and many climate models set the value of Earth’s emissivity to 1. However, a more realistic value is 0.96.^[12] The Earth is a fairly fast rotator so the area ratio can be estimated as 1/4. The other variables are constant. This calculation gives us an effective temperature of the Earth of 252 K (−21 °C). The literature gives a value of 255 K (−18 °C), which is essentially the 239 Wm^-2 outgoing longwave radiation, one of two outgoing energy values of Earth’s energy budget, the other being the reflected energy of 102 W⋅m⁻².^[13] The average temperature of the Earth is 288 K (15 °C). One reason for the difference between the two values is due to the greenhouse effect, which increases the average temperature of the Earth’s surface.

References[edit]

^ Archie E. Roy, David Clarke (2003). Astronomy. CRC Press. ISBN 978-0-7503-0917-2.
^ Stull, R. (2000). Meteorology For Scientists and Engineers. A technical companion book with Ahrens’ Meteorology Today, Brooks/Cole, Belmont CA, ISBN 978-0-534-37214-9., p. 400.
^ Tayler, Roger John (1994). The Stars: Their Structure and Evolution. Cambridge University Press. p. 16. ISBN 0-521-45885-4.
^ Böhm-Vitense, Erika (1992). Introduction to Stellar Astrophysics, Volume 3, Stellar structure and evolution. Cambridge University Press. p. 14. Bibcode:1992isa..book…..B.
^ Baschek (June 1991). “The parameters R and Teff in stellar models and observations”. Astronomy and Astrophysics. 246 (2): 374–382. Bibcode:1991A&A…246..374B.
^ Lide, David R., ed. (2004). “Properties of the Solar System”. CRC Handbook of Chemistry and Physics (85th ed.). CRC Press. p. 14-2. ISBN 9780849304859.
^ Jones, Barrie William (2004). Life in the Solar System and Beyond. Springer. p. 7. ISBN 1-85233-101-1.
^ Prša, Andrej; Harmanec, Petr; Torres, Guillermo; Mamajek, Eric; Asplund, Martin; Capitaine, Nicole; Christensen-Dalsgaard, Jørgen; Depagne, Éric; Haberreiter, Margit; Hekker, Saskia; Hilton, James; Kopp, Greg; Kostov, Veselin; Kurtz, Donald W.; Laskar, Jacques; Mason, Brian D.; Milone, Eugene F.; Montgomery, Michele; Richards, Mercedes; Schmutz, Werner; Schou, Jesper; Stewart, Susan G. (2016). “Nominal Values for Selected Solar and Planetary Quantities: IAU 2015 Resolution B3”. The Astronomical Journal. 152 (2): 41. arXiv:1605.09788. Bibcode:2016AJ….152…41P. doi:10.3847/0004-6256/152/2/41. hdl:1885/108637. S2CID 55319250.
^ Casagrande, Luca (2021). “The GALAH survey: effective temperature calibration from the InfraRed Flux Method in the Gaia system”. MNRAS. 507 (2): 2684–2696. arXiv:2011.02517. Bibcode:2021MNRAS.507.2684C. doi:10.1093/mnras/stab2304.
^ Swihart, Thomas. “Quantitative Astronomy”. Prentice Hall, 1992, Chapter 5, Section 1.
^ “Earth Fact Sheet”. nssdc.gsfc.nasa.gov. Archived from the original on 30 October 2010. Retrieved 8 May 2018.
^ Jin, Menglin and Shunlin Liang, (2006) “An Improved Land Surface Emissivity Parameter for Land Surface Models Using Global Remote Sensing Observations” Journal of Climate, 19 2867-81. (www.glue.umd.edu/~sliang/papers/Jin2006.emissivity.pdf)
^ “Atmospheres and Planetary Temperatures”. American Chemical Society. 2013-07-18. Retrieved 2023-01-03.

External links[edit]

Effective temperature scale for solar type stars
Surface Temperature of Planets
Planet temperature calculator

Источник

Каждая звезда
описывается тремя основными
характеристиками: радиус, масса и
светимость. Рассмотрим основные методы
определения указанных параметров, а
также температуры звезд.

а) Размеры
звезд.

Непосредственные
измерения радиусов звезд, за некоторыми
исключениями, практически невозможны,
так как все звезды настолько далеки от
нас, что их угловые размеры меньше
предела разрешения крупнейших телескопов.
Угловые диаметры нескольких десятков
ближайших звезд определены с помощью
специальных звездных
интерферометров.
Принцип работы этих приборов основан
на интерференции света звезды, отраженного
парой широко расставленных зеркал.

В отдельных случаях
для определения углового диаметра
звезды удается использовать вид
интерференционной картины, возникающей
во время покрытия звезд Луной.

Если для звезды с
известным расстоянием r
найден любым из описанных методов
угловой диаметр ,
выраженный в секундах дуги, то ее линейный
радиус R
может быть вычислен по формуле

(5.24)

где R
выражен в
радиусах Солнца, а r
— в парсеках.

Из формулы (5.15)
следует, что зная эффективную температуру
звезды T_эф
и ее светимость L,
можно вычислить линейный радиус. Запишем
указанное соотношение для звезды и для
Солнца:

;
Деля почленно одно равенство на
другое, после преобразований находим:

(5.25)

где
эффективная температура Солнца T_=
6000 K.

Радиус звезды
можно также определить по ее основному
показателю цвета (BV)
и желтой абсолютной звездной величине
M_V:

(5.26)

где R
— в радиусах Солнца.

Линейные радиусы
можно определить у затменно-переменных
звезд по продолжительности затмения
(см. §
5.12).

Размеры самых
крупных звезд в 1000 и более раз превосходят
солнечные (у звезды VV
Сер (Цефея) в 1600 раз). Звезда, открытая
Лейтеном в созвездии Кита, в 10 раз меньше
Земли по диаметру, а размеры нейтронных
звезд порядка десяти километров.

б) Массы
звезд.

Основой сведений
о массах звезд служат наблюдения двойных
звезд 
физических пар звезд, связанных силами
гравитации и обращающихся вокруг общего
центра масс. В
звездной паре более яркий компонент
называется главной
звездой,
а менее яркий •— звездой-спутником.
Их
расстояния от Земли
и Солнца практически одинаковы, хотя,
конечно, несущественные
различия имеются. По
данным измерений, занимающих несколько
лет (а то и десятки лет), строится видимая
относительная
орбита звезды-спутника: она имеет вид
эллипса, но
главная звезда (S)
расположена вне его фокуса, так как эта
орбита
является проекцией реальной (истинной)
эллиптической орбиты
на плоскость, касательную к небесной
сфере и называемую картинной
плоскостью.
Существуют способы, позволяющие по
видимой орбите вычислить элементы
истинной орбиты: большую полуось а”
(в
секундах дуги),
эксцентриситет е
и
наклонение i
к картинной
плоскости, а период
обращения Т
звезды-спутника
находится непосредственно из
наблюдений ее положений в разные годы.

Если известен
параллакс 
двойной звезды, то легко вычислить
большую полуось а истинной орбиты
в астрономических единицах:

.
Пусть M₁ и
M₂ 
массы компонентов двойной звезды, M_
и M_ масса Солнца и
Земли соответственно. Тогда по третьему
обобщенному закону Кеплера имеем:

(5.27)

где T
и T_ периоды обращения
двойной звезды и Земли соответственно,
а_
большая полуось Земли. Учитывая то, что
масса Солнца во много раз превосходит
земную массу, можно записать:

;
T_= 1 год; а_
= 1 а.е. Приняв это во внимание, выразим
из соотношения (5.27) величину (М₁+М₂),
которая и будет являться массой двойной
звезды:

(5.28)

Чтобы определить
массу каждой компоненты в отдельности,
необходимо найти положение центра масс
системы. Тогда будет справедливо
соотношение

(5.29)

где


расстояния от 1-й и 2-й компонент звезды
до их общего центра масс.

Решая совместно
уравнения (5.28) и (5.29), мы вычислим массу
каждой компоненты.

Если звезда
одиночная, ее массу можно установить
по диаграмме масса-светимость (см.
§ 5.11).

Если измерен радиус
звезды, то по ее спектру можно найти
массу, измерив величину красного
смещения. Данное смещение линий в спектре
происходит из-за эффекта Доплера
вследствие гравитационного сжатия
звезды. Этот метод особенно применим
для тех звезд, у которых красное смещение
велико, — для белых карликов.

Массы звезд
заключены в пределах от 0,1 масс Солнца
до нескольких десятков масс Солнца.

в) Светимости
звезд.

Основным методом
определения светимостей звезд является
фотометрический метод. Если известна
видимая звездная величина звезды и
расстояние до нее,
выраженное в парсеках, то с помощью
формул (5.7) и (5.11) можно определить
светимость этой звезды.

Также светимость
можно вычислить по соотношению (5.15), для
этого необходимо знать радиус звезды
и ее эффективную температуру.

Светимости звезд
заключены в очень широких пределах: от
10^⁵
до 10⁵
светимостей Солнца.

г) Температуры
звезд.

Обычно под
температурой звезды понимают ее
эффективную температуру. Для определения
последней необходимо знать полный поток
излучения (т.е. светимость) и радиус
звезды. Достаточно точно обе эти величины,
а потому и эффективные температуры
могут быть измерены лишь для немногих
звезд. Для остальных звезд эффективные
температуры находят косвенными методами.

Если известны
угловой диаметр звезды 
(в угловых секундах) и ее яркость во всем
диапазоне спектра (т.е. болометрическая
звездная величина m_b),
то эффективная температура звезды (в
кельвинах) может быть найдена из
следующего равенства:

(5.30)

Наиболее просто
найти цветовую температуру звезды,
определив из наблюдений спектральный
класс или показатель цвета этой звезды.
Так, если известен основной показатель
цвета звезды (BV),
то цветовая температура может быть
определена по формуле (5.16).

Температуры звезд
сильно различаются: они лежат в пределах
от 2000 до 50000 К.
Изредка встречаются звезды с температурой
до 100000 К.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Как вычислить температуру звезды на основе данных о её светимости и размерах?

Формула зависимости температуры T, светимости L и радиуса звезды R выводится из формулы закона Стефана-Больцмана:

J = σ*T^4, где J – энергетическая светимость на единицу площади, σ – постоянная Стефана-Больцмана, Т – абсолютная температура.

Поскольку площадь поверхности сферы определяется как S=4ПR^2, то полную светимость можно вычислить по формуле:

L=4*П*R^2*σ*T^4, где L – светимость звезды, R – радиус звезды, σ – постоянная Стефана-Больцмана, Т – абсолютная температура.

Из этой формулы находим температуру:

Т = ∜(L/(4*П*R^2*σ))

979

Комментировать ответ…Комментировать…

Здравствуйте! Методов определения температуры очень много вообще есть…
Для начала напомню, что температура характеризует среднюю кинетическую энергию одной частицы вещества. Вернее сказать, кинетическая температура, потому что температур есть много – и яркостная, и цветовая, и эффективная… много их. Сейчас объясню.
Ваш вопрос сводится к методам определения температуры… Читать далее

1,9 K

Комментировать ответ…Комментировать…

Инженер-радиофизик, преподаватель физической культуры и спорта · 24 июл 2022

По законам физики и довольно точно, Юля Воротынцева подробно описала методы, однако, температура звезды – понятие бессмысленное, так как она в разных местах сильно различается. Строение звёзд, их эволюция и классификация уже давно известны, и можно говорить о температуре фотосферы (тысячи кельвин) и температуре ядра (многие десятки миллионов кельвин), исходя из её… Читать далее

329

Комментировать ответ…Комментировать…

Источник

Обычно под температурой звезды понимают ее эффективную температуру.

Для определения последней необходимо знать полный поток излучения и радиус звезды. Достаточно точно обе эти величины, а потому и эффективные температуры могут быть измерены лишь для немногих звезд. Для остальных звезд эффективные температуры находят косвенными методами на основании изучения их спектров или показателей цвета с помощью шкалы эффективных звездных температур.

Шкалой эффективных температур называется зависимость цветовых характеристик излучения звезд, например спектрального класса или показателя цвета, от эффективных температур (см. приложение 1).

Аналогично вводится шкала цветовых температур. Если известна шкала температур, то, определив из наблюдений спектральный класс или показатель цвета данной звезды, легко найти ее температуру. Температурная шкала определяется эмпирически по звездам с известными, например, эффективными температурами, а также для звезд некоторых типов теоретически.

Радиус

Еще одна существенная характеристика звезды – ее радиус. Радиусы звезд меняются в очень широких пределах. Есть звезды, по своим размерам не превышающие земной шар (так называемые «Белые карлики»), есть огромные «пузыри», внутри которых могла бы свободно поместиться орбита Марса. Мы не случайно назвали такие гигантские звезды «пузырями». Из того факта, что по своим массам звезды отличаются сравнительно незначительно, следует, что при очень большом радиусе средняя плотность вещества должна быть ничтожно малой. Если средняя плотность солнечного вещества равна 1410 кг/м3, то у таких «пузырей» он может быть в миллионы раз меньше, чем у воздуха. В то же время белые карлики имеют огромную среднюю плотность, достигающую десятков и даже сотен миллионов килограммов на кубический метр.

«Зная эффективную температуру Т и светимость L, можно вычислить радиус R звезды по формуле: L=4pR2sT основанной на законе излучения Стефана – Больцмана (s – постоянная Стефана)» [1].

Расстояния до звёзд

«Несмотря на все достижения современной техника, определение расстояний до звезд по-прежнему остается одной из труднейших задач астрономии. Расстояния до звезд настолько велики, что для оценки их не пригодны ни километры, ни даже астрономические единицы (а. е.). Астрономы используют такие единицы расстояний, как световой год (св. год), но чаще парсек (пк; сокращение от двух слов паралакс секунда) – расстояние, с которого радиус земной орбиты, равный 1 а. е., виден под углом в 1″ (секунда дуги). 1 пк = 3,216 св. г. = = 206265 а.с. =; 3.1 * 10″ км. Для целей галактической и внегалактической астрономии используют еще более крупные единицы расстояний: килопарсек (1 кпк = 1000 пк) и мегапарсек (1 Мпк = = i 000000 пк)» [3].

Фотометрический метод определения расстояний.

Освещенности, создаваемые одинаковыми по мощности источниками света, обратно пропорциональны квадратам расстояний до них. Следовательно, видимый блеск одинаковых светил (т. е. освещенность, создаваемая у Земли на единичной площадке, перпендикулярной лучам света) может служить мерой расстояния до них. Выражение освещенностей в звездных величинах (m – видимая звездная величина, М – абсолютная звездная величина) приводит к следующей основной формуле фотометрических расстояний r_ф (пс):

lgr_ф = 0,2 (m – M) + 1.

При определении r _ф по вышеназванной формуле погрешность составляет ~30%.

Определение расстояния по относительным скоростям. Косвенным показателем расстояния до звезд являются их относительные скорости: как правило, чем ближе звезда, тем больше смещается она по небесной сфере. Определить таким способом расстояние, конечно нельзя, но этот способ дает возможность “вылавливать” близкие звезды. Также существует другой метод определения расстояний по скоростям, применимый для звездных скоплений. Он основан на том, что все звезды, принадлежащие одному скоплению, движутся в одном и том же направлении по параллельным траекториям. Измерив лучевую скорость звезд с помощью эффекта Доплера, а также скорость, с которой эти звезды смещаются относительно очень удаленных, то есть условно неподвижных звезд, можно определить расстояние до интересующего нас скопления.

Источник

Эффективная температура Земли[править | править код]

См. также[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Star[edit]