ЛАБОРАТОРНАЯ
РАБОТА 115
ОПРЕДЕЛЕНИЕ
СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО ПРОБЕГА И
ЭФФЕКТИВНОГО ДИАМЕТРА МОЛЕКУЛ ВОЗДУХА
Цель
работы:
определить среднюю длину свободного
пробега и эффективный диаметр молекул
воздуха по его коэффициенту внутреннего
трения, плотности и средней квадратичной
скорости молекул.
Приборы
и принадлежности:
экспериментальная установка, секундомер,
мерный цилиндр, термометр, барометр.
Теория
метода. В
данной работе средняя длина свободного
пробега и эффективный диаметр молекул
определяются по коэффициенту внутреннего
трения (вязкости) воздуха.
Из
молекулярно-кинетической теории следует
формула, связывающая вязкость η газа
со средней длиной
свободного пробега молекул:
,
где ρ –
плотность газа . (1)
Таким
образом,
,
где
–
средняя арифметическая скорость молекул
(2)
Коэффициент
вязкости можно найти по известной
формуле Пуазейля для расчета объема V
жидкости или газа, протекающего ламинарно
через поперечное сечение капилляра
радиуса r за время t при разности Δp
давлений на концах капилляра длиной
l:
. (3)
Откуда:
. (4)
Все величины,
входящие в эту формулу, легко поддаются
измерению.
Среднюю арифметическую
скорость молекул газа, согласно
молекулярно-кинетической теории, можно
рассчитать по формуле:
, (5)
где R – молярная
газовая постоянная, Т – абсолютная
температура в Кельвинах, М – молярная
масса воздуха.
Из уравнения
Менделеева-Клапейрона можно выразить
плотность газа через давление р и
температуру Т:
. (6)
Подставляя
выражения (4), (5), (6) в формулу (2), получим
(в единицах СИ):
(7)
Разность
давлений Δp может быть найдена по формуле:
, (8)
где
h1
и h2
– высоты уровней воды в сосуде А (рис.1),
g – ускорение свободного падения, ρ –
плотность воды.
Для
определения эффективного диаметра d
молекулы воспользуемся формулой для
средней длины

свободного пробега:
, (9)
связывающей
среднюю длину
свободного пробега молекул с их числом
n в единице объема газа.
Молекулярную
концентрацию n при условиях опыта можно
найти из уравнения состояния идеального
газа p = n*k*T:
, (10)
где
n0
= 2,69*1025м
–3
– концентрация молекул (число Лошмидта)
в нормальном состоянии (т.е. при Тн
= 273,15 К и рн
= 760 мм.рт.ст. = 1,013*105
Па)
Из выражений (9) и
(10) получим формулу для расчета эффективного
диаметра молекулы газа (в единицах СИ):
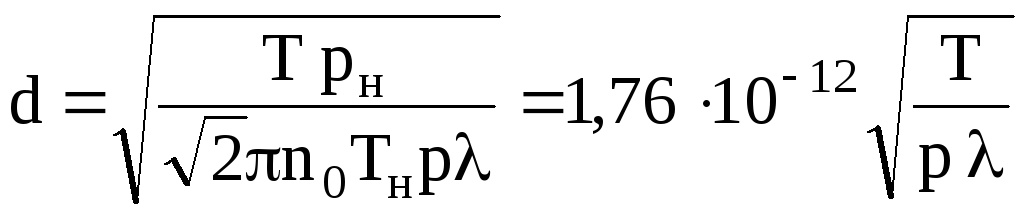
Численное
значение
нами было найдено ранее по формуле (7).
ОПИСАНИЕ УСТАНОВКИ
Д
определения средней длины свободного
пробега и расчета эффективного диаметра
молекул воздуха используется установка,
состоящая из капилляра l, сосуда А с
краном К и мерного цилиндра В (рис. 1).
Сосуд
заполняется водой и закрывается притертой
пробкой с капилляром l.
Если открыть кран К, то вода сначала
будет вытекать из сосуда непрерывной
струей, а затем отдельными каплями. При
этом в капилляре установится течение
воздуха, обусловленное разностью
давлений на его концах:
ратм
– (ратм
– p1gh2)
= p1gh2 (12)
Сосуд снабжен
шкалой, с помощью которой можно определить
уровень воды в нем. Под сосудом
устанавливается мерный цилиндр для
определения объема вытекшей жидкости.
Очевидно, в
установившемся режиме объем воздуха,
поступившего через капилляр в сосуд
воздуха равен объему вытекшей за то же
время из сосуда воды.
ПОРЯДОК ВЫПОЛНЕНИЯ
РАБОТЫ
1.
Поставьте под сосуд химический стакан,
закройте пальцем капилляр и откройте
кран К. Дождавшись, когда вода перестанет
вытекать из сосуда, уберите стакан и
подставьте вместо него мерный цилиндр.
Замерив по шкале начальную высоту уровня
воды h1
в сосуде, откройте капилляр и одновременно
включите секундомер.
2. Через две минуты
закройте кран и остановите секундомер.
3.
Запишите время истечения жидкости t,
конечную высоту уровня воды h2
и объем вытекшей воды V.
4. Опыт проведите
три раза.
5.
Вычислите Δp по формуле 8, приняв за
плотность воды ρ1
= 103 кг/м3.
6. Определите
температуру Т по комнатному термометру
и атмосферное давление Р по барометру.
7.
Для каждого опыта по формуле (7) рассчитайте
среднюю длину
свободного пробега молекул воздуха.
Значения радиуса r и длины l капилляра
приведены на установке.
8.
Найдите среднее арифметическое значение
результатов измерений:
.
9.
Оцените ошибки измерений, окончательный
результат запишите в виде:
,
при δ = 0,95 и N =
3.
Здесь
;
tδ(N)
= 4,30 – коэффициент Стьюдента при
доверительной
вероятности
δ = 0,95 и числе измерений N = 3;
–
средняя
квадратичная погрешность результата
измерений
.
10.
Используя найденное значение
,
по формуле (11) рассчитайте эффективный
диаметр d молекул воздуха.
11. Результаты
измерений и расчетов запишите в таблицу.
ТАБЛИЦА
N |
h1, |
h2, |
t, |
V, м |
T, K |
P,
|
λ, |
d, |
|
1 |
||||||||
|
2 |
||||||||
|
3 |
||||||||
|
λср |
КОНТРОЛЬНЫЕ
ВОПРОСЫ
-
Что
называется средней длиной свободного
пробега молекул газа? Как связаны между
собой эти величины? -
Зависит ли средняя
длина свободного пробега молекул от
температуры газа? давления? Почему? -
Дайте определение
следующих процессов: теплопроводности,
диффузии, вязкости. Почему их называют
явлениями переноса? -
Запишите формулу
Пуазейля для потока вязкой жидкости и
газа. -
Запишите уравнение
состояния идеального газа. -
Какие свойства
теплового движения молекул газа отражает
распределение Максвелла? -
Запишите выражения
для характерных тепловых скоростей
молекул идеального газа в состоянии
равновесия.
ЛИТЕРАТУРА
-
Савельев
И.В. Курс общей физики. Т.1., М.: Наука,
1989, с. 140, 269, 274, 278. -
Трофимова Т.И.
Курс физики. М.: Высш. Школа, 1990, с. 55, 57,
81, 84.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Эффективный диаметр молекулы — минимальное расстояние, на которое сближаются центры двух молекул при столкновении.
При столкновении, молекулы сближаются до некоторого наименьшего расстояния, которое условно считается суммой радиусов взаимодействующих молекул. Столкновение между одинаковыми молекулами может произойти только в том случае, если их центры сблизятся на расстояние, меньшее или равное диаметру 
Через эффективный диаметр молекулы можно выразить эффективное сечение молекулы — как круг радиусом d. Столкновение между молекулами возможно только в том случае, когда центр молекулы окажется внутри круга, представляющего собой эффективное сечение молекулы.
С точки зрения теории межмолекулярных взаимодействий эффективный радиус, представляющий собой половину эффективного диаметра — расстояние от условного центра молекулы, отвечающее минимуму потенциальной энергии в поле этой молекулы.
Для молекул, имеющих точечную симметрию, условный центр может быть определен как центр масс молекулы, для сложных молекул он определяется феноменологически.
В общем случае эффективный радиус — усредненная величина, т.к. в случае, когда молекула не является концентрически симметричной (одноатомная молекула), радиус является функцией от угла в системе, связанной с молекулой.

Лабораторная работа № 206
ОПРЕДЕЛЕНИЕ СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО ПРОБЕГА
И ЭФФЕКТИВНОГО ДИАМЕТРА МОЛЕКУЛ ВОЗДУХА
Цель работы: 1) экспериментальное определение
средней длины свободного пробега молекул воздуха в
лаборатории;
2) определение эффективного диаметра молекул
воздуха.
Приборы и принадлежности:
стеклянный
баллон с краном,
мерный
стакан,
капиллярная
трубка,
линейка,
секундомер,
термометр,
барометр.
1. СРЕДНЯЯ ДЛИНА
СВОБОДНОГО ПРОБЕГА
МОЛЕКУЛ ГАЗА
Молекулы газа, находясь в
состоянии теплового хаотического движения, непрерывно сталкиваются друг с
другом. Термин «столкновение» применительно к молекулам не следует понимать
буквально и представлять себе этот процесс подобным соударению твердых шаров.
Под столкновением молекул подразумевают
процесс взаимодействия между молекулами, в результате которого молекулы
изменяют направление своего движения.
Рис. 1.
На рис. 1а представлен график зависимости
потенциальной энергии eп взаимодействия двух
молекул от расстояния r
между их центрами. Рассмотрим с помощью этого графика процесс сближения
(соударения) молекул. Мысленно поместим центр одной из молекул в начало
координат, а центр второй молекулы представим перемещающимся по оси r. Пусть вторая молекула
летит по направлению к первой из бесконечности, имея начальный запас
кинетической энергии. Приближаясь к
первой молекуле, вторая под действием силы притяжения движется со все
возрастающей скоростью. В результате кинетическая энергия молекулы eк также растет. Однако
полная энергия системы, равная e = eк+eп, остается неизменной
(система двух молекул замкнута), т.к. одновременно уменьшается потенциальная
энергия eп. При прохождении
молекулой точки с координатой r0
силы притяжения сменяются силами отталкивания, вследствие чего молекула
начинает быстро терять скорость (в области отталкивания кривая eп(r) идет очень круто). В
момент, когда потенциальная энергия eп становится равной полной
энергии системы e, скорость молекулы
обращается в нуль. В этот момент имеет место наибольшее сближение молекул
друг с другом. После остановки молекулы все явления протекают в обратной
последовательности: сначала молекула движется со все возрастающей скоростью
под действием силы отталкивания; миновав расстояние r0, молекула попадает под
действие замедляющей ее движение силы притяжения и, наконец, удаляется на
бесконечность, имея первоначальный запас кинетической энергии.
Минимальное расстояние,
на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d (рис. 1b).
Величина
(1)
называется эффективным
сечением молекулы.
Значение d зависит от характера сил
взаимодействия, от энергии сближающихся молекул, т.е. от температуры. С
повышением температуры эффективный диаметр молекул уменьшается.
За секунду молекула
проходит в среднем путь, равный средней скорости . Если за секунду она претерпевает в среднем Z столкновений, то средняя
длина свободного пробега молекулы между двумя последовательными соударениями
будет равна
(2)
Рис. 2.
Для того чтобы подсчитать среднее число столкновений , предположим, что все молекулы газа представляют собой
упругие шарики радиуса r и все молекулы, кроме рассматриваемой, застыли
неподвижно на своих местах. Пусть молекула А движется со средней
скоростью (см. рис. 2). За
единицу времени она столкнется со всеми другими молекулами, центры которых
окажутся внутри цилиндра диаметром D
и высотой L, численно равной средней
скорости . Так молекула А не столкнется с молекулой С,
но испытает соударение с молекулой В. Так как средняя длина
свободного пробега молекул газа много больше, чем эффективный диаметр молекул,
то объем цилиндра можно считать равным
Умножив этот объем на число молекул в единице
объема n, получим среднее число
столкновений за единицу времени движущейся молекулы с неподвижными:
В действительности все
молекулы движутся, вследствие чего число соударений определяется средней
скоростью движения молекул по отношению друг к другу, а не средней скоростью молекул относительно
стенок сосуда:
Поэтому среднее число соударений должно быть
увеличено в раз:
(3)
Из соотношений (2) и (3) получим для средней
длины свободного пробега следующую формулу:
(4)
Из уравнения состояния идеального газа
следует, что концентрация молекул газа равна
Тогда формулу (4) можно записать
(5)
где k
– постоянная Больцмана, Т –
термодинамическая температура, Р –
давление, d – эффективный диаметр
молекул газа. Из формулы (5) видно, что при постоянной температуре с
увеличением давления Р средняя
длина свободного пробега молекул газа уменьшается.
Оценим среднюю длину
свободного пробега молекул газа. Молекулы имеют размеры порядка нескольких
десятых нанометра. Примем эффективный диаметр молекулы равным
Моль газа занимает при нормальных условиях (т.е.
при 0 °С и при Р = 1 атм = 1,013×105 Па) объем, равный
Число молекул в единице объема при этих условиях
равно
где NA – число Авогадро.
Подстановка этих чисел в формулу (4) дает
2. ОПИСАНИЕ РАБОЧЕЙ УСТАНОВКИ И МЕТОДА
ИЗМЕРЕНИЙ
Молекулярно-кинетическая
теория позволила получить формулы, связывающие макроскопические параметры
газа (давление, объем, температура) с его микроскопическими параметрами
(размеры и масса молекулы, ее скорость, средняя длина свободного пробега).
Пользуясь этими формулами, можно на основании измеренных макроскопических
параметров газа найти его микроскопические параметры.
Для нахождения средней
длины свободного пробега молекул газа используют формулу,
выражающую зависимость коэффициента внутреннего трения (вязкости) h от :
(6)
где r – плотность газа.
Из теории Максвелла
следует, что средняя арифметическая скорость молекул газа равна
(7)
где R
– молярная газовая постоянная, Т –
термодинамическая температура, m – масса одного моля.
Состояние идеального газа
описывается уравнением Клапейрона-Менделеева:
Из последнего уравнения плотность газа
(8)
Подставив в формулу (6) значения и r из формул (7) и (8), получим:
(9)
В данной работе
используется зависимость коэффициента вязкости от радиуса r капиллярной трубки, через
которую проходит газ, ее длины l и
разности давлений DР,
возникающих на концах этой трубки. Эта зависимость выражается формулой
Пуазейля:
(10)
где V
– объем газа, в данном случае воздуха, проходящего через трубку за время t.
Из формул (9) и (10)
следует, что средняя длина свободного пробега молекул воздуха равна:
(11)
Из формулы (4)
эффективный диаметр молекулы
Учитывая, что
получим

где Р и
Т – давление и температура, при
которых проводится опыт (определяются по барометру и термометру, находящихся
в лаборатории).
3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ОБРАБОТКА
РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
1.
Наполняют баллон 1 на три четверти водой и плотно
закрывают пробкой 2, в которую вставлен капилляр 3.
2.
Линейкой замеряют первоначальный уровень воды h1. Открывают кран 4
(см. рис. 3) и одновременно включают секундомер.
3.
Когда в мерном стакане 5 будет 100 ¸ 200 мл воды (1 мл = 10–6 м3), закрывают кран и одновременно останавливают
секундомер.
4.
Замеряют уровень жидкости h2
в сосуде. Объем вытесненной из баллона воды в мерном стакане будет равен
объему воздуха V, вошедшего в баллон
через трубку 3.
5.
По формуле (11) рассчитывают среднюю длину свободного пробега молекул
воздуха. Разность давлений вычисляют по формуле:
(13)
где r – плотность воды. Расчет удобнее вести по
формуле (11), записанной в виде:
(14)
где А –
постоянная величина для данного опыта, которая равна
(15)
Рис. 3.
6.
Опыт повторяют три раза с одними и теми же значением V и h1.
7.
По формуле (12) рассчитывают эффективный диаметр молекулы воздуха d. Давление Р и
температуру Т воздуха в лаборатории
берут из показаний барометра и термометра.
8.
Методом расчета погрешностей косвенных измерений находят относительную
Е и абсолютную Dl погрешность средней
длины свободного пробега молекул воздуха. Для простоты расчетов используем
только формулы (14) и (13), считая, что вклад постоянной А (см. формулу (15)) в погрешность измерений незначителен, тогда

,
где и
абсолютные погрешности табличных величин;
и
абсолютные погрешности прямых однократных измерений,
зависящих от цены деления измерительных приборов; абсолютная погрешность прямых многократных измерений
времени.
9.
Данные измерений и вычислений занесите в таблицу.
Таблица
результатов
Температура воздуха Т = ……К, давление Р =……Па.
|
№ |
t, |
h1 |
h2 |
DР |
V |
|
|
Е |
|
|
|
п/п |
с |
м |
м |
Па |
м3 |
м |
м |
% |
м |
м |
Молярная
масса молекул воздуха m = 29×10–3 кг/моль, плотность воды r = 103 кг/м3,
постоянная Больцмана k
= 1,38×10–23 Дж/K,
молярная газовая постоянная R
= 8,31 Дж/(моль×К), 1 мм
рт.ст. = 133 Па.
4. ВОПРОСЫ
ДЛЯ ДОПУСКА К РАБОТЕ
- Сформулируйте цель
работы.
2.
Запишите рабочие формулы для расчета и d, поясните смысл всех
величин, входящих в эти формулы.
3.
Опишите рабочую установку и порядок выполнения работы.
5. ВОПРОСЫ
ДЛЯ ЗАЩИТЫ РАБОТЫ
1.
Что называется эффективным диаметром молекулы? Эффективным сечением?
2.
Дайте определение длины свободного пробега молекул газа.
3.
Выведите формулу для расчета (формулу (5)).
4.
Выведите рабочие формулы (11) и (12).
5.
Используя дифференциальный метод, получите формулу для расчета
относительной погрешности , т.е.




