Как найти экономичный размер партии

Как найти экономичный размер партии

2.1 Модель экономичного размера партии

Если говорить о
проблемах управления запасами в целом,
связанных либо с заказом на партию
деталей внешнему поставщику, либо с
выпуском партии деталей, то стоит
отметить, что политика организации
производства или подачи заказов в этой
ситуации должна быть такой, чтобы общие
издержки были минимальными.

В любой системе
управления запасами уровень последних
изменяется в соответствии с циклической
моделью. Процесс снижения уровня запасов
определяется соответствующей моделью
спроса. В некоторой точке для пополнения
запаса будет сделан новый заказ. По
прошествии некоторого времени, называемого
временем поставки, заказ будет получен,
и уровень запасов возрастет. После этого
начинается новый цикл запасов.

Для упрощения
процесса моделирования в модель вводится
ряд предпосылок:

  1. Спрос на продукцию
    является постоянным, или приблизительно
    постоянным. Если коэффициент использования
    запасов является постоянным, то уровень
    запасов также будет уменьшаться с
    постоянным коэффициентом.

  2. Предполагается,
    что время поставки известно и является
    постоянной величиной. Это означает,
    что заказ можно осуществлять в точке
    с определенными значениями временного
    параметра и размера запаса (уровень
    повторного заказа), которые обеспечивают
    получение заказа в тот момент, когда
    уровень запасов равен нулю.

  3. Отсутствие запасов
    является недопустимым.

  4. В течение каждого
    цикла запасов делается заказ на
    постоянное количество продукции (q).

Компании,
специализирующиеся на выпуске различных
видов товаров, могут организовать
технологический процесс не на непрерывной
основе, а на основе производства партий
продукции. Например, на хлебопекарном
предприятии может быть принято решение
о производстве партии больших батонов
из непросеянной муки, затем – партии
маленьких булочек, за которой должна
следовать партия ячменных лепешек. Если
в компании используется производство
продукции партиями, то приходится решать
вопрос о размере партии продукции,
производимой в течение одного
производственного цикла, и о том, с какой
частотой следует производить партию
определенной продукции. Возникающие
трудности аналогичны проблемам, связанным
с определением экономичного размера
заказа. Вместо заказа определенного
количества продукции у внешнего
поставщика рассматривается объем
производства определенной продукции.

Модель экономичного
размера партии представлена на рис.
2.1.

Рис. 2.1. Модель экономичного размера
партии.

В ходе выпуска
продукции в форме производственных
партий, а не при покупке продукции извне,
возникают издержки, связанные со
стоимостью организации технологического
процесса по выпуску партии продукции
и издержки производства продукции.

Введем следующую
систему обозначений:

D
– спрос на продукцию;

Ch
– издержки хранения единицы продукции,
д.е. на единицу продукции в год;

q
– размер партии продукции.

Общая ежегодная
стоимость производства =

Ежегодная
стоимость организация технологического
процесса +

Годовая сумма
издержек хранения.

Обозначим через
Cs
стоимость организации каждого
производственного цикла, тогда получаем

(д.е.
в год),

где ТС – общая
ежегодная стоимость производства.

Теперь мы должны
определить значение q,
при котором значение общей стоимости
наименьшее.

Оптимальный
размер партии q0

Для определения
оптимального значения q
используем операцию дифференцирования
следующим образом:

,

ТС принимает
минимальное значение, когда

и
;

и

,
если q
> 0.

Положим,

,
тогда
,

следовательно

=;

;

.

Таким образом, ТС
принимает минимальное значение, если
.

Полученное
оптимальное количество продукции в
партии называют экономичным
размером партии (EBQ)
(формула Уилсона).
В настоящее время стало уже традиционным
непосредственное применение формулы
модели EBQ,
а не получение ее каждый раз из уравнения
общей стоимости.

Итак, нам известно,
каким должен быть размер партии, но нам
по-прежнему ничего неизвестно, с какой
частотой их необходимо выпускать.

В течение года
потребуется D
/ q
партий, т.е.

Число партий
продукции в год = Ежегодный спрос / Размер
партии = D
/ q.

Следовательно,
частота выпуска партий равна

Если говорить о
среднегодовых издержках работы системы,
связанных с переналадкой системы и
издержками содержания, то

Среднегодовые
издержки работы системы = Издержки
производства продукции + Общая ежегодная
стоимость производства

Пример 1.
Компания,
производящая изделия из керамики,
выпускает несколько видов кофейников.
Производственный процесс организован
по принципу выпуска партий кофейников
общим объемом 500 штук в неделю. Спрос на
наиболее популярную модель, которую мы
обозначим через Х, составляет 2500 изделий
в год и равномерно распределяется в
течение года. Вне зависимости от того,
в какой момент времени возникает
необходимость в производстве партии
кофейников модели Х, стоимость
производственного процесса составляет
200 ф. ст. По оценкам специалистов компании
стоимость хранения кофейников составляет
1, 50 ф.ст. за единицу.

Каково должна быть
партия кофейников, чтобы затраты на
производство и хранение были минимальными?
Как часто следует возобновлять
производственный цикл и какова его
длительность? Предполагается, что в
году 50 рабочих недель.

Решение

D
= 2500 кофейников в год;

Cs
= 200 ф.ст. на один производственный цикл;

Ch
= 1, 50 ф.ст. за один кофейник в год.

Экономичный размер
партии можно определить следующим
образом:

=
.

Возможно, что
выбранное в качестве EBQ
значение, равное 820, не приведет к
значительному увеличению общей стоимости.
Проверим это.

Для q
= 816,5 единиц имеем:

ТС = 200 * 2500/816,5 + 1,5
* 816,5/2 = 612,37 + 612,37 = 1224,74 ф.ст. в год.

Для q
= 820 единиц имеем:

ТС = 200 * 2500/820 + 1,5 *
820/2 = 609,76 + 615 = 1224,76 ф.ст. в год.

Для q
= 800 единиц имеем:

ТС = 200 * 2500/800 + 1,5 *
800/2 = 625 + 600 = 1225 ф.ст. в год.

Наиболее удобный
размер партии, равный 800 кофейникам, по
сравнению с оптимальным размером
приводит к увеличению общей стоимости
производства и хранения кофейников на
26 пенсов.

Примем в качестве
EBQ
значение, равное 800 кофейникам. Число
производственных циклов в год составит:
2500 / 800 = 3,125 (т.е. 25 циклов за каждые 8 лет),
следовательно, интервал между двумя
любыми производственными циклами равен:
800 * 50 / 2500 = 16 недель. Если объем производства
в неделю равен 500 кофейникам, то процесс
производства одной партии займет 800 /
500 = 1,6 недели.

Пример 2.
Завод выпускает различные типы
лакокрасочных материалов партиями на
одном и том же оборудовании. При переходе
от одного вида материалов к любому
другому приходится нести затраты от
переналадок оборудования, т.е. стоимость
производственного процесса, которые в
среднем равны 300 руб. Средняя потребность
в материалах каждого типа – 3000 т в год,
стоимость 1 т – 160 руб. Издержки содержания
– 2% от стоимости пролеживаемой продукции.
Найти оптимальную партию запуска, его
периодичность и среднегодовые издержки
работы системы.

Итак,

Сs
= 300 руб.;

D
= 3000 т в год;

α = 160 руб. за т;

p
= 0,02 в год.

Решение

Издержки содержания
при выяснении оптимальной партии запуска
могут исчисляться величиной процента
p
от стоимости единицы продукции α, т.е.
Ch
= pα.

Размер партии
запуска продукции:

=
т.;

Периодичность
запуска:

=
года;

Среднегодовые
издержки работы системы, связанные с
переналадкой системы и издержками
содержания:

=
=

= 160*3000 +
руб.
в год.

Источник

Попросили меня тут поделиться мнением о том, каким же должен быть размер партий в одном хорошо известном мне производстве. А я подумал, и решил, что на эту тему много чего можно сказать, поэтому решил записать, чтобы не забыть на потом.

Данная статья не претендует на то, чтобы дать всеобъемлющий ответ на вопрос об оптимальных размерах производственных партий, ее цель — собрать в одно месте некоторые аспекты одно из проблем планирования сложного производства.

Начнем с определения

Вообще, чтобы действительно правильно начать ответ, нужно дать определение производственной партии. И одна только эта попытка может вызвать к жизни несколько крестовых походов и священных войн между адептами того или иного подхода. По крайней мере, в те годы, когда я работал консультантом в консалтинговой компании, мы долго ломали копья по поводу этого определения, пока один из мудрых коллег не предложил 5 вариантов, которые бы более-менее закрыли всё множество вариаций производственных партий.

Партия — это:

  1. Размер заказа клиента – внешнего, или внутреннего (между операциями)
  2. Технологическая партия – одновременно обрабатываемое количество продукции
  3. Количество продукции, выпускаемое между переналадками
  4. Количество продукции, выпускаемой между транспортировками
  5. Объем накопителя или бункера, единовременно загружаемый перед операцией

В общем случае следует говорить о том, что производственная партия — это то количество деталей, изделий, продукции, которое обрабатывается на одном этапе производства без перерывов, остановок и переключения на другой тип деталей, изделий, продукции. Не могу сказать, что это лучшее определение партии, которое можно дать, но для целей этой статьи, думаю, его будет достаточно.

Экономически оптимальный размер партии на одной операции

Для каждого отдельного этапа производства можно достаточно достоверно определить экономически оптимальный размер партии, для чего используют формулу Уилсона

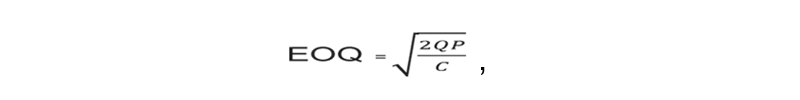
где   EOQ  — экономичный размер заказа (economic order quantity – EOQ)),
Q — количество товара в год (Quantity in annual units),
P — затраты  на реализацию заказа (Placing an order cost),
C — затраты на   складирование единицы товара в год (Carry costs)

или ее аналог формулу Андлера

где   у  min  — оптимальный размер партии,
V  — требуемый объем продукции за период времени (скорость сбыта),
Cr — затраты, связанные со сменой партий  ( условно  — на наладку),
Cl — удельные расходы на складирование  в периоде времени.

Общий вид графика таков:

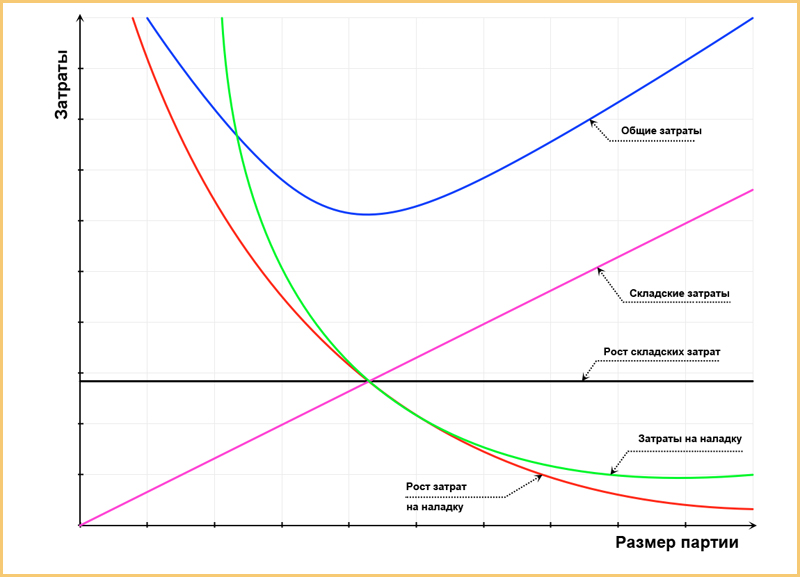
Собственно, тут надо искать минимум кривой «Общие затраты», а значение Х, которое ему соответствует, и будет представлять собой «экономически оптимальный размер партии».

Естественно, это всё выглядит просто только на графике, чтобы посчитать точное значение, нужно хорошо понимать затраты на наладку (зеленая кривая) и величину складских затрат (сиреневая кривая).

В затраты на наладку могут попадать:

  • стоимость простоя оборудования
  • стоимость простоя операторов
  • затраты на наладчиков
  • затраты на инструмент
  • затраты на оснастку
  • дополнительные затраты материалов и энергоносителей на время останова/пуска
  • и т.д.

В величину складских затрат попадают:

  • стоимость хранимых объектов
  • стоимость складских площадей
  • затраты на складской персонал
  • затраты на освещение и отопление
  • затраты на складскую технику (штабелеры / погрузчики)
  • и т.д.

В общем, достаточно много чего нужно учесть.

Кривая общих затрат не имеет излома в токе минимума, а это означает, что если вы получили, к примеру, экономически оптимальный размер партии в 1327 штук, то, скорее всего, вы можете запускать производство партиями от 1300 до 1400 штук без каких-либо существенных отклонений в себестоимости, ну и уж точно если оптимальный размер партии — 4,6 штуки, то можно запускать партии и по 4 штуки и по 5 штук.

Проблема: разные технологии — разные партии

Проблема реального производства заключается в том, что затраты на наладку и складские затраты неодинаковы на всём производственном цикле, и это вносит разногласия в то, каким должен быть размер партии, которая проходит несколько стадий производства, а не только одну.

Например, сырье выгодно привозить фурами, т.к. стоимость транспортного средства «размазывается» на весь объем сырья, сколько бы его ни было, термообработку нужно выполнять для такого количества деталей, которые максимально можно засунуть в печь, а отгрузку нужно делать только в том количестве, которое заказал конкретный заказчик, иначе всё лишнее, что вы ему отправите, просто достанется ему даром.

Хранить мелкие и объемные объекты тоже стоит разные деньги, а если какое-то сырье нужно еще и держать в тепле или других «особых климатических условиях», то стоимость хранения такого сырья будет выше, чем для других видов сырья.

В итоге, если посчитать экономически оптимальный размер партии на четырех участках, можно получить, к примеру, такую картину (по порядку прохождения этапов производства):

  1. 2000 штук в партии
  2. 200 штук в партии
  3. 540 штук в партии
  4. 34 штуки в партии

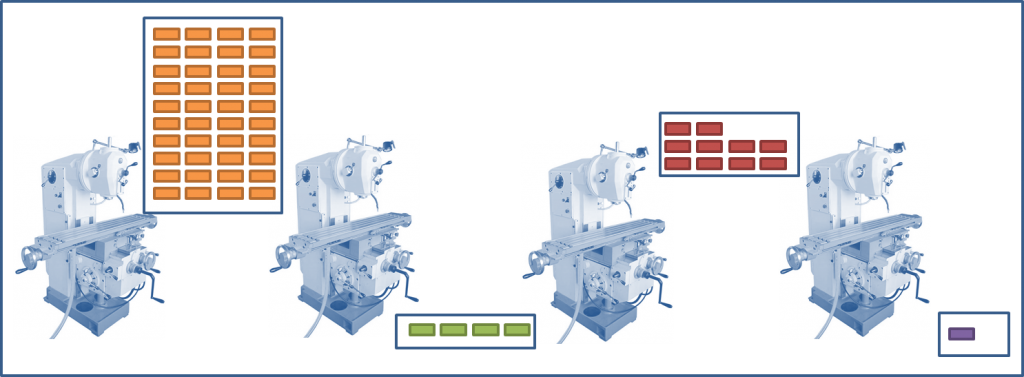
И хорошо еще, если единицы измерений в каждом случае одинаковые. А то ведь может получиться и так:

  1. 2000 кг в партии
  2. 200 штук в партии
  3. 540 пар в партии
  4. 34 комплекта в партии

В этом случае проблема оптимального размера партии только усугубляется.

Крайние варианты решения проблемы

Чтобы не путаться хочется иметь один размер партии на все случаи жизни. Ведь если на одном этапе производства партия состоит из десяти штук, а на другом из тринадцати, нужно организовывать какой-то промежуточный склад для того, чтобы накапливать недостающие штуки полуфабрикатов.

Какие же могут быть крайние варианты?

Их два:

  1. использовать максимальный из расчетных размеров партий
  2. использовать минимальный из расчетных размеров партий

Возьмем пример со штуками, описанный выше (2000, 200, 530 и 34 штуки) и посмотрим, как на нем реализовать оба варианта.

Максимальный размер партии

Максимальный размер партии из всех четырех вариантов — 2000 штук. Согласившись на его использование мы приходим к планированию производства, в котором используются только партии объемом 2000 штук:

  1. 2000 штук в партии
  2. 2000 штук в партии
  3. 2000 штук в партии
  4. 2000 штук в партии

Что при этом получается?

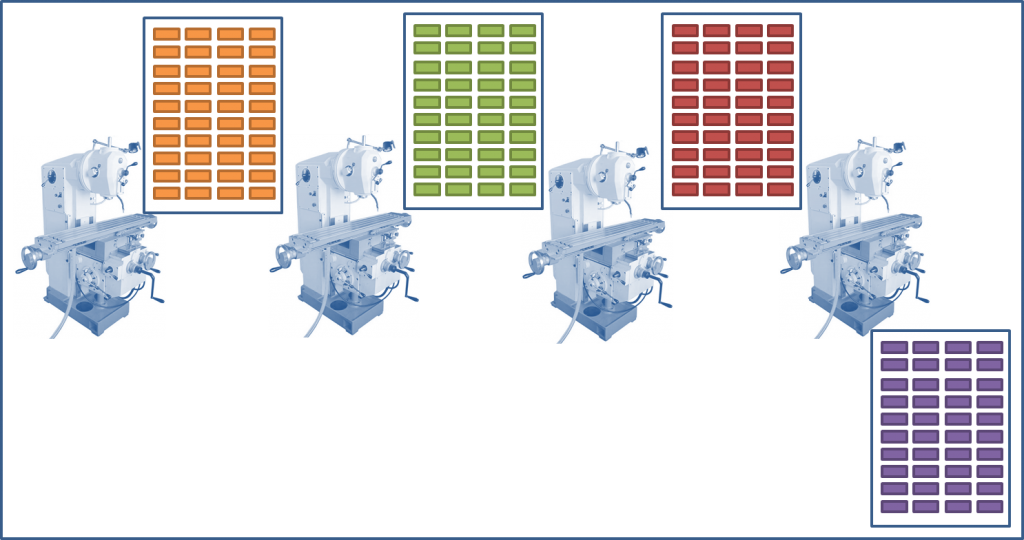
На первом этапе мы получаем оптимальный размер партии — ни больше, ни меньше. И те, кто работают на этом участке, а тем более те, кто им управляет, должны быть абсолютно довольны таким решением.

На втором этапе размер партии в 10 раз превышает оптимальный. Что это означает? Мы тратим в 10 раз меньше времени на переналадку этого этапа производства, но при этом заполняем промежуточный склад между 2 и 3 этапами большим объемом запасов, которые вдесятеро превышают то, что могло бы устроить наших менеджеров.

На третьем этапе размер партии больше оптимального почти в 4 раза, и это тоже может приводить к большому количеству запасов.

Но вот где запасов точно ОЧЕНЬ МНОГО — это после четвертого этапа. Там-то можно работать по 34 штуки, а это означает, что размер партии практически в 60 раз больше оптимального.

Чем хорошо и чем плохо такое решение.

Хороший результат заключается в том, что оборудование будет загружено по полной программе, простои на переналадку будут сведены к минимуму, и если мы сможем синхронизировать переналадку оборудования и пропускать по одной партии через все этапы по порядку, то нам нужно будет только три промежуточных склада на 2000 штук полуфабрикатов (между первым и вторым этапами, между вторым и третьим этапами, между третьим и четвертым этапами) и тогда весь процесс будет работать как конвейер. Если какой-то из этапов остановится, то ограничение в размер промежуточного склада в 2000 штук быстро вынудит остановить всё производство и перепроизводства не произойдет: последующие этапы исчерпают свои запасы полуфабрикатов и остановятся, т.к. аварийный этап не позволит их пополнять, а предыдущие этапы заполнят промежуточные склады и тоже остановятся, т.к. аварийный этап не позволит их освобождать).

Плохой результат в том, что вам скорее всего понадобится очень много складских площадей для организации трех промежуточных складов: чаще всего производство организуют так. что пока все 2000 полуфабрикатов не появятся на предшествующем складе, следующий этап производства не запускается, а это означает, что под эти полуфабрикаты нужно иметь соответствующее пространство (в отдельных случаях можно работать «с колес», т.е. запускать производство на следующем этапе еще до того, как вся партия в 2000 полуфабрикатов завершена, но это возможно не для каждой технологии). Хуже всего дело будет обстоять со складом готовой продукции, т.к. там мы получим катастрофический запас избыточной продукции.

Минимальный размер партии

Минимальный размер партии из всех четырех вариантов — 34 штуки. Согласившись на его использование мы приходим к планированию производства, в котором используются только партии объемом 34 штуки:

  1. 34 штуки в партии
  2. 34 штуки в партии
  3. 34 штуки в партии
  4. 34 штуки в партии

Что при этом получается?

На первом этапе переналадка будет выполняться в 60 раз чаще, чем этого требуется для оптимального варианта. Это очень много. Если каждая переналадка занимает ощутимое время, это может катастрофическим образом сказаться на производительности всего процесса — он просто не будет успевать выпускать всё, что вы хотите от него получить.

Дальше переналадка будет выполняться тоже неоптимально — в 6 раз чаще, чем это требуется для оптимального варианта. Хуже того, если, например, при запуске каждой партии используется дорогостоящая оснастка или материалы, которые расходуются один раз на всю партию, эти расходы существенно возрастут и лягут непомерным грузом на себестоимость продукции.

То же самое будет с третьим этапом, и только на четвертом этапе всё будет так как надо.

В общем случае, весь производственный процесс будет идти медленнее, его будет сдерживать этап с самой длительной переналадкой.

Плюсы данного варианта в том, что вы сводите к минимуму потребности в складских площадях — их нужно только столько, сколько требуется для хранения 3 видов полуфабрикатов по 34 штуки, еще немного — для 34 единиц сырья и 34 единиц готовой продукции. Микроскопическая цифра, по сравнению с предыдущим этапом.

Минусы — возросшие потери оснастки на переналадках и сократившаяся из-за больших потерь времени на переналадку производительность всего процесса в целом.

Давайте оставим всё как есть

Теперь, разобравшись с тем, что происходит в крайних случаях, можно разобраться, а как будет действовать производство, если оставить размеры партий такими, чтобы они были равны экономически оптимальному размеру партии каждого этапа в отдельности:

  1. 2000 штук в партии
  2. 200 штук в партии
  3. 540 штук в партии
  4. 34 штук в партии

Итак, как это будет работать?

Для запуска такого производства нам понадобится 2000 единиц сырья перед первым этапом. Тогда мы сможем выполнить наладку и запустить оптимальную партию в производство и всё будет хорошо.

После этого 2000 полуфабрикатов попадут на промежуточный склад. Из них за первый заход отберут только 200 штук, чтобы начать оптимальным образом второй этап производства. Здесь тоже всё хорошо.

После второго этапа 200 штук лягут в запас и будут ждать следующей партии, поскольку для запуска третьего этапа нужно не меньше 540 штук. И если второй этап будет изготавливать полуфабрикаты того же типа, то потребуется выпустить еще два партии по 200 штук. В этом случае запасы между вторым и третьим этапом достигнут 600 штук и можно будет запустить третий этап производства.

Третий этап производства выдаст 540 полуфабрикатов на последний промежуточный склад и они будут потребляться оттуда небольшими партиями по 34 штуки. В этом случае мы обеспечим минимальные запасы на складе готовой продукции, но всё равно не избавимся от запасов на складе полуфабрикатов между 3 и 4 этапами производства.

Что можно увидеть в этой ситуации?

Размер промежуточного склада пропорционален той из экономически оптимальных партий этих двух этапов, которая больше по количеству.

Т.е. склад полуфабрикатов между первым и вторым этапами производства должен вмещать не менее 2000 изделий. Склад полуфабрикатов между вторым и третьим этапами производства должен вмещать 540, а вовсе не 200 изделий. И склад полуфабрикатов между третьим и четвертым этапами производства тоже должен вмещать 540 изделий. Склад готовой продукции должен вмещать партии в 34 готовых изделия и этого, видимо, в нашем случае будет достаточно.

Интересно, что из этого вытекает первое изменение, которое стоит внести в систему планирования.

Поскольку размер складов у нас больше оптимального (2000, 540, 540 и 34), то нет никакого логического смысла запускать на втором этапе партии по 200 штук, а не по 540 — склад мы всё равно оплачиваем как «на 540» и накапливаем там детали для запуска на следующем этапе по (минимум) 540 штук, поэтому стоит изменить размер экономически оптимальной партии второго этапа с 200 на 540 несмотря на то, что цифру 200 мы получили расчетным путем по вышеприведённой формуле.

В реальности принятие такого решения выглядит так: мастер участка, на котором происходит выполнение второго этапа производства, смотрит на статистику запасов полуфабрикатов на обоих складах и говорит примерно следующее: «а чего мы вообще паримся и всё время переналадки делаем, это же никому не нужно!»

Таким образом, мы плавно переходим к варианту 2:

  1. 2000 штук в партии
  2. 540 штук в партии
  3. 540 штук в партии
  4. 34 штук в партии

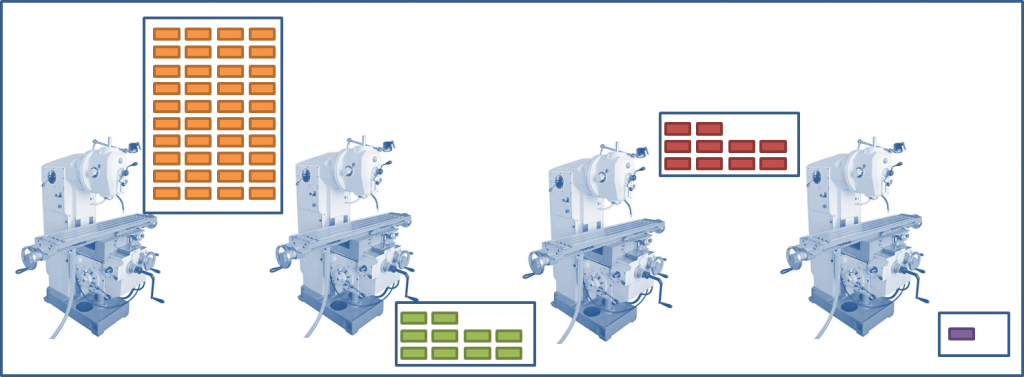
И это не самоуправство, это — просто здравый смысл мастера или планировщика, потому что в данном случае работа партиями по 200 штук действительно не нужна ни для чего кроме для соответствия расчётному экономически обоснованному размеру партии. А если это не игровая ситуация, а жизненная, то на расчётные цифры всем наплевать — ведь очевидно, что в данном случае в расчёте не учли особенностей всего процесса целиком.

Чтобы продемонстрировать это подход другим примером, давайте предположим, что производство состоит не из 4, а из 10 этапов, и оптимальные партии для каждого этапа были рассчитаны следующим образом:

  1. 4000 штук
  2. 70 штук
  3. 320 штук
  4. 15 штук
  5. 645 штук
  6. 90 штук
  7. 425 штук
  8. 64 штук
  9. 130 штук
  10. 70 штук

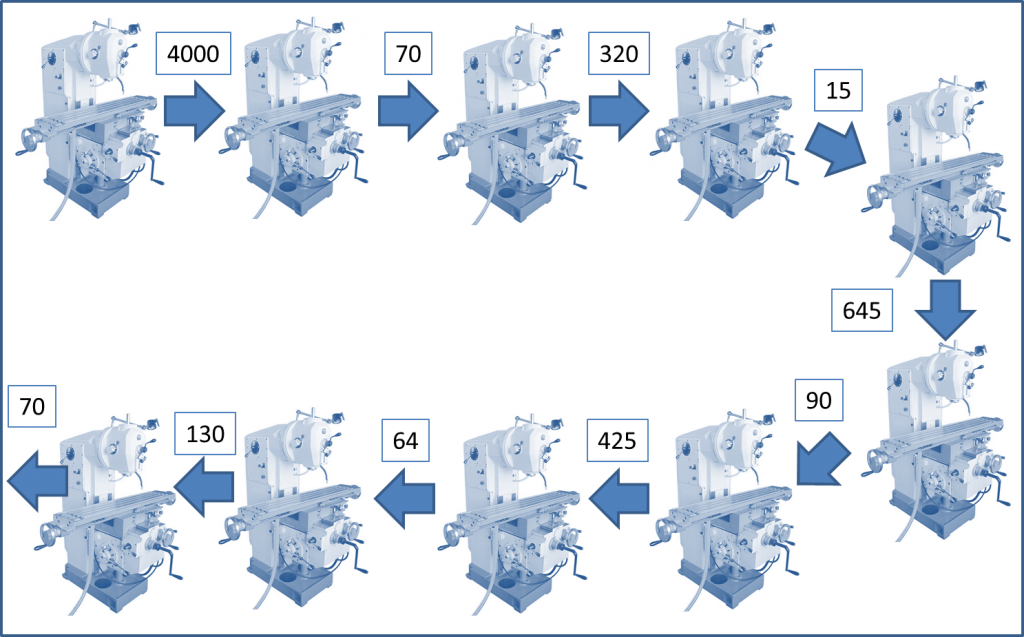
Очевидно, что запасы между этапами должны вмещать не меньше чем:

  • 4000 изделий между первым и вторым этапами
  • 320 изделий между вторым и третьим этапами
  • 320 изделий между третьим и четвертым этапами
  • 645 изделий между четвертым и пятым этапами
  • 645 изделий между пятым и шестым этапами
  • 425 изделий между шестым и седьмым этапами
  • 425 изделий между седьмым и восьмым этапами
  • 130 изделий между восьмым и девятым этапами
  • 130 изделий между девятым и десятым этапами

Поразмышляв немного над оптимальными размерами партий можно прийти к выводу, что с тем же успехом можно выставить размеры партий следующим образом:

  1. 4000 изделий
  2. 320 изделий
  3. 320 изделий
  4. 645 изделий
  5. 645 изделий
  6. 425 изделий
  7. 425 изделий
  8. 130 изделий
  9. 130 изделий
  10. 70 изделий

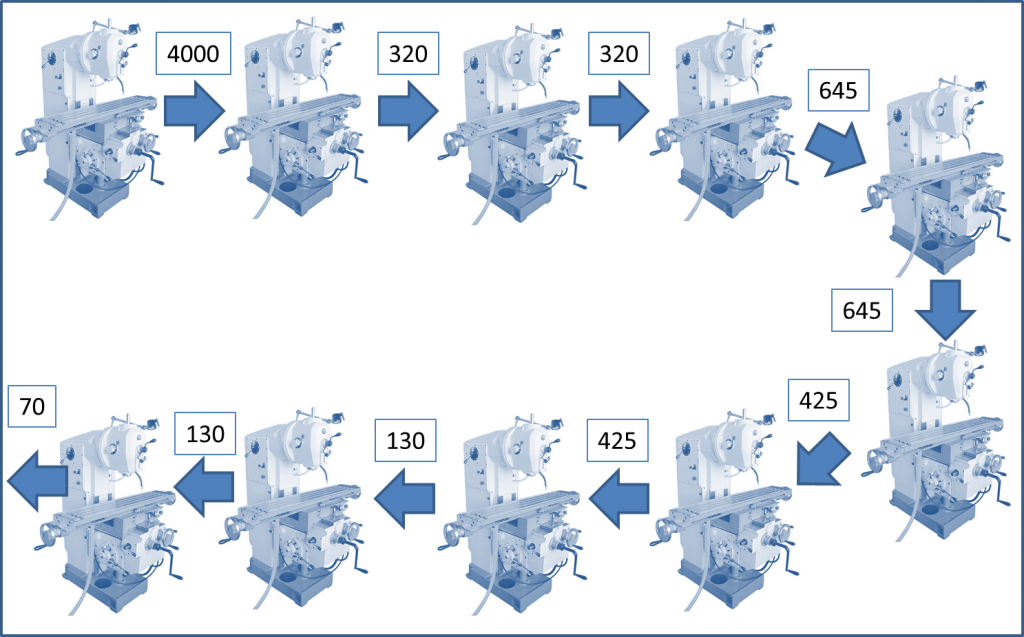
Теперь становится понятным, что между третьим и четвертым этапами нужен буфер в 645 изделий, а потом окажется, что такой же буфер на самом деле нужен и между вторым и третьим этапами производства. В итоге оптимальные размеры производственных партий по этапам будут составлять следующую последовательность:

  1. 4000 изделий
  2. 645 изделий
  3. 645 изделий
  4. 645 изделий
  5. 645 изделий
  6. 425 изделий
  7. 425 изделий
  8. 130 изделий
  9. 130 изделий
  10. 70 изделий

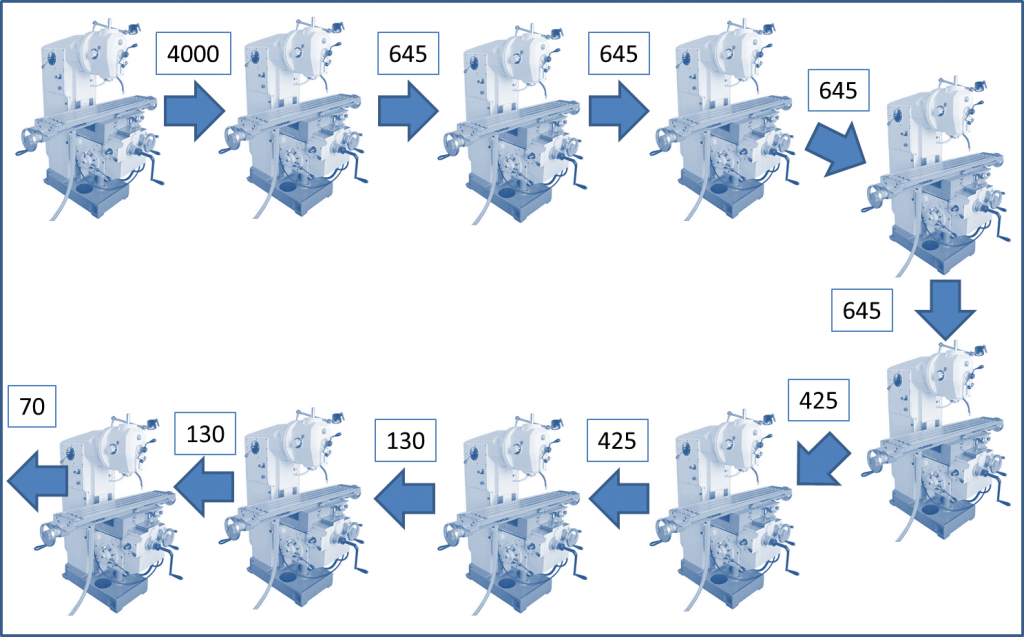
Т.е. в стабильном состоянии любой набор партий на этапах производства стремится к такому набору, когда на следующем этапе размер партии равен или меньше размера партии предыдущего этапа.

Давайте назовем это парадоксом «домашних консервных заготовок»: сначала мы собираем весь урожай, какой можем, и закатываем его по банкам, затем, по праздникам, достаем из запасов банку огурцов, открываем ее, и несколько дней поспешно доедаем открытую банку огурцов, чтобы они не испортились — на каждом этапе «потребления» урожая огурцов размер партии всё меньше и меньше, пока он не достигнет размера партий, которыми забирает продукцию потребитель.

Если бы у нас первоначально размеры партий составляли бы такую последовательность:

  1. 34 штуки
  2. 540 штук
  3. 200 штук
  4. 2000 штук,

то вполне разумно ожидать, что спустя какое-то время набор размеров партий пришел бы к варианту

  1. 2000 штук
  2. 2000 штук
  3. 2000 штук
  4. 2000 штук,

поскольку нет никакой необходимости 10 раз перенастраивать оборудование третьего этапа производства, чтобы запустить одну партию в 2000 одинаковых изделий на четвертом этапе.

Предупреждение о условиях, которые остались «за текстом»

Все эти расклады даны для одного типа изделий без учета других типов изделий — мы просто имеем в виду, что переналадка производится для изготовления «другого» типа продукции.

Парадокс «домашних консервных заготовок» в чистом виде можно увидеть только на том производстве, где производственных и складских площадей достаточно для хранения всех этих разрастающихся запасов. В противном случае они будут ограничиваться физическими масштабами производства, однако при этом суть парадокса будет такой же: размеры партий на предшествующих этапах будут увеличиваться до тех пор, пока не будет достигнут предел занимаемого запасами пространства, либо пока этот самый размер партий не достигнет размера партий последующих этапов.

Важный вывод о предельном оптимальном размере партии

Размер партий на каждом этапе производства будет не меньше размеров партий последнего этапа производства или последнего этапа транспортировки продукции заказчику.

Т.е. если вы отгружаете клиенту зубные велосипедные насосы сорокафутовыми контейнерами, нет никакого смысла производить их партиями по 10 штук, а не по 50 или по 1000 — в конечном итоге вам всё равно нужен будет полный контейнер насосов.

Расчет минимально допустимого размера партии

В логике бережливого производства одной из целью планирования производства является снижение размера партии вплоть до достижения идеального состояния, которое описывается понятием «поток единичных изделий» — One Piece Flow.

Если расчет экономически оптимального размера партий делается в рамках общепринятой логики управления, когда определенные размеры запасов являются благом, а не злом, то в бережливом производстве, когда любые запасы считаются в той или иной степени вредными, вопрос оптимального размера партий ставится немного иначе: насколько маленькими могут быть партии производства при условии сохранения необходимого уровня производительности производства?

Вот расчет.

Предположим, нам надо изготовить за время T определенное количество n изделий или полуфабрикатов. Среднее время цикла составляет CT. В этом случае время, которое мы можем потратить на переналадки будет равно

Tcho  = (T — n x CT)

Если одна переналадка занимает примерно время величиной ChT, то мы можем позволить себе определенное количество переналадок за этот период времени:

Ncho = (T — n x CT) / ChT

И тогда среднее количество изделий в партии будет равно:

Batch = n / Ncho = n x ChT / (T — n x CT)

Для максимума выполняемых за определенный период времени переналадок это будет минимум изделий на одну партию, при котором производство еще успевает выполнить свой план.

Вот пример.

Длительность смены
T = 8 часов или 480 минут

Время цикла
СТ = 1 минута / изделие

Плановый выпуск
n = 400 изделий

Длительность переналадки
Tcho = 5 минут

Batch = 400  x 5 / (480 — 400 x 1) = 400 x 5 / 80 = 25 изделий (округляем вверх)

Для надежности стоит ввести коэффициент доступности оборудования, чтобы учесть время на обслуживание и ремонт.

Тогда формула будет выглядеть так:

Batch = n x ChT / ( T x k — n x CT )

в этом случае, если в наш пример добавить коэффициент доступности 90%, то размер партии будет равен:

Batch = 400 x 5 / (480 x 0,9 — 400 x 1) = 400 x 5 / (432 — 400) = 400 x 5 / 32 = 63 изделий.

Вот несколько следствий из этой формулы:

  • Чем больше плановый выпуск, тем меньше можно сделать переналадок и тем больший размер партий нужно применять.
  • Чем меньше коэффициент доступности, тем меньше переналадок и тем больше размер партий.
  • Чем больше время переналадки, тем меньше переналадок и тем больше размер партий
  • Чем меньше время переналадки, тем больше можно сделать переналадок и тем меньший размер партий можно использовать.

В данной формуле сделаны два упрощения с учетом следующих предположений:

n — общее количество всех изделий одного семейства, которые нужно сделать за данное время, станок выпускает только эти изделия и никакие другие.

CT — усредненное время цикла производства любого одного изделия данного семейства изделий.

Это всё замечательно, но каким должен быть размер партии?

Начнем с конца. Применив последнюю формулу из неэкономического расчета для последнего этапа производства, вы сможете посчитать тот самый предельный оптимальный размер партии.

Размеры партий на предыдущих этапах можно установить таким же образом.

Если для вас критична складская или производственная площадь, то нужно поставить объем партий на каждом этапе под контроль, как и то, сколько пространства занимают промежуточные запасы.

Если это не критично, то размеры оптимальных партий на промежуточных этапах можно увеличить как минимум до предельного оптимального размера партии (рассчитанного для последнего этапа).

Если есть еще возможности хранить запасы — вы можете использовать парадокс «домашних консервных заготовок» и выстроить размеры партий в ниспадающем порядке (от самых больших на первых этапах к предельно оптимальной партии на последнем этапе).

На каждом промежуточном складе между этапами, которые имеют одинаковые размеры оптимальных партий должно единовременно находиться не более одной такой партии продукции. И они должны проходить по таким складам и этапам в режиме FIFO — первый вошел, первый вышел.

Размеры промежуточных складов между этапами, для которых размер оптимальных партий отличается друг от друга, нужно так же установить максимальный допустимый объем хранения и, при возможности, ввести в действие тот же принцип FIFO, чтобы продукция сразу после накопления до нужного количестве попадала на следующий этап.

Сложный случай

Что делать в том случае, если изделия состоят из множества деталей, а самих видов изделий много и они выпускаются последовательно один за другим, перемежаясь переналадками оборудования?

Очевидно, нужно брать базовые модели расчетов и перекладывать их на новые исходные условия. В целом это весьма непростая задача, и дать для нее решение в общем виде в этой статье определённо не получится. Однако я надеюсь, что вышеизложенного будет достаточно для того, чтобы запустить процесс обсуждения деталей системы планирования для тех предприятий, которые пытаются найти для себя ответ на вопрос «какие же партии будут оптимальны для нашего производства».

Если у вас появились вопросы или замечания — вы можете оставить их в комментариях к статье, либо в контактной форме.

Фото взяты здесь, здесь, здесь и здесь.

Кому это может быть интересно

PressFoto_5959641-MediumPressFoto_1251001-MediumPressFoto_725833-Medium

Узнать, кто эти люди…

Источник

Энциклопедия
28 августа 2012

0 комментариев

Размер партии – это величина последовательно произведенного товара без перерывов либо переключений в технологическом процессе. 
В чем значимость определения оптимального размера партии? 
Оптимальный размер партии приводит к уменьшению потерь по складу, процентов на имущество, расходов по перенастройке. Следовательно, разделение объема товаров, производимого за год, на доли приводит к значительному снижению расходов. 
Наилучшему размеру партии для производителя противодействует выгодный размер партии для реализации. Расходы по перенастройке становятся при данном варианте расходами по регистрации заказа. 

В чем заключается особенность серийного производства? 
Серийное производство оптимально для групп товаров сходных по технологическим процессам при изготовлении. Спустя некоторое время возникает необходимость в перенастройке к выпуску иного товара. Вышеприведенный рисунок демонстрирует, что продукция А, В, С производится последовательно на одной технологической линии. 
Перерыв в технологическом процессе для пуска в производство нового товара приводит к простою и появлению не связанных с размером партии расходов – постоянные серийные затраты. Это расходы на перенастройку и наладку производственных мощностей. 
При увеличении размера партии увеличиваются и постоянные серийные затраты. В пересчете на единицу продукции эти расходы сокращаются при увеличении размера партии, производимой без перерывов или перенастройки технологического процесса – дигрессивное поведение затрат. 
Серийное производство требует четкой координации объема производства, серии и последовательности изготовления товаров. Потребности в разных товарах должны исполняться предприятием без задержек. 
Каковы варианты удовлетворения годовой потребности в товаре? 
У бизнесмена есть несколько вариантов насыщения потребности в товаре в течение года: 
1) Единственная партия равная объему годовой потребности:

увеличение пропорциональных серийных затрат, а именно расходов по складу и процентов на имущество;
единичные расходы на перенастройку;
низкий уровень постоянных серийных затрат;
вероятность не насыщения потребностей по другим видам товаров. 

2) Некоторое количество партий, насыщающих годовую потребность:

уменьшение складских расходов и расходов на имущество;
увеличение расходов на перенастройку. 

Итак, главная задача – поиск наиболее эффективного размера партии, при котором единица произведенного товара будет приносить минимальные постоянные и пропорциональные серийные затраты. 
Какие расходы являются основными при серийном производстве? 
При серийном изготовлении товаров на предприятии появляются расходы, нуждающиеся в более полном рассмотрении: 
A) Расходы по складу: 

складские расходы – заработная плата, расходы на поддержание функциональности складских площадей;
калькуляционные проценты – это расходы коррелирующие с объемами хранящегося на складе имущества. 

Обе позиции могут быть снижены путем спланированного сокращения объема товаров на сладе. Нижний предел в данном случае – это страховой запас. 
Уменьшение складских расходов и калькуляционных процентов вызывает противодействие со стороны увеличивающихся расходов на  перенастройку технологического процесса и вероятности не насыщения потребности в определённом виде товаров. Выход из этой ситуации – поиск оптимального размера партии. 
Б) Расходы на перенастройку:

зависят от продолжительности процесса перенастройки;
не зависят от размера партии;
в пересчете на единицу товара уменьшаются с увеличением размера партии;
состоят из: 1) затрат простоя; 2) затрат на необходимые технические средства и оборудование; 3) заработной платы; 4) вспомогательных расходов. 

Этапы нахождения оптимального размера партии
Чтобы найти наиболее приемлемый вариант размера партии нужно: 
1.  Найти количество партий: 

где n – количество партий, M – годовой объем реализуемого товара, m –наиболее приемлимый размер партии, произведенный без перерыва либо перенастройки технологического процесса. 
2. Вычислить постоянные серийные затраты всех серий: 

где KF– общие постоянные затраты на перенастройку всех серий, Kf– серийные затраты для одной партии. 
3. Рассчитать размер суммарных складских расходов (склад и проценты): 

где KL– размер суммарных складских расходов, Kl– ставка расходов по складу и калькуляционных процентов в пересчёте на единицу товара за период. 
4. Определить суммарные затраты (K): 

5. Минимизация суммарных затрат приводит нас к функции: 

6. Наиболее приемлемый размер партии (m) находится при сведении уравнения к дифференциальному виду: 

7. Постановка условия 

8. Решение уравнения относительно m 

Рассмотри на примере. Прогнозируемая реализация в будущем году составит 400 000 единиц товара T. Размер постоянных серийных затрат достигает  6 000 ДМ. Расходы по складу равны 20 ДМ на единицу товара за год. Вычислим наиболее приемлемый вариант размера партии. 

Итак, минимизация затрат будет достигнута при размере партии в 15 491 шт. товара. 
Есть ли допущения в формуле расчета оптимального размера партии? 
Допущения в формуле расчета наиболее приемлемого размера партии:

бесконечность скорости процесса производства;
постоянность скорости реализации;
не учитывались складских потерь;
неизменность постоянных серийных затрат;
прямо пропорциональное изменение прочих расходов по производству;
не учитывались ограничение по складским площадям. 

Является ли расчет оптимального размера партии целесообразным на сегодняшний день? 
Не стоит отказываться от расчета оптимального размера партии под предлогом чрезмерного расходования трудовых ресурсов. Конечно, нет необходимости определять оптимальный размер партии для каждого вида продукции, но для А и B товаров эти расчёты необходимы.
Для начала производится расчет оптимального размера партии для A-товаров, составляющих 5 процентов от объема всей продукции, но дающих около 75 процентов в переводе на доходность. Улучшение планирования и регулировки производства А-товаров приведет к значительному уменьшению затрат. 
Внедрение оптимизации размера партии в сочетании с ABC-анализом значительно уменьшит производственные расходы. Этот эффект будет более значимым при повышении эффективность и снижении расходов склада. 
Широкое распространение и активное использование персональных компьютеров облегчает задачи по поиску оптимального размера партии. 

Размер партии – это величина последовательно произведенного товара без перерывов либо переключений в технологическом процессе. 

В чем значимость определения оптимального размера партии? 

Оптимальный размер партии приводит к уменьшению потерь по складу, процентов на имущество, расходов по перенастройке. Следовательно, разделение объема товаров, производимого за год, на доли приводит к значительному снижению расходов. 

Наилучшему размеру партии для производителя противодействует выгодный размер партии для реализации. Расходы по перенастройке становятся при данном варианте расходами по регистрации заказа. 

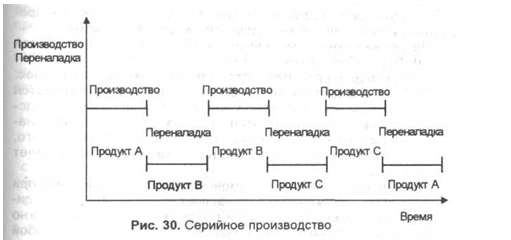
Оптимальный размер партии

В чем заключается особенность серийного производства? 

Серийное производство оптимально для групп товаров сходных по технологическим процессам при изготовлении. Спустя некоторое время возникает необходимость в перенастройке к выпуску иного товара. Вышеприведенный рисунок демонстрирует, что продукция А, В, С производится последовательно на одной технологической линии. 

Перерыв в технологическом процессе для пуска в производство нового товара приводит к простою и появлению не связанных с размером партии расходов – постоянные серийные затраты. Это расходы на перенастройку и наладку производственных мощностей. 

При увеличении размера партии увеличиваются и постоянные серийные затраты. В пересчете на единицу продукции эти расходы сокращаются при увеличении размера партии, производимой без перерывов или перенастройки технологического процесса – дигрессивное поведение затрат. 

Серийное производство требует четкой координации объема производства, серии и последовательности изготовления товаров. Потребности в разных товарах должны исполняться предприятием без задержек. 

Каковы варианты удовлетворения годовой потребности в товаре? 

У бизнесмена есть несколько вариантов насыщения потребности в товаре в течение года: 

1) Единственная партия равная объему годовой потребности:

  • увеличение пропорциональных серийных затрат, а именно расходов по складу и процентов на имущество;
  • единичные расходы на перенастройку;
  • низкий уровень постоянных серийных затрат;
  • вероятность не насыщения потребностей по другим видам товаров. 

2) Некоторое количество партий, насыщающих годовую потребность:

  • уменьшение складских расходов и расходов на имущество;
  • увеличение расходов на перенастройку. 

Итак, главная задача – поиск наиболее эффективного размера партии, при котором единица произведенного товара будет приносить минимальные постоянные и пропорциональные серийные затраты. 

Какие расходы являются основными при серийном производстве? 

При серийном изготовлении товаров на предприятии появляются расходы, нуждающиеся в более полном рассмотрении: 

A) Расходы по складу: 

  • складские расходы – заработная плата, расходы на поддержание функциональности складских площадей;
  • калькуляционные проценты – это расходы коррелирующие с объемами хранящегося на складе имущества. 

Обе позиции могут быть снижены путем спланированного сокращения объема товаров на сладе. Нижний предел в данном случае – это страховой запас. 

Уменьшение складских расходов и калькуляционных процентов вызывает противодействие со стороны увеличивающихся расходов на  перенастройку технологического процесса и вероятности не насыщения потребности в определённом виде товаров. Выход из этой ситуации – поиск оптимального размера партии. 

Б) Расходы на перенастройку:

  • зависят от продолжительности процесса перенастройки;
  • не зависят от размера партии;
  • в пересчете на единицу товара уменьшаются с увеличением размера партии;
  • состоят из: 1) затрат простоя; 2) затрат на необходимые технические средства и оборудование; 3) заработной платы; 4) вспомогательных расходов. 

Этапы нахождения оптимального размера партии

Чтобы найти наиболее приемлемый вариант размера партии нужно: 

1.  Найти количество партий: 

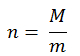
Формула 1

где n – количество партий, M – годовой объем реализуемого товара, m –наиболее приемлимый размер партии, произведенный без перерыва либо перенастройки технологического процесса. 

2. Вычислить постоянные серийные затраты всех серий: 

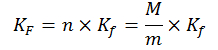
где KF– общие постоянные затраты на перенастройку всех серий, Kf– серийные затраты для одной партии. 

3. Рассчитать размер суммарных складских расходов (склад и проценты): 

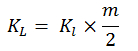
где KL– размер суммарных складских расходов, Kl– ставка расходов по складу и калькуляционных процентов в пересчёте на единицу товара за период. 

4. Определить суммарные затраты (K): 

5. Минимизация суммарных затрат приводит нас к функции: 

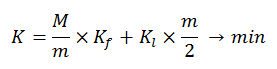
6. Наиболее приемлемый размер партии (m) находится при сведении уравнения к дифференциальному виду: 

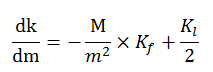
7. Постановка условия 

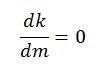
8. Решение уравнения относительно m 

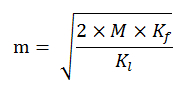
Рассмотри на примере. Прогнозируемая реализация в будущем году составит 400 000 единиц товара T. Размер постоянных серийных затрат достигает  6 000 ДМ. Расходы по складу равны 20 ДМ на единицу товара за год. Вычислим наиболее приемлемый вариант размера партии. 

Итак, минимизация затрат будет достигнута при размере партии в 15 491 шт. товара. 

Есть ли допущения в формуле расчета оптимального размера партии? 

Допущения в формуле расчета наиболее приемлемого размера партии:

  1. бесконечность скорости процесса производства;
  2. постоянность скорости реализации;
  3. не учитывались складских потерь;
  4. неизменность постоянных серийных затрат;
  5. прямо пропорциональное изменение прочих расходов по производству;
  6. не учитывались ограничение по складским площадям. 

Является ли расчет оптимального размера партии целесообразным на сегодняшний день? 

Не стоит отказываться от расчета оптимального размера партии под предлогом чрезмерного расходования трудовых ресурсов. Конечно, нет необходимости определять оптимальный размер партии для каждого вида продукции, но для А и B товаров эти расчёты необходимы.

Для начала производится расчет оптимального размера партии для A-товаров, составляющих 5 процентов от объема всей продукции, но дающих около 75 процентов в переводе на доходность. Улучшение планирования и регулировки производства А-товаров приведет к значительному уменьшению затрат. 

Внедрение оптимизации размера партии в сочетании с ABC-анализом значительно уменьшит производственные расходы. Этот эффект будет более значимым при повышении эффективность и снижении расходов склада. 

Широкое распространение и активное использование персональных компьютеров облегчает задачи по поиску оптимального размера партии. 

Источник

Определение оптимального размера партии
Дмитрий Езепов, менеджер по закупкам компании «Мидвест» © ЛОГИСТИК&система www.logistpro.ru

Одной из самых трудных задач для любого менеджера по закупкам является подбор оптимального размера заказа. Однако реальных инструментов, облегчающих ее решение, очень мало. Конечно, есть формула Вильсона, которая в теоретической литературе преподносится в качестве такого инструмента, но на практике ее использование необходимо корректировать

Автор этой статьи, работая в нескольких крупных торговых фирмах в Минске, нигде не видел, чтобы формула Вильсона применялась на практике. Ее отсутствие в арсенале менеджеров по закупкам никак нельзя объяснить недостатком у них аналитических навыков и умений, так как современные компании уделяют большое внимание квалификации своих сотрудников.

Попробуем выяснить, почему «наиболее распространенный инструмент в управлении запасами» не выходит за рамки научных публикаций и учебников. Ниже представлена известная формула Вильсона, с помощью которой рекомендуется рассчитывать экономичный объем заказа:

формула Вильсона

где Q – объем партии закупки;

S – потребность в материалах или готовой продукции за отчетный период;

О – постоянные затраты, связанные с выполнением одного заказа;

С – затраты на хранение единицы запасов за отчетный период.

Суть данной формулы сводится к тому, чтобы рассчитать, какие должны быть размеры партий (все одинаковые), чтобы доставить заданный объем товаров (то есть общую потребность на отчетный период) в течение данного периода. При этом сумма постоянных и переменных издержек должна быть минимальной.

В решаемой задаче есть по крайней мере четыре начальных условия: 1) заданный объем, который требуется доставить до пункта назначения; 2) заданный период; 3) одинаковые размеры партий; 4) заранее утвержденный состав постоянных и переменных затрат. Такая постановка задачи имеет мало общего с реальными условиями ведения бизнеса. Емкость и динамику рынка заранее не знает никто, поэтому размеры заказываемых партий всегда будут разными. Задавать период для планирования закупок тоже нет смысла, так как коммерческие компании обычно существуют значительно дольше отчетного периода. Состав затрат также подвержен изменениям из-за влияния многих факторов.

Другими словами, условия применения формулы Вильсона в реальности просто не существуют или по крайней мере встречаются очень редко. Нужно ли коммерческим компаниям решение задачи с такими исходными условиями? Думается, что нет. Именно поэтому «распространенный инструмент» реализуется только на бумаге.

МЕНЯЕМ УСЛОВИЯ

В рыночных условиях активность продаж непостоянна, что неизбежно влияет на процесс снабжения. Поэтому как частота, так и размеры закупаемых партий никогда не совпадают с их плановыми показателями в начале отчетного периода. Если же ориентироваться исключительно на план или долгосрочный прогноз (как в формуле Вильсона), то неизбежно возникнет одна из двух ситуаций: либо переполнение склада, либо дефицит продукции. Результатом и того, и другого всегда будет уменьшение чистой прибыли. В первом случае – из-за увеличения расходов на хранение, во втором – из-за дефицита. Поэтому формула расчета оптимального размера заказа должна быть гибкой по отношению к ситуации на рынке, то есть опираться на максимально точный краткосрочный прогноз продаж.

Общие затраты на закупку и хранение запасов состоят из суммы этих же затрат для каждой закупаемой партии. Следовательно, минимизация стоимости доставки и хранения каждой партии в отдельности ведет к минимизации процесса снабжения в целом. А так как расчет объема каждой партии требует именно краткосрочного прогноза продаж (а не на весь отчетный период), то необходимое условие гибкости формулы расчета оптимального размера партии (ОРП) по отношению к ситуации на рынке выполняется. Такое условие задачи соответствует как цели коммерческой фирмы (минимизация затрат), так и реальным условиям ведения бизнеса (изменчивость конъюнктуры рынка). Определения постоянных и переменных затрат для подхода минимизации поставок с точки зрения каждой партии в отдельности приведены во врезке «Виды затрат» на стр. 28.

СОБСТВЕННО РАСЧЕТ

Если допустить, что кредит погашается по мере уменьшения стоимости запасов через плановые промежутки времени (дни, недели, месяц и др.)(1), то, используя формулу суммы членов арифметической прогрессии, можно рассчитать общую стоимость хранения одной партии запасов (плату за пользование кредитом):

общая стоимость хранения одной партии запасов

где K – расходы на хранение запасов;

Q – объем партии закупки;

p – цена закупки единицы товара;

t – время нахождения запаса на складе, которое зависит от краткосрочного прогноза интенсивности продаж;

r – процентная ставка в плановую единицу времени (день, неделя и др.).

Таким образом, общие затраты на доставку и хранение партии заказа составят:

общие затраты на доставку и хранение партии заказа

где Z – общие затраты на доставку и хранение партии.

Минимизировать абсолютную величину стоимости доставки и хранения одной партии нет смысла, так как дешевле было бы просто отказаться от закупок, поэтому следует перейти к относительному показателю затрат на единицу запаса:

где z – стоимость пополнения и хранения единицы запаса.

Виды затрат

Постоянные затраты остаются затратами, которые фирма несет независимо от объема партии. Обозначим их как R (от англ. replenishment – пополнение). Переменные затраты К (от англ. keep – держать) – это затраты на хранение партии. Они зависят не только от стоимости хранимых запасов, но и от времени их нахождения на складе (t). Время t обычно измеряется в каких-либо плановых единицах: днях, неделях, месяцах и др. Для простоты в качестве стоимости хранения запасов возьмем процентную ставку за пользование кредитом (r) в такую же плановую единицу времени, в которой измеряется время t.

Если закупки осуществляются часто, то период продаж для одной партии получается небольшой, и интенсивность продаж в течение этого времени будет относительно постоянной2. Исходя из этого время нахождения запаса на складе рассчитывают как:

где – краткосрочный прогноз средних продаж за плановую единицу времени (день, неделю, месяц и др.).

Обозначение не случайно, так как в качестве прогноза обычно выступают средние продажи в прошлом с учетом различных корректировок (дефицит на складе в прошлом, наличие тенденции и др.).

Таким образом, подставляя формулу (5) в формулу (4), получим целевую функцию минимизации стоимости доставки и хранения единицы запаса:

Приравнивая первую производную к нулю:

находим оптимальный размер партии (ОРП) с учетом краткосрочного прогноза продаж:

оптимальный размер партии

НОВАЯ ФОРМУЛА ВИЛЬСОНА

Формально с математической точки зрения формула (8) – та же формула Вильсона (числитель и знаменатель разделены на одну и ту же величину в зависимости от принятой плановой единицы времени). И если интенсивность продаж не будет меняться, скажем, в течение года, то, заменив годовой потребностью в товаре и r – годовой процентной ставкой, мы получим результат, который будет идентичен расчету ЭОЗ. Однако с функциональной точки зрения формула (8) демонстрирует совершенно иной подход к решаемой задаче. В ней учитывается оперативный прогноз продаж, что делает расчет гибким относительно ситуации на рынке. Остальные параметры формулы ОРП в случае необходимости могут оперативно корректироваться, что также является неоспоримым преимуществом перед классической формулой расчета ЭОЗ.

На политику закупок компании влияют и другие, часто более значимые факторы, чем интенсивность продаж (текущие остатки на собственном складе предприятия, минимальный размер партии, условия доставки и др.). Поэтому, несмотря на то что в предлагаемой формуле устранена основная преграда для расчета оптимального размера заказа, ее использование может быть лишь вспомогательным инструментом эффективного управления запасами.

Высокопрофессиональный менеджер по закупкам опирается на целую систему статистических показателей, в которой формула ОРП играет существенную, но далеко не решающую роль. Однако описание такой системы показателей эффективного управления запасами является отдельной темой, которую мы будем освещать уже в следующих номерах журнала •

1- В реальности так не происходит, поэтому стоимость хранения запасов будет выше. 2- В реальности нужно обращать внимание не на частоту заказа, а на стабильность продаж в рамках краткосрочного периода прогноза продаж. Просто обычно, чем меньше период, тем меньше проявляется сезонность и тенденция.

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 2 августа 2021 года; проверки требуют 4 правки.

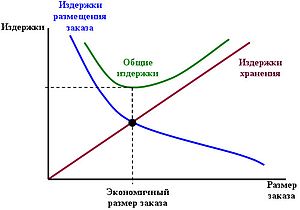
Определение оптимального объема заказа

Экономичный размер заказа (формула Уилсона, EOQ-модель) — модель, определяющая оптимальный объём заказываемого товара, который позволяет минимизировать общие переменные издержки, связанные с заказом и хранением запасов.

Основные предположения[править | править код]

  1. Спрос на продукт известен.
  2. Время реализации заказа (поставки) известно и постоянно.
  3. Получение товара происходит мгновенно.
  4. В модели не учитываются оптовые скидки.
  5. Дефицит не допускается.

Переменные[править | править код]

  • Q * — оптимальный размер заказа
  • C — издержки размещения заказа
  • R — ежегодный (annual) спрос на продукт
  • P — издержки на покупку единицы продукта
  • F — коэффициент издержек хранения запаса; доля издержек на покупку продукта, который используется в качестве издержек хранения (обычно 10-15 %, хотя при определённых обстоятельствах может устанавливаться на уровне от 0 до 1)
  • H — издержки хранения единицы товара в год (H = PF)

Формула[править | править код]

Рисунок показывает взаимоотношение между кривыми издержек размещения заказа, хранения запаса, кривой общих издержек и оптимальным размером заказа.

Формула оптимального размера заказа для единственного продукта может быть представлена как точка минимума следующей функции издержек:

Общие издержки = издержки на закупку + издержки размещения заказа + издержки хранения,

что соответствует:

{displaystyle TC(Q)=PR+{frac {CR}{Q}}+{frac {PFQ}{2}}}

Продифференцировав обе части уравнения и приравняв выражение к нулю, получим:

{displaystyle {frac {dTC(Q)}{dQ}}={frac {d}{dQ}}left(PR+{frac {CR}{Q}}+{frac {PFQ}{2}}right)=0}

В результате получим:

{displaystyle {frac {PF}{2}}-{frac {CR}{Q^{2}}}=0}

Решим относительно Q:

{displaystyle {frac {PF}{2}}={frac {CR}{Q^{2}}}}

{displaystyle Q^{2}={frac {2CR}{PF}}}

{displaystyle Q^{*}={sqrt {frac {2CR}{PF}}}={sqrt {frac {2CR}{H}}}}

Знак (*) означает оптимальный размер заказа.

Расширения[править | править код]

К модели оптимального размера партии могут применяться некоторые расширения, позволяющие учесть издержки задалживания заказов и многономенклатурные запасы.
Следует отметить, что формула Уилсона изначально разработана для крупных промышленных предприятий. А это означает, что она не может быть применена по своему прямому назначению в современных торговых компаниях. Пробовать использовать данную формулу следует на самых весомых в обороте и стабильных товарах. Весомые товары — это группа A (ABC-анализ), стабильные товары — это группа X (XYZ-анализ).

См. также[править | править код]

  • Управление запасами
  • ABC-анализ
  • XYZ-анализ

Ссылки[править | править код]

  • Стерлигова А.Н. Оптимальный размер заказа, или Загадочная формула Вильсона// Логистик &система. – №2. – С. 64-69. – №3. – С. 62-71. – 2005

Примечания[править | править код]

Источник

Добавить комментарий