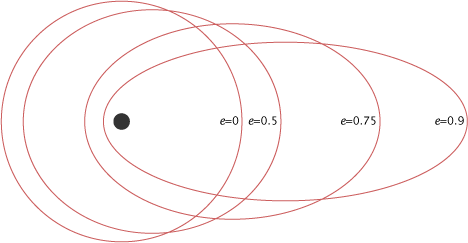
Эллиптическая орбита с эксцентриситетом 0,7 (красным), параболическая орбита (зелёным) и гиперболическая орбита с эксцентриситетом 1,3 (синим)
Эксцентрисите́т орбиты (обозначается «
Вычисление эксцентриситета орбиты[править | править код]
По внешнему виду орбиты можно разделить на пять групп:
Для эллиптических орбит эксцентриситет вычисляется по формуле:
, где
— малая полуось,
— большая полуось эллипса.
Для гиперболических орбит эксцентриситет вычисляется по формуле:
, где
— мнимая полуось,
— действительная полуось гиперболы.
Некоторые эксцентриситеты орбиты[править | править код]
В таблице ниже приведены эксцентриситеты орбиты для некоторых небесных тел (отсортированы по величине большой полуоси орбиты, кроме 1I/Оумуамуа и C/2019 Q4 (Борисова), у которых гиперболические орбиты, и кроме спутников, которые выделены серым цветом).
| Небесное тело | Эксцентриситет орбиты 
|
|
|---|---|---|
| Меркурий | 0,205[1] | |
| Венера | 0,007[1] | |
| Земля | 0,017[1] | |
| Луна | 0,05490[2] | |
| (3200) Фаэтон | 0,8898[3] | |
| Марс | 0,094[1] | |
| Юпитер | 0,049[1] | |
| Ио | 0,004[4] | |
| Европа | 0,009[4] | |
| Ганимед | 0,002[4] | |
| Каллисто | 0,007[4] | |
| Сатурн | 0,057[1] | |
| Титан | 0,029[4] | |
| Комета Галлея | 0,967[5] | |
| Уран | 0,046[1] | |
| Нептун | 0,011[1] | |
| Нереида | 0,7512[4] | |
| Плутон | 0,244[1] | |
| Хаумеа | 0,1902[6] | |
| Макемаке | 0,1549[7] | |
| Эрида | 0,4415[8] | |
| Седна | 0,85245[9] | |
| 1I/Оумуамуа | 1,1995[10] | |
| 2I/Borisov | 3,36[11] |
Эксцентриситет инвариантен относительно движений плоскости и преобразований подобия[12].
См. также[править | править код]
- Элементы орбиты
Примечания[править | править код]
- ↑ 1 2 3 4 5 6 7 8 9 Planetary Fact Sheet
- ↑ Clabon Walter Allen, Arthur N. Cox. Allen’s Astrophysical Quantities. — Springer, 2000. — С. 308. — ISBN 0-387-98746-0.
- ↑ 3200 Phaethon (1983 TB). Jet Propulsion Laboratory (22 октября 2015). Дата обращения: 23 октября 2015.
- ↑ 1 2 3 4 5 6 Clabon Walter Allen, Arthur N. Cox. Allen’s Astrophysical Quantities. — Springer, 2000. — С. 305—306. — ISBN 0-387-98746-0.
- ↑ JPL Small-Body Database Browser: 1P/Halley. Jet Propulsion Laboratory (11 января 1994). Дата обращения: 23 октября 2015. Архивировано 20 августа 2011 года.
- ↑ Jet Propulsion Laboratory Small-Body Database Browser: 136108 Haumea (2003 EL61). Jet Propulsion Laboratory (26 июля 2015). Дата обращения: 23 октября 2015.
- ↑ JPL Small-Body Database Browser: 136472 Makemake (2005 FY9). Jet Propulsion Laboratory (26 июля 2015). Дата обращения: 23 октября 2015.
- ↑ JPL Small-Body Database Browser: 136199 Eris (2003 UB313). Jet Propulsion Laboratory (26 октября 2014). Дата обращения: 23 октября 2015.
- ↑ JPL Small-Body Database Browser: 90377 Sedna (2003 VB12). Jet Propulsion Laboratory (17 ноября 2014). Дата обращения: 23 октября 2015.
- ↑ JPL Small-Body Database Browser: ‘Oumuamua (A/2017 U1). Jet Propulsion Laboratory (17 ноября 2017). Дата обращения: 22 ноября 2017.
- ↑ JPL Small-Body Database Browser: C/2019 Q4 (Borisov). Jet Propulsion Laboratory (16 ноября 2019). Дата обращения: 23 ноября 2019.
- ↑ Акопян А. В., Заславский А. А. Геометрические свойства кривых второго порядка — М.: МЦНМО, 2007. — 136 с.
Сегодня речь пойдет о конфигурации планет.
Конфигурация — характерное взаимное положение Солнца, планет, других небесных тел Солнечной системы на небесной сфере.
Будем называть планеты нижними, если они расположены ближе к Солнцу, чем Земля. Остальные планеты будут верхними – они расположены дальше нашей планеты от Солнца.
Планета может расположиться так, что Земля, Солнце и указанная планета находятся на одной линии. При этом может оказаться, что Солнце расположилось между Землей и рассматриваемой планетой. Такое расположение будем называть верхним соединением. Если же планета оказалась между Землей и Солнцем – то это уже нижнее соединение. Также может быть, что Земля находится между верхней планетой и Солнцем – тогда речь пойдет о противостоянии, или оппозиции.
Элонгация — одна из конфигураций планет, такое положение планеты, при котором её угловое расстояние от Солнца максимально для земного наблюдателя. Различают восточную и западную элонгацию (планета находится, соответственно, к востоку и к западу от Солнца). Об элонгации имеет смысл говорить только для Венеры и Меркурия; наилучшие условия для наблюдения этих планет наступают именно вблизи элонгаций. Из-за того, что орбиты планет не вполне круговые, угловое расстояние от Солнца в момент элонгации может быть разным, для Меркурия — от до
, для Венеры — около
.
Квадратура — в астрономии такая конфигурация Луны или верхней планеты (то есть планеты, более удалённой от Солнца, чем Земля) относительно Земли и Солнца, когда угол планета-Земля-Солнце равен . Если светило при этом находится к востоку от Солнца, конфигурация называется восточной квадратурой, к западу — западной квадратурой.
Сидерический период – это время совершения полного оборота какого-либо тела (планеты, кометы, астероида или искусственного спутника) вокруг главного тела (Солнца или др. планеты для спутника планеты) относительно неподвижных звёзд. Сидерический период также называют годом. Например, Меркурианский год, Юпитерианский год, и т. п.
Синодический же период – это время наблюдения с Земли совершения полного оборота планеты вокруг Солнца или Луны (искусственного спутника) вокруг Земли относительно Солнца ; промежуток времени между двумя последовательными соединениями Луны или какой-нибудь планеты Солнечной системы с Солнцем при наблюдении за ними с Земли. При этом соединения планет с Солнцем должны происходить в фиксированном линейном порядке, что существенно для внутренних планет: например, это будут последовательные верхние соединения, когда планета проходит за Солнцем.
Будем помнить также и о том, что орбиты планет не круговые. Это эллипсы, причем Солнце находится в одном из главных фокусов орбиты планеты.
Перигелий — ближайшая к Солнцу точка орбиты планеты или иного небесного тела Солнечной системы.
Антонимом перигелия является афелий (апогелий) — наиболее удалённая от Солнца точка орбиты. Воображаемую линию между афелием и перигелием называют линией апсид.
Названия апоцентров меняются: эти точки получают конкретные наименования но названию центрального тела, и некоторые из них приведены в нижеследующей таблице:
Задача 9.
| Центральное тело | Греческое название | Наименование перицентра | Наименование апоцентра |
| Солнце | Гелиос | перигелий | афелий |
| Земля | Гея | перигей | апогей |
| Венера | Геспер | перигесперий | апогесперий |
| Марс | Арес | периарий | апоарий |
| Сатурн | Кронос | перикроний | апокроний |
| Луна | Селена | периселений | апоселений |
Теперь обратимся к математике и разберемся, что же такое эксцентрисистет. Будем говорить об эксцентриситете эллипса, поскольку нас пока больше интересуют орбиты планет.
Эксцентриситетом эллипса называется отношение расстояния между фокусами этого эллипса к длине его большой оси; обозначив эксцентриситет буквой , получаем:
Так как , то
, т. е. эксцентриситет каждого эллипса меньше единицы. Заметим, что
, поэтому
Или
И
Следовательно, эксцентриситет определяется отношением осей эллипса, а отношение осей, в свою очередь, определяется эксцентриситетом. Таким образом, эксцентриситет характеризует форму эллипса. Чем ближе эксцентриситет к единице, тем меньше , тем меньше, следовательно, отношение
; значит, чем больше эксцентриситет, тем более эллипс вытянут. В случае окружности
и
.
Радиус перигелия рассчитывается по формуле:
где:
— большая полуось;
— эксцентриситет орбиты.
Скорость в перигелии рассчитывается по формуле:
где:
— гравитационная постоянная;
— масса Солнца;
— большая полуось;
— эксцентриситет орбиты.
Афелийное расстояние рассчитывается по формуле
Следовательно, большая полуось орбиты планеты является средним ее расстоянием от Солнца
Cидерические периоды обращения и
двух планет связаны с их средними расстояниями
и
от Солнца третьим законом Кеплера
Если дается в годах и
— в астрономических единицах, то, принимая для Земли
год и
а. е., получим для любой планеты
Средняя орбитальная, или круговая, скорость планеты
всегда выражается в км/с. Так как обычно задается в астрономических единицах (1 а. е.=
км) и T— в годах (1 год=
с), то
Подставляя , получим:
Где скорость планеты теперь выражена в км/с.
Средняя продолжительность синодического периода обращения планеты связана с сидерическим периодом
уравнением синодического движения: для верхних планет
для нижних планет
где — сидерический период обращения Земли, равный 1 звездному году.
Задача 1.
Найти перигельное и афелийное расстояния, сидерический и синодический периоды обращения, а также круговую скорость малой планеты Поэзии, если большая полуось и эксцентриситет ее орбиты равны 3,12 а. е. и 0,144.
Перигельное расстояние, а.е.
афелийное расстояние, а.е.
Сидерический период обращения
а так как а. е., то планета верхняя и поэтому ее синодический период обращения
вычисляется по формуле
при году:
Круговая скорость, км/с:
Задача 2.
Вычислить перигельное и афелийное расстояния планет Сатурна и Нептуна, если их средние расстояния от Солнца равны 9,54 а. е. и 30,07 а. е., а эксцентриситеты орбит— 0,054 и 0,008.
Перигельное расстояние Сатурна, а.е.
афелийное расстояние Сатурна, а.е.
Перигельное расстояние Нептуна, а.е.
афелийное расстояние Нептуна, а.е.
Ответ: а.е.,
а.е.,
а.е.,
а.е.
Задача 3.
Какая из двух планет — Нептун (а = 30,07 а.е., ) или Плутон (а = 39,52 а. е.,
) — подходит ближе к Солнцу? В скобках даны большая полуось и эксцентриситет орбиты планеты.
Нужно сравнить перигельные расстояния, причем для Нептуна мы его уже вычислили: а.е. Вычислим для Плутона:
Таким образом, Плутон ближе подходит к Солнцу.
Задача 4.
Найти эксцентриситет орбиты и перигельное расстояние планеты Марса и астероида Адониса, если у Марса большая полуось орбиты равна 1,52 а. е. и наибольшее расстояние от Солнца 1,66 а. е., а у Адониса соответственно 1,97 а. е. и 3,50 а. е. Указать, какая из этих двух планет подходит ближе к Солнцу.
Опять определим перигельные расстояния. Наибольшие расстояния от Солнца нам известны – афелийные. Тогда для Марса
Следовательно, перигельное расстояние Марса равно
Для Адониса
Следовательно, перигельное расстояние Адониса равно
Таким образом, Адонис подходит ближе к Солнцу.
Ответ: ,
а.е. ,
,
а.е.
Задача 5.
На каком среднем и наибольшем гелиоцентрическом расстоянии движутся малые планеты Икар и Симеиза, если у Икара перигельное расстояние и эксцентриситет орбиты равны 0,187 а. е. и 0,827, а у Симеизы — 3,219 а. е. и 0,181? У какой из этих планет радиус-вектор изменяется в больших пределах, абсолютно и относительно?
Так как афелийное расстояние у Симеизы больше, то радиус-вектор ее длиннее (абсолютно). Но, так как , то относительно радиус-вектор Икара больше изменяется.
Задача 6.
Вычислить периоды обращения вокруг Солнца планеты Венеры и астероида Европы, у которых средние гелиоцентрические расстояния соответственно равны 0,723 а. е. и 3,10 а. е.
Сидерический период Венеры равен:
Или 224,5 суток.
Сидерический период астероида Европы равен:
Ответ: сидерический период Венеры равен 0,615 года или 224,5 суток, а у Европы 5,458 года.
Задача 7.
Определить периоды обращения вокруг Солнца малой планеты Аполлона и кометы Икейи, если обе они проходят вблизи Солнца почти на одинаковых расстояниях, равных у Аполлона 0,645 а. е., а у кометы 0,633 а. е., но их орбиты имеют эксцентриситеты 0,566 и 0,9933 соответственно.
Определим большие полуоси орбит Аполлона и кометы Икейи:
Тогда сидерический период Аполлона
Тогда сидерический период Икейи
Ответ: года,
лет.
Задача 8.
Первый спутник планеты Юпитера — Ио обращается вокруг нее за 42ч28м на среднем расстоянии в 421 800 км. С какими периодами обращаются вокруг Юпитера его спутники Европа и Ганимед, большие полуоси орбит которых равны 671,1 тыс. км и 1070 тыс. км?
Для спутников справедлив закон Кеплера. Применим его для Европы:
Период 42ч28м= ч.
А теперь то же самое для Ганимеда:
Ответ: Период Европы 85,23 ч, или 3д 55, период Ганимеда 171,59 ч, или 7д 15
Задача 9.
Найти средние расстояние от Сатурна его спутников Мимаса и Реи, обращающихся вокруг планеты с периодами в 22ч37м и 4д,518. Самый крупный спутник планеты — Титан, обращается за 15д,945 по орбите с большой полуосью в 1221 тыс. км.
Переведем периоды в часы: период Мимаса 22,62 ч, период Реи 108,43 ч, период Титана 382, 68 ч.
Применяем закон Кеплера для Титана и Мимаса:
То же для Реи:
Ответ: большая полуось Мимаса 185,27 тыс. км, Реи 526,7 тыс. км.
From Wikipedia, the free encyclopedia
An elliptic, parabolic, and hyperbolic Kepler orbit:
elliptic (eccentricity = 0.7)
parabolic (eccentricity = 1)
hyperbolic orbit (eccentricity = 1.3)
Elliptic orbit by eccentricity
0.0 ·
0.2 ·
0.4 ·
0.6 ·
0.8
In astrodynamics, the orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values between 0 and 1 form an elliptic orbit, 1 is a parabolic escape orbit (or capture orbit), and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections, as every Kepler orbit is a conic section. It is normally used for the isolated two-body problem, but extensions exist for objects following a rosette orbit through the Galaxy.
Definition[edit]
In a two-body problem with inverse-square-law force, every orbit is a Kepler orbit. The eccentricity of this Kepler orbit is a non-negative number that defines its shape.
The eccentricity may take the following values:
- circular orbit: e = 0
- elliptic orbit: 0 < e < 1
- parabolic trajectory: e = 1
- hyperbolic trajectory: e > 1
The eccentricity e is given by[1]
where E is the total orbital energy, L is the angular momentum, mred is the reduced mass, and 
(
or in the case of a gravitational force:[2]: 24
where ε is the specific orbital energy (total energy divided by the reduced mass), μ the standard gravitational parameter based on the total mass, and h the specific relative angular momentum (angular momentum divided by the reduced mass).[2]: 12–17
For values of e from 0 to 1 the orbit’s shape is an increasingly elongated (or flatter) ellipse; for values of e from 1 to infinity the orbit is a hyperbola branch making a total turn of 2 arccsc(e), decreasing from 180 to 0 degrees. Here, the total turn is analogous to turning number, but for open curves (an angle covered by velocity vector). The limit case between an ellipse and a hyperbola, when e equals 1, is parabola.
Radial trajectories are classified as elliptic, parabolic, or hyperbolic based on the energy of the orbit, not the eccentricity. Radial orbits have zero angular momentum and hence eccentricity equal to one. Keeping the energy constant and reducing the angular momentum, elliptic, parabolic, and hyperbolic orbits each tend to the corresponding type of radial trajectory while e tends to 1 (or in the parabolic case, remains 1).
For a repulsive force only the hyperbolic trajectory, including the radial version, is applicable.
For elliptical orbits, a simple proof shows that 
Etymology[edit]
The word “eccentricity” comes from Medieval Latin eccentricus, derived from Greek ἔκκεντρος ekkentros “out of the center”, from ἐκ- ek-, “out of” + κέντρον kentron “center”. “Eccentric” first appeared in English in 1551, with the definition “…a circle in which the earth, sun. etc. deviates from its center”.[citation needed] In 1556, five years later, an adjectival form of the word had developed.
Calculation[edit]
The eccentricity of an orbit can be calculated from the orbital state vectors as the magnitude of the eccentricity vector:
where:
- e is the eccentricity vector (“Hamilton’s vector”).[2]: 25, 62–63
For elliptical orbits it can also be calculated from the periapsis and apoapsis since 

where:
- ra is the radius at apoapsis (also “apofocus”, “aphelion”, “apogee”), i.e., the farthest distance of the orbit to the center of mass of the system, which is a focus of the ellipse.
- rp is the radius at periapsis (or “perifocus” etc.), the closest distance.
The eccentricity of an elliptical orbit can also be used to obtain the ratio of the apoapsis radius to the periapsis radius:
For Earth, orbital eccentricity e ≈ 0.01671, apoapsis is aphelion and periapsis is perihelion, relative to the Sun.
For Earth’s annual orbit path, the ratio of longest radius (ra) / shortest radius (rp) is 
Examples[edit]
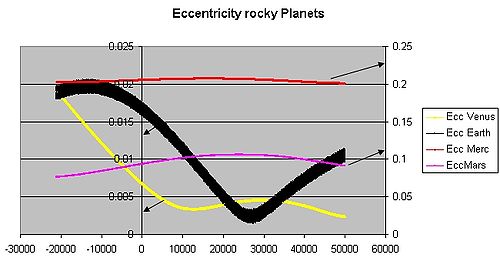
Plot of the changing orbital eccentricity of Mercury, Venus, Earth, and Mars over the next 50000 years. The arrows indicate the different scales used, as the eccentricities of Mercury and Mars are much greater than those of Venus and Earth. The 0 point on this plot is the year 2007.
| Object | eccentricity |
|---|---|
| Triton | 0.00002 |
| Venus | 0.0068 |
| Neptune | 0.0086 |
| Earth | 0.0167 |
| Titan | 0.0288 |
| Uranus | 0.0472 |
| Jupiter | 0.0484 |
| Saturn | 0.0541 |
| Moon | 0.0549 |
| 1 Ceres | 0.0758 |
| 4 Vesta | 0.0887 |
| Mars | 0.0934 |
| 10 Hygiea | 0.1146 |
| Makemake | 0.1559 |
| Haumea | 0.1887 |
| Mercury | 0.2056 |
| 2 Pallas | 0.2313 |
| Pluto | 0.2488 |
| 3 Juno | 0.2555 |
| 324 Bamberga | 0.3400 |
| Eris | 0.4407 |
| Nereid | 0.7507 |
| Sedna | 0.8549 |
| Halley’s Comet | 0.9671 |
| Comet Hale-Bopp | 0.9951 |
| Comet Ikeya-Seki | 0.9999 |
| C/1980 E1 | 1.057 |
| ʻOumuamua | 1.20[a] |
| C/2019 Q4 (Borisov) | 3.5[b] |
The eccentricity of Earth’s orbit is currently about 0.0167; its orbit is nearly circular. Venus and Neptune have even lower eccentricities. Over hundreds of thousands of years, the eccentricity of the Earth’s orbit varies from nearly 0.0034 to almost 0.058 as a result of gravitational attractions among the planets.[3]
The table lists the values for all planets and dwarf planets, and selected asteroids, comets, and moons. Mercury has the greatest orbital eccentricity of any planet in the Solar System (e = 0.2056). Such eccentricity is sufficient for Mercury to receive twice as much solar irradiation at perihelion compared to aphelion. Before its demotion from planet status in 2006, Pluto was considered to be the planet with the most eccentric orbit (e = 0.248). Other Trans-Neptunian objects have significant eccentricity, notably the dwarf planet Eris (0.44). Even further out, Sedna, has an extremely-high eccentricity of 0.855 due to its estimated aphelion of 937 AU and perihelion of about 76 AU.
Most of the Solar System’s asteroids have orbital eccentricities between 0 and 0.35 with an average value of 0.17.[4] Their comparatively high eccentricities are probably due to the influence of Jupiter and to past collisions.
The Moon’s value is 0.0549, the most eccentric of the large moons of the Solar System. The four Galilean moons have an eccentricity of less than 0.01. Neptune’s largest moon Triton has an eccentricity of 1.6×10−5 (0.000016),[5] the smallest eccentricity of any known moon in the Solar System;[citation needed] its orbit is as close to a perfect circle as can be currently[when?] measured. However, smaller moons, particularly irregular moons, can have significant eccentricity, such as Neptune’s third largest moon Nereid (0.75).
Comets have very different values of eccentricity. Periodic comets have eccentricities mostly between 0.2 and 0.7,[6] but some of them have highly eccentric elliptical orbits with eccentricities just below 1; for example, Halley’s Comet has a value of 0.967. Non-periodic comets follow near-parabolic orbits and thus have eccentricities even closer to 1. Examples include Comet Hale–Bopp with a value of 0.995[7] and comet C/2006 P1 (McNaught) with a value of 1.000019.[8] As Hale–Bopp’s value is less than 1, its orbit is elliptical and it will return.[7] Comet McNaught has a hyperbolic orbit while within the influence of the planets,[8] but is still bound to the Sun with an orbital period of about 105 years.[9] Comet C/1980 E1 has the largest eccentricity of any known hyperbolic comet of solar origin with an eccentricity of 1.057,[10] and will eventually leave the Solar System.
ʻOumuamua is the first interstellar object found passing through the Solar System. Its orbital eccentricity of 1.20 indicates that ʻOumuamua has never been gravitationally bound to the Sun. It was discovered 0.2 AU (30000000 km; 19000000 mi) from Earth and is roughly 200 meters in diameter. It has an interstellar speed (velocity at infinity) of 26.33 km/s (58900 mph).
Mean eccentricity[edit]
The mean eccentricity of an object is the average eccentricity as a result of perturbations over a given time period. Neptune currently has an instant (current epoch) eccentricity of 0.0113,[11] but from 1800 to 2050 has a mean eccentricity of 0.00859.[12]
Climatic effect[edit]
Orbital mechanics require that the duration of the seasons be proportional to the area of Earth’s orbit swept between the solstices and equinoxes, so when the orbital eccentricity is extreme, the seasons that occur on the far side of the orbit (aphelion) can be substantially longer in duration. Northern hemisphere autumn and winter occur at closest approach (perihelion), when Earth is moving at its maximum velocity—while the opposite occurs in the southern hemisphere. As a result, in the northern hemisphere, autumn and winter are slightly shorter than spring and summer—but in global terms this is balanced with them being longer below the equator. In 2006, the northern hemisphere summer was 4.66 days longer than winter, and spring was 2.9 days longer than autumn due to the Milankovitch cycles.[13][14]
Apsidal precession also slowly changes the place in Earth’s orbit where the solstices and equinoxes occur. This is a slow change in the orbit of Earth, not the axis of rotation, which is referred to as axial precession. Over the next 10000 years, the northern hemisphere winters will become gradually longer and summers will become shorter. However, any cooling effect in one hemisphere is balanced by warming in the other, and any overall change will be counteracted by the fact that the eccentricity of Earth’s orbit will be almost halved.[15] This will reduce the mean orbital radius and raise temperatures in both hemispheres closer to the mid-interglacial peak.
Exoplanets[edit]
Of the many exoplanets discovered, most have a higher orbital eccentricity than planets in the Solar System. Exoplanets found with low orbital eccentricity (near-circular orbits) are very close to their star and are tidally-locked to the star. All eight planets in the Solar System have near-circular orbits. The exoplanets discovered show that the Solar System, with its unusually-low eccentricity, is rare and unique.[16] One theory attributes this low eccentricity to the high number of planets in the Solar System; another suggests it arose because of its unique asteroid belts. A few other multiplanetary systems have been found, but none resemble the Solar System. The Solar System has unique planetesimal systems, which led the planets to have near-circular orbits. Solar planetesimal systems include the asteroid belt, Hilda family, Kuiper belt, Hills cloud, and the Oort cloud. The exoplanet systems discovered have either no planetesimal systems or one very large one. Low eccentricity is needed for habitability, especially advanced life.[17] High multiplicity planet systems are much more likely to have habitable exoplanets.[18][19] The grand tack hypothesis of the Solar System also helps understand its near-circular orbits and other unique features.[20][21][22][23][24][25][26][27]
See also[edit]
- Equation of time
Footnotes[edit]
- ^ ʻOumuamua was never bound to the Sun, so its orbit is hyperbolic: e ≈ 1.20 > 1 .
- ^ C/2019 Q4 (Borisov) was never bound to the Sun, so its orbit is hyperbolic: e ≈ 3.5 >> 1 .
References[edit]
- ^ Abraham, Ralph (2008). Foundations of mechanics. Jerrold E. Marsden (2nd ed.). Providence, R.I.: AMS Chelsea Pub./American Mathematical Society. ISBN 978-0-8218-4438-0. OCLC 191847156.
- ^ a b c d Bate, Roger R.; Mueller, Donald D.; White, Jerry E.; Saylor, William W. (2020). Fundamentals of Astrodynamics. Courier Dover. ISBN 978-0-486-49704-4. Retrieved 4 March 2022.
- ^ A. Berger & M.F. Loutre (1991). “Graph of the eccentricity of the Earth’s orbit”. Illinois State Museum (Insolation values for the climate of the last 10 million years). Archived from the original on 6 January 2018.
- ^ Asteroids Archived 4 March 2007 at the Wayback Machine
- ^ David R. Williams (22 January 2008). “Neptunian Satellite Fact Sheet”. NASA.
- ^
Lewis, John (2 December 2012). Physics and Chemistry of the Solar System. Academic Press. ISBN 9780323145848. - ^ a b “JPL Small-Body Database Browser: C/1995 O1 (Hale-Bopp)” (2007-10-22 last obs). Retrieved 5 December 2008.
- ^ a b “JPL Small-Body Database Browser: C/2006 P1 (McNaught)” (2007-07-11 last obs). Retrieved 17 December 2009.
- ^ “Comet C/2006 P1 (McNaught) – facts and figures”. Perth Observatory in Australia. 22 January 2007. Archived from the original on 18 February 2011.
- ^ “JPL Small-Body Database Browser: C/1980 E1 (Bowell)” (1986-12-02 last obs). Retrieved 22 March 2010.
- ^ Williams, David R. (29 November 2007). “Neptune Fact Sheet”. NASA.
- ^ “Keplerian elements for 1800 A.D. to 2050 A.D.” JPL Solar System Dynamics. Retrieved 17 December 2009.
- ^ Data from United States Naval Observatory Archived 13 October 2007 at the Wayback Machine
- ^ Berger A.; Loutre M.F.; Mélice J.L. (2006). “Equatorial insolation: from precession harmonics to eccentricity frequencies” (PDF). Clim. Past Discuss. 2 (4): 519–533. doi:10.5194/cpd-2-519-2006.
- ^ “Long Term Climate”. ircamera.as.arizona.edu.
- ^ “ECCENTRICITY”. exoplanets.org.
- ^ Ward, Peter; Brownlee, Donald (2000). Rare Earth: Why Complex Life is Uncommon in the Universe. Springer. pp. 122–123. ISBN 0-387-98701-0.
- ^ Limbach, MA; Turner, EL (2015). “Exoplanet orbital eccentricity: multiplicity relation and the Solar System”. Proc Natl Acad Sci U S A. 112 (1): 20–4. arXiv:1404.2552. Bibcode:2015PNAS..112…20L. doi:10.1073/pnas.1406545111. PMC 4291657. PMID 25512527.
- ^ Youdin, Andrew N.; Rieke, George H. (15 December 2015). “Planetesimals in Debris Disks”. arXiv:1512.04996.
- ^ Zubritsky, Elizabeth. “Jupiter’s Youthful Travels Redefined Solar System”. NASA. Retrieved 4 November 2015.
- ^ Sanders, Ray (23 August 2011). “How Did Jupiter Shape Our Solar System?”. Universe Today. Retrieved 4 November 2015.
- ^ Choi, Charles Q. (23 March 2015). “Jupiter’s ‘Smashing’ Migration May Explain Our Oddball Solar System”. Space.com. Retrieved 4 November 2015.
- ^ Davidsson, Dr. Björn J. R. “Mysteries of the asteroid belt”. The History of the Solar System. Retrieved 7 November 2015.
- ^ Raymond, Sean (2 August 2013). “The Grand Tack”. PlanetPlanet. Retrieved 7 November 2015.
- ^ O’Brien, David P.; Walsh, Kevin J.; Morbidelli, Alessandro; Raymond, Sean N.; Mandell, Avi M. (2014). “Water delivery and giant impacts in the ‘Grand Tack’ scenario”. Icarus. 239: 74–84. arXiv:1407.3290. Bibcode:2014Icar..239…74O. doi:10.1016/j.icarus.2014.05.009. S2CID 51737711.
- ^ Loeb, Abraham; Batista, Rafael; Sloan, David (August 2016). “Relative Likelihood for Life as a Function of Cosmic Time”. Journal of Cosmology and Astroparticle Physics. 2016 (8): 040. arXiv:1606.08448. Bibcode:2016JCAP…08..040L. doi:10.1088/1475-7516/2016/08/040. S2CID 118489638.
- ^ “Is Earthly Life Premature from a Cosmic Perspective?”. Harvard-Smithsonian Center for Astrophysics. 1 August 2016.
Further reading[edit]
- Prussing, John E.; Conway, Bruce A. (1993). Orbital Mechanics. New York: Oxford University Press. ISBN 0-19-507834-9.
External links[edit]
- World of Physics: Eccentricity
- The NOAA page on Climate Forcing Data includes (calculated) data from Berger (1978), Berger and Loutre (1991)[permanent dead link]. Laskar et al. (2004) on Earth orbital variations, Includes eccentricity over the last 50 million years and for the coming 20 million years.
- The orbital simulations by Varadi, Ghil and Runnegar (2003) provides series for Earth orbital eccentricity and orbital inclination.
- Kepler’s Second law’s simulation
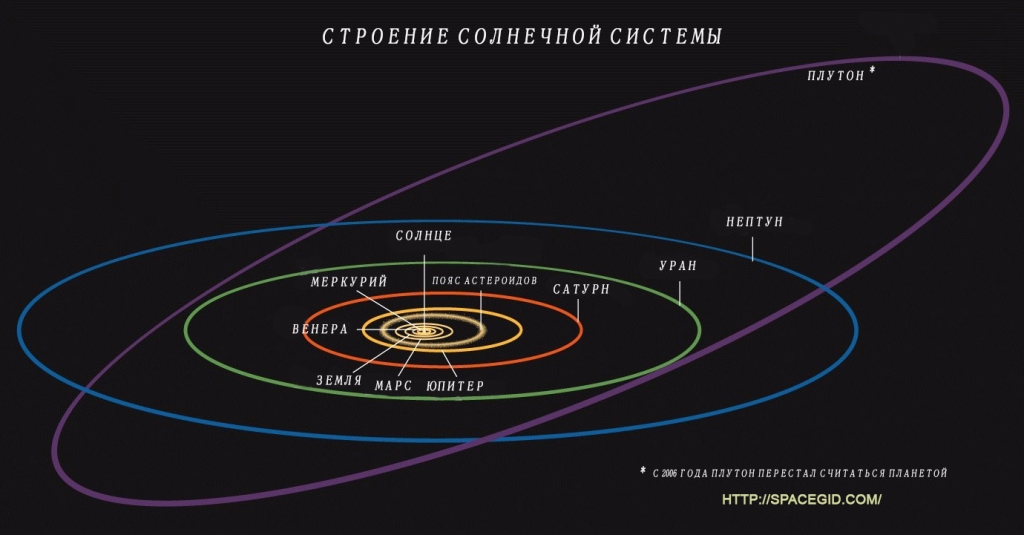
Строение Солнечной системы
Эксцентриситет (обозначается e или ε) входит в шестёрку кеплеровских элементов орбиты. Наряду с большой полуосью он определяют форму орбиты.
Определение эксцентриситета
Первый закон Кеплера гласит о том, что орбиты любой планеты Солнечной системы представляет собой эллипс. Эксцентриситет определяет, насколько орбита отлична от окружности. Он равен отношению расстояния от центра эллипса (c) до его фокуса большой полуоси (a).
Эксцентриситет орбит
У окружности фокус совпадает с центром, т.е. c = 0. Также любого эллипса c<a. Таким образом, при ε = 0 имеет форму окружности, при 0< ε< 1 – эллипса. При ε = 1 орбита является параболой, при ε > 1 – гиперболой. То есть, объект, орбита которого имеет эксцентриситет, равный или больший единицы, уже не обращается вокруг другого объекта. Примером тому являются некоторые кометы, которые, однажды, посетив Солнце, больше никогда к нему не вернуться. При эксцентриситете, равном бесконечности орбита представляет собой прямую линию.
Эксцентриситеты объектов Солнечной Системы
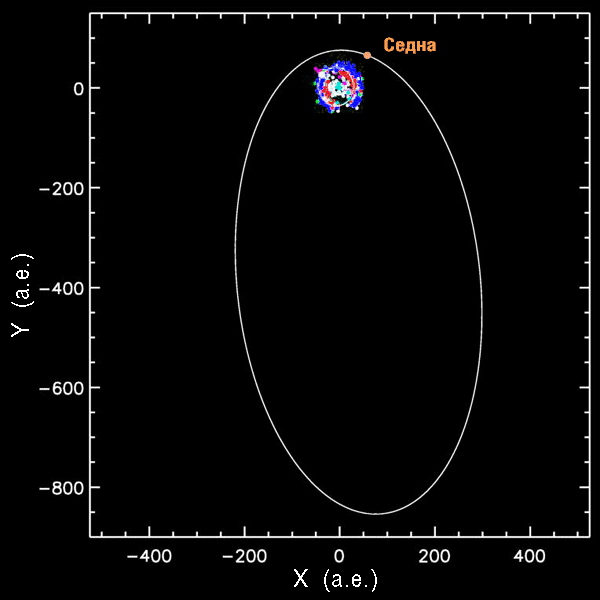
Орбита Седны. В центре координат — Солнечная система, окруженная роем планет и известных объектов пояса Койпера.
В нашей системе орбиты планет ничем не примечательны. Самой «круговой» орбитой обладает Венера. Её афелий всего-лишь на 1,4 млн. км.больше перигелия, а эксцентриситет равен 0,007 (у Земли – 0,016). По довольно вытянутой орбите движется Плутон. Обладая ε = 0,244, он временами приближается к Солнцу даже ближе чем Нептун. Однако, поскольку Плутон не так давно попал в разряд карликовых планет, самую вытянутую орбит среди планет теперь имеет Меркурий, обладающий ε = 0,204.
Среди карликовых планет наиболее примечательна Седна. Обладая ε = 0,86, она делает полный оборот вокруг Солнца почти за 12 тысяч лет, удаляясь от неё в афелии более чем на тысячу астрономический единиц. Однако даже это несравнимо с параметрами орбит долгопериодических комет. Периоды их обращения порой исчисляются миллионами лет, а многих из них и вовсе никогда не вернутся к Солнцу – т.е. обладают эксцентриситетом, большем 1. Облако Оорта может содержать триллионы комет, удалённых от Солнца на 50-100 тысяч астрономических единиц (0,5 – 1 световых лет). На таких расстояниях на нихмогут влиять другие звёзды и галактические приливные силы. Поэтому такие кометы могут обладать очень непредсказуемыми и непостоянными орбитами с самими различными эксцентриситетами.
Наконец, самым интересным является то, что даже Солнце обладает совсем ни круговой орбитой, как это может показаться на первый взгляд. Как известно, Солнце движется вокруг центра Галактики, проделывая свой путь за 223 млн. лет. Причём, из-за бесчисленного взаимодействия со звездами она получила довольно ощутимый эксцентриситет, равный 0,36.
Эксцентриситеты в других системах
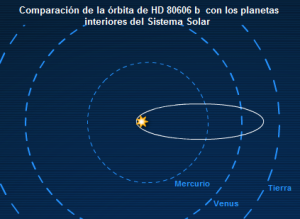
Сравнение орбиты HD 80606 b с внутренними планетами Солнечной системы
Открытие других солнечных систем неизбежно влечёт открытие планет с очень причудливыми параметрами орбит. Примером тому служат эксцентричные юпитеры, газовые гиганты с довольно высокими эксцентриситетами. В системах, имеющие такие планеты невозможно существование планет, подобных Земле. Они неизбежно упадут на гиганты или же статут их спутниками.
Среди обнаруженных на данный момент эксцентричных юпитеров самым большим эксцентриситетом обладает HD 80606b. Он движется вокруг звезды чуть меньшей, чем наше Солнце. Эта планета в перигелии приближается к звезде в 10 раз ближе, чем Меркурий к Солнцу, тогда как в афелии она удаляется от неё почти на астрономическую единицу. Таким образом, она имеет эксцентриситет 0,933.
Стоит отметить, что хоть данная планета и пересекает зону жизни, ни о каких видах привычной биосферы не может идти и речи. Её орбита создаёт на планете экстремальный климат.За короткий период сближения со звездой температура её атмосферы за считанные часы меняется на сотни градусов, в результате чего скорость ветров достигают многих километров в секунду. Подобными условиями обладают прочие планеты с высокими коэффициентами. Тот же Плутон, к примеру, при приближение к Солнцу приобретает обширную атмосферу, которая оседает в виде снега при удалении. В тоже время все Землеподобные планеты обладают орбитами, близкими к круговым. Поэтому эксцентриситет можно назвать одним из параметров, определяющим возможность наличия органической жизни на планете.
Астрономический словарик: шкала космических расстояний, щели Кирквуда, эксцентриситет орбиты
Уровень сложности
Средний
Время на прочтение
8 мин
Количество просмотров 1.8K
Шкала космических расстояний
Иерархия методов определения расстояний во Вселенной (красный цвет – прямые методы, черный – промежуточные, синий – косвенные).
Шкала, или лестница космических расстояний — это последовательность методов, с помощью которых астрономы определяют расстояния до небесных объектов. Прямое измерение расстояния до астрономического объекта возможно только для тех объектов, которые находятся «достаточно близко» (в пределах тысячи парсек) к Земле. Все методы определения расстояний до более удалённых объектов основаны на различных измеренных корреляциях между методами, которые работают на близких расстояниях, и методами, которые работают на больших расстояниях. Некоторые методы основаны на стандартных свечах — астрономических объектах с известной светимостью.
Аналогия с лестницей возникает потому, что ни один метод не может измерить расстояния на всех расстояниях, встречающихся в астрономии. Вместо этого один метод может быть использован для измерения близких расстояний, второй — для измерения близких и промежуточных расстояний и так далее. Каждая ступенька лестницы предоставляет информацию, которая может быть использована для определения расстояний на следующей, более высокой ступеньке.
Расстояние до объекта — одна из основных характеристик, которые определяются из астрономических наблюдений. Более того, только знание расстояний позволяет определять многие характеристики звезд, такие как светимости, массы и прочих.
Шкала расстояний в астрономии основана на знании расстояния между Землей и Солнцем (астрономическая единица, а.е.), которое определяется несколькими способами – старейшим из них является прямое измерение суточного параллакса Солнца. Из-за ряда трудностей (яркость Солнца, тепловые деформации инструмента) этот метод наименее точен. Из третьего закона Кеплера легко определяется взаимное положение планет в Солнечной системе. Остается только масштабировать его, что достигается с высокой точностью определением параллакса Венеры из наблюдений её прохождения по диску Солнца либо радиолокацией планеты.
Расстояния до звезд первоначально определялись тоже только тригонометрическим методом. Определение годичного параллакса опирается именно на надежное знание 1 а.е. Точность наземных измерений параллаксов ограничена земной атмосферой и составляет приблизительно ±0.01″. Также в этих целях используются статистические и групповые параллаксы (параллаксы движущихся скоплений). Последние обладают высокой точностью и лежат в основе шкалы астрономических расстояний, обеспечивая связь между тригонометрическими и фотометрическим методами.
Ступеньки лестницы расстояний обеспечивают разные методы измерения. Расстояния между планетами сегодня измеряются с помощью радиолокации. Межзвездные расстояния вплоть до 100 парсеков раньше измеряли с помощью тригонометрических параллаксов (спутник HIPPARCOS отодвинул эту границу до 1000 парсеков). Вплоть до расстояний в миллион парсеков (1 мпк) используется метод цефеид. Еще более далекие объекты, галактики и квазары, удалены от нас на сотни и тысячи мегапарсеков. Такие расстояния измеряются по красному смещению и требуют знания постоянной Хаббла.
Естественно, при передаче эстафеты от одного метода другому каждый из «старших» методов должен быть проверен с помощью «младшего» метода. Для этого должны существовать области перекрытия, в которых можно применять по крайней мере два метода:
Наиболее надежными годичными параллаксами нас обеспечивают заатмосферные наблюдения – точность спутника HIPPARCOS достигает ±0.001″. В любом случае прямые методы (тригонометрические) позволяют определять расстояния, не превышающие 1кпк.
Более удалённые объекты дистанцируются косвенными методами (фотометрическими): блеск убывает пропорционально квадрату расстояния и, если известна светимость звезды,
можно найти расстояние. Примерами могут служить «спектральные параллаксы» — по статистическим зависимостям интенсивности линий от светимости или «цефеидные параллаксы» — по зависимости «период/светимость». Точность фотометрических методов ограничивается дисперсией эмпирических зависимостей и, как правило, не превышает ±25%.
Основным фотометрическим методом является метод цефеид. Еще в 1908 году Г. Ливитт, изучая переменные в Малом Магеллановом Облаке (ММО) отметила, что более яркие цефеиды имеют больший период. Поскольку все переменные находятся на одном расстоянии (размеры ММО много меньше расстояния до него), то достаточно знать светимость хотя бы одной такой цефеиды, чтобы для любой звезды данного типа по зависимости «период-светимость» определить расстояние.
Однако в окрестности Солнца, доступной для определения расстояний тригонометрическим методом, нет ни одной цефеиды. Поэтому Х. Шепли счел, что переменные в шаровых скоплениях с похожими кривыми блеска (впоследствии – пульсирующие типа RRLyr!), имеют такую же светимость, что и цефеиды. В результате оценка расстояния оказалась заниженной. Её использование привело к существенному занижению размеров туманности Андромеды (М31) и светимости объектов в ней.
Ошибка сохранялась почти 30 лет до тех пор, пока В. Бааде, а затем Д. Ирвин не разрешили эту проблему, создав современную шкалу расстояний во Вселенной. В этом помогло обнаружение нескольких цефеид в рассеянных скоплениях, расстояния до которых уверенно определяются по диаграмме Герцшпрунга – Рассела.
В сфере радиусом 100 парсеков нет ни одной цефеиды (одна из ближайших к нам цефеид – это Полярная звезда, она удалена от нас на 122 парсека). Поэтому до реализации проекта HIPPARCOS шкала расстояний, основанная на цефеидах в скоплениях, не была согласована с результатами прямых измерений до звезд методами тригонометрических параллаксов. Теперь ситуация изменилась: шкала цефеид была уточнена, на основании чего было сделано заключение о том, что принятое в настоящее время значение постоянной Хаббла должно быть уменьшено на 5-10 процентов.
Гравитационные волны, возникающие при постепенном сближении объектов в компактных бинарных системах, таких как нейтронные звезды или чёрные дыры, обладают тем полезным свойством, что энергия, испускаемая в виде гравитационного излучения, зависит исключительно от орбитальной энергии пары, и результирующее сжатие их орбит непосредственно наблюдается как увеличение частоты испускаемых гравитационных волн. Поэтому по аналогии со стандартными свечами расстояние до подобных систем можно оценивать без наличия других методов измерения – только вместо светимости звезды используются характеристики гравитационных волн, в связи с чем такие объекты называют «стандартными сиренами», проводя аналогию между звуковыми и гравитационными волнами.
Как и в случае со стандартными свечами, учитывая амплитуды излучаемой и принимаемой энергии, по закону обратного квадрата определяется расстояние до источника. Однако есть некоторые отличия от стандартных свечей. Гравитационные волны излучаются не изотропно, но измерение поляризации волны даёт достаточно информации для определения угла излучения. Детекторы гравитационных волн также имеют анизотропные антенные диаграммы, поэтому для определения угла приёма необходимо знать положение источника на небе относительно детекторов. Как правило, если волна обнаружена сетью из трёх детекторов в разных местах, это даёт нам достаточно информации, чтобы внести нужные поправки и получить расстояние до объекта. Также, в отличие от стандартных свечей, гравитационные волны не нуждаются в калибровке относительно других мер расстояния.
Удачно, что гравитационные волны не подвержены исчезновению из-за наличия промежуточной поглощающей среды. Но они подвержены гравитационному линзированию, точно так же, как и свет. Если сигнал сильно линзируется, то он может быть принят как несколько событий, разделённых во времени (аналог нескольких изображений квазара, например). Менее легко различить и контролировать эффект слабого линзирования, когда на путь сигнала через пространство влияет множество мелких событий увеличения и размагничивания. Это будет важно для сигналов, возникающих на космологических красных смещениях больше 1. Наконец, сетям детекторов трудно точно измерить поляризацию сигнала, если бинарная система наблюдается почти лицом к лицу — такие сигналы имеют значительно большие ошибки в измерении расстояния. К сожалению, двоичные системы излучают наиболее сильно перпендикулярно плоскости орбиты, поэтому сигналы, направленные в одну сторону, по своей природе сильнее и наблюдаются чаще всего.
Щели Кирквуда
Щели Кирквуда или Кирквуда люки — это определённые области в поясе астероидов, которые создаются резонансным влиянием Юпитера. В этих областях астероиды практически отсутствуют. Эти области соответствуют местам орбитальных резонансов астероидов с Юпитером.
Например, существует очень мало астероидов с большой полуосью около 2,50 AU и периодом 3,95 года. Такие астероиды проходят по три орбиты за каждую орбиту Юпитера (поэтому их орбитальный резонанс называется 3:1). Другие орбитальные резонансы соответствуют орбитальным периодам, длина которых составляет простые доли периода Юпитера.
Впервые эти разрывы были замечены в 1866 году Дэниелом Кирквудом, профессором колледжа Джефферсона в Канонсбурге, штат Пенсильвания. Он, кроме того, правильно объяснил их происхождение орбитальными резонансами с Юпитером.
Большинство разрывов Кирквуда небогаты астероидами — в отличие от средне-двигательных резонансов (MMR) Нептуна или резонанса Юпитера 3:2, которые сохраняют объекты, захваченные во время миграции планет-гигантов.
Совсем недавно было обнаружено относительно небольшое количество астероидов с орбитами высокого эксцентриситета, которые действительно лежат в пределах промежутков Кирквуда. В качестве примера можно привести группы Алинды и Грикуа. Эти орбиты медленно увеличивают свой эксцентриситет в течение десятков миллионов лет и в конце концов выходят из резонанса из-за близкого столкновения с крупной планетой. Именно поэтому астероиды редко встречаются в разрывах Кирквуда.
Эксцентриситет орбиты
В астродинамике орбитальный эксцентриситет астрономического объекта — это безразмерный параметр, определяющий величину отклонения орбиты вокруг другого тела от идеального круга. Значение эксцентриситета, равное 0, соответствует круговой орбите, значения от 0 до 1 образуют эллиптическую орбиту, 1 — параболическую орбиту бегства (или орбиту захвата) объекта, а больше 1 — гиперболу.
Термин получил своё название от параметров конических сечений, поскольку каждая орбита Кеплера — коническое сечение. Обычно он используется для изолированной задачи двух тел, но существуют расширения для объектов, следующих по розетточной орбите через Галактику.
Слово «эксцентричность» происходит от средневекового латинского eccentricus, образованного от греческого ἔκκεντρος «вне центра», от ἐκ- ek-, «из» + κέντρον «центр». Слово «эксцентрик» впервые появилось в английском языке в 1551 году с определением «… круг, в котором земля, солнце и т.д. отклоняются от своего центра». В 1556 году, пять лет спустя, появилась прилагательная форма этого слова.