Содержание
- Как найти эксцентриситет орбиты луны
- Что такое эксцентриситет орбиты
- Как найти эксцентриситет орбиты луны
- 1. Наибольшее расстояние между луной и Землей
- 2. Наименьшее расстояние между луной и Землей
- 3. Эксцентриситет орбиты
- Общий итог
- Как найти эксцентриситет орбиты луны
- Что такое эксцентриситет орбиты
- Способы определения эксцентриситета орбиты луны
- Итог
- Как найти эксцентриситет орбиты Луны
- Понятие эксцентриситета
- Расчет эксцентриситета орбиты Луны
- Применение эксцентриситета орбиты
- Итог
Как найти эксцентриситет орбиты луны
Луна — естественный спутник нашей планеты, вращающийся вокруг Земли. Ее орбита имеет некоторые особенности, включая эксцентриситет, который является важным параметром для изучения орбиты и ее эффектов на Землю. В этой статье мы рассмотрим, что такое эксцентриситет орбиты луны и как его можно найти.
Что такое эксцентриситет орбиты
Эксцентриситет орбиты — это мера того, насколько орбита отклоняется от круговой формы. Круговая орбита имеет эксцентриситет 0, а эллиптическая орбита может иметь эксцентриситет от 0 до 1. Например, орбита Земли имеет эксцентриситет около 0,0167, что означает, что она почти круговая.
Как найти эксцентриситет орбиты луны
Как мы уже знаем, орбита луны является эллиптической. Таким образом, для определения ее эксцентриситета нужно знать две величины: наибольшее и наименьшее расстояние между луной и Землей.
1. Наибольшее расстояние между луной и Землей
Наибольшее расстояние между луной и Землей называется апоцентром. Оно может быть найдено с помощью формулы:
dA = a * (1 + e)
где dA — наибольшее расстояние между луной и Землей, a — большая полуось орбиты луны, e — эксцентриситет орбиты.
Значение большой полуоси орбиты луны составляет около 384 400 км. Таким образом, чтобы найти апоцентр, необходимо знать значение эксцентриситета.
2. Наименьшее расстояние между луной и Землей
Наименьшее расстояние между луной и Землей называется перицентром. Оно может быть найдено с помощью формулы:
dP = a * (1 — e)
где dP — наименьшее расстояние между луной и Землей, a — большая полуось орбиты луны, e — эксцентриситет орбиты.
3. Эксцентриситет орбиты
Как только вы нашли значения апоцентра и перицентра, вы можете найти эксцентриситет орбиты луны с помощью формулы:
e = (dA — dP) / (dA + dP)
где e — эксцентриситет орбиты луны, dA — наибольшее расстояние между луной и Землей, dP — наименьшее расстояние между луной и Землей.
В этой формуле значения расстояний должны быть выражены в одинаковых единицах измерения. Например, если значение расстояний у вас в километрах, то и результат эксцентриситета будет выражен в десятичных долях.
Общий итог
Эксцентриситет орбиты луны — это важный параметр, который может быть найден, зная апоцентр и перицентр орбиты. На основе эксцентриситета можно изучать эффекты орбиты на приливы и другие астрономические явления.
- 1. Чтобы найти апоцентр, используйте формулу dA = a * (1 + e).
- 2. Чтобы найти перицентр, используйте формулу dP = a * (1 — e).
- 3. Чтобы найти эксцентриситет, используйте формулу e = (dA — dP) / (dA + dP).
Зная эксцентриситет орбиты луны, вы можете изучать ее эффекты на приливы и другие астрономические явления. Это также может помочь понять, как орбита луны влияет на жизнь на Земле и в космосе.
Как найти эксцентриситет орбиты луны
Луна всегда была объектом удивления и изучения. Ее орбита вокруг Земли происходит не очень просто. Чтобы понять, как она двигается, нам нужно знать много различных параметров, включая эксцентриситет орбиты, который показывает, насколько круглая или вытянутая она является. В этой статье мы рассмотрим способы определения эксцентриситета орбиты луны.
Что такое эксцентриситет орбиты
Эксцентриситет орбиты — это число, которое показывает, насколько круглая или вытянутая орбита является. Он получен путем измерения различных параметров орбиты, включая ее размер и форму. Если орбита находится ближе к кругу, то эксцентриситет будет равен нулю, если же она является более вытянутой, то эксцентриситет больше нуля.
Способы определения эксцентриситета орбиты луны
- Наблюдения на небе: один из самых простых способов определения эксцентриситета орбиты находящейся на небесах луны — это наблюдение за ее движением. Это может быть выполнено с помощью бинокля или телескопа. Путем наблюдения за фазами луны можно определить ее положение и движение в отношении Земли.
- Радиолокационные измерения: еще один способ определения эксцентриситета орбиты — это использование радиолокационных измерений. Этот способ используется профессиональными астрономами и предполагает использование радаров для измерения скорости луны, расстояния до нее и других параметров ее орбиты.
- Спутниковые наблюдения: использование спутников — это более современный способ определения эксцентриситета орбиты луны. Спутники используются для измерения скорости и расстояния до луны, что позволяет более точно определить ее эксцентриситет.
Итог
Определение эксцентриситета орбиты луны — это важный этап в изучении ее движения и характеристик орбиты в целом. Наблюдения на небе, радиолокационные измерения и спутниковые наблюдения — все они предоставляют способы определения эксцентриситета орбиты. Используя эти методы, мы можем узнать больше о том, как луна движется вокруг Земли и как изменения в ее орбите могут повлиять на нашу планету.
Как найти эксцентриситет орбиты Луны
Орбита Луны вращается вокруг Земли, совершая ежемесячный оборот. Эксцентриситет орбиты Луны отражает степень ее отклонения от круговой формы. Эксцентриситет определяет форму орбиты, включая расстояние Луны от Земли в разное время. Как же вычислить эксцентриситет орбиты Луны?
Понятие эксцентриситета
Эксперты определяют эксцентриситет как отношение расстояния между фокусами орбиты (f) к длине большой оси орбиты (2a). По формуле:
e = f/2a
где e — эксцентриситет орбиты, f — расстояние между фокусами, a — полуось орбиты (зависит от расстояния Луны от Земли в разное время).
Расчет эксцентриситета орбиты Луны
Существует множество методов для расчета эксцентриситета орбиты Луны. Один из них — использование данных о положении Луны в определенные моменты времени.
Первым этапом в расчете эксцентриситета орбиты Луны является измерение расстояния между Землей и Луной в моменты, когда Луна находится в перигее (точке максимального приближения) и апогее (точке максимального удаления). Это расстояние может быть измерено с помощью лазерных измерений или радаров. После получения этих данных можно использовать формулу для вычисления эксцентриситета орбиты Луны.
Второй метод — использование данных о скорости Луны и ее положении в определенный момент времени. Для этой задачи требуется знание скорости обращения Луны вокруг Земли и угла ее положения в определенный момент времени. Из этих данных можно вычислить эксцентриситет орбиты Луны.
Применение эксцентриситета орбиты
Знание эксцентриситета орбиты Луны ценно для изучения влияния Луны на Землю. Например, эксцентриситет орбиты влияет на мощность приливной волны (разницу между высоким и низким приливом). Чем ближе Луна к Земле (больший эксцентриситет), тем выше разница между приливом и отливом. И наоборот.
Эксцентриситет орбиты Луны также влияет на положение Земли в отношении Солнца. В течение года Земля движется вокруг Солнца, и этот путь совершает в форме эллипса. Это означает, что расстояние между Землей и Солнцем колеблется в течение года, причем это колебание усиливается в зависимости от эксцентриситета орбиты Луны. Чем больше эксцентриситет, тем больше разница между ближайшей и дальней точками Земли и Солнца.
Итог
Эксцентриситет орбиты Луны — это важная характеристика орбиты, которую можно вычислить, используя данные о ее положении и скорости в определенные моменты времени. Знание эксцентриситета позволяет более точно изучать влияние Луны на Землю, включая приливную волну и положение Земли относительно Солнца.
У этого термина существуют и другие значения, см. Луна (значения).
| Луна |
||||
|---|---|---|---|---|
| Спутник | ||||
 |
||||
| Орбитальные характеристики | ||||
| Эпоха: J2000.0 | ||||
| Периапсида |
363 104 км (356 400—370 400 км) |
|||
| Апоапсида |
405 696 км (404 000—406 700 км) |
|||
| Большая полуось (a) |
384 399 км 0,00257 а.е. |
|||
| Эксцентриситет орбиты (e) | 0,0549 (средний)[1] | |||
| Сидерический период обращения |
27,321661 дня 27 д 7 ч 43 мин 11,5 сек |
|||
| Синодический период обращения |
29,530588 дня 29 д 12 ч 44,0 мин |
|||
| Орбитальная скорость (v) | 1,023 км/с (средняя)[1] | |||
| Наклонение (i) |
5,145° (4,983—5,317°) отн. эклиптики[2] 6,668° (6,517—6,85°) 18,3—28,6° отн. экватора Земли[2] |
|||
| Долгота восходящего узла (Ω) | (убывание) 1 оборот за 18,6 года | |||
| Аргумент перицентра (ω) | (возрастание) 1 оборот за 8,85 года | |||
| Чей спутник | Земли | |||
| Физические характеристики | ||||
| Полярное сжатие | 0,00125 | |||
| Экваториальный радиус |
1738,14 км 0,273 земных |
|||
| Полярный радиус |
1735,97 км 0,273 земных |
|||
| Средний радиус |
1737,10 км 0,273 земных |
|||
| Окружность большого круга | 10 917 км | |||
| Площадь поверхности (S) |
3,793⋅107 км2 0,074 земной |
|||
| Объём (V) |
2,1958⋅1010 км3 0,020 или 1/50 земного |
|||
| Масса (m) |
7,3477⋅1022 кг 0,0123 или 1/81 земной |
|||
| Средняя плотность (ρ) | 3,3464 г/см3 | |||
| Ускорение свободного падения на экваторе (g) |
1,62 м/с2 0,165 g |
|||
| Первая космическая скорость (v1) | 1,68 км/с | |||
| Вторая космическая скорость (v2) | 2,38 км/с | |||
| Период вращения (T) | синхронизирован (всегда повёрнута к Земле одной стороной) | |||
| Наклон оси | 1,5424° (относительно плоскости эклиптики) | |||
| Альбедо | 0,12 | |||
| Видимая звёздная величина |
−2,5/−12,9 −12,74 (при полной Луне) |
|||
| Температура | ||||
|
||||
| Температура на экваторе[3] |
|
|||
| Атмосфера | ||||
|
Состав: крайне разрежена, имеются следы водорода, гелия, неона и аргона[4] |
||||
Луна́ — единственный естественный спутник Земли. Самый близкий к Солнцу спутник планеты, так как у ближайших к Солнцу планет (Меркурия и Венеры) их нет. Второй по яркости[комм. 1] объект на земном небосводе после Солнца и пятый по величине естественный спутник планеты Солнечной системы. Среднее расстояние между центрами Земли и Луны — 384 467 км (0,00257 а.е., ~30 диаметров Земли).
Видимая звёздная величина полной Луны на земном небе — −12,71m[5]. Освещённость, создаваемая полной Луной возле поверхности Земли при ясной погоде, составляет 0,25—1 лк.
Луна появилась около 4,5 млрд лет назад, немного позже Земли. Наиболее популярна гипотеза о том, что Луна сформировалась из осколков, оставшихся после «Гигантского столкновения» Земли и Тейи — планеты, схожей по размерам с Марсом.
На сегодняшний день Луна является единственным внеземным астрономическим объектом, на котором побывал человек.
Название[править | править код]
Русское слово «Луна» восходит к праслав. *luna < пра-и.е. *louksnā́ «светлая» (женский род прилагательного *louksnós), к этой же индоевропейской форме восходит и лат. lūna «луна»[6].
Греки называли спутник Земли Селеной (др.-греч. Σελήνη), древние египтяне — Ях (Иях)[7], вавилоняне — Син[8], японцы — Цукиёми[9].
Луна как небесное тело[править | править код]
Луна перед закатом солнца
Орбита[править | править код]
С древних времён люди пытались описать и объяснить движение Луны. Со временем появлялись всё более точные теории.
Основой современных расчётов является теория Брауна. Созданная на рубеже XIX—XX веков, она описывала движение Луны с точностью измерительных приборов того времени. При этом в расчёте использовалось более 1400 членов (коэффициентов и аргументов при тригонометрических функциях).
Современная наука может рассчитывать движение Луны и проверять эти расчёты с ещё большей точностью. Методами лазерной локации расстояние до Луны измеряется с ошибкой в несколько сантиметров[10]. Такую точность имеют не только измерения, но и теоретические предсказания положения Луны; для таких расчётов используются выражения с десятками тысяч членов, и не существует предела их количества, если потребуется ещё более высокая точность.
В первом приближении можно считать, что Луна движется по эллиптической орбите с эксцентриситетом 0,0549 и большой полуосью геоцентрической орбиты 384 399 км (в то время как большая полуось в системе относительно центра масс системы «Земля — Луна» составляет 379 730 км). Действительное движение Луны довольно сложное, и при его расчёте необходимо учитывать множество факторов, например, сплюснутость Земли и сильное влияние Солнца, которое притягивает Луну в 2,2 раза сильнее, чем Земля[комм. 2]. Более точно движение Луны вокруг Земли можно представить как сочетание нескольких движений[11]:
- обращение вокруг Земли по эллиптической орбите с периодом 27,32166 суток — это так называемый сидерический месяц (то есть движение измерено относительно звёзд);
- поворот плоскости лунной орбиты: её узлы (точки пересечения орбиты с эклиптикой) смещаются на запад, делая полный оборот за 18,6 года. Это движение является прецессионным;
- поворот большой оси лунной орбиты (линии апсид) с периодом 8,8 года (происходит в противоположном направлении, чем указанное выше движение узлов, то есть долгота перигея увеличивается);
- периодическое изменение наклона лунной орбиты по отношению к эклиптике от 4°59′ до 5°19′;
- периодическое изменение размеров лунной орбиты: перигея — от 356,41 до 369,96 тыс. км, апогея — от 404,18 до 406,74 тыс. км;
- постепенное удаление Луны от Земли вследствие приливного ускорения (на 38 мм в год)[12][13], таким образом, её орбита представляет собой медленно раскручивающуюся спираль[14].
Общее строение[править | править код]
Луна состоит из коры, мантии (астеносферы), свойства которой различны и образуют четыре слоя, кроме того, переходной зоны между мантией и ядром, а также самого ядра, которое имеет внешнюю жидкую и внутреннюю твёрдую[15] части[16]. Атмосфера и гидросфера практически отсутствуют. Поверхность Луны покрыта реголитом — смесью тонкой пыли и скалистых обломков, образующихся в результате столкновений метеоритов с лунной поверхностью. Ударно-взрывные процессы, сопровождающие метеоритную бомбардировку, способствуют взрыхлению и перемешиванию грунта, одновременно спекая и уплотняя частицы грунта. Толщина слоя реголита составляет от долей метра до десятков метров[17].
| Внутреннее твёрдое ядро | 0—230 км |
| Внешнее жидкое ядро | 230—325 км |
| Переходная зона | 325—534 км |
| Мантия | 534—1697 км |
| Кора | 1697—1737 км |
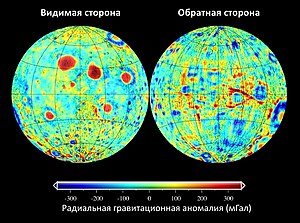
Видимая сторона находится в среднем на 3,2 км ближе к центру масс по сравнению с обратной стороной, смещение центра масс к центру фигуры составляет приблизительно 1,68—1,93 км. Средняя толщина коры в видимом полушарии меньше на 8—12 км. Экваториальная кора в среднем на 9,5 км толще, чем на полюсах[18].
Условия на поверхности[править | править код]
Цветные снимки Луны на разных высотах над горизонтом, полученные бортовой цифровой камерой космического корабля «Колумбия» 26 января 2003 года[19][20]
Атмосфера Луны крайне разрежена. Когда поверхность не освещена Солнцем, содержание газов над ней не превышает 2⋅105 частиц/см3 (для Земли этот показатель составляет 2,7⋅1019 частиц/см3), а после восхода Солнца увеличивается на два порядка за счёт дегазации грунта. Разрежённость атмосферы приводит к высокому перепаду температур на поверхности Луны (от −173 °C ночью до +127 °C в подсолнечной точке)[21], в зависимости от освещённости; при этом температура пород, залегающих на глубине 1 м, постоянна и равна −35 °C. Ввиду практического отсутствия атмосферы небо на Луне всегда чёрное и со звёздами, даже когда Солнце находится над горизонтом. Однако на дневных фотографиях звёзды не видны, так как для их отображения потребовалась бы такая экспозиция, при которой освещённые Солнцем объекты были бы пересвечены.
Около 3,5 млрд лет назад, во время масштабных излияний лавы, лунная атмосфера была плотнее. Расчёты показывают, что высвобождавшиеся из лавы летучие вещества (CO, S, Н2O) могли образовать атмосферу с давлением в 1 % от земного. Время её рассеяния оценивают в 70 млн лет[22].
«На Луне. Восходит Земля»[23] Почтовая марка СССР, 1967 год
Земной диск висит в небе Луны почти неподвижно. Причины небольших ежемесячных колебаний Земли по высоте над лунным горизонтом и по азимуту (примерно по 7°) такие же, как у либраций. Угловой размер Земли при наблюдении с Луны в 3,7 раза больше[24], чем лунный при наблюдении с Земли, а закрываемая Землёй площадь небесной сферы в 13,5 раза больше[25], чем закрываемая Луной. Степень освещённости Земли, видимая с Луны, обратна лунным фазам, видимым на Земле: в полнолуние с Луны видна неосвещённая часть Земли, и наоборот. Освещение отражённым светом Земли теоретически должно быть примерно в 41 раз сильнее[26], чем освещение лунным светом на Земле, однако на практике лишь в 15 раз больше[27]; наибольшая видимая звёздная величина Земли на Луне составляет приблизительно −16m[28].
Лунная поверхность отражает всего 5—18 % солнечного света (как старый асфальт). Цветовые различия на Луне очень малы; её поверхность имеет коричневато-серую или черновато-бурую окраску (данные 1970 года)[29].
Наилучшие на 2017 год колориметрические изображения поверхности Луны были получены широкоугольной, мультиспектральной камерой WAC космического аппарата LRO с использованием фильтров в трёх цветовых каналах: 689 нм — красный, 415 нм — зелёный, и 321 нм — голубой[30] (описание карты[31]). На цветоделительных изображениях буроватый оттенок имеют центральная часть Моря Ясности, восточная часть Моря Дождей, Море Холода и плато Аристарх. Синий оттенок имеют Море Спокойствия, периферийная часть Моря Ясности, северная часть Моря Изобилия, западная часть Моря Дождей, западная и южная части Океана Бурь. Все эти цветовые особенности отдельных районов Луны подтвердились в дальнейшем[32]. Глаз почти не различает цветовые особенности отдельных деталей поверхности. Применение обычной цветной фотографии также не даёт должного эффекта — лунная поверхность выглядит однотонной[33].
Уменьшение альбедо поверхности в коротковолновой части спектра приводит к тому, что зрительно Луна кажется слегка желтоватой[34].
-
Луна с борта МКС 8 марта 2015 года
-
Луна с борта МКС 24 февраля 2005 года
Гравитационное поле[править | править код]
Сила тяжести[править | править код]
Сила тяжести у поверхности Луны составляет 16,5 % от земной (в 6 раз слабее).
Гравитационный потенциал[править | править код]
| C3,1 = −0,000030803810 | S3,1 = −0,000004259329 |
| C3,2 = −0,000004879807 | S3,2 = −0,000001695516 |
| C3,3 = −0,000001770176 | S3,3 = −0,000000270970 |
| C4,1 = −0,000007177801 | S4,1 = −0,000002947434 |
| C4,2 = −0,000001439518 | S4,2 = −0,000002884372 |
| C4,3 = −0,000000085479 | S4,3 = −0,000000718967 |
| C4,4 = −0,000000154904 | S4,4 = −0,000000053404 |
Гравитационный потенциал Луны традиционно записывают как сумму трёх слагаемых[36]:
где δW — приливный потенциал, Q — центробежный потенциал, V — потенциал притяжения. Потенциал притяжения обычно раскладывают по зональным, секторальным и тессеральным гармоникам:
где Pnm — присоединённый полином Лежандра, G — гравитационная постоянная, M — масса Луны, λ и θ — долгота и широта.
Приливы и отливы на Земле[править | править код]
Гравитационное влияние Луны вызывает на Земле некоторые интересные эффекты. Наиболее известный из них — морские приливы и отливы. На противоположных сторонах Земли образуются (в первом приближении) две выпуклости — со стороны, обращённой к Луне, и с противоположной ей. В мировом океане этот эффект выражен намного сильнее, чем в твёрдой коре (выпуклость воды больше). Амплитуда приливов (разность уровней прилива и отлива) на открытых пространствах океана невелика и составляет 30—40 см. Однако вблизи берегов вследствие набега на твёрдое дно приливная волна увеличивает высоту точно так же, как обычные ветровые волны прибоя. Учитывая направление обращения Луны вокруг Земли, можно составить картину следования приливной волны по океану. Сильным приливам больше подвержены восточные побережья материков. Максимальная амплитуда приливной волны на Земле наблюдается в заливе Фанди в Канаде и составляет 18 метров.
Хотя для земного шара величина силы тяготения Солнца почти в 200 раз больше, чем силы тяготения Луны, прили́вные силы, порождаемые Луной, почти вдвое больше порождаемых Солнцем. Это происходит из-за того, что приливные силы зависят не только от величины гравитационного поля, а ещё и от степени его неоднородности. При увеличении расстояния от источника поля неоднородность уменьшается быстрее, чем величина самого поля. Поскольку Солнце почти в 400 раз дальше от Земли, чем Луна, то приливные силы, вызываемые солнечным притяжением, оказываются слабее[37].
Магнитное поле[править | править код]
Считается, что источником магнитного поля планет является тектоническая активность. Например, у Земли поле создаётся движением расплавленного металла в ядре, у Марса — последствиями прошлой активности.
«Луна-1» в 1959 году установила отсутствие однородного магнитного поля на Луне[38]:24. Результаты исследований учёных Массачусетского технологического института подтверждают гипотезу, что у неё было жидкое ядро. Это укладывается в рамки самой популярной гипотезы происхождения Луны — столкновение Земли примерно 4,5 миллиарда лет назад с космическим телом размером с Марс «выбило» из Земли огромный кусок расплавленной материи, который позже превратился в Луну. Экспериментально удалось доказать, что на раннем этапе существования у Луны было аналогичное земному магнитное поле[39].
Программа GRAIL изучения гравитационного поля и внутреннего строения Луны, а также реконструкции её тепловой истории, установило наличие у Луны внутреннего твёрдого и внешнего металлического частей ядра (состоящих из железных и сидерофильных элементов). Очень слабое магнитное поле Луны формируется за счёт остаточного магнетизма в лунных породах, а также приливных сил, действующих на ядро[15].
Наблюдение[править | править код]
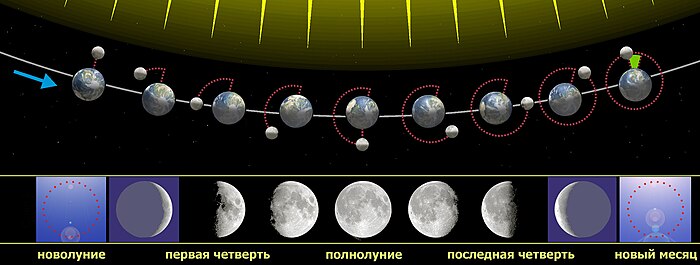
Связь фаз Луны с её положением относительно Солнца и Земли, при наблюдении из Северного полушария Земли. Зелёным цветом выделен угол, на который Луна повернётся с момента окончания сидерического месяца до момента окончания синодического месяца
Так как Луна не светится сама, а лишь отражает солнечный свет, с Земли видна только освещённая Солнцем часть лунной поверхности (в фазах Луны, близких к новолунию, то есть в начале первой четверти и в конце последней четверти, при очень узком серпе можно наблюдать «пепельный свет Луны» — слабое освещение её лучами Солнца, отражёнными от Земли). Луна обращается по орбите вокруг Земли, и тем самым угол между Землёй, Луной и Солнцем изменяется; мы наблюдаем это явление как цикл лунных фаз. Период времени между последовательными новолуниями в среднем составляет 29,5 дней (709 часов) и называется синодический месяц. То, что длительность синодического месяца больше, чем сидерического, объясняется движением Земли вокруг Солнца: когда Луна относительно звёзд совершает полный оборот вокруг Земли, Земля к этому времени проходит уже 1/13 часть своей орбиты, и чтобы Луна снова оказалась между Землёй и Солнцем, ей нужно дополнительно около двух суток.
Хотя Луна и вращается вокруг своей оси, она всегда обращена к Земле одной и той же стороной, то есть обращение Луны вокруг Земли и вращение вокруг собственной оси синхронизировано. Эта синхронизация вызвана трением приливов, которые производила Земля в оболочке Луны[40]. Согласно законам механики, Луна ориентирована в поле тяготения Земли так, что на Землю направлена большая полуось лунного эллипсоида.
Явление либрации, открытое Галилео Галилеем в 1635 году, позволяет наблюдать около 59 % лунной поверхности. Дело в том, что вокруг Земли Луна обращается с переменной угловой скоростью вследствие эксцентриситета лунной орбиты (вблизи перигея движется быстрее, вблизи апогея медленнее), в то время как вращение спутника вокруг собственной оси равномерно. Это позволяет увидеть с Земли западный и восточный края обратной стороны Луны (оптическая либрация по долготе). Кроме того, в связи с наклоном оси вращения Луны к плоскости её орбиты с Земли можно увидеть северный и южный края обратной стороны Луны (оптическая либрация по широте).
Существует ещё физическая либрация, обусловленная колебанием спутника вокруг положения равновесия в связи со смещённым центром тяжести, а также в связи с действием приливных сил со стороны Земли. Эта физическая либрация имеет величину 0,02° по долготе с периодом 1 год и 0,04° по широте с периодом 6 лет.
Из-за рефракции в атмосфере Земли при наблюдении Луны низко над горизонтом наблюдается приплюснутость её диска.
Время (1,255 секунды), за которое свет, пущенный с Земли, достигает Луны. Рисунок выполнен в масштабе
Из-за неровностей рельефа на поверхности Луны во время полного солнечного затмения можно наблюдать чётки Бейли. Когда же, наоборот, Луна попадает в тень Земли, можно наблюдать другой оптический эффект: она краснеет, будучи подсвеченной рассеянным в атмосфере Земли светом.
«Суперлунием» называют астрономическое явление, при котором момент прохождения Луной перигея совпадает с её полной фазой. Менее распространён термин «микролуние», когда Луна в полной фазе находится в апогее, то есть в дальней точке своей орбиты вокруг Земли. Для земного наблюдателя угловой размер диска Луны в момент «суперлуния» больше на 14 % и яркость его на 30 % выше, чем в момент «микролуния».
Селенология[править | править код]
Благодаря её размеру и составу Луну иногда относят к планетам земной группы наряду с Меркурием, Венерой, Землёй и Марсом. Изучая геологическое строение Луны, можно многое узнать о строении и развитии Земли.
Толщина коры Луны в среднем составляет 68 км, изменяясь от 0 км под лунным морем Кризисов до 107 км в северной части кратера Королёва на обратной стороне. Под корой находится мантия и, возможно, малое ядро из сернистого железа (радиусом приблизительно 340 км и массой, составляющей 2 % массы Луны). Любопытно, что центр масс Луны располагается примерно в 2 км от геометрического центра по направлению к Земле. По результатам миссии «Кагуя» было установлено, что в Море Москвы толщина коры наименьшая для всей Луны[41] — почти 0 метров под слоем базальтовой лавы толщиной 600 метров[42].
Измерения скорости спутников «Лунар Орбитер» позволили создать гравитационную карту Луны. С её помощью были обнаружены уникальные лунные объекты, названные масконами (от англ. mass concentration) — это массы вещества повышенной плотности.
Луна не имеет магнитного поля, хотя некоторые из горных пород на её поверхности проявляют остаточный магнетизм, что указывает на возможность существования магнитного поля Луны на ранних стадиях развития.
Не имеющая ни атмосферы, ни магнитного поля, поверхность Луны подвержена непосредственному воздействию солнечного ветра. В течение 4 млрд лет ионы водорода из солнечного ветра внедрялись в реголит Луны. Таким образом, образцы реголита, доставленные миссиями «Аполлон», оказались очень ценными для исследования солнечного ветра.
В феврале 2012 года американские астрономы обнаружили на обратной стороне Луны несколько геологических новообразований. Это свидетельствует о том, что лунные тектонические процессы продолжались ещё как минимум 950 миллионов лет после предполагаемой даты геологической «смерти» Луны[43].
Пещеры[править | править код]
В 2009 году японским зондом Кагуя обнаружено отверстие в поверхности Луны, расположенное недалеко от вулканического плато Холмы Мариуса, предположительно ведущее в тоннель под поверхностью. Диаметр отверстия составляет около 65 метров, а глубина, предположительно, 80 метров[44].
Учёные считают, что такие тоннели сформированы путём затвердевания потоков расплавленной породы, где в центре застыла лава. Данные процессы происходили в период вулканической активности на Луне. Подтверждением этой теории является наличие извилистых борозд на поверхности спутника[44]. Подобные тоннели могут послужить для колонизации, благодаря защите от солнечной радиации и замкнутости пространства, в котором проще поддерживать условия жизнеобеспечения[44]. Похожие отверстия имеются и на Марсе.
Сейсмология[править | править код]
Оставленные на Луне экспедициями «Аполлон-12», «Аполлон-14», «Аполлон-15» и «Аполлон-16» четыре сейсмографа показали наличие сейсмической активности[45]. Исходя из последних расчётов учёных, лунное ядро состоит главным образом из раскалённого железа[46]. Из-за отсутствия воды колебания лунной поверхности продолжительны по времени, могут длиться более часа.
Лунотрясения можно разделить на четыре группы:
- приливные, случаются дважды в месяц, вызваны воздействием приливных сил Солнца и Земли;
- тектонические — нерегулярные, вызваны подвижками в грунте Луны;
- метеоритные — из-за падения метеоритов;
- термальные — их причиной служит резкий нагрев лунной поверхности с восходом Солнца.
Наибольшую опасность для возможных обитаемых станций представляют тектонические лунотрясения. Сейсмографами НАСА за 5 лет исследований было зарегистрировано 28 подобных лунотрясений. Некоторые из них достигают магнитуды 5,5 и длятся более 10 минут. Для сравнения: на Земле подобные землетрясения длятся не более 2 минут[47][48].
Наличие воды[править | править код]
Впервые сведения об обнаружении воды на Луне были опубликованы в 1978 году советскими исследователями в журнале «Геохимия»[49]. Факт был установлен в результате анализа образцов, доставленных зондом «Луна-24» в 1976 году. Количество найденной в образце воды составило 0,1 %[50].
В июле 2008 года группа американских геологов из Института Карнеги и Университета Брауна обнаружила в образцах грунта Луны следы воды, в большом количестве выделявшейся из недр спутника на ранних этапах его существования. Позднее бо́льшая часть этой воды испарилась в космос[51].
Российские учёные, с помощью созданного ими прибора LEND, установленного на зонде LRO, выявили участки Луны, наиболее богатые водородом. На основании этих данных НАСА выбрало место для проведения бомбардировки Луны зондом LCROSS. После проведения эксперимента, 13 ноября 2009 года НАСА сообщило об обнаружении в кратере Кабео в районе южного полюса воды в виде льда[52].
Согласно данным, переданным радаром Mini-SAR, установленным на индийском лунном аппарате Чандраян-1, всего в регионе северного полюса обнаружено не менее 600 млн тонн воды, большая часть которой находится в виде ледяных глыб, покоящихся на дне лунных кратеров. Всего вода была обнаружена в более чем 40 кратерах, диаметр которых варьирует от 2 до 15 км. Сейчас у учёных уже нет никаких сомнений в том, что найденный лёд — водный[53].
Химия пород[править | править код]
Состав лунного грунта существенно отличается в морских и материковых районах Луны. В лунных породах мало воды. Луна также обеднена железом и летучими компонентами[54]. Лунный грунт имеет запах гари и отстрелянных пистонов.
|
|
| Элементы | Доставлен «Луной-20» | Доставлен «Луной-16» |
|---|---|---|
| Si | 20,0 | 20,0 |
| Ti | 0,28 | 1,9 |
| Al | 12,5 | 8,7 |
| Cr | 0,11 | 0,20 |
| Fe | 5,1 | 13,7 |
| Mg | 5,7 | 5,3 |
| Ca | 10,3 | 9,2 |
| Na | 0,26 | 0,32 |
| K | 0,05 | 0,12 |
В лунном реголите также очень много кислорода, входящего в состав оксидов, причём самым распространённым из последних является диоксид кремния— 42,8 %[55]. АМС «Луна-20» доставила грунт из материкового района, «Луна-16» из морского[56].
Селенография[править | править код]
Основные детали на лунном диске, видимые невооружённым глазом: Z — «лунный заяц», A — кратер Тихо, B — кратер Коперник, C — кратер Кеплер, 1 — Океан Бурь, 2 — Море Дождей, 3 — Море Спокойствия, 4 — Море Ясности, 5 — Море Облаков, 6 — Море Изобилия, 7 — Море Кризисов, 8 — Море Влажности
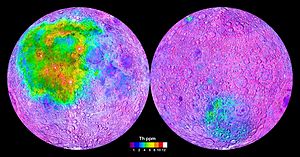
Топография Луны, высота поверхности относительно лунного геоида. Видимая с Земли сторона — слева
Поверхность Луны можно разделить на два типа:
- очень старая гористая местность («лунные материки»),
- относительно гладкие и более молодые лунные моря.
Лунные «моря», которые составляют приблизительно 16 % всей поверхности Луны, — это огромные кратеры, возникшие в результате столкновений с небесными телами, которые были позже затоплены жидкой лавой. Бо́льшая часть поверхности покрыта реголитом. Из-за влияния гравитационного момента при формировании Луны её «моря́», под которыми лунными зондами обнаружены более плотные, тяжёлые породы, сконцентрированы на обращённой к Земле стороне спутника.
Большинство кратеров на обращённой к Земле стороне названо по имени знаменитых людей в истории науки, таких как Тихо Браге, Коперник и Птолемей. Детали рельефа на обратной стороне имеют более современные названия типа Аполлон, Гагарин и Королёв. На обратной стороне Луны расположена огромная впадина Бассейн Южный полюс — Эйткен диаметром 2250 км и глубиной 12 км — это самый большой бассейн в Солнечной системе, появившийся в результате столкновения. Море Восточное в западной части видимой стороны (его можно видеть с Земли) является отличным примером многокольцевого кратера.
Также выделяют второстепенные детали лунного рельефа — купола, хребты, борозды — узкие извилистые долиноподобные понижения рельефа.
Происхождение кратеров[править | править код]
Ударный кратер — углубление, появившееся на поверхности космического тела в результате падения другого тела меньшего размера
Попытки объяснить происхождение кратеров на Луне начались с конца 1780-х годов. Основных гипотез было две — вулканическая и метеоритная[57]. Предтечей обеих гипотез можно считать и Роберта Гука, который в 1667 году производил моделирующие опыты. В одном из них он бросал горошины в жидкую глину, в другом — кипятил масло и наблюдал за его поверхностью[58].
Согласно постулатам вулканической теории, выдвинутой в 1780-х годах немецким астрономом Иоганном Шрётером, лунные кратеры были образованы вследствие мощных извержений на поверхности. Но в 1824 году также немецкий астроном Франц фон Груйтуйзен сформулировал метеоритную теорию, согласно которой при столкновении небесного тела с Луной происходит продавливание поверхности спутника и образование кратера.
До 1920-х годов против метеоритной гипотезы выдвигали тот факт, что кратеры имеют круглую форму, хотя косых ударов по поверхности должно быть больше, чем прямых, а значит при метеоритном происхождении кратеры должны иметь форму эллипса. Однако в 1924 году новозеландский учёный Чарльз Джиффорд впервые дал качественное описание удара о поверхность планеты метеорита, двигающегося с космической скоростью. Получалось, что при таком ударе бо́льшая часть метеорита испаряется вместе с породой на месте удара, и форма кратера не зависит от угла падения. Также в пользу метеоритной гипотезы говорит то, что совпадает зависимость количества лунных кратеров от их диаметра и зависимость количества метеорных тел от их размера. В 1937 году эту теорию привёл к обобщённому научному виду советский студент Кирилл Станюкович, впоследствии ставший доктором наук и профессором. «Взрывная теория» разрабатывалась им самим и группой учёных с 1947 года по 1960 год, а дорабатывалась, в дальнейшем, и другими исследователями.
Полёты к спутнику Земли с 1964 года, совершённые американскими аппаратами «Рейнджер», а также открытие кратеров на других планетах Солнечной системы (Марс, Меркурий, Венера), подвели итог этому вековому спору о происхождении кратеров на Луне. Дело в том, что открытые вулканические кратеры (например, на Венере) сильно отличаются от лунных, схожих с кратерами на Меркурии, которые, в свою очередь, были образованы ударами небесных тел. Поэтому метеоритная теория ныне считается общепринятой.
«Моря»[править | править код]
Лунные моря представляют собой обширные, залитые некогда базальтовой лавой низины. Изначально данные образования считали обычными морями. Впоследствии, когда это было опровергнуто, менять название не стали. Лунные моря занимают около 40 % видимой площади Луны.
| Русское название | Международное название[59] | Сторона Луны | |
|---|---|---|---|
| 1 | Океан Бурь | Oceanus Procellarum | видимая |
| 2 | Залив Зноя (Волнений) | Sinus Aestuum | видимая |
| 3 | Залив Радуги | Sinus Iridum | видимая |
| 4 | Залив Росы | Sinus Roris | видимая |
| 5 | Залив Центральный | Sinus Medium | видимая |
| 6 | Море Влажности | Mare Humorum | видимая |
| 7 | Море Восточное | Mare Orientalis | видимая |
| 8 | Море Дождей | Mare Imbrium | видимая |
| 9 | Море Плодородия (Изобилия) | Mare Foecunditatis | видимая |
| 10 | Море Краевое | Mare Marginis | видимая |
| 11 | Море Кризисов (Опасностей) | Mare Crisium | видимая |
| 12 | Море Мечты | Mare Ingenii | обратная |
| 13 | Море Москвы | Mare Mosquae | обратная |
| 14 | Море Нектара | Mare Nectaris | видимая |
| 15 | Море Облаков | Mare Nubium | видимая |
| 16 | Море Паров | Mare Vaporum | видимая |
| 17 | Море Пены | Mare Spumans | видимая |
| 18 | Море Смита | Mare Smythii | видимая |
| 19 | Море Спокойствия | Mare Tranquillitatis | видимая |
| 20 | Море Холода | Mare Frigorum | видимая |
| 21 | Море Южное | Mare Australe | видимая |
| 22 | Море Ясности | Mare Serenitatis | видимая |
Внутренняя структура[править | править код]
Луна — дифференцированное тело, она имеет геохимически различную кору, мантию и ядро. Оболочка внутреннего ядра богата железом, она имеет радиус 240 км, жидкое внешнее ядро состоит в основном из жидкого железа с радиусом примерно 300—330 километров. Вокруг ядра находится частично расплавленный пограничный слой с радиусом около 480—500 километров[60]. Эта структура, как полагают, появилась в результате фракционной кристаллизации из глобального океана магмы вскоре после образования Луны 4,5 миллиарда лет назад[61]. Лунная кора имеет в среднем толщину около 50 км.
Луна — второй по плотности спутник в Солнечной системе после Ио. Однако внутреннее ядро Луны мало́, его радиус около 350 км; это только ~20 % от радиуса Луны, в отличие от ~50 % у большинства других землеподобных тел.
Карта[править | править код]
Лунный ландшафт своеобразен и уникален. Луна вся покрыта кратерами разного размера — от микроскопических до сотен километров в диаметре. Долгое время учёные не могли получить сведений об обратной стороне Луны. Это стало возможным лишь с появлением космических аппаратов. Сейчас уже созданы очень подробные карты обоих полушарий спутника. Подробные лунные карты составляют для того, чтобы в будущем подготовиться к высадке и колонизации человеком Луны — удачного расположения лунных баз, телескопов, транспорта, поиска полезных ископаемых и т. п.
Происхождение[править | править код]
Эволюция лунной орбиты за последние 4,5 миллиарда лет[62]
Первую научную теорию возникновения Луны выдвинул в 1878 году британский астроном Джордж Говард Дарвин[63]. Согласно этой теории, Луна отделилась от Земли в виде магматического сгустка под действием центробежных сил. Альтернативная «теория захвата» предполагала существование Луны как отдельной планетезимали, захваченной гравитационным полем Земли[63]. Теория совместного формирования предполагает одновременное формирование Земли и Луны из единого массива мелких обломков породы[63]. Анализ грунта, доставленного миссией «Аполлон», показал, что лунный грунт по составу значительно отличается от земного[64]. Кроме того, современные компьютерные модели показали нереальность отделения от Земли массивного тела под действием центробежных сил[64]. Таким образом, ни одна из трёх первоначальных теорий не выдерживает критики.
В 1984 году на Гавайской конференции по планетологии была коллективно выдвинута теория возникновения Луны, получившая название теории Гигантского столкновения. Теория утверждает, что Луна возникла 4,6 млрд лет назад после столкновения Земли с гипотетическим небесным телом, получившим название Тейа[65][66]. Удар пришёлся не по центру, а под углом (почти по касательной). В результате большая часть вещества ударившегося объекта и часть вещества земной мантии были выброшены на околоземную орбиту. Из этих обломков собралась прото-Луна и стала обращаться по орбите с радиусом около 60 000 км (сейчас ~384 тыс. км). Земля в результате удара получила резкий прирост скорости вращения (один оборот за 5 часов) и заметный наклон оси вращения. Хотя у этой теории тоже есть недостатки, в настоящее время она считается основной[67][68].
Подтверждением теории столкновения планет по касательной можно указать:
- диаметр мантии Луны составляет 80 % от общего диаметра. Обычно у подобных космических тел он составляет 50 %;
- мантия Луны преимущественно содержит каменные породы.
По оценкам, основанным на содержании стабильного радиогенного изотопа вольфрама-182 (возникающего при распаде относительно короткоживущего гафния-182) в образцах лунного грунта, в 2005 году учёные-минералоги из Германии и Великобритании определили возраст разделения на силикатную и металлическую оболочки в 4 млрд 527 млн лет (± 10 млн лет)[69], в 2011 году её возраст был определён в 4,36 млрд лет (± 3 млн лет)[66], в 2015 году — в 4,47 миллиарда лет[70], а в 2017 году — в 4,51 млрд лет[71].
В 2020 году учёные определили возраст Луны как 4,425 млрд лет ±25 млн лет[72].
Исследование[править | править код]
Луна привлекала внимание людей с древних времён. Уже во II в. до н. э. Гиппарх исследовал движение Луны по звёздному небу, определив наклон лунной орбиты относительно эклиптики, размеры Луны и расстояние от Земли[73], а также выявил ряд особенностей движения. В III в. до н. э. Аристарх Самосский использовал длительность лунного затмения для вычисления диаметра Луны. По его расчётам, диаметр Луны равен четверти диаметра Земли — то есть примерно 3700 км, что практически идеально совпадает с реальным значением[74].
Изобретение телескопов позволило различить более мелкие детали рельефа Луны. Одну из первых лунных карт составил Джованни Риччиоли в 1651 году, он же дал названия крупным тёмным областям, именовав их «морями», чем мы и пользуемся до сих пор. Данные топонимы отражали давнее представление, будто погода на Луне схожа с земной, и тёмные участки якобы были заполнены лунной водой, а светлые участки считались сушей. Однако в 1753 году хорватский астроном Руджер Бошкович доказал, что Луна не имеет атмосферы. Дело в том, что при покрытии звёзд Луной те исчезают мгновенно. Но если бы у Луны была атмосфера, то звёзды бы гасли постепенно. Это свидетельствовало о том, что у спутника нет атмосферы. А в таком случае жидкой воды на поверхности Луны быть не может, так как она мгновенно бы испарилась.
С лёгкой руки того же Джованни Риччиоли кратерам стали давать имена известных учёных: от Платона, Аристотеля и Архимеда до Вернадского, Циолковского и Павлова.
Новым этапом исследования Луны стало применение фотографии в астрономических наблюдениях, начиная с середины XIX века. Это позволило более детально анализировать поверхность Луны по подробным фотографиям. Такие фотографии были сделаны, в частности, Уорреном де ла Рю (1852) и Льюисом Резерфордом (1865). В 1896—1904 годах Морис Леви, Пьер Пюизё и Шарль Ле Морван издали детальный «Фотографический атлас Луны»[75].
Исследования при помощи космических аппаратов[править | править код]
С началом космической эры количество наших знаний о Луне значительно увеличилось. Стал известен состав лунного грунта, учёные получили его образцы, составлена карта обратной стороны.
Впервые Луны достигла советская межпланетная станция «Луна-2» 13 сентября 1959 года.
Впервые удалось заглянуть на обратную сторону Луны в 1959 году, когда советская станция «Луна-3» пролетела над ней и сфотографировала невидимую с Земли часть её поверхности.
Пилотируемые полёты[править | править код]
В начале 1960-х годов было очевидно, что в освоении космоса США отстают от СССР. Дж. Кеннеди заявил — высадка человека на Луну состоится до 1970 года. Для подготовки к пилотируемому полёту НАСА выполнило несколько космических программ: «Рейнджер» (1961—1965) — фотографирование поверхности, «Сервейер» (1966—1968) — мягкая посадка и съёмки местности и «Лунар орбитер» (1966—1967) — детальное изображение поверхности Луны. В 1965—1966 годах существовал проект НАСА MOON-BLINK по исследованию необычных явлений (аномалий) на поверхности Луны. Работы выполнялись Trident Engineering Associates (Аннаполис, штат Мэриленд) в рамках контракта NAS 5-9613 от 1 июня 1965 года с Goddard Space Flight Center (Гринбелт, штат Мэриленд)[76][77][78].
Американская программа пилотируемого полёта на Луну называлась «Аполлон». Первая посадка произошла 20 июля 1969 года; последняя — в декабре 1972 года, первым человеком, ступившим 21 июля 1969 года на поверхность Луны, стал американец Нил Армстронг, вторым — Эдвин Олдрин; третий член экипажа Майкл Коллинз оставался в орбитальном модуле.
В декабре 1972 года астронавты «Аполлона-17» капитан Джин Сернан и д-р Харрисон Шмитт стали последними (на сегодняшний день) людьми, высадившимися на Луну.
Таким образом, Луна — единственное небесное тело, на котором побывал человек; и первое небесное тело, образцы которого были доставлены на Землю (США доставили 380 килограммов, СССР — 324 грамма лунного грунта)[79].
Луноходы[править | править код]
СССР проводил исследования на поверхности Луны с помощью двух радиоуправляемых самоходных аппаратов: «Луноход-1», запущенный к Луне в ноябре 1970 года, и «Луноход-2» — в январе 1973 года. «Луноход-1» работал 10,5 земных месяцев, «Луноход-2» — 4,5 земных месяцев (то есть 5 лунных дней и 4 лунные ночи), за которые прошёл 42,1 км[80][81] (до 28 июля 2014 года это расстояние оставалось рекордным для внеземных (созданных людьми) аппаратов, пока его не побил марсоход «Оппортьюнити», прошедший 45,16 км[82]). Оба аппарата собрали и передали на Землю большое количество данных о лунном грунте и множество фотоснимков деталей и панорам лунного рельефа[38].
Последующее изучение[править | править код]
После того как в августе 1976 года советская станция «Луна-24» доставила на Землю образцы лунного грунта, следующий аппарат — японский спутник «Hiten» — полетел к Луне лишь в 1990 году. Далее были запущены два американских космических аппарата — Clementine в 1994 году и Lunar Prospector в 1998 году.
Европейское космическое агентство 28 сентября 2003 года запустило свою первую автоматическую межпланетную станцию (АМС) «Смарт-1». 14 сентября 2007 года Япония запустила вторую АМС для исследования Луны «Кагуя». А 24 октября 2007 года в лунную гонку вступила и КНР — был запущен первый китайский спутник Луны «Чанъэ-1». С помощью этой и следующей станций учёные создают объёмную карту лунной поверхности, что в будущем может поспособствовать амбициозному проекту колонизации Луны[83]. 22 октября 2008 года была запущена первая индийская АМС «Чандраян-1». В 2010 году Китай запустил вторую АМС «Чанъэ-2».
Место посадки экспедиции «Аполлон-17». Видны: спускаемый модуль, исследовательское оборудование ALSEP, следы колёс автомобиля и пешие следы космонавтов. Снимок КА LRO, 4 сентября 2011 года
18 июня 2009 года НАСА были запущены лунные орбитальные зонды — Lunar Reconnaissance Orbiter (LRO) и Lunar Crater Observation and Sensing Satellite (LCROSS). Спутники предназначены для сбора информации о лунной поверхности, поиска воды и подходящих мест для будущих лунных экспедиций[84]. К сорокалетию полёта «Аполлона-11» автоматическая межпланетная станция LRO выполнила специальное задание — провела съёмку районов посадок лунных модулей земных экспедиций. В период с 11 по 15 июля LRO сделала и передала на Землю первые в истории детальные орбитальные снимки самих лунных модулей, посадочных площадок, элементов оборудования, оставленных экспедициями на поверхности, и даже следов тележки, ровера и самих землян[85]. За это время были отсняты 5 из 6 мест посадок: экспедиции «Аполлон-11», «-14», «-15», «-16», «-17»[86]. Позднее КА LRO выполнил ещё более подробные снимки поверхности, где ясно видно не только посадочные модули и аппаратуру со следами лунного автомобиля, но и пешие следы самих космонавтов[87]. 9 октября 2009 космический аппарат LCROSS и разгонный блок «Центавр» совершили запланированное падение на поверхность Луны в кратер Кабеус, расположенный примерно в 100 км от южного полюса Луны, а потому постоянно находящийся в глубокой тени. 13 ноября НАСА сообщило о том, что с помощью этого эксперимента на Луне обнаружена вода[88][89].
Прилунение в декабре 2013 года китайского лунохода «Юйту» стало первой мягкой посадкой на Луну с 1976 года, после советской АМС «Луна-24». Кроме того, он стал первым за 40 с лишним лет планетоходом, работающим на Луне, а КНР — третьей державой, осуществившей мягкую посадку на Луну, после СССР и США. Спустя 5 лет, 3 января 2019 года, впервые на обратную сторону Луны была совершена мягкая посадка посадочного модуля «Чанъэ-4» со вторым китайским луноходом «Юйту-2». На посадочном модуле провели уникальный биологический эксперимент по выращиванию картофеля, арабидопсиса, рапса, хлопчатника (удалось прорастить лишь хлопчатник) и выведению мух-дрозофил, а также с дрожжами[90].
Частные проекты[править | править код]
В настоящее время к изучению Луны приступают частные компании. Был объявлен всемирный конкурс Google Lunar X PRIZE по созданию небольшого лунохода, в котором участвовали 16 команд из 11 стран, в том числе российская Селеноход. Стартовав в 2010 году, он должен был продлиться до 2017 года, и несмотря на то, что был продлён до 2018, закончился без победителя: ни одного аппарата в рамках конкурса на Луну послано так и не было.
Есть планы по организации космического туризма с полётами вокруг Луны на российских кораблях — сначала на модернизированных «Союзах», а затем на разрабатываемых перспективных универсальных кораблях серии «Федерация».
Освоение[править | править код]
Международный правовой статус[править | править код]
Большинство правовых вопросов освоения Луны было разрешено в 1967 году Договором о принципах деятельности государств по исследованию и использованию космического пространства, включая Луну и другие небесные тела[91]. Также юридический статус Луны описывает Соглашение о Луне от 1979 года.
Колонизация[править | править код]
Луна является самым близким и лучше всего изученным небесным телом и рассматривается как кандидат для места создания человеческой колонии. НАСА разрабатывала космическую программу «Созвездие», в рамках которой должна разрабатываться новая космическая техника и создаваться необходимая инфраструктура для обеспечения полётов нового космического корабля к МКС, а также полётов на Луну, создания постоянной базы на Луне и в перспективе полётов на Марс[92]. Однако, по решению президента США Барака Обамы от 1 февраля 2010 года, финансирование программы в 2011 году было прекращено[93].
Российские учёные определили 14 наиболее вероятных точек прилунения. Каждое из мест посадки имеет размеры 30×60 км[94]. Будущие лунные базы находятся на стадии эксперимента — в частности, уже проведены первые успешные испытания самозалатывания космических аппаратов в случае попадания в них метеоритов[95]. В будущем Россия собирается применить на полюсах Луны криогенное (низкотемпературное) бурение для доставки на Землю грунта с вкраплениями летучих органических веществ. Данный метод позволит органическим соединениям, которые заморожены на реголите, не испаряться[96].
Сомнительные сделки[править | править код]
Существуют компании, якобы продающие участки на Луне. За определённую плату покупатель получает сертификат о «праве собственности» на некоторую площадь поверхности Луны. Есть мнение, что сейчас сертификаты такого рода не имеют юридической силы из-за нарушения условий Договора о принципах деятельности государств по исследованию и использованию космического пространства 1967 года (запрет на «национальное присвоение» космического пространства, в том числе Луны, согласно статье II Договора). Этот Договор оговаривает лишь деятельность государств, не касаясь деятельности физических лиц, чем и воспользовались в данном случае организации.
Иллюзия Луны[править | править код]
Иллюзия Луны — обман зрения, который заключается в том, что когда Луна находится низко над горизонтом, она кажется намного больше, чем когда она висит высоко в небе. На самом деле, угловой размер Луны практически не меняется с её высотой над горизонтом (а точнее, слабо меняется наоборот: около горизонта он слегка меньше, чем в зените, поскольку в этом случае расстояние от наблюдателя до Луны больше на величину земного радиуса). В настоящее время существует несколько теорий, которые объясняют эту ошибку зрительного восприятия разными причинами.
Кроме кажущихся изменений размера диска Луны в отношении наблюдателя невооружённым глазом с поверхности Земли, при малом угловом расположении Луны над горизонтом, видимый диск Луны кажется жёлтым в тёмное время суток или даже розоватым при рассвете-закате.
Кратковременные явления[править | править код]
Кратковременные лунные явления — это различные непродолжительные локальные аномалии вида лунной поверхности и окололунного пространства, обусловленные нестационарными процессами на Луне.
В навигации[править | править код]
С 1766 года Гринвичская королевская обсерватория издаёт ежегодник «Морской альманах». Наибольшую практическую ценность для навигации в альманахе представляли таблицы угловых расстояний от центра лунного диска до избранных зодиакальных
звёзд или до центра солнечного диска (для дневных измерений), составленные на весь год с интервалом в три часа. Эти таблицы позволяли морякам вплоть до начала XX века определять долготу с точностью до одной угловой минуты (метод лунных расстояний[en])[97].
В культуре[править | править код]
Диалог Плутарха «О лике видимом на лунном диске»[98] (I—II века) передаёт разные теории того времени о природе и свойствах Луны, под конец Плутарх обращается к теории, принятой в Платоновской Академии и Ксенократом, усматривая в Луне родину демонов[99].
В мифологии[править | править код]
В искусстве[править | править код]
Луна не раз вдохновляла поэтов и писателей, художников и музыкантов, режиссёров и сценаристов на создание произведений, связанных с этим единственным естественным спутником Земли.
Луна может выступать как символ таинственности, недоступной красоты, любви.
Сравнение с луной использовалось уже в древней литературе: В Песни песней Соломона (1-е тысячелетие до н. э.) написано:
Кто эта, блистающая, как заря, прекрасная, как луна, светлая, как солнце, грозная, как полки со знамёнами?
Первое фантастическое произведение о Луне (в стихах), известное с античности, приписывается легендарному древнегреческому певцу Орфею:
Он (Зевс) смастерил и иную землю, безграничную, кою Селеной зовут бессмертные, а земные человеки — Луной. Много на ней гор, много городов, много жилищ.
Μήσατο δ’ ἄλλην γαῖαν ἀπείριτον, ἥν τε σελήνην Άθάνατοι κλῄζουσιν, ἐπιχθόνιοι δέ τε μήνην, Ἣ πόλλ’ οὔρε ἔχει, πόλλ’ ἄστεα, πολλά μέλαθρα.
— Прокл. Комментарий к «Тимею» Платона[100].
В настоящее время считается, что эти строки написал пифагореец Керкопс в V веке до н. э.[101]
Тема путешествия на Луну была популярна в фольклоре и в классической литературе, в качестве способа достичь цели фигурируют и заведомо сказочные (бобовый стебель), и сильная буря, и бумажный монгольфьер. Первый технически обоснованный проект полёта на Луну описал Жюль Верн в романах «С Земли на Луну прямым путём за 97 часов 20 минут» (1865) и «Вокруг Луны» (1870).
Лунная тема была одной из главных для фантастов и футурологов на протяжении почти всего XX века[102]. В дореволюционной русской литературе Луна представлялась небесным телом с долинами и зубчатыми скалами, которая была покрыта голубоватой травой и большими белыми цветами[103].
Примечания[править | править код]
- Комментарии
- ↑ Здесь под яркостью понимается звёздная величина, то есть полный световой поток, приходящий от небесного тела (и, как следствие, создаваемая ею освещённость), а не яркость в физическом смысле — значение светового потока на единицу телесного угла объекта. Звёзды и Венера имеют гораздо большее значение последней, но в случае Луны определяющую роль играет её близость к Земле и, следовательно, больший угловой размер.
- ↑ Масса Солнца составляет 333 тыс. масс Земли, а расстояние от Земли до Солнца примерно в 150 млн км / 384 тыс. км ≈ 390 раз больше, чем от Земли до Луны. Соответственно, отношение сил притяжения Солнца и Земли, действующих на Луну, составит 333 000 / 3902 ≈ 2,2 раза.
- Источники
- ↑ 1 2 Солнечная система / Ред.-сост. В. Г. Сурдин. — М.: Физматлит, 2008. — С. 69. — ISBN 978-5-9221-0989-5.
- ↑ 1 2 3 Астрономический Календарь. Постоянная часть / Редактор Абалакин В. К.. — М.: Наука, главная редакция физико-математической литературы, 1981. — С. 555.
- ↑ A. R. Vasavada, D. A. Paige, S. E. Wood. Near-Surface Temperatures on Mercury and the Moon and the Stability of Polar Ice Deposits (англ.) // Icarus : journal. — Elsevier, 1999. — Vol. 141, no. 2. — P. 179—193. — doi:10.1006/icar.1999.6175. — Bibcode: 1999Icar..141..179V.
- ↑ Атмосфера Луны.
- ↑ Михайлов, Виноградов, 1974, с. 61.
- ↑ Фасмер М. Этимологический словарь русского языка. — Прогресс. — М., 1964—1973. — Т. 2. — С. 533.
- ↑ Коростовцев, Михаил Александрович. Религия древнего Египта. — М.: Наука, 1976. — Т. 3. — 336 с.
- ↑ Син, божество // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- ↑ Jeremy Roberts. Japanese Mythology A to Z (англ.). Архивировано 7 сентября 2012 года.
- ↑ В. Е. Жаров, 2002. Сферическая астрономия. 5.6. Пульсарная шкала времени Архивная копия от 5 октября 2012 на Wayback Machine.
- ↑ Дагаев М. М. Солнечные и лунные затмения. — М : Наука, 1978. — С. 50—54.
- ↑ Is the Moon moving away from the Earth? (англ.). Ask the Astronomer (Cornell University) (18 июля 2015). Дата обращения: 16 октября 2015. Архивировано 4 октября 2015 года.
- ↑ When the Moon Becomes Earth’s Nemesis (англ.). Discovery.com (26 июля 2013). — «In the case of the moon, it is moving away from us at a rate of 3.78 centimeters (1.5 inches) per year». Дата обращения: 16 октября 2015. Архивировано 6 марта 2017 года.
- ↑ Алексей Левин. Прекрасная Селена Архивная копия от 5 марта 2018 на Wayback Machine // Популярная механика, № 5, 2008.
- ↑ 1 2 James G. Williams, Dale H. Boggs, Charles F. Yoder, J. Todd Ratcliff, Jean O. Dickey. Lunar rotational dissipation in solid body and molten core (англ.) // Journal of Geophysical Research: Planets. — 2001. — Vol. 106, iss. E11. — P. 27933—27968. — ISSN 2156-2202. — doi:10.1029/2000JE001396.
- ↑ 1 2 James G. Williams, Alexander S. Konopliv, Dale H. Boggs, Ryan S. Park, Dah-Ning Yuan. Lunar interior properties from the GRAIL mission (англ.) // Journal of Geophysical Research: Planets. — 2014. — Vol. 119, iss. 7. — P. 1546—1578. — ISSN 2169-9100. — doi:10.1002/2013JE004559.
- ↑ Галкин И. Н., Шварев В. В. Строение Луны. — М.: Знание, 1977. — 64 с. — (Новое в жизни, науке, технике. Серия «Космонавтика, астрономия», 2. Издается ежемесячно с 1971 г.). — ISBN ?; ББК 526 Г16.
- ↑ D. E. Loper, C. L. Werner. On lunar asymmetries 1. Tilted convection and crustal asymmetry (англ.) // Journal of Geophysical Research (англ.) (рус.. — 2002. — Vol. 107, iss. E6. — doi:10.1029/2000je001441.
- ↑ NASA. STS-107 Shuttle Mission Imagery: STS107-E-05695. Дата обращения: 18 октября 2017. Архивировано из оригинала 30 мая 2016 года.
- ↑ NASA. STS-107 Shuttle Mission Imagery: STS107-E-05697. Дата обращения: 19 октября 2017. Архивировано из оригинала 30 мая 2016 года.
- ↑ Шевченко, 1990, с. 614.
- ↑ Needham D. H., Kring D. A. Lunar volcanism produced a transient atmosphere around the ancient Moon (англ.) // Earth and Planetary Science Letters (англ.) (рус. : journal. — Elsevier, 2017. — Vol. 478. — P. 175—178. — doi:10.1016/j.epsl.2017.09.002. — Bibcode: 2017E&PSL.478..175N.
- ↑ Маковецкий П. В. Смотри в корень! Задача № 36 — Детективно-астрономо-филателистический сюжет. — М.: Наука, 1976.
- ↑ Средний радиус Земли — 6371,0 км, а средний радиус Луны — 1737,1 км; соотношение равно ≈ 3,678.
- ↑ (6371,0 / 1737,1)2 ≈ 13,54.
- ↑ Геометрическое альбедо Земли равно 0,367, а Луны — 0,12. Соотношение альбедо умножаем на соотношение площадей видимых дисков Земли и Луны: (0,367 / 0,12) ⋅ (6371,0 / 1737,1)2 ≈ 41,12.
- ↑ «Фотометрические измерения („Лунохода-2“) привели к несколько неожиданным результатам относительно яркости лунного неба. В частности, было показано, что в дневное время лунное небо загрязнено определённым количеством пыли, и что при свете Земли в ночное время лунное небо в 15 раз ярче, чем небо на Земле при полной Луне» — М. Я. Маров, У. Т. Хантресс Советские роботы в Солнечной системе: технологии и открытия. — М.: Физматлит. — 2017. — С. 263.
- ↑ Соотношение яркости 41,12 соответствует разности видимых звёздных величин −2,5 ⋅ lg(41,12) ≈ −4,035; если звёздная величина Луны при наибольшей яркости равна −12,7, то звёздная величина Земли при наибольшей яркости составит −16,7
- ↑ Первые итоги определения физико-механических свойств грунтов Луны / под ред. проф. д-ра техн. наук В. Г. Булычева. — М.: Госстрой СССР. — 1970. — С. 8.
- ↑ Интерактивная, масштабируемая карта Луны. Активировать слой «WAC Hapke-Normalized Color» или «WAC Color test» Архивная копия от 24 июня 2017 на Wayback Machine.
- ↑ H. Sato et al. Resolved Hapke parametermaps of the Moon (англ.) // Journal of Geophysical Research: Planets : журнал. — 2014. — Vol. 119. — P. 1775—1805. — doi:10.1002/2013JE004580.
- ↑ Шкуратов, 2006, Классическая оптика Луны. Спектрофотометрия и колориметрия, с. 173.
- ↑ Шевченко, 1983, Луна и её наблюдение. Изменение отражательной способности Луны по спектру. Колориметрия, с. 93.
- ↑ Шкуратов, 2006, Классическая оптика Луны. Спектрофотометрия и колориметрия, с. 165.
- ↑ Орбитальные эфемериды Солнца, Луны и планет. 8. Начальные условия Архивная копия от 5 февраля 2011 на Wayback Machine.
- ↑ Астронет: 7.3 Гравитационное поле Луны Архивная копия от 14 мая 2008 на Wayback Machine.
- ↑ Проф. А. В. Некрасов. Морские приливы (недоступная ссылка — история). Дата обращения: 17 июля 2009. Архивировано 4 июля 2012 года.
- ↑ 1 2 И. Н. Галкин. Внеземная сейсмология. — М.: Наука, 1988. — 195 с. — (Планета Земля и Вселенная). — ISBN 502005951X.
- ↑ Учёные раскрыли тайну магнитного поля Луны. Дата обращения: 23 июня 2020. Архивировано 22 июня 2021 года.
- ↑ Э. В. Кононович и В. И. Мороз. Общий курс астрономии — М.: УРСС. — 2001 г. — С. 119.
- ↑ Ishihara, et al. Crustal thickness of the Moon: Implications for farside basin structures (англ.) // Geophysical Research Letters (англ.) (рус. : journal. — 2009. — October (vol. 36). — doi:10.1029/2009GL039708.
- ↑ Manabu Kato, et al. The Kaguya Mission Overview (англ.) // Space Science Reviews. — Springer, 2010. — 25 August. — doi:10.1007/s11214-010-9678-3.
- ↑ На темной стороне Луны найдены следы свежих тектонических процессов. Дата обращения: 20 февраля 2012. Архивировано 21 февраля 2012 года.
- ↑ 1 2 3 «На Луне нашли вход в подземный тоннель» Архивная копия от 9 августа 2020 на Wayback Machine — Лента.ру (26.10.2009)
- ↑ Г. Латем, И. Накамура, Дж. Дорман, Ф. Дьюнебье, М. Юинг, Д. Ламлейн. Результаты пассивного сейсмического эксперимента по программе «Аполлон» // Космохимия Луны и планет. Труды Советско-Американской конференции по космохимии Луны и планет в Москве (4—8 июня 1974 года) / Академия наук СССР, Национальное управление по аэронавтике и исследованию космического пространства США. — М.: Наука, 1975. — С. 299—310.
- ↑ В недрах Луны есть раскаленное металлическое ядро, считают учёные. РИА Новости (8 января 2011). Дата обращения: 8 января 2011. Архивировано 12 января 2011 года.
- ↑ Лунотрясения Архивная копия от 6 августа 2020 на Wayback Machine.
- ↑ Moonquakes Архивная копия от 23 февраля 2018 на Wayback Machine (англ.).
- ↑ Ахманова М. В., Дементьев Б. В., Марков М. Н. Вода в реголите Моря Кризисов («Луна-24»)? // Геохимия. — 1978. — № 2. — С. 285—288.
- ↑ Американский учёный признал приоритет СССР в обнаружении воды на Луне. Lenta.ru (30 мая 2012). Дата обращения: 31 мая 2012. Архивировано 31 мая 2012 года. (Дата обращения: 31 мая 2012)
- ↑ Би-би-си | На Луне была и есть вода. Дата обращения: 11 июля 2008. Архивировано 20 апреля 2014 года.
- ↑ Джонатан Эймос. Научный отдел Би-Би-Си. «На Луне нашли „значительное количество“ воды». Дата обращения: 14 ноября 2009. Архивировано 19 июля 2011 года.
- ↑ «На Луне найдены более 40 водных ледяных кратеров». Дата обращения: 3 марта 2010. Архивировано из оригинала 1 мая 2011 года.
- ↑ Э. Галимов. Научная мысль как планетное явление // Наука и жизнь. — 2018. — № 1. — С. 19.
- ↑ 1 2 А.Цимбальникова, М.Паливцова, И.Франа, А.Машталка. Химический состав фрагментов кристаллических пород и образцов реголита «Луны-16» и «Луны-20» // Космохимия Луны и планет. Труды Советско-Американской конференции по космохимии Луны и планет в Москве (4—8 июня 1974 года) / Академия наук СССР, Национальное управление по аэронавтике и исследованию космического пространства США.. — М.: Наука, 1975. — С. 156—166.
- ↑ Геофизические и геохимические особенности Луны. Дата обращения: 22 июля 2008. Архивировано 12 октября 2008 года.
- ↑ Бронштэн В. А. Метеоры, метеориты, метеороиды.
- ↑ Лунариум / Е. Парнов, Л. Самсоненко. — 2-е. — М.: Молодая гвардия, 1976. — С. 297—298. — 304 с.
- ↑ Дагаев М. М. Введение // Лабораторный практикум по курсу общей астрономии. — 2-е изд. — М.: Высшая школа, 1972. — С. 309. — 424 с.
- ↑ Лунное ядро (NASA) Архивная копия от 11 января 2012 на Wayback Machine (англ.).
- ↑ Кристаллизация лунного океана магмы Архивная копия от 12 апреля 2011 на Wayback Machine (англ.).
- ↑ Ross, M. N. Evolution of the lunar orbit with temperature‐ and frequency‐dependent dissipation : [англ.] / M. N. Ross, G. Schubert // J. Geophys. Res. — 1989. — Vol. 94, no. B7. — P. 9533–9544. — doi:10.1029/JB094iB07p09533.
- ↑ 1 2 3 Хейзен, 2017, с. 49.
- ↑ 1 2 Хейзен, 2017, с. 56.
- ↑ Хейзен, 2017, с. 62.
- ↑ 1 2 Астрономы определили точный возраст Луны. Лента.ру (18 августа 2011). Дата обращения: 19 августа 2011. Архивировано 18 сентября 2011 года.
- ↑ Рождение Луны Архивная копия от 9 сентября 2009 на Wayback Machine. selfire.com.
- ↑ Германские учёные о составе лунных пород Архивная копия от 8 августа 2020 на Wayback Machine.
- ↑ Hf-W Chronometry of Lunar Metals and the Age and Early Differentiation of the Moon Архивная копия от 27 сентября 2007 на Wayback Machine // Science.
- ↑ Учёные узнали точный возраст Луны по метеоритам Архивная копия от 19 апреля 2015 на Wayback Machine. Ореанда-Новости.
- ↑ Ученые оценили возраст Луны в 4,51 млрд лет Архивная копия от 25 октября 2020 на Wayback Machine.
- ↑ Астрономы скорректировали возраст Луны — Российская газета. Дата обращения: 25 ноября 2021. Архивировано 25 ноября 2021 года.
- ↑ Трифонов Е. Д. Как измерили Солнечную систему // Природа. — Наука, 2008. — № 7. — С. 18—24.
- ↑ Асфог, 2021, с. 113.
- ↑ L’Atlas photographique de la Lune, de MM. Loewy et Puiseux (фр.). Cairn.info. Дата обращения: 6 ноября 2017. Архивировано из оригинала 7 ноября 2017 года.
- ↑ Проект в архиве Архивная копия от 27 июня 2011 на Wayback Machine.
- ↑ Официальный веб-сайт Архивная копия от 14 июля 2007 на Wayback Machine (англ.).
- ↑ База фото- и видеоматериалов NASA. Дата обращения: 26 ноября 2012. Архивировано из оригинала 13 ноября 2012 года.
- ↑ Москва: сколько стоит грамм Луны? anomalniy-mir.ru. Архивировано из оригинала 25 сентября 2013 года.
- ↑ Emily Lakdawalla. Is Opportunity near Lunokhod’s distance record? Not as close as we used to think! (англ.). The Planetary Society (21 июня 2013). Дата обращения: 26 июня 2013. Архивировано 25 июня 2013 года.
- ↑ Witze, Alexandra Space rovers in record race (англ.). Nature News (19 июня 2013). Дата обращения: 26 июня 2013. Архивировано 27 июня 2013 года.
- ↑ Update: Spirit and Opportunity (англ.) (24 июня 2014). Дата обращения: 3 июля 2014. Архивировано из оригинала 4 июля 2014 года.
- ↑ Китай запустил свой первый лунный спутник Архивная копия от 18 марта 2009 на Wayback Machine. MEMBRANA, 24 октября 2007.
- ↑ Savage, Donald; Gretchen Cook-Anderson.: NASA Selects Investigations for Lunar Reconnaissance Orbiter (англ.). NASA News (22 декабря 2004). Дата обращения: 18 мая 2006. Архивировано 23 декабря 2004 года.
- ↑ Apollo 17 Lunar Module Landing Site (англ.). NASA. Дата обращения: 23 апреля 2023. Архивировано 14 ноября 2009 года.
- ↑ Соболев И. LRO: первые итоги // Новости космонавтики Архивировано 24 января 2012 года.. — 2009. — Т. 19. — № 10 (321). — С. 36—38. — ISSN 1726-0345.
- ↑ NASA опубликовало ФОТО Луны высокой четкости, на которых видны следы астронавтов и места посадки «Аполлонов» Архивная копия от 25 сентября 2013 на Wayback Machine. NEWSru.com.
- ↑ Jonas Dino. LCROSS Impact Data Indicates Water on Moon (англ.). NASA (13 ноября 2009). Дата обращения: 23 апреля 2023. Архивировано 15 ноября 2009 года.
- ↑ НАСА обнаружило воду в кратере Луны. Интерфакс (13 ноября 2009). Дата обращения: 15 ноября 2009. Архивировано 6 марта 2016 года.
- ↑ СМИ: аппарат «Чанъэ-4» завершил первый биологический эксперимент на Луне. ТАСС (15 января 2019). Дата обращения: 6 февраля 2019. Архивировано 3 февраля 2019 года.
- ↑ Текст договора в Викитеке.
- ↑ Официальная страница проекта «Созвездие» Архивная копия от 12 апреля 2010 на Wayback Machine (англ.).
- ↑ НАСА свернёт полёты шаттлов и лунную программу Архивная копия от 4 февраля 2010 на Wayback Machine // rian.ru.
- ↑ РСН. Россия определилась с местом строительства межпланетных станций на Луне. Ytro.Ru (22 ноября 2010). Дата обращения: 22 ноября 2010. Архивировано 25 ноября 2010 года.
- ↑ Учёные придумали затыкать дыры на Луне пробками. РБК (25 ноября 2010). Дата обращения: 26 ноября 2010. Архивировано из оригинала 20 июня 2013 года.
- ↑ Россия будет искать на Луне водяной лед и летучие вещества на глубине полметра. Интерфакс (7 декабря 2010). Дата обращения: 8 декабря 2010. Архивировано из оригинала 10 декабря 2010 года.
- ↑ Шевченко М. Ю. Луна. Наблюдая за самым знакомым и невероятным небесным объектом. — М.: АСТ, 2020. — С. 115. — 192 с. — ISBN 978-5-17-119739-1.
- ↑ Другое название «Беседа о лице, видимом на диске луны» («Филологическое обозрение» т. VI, кн. 2; 1894)
- ↑ Плутарх / Античные писатели. Словарь. — СПб.: Издательство «Лань», 1999.
- ↑ Proclus. Procli commentarius in Platonis Timaeum graece / Carl Ernst Christoph Schneider. — Vratislaviae: Eduardus Trewendt, 1847. — P. 363,685.
- ↑ А. И. Первушин «Битва за Луну: Правда и ложь о „лунной гонке“», — СПб: Амфора, 2007, С. 14—29. ISBN 978-5-367-00543-1.
- ↑ Первушин А. Лунные хроники Архивная копия от 4 ноября 2017 на Wayback Machine // Если. № 7 (161), 2006. С. 126.
- ↑ Маслов А. Н. Музей восковых фигур. — 1914.
Литература[править | править код]
- Книги
- Болдуин Р. Что мы знаем о Луне? Пер. с англ. К. А. Любарского; Послесл. А. А. Гурштейна.. — М.: Мир, 1967. — 173 с.
- Жарков В.Н., Паньков В.Л., Калачников А.А., Оснач А.И. Введение в физику Луны. — М.: Наука, 1969. — 312 с.
- Физика и астрономия Луны. Под. ред. Копала З., Лейкина Г. А. Пер. с англ.. — М.: Мир, 1973. — 318 с.
- Петров В.П. Здравствуй, Луна! / Петров В.П., Юревич П.П. — Л.: Лениздат, 1967. — 191 с. — 24 500 экз.
- Шевченко В.В. Луна и её наблюдение. — М.: Наука, 1983. — 192 с. — (Библиотека любителя астрономии). — 100 000 экз.
- Уманский С.П. Луна — седьмой континент. — М.: Знание, 1989. — 117 с. — 45 000 экз. — ISBN 5-07-000408-5.
- Шкуратов Ю. Г. Луна далёкая и близкая. — Харьков: Харьковский нац. университет им. В. Н. Каразина, 2006. — 182 с. — ISBN 966-623-370-3.
- Роберт Хейзен. История Земли: От звёздной пыли — к живой планете: Первые 4 500 000 000 лет = Robert Hazen. The Story of Earth. The First 4.5 Billion Years, from Stardust to Living Planet. — М.: Альпина Нон-фикшн, 2017. — 364 p. — ISBN 978-5-91671-706-8.
- Эрик Асфог. Когда у Земли было две Луны. Планеты-каннибалы, ледяные гиганты, грязевые кометы и другие светила ночного неба. = Erik Ian Asphaug. When the Earth Had Two Moons: Cannibal Planets, Icy Giants, Dirty Comets, Dreadful Orbits, and the Origins of the Night Sky. — М.: Альпина нон-фикшн, 2021. — 474 с. — ISBN 978-5-00139-262-0.
- Эйлер Л. Новая теория движения Луны. Пер. с латинского акад. Крылова А.Н.. — М.—Л.: Изд-во АН СССР, 1937. — 248 с.
- Статьи
- Луна / Михайлов А. А., Виноградов А. П. // Большая Советская Энциклопедия / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская Энциклопедия, 1974. — Т. 15 : Ломбард — Мезитол. — С. 60—63. — 629 000 экз.
- Шевченко В. В. Луна // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 613—615. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
- Фильмы
- Что не так с Луной на самом деле?// https://www.youtube.com/watch?v=G6hAxty22kU
См. также[править | править код]
- Законы Кассини (Cassini’s laws (англ.) (рус.)
Ссылки[править | править код]
- Луна — статья из энциклопедии «Кругосвет»
- Фазы Луны, перигеи и апогеи, покрытия звёзд и затмения (англ.)
- Данные о Луне (ГАИШ)
- Бурба Г. Большая одиссея
- Цветная фотография Луны (англ.)
- Фотографии Луны, сделанные с наземных телескопов
- Virtual Moon Atlas Software (GPL) (англ.)
From Wikipedia, the free encyclopedia
An elliptic, parabolic, and hyperbolic Kepler orbit:
elliptic (eccentricity = 0.7)
parabolic (eccentricity = 1)
hyperbolic orbit (eccentricity = 1.3)
Elliptic orbit by eccentricity
0.0 ·
0.2 ·
0.4 ·
0.6 ·
0.8
In astrodynamics, the orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values between 0 and 1 form an elliptic orbit, 1 is a parabolic escape orbit (or capture orbit), and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections, as every Kepler orbit is a conic section. It is normally used for the isolated two-body problem, but extensions exist for objects following a rosette orbit through the Galaxy.
Definition[edit]
In a two-body problem with inverse-square-law force, every orbit is a Kepler orbit. The eccentricity of this Kepler orbit is a non-negative number that defines its shape.
The eccentricity may take the following values:
- circular orbit: e = 0
- elliptic orbit: 0 < e < 1
- parabolic trajectory: e = 1
- hyperbolic trajectory: e > 1
The eccentricity e is given by[1]
where E is the total orbital energy, L is the angular momentum, mred is the reduced mass, and 
(
or in the case of a gravitational force:[2]: 24
where ε is the specific orbital energy (total energy divided by the reduced mass), μ the standard gravitational parameter based on the total mass, and h the specific relative angular momentum (angular momentum divided by the reduced mass).[2]: 12–17
For values of e from 0 to 1 the orbit’s shape is an increasingly elongated (or flatter) ellipse; for values of e from 1 to infinity the orbit is a hyperbola branch making a total turn of 2 arccsc(e), decreasing from 180 to 0 degrees. Here, the total turn is analogous to turning number, but for open curves (an angle covered by velocity vector). The limit case between an ellipse and a hyperbola, when e equals 1, is parabola.
Radial trajectories are classified as elliptic, parabolic, or hyperbolic based on the energy of the orbit, not the eccentricity. Radial orbits have zero angular momentum and hence eccentricity equal to one. Keeping the energy constant and reducing the angular momentum, elliptic, parabolic, and hyperbolic orbits each tend to the corresponding type of radial trajectory while e tends to 1 (or in the parabolic case, remains 1).
For a repulsive force only the hyperbolic trajectory, including the radial version, is applicable.
For elliptical orbits, a simple proof shows that 
Etymology[edit]
The word “eccentricity” comes from Medieval Latin eccentricus, derived from Greek ἔκκεντρος ekkentros “out of the center”, from ἐκ- ek-, “out of” + κέντρον kentron “center”. “Eccentric” first appeared in English in 1551, with the definition “…a circle in which the earth, sun. etc. deviates from its center”.[citation needed] In 1556, five years later, an adjectival form of the word had developed.
Calculation[edit]
The eccentricity of an orbit can be calculated from the orbital state vectors as the magnitude of the eccentricity vector:
where:
- e is the eccentricity vector (“Hamilton’s vector”).[2]: 25, 62–63
For elliptical orbits it can also be calculated from the periapsis and apoapsis since 

where:
- ra is the radius at apoapsis (also “apofocus”, “aphelion”, “apogee”), i.e., the farthest distance of the orbit to the center of mass of the system, which is a focus of the ellipse.
- rp is the radius at periapsis (or “perifocus” etc.), the closest distance.
The eccentricity of an elliptical orbit can also be used to obtain the ratio of the apoapsis radius to the periapsis radius:
For Earth, orbital eccentricity e ≈ 0.01671, apoapsis is aphelion and periapsis is perihelion, relative to the Sun.
For Earth’s annual orbit path, the ratio of longest radius (ra) / shortest radius (rp) is 
Examples[edit]
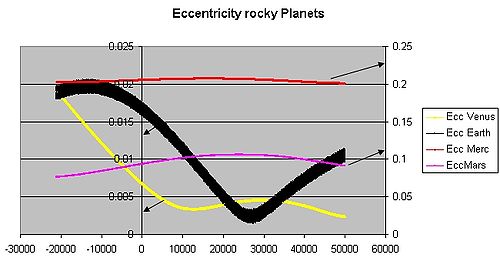
Plot of the changing orbital eccentricity of Mercury, Venus, Earth, and Mars over the next 50000 years. The arrows indicate the different scales used, as the eccentricities of Mercury and Mars are much greater than those of Venus and Earth. The 0 point on this plot is the year 2007.
| Object | eccentricity |
|---|---|
| Triton | 0.00002 |
| Venus | 0.0068 |
| Neptune | 0.0086 |
| Earth | 0.0167 |
| Titan | 0.0288 |
| Uranus | 0.0472 |
| Jupiter | 0.0484 |
| Saturn | 0.0541 |
| Moon | 0.0549 |
| 1 Ceres | 0.0758 |
| 4 Vesta | 0.0887 |
| Mars | 0.0934 |
| 10 Hygiea | 0.1146 |
| Makemake | 0.1559 |
| Haumea | 0.1887 |
| Mercury | 0.2056 |
| 2 Pallas | 0.2313 |
| Pluto | 0.2488 |
| 3 Juno | 0.2555 |
| 324 Bamberga | 0.3400 |
| Eris | 0.4407 |
| Nereid | 0.7507 |
| Sedna | 0.8549 |
| Halley’s Comet | 0.9671 |
| Comet Hale-Bopp | 0.9951 |
| Comet Ikeya-Seki | 0.9999 |
| C/1980 E1 | 1.057 |
| ʻOumuamua | 1.20[a] |
| C/2019 Q4 (Borisov) | 3.5[b] |
The eccentricity of Earth’s orbit is currently about 0.0167; its orbit is nearly circular. Venus and Neptune have even lower eccentricities. Over hundreds of thousands of years, the eccentricity of the Earth’s orbit varies from nearly 0.0034 to almost 0.058 as a result of gravitational attractions among the planets.[3]
The table lists the values for all planets and dwarf planets, and selected asteroids, comets, and moons. Mercury has the greatest orbital eccentricity of any planet in the Solar System (e = 0.2056). Such eccentricity is sufficient for Mercury to receive twice as much solar irradiation at perihelion compared to aphelion. Before its demotion from planet status in 2006, Pluto was considered to be the planet with the most eccentric orbit (e = 0.248). Other Trans-Neptunian objects have significant eccentricity, notably the dwarf planet Eris (0.44). Even further out, Sedna, has an extremely-high eccentricity of 0.855 due to its estimated aphelion of 937 AU and perihelion of about 76 AU.
Most of the Solar System’s asteroids have orbital eccentricities between 0 and 0.35 with an average value of 0.17.[4] Their comparatively high eccentricities are probably due to the influence of Jupiter and to past collisions.
The Moon’s value is 0.0549, the most eccentric of the large moons of the Solar System. The four Galilean moons have an eccentricity of less than 0.01. Neptune’s largest moon Triton has an eccentricity of 1.6×10−5 (0.000016),[5] the smallest eccentricity of any known moon in the Solar System;[citation needed] its orbit is as close to a perfect circle as can be currently[when?] measured. However, smaller moons, particularly irregular moons, can have significant eccentricity, such as Neptune’s third largest moon Nereid (0.75).
Comets have very different values of eccentricity. Periodic comets have eccentricities mostly between 0.2 and 0.7,[6] but some of them have highly eccentric elliptical orbits with eccentricities just below 1; for example, Halley’s Comet has a value of 0.967. Non-periodic comets follow near-parabolic orbits and thus have eccentricities even closer to 1. Examples include Comet Hale–Bopp with a value of 0.995[7] and comet C/2006 P1 (McNaught) with a value of 1.000019.[8] As Hale–Bopp’s value is less than 1, its orbit is elliptical and it will return.[7] Comet McNaught has a hyperbolic orbit while within the influence of the planets,[8] but is still bound to the Sun with an orbital period of about 105 years.[9] Comet C/1980 E1 has the largest eccentricity of any known hyperbolic comet of solar origin with an eccentricity of 1.057,[10] and will eventually leave the Solar System.
ʻOumuamua is the first interstellar object found passing through the Solar System. Its orbital eccentricity of 1.20 indicates that ʻOumuamua has never been gravitationally bound to the Sun. It was discovered 0.2 AU (30000000 km; 19000000 mi) from Earth and is roughly 200 meters in diameter. It has an interstellar speed (velocity at infinity) of 26.33 km/s (58900 mph).
Mean eccentricity[edit]
The mean eccentricity of an object is the average eccentricity as a result of perturbations over a given time period. Neptune currently has an instant (current epoch) eccentricity of 0.0113,[11] but from 1800 to 2050 has a mean eccentricity of 0.00859.[12]
Climatic effect[edit]
Orbital mechanics require that the duration of the seasons be proportional to the area of Earth’s orbit swept between the solstices and equinoxes, so when the orbital eccentricity is extreme, the seasons that occur on the far side of the orbit (aphelion) can be substantially longer in duration. Northern hemisphere autumn and winter occur at closest approach (perihelion), when Earth is moving at its maximum velocity—while the opposite occurs in the southern hemisphere. As a result, in the northern hemisphere, autumn and winter are slightly shorter than spring and summer—but in global terms this is balanced with them being longer below the equator. In 2006, the northern hemisphere summer was 4.66 days longer than winter, and spring was 2.9 days longer than autumn due to the Milankovitch cycles.[13][14]
Apsidal precession also slowly changes the place in Earth’s orbit where the solstices and equinoxes occur. This is a slow change in the orbit of Earth, not the axis of rotation, which is referred to as axial precession. Over the next 10000 years, the northern hemisphere winters will become gradually longer and summers will become shorter. However, any cooling effect in one hemisphere is balanced by warming in the other, and any overall change will be counteracted by the fact that the eccentricity of Earth’s orbit will be almost halved.[15] This will reduce the mean orbital radius and raise temperatures in both hemispheres closer to the mid-interglacial peak.
Exoplanets[edit]
Of the many exoplanets discovered, most have a higher orbital eccentricity than planets in the Solar System. Exoplanets found with low orbital eccentricity (near-circular orbits) are very close to their star and are tidally-locked to the star. All eight planets in the Solar System have near-circular orbits. The exoplanets discovered show that the Solar System, with its unusually-low eccentricity, is rare and unique.[16] One theory attributes this low eccentricity to the high number of planets in the Solar System; another suggests it arose because of its unique asteroid belts. A few other multiplanetary systems have been found, but none resemble the Solar System. The Solar System has unique planetesimal systems, which led the planets to have near-circular orbits. Solar planetesimal systems include the asteroid belt, Hilda family, Kuiper belt, Hills cloud, and the Oort cloud. The exoplanet systems discovered have either no planetesimal systems or one very large one. Low eccentricity is needed for habitability, especially advanced life.[17] High multiplicity planet systems are much more likely to have habitable exoplanets.[18][19] The grand tack hypothesis of the Solar System also helps understand its near-circular orbits and other unique features.[20][21][22][23][24][25][26][27]
See also[edit]
- Equation of time
Footnotes[edit]
- ^ ʻOumuamua was never bound to the Sun, so its orbit is hyperbolic: e ≈ 1.20 > 1 .
- ^ C/2019 Q4 (Borisov) was never bound to the Sun, so its orbit is hyperbolic: e ≈ 3.5 >> 1 .
References[edit]
- ^ Abraham, Ralph (2008). Foundations of mechanics. Jerrold E. Marsden (2nd ed.). Providence, R.I.: AMS Chelsea Pub./American Mathematical Society. ISBN 978-0-8218-4438-0. OCLC 191847156.
- ^ a b c d Bate, Roger R.; Mueller, Donald D.; White, Jerry E.; Saylor, William W. (2020). Fundamentals of Astrodynamics. Courier Dover. ISBN 978-0-486-49704-4. Retrieved 4 March 2022.
- ^ A. Berger & M.F. Loutre (1991). “Graph of the eccentricity of the Earth’s orbit”. Illinois State Museum (Insolation values for the climate of the last 10 million years). Archived from the original on 6 January 2018.
- ^ Asteroids Archived 4 March 2007 at the Wayback Machine
- ^ David R. Williams (22 January 2008). “Neptunian Satellite Fact Sheet”. NASA.
- ^
Lewis, John (2 December 2012). Physics and Chemistry of the Solar System. Academic Press. ISBN 9780323145848. - ^ a b “JPL Small-Body Database Browser: C/1995 O1 (Hale-Bopp)” (2007-10-22 last obs). Retrieved 5 December 2008.
- ^ a b “JPL Small-Body Database Browser: C/2006 P1 (McNaught)” (2007-07-11 last obs). Retrieved 17 December 2009.
- ^ “Comet C/2006 P1 (McNaught) – facts and figures”. Perth Observatory in Australia. 22 January 2007. Archived from the original on 18 February 2011.
- ^ “JPL Small-Body Database Browser: C/1980 E1 (Bowell)” (1986-12-02 last obs). Retrieved 22 March 2010.
- ^ Williams, David R. (29 November 2007). “Neptune Fact Sheet”. NASA.
- ^ “Keplerian elements for 1800 A.D. to 2050 A.D.” JPL Solar System Dynamics. Retrieved 17 December 2009.
- ^ Data from United States Naval Observatory Archived 13 October 2007 at the Wayback Machine
- ^ Berger A.; Loutre M.F.; Mélice J.L. (2006). “Equatorial insolation: from precession harmonics to eccentricity frequencies” (PDF). Clim. Past Discuss. 2 (4): 519–533. doi:10.5194/cpd-2-519-2006.
- ^ “Long Term Climate”. ircamera.as.arizona.edu.
- ^ “ECCENTRICITY”. exoplanets.org.
- ^ Ward, Peter; Brownlee, Donald (2000). Rare Earth: Why Complex Life is Uncommon in the Universe. Springer. pp. 122–123. ISBN 0-387-98701-0.
- ^ Limbach, MA; Turner, EL (2015). “Exoplanet orbital eccentricity: multiplicity relation and the Solar System”. Proc Natl Acad Sci U S A. 112 (1): 20–4. arXiv:1404.2552. Bibcode:2015PNAS..112…20L. doi:10.1073/pnas.1406545111. PMC 4291657. PMID 25512527.
- ^ Youdin, Andrew N.; Rieke, George H. (15 December 2015). “Planetesimals in Debris Disks”. arXiv:1512.04996.
- ^ Zubritsky, Elizabeth. “Jupiter’s Youthful Travels Redefined Solar System”. NASA. Retrieved 4 November 2015.
- ^ Sanders, Ray (23 August 2011). “How Did Jupiter Shape Our Solar System?”. Universe Today. Retrieved 4 November 2015.
- ^ Choi, Charles Q. (23 March 2015). “Jupiter’s ‘Smashing’ Migration May Explain Our Oddball Solar System”. Space.com. Retrieved 4 November 2015.
- ^ Davidsson, Dr. Björn J. R. “Mysteries of the asteroid belt”. The History of the Solar System. Retrieved 7 November 2015.
- ^ Raymond, Sean (2 August 2013). “The Grand Tack”. PlanetPlanet. Retrieved 7 November 2015.
- ^ O’Brien, David P.; Walsh, Kevin J.; Morbidelli, Alessandro; Raymond, Sean N.; Mandell, Avi M. (2014). “Water delivery and giant impacts in the ‘Grand Tack’ scenario”. Icarus. 239: 74–84. arXiv:1407.3290. Bibcode:2014Icar..239…74O. doi:10.1016/j.icarus.2014.05.009. S2CID 51737711.
- ^ Loeb, Abraham; Batista, Rafael; Sloan, David (August 2016). “Relative Likelihood for Life as a Function of Cosmic Time”. Journal of Cosmology and Astroparticle Physics. 2016 (8): 040. arXiv:1606.08448. Bibcode:2016JCAP…08..040L. doi:10.1088/1475-7516/2016/08/040. S2CID 118489638.
- ^ “Is Earthly Life Premature from a Cosmic Perspective?”. Harvard-Smithsonian Center for Astrophysics. 1 August 2016.
Further reading[edit]
- Prussing, John E.; Conway, Bruce A. (1993). Orbital Mechanics. New York: Oxford University Press. ISBN 0-19-507834-9.
External links[edit]
- World of Physics: Eccentricity
- The NOAA page on Climate Forcing Data includes (calculated) data from Berger (1978), Berger and Loutre (1991)[permanent dead link]. Laskar et al. (2004) on Earth orbital variations, Includes eccentricity over the last 50 million years and for the coming 20 million years.
- The orbital simulations by Varadi, Ghil and Runnegar (2003) provides series for Earth orbital eccentricity and orbital inclination.
- Kepler’s Second law’s simulation
Солнечная система > Система Земля-Луна > Спутник Луна > Орбита Луны
Люди всегда с восторгом смотрели на соседний спутник, кажущийся чем-то божественным из-за своей яркости. Луна вращается по орбите вокруг Земли с момента создания, поэтому за ней наблюдали и первые люди. Любопытство и эволюция привели к тому, что появились вычисления и мы начали отмечать шаблоны поведения.
Вращение Луны по орбите
К примеру, ось вращения Луны совпадает с орбитальным. По сути, спутник расположен в гравитационном блоке, то есть, мы всегда смотрим на одну сторону (так возникла идея о загадочной обратной стороне Луны). Из-за эллиптического пути небесное тело периодически кажется больше или меньше.
Орбитальные параметры Луны
Средний лунный эксцентриситет составляет – 0.0549, а значит Луна не проходит вокруг Земли по идеальному кругу. Среднее расстояние от Луны до Земли – 384748 км. Но может меняться от 364397 км до 406748 км.
Сопоставление кажущегося лунного размера в перигее и апогее
Это приводит к перемене угловой скорости и наблюдаемого размера. В фазе полной Луны и на позиции перигелия (ближе всего) мы видим ее на 10% крупнее и на 30% ярче, чем в апогее (максимальная отдаленность).
Средний наклон орбиты по отношению к плоскости эклиптики – 5.155°. Совпадают сидерический период и осевой – 27.3 дней. Это именуют синхронным вращением. Именно поэтому появилась «темная сторона», которую мы просто не видим.
Земля также совершает обороты вокруг Солнца, а Луна вращается вокруг Земли за 29.53 дней. Это синодический период, который подвергается фазам.
Лунный цикл орбиты
Лунный цикл порождает фазы Луны – кажущаяся перемена внешнего вида небесного тела в небе из-за изменения количества освещенности. Когда звезда, планета и спутник выстраиваются в одну линию, то угол между Луной и Солнцем составляет 0 градусов.
Хотите получить индивидуальный расклад?
Опытный таролог ответит на вопросы:
Что ждёт Вас в будущем? Как сложатся отношения? Какое решение — верное?
В этом периоде лунная сторона, повернутая к Солнцу, получает максимум лучей, а обращенная к нам – темная. Далее идет проход и угол растет. После Новолуния объекты разделены на 90 градусов, и мы уже видим иную картину. На нижней схеме можно подробно изучить, как формируются лунные фазы.
Если они расположены в противоположных сторонах, то угол – 180 градусов. Лунный месяц длится 28 дней, во время которого спутник «растет» и «убывает».
При четверти Луна заполнена меньше чем наполовину и растет. Далее идет переход за половину, и она угасает. Мы встречаем последнюю четверть, где освещена уже другая сторона диска.
Будущее лунной орбиты
Мы уже знаем, что спутник постепенно отдаляется по орбите от планеты (1-2 см в год). И это влияет на то, что с каждым веком день у нас становится на 1/500 секунды длиннее. То есть, примерно 620 млн. лет назад Земля могла похвастаться лишь 21 часом.
Сейчас сутки охватывают 24 часа, но Луна не прекращает попыток сбежать. Мы привыкли к спутнику и грустно терять такого напарника. Но отношения между объектами меняются. Интересно лишь, как это отразится на нас.
Читайте также:
- Интересные факты о Луне;
- Что такое Луна?
- Как образовалась Луна;
- Как сформировалась Луна?
- Постройка лунной базы: часть 1
- Постройка лунной базы: часть 2
- Постройка лунной базы: часть 3
- Постройка лунной базы: часть 4
- Как можно уничтожить Луну?
- Как понять, что лунная посадка не была фальшивкой?
- Нужна ли нам Луна для выживания?
- Как заработать на Луне?
- Как в НАСА записали отправку астронавтов с Луны?
- Куда лучше направиться: на Марс или Луну?
- Не пришло ли время вернуться на Луну?
- Какое настоящее название Луны?
Положение и движение Луны
- Орбита Луны;
- Солнце и Луна
- Почему Солнце не поглотит Луну?
- Какие бывают фазы Луны
- Что такое выпуклая Луна?
- Почему Луна кажется такой большой?
- Почему Луна удаляется от нас?
- Почему мы видим Солнце и Луну одновременно?
- Как долго добираться до Луны?
- Расстояние от Земли до Луны;
- Вращение Луны;
- Обратная сторона Луны;
- Второй земной спутник покидает нас
Строение Луны
- Строение Луны
- Размеры Луны;
- Диаметр Луны;
- Масса Луны;
- Является ли Луна планетой?
Поверхность Луны
- Поверхность Луны;
- Вода на Луне
- Новые кратеры на Луне
- Создание Луны: практика формирования кратеров
- Лавовые трубы на Луне
- Первые люди на Луне
- Сколько людей было на Луне?
- Что находится на дальней стороне Луны?
- Старое оборудование НАСА можно рассмотреть на Луне
- Терраформирование Луны
- Токсичность Луны
- Атмосфера Луны;
- Гравитация на Луне;
- Возраст Луны;
- Температура на Луне;
- Почему Луна светит?
- Почему мы видим «человека на Луне»?
- Почему на дальней стороне Луны нет морей?
- Цвет Луны;
- Море Спокойствия;
Ответ: Эксцентриситет лунной орбиты для заданных значений
≈ 0,06666
Объяснение: Дано:
Линейный радиус Луны Rл = 1737,1 км
Угловой радиус Луны в апогее αа” = 14,7′ = 882”
Угловой радиус Луны в перигее αп” = 16,8′ = 1008”
Найти эксцентриситет лунной орбиты е – ?
Расстояние до Луны в апогее: Sа = Rл*206265”/αа” =
= 1737,1 км*206265”/882” ≈ 406239 км.
Расстояние до Луны в перигее: Sп = Rл*206265”/αп” =
= 1737,1 км*206265”/1008” ≈ 355 459 км.
С другой стороны расстояние в апогее Sа = Sср(1 + е), расстояние в перигее Sп = Sср(1 – е). Здесь Sср – среднее расстояние до Луны.
Таким образом, имеем систему уравнений:
Sа = Sср(1 + е) (1)
Sп = Sср(1 – е) (2)
Выразим из уравнения (1) Sср = Sа/(1+е) и подставим это выражение в уравнение (2). Имеем: Sп = Sа(1 – е)/(1+е) или Sп(1+е) = Sа(1 – е) или
Sп + Sп*е = Sа – Sа*е или Sа – Sп = е(Sп+Sа). Отсюда е = (Sа – Sп)/(Sп+Sа) = (406239 – 355 459)/(406239 + 355 459) = 0,06666












![{displaystyle {begin{aligned}V&={frac {GM}{r}}left[1-sum _{n=2}^{infty }J_{n}left({frac {R}{r}}right)^{n}P_{n}(sin theta )right.+\&qquad {}+left.sum _{n=2}^{infty }sum _{m=1}^{n}left({frac {R}{r}}right)^{n}(C_{nm}cos mlambda +S_{nm}sin mlambda )P_{n}^{m}(sin theta )right],end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da5abda8146c8b8e9026fbd7931b4a1e380aee48)