Эллиптическая орбита с эксцентриситетом 0,7 (красным), параболическая орбита (зелёным) и гиперболическая орбита с эксцентриситетом 1,3 (синим)
Эксцентрисите́т орбиты (обозначается «
Вычисление эксцентриситета орбиты[править | править код]
По внешнему виду орбиты можно разделить на пять групп:
Для эллиптических орбит эксцентриситет вычисляется по формуле:
, где
— малая полуось,
— большая полуось эллипса.
Для гиперболических орбит эксцентриситет вычисляется по формуле:
, где
— мнимая полуось,
— действительная полуось гиперболы.
Некоторые эксцентриситеты орбиты[править | править код]
В таблице ниже приведены эксцентриситеты орбиты для некоторых небесных тел (отсортированы по величине большой полуоси орбиты, кроме 1I/Оумуамуа и C/2019 Q4 (Борисова), у которых гиперболические орбиты, и кроме спутников, которые выделены серым цветом).
| Небесное тело | Эксцентриситет орбиты 
|
|
|---|---|---|
| Меркурий | 0,205[1] | |
| Венера | 0,007[1] | |
| Земля | 0,017[1] | |
| Луна | 0,05490[2] | |
| (3200) Фаэтон | 0,8898[3] | |
| Марс | 0,094[1] | |
| Юпитер | 0,049[1] | |
| Ио | 0,004[4] | |
| Европа | 0,009[4] | |
| Ганимед | 0,002[4] | |
| Каллисто | 0,007[4] | |
| Сатурн | 0,057[1] | |
| Титан | 0,029[4] | |
| Комета Галлея | 0,967[5] | |
| Уран | 0,046[1] | |
| Нептун | 0,011[1] | |
| Нереида | 0,7512[4] | |
| Плутон | 0,244[1] | |
| Хаумеа | 0,1902[6] | |
| Макемаке | 0,1549[7] | |
| Эрида | 0,4415[8] | |
| Седна | 0,85245[9] | |
| 1I/Оумуамуа | 1,1995[10] | |
| 2I/Borisov | 3,36[11] |
Эксцентриситет инвариантен относительно движений плоскости и преобразований подобия[12].
См. также[править | править код]
- Элементы орбиты
Примечания[править | править код]
- ↑ 1 2 3 4 5 6 7 8 9 Planetary Fact Sheet
- ↑ Clabon Walter Allen, Arthur N. Cox. Allen’s Astrophysical Quantities. — Springer, 2000. — С. 308. — ISBN 0-387-98746-0.
- ↑ 3200 Phaethon (1983 TB). Jet Propulsion Laboratory (22 октября 2015). Дата обращения: 23 октября 2015.
- ↑ 1 2 3 4 5 6 Clabon Walter Allen, Arthur N. Cox. Allen’s Astrophysical Quantities. — Springer, 2000. — С. 305—306. — ISBN 0-387-98746-0.
- ↑ JPL Small-Body Database Browser: 1P/Halley. Jet Propulsion Laboratory (11 января 1994). Дата обращения: 23 октября 2015. Архивировано 20 августа 2011 года.
- ↑ Jet Propulsion Laboratory Small-Body Database Browser: 136108 Haumea (2003 EL61). Jet Propulsion Laboratory (26 июля 2015). Дата обращения: 23 октября 2015.
- ↑ JPL Small-Body Database Browser: 136472 Makemake (2005 FY9). Jet Propulsion Laboratory (26 июля 2015). Дата обращения: 23 октября 2015.
- ↑ JPL Small-Body Database Browser: 136199 Eris (2003 UB313). Jet Propulsion Laboratory (26 октября 2014). Дата обращения: 23 октября 2015.
- ↑ JPL Small-Body Database Browser: 90377 Sedna (2003 VB12). Jet Propulsion Laboratory (17 ноября 2014). Дата обращения: 23 октября 2015.
- ↑ JPL Small-Body Database Browser: ‘Oumuamua (A/2017 U1). Jet Propulsion Laboratory (17 ноября 2017). Дата обращения: 22 ноября 2017.
- ↑ JPL Small-Body Database Browser: C/2019 Q4 (Borisov). Jet Propulsion Laboratory (16 ноября 2019). Дата обращения: 23 ноября 2019.
- ↑ Акопян А. В., Заславский А. А. Геометрические свойства кривых второго порядка — М.: МЦНМО, 2007. — 136 с.
Величина, на которую орбита отклоняется от кругового кольца 

эксцентриситет орбиты астрономического объекта – это безразмерный параметр, определяющий величину при котором его орбита вокруг другого тела отклоняется от идеальной окружности. Значение 0 – круговая орбита, значения от 0 до 1 образуют эллиптическую орбиту, 1 – параболическая орбита выхода, а больше 1 – гипербола. Термин получил свое название от параметров конических участков, поскольку каждая орбита Кеплера является коническим участком. Обычно он используется для изолированной задачи двух тел, но существуют расширения для объектов, следующих по орбите розетки Клемперера через галактику.
Содержание
- 1 Определение
- 2 Этимология
- 3 Расчет
- 4 Примеры
- 5 Средний эксцентриситет
- 6 Климатическое воздействие
- 7 Экзопланеты
- 8 См. Также
- 9 Сноски
- 10 Ссылки
- 11 Дополнительная литература
- 12 Внешние ссылки
Определение


В задаче двух тел с силой обратного квадрата каждая орбита является орбитой Кеплера. Эксцентриситет этой орбиты Кеплера является неотрицательным числом, определяющим ее форму.
Эксцентриситет может принимать следующие значения:
- круговая орбита : e = 0
- эллиптическая орбита : 0 < e < 1 (see эллипс )
- параболическая траектория : e = 1 (см. парабола )
- гиперболическая траектория : e>1 (см. гипербола )
Эксцентриситет e определяется как
- e = 1 + 2 EL 2 m красный α 2 { displaystyle e = { sqrt {1 + { frac {2EL ^ {2}} {m _ { text {red}} alpha ^ {2}}}}}}
где E – полная орбитальная энергия, L – угловой момент, м красный – это приведенная масса, а α коэффициент закона обратных квадратов центральная сила, например гравитация или электростатика. в классической физике :
- F = α r 2 { displaystyle F = { frac { alpha} {r ^ {2}}}}
- (α отрицательно для привлекательного fo rce, положительный на отталкивающий; см. также задачу Кеплера )
или в случае силы тяжести:
- e = 1 + 2 ε h 2 μ 2 { displaystyle e = { sqrt {1 + { frac {2 varepsilon] h ^ {2}} { mu ^ {2}}}}}}
где ε – удельная орбитальная энергия (полная энергия, деленная на приведенную массу), μ – стандарт гравитационный параметр, основанный на общей массе, и h удельный относительный угловой момент (угловой момент, деленный на приведенную массу).
Для значений e от 0 до 1 форма орбиты представляет собой все более вытянутый (или более плоский) эллипс; для значений e от 1 до бесконечности орбита представляет собой ветвь гиперболы, совершающей полный оборот 2 arccsc e, уменьшаясь от 180 до 0 градусов. Предельный случай между эллипсом и гиперболой, когда е равно 1, – это парабола.
Радиальные траектории классифицируются как эллиптические, параболические или гиперболические в зависимости от энергии орбиты, а не эксцентриситета. Радиальные орбиты имеют нулевой угловой момент и, следовательно, эксцентриситет равен единице. Сохранение постоянной энергии и уменьшение углового момента, эллиптическая, параболическая и гиперболическая орбиты стремятся к соответствующему типу радиальной траектории, в то время как e стремится к 1 (или в параболическом случае остается 1).
Для силы отталкивания применима только гиперболическая траектория, включая радиальный вариант.
Для эллиптических орбит простое доказательство показывает, что arcsin (e { displaystyle e}
Этимология
Слово «эксцентриситет» происходит от средневековой латыни эксцентрик, происходящего от греческого ἔκκεντρος ekkentros «из центра», от ἐκ – эк-, «вне» + κέντρον кентрон «центр». Слово «эксцентричный» впервые появилось в английском языке в 1551 году с определением «… круг, в котором земля, солнце и т. Д. Отклоняются от своего центра». Пятью годами позже, в 1556 году, появилась форма прилагательного слова.
Расчет
эксцентриситет орбиты может быть вычислен из векторов орбитального состояния как величина вектора эксцентриситета :
- e = | е | { displaystyle e = left | mathbf {e} right |}
где:
- e- это вектор эксцентриситета.
Для эллиптических орбит он также может быть вычислен из периапсис и апоапсис, так как r p = a (1 – e) и r a = a (1 + e), где a – большая полуось.
- e = ra – rpra + rp = 1-2 rarp + 1 { displaystyle { begin {align} e = {{r _ { text {a}} – r _ { текст {p}}} over {r _ { text {a}} + r _ { text {p}}}} \ = 1 – { frac {2} {{ frac {r _ { text { a}}} {r _ { text {p}}}} + 1}} end {align}}}
где:
- ra- радиус в апоапсисе (т. е. самый дальний расстояние от орбиты до центра масс системы, который является фокусом эллипса).
- rp- радиус в периапсисе ( самое близкое расстояние).
Эксцентриситет эллиптической орбиты также можно использовать для получения отношения перицентра к апоапсису :
- rpra = 1 – e 1 + e { displaystyle {{r _ { text {p}}} over {r _ { text {a}}}} = {{1-e} over {1 + e}}}
Для Земли, орби Тальный эксцентриситет ≈ 0,0167, апоапсис, – афелий, а периапсис, – перигелий относительно Солнца.
Для годовой орбитальной траектории Земли соотношение r a/rp= наибольший_радиус / наименьший_радиус ≈ 1,034 относительно центральной точки пути.
Примеры
| Объект | эксцентриситет |
|---|---|
| Тритон | 0,00002 |
| Венера | 0,0068 |
| Нептун | 0,0086 |
| Земля | 0,0167 |
| Титан | 0,0288 |
| Уран | 0,0472 |
| Юпитер | 0,0484 |
| Сатурн | 0,0541 |
| Луна | 0,0549 |
| 1 Церера | 0,0758 |
| 4 Веста | 0,0887 |
| Марс | 0,0934 |
| 10 Гигия | 0,1146 |
| Макемаке | 0,1559 |
| Хаумеа | 0,1887 |
| Меркурий | 0,2056 |
| 2 Паллас | 0,2313 |
| Плутон | 0,2488 |
| 3 Юнона | 0,2555 |
| 324 Бамберга | 0,3400 |
| Эрис | 0,4407 |
| Нереида | 0,7507 |
| Седна | 0,8549 |
| Комета Галлея | 0,9671 |
| Комета Хейла-Боппа | 0,9951 |
| Комета Икея-Секи | 0,9999 |
| C / 1980 E1 | 1,057 |
| ʻOumuamua | 1,20 |
| C / 2019 Q4 (Борисов) | 3,5 |
Эксцентриситет Земли. орбита в настоящее время составляет около 0,0167; орбита Земли почти круглая. Венера и Нептун имеют еще меньшие эксцентриситеты. За сотни тысяч лет эксцентриситет земной орбиты изменяется от почти 0,0034 до почти 0,058 в результате гравитационного притяжения планет (см. график ).
В таблице перечислены значения для всех планет и карликовых планет, и избранные астероиды, кометы и луны. Меркурий имеет наибольший эксцентриситет орбиты среди всех планет в Солнечной системе (e = 0,2056). Такой эксцентриситет достаточно, чтобы Меркурий получил вдвое больше сильное солнечное излучение в перигелии по сравнению с афелием. Перед тем, как он был понижен в статусе планеты в 2006 году, Плутон считался планетой с наиболее эксцентричной орбитой (e = 0,248). Other Trans – Нептуновые объекты имеют значительный эксцентриситет, в частности карликовая планета Эрида (0,44). Еще дальше, Седна, имеет чрезвычайно высокий эксцентриситет 0,855 из-за ее предполагаемого афелия 937 а.е. и перигелия около 76 а.е.
Большинство астероидов Солнечной системы имеют орбитальный центричности от 0 до 0,35 со средним значением 0,17. Их сравнительно высокие эксцентриситета, вероятно, связаны с влиянием Юпитера и прошлыми столкновениями.
Значение Луны составляет 0,0549, это самый эксцентричный из больших спутников Солнечной системы. Четыре галилеевых спутника имеют эксцентриситет <0,01. Самый большой спутник Нептуна Тритон имеет эксцентриситет 1,6 × 10 (0,000016), наименьший эксцентриситет из всех известных лун в Солнечной системе; его орбита настолько близка к идеальному кругу, насколько это возможно в настоящее время. Однако более мелкие луны, особенно неправильные луны, могут иметь значительный эксцентриситет, например, третья по величине луна Нептуна Нереида (0,75).
Кометы имеют очень разные значения эксцентриситета. Периодические кометы имеют эксцентриситет в основном от 0,2 до 0,7, но некоторые из них имеют сильно эксцентричные эллиптические орбиты с эксцентриситетом чуть меньше 1, например, комета Галлея имеет значение 0,967. Непериодические кометы следуют по почти параболическим орбитам и поэтому имеют эксцентриситет даже ближе к 1. Примеры включают комету Хейла – Боппа со значением 0,995 и комету C / 2006 P1 (Макнот) со значением 1,000019. Поскольку значение Хейла-Боппа меньше 1, ее орбита эллиптическая, и она вернется. Комета МакНота имеет гиперболическую орбиту, пока находится под влиянием планет, но все еще привязана к Солнце с периодом обращения около 10 лет. По состоянию на 2010 Эпоху, комета C / 1980 E1 имеет самый большой эксцентриситет из всех известных гиперболических комет с эксцентриситетом 1,057 и покинет Солнечную систему в конце концов.
ʻOumuamua – первый межзвездный объект, обнаруженный проходящим через Солнечную систему. Его орбитальный эксцентриситет 1,20 указывает на то, что Оумуамуа никогда не был гравитационно привязан к нашему Солнцу. Он был обнаружен в 0,2 а.е. (30 000 000 км; 19 000 000 миль) от Земли и имеет диаметр примерно 200 метров. Он имеет межзвездную скорость (скорость на бесконечности) 26,33 км / с (58 900 миль в час).
Средний эксцентриситет
Средний эксцентриситет объекта – это средний эксцентриситет в результате возмущений за заданный период времени. В настоящее время Нептун имеет мгновенный (текущая эпоха ) эксцентриситет 0,0113, но с 1800 по 2050 год имеет средний эксцентриситет 0,00859.
Климатический эффект
Орбитальная механика требует, чтобы Продолжительность сезонов пропорциональна площади орбиты Земли, проходящей между солнцестоянием и равноденствием, поэтому, когда эксцентриситет орбиты является экстремальным, сезоны, которые происходят на обратной стороне орбита (афелий ) может быть существенно более продолжительной. Сегодня осень и зима в северном полушарии происходят при самом близком приближении (перигелий ), когда Земля движется с максимальной скоростью, тогда как в южном полушарии происходит противоположное. В результате в северном полушарии осень и зима немного короче, чем весна и лето, но в глобальном плане это уравновешивается тем, что они длиннее ниже экватора. В 2006 году в северном полушарии лето было на 4,66 дня длиннее зимы, а весна была на 2,9 дня дольше, чем осень из-за циклов Миланковича.
Апсидальная прецессия также медленно меняет место на орбите Земли, где происходят солнцестояния. и случаются равноденствия. Обратите внимание, что это медленное изменение орбиты Земли, а не оси вращения, которое называется осевой прецессией (см. Прецессия § Астрономия ). В течение следующих 10 000 лет зимы в северном полушарии будут постепенно удлиняться, а лето – короче. Однако любой охлаждающий эффект в одном полушарии уравновешивается потеплением в другом, и любому общему изменению будет противодействовать тот факт, что эксцентриситет земной орбиты будет почти вдвое меньше. Это уменьшит средний радиус орбиты и повысит температуру в обоих полушариях ближе к среднему межледниковому пику.
Экзопланеты
Из многих обнаруженных экзопланет большинство из них имеют более высокий эксцентриситет орбиты, чем планеты в нашей планетной системе. Обнаруженные экзопланеты с низким эксцентриситетом орбиты (почти круговые орбиты) находятся очень близко к своей звезде и приливно привязаны к звезде. Все восемь планет Солнечной системы имеют почти круглые орбиты. Обнаруженные экзопланеты показывают, что Солнечная система с ее необычно низким эксцентриситетом является редкой и уникальной. Одна из теорий объясняет этот низкий эксцентриситет большим количеством планет в Солнечной системе; другой предполагает, что он возник из-за уникальных поясов астероидов. Было найдено несколько других многопланетных систем, но ни одна из них не похожа на Солнечную систему. В Солнечной системе есть уникальные планетезимальные системы, которые привели планеты к почти круглым орбитам. Солнечные планетезимальные системы включают пояс астероидов, семейство Хильда, пояс Койпера, облако холмов и облако Оорта. Обнаруженные системы экзопланет либо не имеют планетезимальных систем, либо имеют одну очень большую. Низкая эксцентриситет нужна для обитаемости, особенно для продвинутой жизни. В планетных системах с высокой множественностью гораздо больше шансов иметь обитаемые экзопланеты. Гипотеза большого угла Солнечной системы также помогает понять ее почти круговые орбиты и другие уникальные особенности.
См. Также
- Уравнение времени
Сноски
Ссылки
Дополнительная литература
- Prussing, John E.; Конвей, Брюс А. (1993). Орбитальная механика. Нью-Йорк: Издательство Оксфордского университета. ISBN 0-19-507834-9 .
Внешние ссылки
- Мир физики: эксцентриситет
- Страница NOAA по данным климатического воздействия включает (расчетные) данные из Бергер (1978), Бергер и Лутр (1991). Ласкар и др. (2004) об изменениях орбиты Земли, включает эксцентриситет за последние 50 миллионов лет и на ближайшие 20 миллионов лет.
- Моделирование орбиты, проведенное Варади, Гилом и Руннегаром (2003), дает ряды для орбитальной орбиты Земли. эксцентриситет и наклонение орбиты.
- Моделирование Второго закона Кеплера
From Wikipedia, the free encyclopedia
An elliptic, parabolic, and hyperbolic Kepler orbit:
elliptic (eccentricity = 0.7)
parabolic (eccentricity = 1)
hyperbolic orbit (eccentricity = 1.3)
Elliptic orbit by eccentricity
0.0 ·
0.2 ·
0.4 ·
0.6 ·
0.8
In astrodynamics, the orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values between 0 and 1 form an elliptic orbit, 1 is a parabolic escape orbit (or capture orbit), and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections, as every Kepler orbit is a conic section. It is normally used for the isolated two-body problem, but extensions exist for objects following a rosette orbit through the Galaxy.
Definition[edit]
In a two-body problem with inverse-square-law force, every orbit is a Kepler orbit. The eccentricity of this Kepler orbit is a non-negative number that defines its shape.
The eccentricity may take the following values:
- circular orbit: e = 0
- elliptic orbit: 0 < e < 1
- parabolic trajectory: e = 1
- hyperbolic trajectory: e > 1
The eccentricity e is given by[1]
where E is the total orbital energy, L is the angular momentum, mred is the reduced mass, and 
(
or in the case of a gravitational force:[2]: 24
where ε is the specific orbital energy (total energy divided by the reduced mass), μ the standard gravitational parameter based on the total mass, and h the specific relative angular momentum (angular momentum divided by the reduced mass).[2]: 12–17
For values of e from 0 to 1 the orbit’s shape is an increasingly elongated (or flatter) ellipse; for values of e from 1 to infinity the orbit is a hyperbola branch making a total turn of 2 arccsc(e), decreasing from 180 to 0 degrees. Here, the total turn is analogous to turning number, but for open curves (an angle covered by velocity vector). The limit case between an ellipse and a hyperbola, when e equals 1, is parabola.
Radial trajectories are classified as elliptic, parabolic, or hyperbolic based on the energy of the orbit, not the eccentricity. Radial orbits have zero angular momentum and hence eccentricity equal to one. Keeping the energy constant and reducing the angular momentum, elliptic, parabolic, and hyperbolic orbits each tend to the corresponding type of radial trajectory while e tends to 1 (or in the parabolic case, remains 1).
For a repulsive force only the hyperbolic trajectory, including the radial version, is applicable.
For elliptical orbits, a simple proof shows that 
Etymology[edit]
The word “eccentricity” comes from Medieval Latin eccentricus, derived from Greek ἔκκεντρος ekkentros “out of the center”, from ἐκ- ek-, “out of” + κέντρον kentron “center”. “Eccentric” first appeared in English in 1551, with the definition “…a circle in which the earth, sun. etc. deviates from its center”.[citation needed] In 1556, five years later, an adjectival form of the word had developed.
Calculation[edit]
The eccentricity of an orbit can be calculated from the orbital state vectors as the magnitude of the eccentricity vector:
where:
- e is the eccentricity vector (“Hamilton’s vector”).[2]: 25, 62–63
For elliptical orbits it can also be calculated from the periapsis and apoapsis since 

where:
- ra is the radius at apoapsis (also “apofocus”, “aphelion”, “apogee”), i.e., the farthest distance of the orbit to the center of mass of the system, which is a focus of the ellipse.
- rp is the radius at periapsis (or “perifocus” etc.), the closest distance.
The eccentricity of an elliptical orbit can also be used to obtain the ratio of the apoapsis radius to the periapsis radius:
For Earth, orbital eccentricity e ≈ 0.01671, apoapsis is aphelion and periapsis is perihelion, relative to the Sun.
For Earth’s annual orbit path, the ratio of longest radius (ra) / shortest radius (rp) is 
Examples[edit]
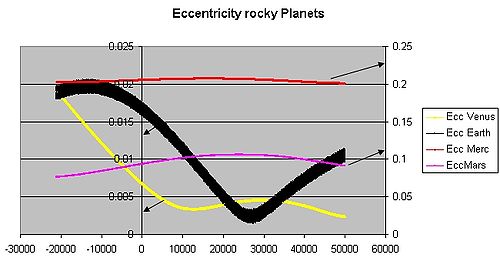
Plot of the changing orbital eccentricity of Mercury, Venus, Earth, and Mars over the next 50000 years. The arrows indicate the different scales used, as the eccentricities of Mercury and Mars are much greater than those of Venus and Earth. The 0 point on this plot is the year 2007.
| Object | eccentricity |
|---|---|
| Triton | 0.00002 |
| Venus | 0.0068 |
| Neptune | 0.0086 |
| Earth | 0.0167 |
| Titan | 0.0288 |
| Uranus | 0.0472 |
| Jupiter | 0.0484 |
| Saturn | 0.0541 |
| Moon | 0.0549 |
| 1 Ceres | 0.0758 |
| 4 Vesta | 0.0887 |
| Mars | 0.0934 |
| 10 Hygiea | 0.1146 |
| Makemake | 0.1559 |
| Haumea | 0.1887 |
| Mercury | 0.2056 |
| 2 Pallas | 0.2313 |
| Pluto | 0.2488 |
| 3 Juno | 0.2555 |
| 324 Bamberga | 0.3400 |
| Eris | 0.4407 |
| Nereid | 0.7507 |
| Sedna | 0.8549 |
| Halley’s Comet | 0.9671 |
| Comet Hale-Bopp | 0.9951 |
| Comet Ikeya-Seki | 0.9999 |
| C/1980 E1 | 1.057 |
| ʻOumuamua | 1.20[a] |
| C/2019 Q4 (Borisov) | 3.5[b] |
The eccentricity of Earth’s orbit is currently about 0.0167; its orbit is nearly circular. Venus and Neptune have even lower eccentricities. Over hundreds of thousands of years, the eccentricity of the Earth’s orbit varies from nearly 0.0034 to almost 0.058 as a result of gravitational attractions among the planets.[3]
The table lists the values for all planets and dwarf planets, and selected asteroids, comets, and moons. Mercury has the greatest orbital eccentricity of any planet in the Solar System (e = 0.2056). Such eccentricity is sufficient for Mercury to receive twice as much solar irradiation at perihelion compared to aphelion. Before its demotion from planet status in 2006, Pluto was considered to be the planet with the most eccentric orbit (e = 0.248). Other Trans-Neptunian objects have significant eccentricity, notably the dwarf planet Eris (0.44). Even further out, Sedna, has an extremely-high eccentricity of 0.855 due to its estimated aphelion of 937 AU and perihelion of about 76 AU.
Most of the Solar System’s asteroids have orbital eccentricities between 0 and 0.35 with an average value of 0.17.[4] Their comparatively high eccentricities are probably due to the influence of Jupiter and to past collisions.
The Moon’s value is 0.0549, the most eccentric of the large moons of the Solar System. The four Galilean moons have an eccentricity of less than 0.01. Neptune’s largest moon Triton has an eccentricity of 1.6×10−5 (0.000016),[5] the smallest eccentricity of any known moon in the Solar System;[citation needed] its orbit is as close to a perfect circle as can be currently[when?] measured. However, smaller moons, particularly irregular moons, can have significant eccentricity, such as Neptune’s third largest moon Nereid (0.75).
Comets have very different values of eccentricity. Periodic comets have eccentricities mostly between 0.2 and 0.7,[6] but some of them have highly eccentric elliptical orbits with eccentricities just below 1; for example, Halley’s Comet has a value of 0.967. Non-periodic comets follow near-parabolic orbits and thus have eccentricities even closer to 1. Examples include Comet Hale–Bopp with a value of 0.995[7] and comet C/2006 P1 (McNaught) with a value of 1.000019.[8] As Hale–Bopp’s value is less than 1, its orbit is elliptical and it will return.[7] Comet McNaught has a hyperbolic orbit while within the influence of the planets,[8] but is still bound to the Sun with an orbital period of about 105 years.[9] Comet C/1980 E1 has the largest eccentricity of any known hyperbolic comet of solar origin with an eccentricity of 1.057,[10] and will eventually leave the Solar System.
ʻOumuamua is the first interstellar object found passing through the Solar System. Its orbital eccentricity of 1.20 indicates that ʻOumuamua has never been gravitationally bound to the Sun. It was discovered 0.2 AU (30000000 km; 19000000 mi) from Earth and is roughly 200 meters in diameter. It has an interstellar speed (velocity at infinity) of 26.33 km/s (58900 mph).
Mean eccentricity[edit]
The mean eccentricity of an object is the average eccentricity as a result of perturbations over a given time period. Neptune currently has an instant (current epoch) eccentricity of 0.0113,[11] but from 1800 to 2050 has a mean eccentricity of 0.00859.[12]
Climatic effect[edit]
Orbital mechanics require that the duration of the seasons be proportional to the area of Earth’s orbit swept between the solstices and equinoxes, so when the orbital eccentricity is extreme, the seasons that occur on the far side of the orbit (aphelion) can be substantially longer in duration. Northern hemisphere autumn and winter occur at closest approach (perihelion), when Earth is moving at its maximum velocity—while the opposite occurs in the southern hemisphere. As a result, in the northern hemisphere, autumn and winter are slightly shorter than spring and summer—but in global terms this is balanced with them being longer below the equator. In 2006, the northern hemisphere summer was 4.66 days longer than winter, and spring was 2.9 days longer than autumn due to the Milankovitch cycles.[13][14]
Apsidal precession also slowly changes the place in Earth’s orbit where the solstices and equinoxes occur. This is a slow change in the orbit of Earth, not the axis of rotation, which is referred to as axial precession. Over the next 10000 years, the northern hemisphere winters will become gradually longer and summers will become shorter. However, any cooling effect in one hemisphere is balanced by warming in the other, and any overall change will be counteracted by the fact that the eccentricity of Earth’s orbit will be almost halved.[15] This will reduce the mean orbital radius and raise temperatures in both hemispheres closer to the mid-interglacial peak.
Exoplanets[edit]
Of the many exoplanets discovered, most have a higher orbital eccentricity than planets in the Solar System. Exoplanets found with low orbital eccentricity (near-circular orbits) are very close to their star and are tidally-locked to the star. All eight planets in the Solar System have near-circular orbits. The exoplanets discovered show that the Solar System, with its unusually-low eccentricity, is rare and unique.[16] One theory attributes this low eccentricity to the high number of planets in the Solar System; another suggests it arose because of its unique asteroid belts. A few other multiplanetary systems have been found, but none resemble the Solar System. The Solar System has unique planetesimal systems, which led the planets to have near-circular orbits. Solar planetesimal systems include the asteroid belt, Hilda family, Kuiper belt, Hills cloud, and the Oort cloud. The exoplanet systems discovered have either no planetesimal systems or one very large one. Low eccentricity is needed for habitability, especially advanced life.[17] High multiplicity planet systems are much more likely to have habitable exoplanets.[18][19] The grand tack hypothesis of the Solar System also helps understand its near-circular orbits and other unique features.[20][21][22][23][24][25][26][27]
See also[edit]
- Equation of time
Footnotes[edit]
- ^ ʻOumuamua was never bound to the Sun, so its orbit is hyperbolic: e ≈ 1.20 > 1 .
- ^ C/2019 Q4 (Borisov) was never bound to the Sun, so its orbit is hyperbolic: e ≈ 3.5 >> 1 .
References[edit]
- ^ Abraham, Ralph (2008). Foundations of mechanics. Jerrold E. Marsden (2nd ed.). Providence, R.I.: AMS Chelsea Pub./American Mathematical Society. ISBN 978-0-8218-4438-0. OCLC 191847156.
- ^ a b c d Bate, Roger R.; Mueller, Donald D.; White, Jerry E.; Saylor, William W. (2020). Fundamentals of Astrodynamics. Courier Dover. ISBN 978-0-486-49704-4. Retrieved 4 March 2022.
- ^ A. Berger & M.F. Loutre (1991). “Graph of the eccentricity of the Earth’s orbit”. Illinois State Museum (Insolation values for the climate of the last 10 million years). Archived from the original on 6 January 2018.
- ^ Asteroids Archived 4 March 2007 at the Wayback Machine
- ^ David R. Williams (22 January 2008). “Neptunian Satellite Fact Sheet”. NASA.
- ^
Lewis, John (2 December 2012). Physics and Chemistry of the Solar System. Academic Press. ISBN 9780323145848. - ^ a b “JPL Small-Body Database Browser: C/1995 O1 (Hale-Bopp)” (2007-10-22 last obs). Retrieved 5 December 2008.
- ^ a b “JPL Small-Body Database Browser: C/2006 P1 (McNaught)” (2007-07-11 last obs). Retrieved 17 December 2009.
- ^ “Comet C/2006 P1 (McNaught) – facts and figures”. Perth Observatory in Australia. 22 January 2007. Archived from the original on 18 February 2011.
- ^ “JPL Small-Body Database Browser: C/1980 E1 (Bowell)” (1986-12-02 last obs). Retrieved 22 March 2010.
- ^ Williams, David R. (29 November 2007). “Neptune Fact Sheet”. NASA.
- ^ “Keplerian elements for 1800 A.D. to 2050 A.D.” JPL Solar System Dynamics. Retrieved 17 December 2009.
- ^ Data from United States Naval Observatory Archived 13 October 2007 at the Wayback Machine
- ^ Berger A.; Loutre M.F.; Mélice J.L. (2006). “Equatorial insolation: from precession harmonics to eccentricity frequencies” (PDF). Clim. Past Discuss. 2 (4): 519–533. doi:10.5194/cpd-2-519-2006.
- ^ “Long Term Climate”. ircamera.as.arizona.edu.
- ^ “ECCENTRICITY”. exoplanets.org.
- ^ Ward, Peter; Brownlee, Donald (2000). Rare Earth: Why Complex Life is Uncommon in the Universe. Springer. pp. 122–123. ISBN 0-387-98701-0.
- ^ Limbach, MA; Turner, EL (2015). “Exoplanet orbital eccentricity: multiplicity relation and the Solar System”. Proc Natl Acad Sci U S A. 112 (1): 20–4. arXiv:1404.2552. Bibcode:2015PNAS..112…20L. doi:10.1073/pnas.1406545111. PMC 4291657. PMID 25512527.
- ^ Youdin, Andrew N.; Rieke, George H. (15 December 2015). “Planetesimals in Debris Disks”. arXiv:1512.04996.
- ^ Zubritsky, Elizabeth. “Jupiter’s Youthful Travels Redefined Solar System”. NASA. Retrieved 4 November 2015.
- ^ Sanders, Ray (23 August 2011). “How Did Jupiter Shape Our Solar System?”. Universe Today. Retrieved 4 November 2015.
- ^ Choi, Charles Q. (23 March 2015). “Jupiter’s ‘Smashing’ Migration May Explain Our Oddball Solar System”. Space.com. Retrieved 4 November 2015.
- ^ Davidsson, Dr. Björn J. R. “Mysteries of the asteroid belt”. The History of the Solar System. Retrieved 7 November 2015.
- ^ Raymond, Sean (2 August 2013). “The Grand Tack”. PlanetPlanet. Retrieved 7 November 2015.
- ^ O’Brien, David P.; Walsh, Kevin J.; Morbidelli, Alessandro; Raymond, Sean N.; Mandell, Avi M. (2014). “Water delivery and giant impacts in the ‘Grand Tack’ scenario”. Icarus. 239: 74–84. arXiv:1407.3290. Bibcode:2014Icar..239…74O. doi:10.1016/j.icarus.2014.05.009. S2CID 51737711.
- ^ Loeb, Abraham; Batista, Rafael; Sloan, David (August 2016). “Relative Likelihood for Life as a Function of Cosmic Time”. Journal of Cosmology and Astroparticle Physics. 2016 (8): 040. arXiv:1606.08448. Bibcode:2016JCAP…08..040L. doi:10.1088/1475-7516/2016/08/040. S2CID 118489638.
- ^ “Is Earthly Life Premature from a Cosmic Perspective?”. Harvard-Smithsonian Center for Astrophysics. 1 August 2016.
Further reading[edit]
- Prussing, John E.; Conway, Bruce A. (1993). Orbital Mechanics. New York: Oxford University Press. ISBN 0-19-507834-9.
External links[edit]
- World of Physics: Eccentricity
- The NOAA page on Climate Forcing Data includes (calculated) data from Berger (1978), Berger and Loutre (1991)[permanent dead link]. Laskar et al. (2004) on Earth orbital variations, Includes eccentricity over the last 50 million years and for the coming 20 million years.
- The orbital simulations by Varadi, Ghil and Runnegar (2003) provides series for Earth orbital eccentricity and orbital inclination.
- Kepler’s Second law’s simulation
Планеты солнечной системы живут своей собственной жизнью. Мы привыкли рассматривать этот процесс через призму земных циклов, однако в таком случае от нас ускользает самое главное и интересное. Попробуем «переместиться» на Меркурий и взглянуть на локальную действительность с местной точки зрения.
В данной статье я использую некоторые термины из области астрономии, объяснение которых можно найти тут.
Астрономические параметры Меркурия
Для того, чтобы понять особенности меркурианского времени, необходимо учесть ряд астрономических фактов (см. схему 1).
Длина орбиты Меркурия составляет 359,9674 млн км (земных).
В виду достаточно большого эксцентриситета, который равен 0,20564, орбита Меркурия сильно «вытянута»; в перигелии она подходит к Солнцу на 46 млн км, в афелии удаляется почти на 70 (69,82) млн км.
Если большую ось орбиты разделить на пять равных частей, на перигелий придется примерно две, а на афелий три таких части. Соответственно соотношение между ними будет близко к 3/2. Как мы увидим ниже, эта числовая константа, 3/2, весьма характерна для времени Меркурия.
Меркурий — самая быстрая планета солнечной системы. Её средняя орбитальная скорость – 47,36 км/с. Орбитальная скорость в перигелии составляет 58,35, в афелии —38,44 км/с. (См. схему 2). Этот момент важно учитывать для понимания локальных процессов, ниже будет понятно, почему.
У Меркурия практически отсутствует наклон оси вращения (всего порядка 0,33°), т.е. плоскость экватора у него почти совпадает с плоскостью орбиты. Поэтому движение видимого Солнца всегда проходит в плоскости экватора. К тому же, на Меркурии нет сезонных изменений климата, продолжительность суток на различных широтах в любое время года остаётся неизменной. Кроме того, тут нет и прецессии с нутацией, точка «весеннего равноденствия» имеет практически постоянную привязку к орбите.
Скорость осевого вращения Меркурия очень небольщая, на экваторе она чуть больше 3 км/с (10,892 км/ч). В СС медленней вокруг своей оси вращается только Венера. (Впрочем, нам пока не известны реальные скорости осевого вращения планет-гигантов, мы видим движение только внешних слоёв их газовых оболочек).
Наклонение плоскости орбиты Меркурия к плоскости орбиты Земли (к эклиптике) составляет 7°. Для ориентации в видимом небе планеты мы вполне можем использовать хорошо знакомые нам на Земле зодиакальные созвездия, движение которых проходит в плоскости местного экватора, как и движение Солнца.
Нужно заметить, что на Меркурии нет атмосферы. Днем лучи Солнца там не рассеиваются, как на Земле. По всей вероятности в светлое время суток тут можно будет наблюдать светило на фоне темного неба и других звёзд, хотя из-за яркости и размеров видимого Солнца (в среднем в 6 раз ярче и в 3 раза больше, чем на Земле) они будут восприниматься, конечно, заметно бледнее, чем ночью.
Цикличность Меркурия
О циклах Меркурия нам достоверно известно следующее:
Сидерический период обращения (длительность меркурианского года) — 87,969 земных суток. Период вращения (звёздные сутки или оборот вокруг своей оси на 360°) — 58,646 земных суток (1407,5 земных часа). Суточный цикл (”от рассвета до рассвета”, солнечные сутки) — 175,942 земных суток.
В качестве единиц измерения тут использованы земные солнечные сутки (ЗСС).
Для понимания локальной цикличности эти данные нам ничего не дают. Чтобы сориентироваться во времени Меркурия, нам необходимо провести несколько несложных вычислений:
87,969 / 175,942 = 0,4999886 ≈ 0,5
87,969 / 58,646 = 1,5
Итак, за один год на Меркурии проходит ровно 1,5 звёздных и 0,5 солнечных суток.
Поразительная математика, не правда ли?!
Это значит, что за два орбитальных витка вокруг Солнца Меркурий совершает три оборота вокруг своей оси на 360° (меркурианские звёздные сутки, МЗС) и всего один привычный для нас суточный цикл «день-ночь» (меркурианские солнечные сутки, МСС). При этом в течение всего первого года заданная точка на поверхности планеты («точка привязки») находится в зоне освещенности, весь второй год — на теневой стороне.
В момент прохождения планетой перигелия Солнце всегда находится в зените на одной и той же долготе, поэтому её называют «горячей долготой». В момент прохождения планетой перигелия горячая долгота попадает в плоскость сечения и видимое Солнце будет находиться над ровно по середине неба, а на следующем орбитальном витке эта же долгота будет находиться ровно на противоположной стороне планеты, т.е. тут будет «строго» полночь. (См. схему 3).
На фоне существенного изменения орбитальной скорости от афелия к перигелию, медленное осевое вращение приводит к интересному явлению: в определённый момент (в диапазоне ±21° от большой оси в районе перигелия) угловая скорость движения Меркурия по орбите становится больше (в перигелии она достигает значения 1,268) угловой скорости его осевого вращения (~1,24).
В следствие этого, видимое Солнце как бы «зависает» и остаётся в районе зенита достаточно продолжительное время. Фактически же оно совершает «обратное» движение, что хорошо заметно на долготе, отстоящей от «горячей» на 90°, где в момент прохождения перигелия наступает рассвет. Здесь краешек Солнца появляется над горизонтом, заходит обратно и затем снова восходит — уже на целый год.
Надо учитывать, что в среднем видимый размер Солнца на Меркурии почти в 3 раза больше, чем на Земле. В перигелии оно почти в 4 раза больше (~2º. т.е занимает примерно 1/90 часть небосвода), чем на нашей планете, а в афелии — в 2,5 (~1,3º). Поэтому в районе горячей долготы «попятное» («ретроградное») движение светила может быть визуально не слишком заметно из-за его огромных размеров на небосклоне.
Напоследок можно отметить ещё один любопытный факт. Орбита Меркурия очень медленно изменяет свое положение относительно звёзд. Такое изменение называется прецессией перигелия. Процесс этот предположительно совершает полный цикл относительно Солнца за 260 000 земных лет, что в меркурианских годах составляет 1 079 500, или почти 540 000 МСС. Соответственно, переход Солнца (восхода Солнца в заданной точке привязки) в следующий знак зодиака происходит примерно раз в 45 000 МСС или 90 000 меркурианских лет.
День и ночь на Меркурии
Схема (4) даёт общее представление о солнечных сутках Меркурия. Рассмотрим этот процесс чуть подробнее.
Предположим, что наша точка привязки находится на «горячей долготе». Тогда восход у нас произойдёт точно в момент прохождения афелия (точка G), и день (МерДень, первая половина солнечных суток от «восхода» до «заката»), который начнётся в этот момент, будет продолжаться целый год.
После «восхода» движение видимого Солнца будет постепенно замедляться, при этом видимый размер его на небе будет постоянно расти.
При подходе планеты к точке L центр Солнца достигнет зенита и перейдёт на западную половину неба, в точке L’ оно «развернётся» и, в момент прохождения перигелия (в точке A), снова окажется в зените, на этот раз во время «ретроградного» движения на восточную половину неба, где, «зависнув» ненадолго в точке А’, снова развернётся и вновь окажется в зените а районе точки B.
Затем этого оно будет неуклонно и постепенно ускоряясь двигаться к закату (при этом визуально уменьшаясь в размерах), пока полностью не скроется за горизонтом в момент следующего прохождения афелия (в точке G). Здесь наступает ночь (МерНочь), которая продлится весь следующий год.
Видимое движение звёзд по небу Меркурия происходит значительно быстрее, чем на Земле, однако, без видимой неравномерности, ибо зависит прежде всего от осевого вращения планеты, не от орбитального. Соответственно, ночью практически невозможно визуально определить изменение её орбитальной скорости.
За ночь мы успеем увидеть все созвездия неба «полтора» раза, т. е. через восток пройдут 18 зодиакальных созвездий. Так, если Солнце восходит, предположим, в Тельце (как в текущую эпоху), то и закат его случится в Тельце, поскольку за один свой день Меркурий сделает 1,5 оборота (540°) вокруг своей оси.
В момент «заката» (в G) на востоке появится Скорпион, который, «пройдя» через всё небо, скроется за горизонт как раз, когда на востоке снова появится Телец (примерно в точке K), но на этот раз «без Солнца». Затем Телец, пройдя через все небо, снова исчезнет на западе в момент повторного появления Скорпиона на востоке (около точки С), который, «пройдя» через все небо, исчезнет за горизонтом на западе в момент следующего восхода Солнца в Тельце (в точке G) и т;д.
В следующей статье все это рассмотрено подробнее:
Как устроено время на планете Меркурий
Также смотрите предыдущую статью, где описаны основные гелиоцентрические параметры орбит планет, которыми я пользуюсь в этой и других статьях:
Космические параметры, которые всем нужно правильно понимать
—
Тимофей Решетов
https://t.me/geliocentric













