Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ЭКСЦЕСС в Microsoft Excel.
Описание
Возвращает эксцесс множества данных. Эксцесс характеризует относительную остроконечность или сглаженность распределения по сравнению с нормальным распределением. Положительный эксцесс обозначает относительно остроконечное распределение. Отрицательный эксцесс обозначает относительно сглаженное распределение.
Синтаксис
ЭКСЦЕСС(число1;[число2];…)
Аргументы функции ЭКСЦЕСС описаны ниже.
-
Число1, число2,… Аргумент “число1” является обязательным, последующие числа необязательные. От 1 до 255 аргументов, для которых вычисляется эксцесс. Вместо аргументов, разделенных запятой, можно использовать один массив или ссылку на массив.
Замечания
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
-
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения пропускаются; однако ячейки, которые содержат нулевые значения, учитываются.
-
Аргументы, представляющие собой значения ошибок или текст, который не может быть преобразован в числа, приводят к возникновению ошибки.
-
Если имеется менее четырех точек данных или стандартное отклонение выборки равно нулю, то #DIV/0! значение ошибки #ЗНАЧ!.
-
Эксцесс определяется следующим образом:
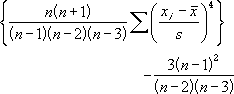
где s — стандартное отклонение выборки.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|
3 |
||
|
4 |
||
|
5 |
||
|
2 |
||
|
3 |
||
|
4 |
||
|
5 |
||
|
6 |
||
|
4 |
||
|
7 |
||
|
Формула |
Описание |
Результат |
|
=ЭКСЦЕСС(A2:A11) |
Эксцесс приведенного выше множества данных |
-0,151799637 |
Нужна дополнительная помощь?
Нужны дополнительные параметры?
Изучите преимущества подписки, просмотрите учебные курсы, узнайте, как защитить свое устройство и т. д.
В сообществах можно задавать вопросы и отвечать на них, отправлять отзывы и консультироваться с экспертами разных профилей.
Функция ЭКСЦЕСС предназначена для анализа значений диапазона данных и возвращает значение коэффициента эксцесса.
Примеры использования функции ЭКСЦЕСС в Excel
Эксцесс является мерой остроты пика в распределении случайных величин. Для любого распределения величин можно рассчитать значение средней величины. В данном контексте коэффициент эксцесса показывает, находятся ли большинство значений распределения в непосредственной близости к средней величине, либо же они распределены отдаленно от нее.
Для нормального распределения величин значение эксцесса равно 0 (нулю). Если значение эксцесса принадлежит к диапазону положительных чисел, анализируемое распределение величин является относительно остроконечным. В противном случае (отрицательный коэффициент) рассматриваемое распределение является относительно сглаженным.
Анализ соотношения цены и спроса по коэффициенту ЭКСЦЕСС в Excel
Пример 1. Проверить теорию о том, что с уменьшением цен на бензин объемы покупок увеличиваются. В таблице представлены сведения о цене и объемах потребления топлива для одной заправочной станции по дням.
Вид таблицы данных:
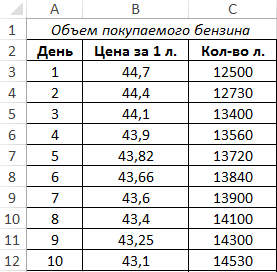
Для расчета эксцесса используем данные из столбца C. Вид формулы:
Результат вычислений:
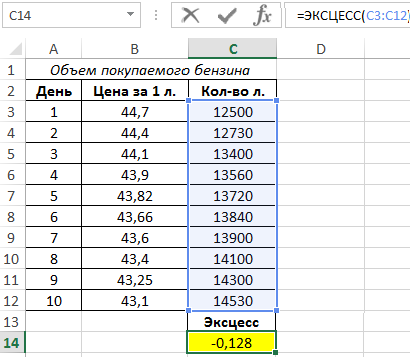
Небольшой отрицательный эксцесс свидетельствует о том, что фактический рост объемов покупок оказался ниже ожидаемого, меньше 14%.
Для наглядного примера выполним визуализацию исходных данных с помощью линейного графика:
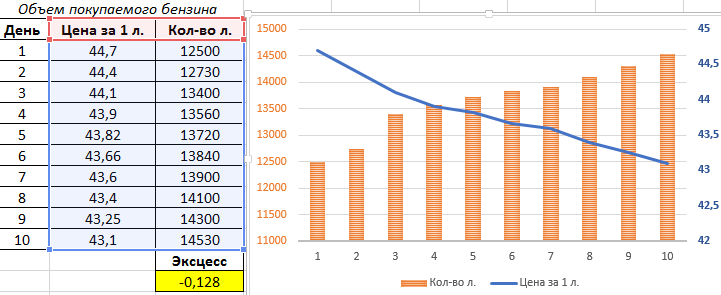
Сложность использования функции ЭКСЦЕСС заключается в правильной трактовке полученных значений. Для формулировки более достоверных выводов в отношении исследуемых данных рассчитывают другие статистические показатели.
Анализ распределения чисел и статистических выбросов в Excel
Пример 2. На основе данных об успеваемости студентов определить, есть ли в группе студенты, сильно отстающие от процесса обучения.
Исходная таблица данных:
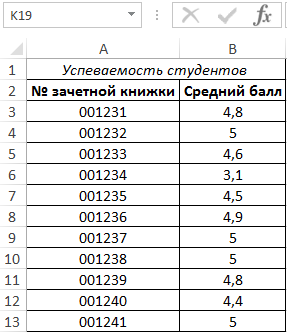
Для расчетов используем формулу:
- B3:B13 – диапазон исследуемых значений (средних баллов студентов).
В результате получаем следующее значение:
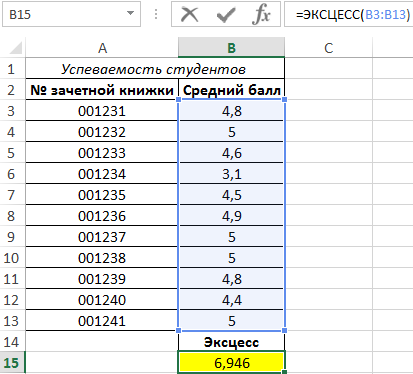
Положительный эксцесс свидетельствует о том, что линия на графике распределения более резкая, нежели у кривой нормального закона распределения, с такой же дисперсией:
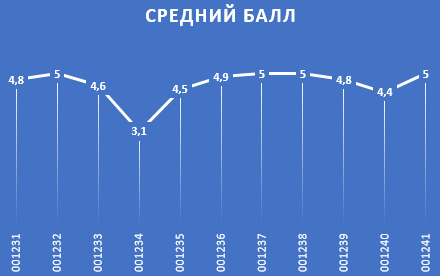
Положительный эксцесс свидетельствует о неравномерности распределения данных, а его довольно большая величина характеризует о имеющемся «скачке», то есть число студентов с низкой успеваемостью небольшое (в данном случае – только один студент).
Правила использования функции ЭКСЦЕСС в Excel
Функция ЭКСЦЕСС имеет следующий вариант синтаксической записи:
=ЭКСЦЕСС(число1;[число2];…)
Описание аргументов:
- число1 – обязательный для заполнения, принимает числовые значения и характеризует первое значение последовательности анализируемых значений.
- [число2];… – второй и последующие аргументы функции, необязательные для заполнения, принимающие числовые значения второго и последующих членов анализируемой последовательности.
Примечания:
- В качестве параметров функции могут быть указаны числовые значения, ссылки на ячейки с числами, массивы, содержащие числа имена.
- Если в списке аргументов имеются логические значения, функция ЭКСЦЕСС выполняет преобразования к числовым (ИСТИНА = 1, ЛОЖЬ = 0) и учитывает их в расчетах. Подобные преобразования выполняются над текстовыми представлениями чисел (например, в качестве параметра указан текст «22»).
- Функция не учитывает пустые ячейки, данные текстового и логического типов, если они содержатся в массиве или ссылке, переданных в качестве параметров этой функции.
- Если. В качестве аргумента был передан не преобразуемый в числовое значение текст или код ошибки, результатом выполнения функции будет являться соответствующий код ошибки.
- При анализе менее 4 точек данных или значение стандартного отклонения выборки равно 0 (нулю), функция вернет код ошибки #ЧИСЛО!
Функция ЭКСЦЕСС возвращает эксцесс множества данных.
Описание функции ЭКСЦЕСС
Возвращает эксцесс множества данных. Эксцесс характеризует относительную остроконечность или сглаженность распределения по сравнению с нормальным распределением. Положительный эксцесс обозначает относительно остроконечное распределение. Отрицательный эксцесс обозначает относительно сглаженное распределение.
Синтаксис
=ЭКСЦЕСС(число1; [число2];…)Аргументы
число1, число2,…
Аргумент «число1» является обязательным, последующие числа необязательные. От 1 до 255 аргументов, для которых вычисляется эксцесс. Вместо аргументов, разделенных запятой, можно использовать один массив или ссылку на массив.
Замечания
- Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
- Учитываются вводимые непосредственно в список аргументов логические значения и текстовые представления чисел.
- Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения игнорируются; ячейки, содержащие нулевые значения, учитываются.
- Аргументы, представляющие собой значения ошибок или текст, который не может быть преобразован в числа, приводят к возникновению ошибки.
- Если задано менее четырех точек данных или если стандартное отклонение выборки равно 0, то функция ЭКСЦЕСС возвращает значение ошибки #ДЕЛ/0!.
- Эксцесс определяется следующим образом:

где s — стандартное отклонение выборки.
Пример
Содержание
- Эксцесс эксель что это
- Функция Kurt — эксцесс в Excel:
- Функция Db — доб в Excel:
- Функция Ddb — ддоб в Excel:
- Как посчитать эксцесс в excel
- Функция ЭКСЦЕСС
- Описание
- Синтаксис
- Замечания
- Пример
- Как посчитать эксцесс в excel
- Описательная статистика в EXCEL
- Надстройка Пакет анализа
- Среднее выборки
- Медиана выборки
- Мода выборки
- Мода и среднее значение
- Дисперсия выборки
- Стандартное отклонение выборки
- Стандартная ошибка
- Асимметричность
- Эксцесс выборки
- Уровень надежности
Эксцесс эксель что это
По численным значениям асимметрии и эксцесса можно приближенно оценить нормальность распределения результатов испытаний. А и Е рассчитывают так:

В Excel А и Е можно рассчитать при помощи статистических функций СКОС (для А) и ЭКСЦЕСС (для Е).
Дисперсии А и Е рассчитывают так:

Если  , то результаты испытаний считают распределёнными нормально.
, то результаты испытаний считают распределёнными нормально.
Пример 14.1. Проверить гипотезу нормальности распределения результатов испытаний: 32,30 31,60 31,70 32,36 32,92 32,61 32,48 32,47 32,46 32,74 32,63 32,68 31,74 32,17 32,25 32,28 32,26 32,29 32,28 31,73.
Возможный вариант расчёта по примеру 14.1 показан на рис 14.1.

Рис.14.1. Вариант расчёта по примеру 14.1.
Вводим в лист MS Excel номера результатов (хотя бы до 1000 – для возможности пересчёта при других данных). Вводим результаты испытаний и сортируем их в вариационный ряд (хотя в данном случае это не обязательно). Рассчитываем объём испытаний n (в Excel функция СЧЁТ), асимметрию (функция СКОС), эксцесс (ЭКСЦЕСС), модуль асимметрии и эксцесса (с использованием функции ABS), дисперсию асимметрии и эксцесса, а также  . Далее выводим сообщение о соответствии или несоответствии распределения нормальному. Для этого используем функцию ЕСЛИ. В строку Логическое_выражение диалогового этой функции вводим неравенство
. Далее выводим сообщение о соответствии или несоответствии распределения нормальному. Для этого используем функцию ЕСЛИ. В строку Логическое_выражение диалогового этой функции вводим неравенство  . После этого в эту же строку вводим функцию И. В открывшемся окне в строку Логическое значение 1 вводим неравенство
. После этого в эту же строку вводим функцию И. В открывшемся окне в строку Логическое значение 1 вводим неравенство  . Затем устанавливаем курсор в строке формул на слово ЕСЛИ. В результате этого возвращаемся в окно функции ЕСЛИ. В этом окне в строке Значение_если_истина вводим «Распределение нормальное», а в строку Значение_если_ложь – «Распределение не нормальное». В результате формула будет выглядеть, как показано на рис. 14.1
. Затем устанавливаем курсор в строке формул на слово ЕСЛИ. В результате этого возвращаемся в окно функции ЕСЛИ. В этом окне в строке Значение_если_истина вводим «Распределение нормальное», а в строку Значение_если_ложь – «Распределение не нормальное». В результате формула будет выглядеть, как показано на рис. 14.1
Задание.
Выполнить расчёты по примеру 14.1.
        Далее     Содержание
Источник
Функция Kurt — эксцесс в Excel:
Возвращает эксцесс множества данных. Эксцесс характеризует относительную остроконечность или сглаженность распределения по сравнению с нормальным распределением. Положительный эксцесс обозначает относительно остроконечное распределение. Отрицательный эксцесс обозначает относительно сглаженное распределение.
Число1, число2, . — это от 1 до 30 аргументов, для которых вычисляется эксцесс. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.
Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа.
Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако, ячейки, которые содержат нулевые значения учитываются.
Если задано менее четырех точек данных или если стандартное отклонение выборки равняется нулю, то функция ЭКСЦЕСС возвращает значение ошибки #ДЕЛ/0!.
Функция Db — доб в Excel:
Возвращает амортизацию имущества на заданный период, используя метод постоянного учета амортизации.
Нач_стоимость — это начальная стоимость имущества.
Ост_стоимость — это стоимость в конце периода амортизации (иногда называется остаточной стоимостью имущества).
Время_эксплуатации — это количество периодов, за которые собственность амортизируется (иногда называется периодом амортизации).
Период — это период, для которого требуется вычислить амортизацию. Период должен быть измерен в тех же единицах, что и время_эксплуатации.
Месяц — это количество месяцев в первом году. Если аргумент месяц опущен, то предполагается, что он равен 12.
Метод постоянного учета амортизации вычисляет амортизацию, используя фиксированную процентную ставку. ДОБ использует следующие формулы для вычисления амортизации за период:
(нач_стоимость — суммарная амортизация за предшествующие периоды) * ставка
ставка = 1 — ((ост_стоимость / нач_стоимость) ^ (1 / время_эксплуатации)), округленное до трех десятичных знаков после запятой
Особым случаем является амортизация за первый и последний периоды. Для первого периода ДОБ использует такую формулу:
нач_стоимость * ставка * месяц / 12
Для последнего периода ДОБ использует такую формулу:
((нач_стоимость — суммарная амортизация за предшествующие периоды) * ставка * (12 — месяц)) / 12.
Функция Ddb — ддоб в Excel:
Возвращает значение амортизации имущества за данный период, используя метод двойного процента со снижающегося остатка или иной явно указанный метод.
Стоимость — это начальная стоимость имущества.
Остаточная_стоимость — это стоимость в конце периода амортизации (иногда называется остаточной стоимостью имущества).
Время_эксплуатации — это количество периодов, за которые собственность амортизируется (иногда называется периодом амортизации).
Период — это период, для которого требуется вычислить амортизацию. Период должен быть измерен в тех же единицах, что и время_эксплуатации.
Коэффициент — это норма снижения балансовой стоимости (амортизации). Если аргумент опущен, то он полагается равным 2 (метод удвоенного процента со снижающегося остатка)
Все пять аргументов должны быть положительными числами.
Метод двойного процента со снижающегося остатка вычисляет амортизацию, используя увеличенный коэффициент. Амортизация максимальна в первый период, в последующие периоды уменьшается. Функция ДДОБ использует следующую формулу для вычисления амортизации за период:
((стоимость — остаточная_стоимость) — суммарная амортизация за предшествующие периоды) * (коэффициент/время_эксплуатации)
Если нужно использовать другой метод вычисления амортизации, измените значение аргумента коэффициент.
Используйте функцию ПДОБ, если необходимо использовать прямую амортизацию в том случае, когда амортизация превышает вычисленную величину амортизации.
Источник
Как посчитать эксцесс в excel
Функция ЭКСЦЕСС
В этой статье описаны синтаксис формулы и использование функции ЭКСЦЕСС в Microsoft Excel.
Описание
Возвращает эксцесс множества данных. Эксцесс характеризует относительную остроконечность или сглаженность распределения по сравнению с нормальным распределением. Положительный эксцесс обозначает относительно остроконечное распределение. Отрицательный эксцесс обозначает относительно сглаженное распределение.
Синтаксис
Аргументы функции ЭКСЦЕСС описаны ниже.
Число1, число2. Аргумент «число1» является обязательным, последующие числа необязательные. От 1 до 255 аргументов, для которых вычисляется эксцесс. Вместо аргументов, разделенных запятой, можно использовать один массив или ссылку на массив.
Замечания
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения пропускаются; однако ячейки, которые содержат нулевые значения, учитываются.
Аргументы, представляющие собой значения ошибок или текст, который не может быть преобразован в числа, приводят к возникновению ошибки.
Если имеется менее четырех точек данных или стандартное отклонение выборки равно нулю, то #DIV/0! значение ошибки #ЗНАЧ!.
Эксцесс определяется следующим образом:
где s — стандартное отклонение выборки.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Как посчитать эксцесс в excel
По численным значениям асимметрии и эксцесса можно приближенно оценить нормальность распределения результатов испытаний. А и Е рассчитывают так:
В Excel А и Е можно рассчитать при помощи статистических функций СКОС (для А) и ЭКСЦЕСС (для Е).
Дисперсии А и Е рассчитывают так:
Если , то результаты испытаний считают распределёнными нормально.
Пример 14.1. Проверить гипотезу нормальности распределения результатов испытаний: 32,30 31,60 31,70 32,36 32,92 32,61 32,48 32,47 32,46 32,74 32,63 32,68 31,74 32,17 32,25 32,28 32,26 32,29 32,28 31,73.
Возможный вариант расчёта по примеру 14.1 показан на рис 14.1.
Рис.14.1. Вариант расчёта по примеру 14.1.
Вводим в лист MS Excel номера результатов (хотя бы до 1000 – для возможности пересчёта при других данных). Вводим результаты испытаний и сортируем их в вариационный ряд (хотя в данном случае это не обязательно). Рассчитываем объём испытаний n (в Excel функция СЧЁТ), асимметрию (функция СКОС), эксцесс (ЭКСЦЕСС), модуль асимметрии и эксцесса (с использованием функции ABS), дисперсию асимметрии и эксцесса, а также . Далее выводим сообщение о соответствии или несоответствии распределения нормальному. Для этого используем функцию ЕСЛИ. В строку Логическое_выражение диалогового этой функции вводим неравенство . После этого в эту же строку вводим функцию И. В открывшемся окне в строку Логическое значение 1 вводим неравенство . Затем устанавливаем курсор в строке формул на слово ЕСЛИ. В результате этого возвращаемся в окно функции ЕСЛИ. В этом окне в строке Значение_если_истина вводим «Распределение нормальное», а в строку Значение_если_ложь – «Распределение не нормальное». В результате формула будет выглядеть, как показано на рис. 14.1
Задание.
Выполнить расчёты по примеру 14.1.
        Далее     Содержание
Источник
Описательная статистика в EXCEL
history 17 ноября 2016 г.
Рассмотрим инструмент Описательная статистика, входящий в надстройку Пакет Анализа. Рассчитаем показатели выборки: среднее, медиана, мода, дисперсия, стандартное отклонение и др.
Задача описательной статистики (descriptive statistics) заключается в том, чтобы с использованием математических инструментов свести сотни значений выборки к нескольким итоговым показателям, которые дают представление о выборке .В качестве таких статистических показателей используются: среднее , медиана , мода , дисперсия, стандартное отклонение и др.
Опишем набор числовых данных с помощью определенных показателей. Для чего нужны эти показатели? Эти показатели позволят сделать определенные статистические выводы о распределении , из которого была взята выборка . Например, если у нас есть выборка значений толщины трубы, которая изготавливается на определенном оборудовании, то на основании анализа этой выборки мы сможем сделать, с некой определенной вероятностью, заключение о состоянии процесса изготовления.
Надстройка Пакет анализа
Для вычисления статистических показателей одномерных выборок , используем надстройку Пакет анализа . Затем, все показатели рассчитанные надстройкой, вычислим с помощью встроенных функций MS EXCEL.
СОВЕТ : Подробнее о других инструментах надстройки Пакет анализа и ее подключении – читайте в статье Надстройка Пакет анализа MS EXCEL .
Выборку разместим на листе Пример в файле примера в диапазоне А6:А55 (50 значений).
Примечание : Для удобства написания формул для диапазона А6:А55 создан Именованный диапазон Выборка.
В диалоговом окне Анализ данных выберите инструмент Описательная статистика .
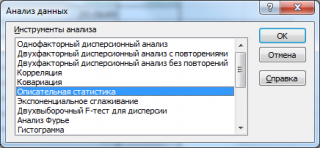
После нажатия кнопки ОК будет выведено другое диалоговое окно,
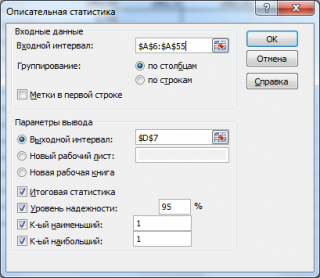
в котором нужно указать:
- входной интервал (Input Range) – это диапазон ячеек, в котором содержится массив данных. Если в указанный диапазон входит текстовый заголовок набора данных, то нужно поставить галочку в поле Метки в первой строке (Labelsinfirstrow). В этом случае заголовок будет выведен в Выходном интервале. Пустые ячейки будут проигнорированы, поэтому нулевые значения необходимо обязательно указывать в ячейках, а не оставлять их пустыми;
- выходной интервал (Output Range). Здесь укажите адрес верхней левой ячейки диапазона, в который будут выведены статистические показатели;
- Итоговая статистика (SummaryStatistics) . Поставьте галочку напротив этого поля – будут выведены основные показатели выборки: среднее, медиана, мода, стандартное отклонение и др.;
- Также можно поставить галочки напротив полей Уровень надежности (ConfidenceLevelforMean) , К-й наименьший (Kth Largest) и К-й наибольший (Kth Smallest).
В результате будут выведены следующие статистические показатели: 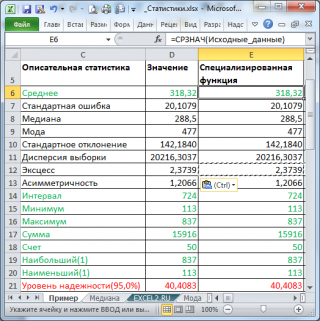
Все показатели выведены в виде значений, а не формул. Если массив данных изменился, то необходимо перезапустить расчет.
Если во входном интервале указать ссылку на несколько столбцов данных, то будет рассчитано соответствующее количество наборов показателей. Такой подход позволяет сравнить несколько наборов данных. При сравнении нескольких наборов данных используйте заголовки (включите их во Входной интервал и установите галочку в поле Метки в первой строке ). Если наборы данных разной длины, то это не проблема — пустые ячейки будут проигнорированы.
Зеленым цветом на картинке выше и в файле примера выделены показатели, которые не требуют особого пояснения. Для большинства из них имеется специализированная функция:
- Интервал (Range) — разница между максимальным и минимальным значениями;
- Минимум (Minimum) – минимальное значение в диапазоне ячеек, указанном во Входном интервале (см. статью про функцию МИН() );
- Максимум (Maximum)– максимальное значение (см. статью про функцию МАКС() );
- Сумма (Sum) – сумма всех значений (см. статью про функцию СУММ() );
- Счет (Count) – количество значений во Входном интервале (пустые ячейки игнорируются, см. статью про функцию СЧЁТ() );
- Наибольший (Kth Largest) – выводится К-й наибольший. Например, 1-й наибольший – это максимальное значение (см. статью про функцию НАИБОЛЬШИЙ() );
- Наименьший (Kth Smallest) – выводится К-й наименьший. Например, 1-й наименьший – это минимальное значение (см. статью про функцию НАИМЕНЬШИЙ() ).
Ниже даны подробные описания остальных показателей.
Среднее выборки
Среднее (mean, average) или выборочное среднее или среднее выборки (sample average) представляет собой арифметическое среднее всех значений массива. В MS EXCEL для вычисления среднего выборки используется функция СРЗНАЧ() . Выборочное среднее является «хорошей» (несмещенной и эффективной) оценкой математического ожидания случайной величины (подробнее см. статью Среднее и Математическое ожидание в MS EXCEL ).
Медиана (Median) – это число, которое является серединой множества чисел (в данном случае выборки): половина чисел множества больше, чем медиана , а половина чисел меньше, чем медиана . Для определения медианы необходимо сначала отсортировать множество чисел . Например, медианой для чисел 2, 3, 3, 4 , 5, 7, 10 будет 4.
Если множество содержит четное количество чисел, то вычисляется среднее для двух чисел, находящихся в середине множества. Например, медианой для чисел 2, 3, 3 , 5 , 7, 10 будет 4, т.к. (3+5)/2.
Если имеется длинный хвост распределения, то Медиана лучше, чем среднее значение , отражает «типичное» или «центральное» значение. Например, рассмотрим несправедливое распределение зарплат в компании, в которой руководство получает существенно больше, чем основная масса сотрудников.
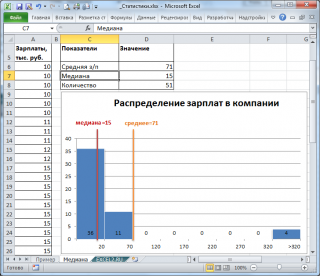 Очевидно, что средняя зарплата (71 тыс. руб.) не отражает тот факт, что 86% сотрудников получает не более 30 тыс. руб. (т.е. 86% сотрудников получает зарплату в более, чем в 2 раза меньше средней!). В то же время медиана (15 тыс. руб.) показывает, что как минимум у 50% сотрудников зарплата меньше или равна 15 тыс. руб.
Очевидно, что средняя зарплата (71 тыс. руб.) не отражает тот факт, что 86% сотрудников получает не более 30 тыс. руб. (т.е. 86% сотрудников получает зарплату в более, чем в 2 раза меньше средней!). В то же время медиана (15 тыс. руб.) показывает, что как минимум у 50% сотрудников зарплата меньше или равна 15 тыс. руб.
Для определения медианы в MS EXCEL существует одноименная функция МЕДИАНА() , английский вариант — MEDIAN().
Медиану также можно вычислить с помощью формул
Подробнее о медиане см. специальную статью Медиана в MS EXCEL .
СОВЕТ : Подробнее про квартили см. статью, про перцентили (процентили) см. статью.
Мода выборки
Мода (Mode) – это наиболее часто встречающееся (повторяющееся) значение в выборке . Например, в массиве (1; 1; 2 ; 2 ; 2 ; 3; 4; 5) число 2 встречается чаще всего – 3 раза. Значит, число 2 – это мода . Для вычисления моды используется функция МОДА() , английский вариант MODE().
Примечание : Если в массиве нет повторяющихся значений, то функция вернет значение ошибки #Н/Д. Это свойство использовано в статье Есть ли повторы в списке?
Начиная с MS EXCEL 2010 вместо функции МОДА() рекомендуется использовать функцию МОДА.ОДН() , которая является ее полным аналогом. Кроме того, в MS EXCEL 2010 появилась новая функция МОДА.НСК() , которая возвращает несколько наиболее часто повторяющихся значений (если количество их повторов совпадает). НСК – это сокращение от слова НеСКолько.
Например, в массиве (1; 1; 2 ; 2 ; 2 ; 3; 4 ; 4 ; 4 ; 5) числа 2 и 4 встречаются наиболее часто – по 3 раза. Значит, оба числа являются модами . Функции МОДА.ОДН() и МОДА() вернут значение 2, т.к. 2 встречается первым, среди наиболее повторяющихся значений (см. файл примера , лист Мода ).
Чтобы исправить эту несправедливость и была введена функция МОДА.НСК() , которая выводит все моды . Для этого ее нужно ввести как формулу массива . 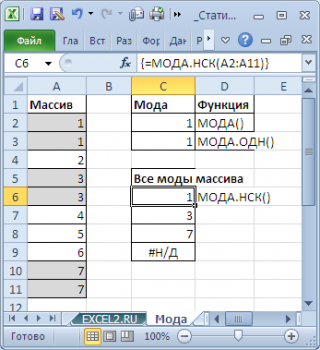
Как видно из картинки выше, функция МОДА.НСК() вернула все три моды из массива чисел в диапазоне A2:A11 : 1; 3 и 7. Для этого, выделите диапазон C6:C9 , в Строку формул введите формулу =МОДА.НСК(A2:A11) и нажмите CTRL+SHIFT+ENTER . Диапазон C 6: C 9 охватывает 4 ячейки, т.е. количество выделяемых ячеек должно быть больше или равно количеству мод . Если ячеек больше чем м о д, то избыточные ячейки будут заполнены значениями ошибки #Н/Д. Если мода только одна, то все выделенные ячейки будут заполнены значением этой моды .
Теперь вспомним, что мы определили моду для выборки, т.е. для конечного множества значений, взятых из генеральной совокупности . Для непрерывных случайных величин вполне может оказаться, что выборка состоит из массива на подобие этого (0,935; 1,211; 2,430; 3,668; 3,874; …), в котором может не оказаться повторов и функция МОДА() вернет ошибку.
Даже в нашем массиве с модой , которая была определена с помощью надстройки Пакет анализа , творится, что-то не то. Действительно, модой нашего массива значений является число 477, т.к. оно встречается 2 раза, остальные значения не повторяются. Но, если мы посмотрим на гистограмму распределения , построенную для нашего массива, то увидим, что 477 не принадлежит интервалу наиболее часто встречающихся значений (от 150 до 250). 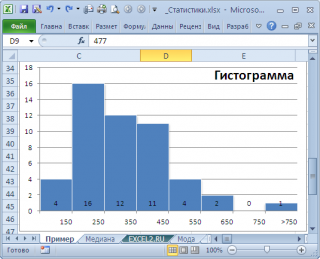
Проблема в том, что мы определили моду как наиболее часто встречающееся значение, а не как наиболее вероятное. Поэтому, моду в учебниках статистики часто определяют не для выборки (массива), а для функции распределения. Например, для логнормального распределения мода (наиболее вероятное значение непрерывной случайной величины х), вычисляется как exp ( m — s 2 ) , где m и s параметры этого распределения. 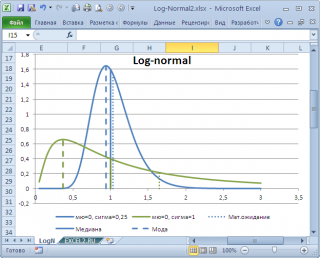
Понятно, что для нашего массива число 477, хотя и является наиболее часто повторяющимся значением, но все же является плохой оценкой для моды распределения, из которого взята выборка (наиболее вероятного значения или для которого плотность вероятности распределения максимальна).
Для того, чтобы получить оценку моды распределения, из генеральной совокупности которого взята выборка , можно, например, построить гистограмму . Оценкой для моды может служить интервал наиболее часто встречающихся значений (самого высокого столбца). Как было сказано выше, в нашем случае это интервал от 150 до 250.
Вывод : Значение моды для выборки , рассчитанное с помощью функции МОДА() , может ввести в заблуждение, особенно для небольших выборок. Эта функция эффективна, когда случайная величина может принимать лишь несколько дискретных значений, а размер выборки существенно превышает количество этих значений.
Например, в рассмотренном примере о распределении заработных плат (см. раздел статьи выше, о Медиане), модой является число 15 (17 значений из 51, т.е. 33%). В этом случае функция МОДА() дает хорошую оценку «наиболее вероятного» значения зарплаты.
Примечание : Строго говоря, в примере с зарплатой мы имеем дело скорее с генеральной совокупностью , чем с выборкой . Т.к. других зарплат в компании просто нет.
О вычислении моды для распределения непрерывной случайной величины читайте статью Мода в MS EXCEL .
Мода и среднее значение
Не смотря на то, что мода – это наиболее вероятное значение случайной величины (вероятность выбрать это значение из Генеральной совокупности максимальна), не следует ожидать, что среднее значение обязательно будет близко к моде .
Примечание : Мода и среднее симметричных распределений совпадает (имеется ввиду симметричность плотности распределения ).
Представим, что мы бросаем некий «неправильный» кубик, у которого на гранях имеются значения (1; 2; 3; 4; 6; 6), т.е. значения 5 нет, а есть вторая 6. Модой является 6, а среднее значение – 3,6666.
Другой пример. Для Логнормального распределения LnN(0;1) мода равна =EXP(m-s2)= EXP(0-1*1)=0,368, а среднее значение 1,649.
Дисперсия выборки
Дисперсия выборки или выборочная дисперсия ( sample variance ) характеризует разброс значений в массиве, отклонение от среднего . 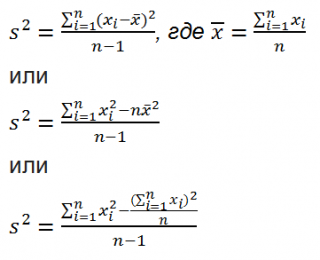
Из формулы №1 видно, что дисперсия выборки это сумма квадратов отклонений каждого значения в массиве от среднего , деленная на размер выборки минус 1.
В MS EXCEL 2007 и более ранних версиях для вычисления дисперсии выборки используется функция ДИСП() . С версии MS EXCEL 2010 рекомендуется использовать ее аналог — функцию ДИСП.В() .
Дисперсию можно также вычислить непосредственно по нижеуказанным формулам (см. файл примера ): =КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) =(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1) – обычная формула =СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1) – формула массива
Дисперсия выборки равна 0, только в том случае, если все значения равны между собой и, соответственно, равны среднему значению .
Чем больше величина дисперсии , тем больше разброс значений в массиве относительно среднего .
Размерность дисперсии соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность дисперсии будет кг 2 . Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из дисперсии – стандартное отклонение .
Стандартное отклонение выборки
Стандартное отклонение выборки (Standard Deviation), как и дисперсия , — это мера того, насколько широко разбросаны значения в выборке относительно их среднего .
По определению, стандартное отклонение равно квадратному корню из дисперсии : 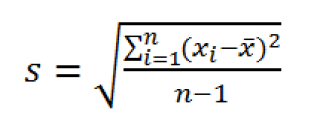
Стандартное отклонение не учитывает величину значений в выборке , а только степень рассеивания значений вокруг их среднего . Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х выборок : (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у выборок существенно отличается.
В MS EXCEL 2007 и более ранних версиях для вычисления Стандартного отклонения выборки используется функция СТАНДОТКЛОН() . С версии MS EXCEL 2010 рекомендуется использовать ее аналог СТАНДОТКЛОН.В() .
Стандартное отклонение можно также вычислить непосредственно по нижеуказанным формулам (см. файл примера ): =КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))
Стандартная ошибка
В Пакете анализа под термином стандартная ошибка имеется ввиду Стандартная ошибка среднего (Standard Error of the Mean, SEM). Стандартная ошибка среднего — это оценка стандартного отклонения распределения выборочного среднего .
Примечание : Чтобы разобраться с понятием Стандартная ошибка среднего необходимо прочитать о выборочном распределении (см. статью Статистики, их выборочные распределения и точечные оценки параметров распределений в MS EXCEL ) и статью про Центральную предельную теорему .
Стандартное отклонение распределения выборочного среднего вычисляется по формуле σ/√n, где n — объём выборки, σ — стандартное отклонение исходного распределения, из которого взята выборка . Т.к. обычно стандартное отклонение исходного распределения неизвестно, то в расчетах вместо σ используют ее оценку s — стандартное отклонение выборки . А соответствующая величина s/√n имеет специальное название — Стандартная ошибка среднего. Именно эта величина вычисляется в Пакете анализа.
В MS EXCEL стандартную ошибку среднего можно также вычислить по формуле =СТАНДОТКЛОН.В(Выборка)/ КОРЕНЬ(СЧЁТ(Выборка))
Асимметричность
Асимметричность или коэффициент асимметрии (skewness) характеризует степень несимметричности распределения ( плотности распределения ) относительно его среднего .
Положительное значение коэффициента асимметрии указывает, что размер правого «хвоста» распределения больше, чем левого (относительно среднего). Отрицательная асимметрия, наоборот, указывает на то, что левый хвост распределения больше правого. Коэффициент асимметрии идеально симметричного распределения или выборки равно 0. 
Примечание : Асимметрия выборки может отличаться расчетного значения асимметрии теоретического распределения. Например, Нормальное распределение является симметричным распределением ( плотность его распределения симметрична относительно среднего ) и, поэтому имеет асимметрию равную 0. Понятно, что при этом значения в выборке из соответствующей генеральной совокупности не обязательно должны располагаться совершенно симметрично относительно среднего . Поэтому, асимметрия выборки , являющейся оценкой асимметрии распределения , может отличаться от 0.
Функция СКОС() , английский вариант SKEW(), возвращает коэффициент асимметрии выборки , являющейся оценкой асимметрии соответствующего распределения, и определяется следующим образом: 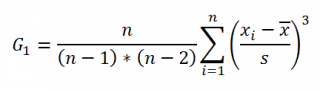
где n – размер выборки , s – стандартное отклонение выборки .
В файле примера на листе СКОС приведен расчет коэффициента асимметрии на примере случайной выборки из распределения Вейбулла , которое имеет значительную положительную асимметрию при параметрах распределения W(1,5; 1).
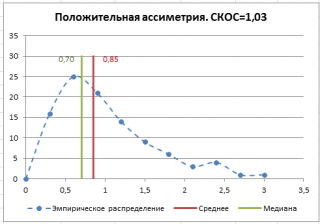
Эксцесс выборки
Эксцесс показывает относительный вес «хвостов» распределения относительно его центральной части.
Для того чтобы определить, что относится к хвостам распределения, а что к его центральной части, можно использовать границы μ +/- σ .
Примечание : Не смотря на старания профессиональных статистиков, в литературе еще попадается определение Эксцесса как меры «остроконечности» (peakedness) или сглаженности распределения. Но, на самом деле, значение Эксцесса ничего не говорит о форме пика распределения.
Согласно определения, Эксцесс равен четвертому стандартизированному моменту: 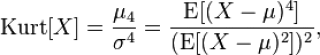
Для нормального распределения четвертый момент равен 3*σ 4 , следовательно, Эксцесс равен 3. Многие компьютерные программы используют для расчетов не сам Эксцесс , а так называемый Kurtosis excess, который меньше на 3. Т.е. для нормального распределения Kurtosis excess равен 0. Необходимо быть внимательным, т.к. часто не очевидно, какая формула лежит в основе расчетов.
Примечание : Еще большую путаницу вносит перевод этих терминов на русский язык. Термин Kurtosis происходит от греческого слова «изогнутый», «имеющий арку». Так сложилось, что на русский язык оба термина Kurtosis и Kurtosis excess переводятся как Эксцесс (от англ. excess — «излишек»). Например, функция MS EXCEL ЭКСЦЕСС() на самом деле вычисляет Kurtosis excess.
Функция ЭКСЦЕСС() , английский вариант KURT(), вычисляет на основе значений выборки несмещенную оценку эксцесса распределения случайной величины и определяется следующим образом: 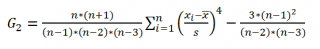
Как видно из формулы MS EXCEL использует именно Kurtosis excess, т.е. для выборки из нормального распределения формула вернет близкое к 0 значение.
Если задано менее четырех точек данных, то функция ЭКСЦЕСС() возвращает значение ошибки #ДЕЛ/0!
Вернемся к распределениям случайной величины . Эксцесс (Kurtosis excess) для нормального распределения всегда равен 0, т.е. не зависит от параметров распределения μ и σ. Для большинства других распределений Эксцесс зависит от параметров распределения: см., например, распределение Вейбулла или распределение Пуассона , для котрого Эксцесс = 1/λ.
Уровень надежности
Уровень надежности — означает вероятность того, что доверительный интервал содержит истинное значение оцениваемого параметра распределения.
Вместо термина Уровень надежности часто используется термин Уровень доверия . Про Уровень надежности (Confidence Level for Mean) читайте статью Уровень значимости и уровень надежности в MS EXCEL .
Задав значение Уровня надежности в окне надстройки Пакет анализа , MS EXCEL вычислит половину ширины доверительного интервала для оценки среднего (дисперсия неизвестна) .
Тот же результат можно получить по формуле (см. файл примера ): =ДОВЕРИТ.СТЬЮДЕНТ(1-0,95;s;n) s — стандартное отклонение выборки , n – объем выборки .
Источник
17 авг. 2022 г.
читать 2 мин
Асимметрия — это мера асимметрии набора данных или распределения. Это значение может быть положительным или отрицательным. Это полезно знать, потому что это помогает нам понять форму распределения.
Отрицательная асимметрия указывает на то, что хвост находится в левой части распределения, которая простирается в сторону более отрицательных значений.
Положительная асимметрия указывает на то, что хвост находится на правой стороне распределения, которая простирается в сторону более положительных значений.
Нулевое значение указывает на то, что в распределении вообще нет асимметрии, что означает, что распределение совершенно симметрично. Это необычно и редко встречается на практике.
Как рассчитать асимметрию в Excel
Excel предлагает следующую встроенную функцию для вычисления асимметрии распределения:
=СКОС(массив значений)
Эта функция использует следующую формулу для вычисления асимметрии:
Асимметрия = [n/(n-1)(n-2)] * Σ[(x i – x )/s] 3
куда:
n = размер выборки
Σ = причудливый символ, означающий «сумма»
x i = значение i -го значения в наборе данных
х = среднее
с = стандартное отклонение
Формула немного сложна, но, к счастью, Excel выполняет этот расчет за вас, так что вам не нужно делать это вручную.
Пример: расчет асимметрии в Excel
Предположим, у нас есть следующий набор данных, содержащий экзаменационные оценки 20 студентов:
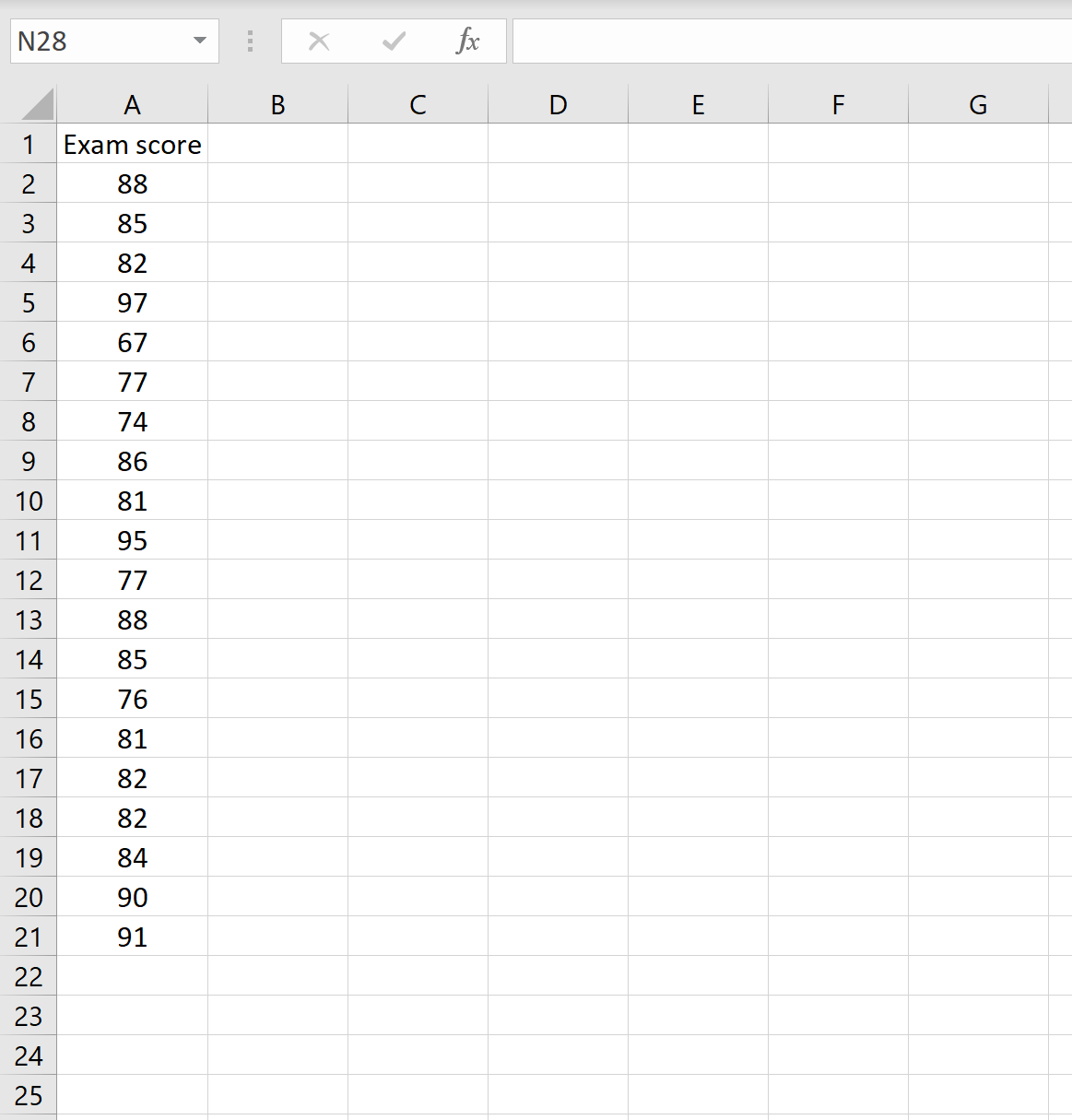
Мы можем рассчитать асимметрию распределения, используя =SKEW(A2:A21)
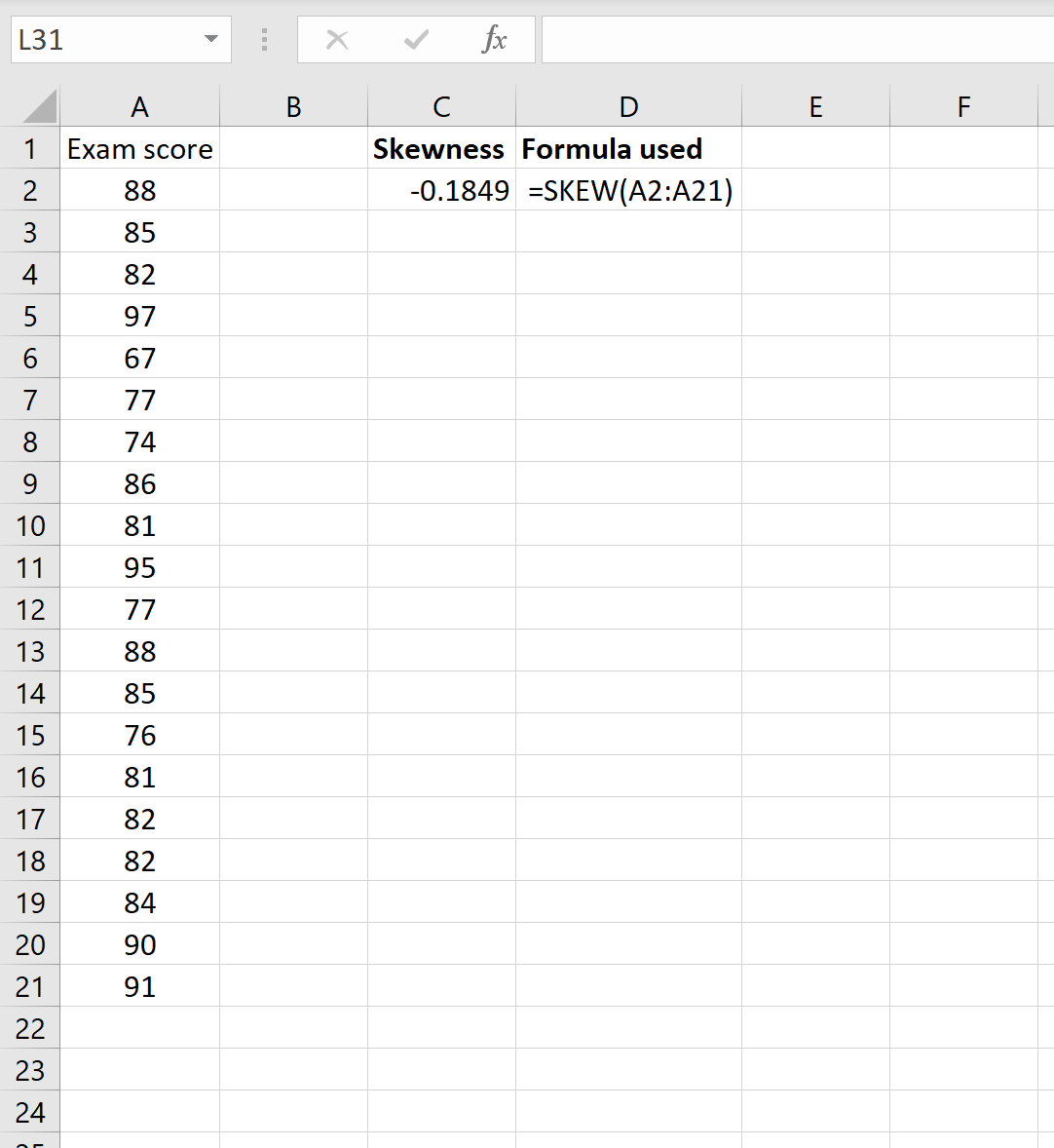
Это говорит нам о том, что асимметрия этого набора данных составляет -0,1849.Поскольку это значение отрицательное, мы знаем, что хвост распределения простирается влево.
Техническое примечание:
Функция SKEW() вернет ошибку #DIV/0! в следующих двух сценариях:
- Если имеется менее трех точек данных
- Если стандартное отклонение выборки равно нулю
Дополнительный ресурс: Калькулятор асимметрии и эксцесса
Вы также можете рассчитать асимметрию для заданного набора данных с помощью статистического калькулятора асимметрии и эксцесса, который автоматически вычисляет как асимметрию, так и эксцесс для заданного набора данных. Вы просто вводите необработанные значения данных для своего набора данных в поле ввода, затем нажимаете «Рассчитать».
Например, вот как рассчитать асимметрию для набора данных из приведенного выше примера:

Обратите внимание, что значение асимметрии из калькулятора совпадает со значением асимметрии, которое мы нашли в Excel.

