Распределение коммерческих банков по размеру активов характеризуется следующими данными:
| Размер активов, млн руб. | До 200 | 200 – 300 | 300 – 400 | 400 – 500 | 500 – 600 | 600 и более | Итого |
|---|---|---|---|---|---|---|---|
| Удельный вес банков, % к итогу | 8 | 25 | 52 | 7 | 5 | 3 | 100 |
Определите характеристики распределения:
а) среднюю;
б) моду;
в) среднее квадратическое отклонение;
г) коэффициент вариации;
д) коэффициент асимметрии и эксцесс.
Решение:
Данный интервальный вариационный ряд содержит открытые интервалы, которые предварительно необходимо закрыть. Для этого из величины верхней границы первого интервала надо вычесть величину второго интервала. Получим нижнюю границу первого интервала.
200 – 100 = 100.
Первый интервал: 100 – 200.
Теперь к нижней границе последнего интервала прибавляем величину предшествующего интервала:
600 + 100 = 700
Последний интервал: 600 – 700.
а) Определение средней по сгруппированным данным производится по формуле средней арифметической взвешенной:
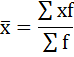
Чтобы применить эту формулу, необходимо варианты признака выразить одним числом (дискретным). За такое дискретное число принимается средняя арифметическая простая из верхнего и нижнего значения каждого интервала.
Так, например, дискретная величина х для первого интервала будет равна: (100 + 200) / 2 = 150.
Построим таблицу рассчётных данных:
Дальнейший расчёт производится обычным методом определения средней арифметической взвешенной.
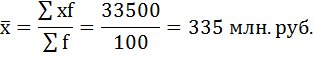
б) Определим моду.
Мода – это величина признака наиболее часто встречающегося в совокупности.
В интервальных рядах распределения с равными интервалами мода определяется по формуле:
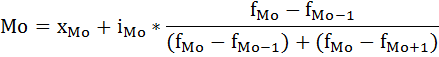
где
хМо – начальное значение интервала, содержащего моду;
iМо – величина модального интервала,
fМо – частота модального интервала,
fМо-1 – частота интервала, предшествующего модальному,
fМо+1 – частота интервала, следующего за модальным.
Мода содержится в интервале от 300 до 400, так как у этого интервала наибоьшая частота
f = 52.
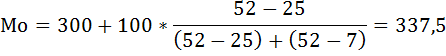млн. руб.
в) Найдём среднее квадратическое отклонение:
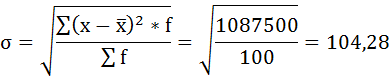
Значения размера активов в ряду распределения могут отличаться от среднего значения на 104,28 млн. руб.
Дисперсия будет равна:
σ2 = 10 875
г) Коэффициент вариации рассчитаем по формуле:
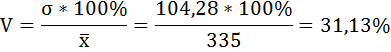
Совокупность однородна, так как коэффициент вариации не превышает 33%.
д) Рассчитаем показатель асимметрии через отношение центрального момента третьего порядка к среднему квадратическому отклонению данного ряда в кубе, то есть
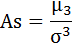
где μ3 – центральный момент третьего порядка, рассчитываемый по формуле:
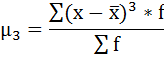
μ3 = 88 275 000 / 100 = 882 750
As = 882 750 / 104,283 = 0,78
Так как величина показателя асимметрии положительна, следовательно, речь идёт о правосторонней асимметрии.
Полученный результат свидетельствует о наличии несущественной по величине и положительной по своему характеру асимметрии.
Далее рассчитаем показатель эксцесса (Еk). Наиболее точно он определяется по формуле с использованием центрального момента четвёртого порядка:
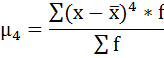
μ4 = 52 123 312 500 / 100 = 521 233 125
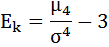
σ4 = 118 265 625
Ek = 521 233 125 / 118 265 625 – 3 = 4,41 – 3 = 1,41
Так как Ek > 0 распределение является островершинным.
Коэффициент асимметрии. Эксцесс распределения
Краткая теория
При изучении распределений, отличных от нормального,
возникает необходимость количественно оценить это различие. С этой целью вводят
специальные характеристики, в частности асимметрию и эксцесс. Для нормального
распределения эти характеристики равны нулю. Поэтому если для изучаемого
распределения асимметрия и эксцесс имеют небольшие значения, то можно
предположить близость этого распределения к нормальному.
Наоборот, большие значения асимметрии и эксцесса указывают на значительное
отклонение от нормального.
Асимметрией теоретического распределения называют отношение
центрального момента третьего порядка к кубу среднего квадратического
отклонения:
Коэффициент асимметрии характеризует скошенность
распределения по отношению к математическому ожиданию. Асимметрия положительна,
если «длинная часть» кривой распределения расположена справа от математического
ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева
от математического ожидания.
На рисунке показаны две кривые распределения: I и II. Кривая I имеет
положительную (правостороннюю) асимметрию
,
а кривая II – отрицательную (левостороннюю)
.
Кроме вышеописанного коэффициента, для характеристики асимметрии
рассчитывают также показатель асимметрии Пирсона:
Коэффициент асимметрии Пирсона характеризует асимметрию только в
центральной части распределения, поэтому более распространенным и более точным
является коэффициент асимметрии, рассчитанный на основе центрального момента третьего
порядка.
Для оценки «крутости», т. е. большего или меньшего подъема кривой
теоретического распределения по сравнению с нормальной кривой, пользуются
характеристикой – эксцессом.
Эксцессом (или коэффициентом эксцесса) случайной величины
называется число:
Число 3 вычитается из отношения
потому, что для наиболее часто встречающегося
нормального распределения отношение
.
Кривые, более островершинные, чем нормальная,
обладают положительным эксцессом, более плосковершинные – отрицательным
эксцессом.
Примеры решения задач
Задача 1
Для заданного
вариационного ряда вычислить коэффициенты асимметрии и эксцесса.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Составим расчетную
таблицу
Средняя:
Найдем моду – варианту, которой соответствует наибольшая частота.
Дисперсия:
Среднее квадратическое
отклонение:
Коэффициент асимметрии Пирсона:
Коэффициент асимметрии можно найти по формуле:
Центральный момент
3-го порядка:
Получаем:
Эксцесс можно найти по формуле:
Центральный момент
4-го порядка:
Получаем:
Задача 2
Для заданного
вариационного ряда (см. условие задачи 1) вычислить коэффициенты асимметрии и
эксцесса методом произведений, используя условные моменты.
Решение
Составим расчетную таблицу
Перейдем к условным вариантам
В качестве ложного нуля возьмем
3-ю варианту
0
Условные варианты вычислим по
формуле:
где
4
(разность между соседними вариантами)
Условный момент 1-го порядка:
Средняя:
Условный момент 2-го порядка:
Дисперсия:
Среднее квадратическое
отклонение:
Коэффициент асимметрии можно найти
по формуле:
Условный момент 3-го порядка:
Центральный момент 3-го порядка:
Получаем:
Эксцесс можно найти по формуле:
Условный момент 4-го порядка:
Центральный момент 4-го порядка:
Получаем:
58. Коэффициенты асимметрии и эксцесса.
Центральные
моменты распределения
Для дальнейшего изучения характера
вариации используются средние значения
разных степеней отклонений отдельных
величин признака от его средней
арифметической величины. Эти показатели
получили название центральных
моментов распределения порядка,
соответствующего степени, в которую
возводятся отклонения,
или просто моментов.
Показатели формы распределения
-
Асимметрия – Коэффициент
асимметрии
характеризует асимметричность
(«скошенность») распределения признака
в совокупности -
Эксцесс – Показатель эксцесса
представляет собой отклонение вершины
эмпирического распределения вверх или
вниз («крутость») от вершины кривой
нормального распределения
Асимметрия распределения
-
При
=0
распределение считается нормальным. -
При
> 0 правосторонняя асимметрия. -
При
<0
левосторонняя асимметрия. -
Если асимметрия более 0,5, то независимо
от знака она считается значительной -
Если асимметрия меньше 0,25, то она
считается незначительной
=0
<0
|
Асимметрия |
|
|
является |
|
Расчет |
|
т.е. – нормированный |
Показатель Пирсона зависит от степени
асимметричности в средней части ряда
распределения, а показатель асимметрии,
основанный на моменте третьего порядка,
– от крайних значений признака.
Оценка существенности асимметрии
Для оценки существенности асимметрии
вычисляют показатель средней квадратической
ошибки коэффициента асимметрии
Если отношение
имеет значение больше 2, то это
свидетельствует о существенном характере
асимметрии
Эксцесс распределения
Показатель эксцесса
представляет собой отклонение вершины
эмпирического распределения вверх или
вниз («крутость») от вершины кривой
нормального распределения, НО! График
распределения может выглядеть сколь
угодно крутым в зависимости от силы
вариации признака: чем слабее вариация,
тем круче кривая распределения при
данном масштабе. Не говоря уже о том,
что, изменяя масштабы по оси абсцисс и
по оси ординат, любое распределение
можно искусствен но сделать «крутым»
и «пологим». Чтобы показать, в чем состоит
эксцесс распределения, и правильно его
интерпретировать, нужно сравнить ряды
с одинаковой силой вариации (одной и
той же величиной σ) и разными показателями
эксцесса. Чтобы не смешать эксцесс с
асимметрией, все сравниваемые ряды
должны быть симметричными. Такое
сравнение изображено на рис.
Поскольку эксцесс нормального
распределения равен 3, показатель
эксцесса вычисляется по формуле
|
|
или |
где |
-
При
>0
– высоковершинный эксцесс распределения -
При
<0
– низковершинный эксцесс распределение -
При
=0 – нормальное распределение
>0
<0
Оценка существенности эксцесса
Для оценки существенности эксцесса
вычисляют показатель его средней
квадратической ошибки
Если отношение
имеет значение больше 3, то это
свидетельствует о существенном характере
эксцесса
У этого термина существуют и другие значения, см. Эксцесс (значения).
Несколько распределений и их коэффициенты эксцесса. В порядке уменьшения высоты пика (значения в нуле):
распределение Лапласа;
Hyperbolic secant distribution (англ.) (рус.;
Логистическое распределение;
Нормальное распределение;
Raised cosine distribution (англ.) (рус.;
Полукруговой закон Вигнера;
Равномерное распределение
Коэффицие́нт эксце́сса (коэффициент островершинности) в теории вероятностей — мера остроты пика распределения случайной величины.
Содержание
- 1 Определение
- 2 Замечание
- 3 Свойства коэффициента эксцесса
- 4 См. также
Определение[править | править код]
|
В Викисловаре есть статья «эксцесс» |
|---|
Пусть задана случайная величина 
, такая что 
. Пусть 
обозначает четвёртый центральный момент: ![mu _{4}={mathbb {E}}left[(X-{mathbb {E}}X)^{4}right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9489a32f8e9d80d6af515720e27d5888353513d)
, а ![sigma ={sqrt {{mathrm {D}}[X]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb1d09ce7db9875c167d4b8df03e4608460e3dab)
— стандартное отклонение . Тогда коэффициент эксцесса задаётся формулой:
.
Замечание[править | править код]
- «Минус три» в конце формулы введено для того, чтобы коэффициент эксцесса стандартного нормального распределения был равен нулю. Он положителен, если пик распределения около математического ожидания острый, и отрицателен, если пик очень гладкий.
Свойства коэффициента эксцесса[править | править код]
- .
- Пусть — независимые случайные величины с равной дисперсией. Пусть . Тогда
- ,
где 
— коэффициенты эксцесса соответствующих случайных величин.
См. также[править | править код]
- Моменты случайной величины.
Может ли эксцесс быть отрицательным?
17 авг. 2022 г.
читать 2 мин
В статистике эксцесс используется для описания формы распределения вероятностей.
В частности, он сообщает нам, в какой степени значения данных группируются в хвостах или пиках распределения.
Эксцесс распределения может быть отрицательным, равным нулю или положительным.
Нулевой эксцесс
Если эксцесс распределения равен 0, то он равен нормальному распределению, которое имеет следующую колоколообразную форму:
Положительный эксцесс
Если распределение имеет положительный эксцесс, говорят, что оно лептокуртическое , что означает, что оно имеет более острый пик и более тяжелые хвосты по сравнению с нормальным распределением.
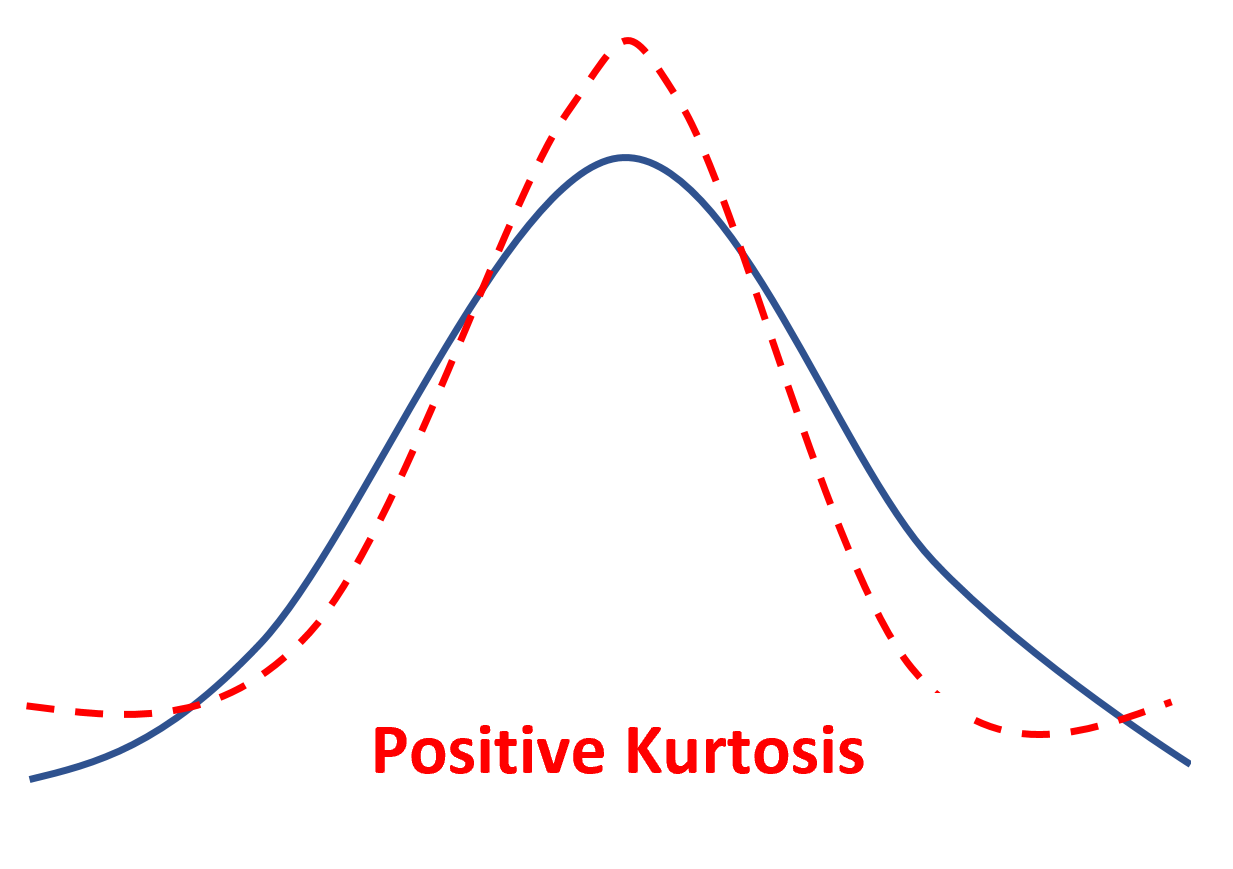
Это просто означает, что меньше значений данных находится рядом со средним значением, а больше значений данных находится на хвостах.
Наиболее известным распределением с положительным эксцессом является t-распределение, которое имеет более острый пик и более тяжелые хвосты по сравнению с нормальным распределением.
Отрицательный эксцесс
Если распределение имеет отрицательный эксцесс, говорят, что оно платикуртическое , что означает, что у него более плоский пик и более тонкие хвосты по сравнению с нормальным распределением.
Это просто означает, что больше значений данных находится рядом со средним значением и меньше значений данных находится на хвостах.
Одним крайним примером распределения с отрицательным эксцессом является равномерное распределение , которое вообще не имеет пика и является полностью плоским распределением.
Когда использовать эксцесс на практике
На практике мы часто измеряем эксцесс распределения на исследовательской фазе анализа, когда просто пытаемся лучше понять данные.
Таким образом, если мы видим, что эксцесс положительный, то мы знаем, что работаем с распределением, в котором меньше значений данных расположены ближе к центру и больше значений данных разбросаны вдоль хвостов.
И наоборот, если мы видим, что эксцесс отрицательный, то мы знаем, что работаем с распределением, в котором больше значений данных расположено ближе к центру и меньше значений данных в хвостах.
Дополнительные ресурсы
Чтобы найти асимметрию и эксцесс для данного распределения, вы можете ввести необработанные значения данных в этот Калькулятор асимметрии и эксцесса, который сообщит вам как асимметрию, так и эксцесс для распределения.
Одним из самых популярных статистических тестов, который используется для определения того, имеет ли конкретное распределение асимметрию и эксцесс, соответствующие нормальному распределению, является тест Харке-Бера .
У Академии Хана также есть отличная серия видео , в которой рассказывается, как классифицировать формы распределений.
