Как найти экспоненту формула - Сайт, где вы сможете решить свои вопросы

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 27 августа 2022 года; проверки требуют 5 правок.

Запрос «EXP» перенаправляется сюда; о классе сложности см. Класс EXPTIME.

Экспоне́нта — показательная функция $f(x)=exp(x)=e^{x}$ , где — число Эйлера.

Определение[править | править код]

Экспоненциальная функция может быть определена различными эквивалентными способами. Например, через ряд Тейлора:

$e^{x}=1+sum _{{n=1}}^{{infty }}{x^{n} over n!}=1+x+{x^{2} over 2!}+{x^{3} over 3!}+{x^{4} over 4!}+cdots$

или через предел:

$e^{x}=lim _{{nrightarrow infty }}left(1+{frac {x}{n}}right)^{n}$

Здесь — любое комплексное число.

Происхождение понятия[править | править код]

Слово экспонента происходит от лат. “exponere”, что переводится как “выставить вперёд; показать“, которое в свою очередь произошло от лат. приставки “ex-“ (“впереди”) и лат. слова “ponere” (“ставить, расположить”);^[1] Смысл использования такого слова для показателя степени заключается в том, что знак экспоненты “ставят вне” привычной линии письма $a^{x}$ (немного выше и правее места, где обычно должна быть поставлена цифра).

Свойства[править | править код]

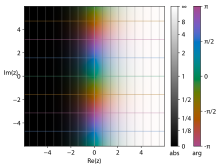
Комплексная экспонента[править | править код]

График экспоненты в комплексной плоскости.
Легенда

Комплексная экспонента — математическая функция, задаваемая соотношением $f(z)=e^{z}$ , где есть комплексное число. Комплексная экспонента определяется как аналитическое продолжение экспоненты $f(x)=e^{x}$ вещественного переменного :

Определим формальное выражение

$e^{z}=e^{{x+iy}}=e^{x}cdot e^{{iy}}$

Определённое таким образом выражение на вещественной оси будет совпадать с классической вещественной экспонентой. Для полной корректности построения необходимо доказать аналитичность функции $e^{z}$ , то есть показать, что $e^{z}$ разлагается в некоторый сходящийся к данной функции ряд. Покажем это:

$f(z)=e^{z}=e^{x}cdot e^{{iy}}=e^{{iy}}sum _{{n=0}}^{infty }{frac {x^{n}}{n!}}$

Сходимость данного ряда легко доказывается:

${displaystyle left|e^{iy}sum _{n=0}^{infty }{frac {x^{n}}{n!}}right|leq left|sum _{n=0}^{infty }{frac {x^{n}}{n!}}right|leq sum _{n=0}^{infty }left|{frac {x^{n}}{n!}}right|=sum _{n=0}^{infty }{dfrac {|x|^{n}}{n!}}=e^{|x|}}$

Ряд всюду сходится абсолютно, то есть вообще всюду сходится, таким образом, сумма этого ряда в каждой конкретной точке будет определять значение аналитической функции $f(z)=e^{z}$ . Согласно теореме единственности, полученное продолжение будет единственно, следовательно, на комплексной плоскости функция $e^{z}$ всюду определена и аналитична.

Свойства[править | править код]

Вариации и обобщения[править | править код]

Аналогично экспонента определяется для элемента произвольной ассоциативной алгебры.
В конкретном случае требуется также доказательство того, что указанные пределы существуют.

Матричная экспонента[править | править код]

Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:

$exp A=sum _{{k=0}}^{{infty }}{frac {A^{k}}{k!}}.$

Определённый таким образом ряд сходится для любого оператора с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы Следовательно, экспонента от матрицы ${displaystyle Ain mathbb {R} ^{ntimes n}}$ всегда определена и сама является матрицей.

С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение ${dot x}=Ax,~~~xin {mathbb R}^{n}$ с начальным условием $x(0)=x_{0}$ имеет своим решением $x(t)=exp(At)x_{0}.$

h-экспонента[править | править код]

Введение -экспоненты основано на втором замечательном пределе:

$e_{{h}}(x)=(1+h)^{{frac {x}{h}}}.$

При hto 0 получается обычная экспонента^[2].

Обратная функция[править | править код]

Обратная функция к экспоненциальной функции — натуральный логарифм.
Обозначается ln x :

$ln x=log _{{e}}x.$

См. также[править | править код]

Показательная функция
Список интегралов от экспоненциальных функций
Экспоненциальный рост

Примечания[править | править код]

↑ exponent (n.) (англ.).
↑ A.I. Olemskoi, S.S. Borysov, a, and I.A. Shuda. Statistical field theories deformed within different calculi

Литература[править | править код]

Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. — Издание 5-е, исправленное. — М.: Наука, 1987. — 688 с.
Хапланов М. Г. Теория функции комплексного переменного (краткий курс). — Издание 2-е, исправленное. — М.: Просвещение, 1965. — 209 с.

Ссылки[править | править код]

An Intuitive Guide To Exponential Functions & e | BetterExplained (англ.)

Источник

Посчитать экспоненту

Главная
/
Математика
/
Арифметика
/
Посчитать экспоненту

Для того чтобы посчитать экспоненту воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор

Чему равна

exp()?

Ответ:

Просто введите число для которого нужно посчитать экспоненту и получите ответ.

Теория

Экспонента является показательной функцией ƒ(x) = e^x, где число e (число Эйлера, e ≈ 2,718) – основание степени, а х – степень в которую нужно его возвести.

Формула

exp(x) = e^x

Пример

К примеру, посчитаем экспоненту числа 2:

exp(2) = e² = 2,7182818284² ≈ 7.389

См. также

Источник

В данной публикации мы рассмотрим, что такое экспонента, как выглядит ее график, приведем формулу, с помощью которой задается экспоненциальная функция, а также перечислим ее основные свойства.

Определение и формула экспоненты
График экспоненты
Свойства экспоненциальной функции

Определение и формула экспоненты

Экспонента – это показательная функция, формула которой выглядит следующим образом:

f (x) = exp(x) = e^x

где e – число Эйлера.

Экспоненциальная функция (так часто называют экспоненту) может быть определена:

Через предел (lim):

Через степенной ряд Тейлора:

График экспоненты

Ниже представлен график экспоненциальной функции y = e^x.

Как мы видим график (синяя линия) является выпуклым, строго возрастающим, т.е. при увеличении x увеличивается значение y.

Асимптотой является ось абсцисс, т.е. график во II четверти координатной плоскости стремится к оси Ox, но никогда не пересечет и не коснется ее.

Пересечение с осью ординат Oy – в точке (0, 1), так как e⁰ = 1.

Касательная (зеленая линия) к экспоненте проходит под углом 45 градусов в точке касания.

Свойства экспоненциальной функции

Экспонента определена для всех x, причем функция везде возрастает, и ее значение всегда больше нуля. То есть:
- область определения: – ∞ < x + ∞;
- область значений: 0 < y < + ∞.
Обратная к экспоненте функция – это натуральный логарифм (ln x).
- ln e ^x = x;
- e^{ln x} = x, где x > 0.
Для экспоненты применимы правила операций с показателями, например: e^{(a + b)} = e^a ⋅ e^b.
Производная экспоненты:
- (e^x)‘ = e^x.
- если вместо x – сложная функция u: (e^u)‘ = e^u + u‘.
Интеграл экспоненты: ∫ e^x dx = e^x + C, где C – константа интегрирования.

Источник

This article is about the function f(x) = e^x and its generalizations. For functions of the form f(x) = x^r, see Power function. For the bivariate function f(x,y) = x^y, see Exponentiation. For the representation of scientific numbers, see E notation.

Exponential
The natural exponential function along part of the real axis
General information
General definition	${displaystyle exp z=e^{z}}$
Motivation of invention	Analytic proofs
Fields of application	Pure and applied mathematics
Domain, Codomain and Image
Domain
Image	${displaystyle {begin{cases}(0,infty )&{text{for }}zin mathbb {R} \mathbb {C} setminus {0}&{text{for }}zin mathbb {C} end{cases}}}$
Specific values
At zero	1
Value at 1	e
Specific features
Fixed point	−W_n(−1) for
Related functions
Reciprocal
Inverse	Complex logarithm
Derivative
Antiderivative
Series definition
Taylor series	${displaystyle exp z=sum _{n=0}^{infty }{frac {z^{n}}{n!}}}$

Exponential functions with bases 2 and 1/2

The exponential function is a mathematical function denoted by or $e^{x}$ (where the argument x is written as an exponent). Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, although it can be extended to the complex numbers or generalized to other mathematical objects like matrices or Lie algebras. The exponential function originated from the notion of exponentiation (repeated multiplication), but modern definitions (there are several equivalent characterizations) allow it to be rigorously extended to all real arguments, including irrational numbers. Its ubiquitous occurrence in pure and applied mathematics led mathematician Walter Rudin to opine that the exponential function is “the most important function in mathematics”.^[1]

The exponential function satisfies the exponentiation identity

${displaystyle e^{x+y}=e^{x}e^{y}{text{ for all }}x,yin mathbb {R} ,}$

which, along with the definition , shows that ${displaystyle e^{n}=underbrace {etimes cdots times e} _{n{text{ factors}}}}$ for positive integers n, and relates the exponential function to the elementary notion of exponentiation. The base of the exponential function, its value at 1, , is a ubiquitous mathematical constant called Euler’s number.

While other continuous nonzero functions that satisfy the exponentiation identity are also known as exponential functions, the exponential function exp is the unique real-valued function of a real variable whose derivative is itself and whose value at 0 is 1; that is, for all real x, and Thus, exp is sometimes called the natural exponential function to distinguish it from these other exponential functions, which are the functions of the form ${displaystyle f(x)=ab^{x},}$ where the base b is a positive real number. The relation ${displaystyle b^{x}=e^{xln b}}$ for positive b and real or complex x establishes a strong relationship between these functions, which explains this ambiguous terminology.

The real exponential function can also be defined as a power series. This power series definition is readily extended to complex arguments to allow the complex exponential function to be defined. The complex exponential function takes on all complex values except for 0 and is closely related to the complex trigonometric functions, as shown by Euler’s formula.

Motivated by more abstract properties and characterizations of the exponential function, the exponential can be generalized to and defined for entirely different kinds of mathematical objects (for example, a square matrix or a Lie algebra).

In applied settings, exponential functions model a relationship in which a constant change in the independent variable gives the same proportional change (that is, percentage increase or decrease) in the dependent variable. This occurs widely in the natural and social sciences, as in a self-reproducing population, a fund accruing compound interest, or a growing body of manufacturing expertise. Thus, the exponential function also appears in a variety of contexts within physics, computer science, chemistry, engineering, mathematical biology, and economics.

The real exponential function is a bijection from to .^[2] Its inverse function is the natural logarithm, denoted ^{[nb 1]} ^{[nb 2]} or ${displaystyle log _{e};}$ because of this, some old texts^[3] refer to the exponential function as the antilogarithm.

Graph[edit]

The graph of $y=e^{x}$ is upward-sloping, and increases faster as x increases.^[4] The graph always lies above the x-axis, but becomes arbitrarily close to it for large negative x; thus, the x-axis is a horizontal asymptote. The equation ${displaystyle {tfrac {d}{dx}}e^{x}=e^{x}}$ means that the slope of the tangent to the graph at each point is equal to its y-coordinate at that point.

Relation to more general exponential functions[edit]

The exponential function $f(x)=e^{x}$ is sometimes called the natural exponential function for distinguishing it from the other exponential functions. The study of any exponential function can easily be reduced to that of the natural exponential function, since per definition, for positive b,

${displaystyle ab^{x}:=ae^{xln b}}$

As functions of a real variable, exponential functions are uniquely characterized by the fact that the derivative of such a function is directly proportional to the value of the function. The constant of proportionality of this relationship is the natural logarithm of the base b:

${displaystyle {frac {d}{dx}}b^{x} {stackrel {text{def}}{=}} {frac {d}{dx}}e^{xln(b)}=e^{xln(b)}ln(b)=b^{x}ln(b).}$

For b > 1, the function b^x is increasing (as depicted for b = e and b = 2), because makes the derivative always positive; while for b < 1, the function is decreasing (as depicted for b = 1/2); and for b = 1 the function is constant.

Euler’s number e = 2.71828… is the unique base for which the constant of proportionality is 1, since ln(e)=1 , so that the function is its own derivative:

${displaystyle {frac {d}{dx}}e^{x}=e^{x}ln(e)=e^{x}.}$

This function, also denoted as exp x, is called the “natural exponential function”,^[5]^[6] or simply “the exponential function”. Since any exponential function can be written in terms of the natural exponential as ${displaystyle b^{x}=e^{xln b}}$ , it is computationally and conceptually convenient to reduce the study of exponential functions to this particular one. The natural exponential is hence denoted by

${displaystyle xmapsto e^{x}}$

The former notation is commonly used for simpler exponents, while the latter is preferred when the exponent is more complicated and harder to read in a small font.

For real numbers c and d, a function of the form ${displaystyle f(x)=ab^{cx+d}}$ is also an exponential function, since it can be rewritten as

${displaystyle ab^{cx+d}=left(ab^{d}right)left(b^{c}right)^{x}.}$

Formal definition[edit]

The exponential function (in blue), and the sum of the first n + 1 terms of its power series (in red).

The real exponential function can be characterized in a variety of equivalent ways. It is commonly defined by the following power series:^[1]^[7]

${displaystyle exp x:=sum _{k=0}^{infty }{frac {x^{k}}{k!}}=1+x+{frac {x^{2}}{2}}+{frac {x^{3}}{6}}+{frac {x^{4}}{24}}+cdots }$

Since the radius of convergence of this power series is infinite, this definition is, in fact, applicable to all complex numbers; see § Complex plane for the extension of exp x to the complex plane. Using the power series, the constant e can be defined as ${textstyle e=exp 1=sum _{k=0}^{infty }(1/k!).}$

The term-by-term differentiation of this power series reveals that ${textstyle {frac {d}{dx}}exp x=exp x}$ for all real x, leading to another common characterization of exp x as the unique solution of the differential equation

that satisfies the initial condition

Based on this characterization, the chain rule shows that its inverse function, the natural logarithm, satisfies ${textstyle {frac {d}{dy}}ln y=1/y}$ for or ${textstyle ln y=int _{1}^{y}{frac {dt}{t}},.}$ This relationship leads to a less common definition of the real exponential function exp x as the solution to the equation

${displaystyle x=int _{1}^{y}{frac {1}{t}},dt.}$

By way of the binomial theorem and the power series definition, the exponential function can also be defined as the following limit:^[8]^[7]

${displaystyle exp x=lim _{nto infty }left(1+{frac {x}{n}}right)^{n}.}$

It can be shown that every continuous, nonzero solution of the functional equation for is an exponential function, $f(x)=e^{{kx}}$ with

Overview[edit]

The red curve is the exponential function. The black horizontal lines show where it crosses the green vertical lines.

The exponential function arises whenever a quantity grows or decays at a rate proportional to its current value. One such situation is continuously compounded interest, and in fact it was this observation that led Jacob Bernoulli in 1683^[9] to the number

${displaystyle lim _{nto infty }left(1+{frac {1}{n}}right)^{n}}$

now known as e. Later, in 1697, Johann Bernoulli studied the calculus of the exponential function.^[9]

If a principal amount of 1 earns interest at an annual rate of x compounded monthly, then the interest earned each month is x/12 times the current value, so each month the total value is multiplied by (1 + x/12), and the value at the end of the year is (1 + x/12)¹². If instead interest is compounded daily, this becomes (1 + x/365)³⁶⁵. Letting the number of time intervals per year grow without bound leads to the limit definition of the exponential function,

${displaystyle exp x=lim _{nto infty }left(1+{frac {x}{n}}right)^{n}}$

first given by Leonhard Euler.^[8]
This is one of a number of characterizations of the exponential function; others involve series or differential equations.

From any of these definitions it can be shown that the exponential function obeys the basic exponentiation identity,

which justifies the notation e^x for exp x.

The derivative (rate of change) of the exponential function is the exponential function itself. More generally, a function with a rate of change proportional to the function itself (rather than equal to it) is expressible in terms of the exponential function. This function property leads to exponential growth or exponential decay.

The exponential function extends to an entire function on the complex plane. Euler’s formula relates its values at purely imaginary arguments to trigonometric functions. The exponential function also has analogues for which the argument is a matrix, or even an element of a Banach algebra or a Lie algebra.

Derivatives and differential equations[edit]

The derivative of the exponential function is equal to the value of the function. From any point P on the curve (blue), let a tangent line (red), and a vertical line (green) with height h be drawn, forming a right triangle with a base b on the x-axis. Since the slope of the red tangent line (the derivative) at P is equal to the ratio of the triangle’s height to the triangle’s base (rise over run), and the derivative is equal to the value of the function, h must be equal to the ratio of h to b. Therefore, the base b must always be 1.

The importance of the exponential function in mathematics and the sciences stems mainly from its property as the unique function which is equal to its derivative and is equal to 1 when x = 0. That is,

${displaystyle {frac {d}{dx}}e^{x}=e^{x}quad {text{and}}quad e^{0}=1.}$

Functions of the form ce^x for constant c are the only functions that are equal to their derivative (by the Picard–Lindelöf theorem). Other ways of saying the same thing include:

The slope of the graph at any point is the height of the function at that point.
The rate of increase of the function at x is equal to the value of the function at x.
The function solves the differential equation y′ = y.
exp is a fixed point of derivative as a functional.

If a variable’s growth or decay rate is proportional to its size—as is the case in unlimited population growth (see Malthusian catastrophe), continuously compounded interest, or radioactive decay—then the variable can be written as a constant times an exponential function of time. Explicitly for any real constant k, a function f: R → R satisfies f′ = kf if and only if f(x) = ce^kx for some constant c. The constant k is called the decay constant, disintegration constant,^[10] rate constant,^[11] or transformation constant.^[12]

Furthermore, for any differentiable function f, we find, by the chain rule:

${displaystyle {frac {d}{dx}}e^{f(x)}=f'(x)e^{f(x)}.}$

Continued fractions for e^x[edit]

A continued fraction for e^x can be obtained via an identity of Euler:

${displaystyle e^{x}=1+{cfrac {x}{1-{cfrac {x}{x+2-{cfrac {2x}{x+3-{cfrac {3x}{x+4-ddots }}}}}}}}}$

The following generalized continued fraction for e^z converges more quickly:^[13]

${displaystyle e^{z}=1+{cfrac {2z}{2-z+{cfrac {z^{2}}{6+{cfrac {z^{2}}{10+{cfrac {z^{2}}{14+ddots }}}}}}}}}$

or, by applying the substitution z = x/y:

${displaystyle e^{frac {x}{y}}=1+{cfrac {2x}{2y-x+{cfrac {x^{2}}{6y+{cfrac {x^{2}}{10y+{cfrac {x^{2}}{14y+ddots }}}}}}}}}$

with a special case for z = 2:

${displaystyle e^{2}=1+{cfrac {4}{0+{cfrac {2^{2}}{6+{cfrac {2^{2}}{10+{cfrac {2^{2}}{14+ddots ,}}}}}}}}=7+{cfrac {2}{5+{cfrac {1}{7+{cfrac {1}{9+{cfrac {1}{11+ddots ,}}}}}}}}}$

This formula also converges, though more slowly, for z > 2. For example:

${displaystyle e^{3}=1+{cfrac {6}{-1+{cfrac {3^{2}}{6+{cfrac {3^{2}}{10+{cfrac {3^{2}}{14+ddots ,}}}}}}}}=13+{cfrac {54}{7+{cfrac {9}{14+{cfrac {9}{18+{cfrac {9}{22+ddots ,}}}}}}}}}$

Complex plane[edit]

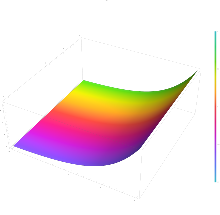
The exponential function e^z plotted in the complex plane from -2-2i to 2+2i

As in the real case, the exponential function can be defined on the complex plane in several equivalent forms.

The most common definition of the complex exponential function parallels the power series definition for real arguments, where the real variable is replaced by a complex one:

${displaystyle exp z:=sum _{k=0}^{infty }{frac {z^{k}}{k!}}}$

Alternatively, the complex exponential function may be defined by modelling the limit definition for real arguments, but with the real variable replaced by a complex one:

${displaystyle exp z:=lim _{nto infty }left(1+{frac {z}{n}}right)^{n}}$

For the power series definition, term-wise multiplication of two copies of this power series in the Cauchy sense, permitted by Mertens’ theorem, shows that the defining multiplicative property of exponential functions continues to hold for all complex arguments:

The definition of the complex exponential function in turn leads to the appropriate definitions extending the trigonometric functions to complex arguments.

In particular, when z = it (t real), the series definition yields the expansion

${displaystyle exp(it)=left(1-{frac {t^{2}}{2!}}+{frac {t^{4}}{4!}}-{frac {t^{6}}{6!}}+cdots right)+ileft(t-{frac {t^{3}}{3!}}+{frac {t^{5}}{5!}}-{frac {t^{7}}{7!}}+cdots right).}$

In this expansion, the rearrangement of the terms into real and imaginary parts is justified by the absolute convergence of the series. The real and imaginary parts of the above expression in fact correspond to the series expansions of cos t and sin t, respectively.

This correspondence provides motivation for defining cosine and sine for all complex arguments in terms of and the equivalent power series:^[14]

${displaystyle {begin{aligned}&cos z:={frac {exp(iz)+exp(-iz)}{2}}=sum _{k=0}^{infty }(-1)^{k}{frac {z^{2k}}{(2k)!}},\[5pt]{text{and }}quad &sin z:={frac {exp(iz)-exp(-iz)}{2i}}=sum _{k=0}^{infty }(-1)^{k}{frac {z^{2k+1}}{(2k+1)!}}end{aligned}}}$

for all

The functions exp, cos, and sin so defined have infinite radii of convergence by the ratio test and are therefore entire functions (that is, holomorphic on ). The range of the exponential function is , while the ranges of the complex sine and cosine functions are both in its entirety, in accord with Picard’s theorem, which asserts that the range of a nonconstant entire function is either all of , or excluding one lacunary value.

These definitions for the exponential and trigonometric functions lead trivially to Euler’s formula:

We could alternatively define the complex exponential function based on this relationship. If z = x + iy, where x and y are both real, then we could define its exponential as

where exp, cos, and sin on the right-hand side of the definition sign are to be interpreted as functions of a real variable, previously defined by other means.^[15]

For tinR , the relationship holds, so that for real and maps the real line (mod 2π) to the unit circle in the complex plane. Moreover, going from t=0 to $t=t_{0}$ , the curve defined by traces a segment of the unit circle of length

${displaystyle int _{0}^{t_{0}}|gamma '(t)|,dt=int _{0}^{t_{0}}|iexp(it)|,dt=t_{0},}$

starting from z = 1 in the complex plane and going counterclockwise. Based on these observations and the fact that the measure of an angle in radians is the arc length on the unit circle subtended by the angle, it is easy to see that, restricted to real arguments, the sine and cosine functions as defined above coincide with the sine and cosine functions as introduced in elementary mathematics via geometric notions.

The complex exponential function is periodic with period 2πi and holds for all .

When its domain is extended from the real line to the complex plane, the exponential function retains the following properties:

${displaystyle {begin{aligned}&e^{z+w}=e^{z}e^{w},\[5pt]&e^{0}=1,\[5pt]&e^{z}neq 0\[5pt]&{frac {d}{dz}}e^{z}=e^{z}\[5pt]&left(e^{z}right)^{n}=e^{nz},nin mathbb {Z} end{aligned}}}$

for all

Extending the natural logarithm to complex arguments yields the complex logarithm log z, which is a multivalued function.

We can then define a more general exponentiation:

${displaystyle z^{w}=e^{wlog z}}$

for all complex numbers z and w. This is also a multivalued function, even when z is real. This distinction is problematic, as the multivalued functions log z and z^w are easily confused with their single-valued equivalents when substituting a real number for z. The rule about multiplying exponents for the case of positive real numbers must be modified in a multivalued context:

(e^z)^w
≠ e^zw, but rather (e^z)^w
= e^{(z + 2niπ)w} multivalued over integers n

See failure of power and logarithm identities for more about problems with combining powers.

The exponential function maps any line in the complex plane to a logarithmic spiral in the complex plane with the center at the origin. Two special cases exist: when the original line is parallel to the real axis, the resulting spiral never closes in on itself; when the original line is parallel to the imaginary axis, the resulting spiral is a circle of some radius.

3D plots of real part, imaginary part, and modulus of the exponential function
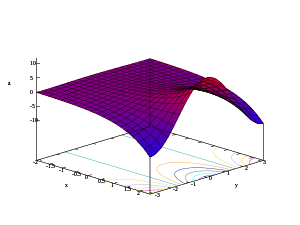
z = Re(e^{x + iy})
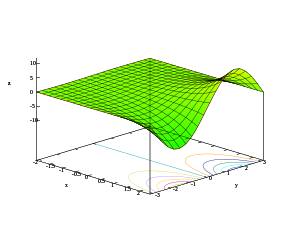
z = Im(e^{x + iy})
z = |e^{x + iy}|

Considering the complex exponential function as a function involving four real variables:

the graph of the exponential function is a two-dimensional surface curving through four dimensions.

Starting with a color-coded portion of the domain, the following are depictions of the graph as variously projected into two or three dimensions.

Graphs of the complex exponential function
Projection onto the range complex plane (V/W). Compare to the next, perspective picture.
Projection into the , , and dimensions, producing a flared horn or funnel shape (envisioned as 2-D perspective image).

The second image shows how the domain complex plane is mapped into the range complex plane:

The third and fourth images show how the graph in the second image extends into one of the other two dimensions not shown in the second image.

The third image shows the graph extended along the real axis. It shows the graph is a surface of revolution about the axis of the graph of the real exponential function, producing a horn or funnel shape.

The fourth image shows the graph extended along the imaginary axis. It shows that the graph’s surface for positive and negative values doesn’t really meet along the negative real axis, but instead forms a spiral surface about the axis. Because its values have been extended to ±2π, this image also better depicts the 2π periodicity in the imaginary value.

Computation of a^b where both a and b are complex[edit]

Complex exponentiation a^b can be defined by converting a to polar coordinates and using the identity (e^{ln a})^b
= a^b:

${displaystyle a^{b}=left(re^{theta i}right)^{b}=left(e^{(ln r)+theta i}right)^{b}=e^{left((ln r)+theta iright)b}}$

However, when b is not an integer, this function is multivalued, because θ is not unique (see failure of power and logarithm identities).

Matrices and Banach algebras[edit]

The power series definition of the exponential function makes sense for square matrices (for which the function is called the matrix exponential) and more generally in any unital Banach algebra B. In this setting, e⁰ = 1, and e^x is invertible with inverse e^−x for any x in B. If xy = yx, then e^{x + y} = e^xe^y, but this identity can fail for noncommuting x and y.

Some alternative definitions lead to the same function. For instance, e^x can be defined as

${displaystyle lim _{nto infty }left(1+{frac {x}{n}}right)^{n}.}$

Or e^x can be defined as f_x(1), where f_x : R → B is the solution to the differential equation df_x/dt(t) = x f_x(t), with initial condition f_x(0) = 1; it follows that f_x(t) = e^tx for every t in R.

Lie algebras[edit]

Given a Lie group G and its associated Lie algebra , the exponential map is a map ↦ G satisfying similar properties. In fact, since R is the Lie algebra of the Lie group of all positive real numbers under multiplication, the ordinary exponential function for real arguments is a special case of the Lie algebra situation. Similarly, since the Lie group GL(n,R) of invertible n × n matrices has as Lie algebra M(n,R), the space of all n × n matrices, the exponential function for square matrices is a special case of the Lie algebra exponential map.

The identity exp(x + y) = exp x exp y can fail for Lie algebra elements x and y that do not commute; the Baker–Campbell–Hausdorff formula supplies the necessary correction terms.

Transcendency[edit]

The function e^z is not in C(z) (that is, is not the quotient of two polynomials with complex coefficients).

If a₁, …, a_n are distinct complex numbers, then e^a₁z, …, e^a_nz are linearly independent over C(z). It follows that e^z is transcendental over C(z).

Computation[edit]

When computing (an approximation of) the exponential function near the argument 0, the result will be close to 1, and computing the value of the difference $e^{x}-1$ with floating-point arithmetic may lead to the loss of (possibly all) significant figures, producing a large calculation error, possibly even a meaningless result.

Following a proposal by William Kahan, it may thus be useful to have a dedicated routine, often called expm1, for computing e^x − 1 directly, bypassing computation of e^x. For example, if the exponential is computed by using its Taylor series

${displaystyle e^{x}=1+x+{frac {x^{2}}{2}}+{frac {x^{3}}{6}}+cdots +{frac {x^{n}}{n!}}+cdots ,}$

one may use the Taylor series of $e^{x}-1$ :

${displaystyle e^{x}-1=x+{frac {x^{2}}{2}}+{frac {x^{3}}{6}}+cdots +{frac {x^{n}}{n!}}+cdots .}$

This was first implemented in 1979 in the Hewlett-Packard HP-41C calculator, and provided by several calculators,^[16]^[17] operating systems (for example Berkeley UNIX 4.3BSD^[18]), computer algebra systems, and programming languages (for example C99).^[19]

In addition to base e, the IEEE 754-2008 standard defines similar exponential functions near 0 for base 2 and 10: $2^{x}-1$ and ${displaystyle 10^{x}-1}$ .

A similar approach has been used for the logarithm (see lnp1).^{[nb 3]}

An identity in terms of the hyperbolic tangent,

${displaystyle operatorname {expm1} (x)=e^{x}-1={frac {2tanh(x/2)}{1-tanh(x/2)}},}$

gives a high-precision value for small values of x on systems that do not implement expm1(x).

Notes[edit]

^ The notation ln x is the ISO standard and is prevalent in the natural sciences and secondary education (US). However, some mathematicians (for example, Paul Halmos) have criticized this notation and prefer to use log x for the natural logarithm of x.
^ In pure mathematics, the notation log x generally refers to the natural logarithm of x or a logarithm in general if the base is immaterial.
^ A similar approach to reduce round-off errors of calculations for certain input values of trigonometric functions consists of using the less common trigonometric functions versine, vercosine, coversine, covercosine, haversine, havercosine, hacoversine, hacovercosine, exsecant and excosecant.

References[edit]

^ ^a ^b Rudin, Walter (1987). Real and complex analysis (3rd ed.). New York: McGraw-Hill. p. 1. ISBN 978-0-07-054234-1.
^ Meier, John; Smith, Derek (2017-08-07). Exploring Mathematics. Cambridge University Press. p. 167. ISBN 978-1-107-12898-9.
^ Converse, Henry Augustus; Durell, Fletcher (1911). Plane and Spherical Trigonometry. Durell’s mathematical series. C. E. Merrill Company. p. 12. Inverse Use of a Table of Logarithms; that is, given a logarithm, to find the number corresponding to it, (called its antilogarithm) … [1]
^ “Exponential Function Reference”. www.mathsisfun.com. Retrieved 2020-08-28.
^ Goldstein, Larry Joel; Lay, David C.; Schneider, David I.; Asmar, Nakhle H. (2006). Brief calculus and its applications (11th ed.). Prentice–Hall. ISBN 978-0-13-191965-5. (467 pages)
^ Courant; Robbins (1996). Stewart (ed.). What is Mathematics? An Elementary Approach to Ideas and Methods (2nd revised ed.). Oxford University Press. p. 448. ISBN 978-0-13-191965-5. This natural exponential function is identical with its derivative. This is really the source of all the properties of the exponential function, and the basic reason for its importance in applications…
^ ^a ^b Weisstein, Eric W. “Exponential Function”. mathworld.wolfram.com. Retrieved 2020-08-28.
^ ^a ^b Maor, Eli. e: the Story of a Number. p. 156.
^ ^a ^b O’Connor, John J.; Robertson, Edmund F. (September 2001). “The number e”. School of Mathematics and Statistics. University of St Andrews, Scotland. Retrieved 2011-06-13.
^ Serway, Raymond A.; Moses, Clement J.; Moyer, Curt A. (1989). Modern Physics. Fort Worth: Harcourt Brace Jovanovich. p. 384. ISBN 0-03-004844-3.
^ Simmons, George F. (1972). Differential Equations with Applications and Historical Notes. New York: McGraw-Hill. p. 15. LCCN 75173716.
^ McGraw-Hill Encyclopedia of Science & Technology (10th ed.). New York: McGraw-Hill. 2007. ISBN 978-0-07-144143-8.
^ Lorentzen, L.; Waadeland, H. (2008). “A.2.2 The exponential function.”. Continued Fractions. Atlantis Studies in Mathematics. Vol. 1. p. 268. doi:10.2991/978-94-91216-37-4. ISBN 978-94-91216-37-4.
^ Rudin, Walter (1976). Principles of Mathematical Analysis. New York: McGraw-Hill. p. 182. ISBN 978-0-07-054235-8.
^ Apostol, Tom M. (1974). Mathematical Analysis (2nd ed.). Reading, Mass.: Addison Wesley. pp. 19. ISBN 978-0-201-00288-1.
^ HP 48G Series – Advanced User’s Reference Manual (AUR) (4 ed.). Hewlett-Packard. December 1994 [1993]. HP 00048-90136, 0-88698-01574-2. Retrieved 2015-09-06.
^ HP 50g / 49g+ / 48gII graphing calculator advanced user’s reference manual (AUR) (2 ed.). Hewlett-Packard. 2009-07-14 [2005]. HP F2228-90010. Retrieved 2015-10-10. [2]
^ Beebe, Nelson H. F. (2017-08-22). “Chapter 10.2. Exponential near zero”. The Mathematical-Function Computation Handbook – Programming Using the MathCW Portable Software Library (1 ed.). Salt Lake City, UT, USA: Springer International Publishing AG. pp. 273–282. doi:10.1007/978-3-319-64110-2. ISBN 978-3-319-64109-6. LCCN 2017947446. S2CID 30244721. Berkeley UNIX 4.3BSD introduced the expm1() function in 1987.
^ Beebe, Nelson H. F. (2002-07-09). “Computation of expm1 = exp(x)−1” (PDF). 1.00. Salt Lake City, Utah, USA: Department of Mathematics, Center for Scientific Computing, University of Utah. Retrieved 2015-11-02.

External links[edit]

“Exponential function”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]

Источник

Экспонента (экспоненциальная функция) — это математическая функция вида y = e×, или у = exp(x), или у = Exp(x) (где основанием степени является число е).

е — это число Эйлера, у него бесконечное количество цифр после запятой, оно трансцендентное и иррациональное. Оно равно округлённо 2,72 (а полностью — 2,718281828459045…).

Трансцендентным число называется, если оно не удовлетворяет ни одному алгебраическому уравнению. Иррациональным — если его нельзя представить в виде дроби m/n, где n не равно 0.

Несмотря на свою бесконечность, число е является константой. То есть значением, которое никогда не изменяется.

Показательная функция — это математическая функция вида y = a×.

График экспоненты выглядит следующим образом:

Для чего используется экспонента?

Экспонента применяется и в физике, и в технике, и в экономике, особенно при решении задач, связанных с процентами.

Экспоненциальный рост

Мы используем термин экспоненциальный рост, чтобы сказать о стремительном росте чего-либо. Словосочетание чаще всего употребляется по отношению к росту популяции людей или животных/птиц.

Что такое второй замечательный предел

Швейцарский математик Якоб Бернулли (1655–1705 гг.) вывел число е, когда пытался решить финансовый вопрос. В частности, он пытался понять, как должны начисляться проценты на сумму вклада в банке, чтобы это было наиболее прибыльно для владельца денег.

Он также пытался понять, есть ли лимит у дохода, получаемого в процентах, или он будет увеличиваться бесконечно.

Решая эту задачу, он использовал предел последовательности, а именно второй замечательный предел. Формулу для вычисления числа е можно записать следующим образом (где n — это число, стремящееся к бесконечности):

Второй замечательный предел

То есть числу е равняется предел, где n стремится к бесконечности, от 1, плюс 1, разделённый на n, и всё возвести в степень n.

Если подставить в данную формулу вместо n какую-нибудь очень большую цифру, можно получить очень хорошее приближение к е.
Например, подставим 1.000.000 и посчитаем на калькуляторе:

(1 + 1/1000000) ^ 1000000 = 2.7182804691

Как видите, с n = 1.000.000 мы получили достаточно хорошее приближение, с правильными 5 знаками после запятой.

Как определить число е?

Помимо второго замечательного предела, существуют и другие способы для определения числа е:

через сумму ряда;
через формулу Муавра — Стирлинга;
другие.

Сумма ряда

Существует мнение, что этот метод использовал сам Эйлер, когда высчитывал е.

Можно получить приближение е, рассчитав первые 7 частей этой суммы:

И эти вычисления дали нам следующий результат:

otvet

Этот метод дал нам точных 4 знака после запятой, и его достаточно легко запомнить.

Формула Муавра — Стирлинга

Также называется просто формула Стирлинга:

И в этом случае чем больше n, тем точнее будет результат.

Как запомнить число е

Можно легко запомнить 9 знаков после запятой, если заметить удивительную закономерность: после “2,7” число “1828” появляется дважды (2,7 1828 1828). В 1828 году родились Лев Толстой и Жюль Верн, а Франц Шуберт умер.

Хотите дальше? Можно и дальше! 15 знаков после запятой! Последующие цифры — это градусы углов в равнобедренном прямоугольном треугольнике ( 45°, 90°, 45°): 2,7 1828 1828 45 90 45.

Интересные факты

Экспоненциальную функцию также называют экспонента.

Показательная функция — это функция вида y=a×, где a — заданное число (основание), x — это переменная.

А если основание = е, с переменной x, то математически логарифм записывается как ln, а не как log. И его называют натуральный логарифм (логарифм с основанием е):

Логарифмическая функция, что обратная к показательной функции y = a×, a > 0, a≠1, пишется как .

Производная и первообразная экспоненциальной функции равны ей самой, т. е. (e×)’ = e×, но (a×)’ = (a×)*ln(a).

Якобу Бернулли в расчётах помогал его брат Иоганн. Один из кратеров на Луне носит их имя.

Число Непера и число Эйлера

Число Непера или Неперово число, число Эйлера — это названия для одного и того же числа е.

Шотландский математик Джон Непер придумал логарифмы. Так как число е является основанием натурального логарифма (ln x), то этому числу присвоили имя математика из Шотландии. Хотя Непер и не вычислял его.

Джон Непер — шотландский математик (1550–1617 гг.)

Сам символ e был придуман в 1731 году швейцарским математиком Леонардом Эйлером. Эйлер занимался вычислениями алгоритмов и вывел его основание. А точнее основание натурального логарифма, которым и является число е.

Леонард Эйлер — швейцарский математик (1707–1783 гг.)

Изобретение логарифмов в XVII веке (1614 год) шотландским математиком Джоном Непером стало одним из важнейших событий в истории математики.

Узнайте также, что такое Число Пи, Натуральные числа и Логарифм.

Источник

Определение[править | править код]

Происхождение понятия[править | править код]

Свойства[править | править код]

Комплексная экспонента[править | править код]

Свойства[править | править код]

Вариации и обобщения[править | править код]

Матричная экспонента[править | править код]

h-экспонента[править | править код]

Обратная функция[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Посчитать экспоненту

Онлайн калькулятор

Теория

Формула

Пример

См. также

Определение и формула экспоненты

График экспоненты

Свойства экспоненциальной функции

Graph[edit]

Relation to more general exponential functions[edit]

Formal definition[edit]

Overview[edit]

Derivatives and differential equations[edit]

Continued fractions for ex[edit]

Complex plane[edit]

Computation of ab where both a and b are complex[edit]

Matrices and Banach algebras[edit]

Lie algebras[edit]

Transcendency[edit]

Computation[edit]

See also[edit]

Notes[edit]

References[edit]

External links[edit]

Для чего используется экспонента?

Экспоненциальный рост

Что такое второй замечательный предел

Как определить число е?

Сумма ряда

Формула Муавра — Стирлинга

Как запомнить число е

Интересные факты

Число Непера и число Эйлера

Вам также может понравиться

Как исправить ошибку android process acore на телефоне zte

Как составить кроссворд в школу для 3 класса

Как можно найти работу без образования

Добавить комментарий Отменить ответ

Continued fractions for e^x[edit]

Computation of a^b where both a and b are complex[edit]