Постановка задачи
Данная задача чаще всего формулируется так:
Найти экстремали функционала
J[y]=∫x0x1L(x,y,y′)dxJ [y]=intlimits_{x_0}^{x_1}L (x, y, y’)dx
y(x0)=y0, y(x1)=y1y(x_0)=y_0,,,y(x_1)=y_1
Шаблон решения
Вычисление производных. Уравнение Эйлера
Уравнение Эйлера для данного функционала:
ddx∂∂y′L(x,y,y′)=∂∂yL(x,y,y′)frac{d}{dx}frac{partial}{partial y’}L(x,y,y’)=frac{partial}{partial y}L(x,y,y’)
Вычисляем производные:
∂∂yL(x,y,y′)frac{partial}{partial y}Lleft(x,y,y’right),
∂∂y′L(x,y,y′)frac{partial}{partial y’}Lleft(x,y,y’right),
ddx∂∂y′L(x,y,y′)frac{d}{dx}frac{partial}{partial y’}Lleft(x,y,y’right)
Выписываем уравнение Эйлера и приводим его к максимально простому виду.
Решение уравнения
Решаем полученное уравнение и выписываем общее решение:
y=y(x,C1,C2)y=y(x,C_1,C_2).
Определение констант
Используя граничные условия, получаем систему для определения постоянных:
{y(x0,C1,C2)=y0y(x1,C1,C2)=y1left{begin{array}{l}
yleft(x_0,C_1,C_2right)=y_0\
yleft(x_1,C_1,C_2right)=y_1
end{array}right.
Решая данную систему, получаем значения констант
C1=C1(x0,x1,y0,y1)C_1=C_1(x_0,x_1,y_0,y_1),
C2=C2(x0,x1,y0,y1)C_2=C_2(x_0,x_1,y_0,y_1).
Уравнение экстремали
Подставляем найденные в предыдущем пункте значения констант в общее решение и получаем уравнение экстремали функционала
y∗(x)=y(x,C1(x0,x1,y0,y1),C2(x0,x1,y0,y1))y_*(x)=y(x,C_1(x_0,x_1,y_0,y_1), C_2(x_0,x_1,y_0,y_1)).
Если подинтегральная функция L(x,y,y′)Lleft(x,y,y’right) не зависит от первого аргумента, то уравнение Эйлера имеет первый интеграл
y′∂L(y,y′)∂y′−L(y,y′)=C1y’frac{partial Lleft(y,y’right)}{partial y’}-Lleft(y,y’right)=C_1
Данное выражение определяет дифференциальное уравнение первого порядка, общее решение которого (зависящее от некоторой постоянной C2C_2) совпадает с решением уравнения Эйлера (См. пример 2 ниже).
Примеры
Пример 1
Найти экстремали функционала
J[y]=∫0π/2(4ycosx+y′2−y2)dxJ [y]=intlimits_{0}^{pi/2}(4y cos x+y’^2 – y^2) dx
y(0)=0, y(π/2)=1y(0)=0,,,y(pi/2)=1.
Решение
- Уравнение Эйлера для данного функционала имеет вид:
ddx∂∂y′(4ycosx+y′2−y2=∂∂y(4ycosx+y′2−y2){frac{d}{dx} frac{partial }{partial y{‘} }(4ycos x+y{‘} ^{2} -y^{2} =frac{partial }{partial y} (4ycos x+y{‘} ^{2} -y^{2}})
Вычислим производные:
∂∂y(4ycosx+y′2−y2)=4cosx−2y,∂∂y′(4ycosx+y′2−y2)=2y′,frac{partial}{partial y}left(4ycos x+y{‘} ^{2} -y^{2}right)=4cos x-2y,quadfrac{partial}{partial y’}left(4ycos x+y{‘}^{2} -y^{2}right)=2y’,
ddx∂∂y′(4ycosx+y′2−y2)=ddx(2y′)=2y′′.frac{d}{dx}frac{partial}{partial y’}left(4ycos x+y{‘} ^{2} -y^{2}right)=frac{d}{dx}left(2y’right)=2y”.
Таким образом, уравнение может быть записано как
2y′′=4cosx−2y ⇔ y′′+y=2cosx2y”=4cos x-2y,,Leftrightarrow,,
y”+y=2cos x
- Уравнение Эйлера является неоднородным ЛОДУ второго порядка с постоянными коэффициентами.
Общее решение соответствующего однородного уравнения
y0=C1cosx+C2sinx.y_{0} =C_{1} cos x+C_{2} sin x.
Решение неоднородного уравнения ищем в виде
y1=Axcosx+Bxsinx.y_{1} =Axcos x+Bxsin x.
Подстановка в уравнение Эйлера дает
y′′+y=−2Asinx+2Bcosx=2cosx.y”+y=-2Asin x+2Bcos x=2cos x.
Следовательно, A=0A=0 и B=1B=1.
Таким образом, общее решение уравнения Эйлера
y=C1cosx+C2sinx+xsinx.y=C_{1} cos x+C_{2} sin x+xsin x.
- Используя граничные условия, получаем систему для определения постоянных
{C1cos0+C2sin0+0sin0=0C1cosπ/2+C2sinπ/2+(π/2)sinπ/2=1left{begin{array}{l}
C_{1} cos 0+C_{2} sin 0+0sin 0=0\
C_{1} cos pi/2+C_{2} sin pi/2+left(pi/2right)sin pi/2=1
end{array}right.
Решая данную систему, получим
{C1=0C2+π/2=1⇔{C1=0C2=1−π/2left{begin{array}{l}
C_{1}=0\
C_{2}+pi/2=1
end{array}right.Leftrightarrow left{begin{array}{l}
C_{1}=0\
C_{2}=1-{pi}/{2}
end{array}right.
- Подставляем найденные в предыдущем пункте значения констант в общее решение и получаем уравнение экстремали функционала JJ
y∗(x)=(x+1−π2)sinx.y_*(x)=left(x+1-frac{pi}{2}right) sin x.
Пример 2
Найти экстремали функционала
J[y]=∫021+y′2ydx,J[y]=intlimits_{0}^{2}frac{sqrt{1+y’^2}}{y}dx,
y(0)=0, y(2)=4.y(0)=0,,,y(2)=4.
Решение
1, 2. Подинтегральная функция L(x,y,y′)=1+y′2yLleft(x,y,y’right)=frac{sqrt{1+y’^2}}{y} не зависит от переменной xx, поэтому уравнение Эйлера для данного функционала имеет первый интеграл
y′∂∂y′1+y′2y−1+y′2y=C,y’frac{partial }{partial y’}frac{sqrt{1+y’^2}}{y}-frac{sqrt{1+y’^2}}{y}=C,
где CC – некоторая постоянная.
Вычислив частную производную и выполнив элементарные преобразования, получим уравнение
y′=C12y2−1y’=sqrt{frac{C_1^2}{y^2}-1},
где C1=1/CC_1=1/C.
Отсюда следует, что
dx=ydyC12−y2.dx=frac{yd y}{sqrt{C_1^2-y^2}}.
Интегрируя, получим
x=∫ydyC12−y2=−12∫d(C12−y2)C12−y2=−C12−y2+C2.x=intfrac{y d y}{sqrt{C_1^2-y^2}}=-frac{1}{2}intfrac{d (C_1^2-y^2)}{sqrt{C_1^2-y^2}}=-sqrt{C_1^2-y^2}+C_2.
Таким образом, общее решение уравнения Эйлера
y(x)=C12−(x−C2)2.y(x)=sqrt{C_1^2-(x-C_2)^2}.
- Используя граничные условия, получаем систему для определения постоянных
{0=C12−(0−C2)24=C12−(2−C2)2⇔{C1=±C216=4C2−4⇔{C1=±5C2=5left{begin{array}{l}
0=sqrt{C_1^2-(0-C_2)^2}\
4=sqrt{C_1^2-(2-C_2)^2}
end{array}right.Leftrightarrow left{begin{array}{l}
C_1=pm C_2\
16=4C_2-4end{array}right.
Leftrightarrow left{begin{array}{l}
C_1=pm 5\
C_2=5
end{array}right.
- Подставляем найденные в предыдущем пункте значения констант в общее решение и получаем уравнение экстремали функционала JJ
y∗(x)=10x−x2.y_*(x)=sqrt{10x-x^2}.
Экстремаль является дугой окружности радиуса 5 с центром в точке (5,0)(5,0).
Пример 3
Важно отметить, что существуют функционалы, у которых нет экстремалей, удовлетворяющих данным граничным условиям.
Найти экстремали функционала
J[y]=∫01(xy+y2−2y2y′)dxJ[y]=intlimits_{0}^{1}(xy+y^2-2y^2y’)d x,
y(0)=y0, y(1)=y1.y(0)=y_0,,,y(1)=y_1.
Решение
Уравнение Эйлера для данного функционала имеет вид
ddx∂∂y′(xy+y2−2y2y′)=∂∂y(xy+y2−2y2y′)frac{d}{dx} frac{partial }{partial y{‘} } left(xy+y^2-2y^2y’right)=frac{partial }{partial y} left(xy+y^2-2y^2y’right)
Вычислим производные:
∂∂y(xy+y2−2y2y′)=x+2y−4yy′,∂∂y′(xy+y2−2y2y′)=−2y2,frac{partial}{partial y}left(xy+y^2-2y^2y’right)=x+2y-4yy’,quadfrac{partial}{partial y’}left(xy+y^2-2y^2y’right)=-2y^2,
ddx∂∂y′(xy+y2−2y2y′)=ddx(−2y2)=−4yy′.frac{d}{dx}frac{partial}{partial y’}left(xy+y^2-2y^2y’right)=frac{d}{dx}left(-2y^2right)=-4yy’.
Таким образом, уравнение Эйлера может быть записано как
x+2y−4yy′=−4yy′ ⇔ y=−x2x+2y-4yy’=-4yy’,,Leftrightarrow,,
y=-frac{x}{2}
и по сути не является дифференциальным.
Исходный функционал имеет только одну экстремаль y=−x2y=-frac{x}{2}. Поставленная задача имеет решение только если y0=0y_0=0 и y1=−12y_1=-frac{1}{2}.
Тест по теме «Одномерная задача с закрепленными концами»
Найти
экстремаль функционала
![]() (1.0)
(1.0)
Исследовать
полученную экстремаль на достаточные
условия экстремума. Построить график
решения.
В этом
примере подынтегральная функция
F(x,y,y)
является функцией общего вида, поэтому
составим уравнение Эйлера в виде (1.5) и
решим его. Затем построим график решения.
Попутно исследуем на выполнение
достаточных условия экстремума.
Ответ.Уравнение Эйлера после сокращения на
–2 будет:
![]() . (1.0)
. (1.0)
Его аналитическое
решение
![]() . (1.0)
. (1.0)
После подстановки
значений произвольных постоянных
экстремаль функционала (1.6) имеет вид
![]() . (1.0)
. (1.0)
График
её показан на рис.1.1. Так
как Fyy2>0,
и это условие выполняется y(x)
и y(x),
то всоответствии с достаточным
условием Лежандра найденная экстремаль
доставляет сильный минимум функционалу
(1.6).
Пример 1b
Найти экстремаль
функционала
![]() (1.0)
(1.0)
Исследовать на
выполнение достаточных условий
экстремума. Построить график решения.
В этом примере
подынтегральная функция F(x,y,y)
не зависит явно от y.
Первый интеграл уравнения Эйлера
имеет видFyC1.
Составим программу для решения этой
вариационной задачи. Вначале введём
исходные данные.
Ответ. Первый интеграл
дифференциального уравнения Эйлера
![]() . (1.0)
. (1.0)
Экстремаль функционала (1.11)
имеет вид
![]() . (1.0)
. (1.0)
График её
показан на рис.1.2. Так как
Fy’y’2>0,
и это выполняется y(x)
и y(x),
то подостаточному условию Лежандра
имеем сильный минимум.
Пример 1c
Найти экстремаль
функционала
![]() (1.0)
(1.0)
Исследовать на
достаточные условия. Построить график
решения.
Здесь подынтегральная
функция F(x,y,y)
не зависит явно от x.
Первый интеграл уравнения Эйлера
имеет видFyFyC1.
Составим программу для
решения этого примера. Вначале введём
исходные данные задачи.
Ответ. Первый интеграл
дифференциального уравнения Эйлера
![]() . (1.0)
. (1.0)
Экстремаль функционала (1.13)
имеет вид
![]() . (1.0)
. (1.0)
График её
показан на рис.1.3. Так как Fy’y’2y2>0,
имеем сильный минимум.
Задание
Для своего варианта
функционалов a), b), c) найти экстремали,
построить их графики и исследовать на
выполнение достаточных условий
экстремума.
Варианты заданий
Вариант 1.
a).
![]()
b).
![]()
c).
![]()
Вариант 2.
a).
![]()
b).
![]()
c).
![]()
Вариант 3.
a).
![]()
b).
![]()
c).
![]()
Вариант 4.
a).
![]()
b).
![]()
c).
![]()
Вариант 5.
a).
![]()
b).
![]()
c).
![]()
Вариант 6.
a).
![]()
b).
![]()
c).
![]()
Вариант 7.
a).
![]()
b).
![]()
c).
![]()
Вариант 8.
a).
![]()
b).
![]()
c).
![]()
Вариант 9.
a).
![]()
b).
![]()
c).
![]()
Вариант 10.
a).
![]()
b).
![]()
c).
![]()
Вариант 11.
a).
![]()
b).
![]()
c).
![]()
Вариант 12.
a).
![]()
b).
![]()
c).
![]()
Вариант 13.
a).
![]()
b).
![]()
c).
![]()
Вариант 14.
a).
![]()
b).
![]()
c).
![]()
Вариант 15.
a).
![]()
b).
![]()
c).
![]()
Вариант 16.
a).
![]()
b).
![]()
c).
![]()
Вариант 17.
a).
![]()
b).
![]()
c).
![]()
Вариант 18.
a).
![]()
b).
![]()
c).
![]()
Вариант 19.
a).
![]()
b).
![]()
c).
![]()
Вариант 20.
a).![]()
b).

c).
![]()
Вариант 21.
a).
![]()
b).
![]()
c).
![]()
Вариант 22.
a).
![]()
b).
![]()
c).
![]()
Вариант 23.
a).
![]()
b).
![]()
c).
![]()
Вариант 24.
a).
![]()
b).
![]()
c).
![]()
Вариант 25.
a).
![]()
b).
![]()
c).
![]()
Вариант 26.
a).
![]()
b).
![]()
c).
![]()
Вариант 27.
a).
![]()
b).
![]()
c).
![]()
Вариант 28.
a).
![]()
b).
![]()
c).
![]()
Вариант 29.
a).
![]()
b).
![]()
c).
![]()
Вариант 30.
a).![]()
b).
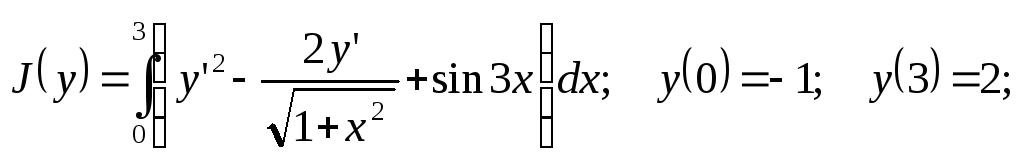
c).
![]()
-
Экстремаль функционала, зависящего от нескольких функций Краткие теоретические сведения
Рассмотрим
задачу отыскания экстремума функционала,
зависящего от нескольких функций одной
переменной и их первыхпроизводных:
 .(2.0)
.(2.0)
Экстремаль
функционала должна удовлетворять в
общем случае 2nграничным условиям:
 (2.0)
(2.0)
Как и ранее (см. глава
1), необходимое условием экстремума
такого функционала – равенство нулю
его вариации, вычисленной на экстремали
{y10(x),y20(x),…,yn0(x)}.
Так как функционал достигает экстремума
на множестве варьируемых функций с
закреплёнными концами, то он тем более
будет достигать экстремума на более
узком классе функций: когда варьируется
только одна из них, а остальные
зафиксированы. Значит, каждая из функцийyi(x) должна удовлетворять
уравнению Эйлера (1.5). Таким образом, для
нахожденияэкстремалей
мы получаем системуnдифференциальных
уравнений Эйлера
 (2.0)
(2.0)
дополненную 2nграничными условиями (2.2).
Данную вариационную
задачу при n=2 можно интерпретировать
геометрически. Обозначим функции черезy(x) иz(x). Тогда задача
сводится к отысканию линии, проходящей
через заданные две точкиM1(x1,y1,z1)
иM2(x2,y2,z2),
и доставляющей экстремум функционалу
(2.1).
Вариационное исчисление: примеры и задачи
Вариационное исчисление для чайников
Древнейшей из задач на максимум и минимум является задача отыскания среди плоских замкнутных кривых заданной длины такую, которая охватывает наибольшую площадь (5 в до н.э.) – и это классическая изопериметрическая задача вариационного исчисления. Началось же классическое вариационное исчисление с задачи о кривой наискорейшего спуска (брахистохроне) в 1696 г. с публикации Иоганна Бернулли.
Общие принципы и методы решения задач вариационного исчисления были введены в 18 веке Эйлером и Лангранжем, они же установили тесную связь между ВИ и естествознанием. Далее на протяжении более чем двух столетий они разрабатывались, были найдены помимо необходимых условий первого порядка (уравнений Эйлера-Лагранжа) необходимые и достаточные услвоия второго порядка для сильных и слабых экстремумов.
На этой странице мы рассмотрим примеры с подробным решением следующих типов: простейшая задача вариационного исчисления, задача Больца, изопериметрическая задача, задача со старшими производными. А также научимся находить вариацию и допустимые экстремали функционала. Все это относится к классическому вариационному исчислению.
Смежные задачи вы можете найти в соответствующих разделах: Нелинейное программирование, Многокритериальная оптимизация, Математическое программирование и т.д.
Понравилось? Добавьте в закладки
Вариационное исчисление: задачи с решениями
Задача 1. Решить классическую задачу вариационного исчисления:
$$
int_0^1 dot{x}^2 dt to extr, quad x(0)=1, x(1)=0.
$$
Задача 2. Решить задачу Больца
$$
int_0^1 dot{x}^2 dt +alpha x^2(1) to extr, quad x(0)=1.
$$
Задача 3. Решить изопериметрическую задачу
$$
int_0^1 dot{x}^2 dt to extr, int_0^1 x^2 dt =3, quad x(0)=1, x(1)=6.
$$
Задача 4. Решить задачу со старшими производными
$$
int_0^pi (ddot{x}^2+4x^2) dt to extr, quad x(0) = dot x(0)=0, , dot x(pi)=sh(pi).
$$
Задача 5. Найти все экстремали функционала $J(y)$, удовлетворяющие указанным граничным условиям
$$
J(y)=int_0^1 (e^y +xy’)dx, quad y(0)=0, y(1)=1.
$$
Задача 6. Найти все экстремали функционала $J(y)$, удовлетворяющие указанным граничным условиям
$$
J(y)=int_0^1 e^{-x}cdot y” ^2 dx, quad y(0)=0, y'(0)=1, y(1)=e, y'(1)=2e.
$$
Задача 7. Для указанной вариационной задачи записать уравнение Эйлера и найти экстремаль, удовлетворяющую условиям $y(0) = 19, y(1)=30$
$$int_0^1 (1+y’^2)dx.$$
Задача 8. Найти вариацию функционала
$$int_0^1 (x+y’)ln sin y’ dx.$$
Задача 9. Найти все экстремали функционала $J(y)$, удовлетворяющие указанным граничным условиям
$$
J(y)=int_0^{pi/4} (4ysin x +y’^2-y^2)dx, quad y(0)=0, y(pi/4)=0.
$$
Консультации и помощь
Нужно выполнить контрольную работу или задачи по вариационному исчислению и смежным предметам? Нет проблем! Стоимость консультации по решению – от 150 рублей, подробное оформление согласно требованиям методички в Word.
Решение задач вариационного исчисления на заказ
Полезные ссылки
- Вариационное исчисление: задачи, алгоритмы, примеры Крайне удобная для решения задач методичка: для каждого типа задач есть теория, краткий алгоритм и пример решения нескольких задач. Рекомендуем.
- Вариационное исчисление и основы теории управления Краткое учебное пособие с примерами задач по ВИ
- Эльсгольц Л.Э. Вариационное исчисление Классический учебник, теория изложена на простом уровне, множество разобранных примеров по каждому разделу.
- Изопериметрическая задача: теория и примеры решения
Уравнение Эйлера
В многомерном случае основная задача вариационного исчисления записывается в виде системы n уравнений:
i=1:n. (9.10»)
Уравнение (9.10) называется уравнением Эйлера. Оно было найдено Эйлером в 1744г. и играет центральную роль в вариационном исчислении.
Решения уравнения Эйлера называются экстремалями. Только на экстремалях может достигаться экстремум функционала.
Уравнение Эйлера является только необходимым, но не достаточным условием экстремума. Оно не дает гарантии того, что на экстремали действительно достигается экстремум (подобно тому, как в дифференциальном исчислении точки, где y‘ = 0, не обязательно доставляют экстремум функции y(t)).
Таким образом, с помощью уравнения Эйлера можно фактически определить функцию, на которой может достигаться экстремум, но не всякое решение уравнения Эйлера является решением поставленной вариационной задачи.
Пример 9.1. Определить функцию, на которой может достигаться экстремум функционала
при граничных (краевых) условиях
y(0) = 0, y(1) = 1.
Решение. В рассматриваемом примере F = y 2 + y‘ 2 , поэтому
В результате уравнение Эйлера будет иметь вид
y» – y = 0.
Решение полученного уравнения ищем в виде y = e rx . В результате получаем уравнение r 2 – 1 = 0. Откуда r = ± 1, r1 = 1, r2 = -1.
В общем виде решение уравнения Эйлера имеет вид
y(х) = С1e r 1 x +С2e r 2 x
y(х) = С1e x +С2e -х .
Из граничных условий получаем
Окончательно, экстремаль имеет вид
Пример 9.2.Нужно определить кратчайшую линию y(x), соединяющую точки на плоскости – (0;0) и (1;1).
Решение. Длина кривой выражается интегралом
т.е. в данном случае ; , , и уравнение Эйлера принимает вид:
т.е. , где С и – постоянные интегрирования.
Таким, образом, уравнение Эйлера позволило нам определить, что кратчайшим путем, соединяющим две точки на плоскости, может быть только прямая линия. Две произвольные постоянные в формуле (9.11) находятся из условий прохождения линии через две заданные точки.
В данном случае = 0; C = 1 и y = x.
Пример 9.3.Найти экстремали функционала
удовлетворяющие граничным условиям y(1) = 1, y(3) = 4,5.
Решение.Fy = 3x-2y, Fy‘ = 0.
Уравнение Эйлера имеет вид 3x-2y = 0, откуда y(x) = x – экстремаль.
Так как найденная экстремаль не удовлетворяет граничному условию y(1) = 1, то вариационная задача решения не имеет.
Как найти экстремаль функционала
Библиографическая ссылка на статью:
Абдрахманов В.Г., Рабчук А.В., Князева Н.Г. Решение некоторых задач вариационного исчисления. Часть 1 // Современная педагогика. 2013. № 2 [Электронный ресурс]. URL: https://pedagogika.snauka.ru/2013/02/1407 (дата обращения: 25.01.2022).
1. ПРОСТЕЙШАЯ ЗАДАЧА ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
Дан функционал J[y]= 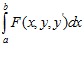 (1)
(1)
при граничных условиях у (а )= у 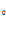 , у (в) = у
, у (в) = у 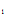 (2)
(2)
Задача отыскания экстремума этого функционала называется простейшей задачей вариационного исчисления. Основой для решения задачи является утверждение: Если функция у(х) дает экстремум (1) то она является решением уравнения Эйлера
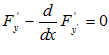
Решение уравнения Эйлера – это семейство кривых у = у (х, С 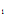 ,С
,С 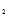 ) которые называются экстремалями функционала (1). Константы С
) которые называются экстремалями функционала (1). Константы С 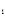 и С
и С  находятся из граничных условий (2).
находятся из граничных условий (2).

Пример 1. 
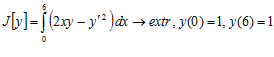 .
.
□ 
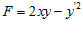
(Рассматриваем 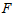 как функцию трех переменных x, y, y
как функцию трех переменных x, y, y ).
).
а) 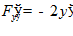 ;
;
б) 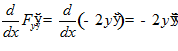 ;
;
в) 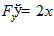 .
.
Составляем уравнение Эйлера
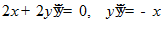 . Интегрируем дважды:
. Интегрируем дважды:

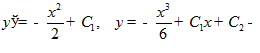 экстремали (множество кривых).
экстремали (множество кривых).
Используя краевые условия, находим
1 = C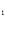 , 1= -216/6 +6 C
, 1= -216/6 +6 C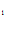 + C
+ C
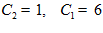 .
.
Единственная экстремаль 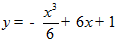

Пример 2. 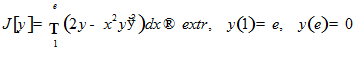
□ Уравнение Эйлера 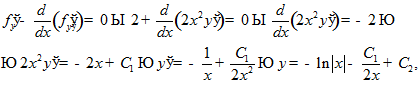

или, с учетом 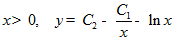 .
.
Используем краевые условия:
e = C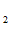 — C
— C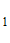 , 0= C
, 0= C 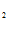 – C
– C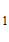 /e -1, откуда C
/e -1, откуда C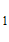 =-е, C
=-е, C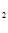 =0.
=0.
Единственная экстремаль 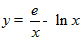 .■
.■
2. ОБОБЩЕНИЕ ПРОСТЕЙШЕЙ ЗАДАЧИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ.
1. Дан функционал вида
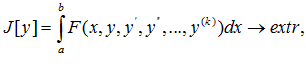
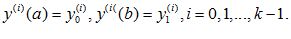
Если функция у(х) дает экстремум данному функционалу , то она является решением уравнения Эйлера-Пуассона
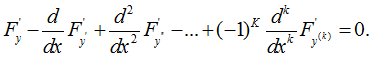
Пример 3. 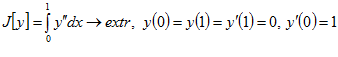 .
.
□ . Уравнение Эйлера-Пуассона,
. Уравнение Эйлера-Пуассона, 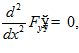 т.е.
т.е. 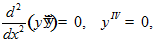 отсюда
отсюда 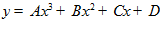 ,
, 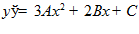 .
.
Для нахождения коэффициентов используем граничные условия:
A + B + C + D = 0, откуда A = 1, B = – 2, C= 1, D = 0.
Получаем единственную экстремаль
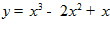 .
.
Пример 4. 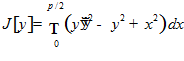
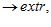
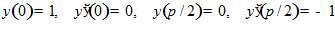 .
.
□ 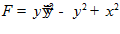 .
.
Уравнение Эйлера-Пуассона: 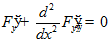 ,
,
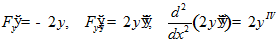 ,
,
так что уравнение имеет вид 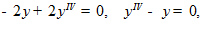
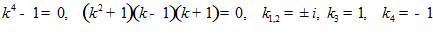 ,
,
y=C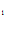 COSX + C
COSX + C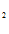 SINX + C
SINX + C 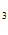 e
e 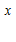 + C
+ C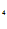 e
e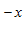
y  = – C
= – C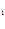 SINX + C
SINX + C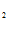 COSX + C
COSX + C 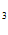 e
e 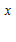 – C
– C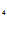 e
e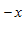
Используем граничные условия:
C 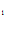 +C
+C +C
+C 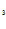 =1,
=1,
C +C
+C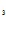 — C
— C 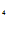 = 0, из системы C==1, C
= 0, из системы C==1, C =0, C
=0, C 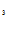 =0, C
=0, C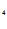 =0.
=0.
C +C
+C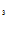 e
e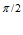 +C
+C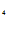 e
e 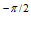 =0,
=0,
-C 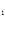 +C
+C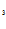 e
e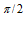 -C
-C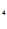 e
e 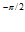 =-1.
=-1.
Единственная экстремаль 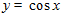 . ■
. ■
2. Дан функционал вида
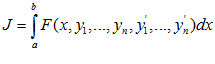
Граничные условия 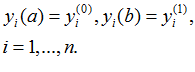
Экстремали находим из системы уравнений Эйлера
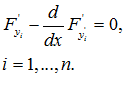
Пример 5. 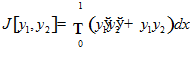
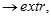
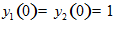 ,
, 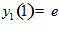 ,
, 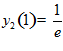 .
.
□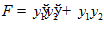 ,
, 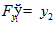 ,
, 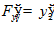 ,
, 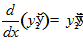 ,
,
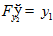 ,
, 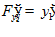 ,
, 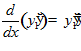 .
.
Система уравнений Эйлера имеет вид: y 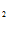 – y
– y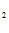
 =0,
=0,
y 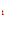 – y
– y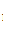
 = 0.
= 0.
Рассмотрим второе уравнение 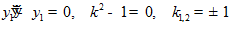 , отсюда
, отсюда 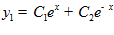 , аналогично
, аналогично 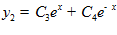 .
.
Для определения констант используем граничные условия
C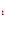 +C
+C =1 откуда
=1 откуда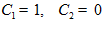 .
.
C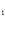 e+ C
e+ C /e = e
/e = e
C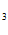 +C
+C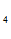 =1, C
=1, C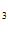 + C
+ C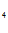 /e = 1/e
/e = 1/e
откуда 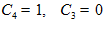 .
.
Получаем 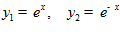 . ■
. ■
Задачи для самостоятельного решения
1. 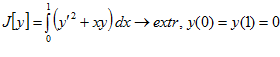 .
.
2. 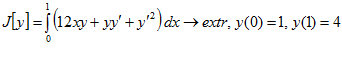 .
.
3. 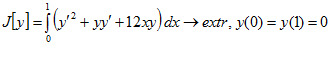 .
.
4. 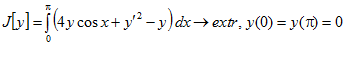 .
.
5. 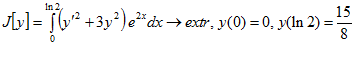 .
.
6. 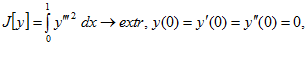
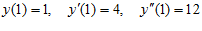 .
.
7. 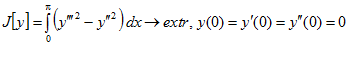 ,
,
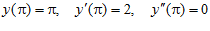 .
.
8. 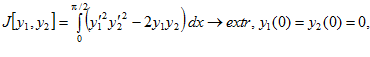
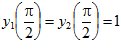 .
.
9. 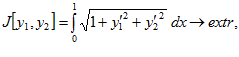
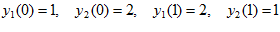 .
.
ЗАДАНИЕ 1
а) Вычислить функционал 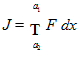 для заданных функций
для заданных функций 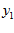 и
и 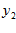 .
.
б) Написать уравнение Эйлера для функций 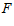 (Таблица 1).
(Таблица 1).
Как найти экстремаль функционала
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 71a9e11d9ac59018 • Your IP : 82.102.23.104 • Performance & security by Cloudflare
