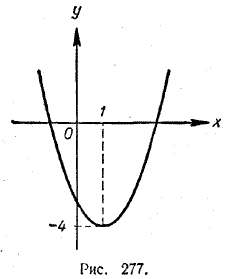Как найти экстремальное значение скорости тела

1.3.1.Отличать
среднюю скорость на данном участке пути
от
мгновенной
скорости.

1.3.2.Записывать
уравнение координаты по известным
начальной
координате, скорости и
ускорению.

1.3.3.Решать
задачи координатным методом.

1.3.4.Рассчитывать
скорости и ускорения при поступательном
и
вращательном
движении тел методом дифференцирования.

1.4.Примеры решения задач.

К
наиболее
типичным задачам по кинематике
принадлежат:

1.4.1
Задачи на определение средней скорости.

1.4.2.
Задачи о поступательном движении или
о вращении твер­дого
тела вокруг оси, в которых заданы их
уравнения движения.

1.4.3.Задачи, в которых
требуется определить максимальное
или
минимальное
значение одной из кинематических
величин.

1.4.5. Задачи на
движение тел в гравитационном поле
Земли.

При
решении задач (1.4.1.)
нужно уметь ориентироваться в си­туации,
когда даны части пути, пройденного телом
или время про­хождения
каждой части пути. Если даны части пути,
то в скалярной формуле
средней скорости
(гдеS
— весь путь, t
–
все время движения,
включая время остановок) нужно выразить
время
t
через данные части пути и скорости, а
если даны доли времени, то необ­ходимо
общий путь S
выразить через скорости и доли времени

Решение
задач (1.4.2.) основано на использовании
формул пере­меним,
скорости, ускорения, где неизвестные
находятся путем дифференцирования.

Задачи
(1.4.3.)
требуют применения методов математического
анализа к
исследованию функции на экстремум. В
них нужно полу­чить
алгебраическое выражение искомой
величины в произвольный момент времени,
записав ее через данные характеристики
движения. Что6ы
найти
максимум или минимум этой величины или
условие, при
котором она будет экстремальной, нужно
продифференцировать полученное
выражение и приравнять производную к
нулю. В результате
мы получим уравнение, из которого можно
найти значение параметра,
определяющего минимальное или максимальное
значе­ние
искомой величины. Будет ли функция иметь
максимум или минимум,
можно иногда определить из физических
соображений, а в общем
случае – по второй производной.

Если
вторая производная окажется больше
нуля, функция имеет минимум,
если меньше – максимум. Подставляя
найденное значение 11
исходную формулу, мы получим экстремальное
значение искомой величины.
Этот прием особенно часто применяется
при решении задач
на кинематику колебательного движения,
изучение которого предусмотрено
в третьем семестре.

К
задачам (1.4.5.) относятся задачи на
свободное падение тел, движение
тел, подброшенных вверх, брошенных
горизонтально и мод
углом к горизонту и др.

Эти
задачи удобно решать координатным
методом по следующе­му
плану:

1.Выбрать тело
отсчета, систему координат (ось X
направить по
направлению
начальной скорости).

2. Записать
уравнение координаты в общем виде для
каждого тела:

1. Найти
   начальные условия и подставить их в
   уравнение коор­динаты.

,

.

3.
Записать уравнение координаты для
данного движения (с уче­том
начальных условий).

4.Найти искомое
неизвестное, используя, если нужно,
уравнение

проекции
скорости (,)

,

или=const.

Движение тел,
брошенных горизонтально или под углом
к гори­зонту,
можно представить как результат двух
одновременных неза­висимых
прямолинейных движений: одного вдоль
поверхности Зем­ли,
второго – в направлении перпендикулярном
поверхности Земли. Иными
словами, сложное прямолинейное движение
можно разло­жить
на два простых, которые происходят в
одно и то же время. По­этому решение
таких задач необходимо начинать с
разложения век­тора
начальной скорости по двум взаимно
перпендикулярным осям ОХ
и OY,
применив алгоритм решения к проекциям
величин по осям
ОХ и OY.

Задача
1.4.1
(а)
Первую половину своего пути автомобиль
дви­гался
со скоростью
=
72к.м/ч, а
вторую половину пути – со

скоростью

км/ч.
Какова
средняя скорость движения авто­мобиля?

Дано:
;;км/ч;
3
6 км/ч.

?

Анализ и решение:

Путь
пройденный телом, состоит из двух равных
частей поS
каждая. Потому время,
в течение которого автомобиль прошел
первую
половину пути, равно

,
вторую
–
.

Подставив эти
значения в формулу
скалярной величины средней скорости,
получим:

Произведем
вычисления, переведя в систему СИ

м/с;
10м/с.

м/с.

Задача
1.4.1(6)
Велосипедист
ехал из одного пункта в другой. Первую
часть пути он проехал со скоростью
= 18км/ч.
Далее
половину
оставшегося
времени он ехал со скоростью

=
22км/Iч,
после чего до конечного пункта он шел
пешком со скоростью
=5
км/ч. Определить
среднюю скорость
велосипедиста.

Дано:

= 18км/ч;

=
22км/Iч;

=5
км/ч;

;.

-?

Анализ и решение:

где
S
– весь путь , t
– все время. Первую треть пути велосипедист
проехал за время
.
ОставшиесяS
он первую половину времени ехал со
скоростью
,
а вторую половину со скоростью,
поэтому средняя скорость на этом пути.

Подставив это
значение в общую формулу, получим:

.

Выразим величины
скоростей в СИ и произведем вычисления

5
м/с;6,1м/с;
1,6м/с.

м/с.

Задача
1.4.2(а) Зависимость
пройденного пути S
от времени да­ется
уравнением: S=
At
— Bt²
+
Ct³,
где
A=2
м/с, В=3 м/с ²,
С=4 м/с³.

Найти:
а) зависимость скорости и ускорения от
времени,

б)
скорость и ускорение за t=2
с от начала движения.

Построить
график зависи­мости
скорости и ускорения от времени для
интервала 0
t
<3
счерез
0,5 с.

Дано:
А=2 м/с.;В=3м/с;
С=4м/с.

;
(t)
– ?;
– ?;– ?

Анализ
и решение:

Так
как путь задан уравнением
,скорость
определим,

продиффенцировав
по времени
Соответственно
ускорение.

Подставив значение
постоянных величин получим скорость и
ускорение:

и
.Следовательно,
через 2 с от на­чала
движения

м/с.

Построим
графики зависимостей v(t)
и a(t):

Задача
1.4.2(6) Колесо
радиусом R=0,l
м
вращается так, что за­висимость угла
поворота радиуса колеса от времени
дается уравне­нием
,
где В=2рад/с,
С=1 рад/.
Для точек, лежащихна
ободе колеса, найти через время t=2
с после начала движения: а)
угловую скорость
,
б)
линейную скорость v,
в) угловое ускоре­ние
,
д) тангенциальное и нормальное ускорение.

Дано:
R=0,1
м;
B=2
рад/с;
C=1
рад/;t=2
c.

?,
V-?,
-?,-?,-?

Анализ и решение:

Угловую скорость
найдем дифференцированием.

;
Линейная скорость связана с угловой:
.

Угловое
ускорение – первая производная от
угловой скорости.
.

Тангенциальное
и нормальное ускорения можно найти по
формулам:

,

.
Подставим в формулы числовые значения
величин и рассчитаем.

Получим:
14рад/с,
v=1.4м/с

=12рад/,
=1,2м/с,

=19,6
м/

Задача 1.4.2(в)
Тело вращается вокруг неподвижной оси
по зако­ну
,
где А=10рад,
В=20 рад/с,
С= -2 рад/.
Найти полное ускорение точки, находящейся
на расстоянии R=
0,1 м
от оси вращения, для момента времени
t=4
с.

Дано: A=10
рад; В=20
рад/с,
С=-2рад/

а-?

Анализ и решение:

Полное ускорение
точки, движущейся по кривой линии, может
быть найдено как геометрическая сумма
тангенциального и нор­мального
ускорений.

.

Так как векторы
ивзаимно перпендикулярны, то модуль
ускорения.

Но
,

поэтому

Угловую скорость
найдем, взяв производную угла поворота
по времени:

.
В момент времени t=4
с
угловая скорость:

=
20 + 2(-2) 4 =4 (рад/с).
Угловое ускорение найдем, взяв
первую производную от угловой
скорости по времени:

(рад/с)
. Подставляя значения
ив формулу ускорения, получим:=l,65(м/).

Задача 1.4.3(а)
Зависимость пройденного телом пути от
времени выражается уравнением S=.
Найти

экстремальное
значение скорости тела. Построить график
зависимости скорости от вре­мени за
первые 5 с движения, если а=0,25м/,
b=9
м/.

Дано: а=0,25м/,
b=9
м/.

-?

Анализ и решение:

Найдем зависимость
скорости от времени, определив производную
и подставив числовые значения а
и b.
.
Для нахождения экстремума возьмем
производную от скорости по времени и
приравняем ее нулю:–
18 = 0;

.
Нас интересует положительный корень:
t=2,45
с;

поэтому
= -29,3м /с.

a	t
0	0
1	-17
2	-28
2,45	-29,3
3	-27
4	8
5 5	35

Задача 1.4.4(а)
С аэростата, находящегося на высоте 300
м, упал камень. Через сколько времени
камень достигнет Земли, если: 1) аэростат
поднимается со скоростью 5 м/с, 2) аэростат
опускается со скоростью 5 м/с, 3) аэростат
неподвижен. Сопро­тивлением воздуха
пренебречь.

Дано:
h=300
м,
v=5
м/с

–
?
–
?–
?

Анализ и решение:

В данной задаче
рассматривается свобод­ное падение
тела. Воспользуемся приведен­ным выше
планом решения.

1. Выберем в
качестве тела отсчета аэростат в
начальный момент времени. Так как
движе­ние происходит в одном направлении,

2. Запишем
уравнение координаты данного
равноускоренного движения (свободного
па­дения) для камня:

3. Найдем начальные
условия для ответа на первый вопрос
зада­чи:=
0,

=
-5м/с,
а
= g.

0Проекция начальной скорости камня
по модулю равна скорости аэростата и
имеет знак «-», так как скорость направлена
против осиOY.

4. Подставим
начальные условия в уравнение координаты:

.

y

1. Конечная координата
   известна (y
   = ЗОО м),
   поэтому
   

Решая это уравнение,
находим искомое неизвестное

Подставив числовые
значения, получим:

с

Отбрасывая
отрицательный корень, получим
8,3 с .

Ответы на второй
и третий вопросы задачи предлагаются
студентам для самостоятельной работы.
Приведем эти решения:

2.
,=0
.=5м/с,

,

,7,3с.

3.
=0,=0,a=g,

,,7,8с.

Задача 1.4.4(6)
Тело брошено вертикально вверх с
начальной ско­ростью
=4м/с.
Когда оно достигло верхней точки полета
из того же начального пункта, с той же
начальной скоростью
вертикально
вверх брошено второе тело. На каком
расстоянииh
от начального пункта встретятся тела?
Сопротивление воздуха не учитывать.

Дано:
=4м/с,
a=,

.

h-?

Анализ и решение:

Y
Выберем ось OY
снизу вверх по

направлению
движения первого тела.

h
Уравнение координаты в общем виде
.

Для
первого тела начальные условия согласно

выбранному
направлению оси
=
0,=4м/с,
a=
–g.

0
Следовательно уравнение координаты
первого тела

(1)

Для второго тела
уравнение координаты будут отличаться
только значением времени:

Определим время
t,
исходя из того, что скорость в наи­высшей
точке v=0

,
v=0,
a=-g
поэтому
,

Но время движения
второго тела как раз на эту величину
меньше времени движения первого тела:

,
поэтому
(2)

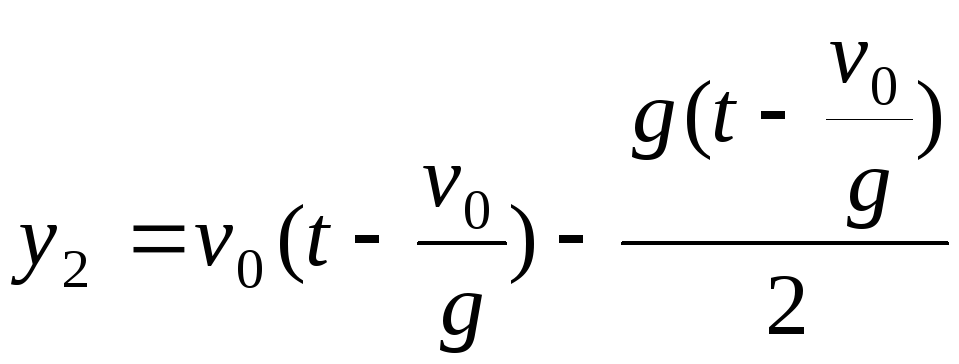
При встрече тел
их координата будет одной и той же,
.
Приравняв (1) и (2), получим:

Определим время
встречи тел t:

,

Поскольку
расстояние от начального пункта, на
котором встретятся тела,

,
то

м.

Задача 1.4.4(в)
С башни высотой h=25
м горизонтально
брошен камень со скоростью
=
15м/с. Какое
время t
камень будет
в движении? На каком расстоянии х от
основания башни он упадет на землю? С
какой скоростью он упадет на землю?
Какой угол составит траектория камня
с горизонтом в точке его падения?

Дано:
=
15м/с,
h=25
м.

t-?,
x-?,
v-?,
-?

Анализ и решение:

Y

A

0

X

v

Вдоль оси OY
камень двигался равноускоренно:
.

Начальные условия:
=h,
0,a=-g.
Поэтому
.
Но конечная координатаy=0
и
.
Время движения тела:с.

По оси ОХ тело
движется равномерно. Поэтому расстояние,
на котором оно упадет на землю
.

Но
0,33,9м.

Чтобы определить
скорость, с какой тело упадет на землю,
нужно найти скорость в точке А по
вертикали
,
поэтому

26,7
м/с.

Угол
,
который составит траектория камня с
горизонтом, определится так:

sin=
0,827, откуда
= 55°48′.

Соседние файлы в папке Пр.зан,СРС

• #
• #
• #
• #
• #
• #

1.3.Что надо уметь:

1.3.1.Отличать среднюю скорость на данном участке пути от мгновенной скорости.

1.3.2.Записывать уравнение координаты по известным начальной координате, скорости и ускорению.

1.3.3.Решать задачи координатным методом.

1.3.4.Рассчитывать скорости и ускорения при поступательном и вращательном движении тел методом дифференцирования.

1.4.Примеры решения задач.

К наиболее типичным задачам по кинематике принадлежат:

1.4.1 Задачи на определение средней скорости.

1.4.2. Задачи о поступательном движении или о вращении твер­дого тела вокруг оси, в которых заданы их уравнения движения.

1.4.3.Задачи, в которых требуется определить максимальное или минимальное значение одной из кинематических величин.

1.4.5. Задачи на движение тел в гравитационном поле Земли.

При решении задач (1.4.1.) нужно уметь ориентироваться в си­туации, когда даны части пути, пройденного телом или время про­хождения каждой части пути. Если даны части пути, то в скалярной формуле средней скорости (гдеS — весь путь, t — все время движения, включая время остановок) нужно выразить время t через данные части пути и скорости, а если даны доли времени, то необ­ходимо общий путь S выразить через скорости и доли времени

Решение задач (1.4.2.) основано на использовании формул пере­меним, скорости, ускорения, где неизвестные находятся путем дифференцирования.

Задачи (1.4.3.) требуют применения методов математического анализа к исследованию функции на экстремум. В них нужно полу­чить алгебраическое выражение искомой величины в произвольный момент времени, записав ее через данные характеристики движения. Что6ы найти максимум или минимум этой величины или условие, при котором она будет экстремальной, нужно продифференцировать полученное выражение и приравнять производную к нулю. В результате мы получим уравнение, из которого можно найти значение параметра, определяющего минимальное или максимальное значе­ние искомой величины. Будет ли функция иметь максимум или минимум, можно иногда определить из физических соображений, а в общем случае — по второй производной.

Если вторая производная окажется больше нуля, функция имеет минимум, если меньше — максимум. Подставляя найденное значение 11 исходную формулу, мы получим экстремальное значение искомой величины. Этот прием особенно часто применяется при решении задач на кинематику колебательного движения, изучение которого предусмотрено в третьем семестре.

К задачам (1.4.5.) относятся задачи на свободное падение тел, движение тел, подброшенных вверх, брошенных горизонтально и мод углом к горизонту и др.

Эти задачи удобно решать координатным методом по следующе­му плану:

1.Выбрать тело отсчета, систему координат (ось X направить по направлению начальной скорости).

2. Записать уравнение координаты в общем виде для каждого тела:

Найти начальные условия и подставить их в уравнение коор­динаты.

, .

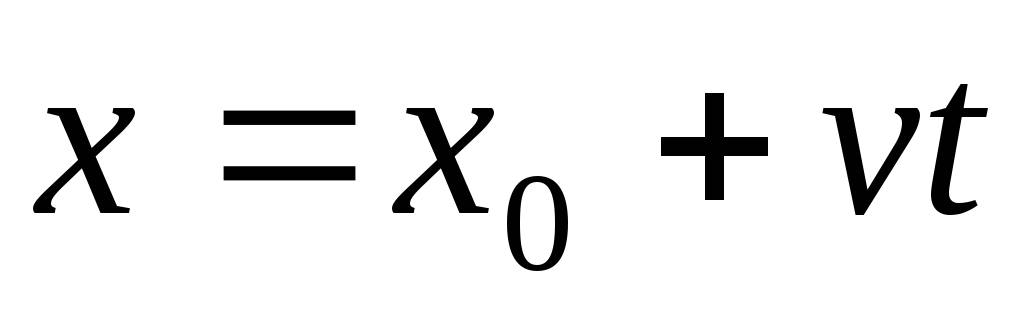
3. Записать уравнение координаты для данного движения (с уче­том начальных условий).

4.Найти искомое неизвестное, используя, если нужно, уравнение

проекции скорости (,)

, или=const.

Движение тел, брошенных горизонтально или под углом к гори­зонту, можно представить как результат двух одновременных неза­висимых прямолинейных движений: одного вдоль поверхности Зем­ли, второго — в направлении перпендикулярном поверхности Земли. Иными словами, сложное прямолинейное движение можно разло­жить на два простых, которые происходят в одно и то же время. По­этому решение таких задач необходимо начинать с разложения век­тора начальной скорости по двум взаимно перпендикулярным осям ОХ и OY, применив алгоритм решения к проекциям величин по осям ОХ и OY.

Задача 1.4.1 (а) Первую половину своего пути автомобиль дви­гался со скоростью = 72к.м/ч, а вторую половину пути — со

скоростью км/ч. Какова средняя скорость движения авто­мобиля?

Дано: ;;км/ч; 3 6 км/ч.

?

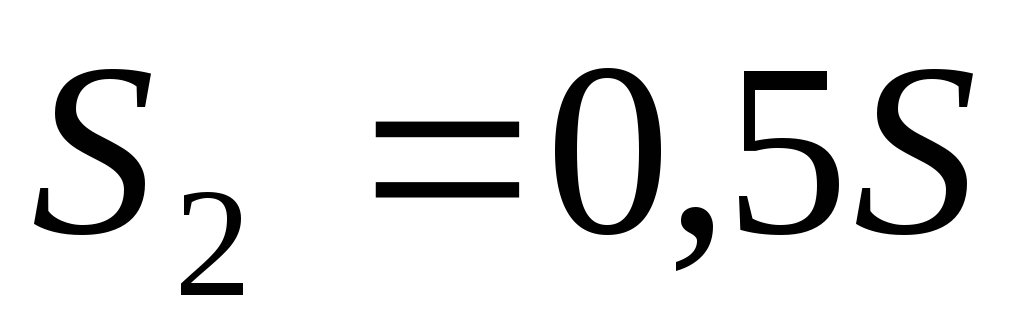
Анализ и решение:

Путь пройденный телом, состоит из двух равных частей поS каждая. Потому время, в течение которого автомобиль прошел первую половину пути, равно

, вторую — .

Подставив эти значения в формулу скалярной величины средней скорости, получим:

Произведем вычисления, переведя в систему СИ

м/с; 10м/с.

м/с.

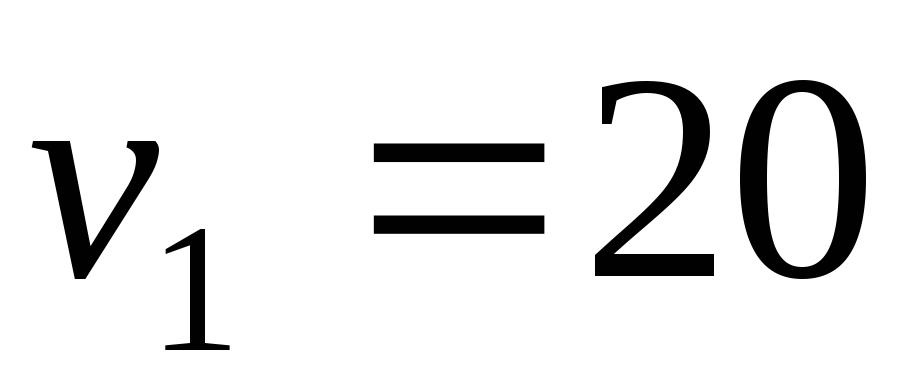
Задача 1.4.1(6) Велосипедист ехал из одного пункта в другой. Первую часть пути он проехал со скоростью = 18км/ч. Далее половину оставшегося времени он ехал со скоростью = 22км/Iч, после чего до конечного пункта он шел пешком со скоростью =5 км/ч. Определить среднюю скорость велосипедиста.

Дано: = 18км/ч; = 22км/Iч; =5 км/ч; ;.

-?

Анализ и решение:

где S – весь путь , t – все время. Первую треть пути велосипедист проехал за время . ОставшиесяS он первую половину времени ехал со скоростью , а вторую половину со скоростью, поэтому средняя скорость на этом пути.

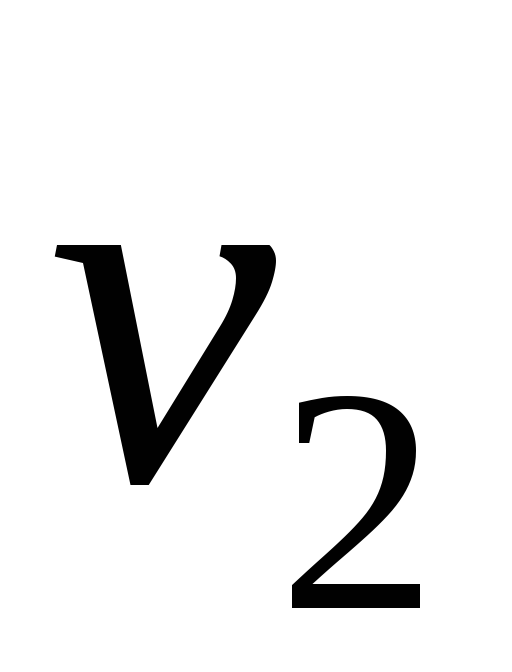
Подставив это значение в общую формулу, получим:

.

Выразим величины скоростей в СИ и произведем вычисления

5 м/с;6,1м/с; 1,6м/с.

м/с.

Задача 1.4.2(а) Зависимость пройденного пути S от времени да­ется уравнением: S= At — Bt 2 + Ct 3 , где A=2 м/с, В=3 м/с 2 , С=4 м/с 3 .

Найти: а) зависимость скорости и ускорения от времени,

б) скорость и ускорение за t=2 с от начала движения.

Построить график зависи­мости скорости и ускорения от времени для интервала 0 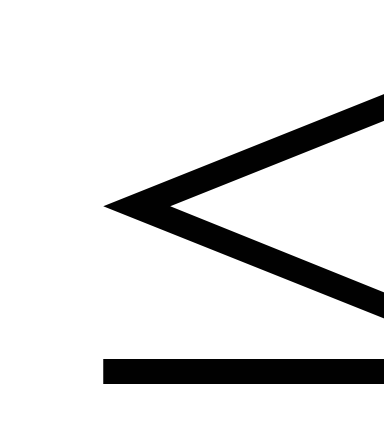t

Источник

Что значит экстремальное значение скорости

ФУНКЦИИ И ПРЕДЕЛЫ IX

§ 205. Экстремальные значения функции

В этом параграфе мы изучим некоторые вопросы поведения функции у = f (х) в интервале [а, b]. При этом, конечно, мы будем предполагать, что функция f (х) определена в каждой точке этого интервала.

Наибольшее из всех тех значений, которые принимает функция у = f (х) в интервале [а, b], называется ее абсолютным максимумом, а наименьшее — абсолютным минимумом в данном интервале.

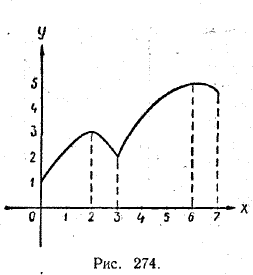
Например, для функции у = f (х) , графически представленной на рисунке 274, абсолютным минимумом в интервале [0,7] является значение f (0) = 1, а абсолютным максимумом — значение f (6) =5.

Наряду с абсолютным максимумом и абсолютным минимумом в математике часто говорят о локальных (т. е. местных) максимумах и минимумах.

Точка х = с, лежащая внутри интервала [а, b], называется точкой локального максимума функции у = f (х) , если для всех значений х, достаточно близких к с,

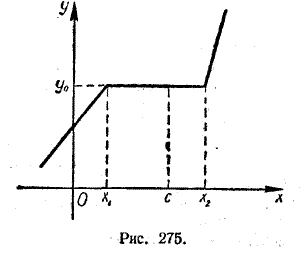
Для функции у = f (х), графически представленной на рисунке 275, точкой локального максимума будет, например, точка х = с. Для всех х, достаточно близких к с,

так что условие (1) выполняется.

Точка х = с, лежащая внутри интервала [а, b], называется точкой локального минимума функции у = f (х), если для всех значений х, достаточно близких к с,

Значения функции в точках еe локальных минимумов называются локальными минимумами этой функции.

Например, для функции у = f (х), графически представленной на рисунке 274, точкой локального минимума является точка х = 3, а самим локальным минимумом — значение f (3) = 2.

Точка х = с, отмеченная нами выше как точка локального максимума, является вместе с тем и точкой локального минимума. Ведь для всех точек х, достаточно близких к ней,

Точки минимумов и точки максимумов функции f (х) называются точками экстремумов этой функции. Значения функции f (х) в точках экстремумов называются экстремальными значениями этой функции.

Рисунок 274 показывает различие между абсолютными и локальными экстремумами. Функция у = f (х), изображенная на этом рисунке, имеет в точке х = 2 локальный максимум, который не является абсолютным максимумом в интервале [0, 7]. Точно так же и точке х = 3 эта функция имеет локальный минимум, не являющийся абсолютным минимумом в интервале [0, 7].

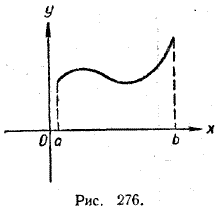
Если абсолютный максимум функции у = f (х) в интервале [а, b] достигается во внутренней точке этого интервала, то этот абсолютный максимум является, очевидно, и локальным максимумом (см., например, рис. 274 в точке х = 6). Но может случиться, что этот абсолютный максимум достигается не внутри интервала [a, b], а в какой-нибудь крайней его точке (рис. 276).

Тогда он не является локальным максимумом. Отсюда вытекает следующее правило для нахождения абсолютного максимума функции у = f (х) в интервале [a, b],

1. Находим все локальные максимумы функции у = f (х) в данном интервале.

2. К полученным значениям добавляем значения этой функции в концах данного интервала, то есть значения f (а) и f (b).

Наибольшее из всех этих значений и даст нам абсолютный максимум функции у = f (х) в интервале [a, b] . Аналогично находится и абсолютный минимум функции у = f (х) в интервале [a, b].

Пример. Найти все локальные экстремумы функции у = x 2 — 2х — 3. Каковы наибольшее и наименьшее значения этой функции в интервале [0, 5]?

Преобразуем данную функцию, выделив полный квадрат:

Теперь легко построить ее график. Это будет направленная вверх парабола с вершиной в точке (1, —4) (рис. 277).

Единственной точкой локального экстремума является точка х = 1. В этой точке функция имеет локальный минимум, равный —4. Чтобы найти наибольшее и наименьшее значения данной функции в интервале [0, 5], заметим, что при x = 0 у = — 3, а при х = 5 у = 12. Из трех значений —4, —3 и 12 наименьшим является —4, а наибольшим 12. Таким образом, наименьшее значение (абсолютный минимум) данной функции в интервале [0, 5] равно —4; оно достигается при х = 1. Наибольшее значение (абсолютный максимум) данной функции в интервале [0, 5] равно 12; оно достигается при х = 5.

1589. Какие из известных вам функций на всей числовой прямой:

а) совсем не имеют локальных экстремумов;

б) имеют ровно один локальный экстремум;

в) имеют бесконечное множество локальных экстремумов?

В упражнениях № 1590—1600 найти точки локальных экстремумов и сами локальные экстремумы данных функций. Выяснить, какие это экстремумы (максимумы или минимумы):

Найти абсолютные экстремумы данных функций в указанных интервалах (№ 1601—1603):

Источник

Как найти предельную скорость

wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 11 человек(а).

Количество просмотров этой статьи: 34 506.

Вы никогда не задумывались, почему при падении парашютисты в конечном итоге достигают предельной максимальной скорости, хотя сила тяжести в вакууме заставляет тело постоянно ускоряться? Падающее тело достигает предельной скорости, когда есть некая сдерживающая сила, такая, как сопротивление воздуха. Сила тяжести действует на тело с постоянной величиной, но сила сопротивления воздуха увеличивается с увеличением скорости падения тела. Если свободное падение длится достаточно долго, то скорость падения тела достигнет такой величины, при которой сила сопротивления станет равна силе тяжести, и эти силы будут компенсировать друг друга; в результате этого тело будет продолжать падение с постоянной скоростью, пока не коснется земли. Такая скорость называется предельной скоростью.

Как определить максимальную и минимальную скорости движущихся объектов — манекены — Бизнес — 2022

Одним из наиболее практических применений дифференциации является поиск максимальных или минимальных значений функции реального мира, например максимальной и минимальной скоростей движущегося объекта.

Вы можете представить v elocity как более техническую версию скорость .

Вот пример. Йо-йо движется прямо вверх и вниз. Его высота над землей, как функция времени, задается функцией H ( t ) = t 3 — 6 t 2 + 5 t + 30, где t находится в секундах и H ( t ) находится в дюймов. При t = 0 yo-yo составляет 30 дюймов над землей, а через 4 секунды он находится на высоте 18 дюймов, как показано на этом рисунке.

Высота yo-yo, от 0 до 4 секунд.

Чтобы определить общее расстояние, пройденное yo-yo, вам нужно добавить расстояния, пройденные на каждой ноге поездки yo-yo: вверх нога, нога и вторая нога.

Во-первых, йо-йо поднимается с высоты от 30 дюймов до 31 дюймов (где первая точка поворота). Это расстояние около 1,1 дюйма. Затем он опускается примерно с 31. 1 до 16. 9 (высота второй точки поворота). Это расстояние 31. 1 минус 16. 9, или около 14. 2 дюйма. Наконец, yo-yo снова поднимается с 16 дюймов до конечной высоты 18 дюймов. Это еще 1 дюйм. Добавьте эти три расстояния, чтобы получить общее пройденное расстояние:

Примечание: Сравните этот ответ с общим объемом перемещения — 12, который вы получаете от вычитания конечной высоты yo-yo, 18 дюймов, от ее начальная высота 30 дюймов. Смещение отрицательно, потому что движение сети вниз. И положительная величина смещения (а именно 12) меньше расстояния, пройденного 16. 4, потому что при смещении верхние ноги рейса yo-yo отменяют часть расстояния вниз. Посмотрите математику:

Средняя скорость yo-yo определяется общим пройденным пройденным расстоянием, деленным на прошедшее время. Таким образом,

Скажем, вы определяете, что максимальная скорость yo-yo составляет 5 дюймов в секунду, а ее минимальная скорость составляет -7 дюймов в секунду. Скорость -7 — это скорость 7, так что это максимальная скорость yo-yo. Его минимальная скорость равна нулю в двух оборотных точках.

Хорошим способом анализа максимальной и минимальной скорости является рассмотрение функции скорости и ее графика. (Или, если вы являетесь обжором для наказания, ознакомьтесь со следующим mumbo jumbo.) Скорость равна абсолютному значению скорости.

Velocity, V ( t ), является производной от позиции (высота, в этой задаче). Таким образом:

Итак, для задачи yo-yo, функция скорости,

Посмотрите на график S ( t ) на следующем рисунке.

Функция скорости yo-yo S ( t )

Глядя на этот график , легко видеть, что максимальная скорость yo-yo происходит при t = 2

и что минимальная скорость равна нулю на двух x -перехватах.

Минимальная и максимальная скорость: Для непрерывной функции скорость минимальная скорость равна нулю всякий раз, когда максимальная и минимальная скорости имеют противоположные знаки или когда один из них нуль. Когда максимальная и минимальная скорости являются как положительными, так и отрицательными, скорость минимум меньше абсолютных значений максимальной и минимальной скоростей. Во всех случаях максимальная скорость представляет собой больше абсолютных значений максимальной и минимальной скоростей. Это глоток или что?

Как найти максимальную скорость по графику

Чтобы узнать знак производной, рисуем координатную прямую, отмечаем точку 1/2 и определяем знаки производной подбором.

Берем любую точку, например, 0.

— 60 * 0 + 30 = 30 (производная положительна, функция возрастает)

Берем например, точку 1.

— 60 * 1 + 30 = — 30 (производная отрицательна, функция убывает)

Значит, t = 1/2 — это точка максимума.

Подставим это значение в уравнение скорости.

v = — 30t 2 + 30t + 2

v = — 30(1/2) 2 + 30 * 1/2 + 2 = — 7,5 + 15 + 2 = 9,5.

Ответ: максимальная скорость движения равна 9,5.

Из уравнения S = — 10t^3 + 15t^2 + 2t сначала найдем производную пути по времени(это будет уравнение скорости точки): S'(t) = V(t) = — 30t^2 + 30t + 2. Графиком функции данного уравнения является парабола и как видим около t^2(то есть коэффициент а) стоит отрицательное число, значит ветки параболы направлены вниз и максимальное значение t достигается на вершине параболы, найдем ее: tmax = — b / 2a = 30 / 30 * 2 = 0,5. Подставим в уравнение скорости и найдем Vmax получим Vmax = — 30 * 0,5^2 + 30 * 0,5 + 2 = 9,5.

• Попроси больше объяснений
• Следить
• Отметить нарушение

Ответ

Ответ:

Объяснение:

Находим L. Разделим путь на три отрезка(как на графике)(с 0 по 1 секунду, потом с 1 до 4 секунды и с 4 по 5 секунду)

1. S = Vot(начальная скорость умноженная на время) + at²/2 ; a(ускорение) = ΔV/Δt = 15 м/с²

S = 0 + 15*1/2 = 7,5 м

2. S = V*t = 15*3 = 45 м

3. S = Vot + at²/2 ; a = ΔV/Δt = — 15 м/с² (тело тормозит)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

То есть ускорение – это величина, которая определяется изменением скорости за время, в течение которого это изменение произошло.

Еще раз о том, что такое равноускоренное движение

Автомобиль за каждую секунду увеличивает свою скорость на . Движется ли автомобиль равноускоренно?

На первый взгляд, кажется, да, ведь за равные промежутки времени скорость увеличивается на равные величины. Давайте рассмотрим подробнее движение на протяжении 1 с. Возможен такой случай, что первые 0,5 с автомобиль двигался равномерно и увеличил свою скорость на Часто равноускоренным называют такое движение, при котором тело двигается с постоянным ускорением . Самым простым примером равноускоренного движения является свободное падение тела (тело падает под действием силы тяжести).

Уравнение скорости

Воспользовавшись уравнением, определяющим ускорение , удобно записать формулу для вычисления мгновенной скорости любого промежутка и для любого момента времени:

Уравнение скорости в проекциях имеет вид:

Это уравнение дает возможность определить скорость в любой момент движения тела. При работе с законом изменения скорости от времени необходимо учитывать направление скорости по отношению к выбранной СО.

К вопросу о направлении скорости и ускорения

В равномерном движении направление скорости и перемещения всегда совпадают. В случае равноускоренного движения направление скорости не всегда совпадает с направлением ускорения и не всегда направление ускорения указывает направление движения тела.

Рассмотрим наиболее типичные примеры направления скорости и ускорения.

1. Скорость и ускорение направлены в одну сторону вдоль одной прямой (рис. 1).

Рис. 1. Скорость и ускорение направлены в одну сторону вдоль одной прямой

В данном случае тело разгоняется. Примерами такого движения могут быть свободное падение, начало движения и разгон автобуса, старт и разгон ракеты.

2. Скорость и ускорение направлены в разные стороны вдоль одной прямой (рис. 2).

Рис. 2. Скорость и ускорение направлены в разные стороны вдоль одной прямой

Такое движение иногда называют равнозамедленным. В таком случае говорят, что тело тормозит. В конечном итоге оно либо остановится, либо начнет двигаться в противоположном направлении. Пример такого движения – камень, подброшенный вертикально вверх.

3. Скорость и ускорение взаимно перпендикулярны (рис. 3).

Рис. 3. Скорость и ускорение взаимно перпендикулярны

Примерами такого движения является движение Земли вокруг Солнца и движение Луны вокруг Земли. В этом случаи траекторией движения будет окружность.

Таким образом, направление ускорения не всегда совпадает с направлением скорости, но всегда совпадает с направлением изменения скорости.

График скорости

График скорости (проекции скорости) представляет собой закон изменения скорости (проекции скорости) от времени для равноускоренного прямолинейного движения, представленный графически.

Рис. 4. Графики зависимости проекции скорости от времени для равноускоренного прямолинейного движения

Проанализируем различные графики.

Первый. Уравнение проекции скорости:

Второй – это зависимость при отрицательном значении проекции ускорения, когда движение замедленно, то есть скорость по модулю сначала уменьшается. В этом случае уравнение выглядит так:

График начинается в точке

Где

Рис. 5. График функции

Это уравнение прямой, что подтверждается графиками, рассмотренными нами.

Некоторые частные случаи

Чтобы окончательно разобраться с графиком скорости, рассмотрим частные случаи. На первом графике зависимость скорости от времени связана с тем, что начальная скорость, , равняется нулю, проекция ускорения больше нуля.

Запись этого уравнения . А сам вид графика достаточно простой (график 1).

Рис. 6. Различные случаи равноускоренного движения

Еще два случая равноускоренного движения представлены на следующих двух графиках. Второй случай – это ситуация, когда сначала тело двигалось с отрицательной проекцией ускорения, а затем начало разгоняться в положительном направлении оси.

Третий случай – это ситуация, когда проекция ускорения меньше нуля и тело непрерывно движется в направлении, противоположном положительному направлению оси . При этом модуль скорости постоянно возрастает, тело ускоряется.

График зависимости ускорения от времени

Равноускоренное движение – это движение, при котором ускорение тела не меняется.

Рис. 7. График зависимости проекций ускорения от времени

Если какая-либо зависимость является постоянной, то на графике она изображается прямой, параллельной оси абсцисс. Прямые I и II – прямые движения для двух разных тел. Обратите внимание, что прямая I лежит выше прямой абсцисс (проекция ускорения положительна), а прямая II – ниже (проекция ускорения отрицательна). Если бы движение было равномерным, то проекция ускорения совпала бы с осью абсцисс.

Рассмотрим рис. 8. Площадь фигуры, ограниченной осями, графиком и перпендикуляром к оси абсцисс, равна:

Произведение ускорения и времени –это изменение скорости за данное время.

Рис. 8. Изменение скорости

Площадь фигуры, ограниченной осями, зависимостью и перпендикуляром к оси абсцисс, численно равна изменению скорости тела.

Мы использовали слово «численно», поскольку единицы измерения площади и изменения скорости не совпадают.

Заключение

На данном уроке мы познакомились с уравнением скорости и научились графически изображать данное уравнение.

1. Кикоин И.К., Кикоин А.К. Физика: Учебник для 9 класса средней школы. – М.: «Просвещение».
2. Перышкин А.В., Гутник Е.М., Физика. 9 кл.: учебник для общеобразоват. учреждений/А.В. Перышкин, Е.М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300 с.
3. Соколович Ю.А., Богданова Г.С. Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «class-fizika.narod.ru» (Источник)
2. Интернет-портал «youtube.com» (Источник)
3. Интернет-портал «fizmat.by» (Источник)
4. Интернет-портал «sverh-zadacha.ucoz.ru» (Источник)

1. Что такое равноускоренное движение?

2. Охарактеризуйте движение тела и определите пройденный путь тела по графику за 2 с от начала движения:

3. На каком из графиков изображена зависимость проекции скорости тела от времени при равноускоренном движении при ?

Была ли эта статья полезной?