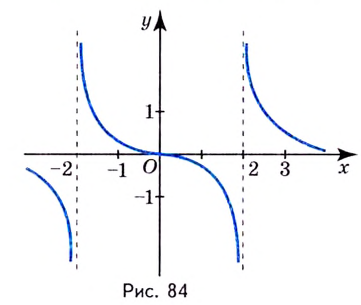
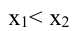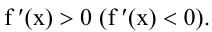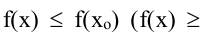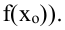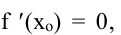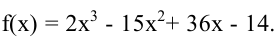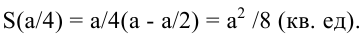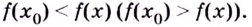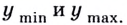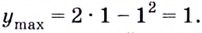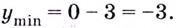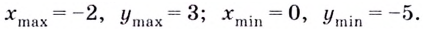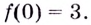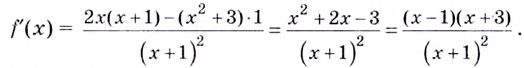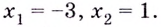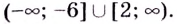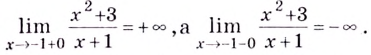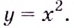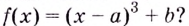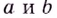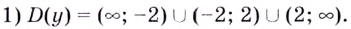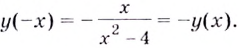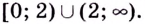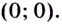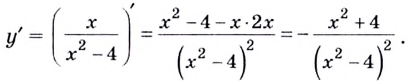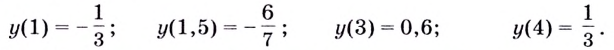Опр. Функция
называетсядифференцируемой
в данной точке
,
если приращениеэтой
функции в точке,
соответствующее приращению аргумента,
может быть представлено в виде,(9)
где
–
некоторое число, не зависящее от,
а– функция аргумента
,
являющаяся бесконечно малой при.
Заметим, что функция
(
)
может принимать в точке=0
какое угодно значение. Ради определенности
можно положить(0)=0
(при этом частное значение функции(
)
в точке=0
будет совпадать с ее предельным значением
в этой точке).
Так как произведение
двух бесконечно малых
является бесконечно малой более высокого
порядка, чем,
т.е.=0(
),
то формулу (9) можно переписать в виде.
Пусть функция
определена
всюду в некоторой окрестности точки.
Опр. Говорят,
что функция
имеет
в точкелокальный
максимум (минимум),
если найдется такая окрестность точки
,
в пределах которой значениеявляется наибольшим (наименьшим) среди
всех значений этой функции.
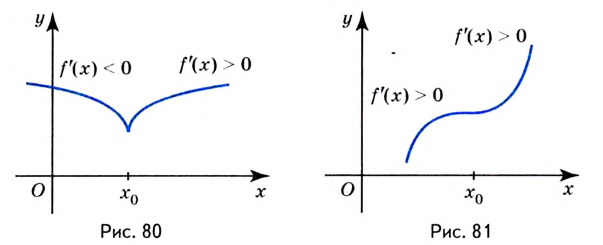
На рис.1 изображена
функция
,
имеющая локальный максимум в точке.
Локальный максимум
и локальный минимум объединяются общим
названием локальный
экстремум.
Теоремы0(
о достаточном условии возрастания
(убывания) функции
в точке
):если функция
дифференцируема в точке
и
,
то эта функция возрастает (убывает) в
точке.
Опр. Говорят,
что функция
возрастает
(убывает)
в точке
,
если найдется такая окрестность точки,
в пределах которойпри
и
при
(
при
и
при
).
Установим необходимое
условие экстремума
дифференцируемой функции.
Теорема1.
Если функция
дифференцируема в точке
и имеет в этой точке локальный экстремум,
то.
Доказательство.
Так как функция
имеет локальный экстремум в точке
,
тоне может в этой точке ни возрастать, ни
убывать. Стало быть, в силутеоремы0
производная
не может быть ни положительна, ни
отрицательна, т.е..
Теорема1 имеет
простой геометрический смысл: она
утверждает, что если в точке кривой
,
которой соответствует локальный
экстремум функции,
существует касательная параллельно
оси(рис.1).
касательная
–
Таким образом, для
отыскания у дифференцируемой функции
точек возможного экстремума следует
найти все корни уравнения(т.е. найти все нули производной
).
Впредь мы будем называть корни уравненияточкамивозможного
экстремума функции
(иногда
корни уравненияназываютсястационарными
точками).
-
Первое достаточное
условие экстремума
Теорема2.
Пусть точка
является точкой возможного экстремума
функции,
и пусть функциядифференцируема всюду в некоторой
окрестности точки.
Тогда, если в пределах указанной
окрестности производнаяположительна
(отрицательна) слева от точкии отрицательна (положительна) справа
от точки,
то функцияимеет в точке
локальный максимум (минимум). Если же
имеет
один и тот же знак слева и справа от
точки,
то экстремума в точкенет.
Доказательство.
1) Пусть сначала производная
в
пределах рассматриваемой окрестности
положительна (отрицательна) слева оти отрицательна (положительна) справа
от.
Требуется доказать, что значениеявляется наибольшим (наименьшим) среди
всех значенийв рассматриваемой окрестности. Обозначим
любое
значение аргумента из рассматриваемой
окрестности, отличное от
.
Достаточно доказать, что.
Функция
дифференцируема (а столь быть, и
непрерывна) на сегменте.
Применяя кпо сегменту
теорему Лагранжа (см. 4 вопрос), будем
иметь
,
(10)
где
–
некоторое значение аргумента междуи
.
Поскольку производная положительна
(отрицательна) при<
и отрицательна (положительна) при
>
,
правая часть (10) положительна (отрицательна).
2) Пусть теперь
производная
имеет один и тот же знак слева и справа
от.
Обозначая, как выше, черезлюбое
значение аргумента, отличное от
,
и повторяя проведение выше рассуждения,
мы теперь докажем, что правая часть (10)
имеетразные
знаки при
<
и при
>
.
Это отсутствие экстремума в точке.
Вытекающее из
теоремы2 правило можно кратко сформулировать
так: 1) если при переходе через данную
точку
возможного экстремума производная
меняет
знак с плюса на минус (с минуса на плюс),
то функцияимеет в точке
локальный максимум (минимум); 2) если же
при переходе через данную точкувозможного экстремума производная
не
меняет знака, то экстремума в точкенет.
Примеры.
1) Предполагая, что консервная банка
имеет форму круглого цилиндра радиуса
r
и высоты h,
определитель, при каком соотношении
между r
и h
консервная банка с постоянной площадью
полной поверхности имеет наибольший
объем.
Обозначим площадь
полной поверхности консервной банки
через S.
Тогда
. (11)
Из этого равенства
находим, что
.
Таким образом, мы
можем выразить объем V
консервной банки как функцию радиуса
r:
.
Задача сведена к отысканию максимума
функции.
Приравнивая к нулю производнуюи учитывая, чтоr<0,
находим точку возможного экстремума
.
(12)
Хотя по смыслу
задача и ясно, что единственная точка
возможного экстремума является точкой
максимума функции V(r),
мы можем строго убедиться в этом,
используя теорему1 и замечая, что
производная
положительна при
и отрицательна при
.
Установим теперь, при каком соотношении
между радиусомr
и высотой h
реализуется наибольший объем V(r)
консервной банки. Для этого равенство
(11) на r2
и в правой части полученного при этом
равенства воспользуемся соотношением
(12). При этом получим h/r=2,
т.е. h=2r.
Таким образом,
наибольший
объем будет у той консервной банки, у
которой высота равна диаметру.
2) Найти точки
экстремума функции
.
Поскольку,
то единственной точкой возможного
экстремума является точкойx=2.
Так как
положительна,
как слева, так и справа от этой точки,
то функциявовсе
не имеет точек экстремума.
-
Второе достаточное
условие экстремума.
Иногда вызывает
затруднение исследование знака первой
производной
слева
и справа от точки возможного экстремума.
На этот случай мы укажем другое достаточное
условие наличия экстремума в данной
точкевозможного экстремума, не требующее
исследования знакав окрестности
,
но зато предполагающее существование
в точкеотличной от нуля конечной второй
производной.
Теорема3.
Пусть функция
имеет в данной точке
возможного экстремума конечную вторую
производную. Тогда функцияимеет в точке
максимум, если
<0,
и минимум, если>0.
Доказательство.
Из условия
<0
(>0)
и изтеоремы0
вытекает, что функция
убывает (возрастает) в точке
.
Поскольку по условию,
то найдется такая окрестность точки,
в пределах которойположительна
(отрицательна) слева оти отрицательна (положительна)справа от
.
Но тогда по предыдущей теоремеимеет в точке
максимум (минимум).
Замечание.Теорема3
имеет более узкую сферу действия, чем
теорема2. Так, теорема3 не решает вопроса
об экстремуме для случая, когда вторая
производная
не существует в точке
,
а также для случая, когда=0.
В последнем случае для решения вопроса
о наличии экстремума нужно изучить
поведение в точкепроизводных высших порядков.
Пример.
Найти экстремальные значения функции
.
Так как,
то функцияимеет
две точки возможного экстремума:и
.
Поскольку знакслева
и справа от этих точек легко выясняется,
можно решить вопрос об экстремуме при
помощи теоремы2 (первого достаточного
условия). Но мы предпочитаем привлечь
теорему3 ( второе достаточное условие).
Имеет
.Таким
образом, функция
имеет максимум в точке 0 и минимум в
точке 2. Экстремальные значения этой
функции равны
Соседние файлы в папке шпоры
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Экстремум функции
Функция y=f(x) называется возрастающей (убывающей) в некотором интервале, если при
Если дифференцируемая функция у = f(x) на отрезке 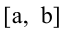
Точка 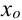
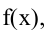
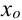
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках – ее экстремумами.
Необходимые условия экстремума. Если точка хо является точкой экстремума функции 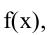
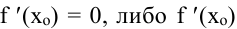
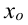


Второе достаточное условие. Пусть функция 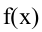

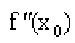

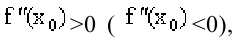

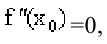
На отрезке 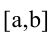
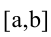
Пример:
Найти экстремумы функции
Решение:
Так как 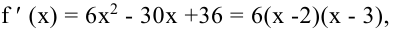
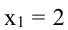
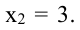
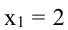
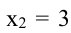
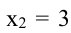
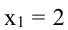
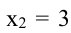
Пример:
Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, а четвертой стороной примыкала к стене. Для этого имеется а погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?
Решение:
Обозначим стороны площадки через 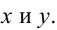
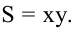
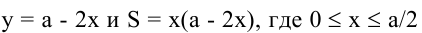
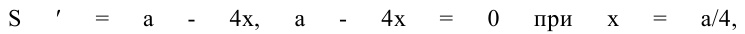
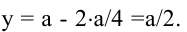
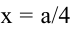
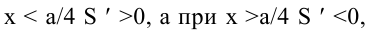
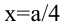
Поскольку S непрерывна на 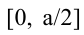
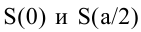
Таким образом, наиболее выгодным соотношением сторон площадки при данных условиях задачи является у = 2х.
Пример:
Требуется изготовить закрытый цилиндрический бак вместимостью 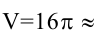
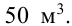
Решение:
Площадь полной поверхности цилиндра равна 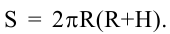
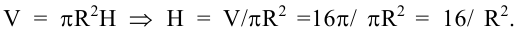
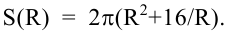
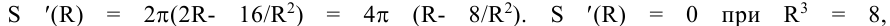
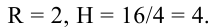
Экстремумы функции
Введём несколько новых понятий. Окрестностью точки 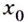
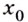
Точка 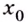
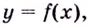
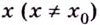
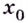
Точки минимума и максимума обозначают 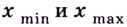
Значение функции в точке минимума называется минимумом функции, а в точке максимума — максимумом функции. Обозначают их:
Точки минимума и максимума функции называют точками экстремума (лат. extremum — край, конец). Значения функции в точках её экстремума — её экстремальные значения, или экстремумы.
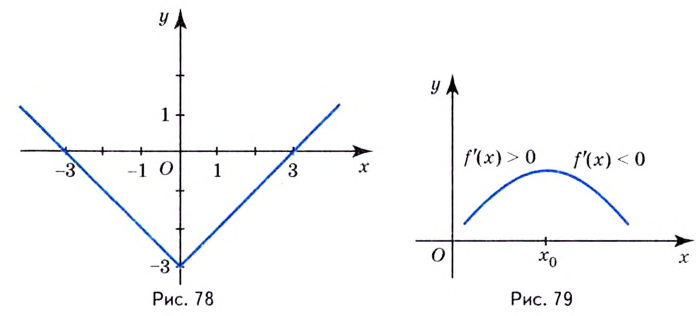
Например, для функции 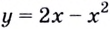

Для функции 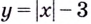
Функция, график которой изображён на рисунке 75, имеет четыре экстремальные точки: 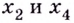
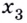
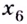
Точка экстремума функции не может принадлежать промежутку, на котором эта функция возрастает или убывает (почему?). Следовательно, те точки, в которых производная функции положительная или отрицательная, не могут быть точками её экстремума. Все остальные точки области определения функции являются её критическими точками. Поэтому точками экстремума функции могут быть только её критические точки. Это — необходимое условие существования экстремума.
Выбрать из критических точек функции точки экстремума позволяет достаточное условие существования экстремума.
Пусть функция 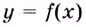
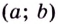
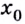
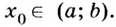
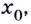
Действительно, если производная функции 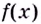
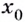
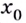
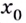
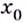
Если же производная функции в точке 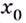
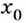
- Заказать решение задач по высшей математике
Пример №552
Найдите точки экстремума и экстремальные значения функции
Решение:
Критические точки функции: 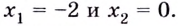
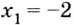
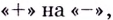
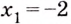
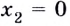
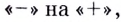
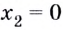
Ответ.
Нахождение экстремумов функции можно оформлять в виде таблицы, как на с. 176. Особенно это удобно при общем исследовании функции, когда находят не только её экстремумы, но и другие свойства, строят её график.
Чтобы исследовать функцию, можно пользоваться следующей схемой:
- найти область определения функции;
- исследовать функцию на чётность, нечётность, периодичность;
- найти точки пересечения графика функции с осями координат;
- исследовать функцию на монотонность, то есть найти промежутки возрастания и убывания функции;
- найти точки экстремума и экстремальные значения функции;
- найти асимптоты графика функции;
- построить график функции.
Пример №553
Исследуйте функцию 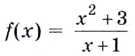
Решение:
Область определения функции — все действительные числа, кроме 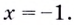
Уравнение 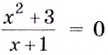
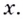
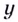
Критические точки:
Составим и заполним таблицу.
На промежутках 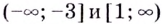
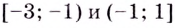

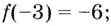
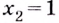
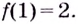
Область значений функции:
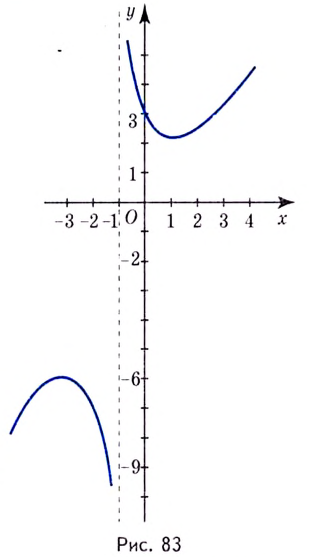
График функции имеет вертикальную асимптоту 
График этой функции изображён на рисунке 83.
Пример №554
Может ли нечётная функция иметь экстремум в точке 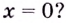
Решение:
Нечётная функция не может. Если в окрестности точки 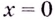

Пример №555
Существуют ли такие числа 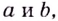
Решение:
При любых действительных значениях 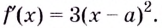
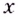
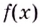
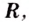
Ответ. Не существуют.
Пример №556
Исследуйте функцию 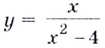
Решение.
2) Функция — нечётная, поскольку
Следовательно, её график симметричен относительно начала координат и достаточно исследовать функцию на промежутке
3) если 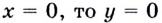
4) Найдём производную функции:
Очевидно, что 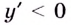
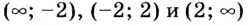
Для более точного построения вычислим значение функции в нескольких точках:
График функции имеет вертикальные асимптоты 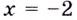
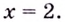
График функции изображён на рисунке 84.
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Определитель матрицы
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
Пример 1:
Исследовать функцию на экстремум и вычислить значение функции в точках экстремума:
Решение от преподавателя:
Решение.
Пример 2:
Исследуйте на экстремум функцию.
y = х2 – 10х + 5
Решение от преподавателя:
Пример 3:
Найти экстремумы функций двух переменных
z = 2x3 + 6xy2 – 30x – 24y.
Решение от преподавателя:
Пример 4:
Исследовать на экстремум:
Решение от преподавателя:
Необходимое условие экстремума функции одной переменной.
Уравнение f’0(x*) = 0 – это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки xс, в которых функция не возрастает и не убывает.
Достаточное условие экстремума функции одной переменной.
Пусть f0(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие:
f’0(x*) = 0
f”0(x*) > 0
то точка x* является точкой локального (глобального) минимума функции.
Если в точке x* выполняется условие:
f’0(x*) = 0
f”0(x*) < 0
то точка x* – локальный (глобальный) максимум.
Решение.
Находим первую производную функции:
y’ = 6x2+6x
или
y’ = 6x(x+1)
Приравниваем ее к нулю:
6x2+6x = 0
x1 = 0
x2 = -1
Вычисляем значения функции
f(0) = -11
f(-1) = -10
Ответ:
fmin = -11, fmax = -10
Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную:
y” = 12x+6
Вычисляем:
y”(0) = 6>0 – значит точка x = 0 точка минимума функции.
y”(-1) = -6<0 – значит точка x = -1 точка максимума функции.
Пример 5:
Найти стационарные точки и исследовать на экстремум функцию
z = x2 + y2 – 2x – 2y+ 8
Решение от преподавателя:
Исследовать на экстремум функцию z = x2 + y2 – 2x – 2y+ 8
1. Найдем частные производные.
2. Решим систему уравнений.
2x-2 = 0
2y-2 = 0
Получим: x = 1, y = 1
критическая точка M1(1;1)
3. Найдем частные производные второго порядка.
4. Вычислим значение этих частных производных второго порядка в критических точках M(x0;y0).
Вычисляем значения для точки M1(1;1)
AC – B2 = 4 > 0 и A > 0 , то в точке M1(1;1) имеется минимум z(1;1) = 6
Вывод: В точке M1(1;1) имеется минимум z(1;1) = 6;
Пример 6:
Исследовать на экстремум функцию:
Решение от преподавателя:
Пример 7:
Исследовать функцию z(x,y) на экстремум
Решение от преподавателя:
Пример 8:
Исследовать на экстремум функцию:
Решение от преподавателя:
Вычислим производную этой функции и найдем стационарные точки, в которых она обращается в нуль:
Решая это уравнение, находим корни x1 = 1 и x2 = 2. Они являются подозрительными на экстремум в данной задаче. При этом знаки производной нашей функции распределены следующим образом:
Согласно теореме о достаточном условии экстремума первого порядка, полученные точки являются точками локального экстремума, а именно: x1 = 1 — точка локального максимума, причем f(x1) = 11, а x2 = 2 — точка локального минимума, причем f(x2) = 10.
Глобальных экстремумов в этой задаче нет. Это видно из того, что
Итак, локальный максимум достигается в точке x = 1 и равен 11, локальный минимум достигается в точке x = 2, и равен 10.
Пример 9:
Исследуйте на экстремум функцию z = z(x;y).
Решение от преподавателя:
Пример 10:
Исследовать на экстремум:
y = (2*x-8)*(9*x+1)
Решение от преподавателя:
Необходимое условие экстремума функции одной переменной.
Уравнение f’0(x*) = 0 – это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки xс, в которых функция не возрастает и не убывает.
Достаточное условие экстремума функции одной переменной.
Пусть f0(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие:
f’0(x*) = 0
f”0(x*) > 0
то точка x* является точкой локального (глобального) минимума функции.
Если в точке x* выполняется условие:
f’0(x*) = 0
f”0(x*) < 0
то точка x* – локальный (глобальный) максимум.
Решение.
Находим первую производную функции:
y’ = 36x-70
Приравниваем ее к нулю:
36x-70 = 0
Вычисляем значения функции
Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную:
y” = 36
Вычисляем:
значит эта точка – минимума функции.
Пример 11:
Найти экстремумы функции z(x,y) при данном условии:
Решение от преподавателя:
Пример 12:
Исследовать на экстремум функцию:
Решение от преподавателя:
Найдем производную f′ (x) = ex − e−x . Чтобы найти критические точки функции f(x), приравняем эту производную к нулю:
Очевидно, что точка x = 0 является решением последнего уравнения. Функция f′(x) строго возрастает (поскольку 
Следовательно, точка x = 0 является точкой строгого локального минимума функции f(x), и f(0) = 2 — соответствующее минимальное значение.
В данной ситуации можно также применить теорему о достаточном условии экстремума второго порядка. Поскольку f′′(0) = 2 > 0, функция f(x) имеет строгий локальный минимум в точке x = 0.
Кроме того, этот минимум глобальный, потому что
Ответ: точка x = 0 является точкой глобального минимума для исследуемой функции и fmin = f(0) = 2.
Пример 13:
Найти наибольшее и наименьшее значения функции z(x,y) в области D:
Решение от преподавателя:
Пример 14:
Исследовать на экстремум функцию:
y = x3+6*x2-4, [-4;1].
Решение от преподавателя:
Необходимое условие экстремума функции одной переменной.
Уравнение f’0(x*) = 0 – это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки xс, в которых функция не возрастает и не убывает.
Достаточное условие экстремума функции одной переменной.
Пусть f0(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие:
f’0(x*) = 0
f”0(x*) > 0
то точка x* является точкой локального (глобального) минимума функции.
Если в точке x* выполняется условие:
f’0(x*) = 0
f”0(x*) < 0
то точка x* – локальный (глобальный) максимум.
Решение.
Находим первую производную функции:
y’ = 3x2+12x
или
y’ = 3x(x+4)
Приравниваем ее к нулю:
3x(x+4) = 0
x1 = 0
x2 = -4
Вычисляем значения функции на концах отрезка
f(0) = -4
f(-4) = 28
f(-4) = 28.0000000000000
f(1) = 3.00000000000000
Ответ: fmin = -4, fmax = 28.
Пример 15:
Исследовать на экстремум функцию
Решение от преподавателя:
Как обычно, начнем с нахождения производной исследуемой функции и точек, подозрительных на экстремум:
Легко видеть, что точка x = 0 является критической.
Найдем вторую производную:
Очевидно, f′′(0) = 0. Воспользуемся теоремой о достаточном условии экстремума n-го порядка и будем дифференцировать функцию до того момента, пока не появится отличная от нуля производная:
Значит, x = 0 — точка локального минимума функции f(x).
Из предыдущего примера следует, что при
. В то же время
. Поэтому f′′(x) > 0 при
. Отсюда следует, что производная f′(x) обращается в нуль в единственной точке x = 0.
Так как , минимум в точке x = 0 является глобальным.
Ответ: есть один глобальный минимум f(0) = 4.
Пример 16:
С помощью второй производной исследуйте на экстремум функцию 
Решение от преподавателя:
Определяем критические точки
Определяем вторую производную функции
Определяем знаки второй производной в критических точках
Т. к. вторая производная положительная, то в точке х=0 минимум
Т. к. вторая производная отрицательная, то в точке х=1 максимум
Наибольшее М и наименьшее m значения этой функции на отрезке [-1, 2]
Т. к. обе критические точки принадлежат указанному отрезку, то определяем значения функции в полученных точках и на концах отрезка
Т. о., М=у(-1)=6 m=у(2)=-3
Пример 17:
Исследовать на экстремум функцию:
Решение от преподавателя:
Подозрительные на экстремум точки найдем с помощью леммы Ферма. Так как
то единственная подозрительная на экстремум точка (в которой все частные производные обращаются в нуль) — это точка a = (3, −2, −1).
Определим, есть ли в этой точке экстремум. Для этого найдем все частные производные второго порядка
и составим из них матрицу полной второй производной f′′(a):
Главные миноры этой матрицы чередуют знаки:
По теореме (достаточное условие экстремума второго порядка) в точке a локальный максимум. Ответ: локальный максимум достигается в точке a = (3, −2, −1) и равен 14.
Ответ: локальный максимум достигается в точке a = (3, −2, −1) и равен 14.
Пример 18:
Найти экстремумы функции:
Решение от преподавателя:
Подозрительные на экстремум точки найдем с помощью леммы Ферма. Так как
то единственной стационарной точкой будет точка a = (0, 0).
Посмотрим, есть ли в ней экстремум. Для этого вычислим частные производные второго порядка
и составим из них матрицу второй производной в точке a:
Очевидно, ее определитель равен нулю. Значит, достаточные условия экстремума из теоремы (достаточное условие экстремума второго порядка) в данном случае не применимы.
Придется использовать определение экстремума. Рассмотрим разность . Она больше нуля при всех y > 0 и меньше нуля при y < 0. Поэтому в точке a = (0, 0) нет экстремума.
Ответ: у функции f нет экстремумов.
Пример 19:
Найти экстремумы функции
Решение от преподавателя:
Очевидно,
и единственная стационарная точка — это a = (0, 0).
Далее вычисляем частные производные второго порядка
и выписываем матрицу второй производной в точке a:
Ее определитель равен нулю. Достаточные условия экстремума опять не работают. С другой стороны, 
Ответ: есть один глобальный минимум f(0, 0) = 0.
Пример 20:
Исследовать на экстремумы функцию.
Решение от преподавателя:
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).


Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
– Производная положительна там, где функция возрастает.
– Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после – производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.
(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.
(- 9): функция возрастает, а потом убывает – максимум.
(-7): минимум.
(3): максимум.
Все вышесказанное можно обобщить следующими выводами:
– Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
– Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции (f'(x)).
- Найдите корни уравнения (f'(x)=0).
- Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
– если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
– если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
– если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:
(15x^4-60x^2=0) (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0) (x^2-4=0)
(x=±2)
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является (-2).
Ответ. (-2).
Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов
Скачать статью