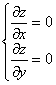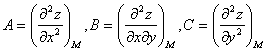Как найти экстремум функции двух переменных калькулятор

Как найти экстремум функции двух переменных калькулятор

Экстремум функции двух переменных

Назначение сервиса. Онлайн-калькулятор используется для нахождения в онлайн режиме наибольшего и наименьшего значения функции двух переменных (см. пример). Решение оформляется в формате Word.

  • Решение онлайн
  • Видеоинструкция
  • Оформление Word

Для функции трех переменных можно использовать матрицу Гессе.

Алгоритм исследования функции двух переменных на экстремум

Функция z = f(x,y) имеет максимум в точке M0(x0;y0), если f(x0;y0) > f(x;y) для всех точек (x;y), достаточно близких к точке (x0;y0) и отличных от неё. Функция z = f(x,y) имеет минимум в точке M0(x0;y0), если f(x0;y0) < f(x;y) для всех точек (x;y), достаточно близких к точке (x0;y0) и отличных от неё. Максимум и минимум функции называются экстремумами функции.

Исследование функции двух переменных на экстремум проводят по следующей схеме.

1. Находят частные производные dz/dx и dz/dy.

2. Решают систему уравнений:

и таким образом находят критические точки функции.

3. Находят частные производные второго порядка:

4. Вычисляют значения этих частных производных второго порядка в каждой из найденных в п.2 критических точках M(x0;y0).

5. Делаю вывод о наличии экстремумов:

а) если AC – B2 > 0 и A < 0 , то в точке M имеется максимум;

б) если AC – B2 > 0 и A > 0 , то в точке M имеется минимум;

в) если AC – B2 < 0, то экстремума нет;

г) если AC – B2 = 0, то вопрос о наличии экстремума остается открытым;

Пример №1. Найти экстремумы функции f(x,y)=x3+xy2+x2+y2 и определить по критерию Сильвестра их тип.

Решение.

1. Найдем первые частные производные.





2. Решим систему уравнений.

3x2+2x+y2=0

2xy+2y=0

Получим:

а) Из первого уравнения выражаем x и подставляем во второе уравнение:

x = -1

y2+1=0

Данная система уравнений не имеет решения.

б) Из первого уравнения выражаем y и подставляем во второе уравнение:





или





или

Откуда x1 = -2/3; x2 = 0; x3 = -2/3; x4 = 0

Данные значения x подставляем в выражение для y. Получаем: y1 = 0; y2 = 0; y3 = 0; y4 = 0

Количество критических точек равно 2: M1(-2/3;0), M2(0;0)

3. Найдем частные производные второго порядка.







4. Вычислим значение этих частных производных второго порядка в критических точках M(x0;y0).

Вычисляем значения для точки M1(-2/3;0)







AC – B2 = -4/3 < 0, то глобального экстремума нет.

Вычисляем значения для точки M2(0;0)







AC – B2 = 4 > 0 и A > 0 , то в точке M2(0;0) имеется минимум z(0;0) = 0

Вывод: В точке M2(0;0) имеется минимум z(0;0) = 0

Пример №2. Исследовать функцию на экстремум классическим методом: Z=8x2+2xy-5x+6.

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Источник
bold{mathrm{Basic}} bold{alphabetagamma} bold{mathrm{ABGamma}} bold{sincos} bold{gedivrightarrow} bold{overline{x}spacemathbb{C}forall} bold{sumspaceintspaceproduct} bold{begin{pmatrix}square&square\square&squareend{pmatrix}} bold{H_{2}O}
square^{2} x^{square} sqrt{square} nthroot[msquare]{square} frac{msquare}{msquare} log_{msquare} pi theta infty int frac{d}{dx}
ge le cdot div x^{circ} (square) |square| (f:circ:g) f(x) ln e^{square}
left(squareright)^{‘} frac{partial}{partial x} int_{msquare}^{msquare} lim sum sin cos tan cot csc sec
alpha beta gamma delta zeta eta theta iota kappa lambda mu
nu xi pi rho sigma tau upsilon phi chi psi omega
A B Gamma Delta E Z H Theta K Lambda M
N Xi Pi P Sigma T Upsilon Phi X Psi Omega
sin cos tan cot sec csc sinh cosh tanh coth sech
arcsin arccos arctan arccot arcsec arccsc arcsinh arccosh arctanh arccoth arcsech
begin{cases}square\squareend{cases} begin{cases}square\square\squareend{cases} = ne div cdot times < > le ge
(square) [square] ▭:longdivision{▭} times twostack{▭}{▭} + twostack{▭}{▭} – twostack{▭}{▭} square! x^{circ} rightarrow lfloorsquarerfloor lceilsquarerceil
overline{square} vec{square} in forall notin exist mathbb{R} mathbb{C} mathbb{N} mathbb{Z} emptyset
vee wedge neg oplus cap cup square^{c} subset subsete superset supersete
int intint intintint int_{square}^{square} int_{square}^{square}int_{square}^{square} int_{square}^{square}int_{square}^{square}int_{square}^{square} sum prod
lim lim _{xto infty } lim _{xto 0+} lim _{xto 0-} frac{d}{dx} frac{d^2}{dx^2} left(squareright)^{‘} left(squareright)^{”} frac{partial}{partial x}
(2times2) (2times3) (3times3) (3times2) (4times2) (4times3) (4times4) (3times4) (2times4) (5times5)
(1times2) (1times3) (1times4) (1times5) (1times6) (2times1) (3times1) (4times1) (5times1) (6times1) (7times1)
mathrm{Радианы} mathrm{Степени} square! ( ) % mathrm{очистить}
arcsin sin sqrt{square} 7 8 9 div
arccos cos ln 4 5 6 times
arctan tan log 1 2 3 –
pi e x^{square} 0 . bold{=} +

Подпишитесь, чтобы подтвердить свой ответ

Подписаться

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

  • extreme:f(x,y)=3x^{2}y+y^{3}−3x^{2}−3y^{2}+2

  • extreme:f(x,y)=x^{2}+y^{2}

Описание

Шаг за шагом найдите экстремальные и седловые точки функций с несколькими переменными

multi-var-function-extreme-points-calculator

ru

Блог-сообщения, имеющие отношение к Symbolab

  • High School Math Solutions – Derivative Calculator, the Basics

    Differentiation is a method to calculate the rate of change (or the slope at a point on the graph); we will not…

    Read More

    • Введите Задачу

    Сохранить в блокнот!

    Войти

    Источник

    Ключевые слова: калькулятор экстремумов, найти экстремум функции двух переменных, частные производные первого и второго порядков, стационарные точки, калькулятор частных производных.

    Пример 1. Исследовать на экстремум функцию:

    Алгоритм решения следующий:

    1) находим частные производные первого порядка:

    Примечание: найти частные производные онлайн  (первого и второго порядка) можно с помощью калькулятора.

    2). Решаем систему уравнений:

    и таким образом находим стационарные точки функции.

    Точки, в которых значение производной функции равно нулю, называются стационарными точками.

    Для данного примера  получаем систему уравнений:

    стационарная точка: (-1;1)

    3) Находим вторые частные производные

    Вычисляем значения этих частных производных второго порядка в каждой из найденных в п.2 стационарных точках M(x0;y0).

    Для данного примера, получаем

    4) Делаем вывод о наличии экстремумов:
    а) если AC – B2 > 0 и A < 0 , то в точке M имеется максимум;
    б) если AC – B2 > 0 и A > 0 , то в точке M имеется минимум;
    в) если AC – B2 < 0, то экстремума нет;
    г) если AC – B2 = 0, то вопрос о наличии экстремума остается открытым;

    Тогда в точке    x=-1, y=1

    Следовательно в точке x=-1, y=1 функция имеет локальный минимум

    Ответ: min{z}=0

    Проверить правильность решения можно с помощью калькулятора “экстремум функции”.

    Источник

    The calculator will try to find the maxima and minima of the two- or three-variable function, subject to the given constraints, using the method of Lagrange multipliers, with steps shown.

    Related calculator:

    Critical Points, Extrema, and Saddle Points Calculator

    Your Input

    Find the maximum and minimum values of $$$f{left(x,y right)} = 3 x + 4 y$$$ subject to the constraint $$$x^{2} + y^{2} = 25$$$.

    Solution

    Attention! This calculator doesn’t check the conditions for applying the method of Lagrange multipliers. Use it at your own risk: the answer may be incorrect.

    Rewrite the constraint $$$x^{2} + y^{2} = 25$$$ as $$$x^{2} + y^{2} – 25 = 0$$$.

    Form the Lagrangian: $$$L{left(x,y,lambda right)} = left(3 x + 4 yright) + lambda left(x^{2} + y^{2} – 25right)$$$.

    Find all the first-order partial derivatives:

    $$$frac{partial}{partial x} left(left(3 x + 4 yright) + lambda left(x^{2} + y^{2} – 25right)right) = 2 lambda x + 3$$$ (for steps, see partial derivative calculator).

    $$$frac{partial}{partial y} left(left(3 x + 4 yright) + lambda left(x^{2} + y^{2} – 25right)right) = 2 lambda y + 4$$$ (for steps, see partial derivative calculator).

    $$$frac{partial}{partial lambda} left(left(3 x + 4 yright) + lambda left(x^{2} + y^{2} – 25right)right) = x^{2} + y^{2} – 25$$$ (for steps, see partial derivative calculator).

    Next, solve the system $$$begin{cases} frac{partial L}{partial x} = 0 \ frac{partial L}{partial y} = 0 \ frac{partial L}{partial lambda} = 0 end{cases}$$$, or $$$begin{cases} 2 lambda x + 3 = 0 \ 2 lambda y + 4 = 0 \ x^{2} + y^{2} – 25 = 0 end{cases}$$$.

    The system has the following real solutions: $$$left(x, yright) = left(-3, -4right)$$$, $$$left(x, yright) = left(3, 4right)$$$.

    $$$f{left(-3,-4 right)} = -25$$$

    $$$f{left(3,4 right)} = 25$$$

    Thus, the minimum value is $$$-25$$$, and the maximum value is $$$25$$$.

    Answer

    Maximum

    $$$25$$$A at $$$left(x, yright) = left(3, 4right)$$$A.

    Minimum

    $$$-25$$$A at $$$left(x, yright) = left(-3, -4right)$$$A.

    Источник

    Найти экстремумы функции

    Данный калькулятор предназначен для нахождения экстремумов функции.
    Следует различать понятия точек экстремума и экстремумов функции. Точки экстремума – точки максимума и минимума функции, это значения на оси Ox. Точка x0 является точкой максимума функции y=f(x), если для всех x из ее окрестности выполняется неравенство f(x0)≥f(x). Точка x0 является точкой минимума функции y=f(x), если из ее окрестности для всех x выполняется неравенство f(x0)≤f(x). Значения функции, которые соответствуют точкам экстремума, называются экстремумами функции, это значения на оси Oy.
    Для того чтобы найти экстремумы функции можно использовать любой из трех условий экстремума, если функция удовлетворяет эти условиям.
    Первым достаточным условием экстремума являются следующие утверждения: если в точке x0 функция непрерывна, и в ней производная меняет знак с плюса на минус, то точка x0 является точкой максимума, а если в данной точке производная меняет знак с минуса на плюс, то x0 – точка минимума.

    Вторым признаком экстремума является следующее утверждение: если производная второго порядка от x0 больше нуля, то x0 – точка минимума; если меньше нуля, то x0 – точка максимума.
    Третье достаточное условие экстремума функции заключается в следующем. Пусть функция y=f(x) имеет производные до n-ого порядка в окрестности точки x0 и производные до n+1-ого порядка в самой точке x0; пусть f’(x0)= f’’(x0)= f’’’(x0)=…=f(n)( x0)=0 и f(n+1)( x0)≠0. Тогда, если n – нечетное, то x0 – точка экстремума. Если f(n+1)( x0)>0, то x0 – точка минимума, а, если f(n+1)( x0)<0, то x0 – точка максимума.
    Для того чтобы найти экстремумы функции, введите эту функцию в ячейку. Основные примеры ввода функций для данного калькулятора указаны ниже.

    Для получения полного хода решения нажимаем в ответе Step-by-step.

    ×

    Пожалуйста напишите с чем связна такая низкая оценка:

    ×

    Для установки калькулятора на iPhone – просто добавьте страницу
    «На главный экран»

    Для установки калькулятора на Android – просто добавьте страницу
    «На главный экран»

    Источник

    Добавить комментарий