Условный экстремум. Метод множителей Лагранжа. Первая часть.
Для начала рассмотрим случай функции двух переменных. Условным экстремумом функции $z=f(x,y)$ в точке $M_0(x_0;y_0)$ называется экстремум этой функции, достигнутый при условии, что переменные $x$ и $y$ в окрестности данной точки удовлетворяют уравнению связи $varphi (x,y)=0$.
Название «условный» экстремум связано с тем, что на переменные наложено дополнительное условие $varphi(x,y)=0$. Если из уравнения связи можно выразить одну переменную через другую, то задача определения условного экстремума сводится к задаче на обычный экстремум функции одной переменной. Например, если из уравнения связи следует $y=psi(x)$, то подставив $y=psi(x)$ в $z=f(x,y)$, получим функцию одной переменной $z=fleft(x,psi(x)right)$. В общем случае, однако, такой метод малопригоден, поэтому требуется введение нового алгоритма.
Метод множителей Лагранжа для функций двух переменных.
Метод множителей Лагранжа состоит в том, что для отыскания условного экстремума составляют функцию Лагранжа: $F(x,y)=f(x,y)+lambdavarphi(x,y)$ (параметр $lambda$ называют множителем Лагранжа). Необходимые условия экстремума задаются системой уравнений, из которой определяются стационарные точки:
$$
left { begin{aligned}
& frac{partial F}{partial x}=0;\
& frac{partial F}{partial y}=0;\
& varphi (x,y)=0.
end{aligned} right.
$$
Достаточным условием, из которого можно выяснить характер экстремума, служит знак $d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2$. Если в стационарной точке $d^2F > 0$, то функция $z=f(x,y)$ имеет в данной точке условный минимум, если же $d^2F < 0$, то условный максимум.
Есть и другой способ для определения характера экстремума. Из уравнения связи получаем: $varphi_{x}^{‘}dx+varphi_{y}^{‘}dy=0$, $dy=-frac{varphi_{x}^{‘}}{varphi_{y}^{‘}}dx$, поэтому в любой стационарной точке имеем:
$$d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2=F_{xx}^{”}dx^2+2F_{xy}^{”}dxleft( -frac{varphi_{x}^{‘}}{varphi_{y}^{‘}}dxright)+F_{yy}^{”}left( -frac{varphi_{x}^{‘}}{varphi_{y}^{‘}}dxright)^2=\
=-frac{dx^2}{left(varphi_{y}^{‘} right)^2}cdotleft( -(varphi_{y}^{‘})^2 F_{xx}^{”}+2varphi_{x}^{‘}varphi_{y}^{‘}F_{xy}^{”}-(varphi_{x}^{‘})^2 F_{yy}^{”} right)$$
Второй сомножитель (расположенный в скобке) можно представить в такой форме:
$$
H=left| begin{array} {ccc}
0 & varphi_{x}^{‘} & varphi_{y}^{‘}\
varphi_{x}^{‘} & normred{F_{xx}^{”}} & normred{F_{xy}^{”}} \
varphi_{y}^{‘} & normred{F_{xy}^{”}} & normred{F_{yy}^{”}} end{array} right|
$$
Красным цветом выделены элементы определителя $left| begin{array} {cc} F_{xx}^{”} & F_{xy}^{”} \ F_{xy}^{”} & F_{yy}^{”} end{array} right|$, который является гессианом функции Лагранжа. Если $H > 0$, то $d^2F < 0$, что указывает на условный максимум. Аналогично, при $H < 0$ имеем $d^2F > 0$, т.е. имеем условный минимум функции $z=f(x,y)$.
Примечание относительно формы записи определителя $H$. показатьскрыть
Алгоритм исследования функции двух переменных на условный экстремум
- Составить функцию Лагранжа $F(x,y)=f(x,y)+lambdavarphi(x,y)$
- Решить систему $
left { begin{aligned}
& frac{partial F}{partial x}=0;\
& frac{partial F}{partial y}=0;\
& varphi (x,y)=0.
end{aligned} right.$ - Определить характер экстремума в каждой из найденных в предыдущем пункте стационарных точек. Для этого применить любой из указанных способов:
- Составить определитель $H$ и выяснить его знак
- С учетом уравнения связи вычислить знак $d^2F$
Метод множителей Лагранжа для функций n переменных
Допустим, мы имеем функцию $n$ переменных $z=f(x_1,x_2,ldots,x_n)$ и $m$ уравнений связи ($n > m$):
$$varphi_1(x_1,x_2,ldots,x_n)=0; ; varphi_2(x_1,x_2,ldots,x_n)=0,ldots,varphi_m(x_1,x_2,ldots,x_n)=0.$$
Обозначив множители Лагранжа как $lambda_1,lambda_2,ldots,lambda_m$, составим функцию Лагранжа:
$$F(x_1,x_2,ldots,x_n,lambda_1,lambda_2,ldots,lambda_m)=f+lambda_1varphi_1+lambda_2varphi_2+ldots+lambda_mvarphi_m$$
Необходимые условия наличия условного экстремума задаются системой уравнений, из которой находятся координаты стационарных точек и значения множителей Лагранжа:
$$left{begin{aligned}
& frac{partial F}{partial x_i}=0; (i=overline{1,n})\
& varphi_j=0; (j=overline{1,m})
end{aligned} right.$$
Выяснить, условный минимум или условный максимум имеет функция в найденной точке, можно, как и ранее, посредством знака $d^2F$. Если в найденной точке $d^2F > 0$, то функция имеет условный минимум, если же $d^2F < 0$, – то условный максимум. Можно пойти иным путем, рассмотрев следующую матрицу:
Определитель матрицы
$$left| begin{array} {ccccc} frac{partial^2F}{partial x_{1}^{2}} & frac{partial^2F}{partial x_{1}partial x_{2}} & frac{partial^2F}{partial x_{1}partial x_{3}} &ldots & frac{partial^2F}{partial x_{1}partial x_{n}}\
frac{partial^2F}{partial x_{2}partial x_1} & frac{partial^2F}{partial x_{2}^{2}} & frac{partial^2F}{partial x_{2}partial x_{3}} &ldots & frac{partial^2F}{partial x_{2}partial x_{n}}\
frac{partial^2F}{partial x_{3} partial x_{1}} & frac{partial^2F}{partial x_{3}partial x_{2}} & frac{partial^2F}{partial x_{3}^{2}} &ldots & frac{partial^2F}{partial x_{3}partial x_{n}}\
ldots & ldots & ldots &ldots & ldots\
frac{partial^2F}{partial x_{n}partial x_{1}} & frac{partial^2F}{partial x_{n}partial x_{2}} & frac{partial^2F}{partial x_{n}partial x_{3}} &ldots & frac{partial^2F}{partial x_{n}^{2}}\
end{array} right|,$$
выделенной в матрице $L$ красным цветом, есть гессиан функции Лагранжа. Используем следующее правило:
- Если знаки угловых миноров $H_{2m+1},; H_{2m+2},ldots,H_{m+n}$ матрицы $L$ совпадают с знаком $(-1)^m$, то исследуемая стационарная точка является точкой условного минимума функции $z=f(x_1,x_2,x_3,ldots,x_n)$.
- Если знаки угловых миноров $H_{2m+1},; H_{2m+2},ldots,H_{m+n}$ чередуются, причём знак минора $H_{2m+1}$ совпадает с знаком числа $(-1)^{m+1}$, то исследуемая стационарная точка является точкой условного максимума функции $z=f(x_1,x_2,x_3,ldots,x_n)$.
Пример №1
Найти условный экстремум функции $z(x,y)=x+3y$ при условии $x^2+y^2=10$.
Решение
Геометрическая интерпретация данной задачи такова: требуется найти наибольшее и наименьшее значение аппликаты плоскости $z=x+3y$ для точек ее пересечения с цилиндром $x^2+y^2=10$.
Выразить одну переменную через другую из уравнения связи и подставить ее в функцию $z(x,y)=x+3y$ несколько затруднительно, поэтому будем использовать метод Лагранжа.
Обозначив $varphi(x,y)=x^2+y^2-10$, составим функцию Лагранжа:
$$
F(x,y)=z(x,y)+lambda varphi(x,y)=x+3y+lambda(x^2+y^2-10);\
frac{partial F}{partial x}=1+2lambda x; frac{partial F}{partial y}=3+2lambda y.
$$
Запишем систему уравнений для определения стационарных точек функции Лагранжа:
$$
left { begin{aligned}
& 1+2lambda x=0;\
& 3+2lambda y=0;\
& x^2+y^2-10=0.
end{aligned} right.
$$
Если предположить $lambda=0$, то первое уравнение станет таким: $1=0$. Полученное противоречие говорит о том, что $lambdaneq 0$. При условии $lambdaneq 0$ из первого и второго уравнений имеем: $x=-frac{1}{2lambda}$, $y=-frac{3}{2lambda}$. Подставляя полученные значения в третье уравнение, получим:
$$
left( -frac{1}{2lambda} right)^2+left( -frac{3}{2lambda} right)^2-10=0;\
frac{1}{4lambda^2}+frac{9}{4lambda^2}=10; lambda^2=frac{1}{4}; left[ begin{aligned} & lambda_1=-frac{1}{2};\ & lambda_2=frac{1}{2}. end{aligned} right.\
begin{aligned}
& lambda_1=-frac{1}{2}; ; x_1=-frac{1}{2lambda_1}=1; ; y_1=-frac{3}{2lambda_1}=3;\
& lambda_2=frac{1}{2}; ; x_2=-frac{1}{2lambda_2}=-1; ; y_2=-frac{3}{2lambda_2}=-3.end{aligned}
$$
Итак, система имеет два решения: $x_1=1;; y_1=3;; lambda_1=-frac{1}{2}$ и $x_2=-1;; y_2=-3;; lambda_2=frac{1}{2}$. Выясним характер экстремума в каждой стационарной точке: $M_1(1;3)$ и $M_2(-1;-3)$. Для этого вычислим определитель $H$ в каждой из точек.
$$
varphi_{x}^{‘}=2x;; varphi_{y}^{‘}=2y;; F_{xx}^{”}=2lambda;; F_{xy}^{”}=0;; F_{yy}^{”}=2lambda.\
H=left| begin{array} {ccc} 0 & varphi_{x}^{‘} & varphi_{y}^{‘}\ varphi_{x}^{‘} & F_{xx}^{”} & F_{xy}^{”} \ varphi_{y}^{‘} & F_{xy}^{”} & F_{yy}^{”} end{array} right|=
left| begin{array} {ccc} 0 & 2x & 2y\ 2x & 2lambda & 0 \ 2y & 0 & 2lambda end{array} right|=
8cdotleft| begin{array} {ccc} 0 & x & y\ x & lambda & 0 \ y & 0 & lambda end{array} right|
$$
В точке $M_1(1;3)$ получим:
$$H=8cdotleft| begin{array} {ccc} 0 & x & y\ x & lambda & 0 \ y & 0 & lambda end{array} right|=
8cdotleft| begin{array} {ccc} 0 & 1 & 3\ 1 & -1/2 & 0 \ 3 & 0 & -1/2 end{array} right|=40 > 0.$$
Следовательно, в точке $M_1(1;3)$ функция $z(x,y)=x+3y$ имеет условный максимум, $z_{max}=z(1;3)=10$.
Аналогично, в точке $M_2(-1;-3)$ найдем:
$$H=8cdotleft| begin{array} {ccc} 0 & x & y\ x & lambda & 0 \ y & 0 & lambda end{array} right|=
8cdotleft| begin{array} {ccc} 0 & -1 & -3\ -1 & 1/2 & 0 \ -3 & 0 & 1/2 end{array} right|=-40$$
Так как $H < 0$, то в точке $M_2(-1;-3)$ имеем условный минимум функции $z(x,y)=x+3y$, а именно: $z_{min}=z(-1;-3)=-10$.
Отмечу, что вместо вычисления значения определителя $H$ в каждой точке, гораздо удобнее раскрыть его в общем виде. Дабы не загромождать текст подробностями, этот способ скрою под примечание.
Запись определителя $H$ в общем виде. показатьскрыть
Вопрос о характере экстремума в стационарных точках $M_1(1;3)$ и $M_2(-1;-3)$ можно решить и без использования определителя $H$. Найдем знак $d^2F$ в каждой стационарной точке:
$$
d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2=2lambda left( dx^2+dy^2right)
$$
Отмечу, что запись $dx^2$ означает именно $dx$, возведённый в вторую степень, т.е. $left( dx right)^2$. Отсюда имеем: $dx^2+dy^2>0$, посему при $lambda_1=-frac{1}{2}$ получим $d^2F < 0$. Следовательно, функция имеет в точке $M_1(1;3)$ условный максимум. Аналогично, в точке $M_2(-1;-3)$ получим условный минимум функции $z(x,y)=x+3y$. Отметим, что для определения знака $d^2F$ не пришлось учитывать связь между $dx$ и $dy$, ибо знак $d^2F$ очевиден без дополнительных преобразований. В следующем примере для определения знака $d^2F$ уже будет необходимо учесть связь между $dx$ и $dy$.
Ответ: в точке $(-1;-3)$ функция имеет условный минимум, $z_{min}=-10$. В точке $(1;3)$ функция имеет условный максимум, $z_{max}=10$.
Пример №2
Найти условный экстремум функции $z(x,y)=3y^3+4x^2-xy$ при условии $x+y=0$.
Решение
Первый способ (метод множителей Лагранжа)
Обозначив $varphi(x,y)=x+y$ составим функцию Лагранжа:
$$F(x,y)=z(x,y)+lambda varphi(x,y)=3y^3+4x^2-xy+lambda(x+y).$$
$$
frac{partial F}{partial x}=8x-y+lambda; ; frac{partial F}{partial y}=9y^2-x+lambda.\
left { begin{aligned} & 8x-y+lambda=0;\ & 9y^2-x+lambda=0; \ & x+y=0. end{aligned} right.
$$
Решив систему, получим: $x_1=0$, $y_1=0$, $lambda_1=0$ и $x_2=frac{10}{9}$, $y_2=-frac{10}{9}$, $lambda_2=-10$. Имеем две стационарные точки: $M_1(0;0)$ и $M_2 left(frac{10}{9};-frac{10}{9} right)$. Выясним характер экстремума в каждой стационарной точке с использованием определителя $H$.
$$
H=left| begin{array} {ccc} 0 & varphi_{x}^{‘} & varphi_{y}^{‘}\ varphi_{x}^{‘} & F_{xx}^{”} & F_{xy}^{”} \ varphi_{y}^{‘} & F_{xy}^{”} & F_{yy}^{”} end{array} right|=
left| begin{array} {ccc} 0 & 1 & 1\ 1 & 8 & -1 \ 1 & -1 & 18y end{array} right|=-10-18y
$$
В точке $M_1(0;0)$ $H=-10-18cdot 0=-10 < 0$, поэтому $M_1(0;0)$ есть точка условного минимума функции $z(x,y)=3y^3+4x^2-xy$, $z_{min}=0$. В точке $M_2left(frac{10}{9};-frac{10}{9}right)$ $H=10 > 0$, посему в данной точке функция имеет условный максимум, $z_{max}=frac{500}{243}$.
Исследуем характер экстремума в каждой из точек иным методом, основываясь на знаке $d^2F$:
$$
d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2=8dx^2-2dxdy+18ydy^2
$$
Из уравнения связи $x+y=0$ имеем: $d(x+y)=0$, $dx+dy=0$, $dy=-dx$.
$$
d^2 F=8dx^2-2dxdy+18ydy^2=8dx^2-2dx(-dx)+18y(-dx)^2=(10+18y)dx^2
$$
Так как $ d^2F Bigr|_{M_1}=10 dx^2 > 0$, то $M_1(0;0)$ является точкой условного минимума функции $z(x,y)=3y^3+4x^2-xy$. Аналогично, $d^2F Bigr|_{M_2}=-10 dx^2 < 0$, т.е. $M_2left(frac{10}{9}; -frac{10}{9} right)$ – точка условного максимума.
Второй способ
Из уравнения связи $x+y=0$ получим: $y=-x$. Подставив $y=-x$ в функцию $z(x,y)=3y^3+4x^2-xy$, получим некоторую функцию переменной $x$. Обозначим эту функцию как $u(x)$:
$$
u(x)=z(x,-x)=3cdot(-x)^3+4x^2-xcdot(-x)=-3x^3+5x^2.
$$
Таким образом задачу о нахождении условного экстремума функции двух переменных мы свели к задаче определения экстремума функции одной переменной.
$$
u_{x}^{‘}=-9x^2+10x;\
-9x^2+10x=0; ; xcdot(-9x+10)=0;\
x_1=0; ; y_1=-x_1=0;\
x_2=frac{10}{9}; ; y_2=-x_2=-frac{10}{9}.
$$
Получили точки $M_1(0;0)$ и $M_2left(frac{10}{9}; -frac{10}{9}right)$. Дальнейшее исследование известно из курса дифференциального исчисления функций одной переменой. Исследуя знак $u_{xx}^{”}$ в каждой стационарной точке или проверяя смену знака $u_{x}^{‘}$ в найденных точках, получим те же выводы, что и при решении первым способом. Например, проверим знак $u_{xx}^{”}$:
$$u_{xx}^{”}=-18x+10;\
u_{xx}^{”}(M_1)=10;;u_{xx}^{”}(M_2)=-10.$$
Так как $u_{xx}^{”}(M_1)>0$, то $M_1$ – точка минимума функции $u(x)$, при этом $u_{min}=u(0)=0$. Так как $u_{xx}^{”}(M_2)<0$, то $M_2$ – точка максимума функции $u(x)$, причём $u_{max}=uleft(frac{10}{9}right)=frac{500}{243}$.
Значения функции $u(x)$ при заданном условии связи совпадают с значениями функции $z(x,y)$, т.е. найденные экстремумы функции $u(x)$ и есть искомые условные экстремумы функции $z(x,y)$.
Ответ: в точке $(0;0)$ функция имеет условный минимум, $z_{min}=0$. В точке $left(frac{10}{9}; -frac{10}{9} right)$ функция имеет условный максимум, $z_{max}=frac{500}{243}$.
Рассмотрим еще один пример, в котором характер экстремума выясним посредством определения знака $d^2F$.
Пример №3
Найти наибольшее и наименьшее значения функции $z=5xy-4$, если переменные $x$ и $y$ положительны и удовлетворяют уравнению связи $frac{x^2}{8}+frac{y^2}{2}-1=0$.
Решение
Составим функцию Лагранжа: $F=5xy-4+lambda left( frac{x^2}{8}+frac{y^2}{2}-1 right)$. Найдем стационарные точки функции Лагранжа:
$$
F_{x}^{‘}=5y+frac{lambda x}{4}; ; F_{y}^{‘}=5x+lambda y.\
left { begin{aligned}
& 5y+frac{lambda x}{4}=0;\
& 5x+lambda y=0;\
& frac{x^2}{8}+frac{y^2}{2}-1=0;\
& x > 0; ; y > 0.
end{aligned} right.
$$
Все дальнейшие преобразования осуществляются с учетом $x > 0; ; y > 0$ (это оговорено в условии задачи). Из второго уравнения выразим $lambda=-frac{5x}{y}$ и подставим найденное значение в первое уравнение: $5y-frac{5x}{y}cdot frac{x}{4}=0$, $4y^2-x^2=0$, $x=2y$. Подставляя $x=2y$ в третье уравнение, получим: $frac{4y^2}{8}+frac{y^2}{2}-1=0$, $y^2=1$, $y=1$.
Так как $y=1$, то $x=2$, $lambda=-10$. Характер экстремума в точке $(2;1)$ определим, исходя из знака $d^2F$.
$$
F_{xx}^{”}=frac{lambda}{4}; ; F_{xy}^{”}=5; ; F_{yy}^{”}=lambda.
$$
Так как $frac{x^2}{8}+frac{y^2}{2}-1=0$, то:
$$
dleft( frac{x^2}{8}+frac{y^2}{2}-1right)=0; ; dleft( frac{x^2}{8} right)+dleft( frac{y^2}{2} right)=0; ; frac{x}{4}dx+ydy=0; ; dy=-frac{xdx}{4y}.
$$
В принципе, здесь можно сразу подставить координаты стационарной точки $x=2$, $y=1$ и параметра $lambda=-10$, получив при этом:
$$
F_{xx}^{”}=frac{-5}{2}; ; F_{xy}^{”}=-10; ; dy=-frac{dx}{2}.\
d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2=-frac{5}{2}dx^2+10dxcdot left(-frac{dx}{2} right)-10cdot left(-frac{dx}{2} right)^2=\
=-frac{5}{2}dx^2-5dx^2-frac{5}{2}dx^2=-10dx^2.
$$
Однако в других задачах на условный экстремум стационарных точек может быть несколько. В таких случаях лучше $d^2F$ представить в общем виде, а потом подставлять в полученное выражение координаты каждой из найденных стационарных точек:
$$
d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2=frac{lambda}{4}dx^2+10cdot dxcdot frac{-xdx}{4y} +lambdacdot left(-frac{xdx}{4y} right)^2=\
=frac{lambda}{4}dx^2-frac{5x}{2y}dx^2+lambda cdot frac{x^2dx^2}{16y^2}=left( frac{lambda}{4}-frac{5x}{2y}+frac{lambda cdot x^2}{16y^2} right)cdot dx^2
$$
Подставляя $x=2$, $y=1$, $lambda=-10$, получим:
$$
d^2 F=left( frac{-10}{4}-frac{10}{2}-frac{10 cdot 4}{16} right)cdot dx^2=-10dx^2.
$$
Так как $d^2F=-10cdot dx^2 < 0$, то точка $(2;1)$ есть точкой условного максимума функции $z=5xy-4$, причём $z_{max}=10-4=6$.
Ответ: в точке $(2;1)$ функция имеет условный максимум, $z_{max}=6$.
В следующей части рассмотрим применение метода Лагранжа для функций большего количества переменных.
Метод множителей Лагранжа, применяемый для решения задач математического программирования (в частности, линейного программирования) — метод нахождения условного экстремума функции 
, где 
, относительно 
ограничений 
, где 
меняется от единицы до .
Описание метода[править | править код]
- где .
Обоснование[править | править код]
Нижеприведенное обоснование метода множителей Лагранжа не является его строгим доказательством. Оно содержит эвристические рассуждения, помогающие понять геометрический смысл метода.
Двумерный случай[править | править код]
Пусть требуется найти экстремум функции 
при условии, заданном уравнением 
.
Будем считать, что
- 1) функция непрерывно дифференцируема,
- 2) функция непрерывно дифференцируема, с частными производными, не равными нулю одновременно, то есть уравнение задаёт гладкую кривую из обыкновенных точек на плоскости .
- 3) кривая не проходит через точки, в которых градиент обращается в .
Нарисуем на плоскости 
линии уровня функции 
(то есть кривые 
). Из геометрических соображений следует, что точкой (возможно — точками) условного экстремума функции может быть только точка касания кривой 
и некоторой линии уровня, то есть точкой, в которой касательная к и касательная к этой линии уровня — совпадают. Действительно, если в некоторой точке 
кривая пересекает линию уровня 
трансверсально (то есть под некоторым ненулевым углом), то при движении по кривой из точки можно попасть как на линии уровня, соответствующие значению, большему 
, так и на линии уровня, соответствующие значению, меньшему . Следовательно, такая точка не может быть точкой экстремума.
Тем самым, необходимым условием экстремума в рассматриваемом случае будет совпадение касательных. Чтобы записать его в аналитической форме, заметим, что оно эквивалентно параллельности градиентов функций и 
в данной точке, поскольку вектор градиента перпендикулярен касательной к линии уровня. Это условие выражается в следующей форме:
где 
— некоторое число, отличное от нуля, и являющееся множителем Лагранжа.
Рассмотрим теперь функцию Лагранжа , зависящую от 
и :
Необходимым условием её экстремума является равенство нулю градиента 
. В соответствии с правилами дифференцирования оно записывается в виде
В полученной системе первые два уравнения эквивалентны необходимому условию локального экстремума (1), а третье — уравнению . Из неё можно найти 
. При этом 
, поскольку в противном случае градиент функции обращается в нуль в точке 
, что противоречит предположениям.
Замечание. Найденные таким способом точки могут и не являться точками условного экстремума — записанное дифференциальное условие носит необходимый, но не достаточный характер.
Вышеприведённые рассуждения о нахождении условного экстремума с помощью вспомогательной функции 
составляют
основу метода множителей Лагранжа и обобщаются на случай произвольного числа переменных и уравнений, задающих условия.
На основе метода множителей Лагранжа можно получить достаточные условия условного экстремума, требующие анализа (в простейшем случае) вторых производных функции Лагранжа .
Применение[править | править код]
- Метод множителей Лагранжа применяется при решении задач нелинейного программирования, возникающих во многих областях (например, в экономике).
- Основной метод решения задачи об оптимизации качества кодирования аудио и видео информации при заданном среднем битрейте (см. Оптимизация искажений (англ.) (рус.).
См. также[править | править код]
- Математическое программирование
- Линейное программирование
- Условия Каруша — Куна — Таккера
Литература[править | править код]
- Акулич И.Л. Глава 3. Задачи нелинейного программирования // Математическое программирование в примерах и задачах. — М.: Высшая школа, 1986. — 319 с. — ISBN 5-06-002663-9..
- Зорич В. А. Математический анализ. Часть 1. — изд. 2-е, испр. и доп. — М.: ФАЗИС, 1997.
- Протасов В. Ю. Максимумы и минимумы в геометрии. — М.: МЦНМО. — 56 с. — (Библиотека «Математическое просвещение», выпуск 31).
Условный экстремум
4 раздела
от теории до практики
2 примера
Примеры решения задач
видео
Примеры решения задач
-
Понятие условного экстремума.
Начать изучение
-
Прямой метод отыскания точек условного экстремума.
Начать изучение
-
Метод множителей Лагранжа.
Начать изучение
-
Несколько замечаний о методе множителей Лагранжа.
Начать изучение
Понятие условного экстремума.
Пусть на открытом множестве (G subset boldsymbol{R}^{n}) заданы функции (f_{0}(x)), (f_{1}(x), ldots, f_{m}(x)), причем (m < n), и пусть (E) — множество точек множества (G), удовлетворяющих системе уравнений
$$
f_{1}(x) = 0, ldots, f_{m}(x) = 0.label{ref1}
$$
Уравнения eqref{ref1} будем называть уравнениями связей (или просто связями).
Определение 1.
Точка (x^{0} = (x_{1}^{0}, ldots, x_{n}^{0}) in G) называется точкой условного минимума функции (f_{0}(x)) при наличии связей eqref{ref1}, если найдется такая окрестность (S_{delta}(x^{0})), что для всех (x in G cap S_{delta}(x^{0})) выполнено неравенство (f_{0}(x) geq f_{0}(x^{0})).
Определение 2.
Точка (x^{0} in G) называется точкой строгого условного минимума функции (f_{0}(x)) при наличии связей eqref{ref1}, если найдется такая окрестность (S_{delta}(x^{0})), что для всех (x in dot{S}_{delta}(x^{0}) cap G) выполнено неравенство (f_{0}(x) geq f_{0}(x^{0})).
Аналогично определяются точки условного максимума. Точки условного максимума и минимума называются точками условного экстремума.
Прямой метод отыскания точек условного экстремума.
Предположим, что из системы уравнений eqref{ref1} можно выразить какие-либо (m) переменных (x_{i}) через остальные переменные. Тогда, подставив вместо соответствующих переменных (x_{i}) их выражения через остальные (n-m) переменных в функцию (f_{0}(x)), получим функцию (F) от (n-m) переменных.
Задача о нахождении точек экстремума функции (f_{0}(x)) при наличии связей eqref{ref1} сведется к задаче нахождения обычного (безусловного) экстремума функции (F), зависящей от (n-m) переменных.
Пример 1.
Найти точки условного экстремума функции (z = 1-x^{2}-y^{2}), если (x+y = 1).
Решение.
(vartriangle) Уравнение связи (x+y = 1) легко разрешается относительно переменной (y), а именно (y = 1-x). Подставив это выражение для (y) в функцию (z = 1-x^{2}-y^{2}), получаем, что (z = 1-x^{2}-(1-x)^{2} = 2x-2x^{2}). Функция (2x-2x^{2}) имеет максимум при (x = frac{1}{2}). Точка ((frac{1}{2}, frac{1}{2})) является точкой условного максимума функции (z(x, y)) при наличии связи (x+y = 1), причем (z_{max} = displaystylefrac{1}{2}). (blacktriangle)
Замечание 1.
Прямой метод нахождения условного экстремума редко бывает эффективным ввиду трудности разрешения уравнений связей относительно какой-либо группы переменных.
Метод множителей Лагранжа.
Определение 3.
Рассмотрим функцию (n+m) переменных
$$
L(x, lambda) = f_{0}(x)+lambda_{1}f_{1}(x)+ldots+lambda_{m}f_{m}(x),nonumber
$$
где (x in G), а (lambda = (lambda_{1}, ldots, lambda_{m}) in boldsymbol{R}^{m}). Числа (lambda_{1}, ldots, lambda_{m}) называются множителями Лагранжа, а функция (L(x, lambda)) называется функцией Лагранжа.
Будем говорить, что ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа, если
$$
begin{array}{cc}
& displaystylefrac{partial L}{partial x_{1}} (x^{0}, lambda^{0}) = 0, ldots, frac{partial L}{partial x_{n}} (x^{0}, lambda^{0}) = 0\
&\
& displaystylefrac{partial L}{partial lambda_{1}} (x^{0}, lambda^{0}) = f_{1}(x^{0}) = 0, ldots, frac{partial L}{partial lambda_{m}} (x^{0}, lambda^{0}) = f_{m}(x^{0}) = 0.
end{array}label{ref2}
$$
Теорема 1.
(Теорема Лагранжа).
Пусть (x^{0}) — точка условного экстремума функции (f_{0}(x)) при наличии связей eqref{ref1}, и пусть функции (f_{i}(x)), (i = overline{0, m}), непрерывно дифференцируемы в окрестности точки (x^{0}), причем в точке (x^{0}) ранг матрицы Якоби
$$
A = begin{pmatrix}displaystylefrac{partial f_{1}}{partial x_{1}}(x)&ldots&displaystylefrac{partial f_{1}}{partial x_{n}}(x)\………&…..&…….\displaystylefrac{partial f_{m}}{partial x_{1}}(x)&ldots&displaystylefrac{partial f_{m}}{partial x_{n}}(x)end{pmatrix}label{ref3}
$$
равен (m).
Тогда найдутся такие множители Лагранжа (lambda_{1}^{0}, ldots, lambda_{m}^{0}), что ((x^0, lambda^0)) будет стационарной точкой функции Лагранжа.
Доказательство.
(circ) Так как (m < n), а ранг матрицы Якоби в точке (x^{0}) равен (m), то хотя бы один из миноров этой матрицы порядка (m) отличен от нуля.
Без ограничения общности можно считать, что
$$
begin{vmatrix}displaystylefrac{partial f_{1}}{partial x_{1}}(x^{0})&ldots&displaystylefrac{partial f_{1}}{partial x_{m}}(x^{0})\………&…..&…….\displaystylefrac{partial f_{m}}{partial x_{1}}(x^{0})&ldots&displaystylefrac{partial f_{m}}{partial x_{m}}(x^{0})end{vmatrix} neq 0,label{ref4}
$$
так как выполнения условия eqref{ref4} всегда можно добиться, перенумеровывая переменные и уравнения связей в нужном порядке.
Пусть (x^{0}) есть точка условного минимума функции (f_{0}(x)). Тогда существует окрестность (K'(x^{0}) = K’_{1}(x_{1}^{0}, ldots, x_{m}^{0}) times K’_{2}(x_{m+1}^{0}, ldots, x_{n}^{0})) такая, что
$$
f_{0}(x)-f_{0}(x^{0}) geq 0 mbox{при всех} x in E cap K’ (x^{0}).label{ref5}
$$
В силу непрерывности частных производных и выполнения условия eqref{ref4} можно применить теорему о неявных функциях. В силу этой теоремы найдется такая окрестность
$$
K(x^{0}) = K_{1}(x_{1}^{0}, ldots, x_{m}^{0}) times K_{2}(x_{m+1}^{0}, ldots, x_{n}^{0}) subset K'(x^{0}),nonumber
$$
в которой система уравнений связей eqref{ref1} определяет переменные (x_{1}, ldots, x_{m}) как неявные функции переменных (x_{m+1}, ldots, x_{m}). Это означает, что найдется единственный набор непрерывно дифференцируемых в окрестности (K’_{2}(x_{m+1}^{0}, ldots, x_{n}^{0})) функций (varphi_{i}(x_{m+1}, ldots, x_{n})), (i = overline{1, m}), таких, что
$$
varphi_{i}(x_{m+1}^{0}, ldots, x_{m}^{0}) = x_{i}^{0}, i = overline{1, m};label{ref6}
$$
$$
f_{i}(varphi_{1}(x_{m+1}, ldots, x_{n}), ldots, varphi_{m}(x_{m+1}, ldots, x_{n}), x_{m+1}, ldots, x_{n}) equiv 0,label{ref7}
$$
$$
(varphi_{1}(x_{m+1}, ldots, x_{n}), ldots, varphi_{m}(x_{m+1}, ldots, x_{n})) in K_{1}(x_{1}^{0}, ldots, x_{m}^{0})nonumber
$$
при ((x_{m+1}, ldots, x_{n}) in K_{2}(x_{1}^{0}, ldots, x_{m}^{0})), (i = overline{1, m}).
Другими словами, множество (E cap K(x^{0})) можно задать следующим образом:
$$
begin{array}{cc}
& E cap K(x^{0}) = {x: x = (x_{1}, ldots, x_{n}), (x_{m+1}, ldots, x_{n}) in K_{2}(x_{m+1}^{0}, ldots, x_{n}^{0}),\
& \
& x_{i} = varphi_{i}(x_{m+1}, ldots, x_{n}), i = overline{1, m}}.
end{array}label{ref8}
$$
Так как (K(x^{0}) subset K'(x^{0})), то из неравенства eqref{ref5} следует, что функция (f_{0}(x)) принимает на множестве (E cap K(x^{0})) наименьшее значение в точке (x^{0}). Если взять представление множества (E cap K(x^{0})) в виде eqref{ref8}, то сложная функция
$$
F(x_{m+1}, ldots, x_{n}) = f_{0}(varphi_{1}(x_{m+1}, ldots, x_{n}), ldots, varphi_{m}(x_{m+1}, ldots, x_{n}), x_{m+1}, ldots, x_{n})label{ref9}
$$
определена в окрестности (K_{2}(x_{m+1}^{0}, ldots, x_{n}^{0})) и принимает в этой окрестности наименьшее значение в точке ((x_{m+1}^{0}, ldots, x_{n}^{0})). Следовательно, в силу необходимых условий экстремума должно выполняться равенство (dF(x_{m+1}^{0}, ldots, x_{n}^{0}) = 0). Воспользовавшись инвариантностью формы первого дифференциала и равенством eqref{ref9}, получаем, что
$$
sum_{k=1}^{n} frac{partial f_{0}(x^{0})}{partial x_{k}} dx_{k} = 0.label{ref10}
$$
В равенстве eqref{ref10} (dx_{m+1}, ldots, dx_{n}) есть дифференциалы независимых переменных, a (dx_{1}, ldots, dx_{n}) — дифференциалы функций (varphi_{i}, ldots, varphi_{m}), зависящих от (x_{m+1}, ldots, x_{n}). Для краткости будем говорить о независимых и зависимых дифференциалах.
Найдем связи между зависимыми и независимыми дифференциалами. Дифференцируя тождества eqref{ref7} в точке ((x_{m+1}^{0}, ldots, x_{n}^{0})) и пользуясь инвариантностью формы первого дифференциала, получаем
$$
sum_{k=1}^{n} frac{partial f_{i}(x^{0})}{partial x_{k}} dx_{k} = 0, i = overline{1, m}.label{ref11}
$$
Умножая равенства eqref{ref11} на множители (lambda_{i}) и складывая полученные равенства с равенством eqref{ref10}, находим
$$
0 = sum_{k=1}^{n} left(frac{partial f_{0}}{partial x_{k}}+sum_{i=1}^{m} frac{partial f_{i}}{partial x_{k}} lambda_{i}right)_{x = x^{0}} dx_{k} = sum_{k=1}^{n} frac{partial L(x^{0}, lambda)}{partial x_{k}} dx_{k},label{ref12}
$$
где (L(x^{0}, lambda)) есть функция Лагранжа.
Подберем множители (lambda_{1}^{0}, ldots, lambda_{m}^{0}) так, чтобы коэффициенты при зависимых дифференциалах в равенстве eqref{ref12} обратились в нуль, то есть
$$
frac{partial L(x^{0}, lambda)}{partial x_{k}} = frac{partial f_{0}(x^{0})}{partial x_{k}}+sum_{i=1}^{m} lambda_{i}^{0} frac{partial f_{i}(x^0)}{partial x_{k}} = 0, k = overline{1, m}.label{ref13}
$$
Система уравнений eqref{ref13} единственным образом определяет множители (lambda_{1}^{0}, ldots, lambda_{m}^{0}), так как ее определитель eqref{ref4} отличен от нуля.
При выполнении условий eqref{ref13} уравнение eqref{ref12} примет вид
$$
sum_{k=m+1}^{n} frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} dx_{k} = 0.label{ref14}
$$
Так как дифференциалы независимых переменных (dx_{m+1}, ldots, dx_{n}), могут принимать любые значения, то из eqref{ref14} следует, что
$$
frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} = 0, k = m+1, ldots, n.label{ref15}
$$
Объединяя равенства eqref{ref13} и eqref{ref15}, получаем
$$
frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} = 0, k = overline{1, n}.nonumber
$$
Так как точка (x^{0} in E) и, следовательно, удовлетворяет уравнениям связей, то
$$
frac{partial L(x^{0}, lambda^{0})}{partial lambda_{j}} = f_{i}(x^{0}) = 0, j = overline{1, m}.nonumber
$$
Таким образом, ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа (L(x, lambda)). (bullet)
Второй дифференциал функции Лагранжа, вычисленный при фиксированных (lambda_{1}^{0}, ldots, lambda_{m}^{0}) по переменным ((x_{1}, ldots, x_{n})) в точке ((x_{1}^{0}, ldots, x_{n}^{0})), будем обозначать через (d_{xx}^{2}L(x^{0}, lambda^{0})).
Таким образом,
$$
d_{xx}^{2}L(x^{0}, lambda^{0}) = sum_{k=1}^{n} sum_{j=1}^{n} frac{partial^{2} L(x^{0}, lambda^{0})}{partial x_{k} partial x_{j}} dx_{k} dx_{j}.label{ref16}
$$
Иногда вместо (d_{xx}^{2}L(x^{0}, lambda^{0})) будем писать (d^{2}L(x^{0}, lambda^{0})).
Обозначим через (E_{T}) следующее линейное многообразие в (boldsymbol{R}^{n}):
$$
E_{T} = left{xi = (xi_{1}, ldots, xi_{n}) in boldsymbol{R}^{n}: sum_{k=1}^{n} frac{partial f_{i}(x^{0})}{partial x_{k}} xi_{k} = 0, i = overline{1, m}right}.label{ref17}
$$
Равенства eqref{ref11} означают, что (dx = (dx_{1}, ldots, dx_{n}) in E_{T}).
Теорема 2.
Пусть (x^{0}) есть точка условного минимума функции (f_{0}(x)) при наличии связей eqref{ref1}, и пусть функции (f_{i}(x)), (i = overline{1, m}), имеют непрерывные частные производные второго порядка в окрестности точки (x^{0}), причем в точке (x^{0}) ранг функциональной матрицы eqref{ref3} равен (m).
Тогда найдутся множители Лагранжа (lambda_{1}^{0}, ldots, lambda_{m}^{0}) такие, что ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа, a (d^{2}L(x^{0}, lambda^{0}) geq 0) при ((dx_{1}, ldots, dx_{n}) in E_{T}).
Доказательство.
(circ) Так как выполнены все условия теоремы 1, то найдутся множители Лагранжа (lambda_{1}^{0}, ldots, lambda_{m}^{0}) такие, что ((x^{0}, lambda^{0})) будет стационарной точкой функции Лагранжа, то есть выполняются условия eqref{ref2}. Повторяя рассуждения теоремы 1, рассмотрим сложную функцию eqref{ref9}, имеющую безусловный экстремум в точке ((x_{m+1}^{0}, ldots, x_{n}^{0})). Так как эта функция имеет непрерывные частные производные второго порядка, то, в силу теоремы о необходимом условии минимума должно быть выполнено условие (d^{2}F(x_{m+1}^{0}, ldots, x_{n}^{0}) geq 0).
Воспользовавшись правилом нахождения второго дифференциала сложной функции и формулой eqref{ref9}, находим, что
$$
sum_{k=1}^{n} sum_{j=1}^{n} frac{partial^{2} f_{0}(x^{0})}{partial x_{k} partial x_{j}} dx_{k} dx_{j}+sum_{k=1}^{n} frac{partial^{2} f_{0}}{partial x_{k}}(x^{0}) d^{2}x_{k} geq 0.label{ref18}
$$
Дифференцируя два раза в точке (x_{m+1}^{0}, ldots, x_{n}^{0}) тождества eqref{ref7}, получаем равенства
$$
sum_{k=1}^{n} sum_{j=1}^{n} frac{partial^{2} f_{i}(x^{0})}{partial x_{k} partial x_{j}} dx_{k} dx_{j}+sum_{k=1}^{n} frac{partial^{2} f_{i}}{partial x_{k}}(x^{0}) d^{2}x_{k} = 0.label{ref19}
$$
Если умножить каждое из равенств eqref{ref19} на соответствующий множитель Лагранжа (lambda_{i}^{0}) и сложить с неравенством eqref{ref18}, то получаем неравенство
$$
d_{xx}^{2}L(x^{0}, lambda^{0})+sum_{k=1}^{n} frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} d^{2}x_{k} geq 0.label{ref20}
$$
Последняя сумма в неравенстве eqref{ref20} равна нулю, так как ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа и в ней выполняются условия eqref{ref2}. Таким образом, (d_{xx}^{2}L(x^{0}, lambda^{0}) geq 0) при ((dx_{1}, ldots, dx_{n}) in E_{T}). (bullet)
Теорема 3.
(Достаточные условия условного экстремума).
Пусть функции (f_{i}(x)), (i = overline{0, m}), имеют непрерывные частные производные второго порядка в окрестности точки (x^{0} in boldsymbol{R}^{n}), причем в точке (x^{0}) ранг функциональной матрицы (3) равен (m), и пусть ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа (L(x, lambda)).
Тогда если (d_{xx}L(x^{0}, lambda^{0})) есть положительно определенная квадратичная форма при (dx in E_{T}), то (x^{0}) является точкой условного строгого минимума функции (f_{0}(x)) при наличии связей eqref{ref1}. Если (d_{xx}L(x^{0}, lambda^{0})) есть отрицательно определенная квадратичная форма при (dx in E_{T}), то (x^{0}) — точка условного строгого максимума. Если (d_{xx}L(x^{0}, lambda^{0})) есть неопределенная квадратичная форма при (dx in E_{T}), то (x^{0}) не есть точна условного экстремума функции (f_{0}(x)) при наличии связей eqref{ref1}.
Доказательство.
(circ) Пусть
$$
E = {x: f_{i}(x) = 0, i = overline{1, m}}.label{ref21}
$$
По условию теоремы функции (f_{i}(x)), (i = overline{0, m}), имеют непрерывные частные производные второго порядка, а ранг функциональной матрицы eqref{ref3} равен (m). Повторяя рассуждения теоремы 1, можем без ограничения общности считать, что выполнено условие eqref{ref4} и что найдется такая окрестность (K(x^{0}) = K_{1}(x_{1}^{0}, ldots, x_{m}^{0}) times K_{2}(x_{m+1}^{0}, ldots, x_{n}^{0})), что множество (E cap K(x^{0})) можно задать формулой eqref{ref8}. На (E cap K(x^{0})) функция (f_{0}(x)) становится функцией (n-m) переменных (F(x_{m+1}^{0}, ldots, x_{n}^{0})), определенной формулой eqref{ref9} и имеющей непрерывные частные производные второго порядка.
По условию теоремы ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа, то есть
$$
begin{array}{cc}
& displaystylefrac{partial L}{partial x_{k}} (x^{0}, lambda^{0}) = 0, k = overline{1, n};\
&\
& displaystylefrac{partial L}{partial lambda_{i}} (x^{0}, lambda^{0}) = f_{i}(x^{0}) = 0, i = overline{1, m}.
end{array}label{ref22}
$$
Из формул eqref{ref22} следует, что (x^{0} in E) и что
$$
d_{x}L(x^{0}, lambda^{0}) = sum_{k=1}^{n} frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} d^{2}x_{k} = 0.label{ref23}
$$
Рассмотрим функцию (L(x, lambda^{0})) на множестве (E cap K(x^{0})). Очевидно, что
$$
L(x, lambda^{0}) = f_{0}(x) = F(x_{m+1}, ldots, x_{n}) mbox{при} x in E cap K(x^{0}).label{ref24}
$$
В силу инвариантности формы первого дифференциала из формулы eqref{ref24} следует, что
$$
dF(x_{m+1}^{0}, ldots, x_{n}^{0}) = d_{x}L(x^{0}, lambda^{0}) = 0.label{ref25}
$$
Находя второй дифференциал от обеих частей равенства eqref{ref24} и используя равенства eqref{ref22}, получаем
$$
d^{2}F(x_{m+1}^{0}, ldots, x_{n}^{0}) = sum_{k=1}^{n} sum_{j=1}^{n} frac{partial^{2} L(x^{0}, lambda^{0})}{partial x_{j} partial x_{k}} dx_{j} dx_{k}+sum_{k=1}^{n} frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} d^{2}x_{k} = d_{xx}^{2}L(x^{0}, lambda^{0}).label{ref26}
$$
Пусть (d_{xx}^{2}L(x^{0}, lambda^{0}) > 0) при (dx in E_{T}), (dx neq 0). Так как множество (E cap K(x^{0})) можно задать в форме eqref{ref8}, то, выбирая (dx_{m+1}, ldots, dx_{n}) произвольным образом, получим, что дифференциалы (dx_{1},…, dx_{m}) зависят от ((dx_{m+1}, ldots, dx_{n})). Дифференцируя тождества eqref{ref7} в точке (x^{0}), получаем соотношения eqref{ref11}, которые означают, что (dx in E_{T}).
Из формулы eqref{ref26} тогда следует, что
$$
d^{2}F(x_{m+1}^{0}, ldots, x_{n}^{0}) > 0 mbox{при} dx_{m+1}^{2}+ldots+dx_{n}^{2} > 0.label{ref27}
$$
Из eqref{ref25} и eqref{ref27} получаем, что ((x_{m+1}^{0}, ldots, x_{n}^{0})) есть точка строгого минимума функции (F(x_{m+1}, ldots, x_{n})), то есть (x^{0}) есть точка строгого минимума функции (f_{0}(x)) на множестве (E cap K(x^{0})). Таким образом, (x^{0}) есть точка строгого условного минимума функции (f_{0}(x)) при наличии связей eqref{ref1}.
Аналогично рассматривается случай, когда (d_{xx}^{2}L(x^{0}, lambda^{0}) < 0), (dx in E_{T}), (dx neq 0). Если же (d_{xx}^{2}L(x^{0}, lambda^{0})) при (dx in E_{T}) есть неопределенная квадратичная форма, то не выполняется условие (d_{xx}^{2}L(x^{0}, lambda^{0}) geq 0) при (dx in E_{T}), являющееся, в силу теоремы 2, необходимым условием минимума. Поэтому (x^{0}) не есть точка условного минимума функции (f_{0}(x)) при связях eqref{ref1}. Аналогично доказывается, что (x^{0}) не может быть точкой условного минимума функции (-f_{0}(x)), а следовательно, и точкой условного максимума функции (f_{0}(x)) при связях eqref{ref1}. (bullet)
Замечание.
Если окажется, что (d_{xx}^{2}L(x^{0}, lambda^{0})) есть положительно определенная квадратичная форма на всем пространстве (boldsymbol{R}^{n}), то (d_{xx}^{2}L(x^{0}, lambda^{0}) > 0) при (dx in E_{T}), (dx neq 0). Поэтому в этом случае в квадратичной форме (d_{xx}^{2}L(x^{0}, lambda^{0})) не нужно исключать зависимые дифференциалы.
Пример 1.
Найти экстремумы функции (x-2y+2z = u) и на сфере (x^{2}+y^{2}+z^{2} = 1).
Решение.
(vartriangle) Строим функцию Лагранжа
$$
L(x, y, z, lambda) = x-2y+2z+lambda(x^{2}+y^{2}+x^{2}-1)nonumber
$$
Стационарные точки функции Лагранжа находим, решая систему уравнений
$$
frac{partial L}{partial x} = 1+2lambda x = 0,quad frac{partial L}{partial y} = -2+2lambda y = 0,quad frac{partial L}{partial z} = 2+2lambda z = 0,nonumber
$$
$$
frac{partial L}{partial lambda} = x^{2}+y^{2}+z^{2}-1 = 0.nonumber
$$
Исключая из этой системы (x, y, z), получаем (displaystyleleft(frac{1}{2lambda}right)^{2}+left(frac{1}{lambda}right)^{2}+left(frac{1}{lambda}right)^{2}-1 = 0), откуда (lambda_{1} = displaystylefrac{3}{2}), (lambda_{2} = -displaystylefrac{3}{2}).
У функции Лагранжа есть две стационарные точки,
$$
M_{1} = left(-frac{1}{3}, frac{2}{3}, -frac{2}{3}, frac{3}{2}right)quad mbox{и}quad M_{2} = left(frac{1}{3}, -frac{2}{3}, frac{2}{3}, -frac{3}{2}right).nonumber
$$
Так как (d^{2}L(M_{1}) = 3(dx^{2}+dy^{2}+dz^{2}) > 0), a (d^{2}L(M_{2}) = -3(dx^{2}+dy^{2}+dz^{2}) < 0) при (dx^{2}+dy^{2}+dz^{2} > 0), тo (displaystyleleft(-frac{1}{3}, frac{2}{3}, -frac{2}{3}, frac{3}{2}right)) — точка условного минимума, a (displaystyleleft(frac{1}{3}, -frac{2}{3}, frac{2}{3}, -frac{3}{2}right)) — точка условного максимума функции (u = x-2y+2x) при наличии ограничения (x^{2}+y^{2}+z^{2}-1 = 0), Причем (u_{min} = -3), (u_{max} = 3). (blacktriangle)
Пример 2.
Найти условные экстремумы функции (f_{0}(x, y) = e^{axy}), (a neq 0), при наличии ограничения (f_{i}(x, y) = x^{3}+y^{3}+x+y-4 = 0).
Решение.
(vartriangle) Построим функцию Лагранжа:
$$
L(x, y) = e^{axy}+lambda(x^{3}+y^{3}+x+y-4).nonumber
$$
Стационарные точки функции Лагранжа определяются из системы уравнений
$$
begin{array}{cc}
& displaystylefrac{partial L}{partial x} = aye^{axy}+lambda(3x^{2}+1) = 0,\
&\
& displaystylefrac{partial L}{partial y} = axe^{axy}+lambda(3y^{2}+1) = 0,\
&\
& displaystylefrac{partial L}{partial lambda} = x^{3}+y^{3}+x+y-4 = 0.
end{array}label{ref28}
$$
Умножая первое уравнение на (x), а второе на (y) и вычитая, получаем
$$
lambda(3x^{3}-3y^{3}+x-y) = lambda(x-y)(3x^{2}+3xy+3y^{2}+1) = 0.label{ref29}
$$
Если (lambda = 0), то из первых двух уравнений eqref{ref28} получаем (x = y = 0). Но (x = y = 0) не удовлетворяет уравнению связи. Итак, (lambda neq 0), поэтому из eqref{ref29} следует, что (x = y) (второй сомножитель всегда положителен: (3(x^{2}+xy+y^{2})+1 > 0)). Подставляя (x = y) в уравнение связи, получаем (x^{3}+x = 2), (x = y = 1). Первое из уравнений eqref{ref28} дает при (x = y = 1) значение (lambda = -displaystylefrac{a}{4} e^{a}).
Итак, ((1, 1, -displaystylefrac{a}{4} e^{a})) есть единственная стационарная точка функции Лагранжа.
Так как
$$
d(e^{axy}) = a(x dy+y dx) e^{axy},nonumber
$$
$$
d^{2}(e^{axy}) = a^{2}(x dy+y dx)^{2} e^{axy}+2a dx dy e^{axy},nonumber
$$
$$
d^{2}(x^{3}+y^{3}+x+y-4) = 6x dx^{2}+6y dy^{2},nonumber
$$
то для второго дифференциала функции Лагранжа при (lambda_{0} = -displaystylefrac{a}{4} e^{a}) и (x = y = 1) получается следующее выражение:
$$
d^{2}L(1, 1, lambda_{0}) = ae^{a}left[a(dx+dy)^{2}+2 dx dy-frac{3}{2}(dx^{2}+dy^{2})right].label{ref30}
$$
Дифференцируя уравнение связи при (x = y = 1), получаем, что (dy+dx = 0). Подставляя (dy = -dx) в уравнение eqref{ref30}, получаем равенство
$$
d^{2}L(1, 1, lambda_{0}) = -5ae^{a}dx^{2}.label{ref31}
$$
Поэтому при (a < 0) в точке (1,1) будет условный минимум, а при (a > 0) — условный максимум функции (f_{0}(x, y)) при наличии связи (x^{3}+y^{3}+x+y = 4), причем экстремальное значение функции равно (e^{a}). (blacktriangle)
Замечание.
Уравнение связи (x^{3}+y^{3}+x+y = 4) было бы затруднительно разрешить относительно одной из переменных. Метод Лагранжа для примера 2 более эффективен, чем прямой метод исключения зависимых переменных.
Несколько замечаний о методе множителей Лагранжа.
Задачи об отыскании экстремумов функций (как числовых, так и функций более общей природы) при наличии ограничений являются весьма распространенными. Теория экстремальных задач интенсивно развивается и находит широкий круг приложений. Здесь были рассмотрены ограничения типа равенств, задаваемые достаточно гладкими функциями (гладкие связи). Метод множителей Лагранжа имеет глубокие обобщения и на более общий случай, когда ограничения задаются системой равенств и неравенств при помощи недифференцируемых в обычном смысле функций.
В конкретных прикладных вопросах множители Лагранжа имеют содержательную интерпретацию. Так, в механике множители Лагранжа задают реакции связей, а в математической экономике — цены на продукты производства. Широко развиты приближенные методы решения экстремальных задач, использующие современную вычислительную технику.
Приветствую Вас, уважаемые Читатели! В школе каждый из Вас сталкивался с экстремальными задачами на поиск минимумов и максимумов. Все, так или иначе, научились находить производные, приравнивать их к нулю и анализировать полученные точки.
Но что, если мы имеем, например, функцию двух переменных, да еще и с ограничениями, заданными неявно. Например, требуется исследовать на экстремумы следующую конструкцию:
Конечно, можно пытаться выразить одну переменную через другую, но тогда получится не совсем красивая функция, с которой лень возиться. К счастью, у нас есть возможность использовать замечательный метод множителей Лагранжа. Давайте рассмотрим его, так сказать, на пальцах. Для начала запишем следующую вспомогательную функцию:
Теперь необходимо найти частные производные и решить систему уравнений:
Теперь при полученных значениях множителя находим точки, которые будем исследовать дополнительно:
Точки, найденные нами называются стационарными, а дальнейшие изыскания связаны с вычислением знака второй производной функции F в этих точках. Простейшая запись этих условий сводится к вычислению определителя:
Подставляем и вычисляем определитель в общем виде, что значительно удобнее:
Теперь, если определитель больше нуля, мы получим точку максимума, в обратном случае – минимум:
Вычисляем значения функции в найденных экстремальных точках:
Теперь посмотрим на геометрическую интерпретацию:
Как видно из рисунка, нужно найти наибольшее и наименьшее значение аппликаты плоскости z=x+2y для точек ее пересечения с цилиндром. Спасибо за внимание!
- TELEGRAM и Вконтакте– там я публикую не только интересные статьи, но и математический юмор и многое другое!
Метод множителей Лагранжа (в англ. литературе «LaGrange’s method of undetermined multipliers») ˗ это численный метод решения оптимизационных задач, который позволяет определить «условный» экстремум целевой функции (минимальное или максимальное значение)
при наличии заданных ограничений на ее переменные в виде равенств (т.е. определена область допустимых значений)
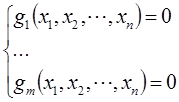
˗ это значения аргумента функции (управляемые параметры) на вещественной области при котором значение функции стремится к экстремуму. Применение названия «условный» экстремум связано с тем, что на переменные наложено дополнительное условие, которое ограничивает область допустимых значений при поиске экстремума функции.
Метод множителей Лагранжа позволяет задачу поиска условного экстремума целевой функции на множестве допустимых значений преобразовать к задаче безусловной оптимизации функции.
В случае если функции 
и 
непрерывны вместе со своими частными производными, то существуют такие переменные λ не равные одновременно нулю, при которых выполняется следующее условие:
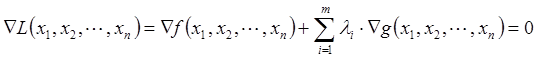
Таким образом, в соответствии с методом множителей Лагранжа для поиска экстремума целевой функции на множестве допустимых значений составляю функцию Лагранжа L(х, λ), которую в дальнейшем оптимизируют:
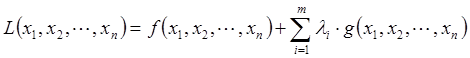
где λ ˗ вектор дополнительных переменных, называемых неопределенными множителями Лагранжа.
Таким образом, задача нахождения условного экстремума функции f(x) свелась к задаче поиска безусловного экстремума функции L(x, λ).
Далее в соответствии с методом определяют частные производные функции Лагранжа:
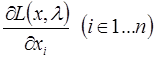и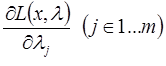 
Необходимое условие экстремума функции Лагранжа задается системой уравнений (система состоит из «n + m» уравнений):
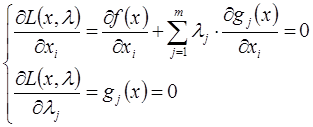
Решение данной системы уравнений позволяет определить аргументы функции (Х), при которых значение функции L(x, λ), а также значение целевой функции f(x) соответствуют экстремуму.
Величина множителей Лагранжа (λ) имеет практический интерес в случае, если ограничения представлены в форме со свободным членом уравнения (константой). В этом случае можно рассматривать дальнейшее (увеличение/уменьшение) значения целевой функции за счет изменения значения константы в системе уравнения 
. Таким образом, множитель Лагранжа характеризует скорость изменения максимума целевой функции при изменении ограничивающей константы.
Существует несколько способов определения характера экстремума полученной функции:
Первый способ: Пусть 
– координаты точки экстремума, а 
– соответствующее значение целевой функции. Берется точка 
, близкая к точке , и вычисляется значение целевой функции 
:
– Если 
, то в точке 
имеет место максимум.
– Если 
, то в точке имеет место минимум.
Второй способ: Достаточным условием, из которого можно выяснить характер экстремума, является знак второго дифференциала функции Лагранжа. Второй дифференциал функции Лагранжа определяется следующим образом:
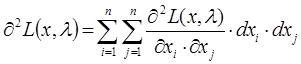
Если в заданной точке 
, то целевая функция f(x) имеет в данной точке условный минимум, если же 
, то целевая функция f(x) имеет в данной точке условный максимум.
Третий способ: Также характер экстремума функции можно выяснить рассмотрев гессиан функции Лагранжа. Матрица Гессе представляет собой симметричную квадратную матрицу вторых частных производных функции в точке 
, в которой элементы матрицы симметричны относительно главной диагонали.
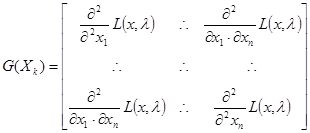
Для определения типа экстремума (максимум или минимум функции) можно воспользоваться правилом Сильвестра:
1. Для того, чтобы второй дифференциал функции Лагранжа был знакоположителен 
необходимо, чтобы угловые миноры функции были положительными 
. При таких условиях функция в этой точке имеет минимум.
2. Для того, чтобы второй дифференциал функции Лагранжа был знакоотрицателен 
, необходимо, чтобы угловые миноры функции чередовались, причем первый элемент матрицы должен быть отрицательнsv 
. При таких условиях функция в этой точке имеет максимум.
Под угловым минором понимаем минор, расположенный в первых k строках и k столбцах исходной матрицы.
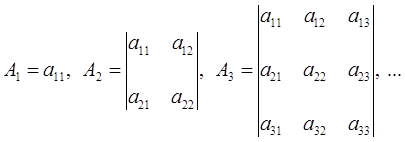
Основное практическое значение метода Лагранжа заключается в том, что он позволяет перейти от условной оптимизации к безусловной и, соответственно, расширить арсенал доступных методов решения задачи. Однако задача решения системы уравнений, к которой сводится данный метод, в общем случае не проще исходной задачи поиска экстремума. Такие методы называются непрямыми. Их применение объясняется необходимостью получить решение экстремальной задачи в аналитической форме (допустим, для тех или иных теоретических выкладок). При решении конкретных практических задач обычно используются прямые методы, основанные на итеративных процессах вычисления и сравнения значений оптимизируемых функций.
Методика расчета
1 шаг: Определяем функцию Лагранжа из заданной целевой функции и системы ограничений:
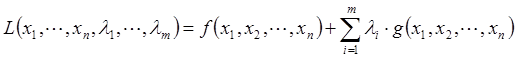
2 шаг: Определение аналитических соотношений (в символьном виде) для поиска безусловного экстремума функции L(x, λ).
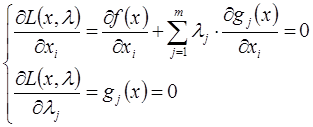
3 шаг: Решаем полученную систему линейных или нелинейных уравнений, используя соответствующие методы решения.
4 шаг: Определяем характер экстремума (максимум или минимум целевой функции) по любому из представленных выше методов.
