Загрузить PDF
Загрузить PDF
Во многих задачах требуется вычислить максимальное или минимальное значение квадратичной функции. Максимум или минимум можно найти, если исходная функция записана в стандартном виде: 

-
1
Запишите функцию в стандартном виде. Квадратичная функция – это функция, уравнение которой включает переменную
. Уравнение может включать или не включать переменную
. Если уравнение включает переменную с показателем степени больше 2, оно не описывает квадратичную функцию. Если нужно, приведите подобные члены и переставьте их, чтобы записать функцию в стандартном виде.[1]
-
2
-
3
-
4
Найдите соответствующее значение f(x). Подставьте найденное значение «x» в исходную функцию, чтобы найти соответствующее значение f(x). Так вы найдете минимум или максимум функции.
-
5
Реклама
-
1
Запишите квадратичную функцию через координаты вершины параболы. Такое уравнение имеет следующий вид:[3]
-
2
-
3
Найдите минимальное или максимальное значение функции. Если функция записана через координаты вершины параболы, минимум или максимум равен значению коэффициента
. В приведенных выше примерах:
-
4
Реклама
-
1
Сначала рассмотрим стандартный вид уравнения. Запишите квадратичную функцию в стандартном виде:
. Если нужно, приведите подобные члены и переставьте их, чтобы получить стандартное уравнение.[5]
- Например:
.
- Например:
-
2
Найдите первую производную. Первая производная квадратичной функции, которая записана в стандартном виде, равна
.[6]
-
3
Производную приравняйте к нулю. Напомним, что производная функции равна угловому коэффициенту функции в определенной точке. В минимуме или максимуме угловой коэффициент равен нулю. Поэтому, чтобы найти минимальное или максимальное значение функции, производную нужно приравнять к нулю. В нашем примере:[7]
-
4
-
5
-
6
Запишите ответ. Вы вычислили максимум или минимум функции. В нашем примере
координаты вершины равны
. Коэффициент
положительный, поэтому парабола направлена вверх. Следовательно, минимальное значение функции – это координата «у» вершины, которая равна
.[10]
Реклама
Советы
- Ось симметрии параболы описывается уравнением x=h.
Реклама
Об этой статье
Эту страницу просматривали 95 930 раз.
Была ли эта статья полезной?
Экстремумы функции
Необходимое условие экстремума функции одной переменной
Достаточное условие экстремума функции одной переменной
Если в точке x * выполняется условие:
Пример №1 . Найти наибольшее и наименьшее значения функции: 
Решение.
Критическая точка одна x1 = 2 (f’(x)=0). Эта точка принадлежит отрезку [1;3]. (Точка x=0 не является критической, так как 0∉[1;3]).
Вычисляем значения функции на концах отрезка и в критической точке.
f(1)=9, f(2)= 5 /2, f(3)=3 8 /81
Ответ: fmin= 5 /2 при x=2; fmax=9 при x=1
Пример №2 . С помощью производных высших порядков найти экстремум функции y=x-2sin(x) .
Решение.
Находим производную функции: y’=1-2cos(x) . Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=± π /3+2πk, k∈Z. Находим y’’=2sin(x), вычисляем 

Пример №3 . Исследовать на экстремум фцнкцию в окрестностях точки x=0.
Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0 , то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).
Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x0 или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.
Пример №4 . Разбить число 49 на два слагаемых, произведение которых будет наибольшим.
Решение. Обозначим x – первое слагаемое. Тогда (49-x) – второе слагаемое.
Произведение будет максимальным: x·(49-x) → max
или
49x – x 2
Как решать задачи B15 без производных
Иногда в задачах B15 попадаются «плохие» функции, для которых сложно найти производную. Раньше такое было лишь на пробниках, но сейчас эти задачи настолько распространены, что уже не могут быть игнорированы при подготовке к настоящему ЕГЭ.
В этом случае работают другие приемы, один из которых — монотонность.
Функция f ( x ) называется на отрезке если для любых точек этого отрезка выполняется следующее:
Функция f ( x ) называется на отрезке если для любых точек этого отрезка выполняется следующее:
Другими словами, для возрастающей функции Для убывающей функции все наоборот:
Например, логарифм монотонно возрастает, если основание и монотонно убывает, если Не забывайте про область допустимых значений логарифма:
f ( x ) = log a x ( a > 0; a ≠ 1; x > 0)
Арифметический квадратный (и не только квадратный) корень монотонно возрастает на всей области определения:
Показательная функция ведет себя аналогично логарифму: растет и убывает Но в отличие от логарифма, показательная функция определена для всех чисел, а не только
f ( x ) = a x (a > 0)
Наконец, степени с отрицательным показателем. Можно записывать их как дробь. Имеют точку разрыва, в которой монотонность нарушается.
Все эти функции никогда не встречаются в чистом виде. В них добавляют многочлены, дроби и прочий бред, становится тяжело считать производную. Что при этом происходит — сейчас разберем.
Координаты вершины параболы
Чаще всего аргумент функции заменяется на квадратный трехчлен вида Его график — стандартная парабола, в которой нас интересуют:
- Ветви параболы — могут уходить вверх или вниз Задают направление, в котором функция может принимать бесконечные значения;
- Вершина параболы — точка экстремума квадратичной функции, в которой эта функция принимает свое наименьшее или наибольшее значение.
Наибольший интерес представляет именно вершина параболы, абсцисса которой рассчитывается по формуле:
Итак, мы нашли точку экстремума квадратичной функции. Но если исходная функция монотонна, для нее тоже будет точкой экстремума. Таким образом, сформулируем ключевое правило:
Точки экстремума квадратного трехчлена и сложной функции, в которую он входит, совпадают. Поэтому можно для квадратного трехчлена, а на функцию — забить.
Из приведенных рассуждений остается непонятным, какую именно точку мы получаем: максимума или минимума. Однако задачи специально составляются так, что это не имеет значения. Судите сами:
- Отрезок [ a ; b ] в условии задачи отсутствует. Следовательно, вычислять не требуется. Остается рассмотреть лишь точки экстремума;
- Но таких точек всего одна — это вершина параболы координаты которой вычисляются буквально устно и без всяких производных.
Таким образом, решение задачи резко упрощается и сводится всего к двум шагам:
- Выписать уравнение параболы и найти ее вершину по формуле:
- Найти значение исходной функции в этой точке: Если никаких дополнительных условий нет, это и будет ответом.
На первый взгляд, этот алгоритм и его обоснование могут показаться сложными. Я намеренно не выкладываю «голую» схему решения, поскольку бездумное применение таких правил чревато ошибками.
Рассмотрим настоящие задачи из пробного ЕГЭ по математике — именно там данный прием встречается чаще всего. Заодно убедимся, что таким образом многие задачи B15 становятся почти устными.
Задача. Найдите наименьшее значение функции:
Под корнем стоит квадратичная функция График этой функции − парабола ветвями вверх, поскольку коэффициент
x 0 = − b /(2 a ) = −6/(2 · 1) = −6/2 = −3
Поскольку ветви параболы направлены вверх, в точке функция принимает наименьшее значение.
Корень монотонно возрастает, значит точка минимума всей функции. Имеем:
Задача. Найдите наименьшее значение функции:
Под логарифмом снова квадратичная функция: График — парабола ветвями вверх,
x 0 = − b /(2 a ) = −2/(2 · 1) = −2/2 = −1
Итак, в точке квадратичная функция принимает наименьшее значение. Но функция монотонная, поэтому:
y min = y (−1) = log 2 ((−1) 2 + 2 · (−1) + 9) = . = log 2 8 = 3
Задача. Найдите наибольшее значение функции:
В показателе стоит квадратичная функция Перепишем ее в нормальном виде:
Очевидно, что график этой функции — парабола, ветви вниз Поэтому вершина будет точкой максимума:
Исходная функция — показательная, она монотонна, поэтому наибольшее значение будет в найденной точке
Внимательный читатель наверняка заметит, что мы не выписывали область допустимых значений корня и логарифма. Но этого и не требовалось: внутри стоят функции, значения которых всегда положительны.
Следствия из области определения функции
Иногда для решения задачи B15 недостаточно просто найти вершину параболы. Искомое значение может лежать на конце отрезка, а вовсе не в точке экстремума. Если в задаче вообще не указан отрезок, смотрим на область допустимых значений исходной функции. А именно:
Аргумент логарифма должен быть положительным:
y = log a f ( x ) ⇒ f ( x ) > 0
Арифметический квадратный корень существует только из неотрицательных чисел:
Знаменатель дроби не должен равняться нулю:
Обратите внимание еще раз: ноль вполне может быть под корнем, но в логарифме или знаменателе дроби — никогда. Посмотрим, как это работает на конкретных примерах:
Задача. Найдите наибольшее значение функции:
Под корнем снова квадратичная функция: Ее график — парабола, но ветви вниз, поскольку Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический квадратный корень из отрицательного числа не существует.
Выписываем область допустимых значений (ОДЗ):
3 − 2 x − x 2 ≥ 0 ⇒ x 2 + 2 x − 3 ≤ 0 ⇒
Теперь найдем вершину параболы:
Точка принадлежит отрезку ОДЗ — и это хорошо. Теперь считаем значение функции а также на концах ОДЗ:
Итак, получили числа 2 и 0. Нас просят найти наибольшее — это число 2.
Задача. Найдите наименьшее значение функции:
Внутри логарифма стоит квадратичная функция Это парабола ветвями вниз, но в логарифме не может быть отрицательных чисел, поэтому выписываем ОДЗ:
6 x − x 2 − 5 > 0 ⇒ x 2 − 6 x + 5 x 0 = − b /(2 a ) = −6/(2 · (−1)) = −6/(−2) = 3
Вершина параболы подходит по ОДЗ: Но поскольку концы отрезка нас не интересуют, считаем значение функции только
y min = y (3) = log 0,5 (6 · 3 − 3 2 − 5) =
Максимумы, минимумы и экстремумы функций
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.
Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:
У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).
Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
– Производная положительна там, где функция возрастает.
– Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.
Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.
Начнем с (-13): до (-13) производная положительна т.е. функция растет, после – производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.
(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.
(- 9): функция возрастает, а потом убывает – максимум.
Все вышесказанное можно обобщить следующими выводами:
– Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
– Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции (f'(x)).
- Найдите корни уравнения (f'(x)=0).
- Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
– если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
– если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
– если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.
Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.
Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является (-2).
[spoiler title=”источники:”]
http://www.berdov.com/ege/extremum/other_way/
http://cos-cos.ru/math/327/
[/spoiler]
Эта статья — о числовой функции одной переменной. О функции второй степени с несколькими переменными см. Квадратичная форма; о геометрическом месте точек см. Парабола.
График функции
Квадратичная функция — целая рациональная функция второй степени вида 


Обзор основных свойств[править | править код]
Многие свойства квадратичной функции 

| Свойство | 
|

|
|---|---|---|
| Область определения функции | 
|
|
| Множество значений функции | 
|
![{displaystyle E(f)=left(-infty ;-{frac {b^{2}-4ac}{4a}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80574007c87fd2e0a084cba4db58f5eaa2f68950)
|
| Чётность функции | Чётная функция при  ; ни чётная, ни нечётная при ; ни чётная, ни нечётная при 
|
|
| Периодичность функции | Непериодическая функция | |
| Непрерывность функции | Всюду непрерывная функция, точек разрыва нет | |
| Нули функции |  , если , если  нет действительных нулей, если 
|
|
Предел функции при 
|
 при при 
|
 при при 
|
| Дифференцируемость функции | Всюду многократно дифференцируема:
|
|
| Точки экстремума (абсолютный экстремум) |  (минимум) (минимум)
|
 (максимум) (максимум)
|
| Интервалы строгой монотонности | убывает на ![{displaystyle left(-infty ;-{frac {b}{2a}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae6b6c026c5999b70af07f10b99f04c9f3eb4cc4) возрастает на 
|
возрастает на ![{displaystyle left(-infty ;-{frac {b}{2a}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae6b6c026c5999b70af07f10b99f04c9f3eb4cc4) убывает на 
|
| Выпуклость функции | Всюду выпуклая вниз функция | Всюду выпуклая вверх функция |
| Точки перегиба | Точки перегиба отсутствуют | |
| Ограниченность функции | Ограничена снизу | Ограничена сверху |
| Наибольшее значение функции | Отсутствует (неограничена сверху) | 
|
| Наименьшее значение функции | 
|
Отсутствует (неограничена снизу) |
| Положительные значения функции | 
|

|
| Отрицательные значения функции | 
|

|
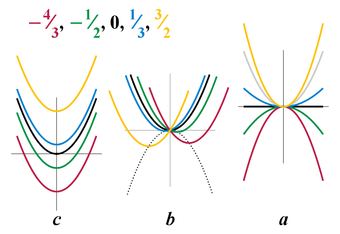
Влияние коэффициентов на трансформацию графика[править | править код]
Стандартная запись уравнения квадратичной функции[править | править код]
Влияние коэффициентов 


Действительные числа 




По значению коэффициента 
- Если
, то ветви параболы направлены вверх, то есть её вершина расположена снизу.
- Если
, то ветви параболы направлены вниз, то есть её вершина расположена сверху.
- Если
, то парабола сжата по оси ординат, то есть кажется более широкой и плоской.
- Если
, то парабола растянута по оси ординат, то есть кажется более узкой и крутой.
Влияние значения коэффициента 




Изменение коэффициента 








Коэффициент 



Запись квадратичной функции через координаты вершины параболы[править | править код]
Любая квадратичная функция 













Влияние коэффициентов в записи вида 
Преобразовать произвольную квадратичную функцию вида 

-
, где
и
-
Сравнивая значения для 

Недостатком данного метода является его громоздкость, особенно в случае, когда в результате вынесения за скобки приходится работать с дробями. Также он требует определённого навыка в обращении с формулами сокращённого умножения.
Однако, рассмотренное выше доказательство в общем виде приводит к более простому способу вычисления координат вершины параболы с помощью формул 


.
Таким образом, 
Нули функции[править | править код]
Число нулей квадратичной функции[править | править код]
Число действительных нулей квадратичной функции в случае
Квадратичная функция является целой рациональной функцией второй степени, поэтому она может иметь не более двух нулей в действительной области. В случае расширения на комплексную область можно говорить о том, что квадратичная функция в любом случае имеет ровно два комплексных нуля, которые могут быть строго действительными числами или содержать мнимую единицу.
Определить число нулей квадратичной функции без решения соответствующего квадратного уравнения можно с помощью вычисления дискриминанта. При этом имеются различные вариации его вычисления: обычный (применим всегда), сокращённый (удобен в случае чётного коэффициента 
| Полный дискриминант | Сокращённый дискриминант | Приведённый дискриминант |
|---|---|---|
 |
 |

|
 |
 |

|
Независимо от вычисления дискриминанта будут справедливы следующие утверждения:
Например, для функции 
.
Это означает, что данная функция имеет два действительных нуля, то есть её парабола пересекает ось абсцисс в двух точках.
Методы вычисления нулей квадратичной функции[править | править код]
Нахождение нулей квадратичной функции сводится к решению квадратного уравнения 

- В наиболее общем случае применяется универсальная формула:
-
- Получить приведённую форму из общей можно, поделив исходное уравнение
на
. При этом, очевидно,
и
.
Чётность и симметрия квадратичной функции[править | править код]
Симметрия относительно оси ординат[править | править код]
График функции 


Квадратичная функция 

Кроме того, очевидно, что квадратичная функция является чётной только при отсутствии показателя 1, что означает 

, то есть
.
Таким образом, квадратичная функция является симметричной относительно оси ординат только тогда, когда 



Во всех других случаях квадратичная функция не будет ни чётной, ни нечётной, то есть является функцией общего вида. Это также легко можно показать с помощью определения чётности функции:
, то есть
.
, то есть
.
Осевая симметрия в общем случае[править | править код]
Осью симметрии любой параболы является прямая, проходящая через её вершину параллельно оси ординат
В то же время график любой квадратичной функции обладает осевой симметрией. Как известно, если для некоторой функции 







Доказательство этого факта также не является сложным:
К аналогичному результату приводит и преобразование:
Таким образом, 

Вычисление вершины параболы с помощью нулей функции[править | править код]
Нули функции расположены симметрично к оси, проходящей через вершину параболы параллельно оси ординат
Так как ось симметрии параболы всегда проходит через её вершину, то, очевидно, что нули квадратичной функции также всегда симметричны относительно абсциссы вершины параболы. Этот факт позволяет легко вычислить координаты вершины параболы с помощью известных нулей функции. В поле действительных чисел этот способ действует только тогда, когда парабола пересекает ось абсцисс или касается её, то есть имеет нули из действительной области.
В случае, когда квадратичная функция имеет лишь один нуль (кратности 2), то он, очевидно, сам и является вершиной параболы. Если же парабола имеет нули 


Особенно удобным этот способ будет в случае, когда квадратичная функция заданна в её факторизированном виде. Так, например, парабола функции 
При этом даже не требуется преобразовывать уравнение функции к общему виду.
Исследование методами дифференциального и интегрального анализа[править | править код]
Производная и первообразная[править | править код]
Квадратичная функция (красный график), её производная (синий) и первообразная (чёрный)
Угловой коэффициент касательной параболы в точке 

Как и любая целая рациональная функция квадратичная функция 





Квадратичная функция как и любая целая рациональная функция также и интегрируема во всей своей области определения. Её первообразная, очевидно, является кубической функцией:
, где
.
Монотонность и точки экстремума[править | править код]
Очевидно, что вершина параболы является её наивысшей или наинизшей точкой, то есть абсолютным экстремумом квадратичной функции (минимумом при 


Согласно необходимому и достаточному условию для существования экстремума, получаем: 








Вершина параболы разбивает область определения квадратичной функции на два монотонных интервала: 



При этом можно вовсе не запоминать данные формулы, а просто каждый раз пользоваться критериями существования экстремума для каждой конкретной квадратичной функции. Или же рекомендуется запоминать только формулу 
Например, для функции 
.
Таким образом, вершина параболы данной функции имеет координаты 


Выпуклость и точки перегиба[править | править код]
Так как вторая производная квадратичной функции 



Обратимость квадратичной функции[править | править код]
Функция 

Так как квадратичная функция не является строго монотонной функцией, то она является необратимой. Так как любую непрерывную функцию, однако, можно обратить на её интервалах строгой монотонности, то для любой квадратичной функции существуют две обратные функции, соответствующие двум её интервалам монотонности. Обратными для квадратичной функции на каждом из её интервалов монотонности являются функции арифметического квадратного корня[2].
Так, функция арифметического квадратного корня 




![{displaystyle (-infty ;0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72c148ad1ad5af487ca5ae78ee670d0d3605a243)



Функция 

Для нахождения обратных функций для произвольной квадратичной функции 






Таким образом, обратной к 


На интервале ![{displaystyle (-infty ;x_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b851e43347b4ceced99ed4c5b14a71e746675021)


Например, для функции 

на интервале
.
на интервале
.
Примеры появления на практике[править | править код]
- Зависимость высоты свободно падающего тела от времени.
- Зависимость площади круга от её линейных размеров (например, радиуса).
- Зависимость расстояния от времени при равноускоренном движении.
- Зависимость напора от расхода (напорная характеристика центробежного насоса).
Обобщение[править | править код]
Обобщение на случай многих переменных служат поверхности второго порядка, в общем виде такое уравнение можно записать, как:
.
Здесь: 


Свойства функции, так же как и в одномерном случае, определяются главным коэффициентом — матрицей 
См. также[править | править код]
- Аффинно-квадратичная функция
Примечания[править | править код]
- ↑ Квадратичная функция // Большая школьная энциклопедия. — М. : «Русское энциклопедическое товарищество», 2004. — С. 118—119.
- ↑ Rolf Baumann. Quadratwutzelfunktion // Algebra: Potenzfunktionen, Exponential- und Logarithmusgleichungen, Stochastik : [нем.]. — München : Mentor, 1999. — Т. 9. — С. 17—19. — 167 с. — ISBN 3-580-63631-6.
Литература[править | править код]
- Сканави М.И. График квадратного трёхчлена // Элементарная математика. — 2-е изд., перераб. и доп. — М., 1974. — С. 130—133. — 592 с.
- Каплан И.А. Тридцать третье практическое занятие (экстремум квадратичной функции) // Практические занятия по высшей математике. — 3-е изд. — Харьков, 1974. — С. 449—451.
29 января 2012
Иногда в задачах B15 попадаются «плохие» функции, для которых сложно найти производную. Раньше такое было лишь на пробниках, но сейчас эти задачи настолько распространены, что уже не могут быть игнорированы при подготовке к настоящему ЕГЭ.
В этом случае работают другие приемы, один из которых — монотонность.
Функция f (x) называется монотонно возрастающей на отрезке [a; b], если для любых точек x1 и x2 этого отрезка выполняется следующее:
x1 < x2 ⇒ f (x1) < f (x2).
Функция f (x) называется монотонно убывающей на отрезке [a; b], если для любых точек x1 и x2 этого отрезка выполняется следующее:
x1 < x2 ⇒ f (x1) > f (x2).
Другими словами, для возрастающей функции чем больше x, тем больше f (x). Для убывающей функции все наоборот: чем больше x, тем меньше f (x).
Например, логарифм монотонно возрастает, если основание a > 1, и монотонно убывает, если 0 < a < 1. Не забывайте про область допустимых значений логарифма: x > 0.
f (x) = loga x (a > 0; a ≠ 1; x > 0)
Арифметический квадратный (и не только квадратный) корень монотонно возрастает на всей области определения:
Показательная функция ведет себя аналогично логарифму: растет при a > 1 и убывает при 0 < a < 1. Но в отличие от логарифма, показательная функция определена для всех чисел, а не только для x > 0:
f (x) = a x (a > 0)
Наконец, степени с отрицательным показателем. Можно записывать их как дробь. Имеют точку разрыва, в которой монотонность нарушается.
Все эти функции никогда не встречаются в чистом виде. В них добавляют многочлены, дроби и прочий бред, из-за которого становится тяжело считать производную. Что при этом происходит — сейчас разберем.
Координаты вершины параболы
Чаще всего аргумент функции заменяется на квадратный трехчлен вида y = ax2 + bx + c. Его график — стандартная парабола, в которой нас интересуют:
- Ветви параболы — могут уходить вверх (при a > 0) или вниз (a < 0). Задают направление, в котором функция может принимать бесконечные значения;
- Вершина параболы — точка экстремума квадратичной функции, в которой эта функция принимает свое наименьшее (для a > 0) или наибольшее (a < 0) значение.
Наибольший интерес представляет именно вершина параболы, абсцисса которой рассчитывается по формуле:
Итак, мы нашли точку экстремума квадратичной функции. Но если исходная функция монотонна, для нее точка x0 тоже будет точкой экстремума. Таким образом, сформулируем ключевое правило:
Точки экстремума квадратного трехчлена и сложной функции, в которую он входит, совпадают. Поэтому можно искать x0 для квадратного трехчлена, а на функцию — забить.
Из приведенных рассуждений остается непонятным, какую именно точку мы получаем: максимума или минимума. Однако задачи специально составляются так, что это не имеет значения. Судите сами:
- Отрезок [a; b] в условии задачи отсутствует. Следовательно, вычислять f (a) и f (b) не требуется. Остается рассмотреть лишь точки экстремума;
- Но таких точек всего одна — это вершина параболы x0, координаты которой вычисляются буквально устно и без всяких производных.
Таким образом, решение задачи резко упрощается и сводится всего к двум шагам:
- Выписать уравнение параболы y = ax2 + bx + c и найти ее вершину по формуле: x0 = −b/2a;
- Найти значение исходной функции в этой точке: f (x0). Если никаких дополнительных условий нет, это и будет ответом.
На первый взгляд, этот алгоритм и его обоснование могут показаться сложными. Я намеренно не выкладываю «голую» схему решения, поскольку бездумное применение таких правил чревато ошибками.
Рассмотрим настоящие задачи из пробного ЕГЭ по математике — именно там данный прием встречается чаще всего. Заодно убедимся, что таким образом многие задачи B15 становятся почти устными.
Задача. Найдите наименьшее значение функции:

Под корнем стоит квадратичная функция y = x2 + 6x + 13. График этой функции − парабола ветвями вверх, поскольку коэффициент a = 1 > 0.
Вершина параболы:
x0 = −b/(2a) = −6/(2 · 1) = −6/2 = −3
Поскольку ветви параболы направлены вверх, в точке x0 = −3 функция y = x2 + 6x + 13 принимает наименьшее значение.
Корень монотонно возрастает, значит x0 — точка минимума всей функции. Имеем:
Задача. Найдите наименьшее значение функции:
y = log 2 (x2 + 2x + 9)
Под логарифмом снова квадратичная функция: y = x2 + 2x + 9. График — парабола ветвями вверх, т.к. a = 1 > 0.
Вершина параболы:
x0 = −b/(2a) = −2/(2 · 1) = −2/2 = −1
Итак, в точке x0 = −1 квадратичная функция принимает наименьшее значение. Но функция y = log 2 x — монотонная, поэтому:
ymin = y(−1) = log 2 ((−1)2 + 2 · (−1) + 9) = … = log 2 8 = 3
Задача. Найдите наибольшее значение функции:

В показателе стоит квадратичная функция y = 1 − 4x − x2. Перепишем ее в нормальном виде: y = −x2 − 4x + 1.
Очевидно, что график этой функции — парабола, ветви вниз (a = −1 < 0). Поэтому вершина будет точкой максимума:
x0 = −b/(2a) = −(−4)/(2 · (−1)) = 4/(−2) = −2
Исходная функция — показательная, она монотонна, поэтому наибольшее значение будет в найденной точке x0 = −2:
Внимательный читатель наверняка заметит, что мы не выписывали область допустимых значений корня и логарифма. Но этого и не требовалось: внутри стоят функции, значения которых всегда положительны.
Следствия из области определения функции
Иногда для решения задачи B15 недостаточно просто найти вершину параболы. Искомое значение может лежать на конце отрезка, а вовсе не в точке экстремума. Если в задаче вообще не указан отрезок, смотрим на область допустимых значений исходной функции. А именно:
-
Аргумент логарифма должен быть положительным:
y = loga f (x) ⇒ f (x) > 0
-
Арифметический квадратный корень существует только из неотрицательных чисел:
-
Знаменатель дроби не должен равняться нулю:
Обратите внимание еще раз: ноль вполне может быть под корнем, но в логарифме или знаменателе дроби — никогда. Посмотрим, как это работает на конкретных примерах:
Задача. Найдите наибольшее значение функции:

Под корнем снова квадратичная функция: y = 3 − 2x − x2. Ее график — парабола, но ветви вниз, поскольку a = −1 < 0. Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический квадратный корень из отрицательного числа не существует.
Выписываем область допустимых значений (ОДЗ):
3 − 2x − x2 ≥ 0 ⇒ x2 + 2x − 3 ≤ 0 ⇒ (x + 3)(x − 1) ≤ 0 ⇒ x ∈ [−3; 1]
Теперь найдем вершину параболы:
x0 = −b/(2a) = −(−2)/(2 · (−1)) = 2/(−2) = −1
Точка x0 = −1 принадлежит отрезку ОДЗ — и это хорошо. Теперь считаем значение функции в точке x0, а также на концах ОДЗ:
y(−3) = y(1) = 0
Итак, получили числа 2 и 0. Нас просят найти наибольшее — это число 2.
Задача. Найдите наименьшее значение функции:
y = log 0,5 (6x − x2 − 5)
Внутри логарифма стоит квадратичная функция y = 6x − x2 − 5. Это парабола ветвями вниз, но в логарифме не может быть отрицательных чисел, поэтому выписываем ОДЗ:
6x − x2 − 5 > 0 ⇒ x2 − 6x + 5 < 0 ⇒ (x − 1)(x − 5) < 0 ⇒ x ∈ (1; 5)
Обратите внимание: неравенство строгое, поэтому концы не принадлежат ОДЗ. Этим логарифм отличается от корня, где концы отрезка нас вполне устраивают.
Ищем вершину параболы:
x0 = −b/(2a) = −6/(2 · (−1)) = −6/(−2) = 3
Вершина параболы подходит по ОДЗ: x0 = 3 ∈ (1; 5). Но поскольку концы отрезка нас не интересуют, считаем значение функции только в точке x0:
ymin = y(3) = log 0,5 (6 · 3 − 32 − 5) = log 0,5 (18 − 9 − 5) = log 0,5 4 = −2
Смотрите также:
- Показательные функции в задаче B15: хитрости решения
- Задача B15: работаем с показательной функцией без производной
- Тест к уроку «Сложные выражения с дробями» (легкий)
- Четырехугольная пирамида в задаче C2
- Задача B5: площадь кольца
- Решение задач на движение по воде
Что такое экстремум функции и каково необходимое условие экстремума?
Экстремумом функции называется максимум и минимум функции.
Необходимое условие максимума и минимума (экстремума) функции следующее: если функция f(x) имеет экстремум в точке х = а, то в этой точке производная либо равна нулю, либо бесконечна, либо не существует.
Это условие необходимое, но не достаточное. Производная в точке х = а может обращаться в нуль, в бесконечность или не существовать без того, чтобы функция имела экстремум в этой точке.
Каково достаточное условие экстремума функции (максимума или минимума)?
Первое условие:
Если в достаточной близости от точки х = а производная f?(x) положительна слева от а и отрицательна справа от а, то в самой точке х = а функция f(x) имеет максимум при условии, что функция f(x) здесь непрерывна.
Если в достаточной близости от точки х = а производная f?(x) отрицательна слева от а и положительна справа от а, то в самой точке х = а функция f(x) имеет минимум при условии, что функция f(x) здесь непрерывна.
Вместо этого можно воспользоваться вторым достаточным условием экстремума функции:
Пусть в точке х = а первая производная f?(x) обращается в нуль; если при этом вторая производная f??(а) отрицательна, то функция f(x) имеет в точке x = a максимум, если положительна – то минимум.
О случае f??(а) = 0 можно прочитать в Справочнике по высшей математике М.Я. Выгодского.
Что такое критическая точка функции и как её найти?
Это значение аргумента функции, при котором функция имеет экстремум (т.е. максимум или минимум). Чтобы его найти, нужно найти производную функции f?(x) и, приравняв её к нулю, решить уравнение f?(x) = 0. Корни этого уравнения, а также те точки, в которых не существует производная данной функции, являются критическими точками, т. е. значениями аргумента, при которых может быть экстремум. Их можно легко определить, взглянув на график производной: нас интересуют те значения аргумента, при которых график функции пересекает ось абсцисс (ось Ох) и те, при которых график терпит разрывы.
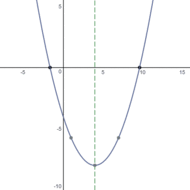
Для примера найдём экстремум параболы.
Функция y(x) = 3x2 + 2x – 50.
Производная функции: y?(x) = 6x + 2
Решаем уравнение: y?(x) = 0
6х + 2 = 0, 6х = -2, х=-2/6 = -1/3
В данном случае критическая точка – это х0=-1/3. Именно при этом значении аргумента функция имеет экстремум. Чтобы его найти, подставляем в выражение для функции вместо «х» найдённое число:
y0 = 3*(-1/3)2 + 2*(-1/3) – 50 = 3*1/9 – 2/3 – 50 = 1/3 – 2/3 – 50 = -1/3 – 50 = -50,333.
Как определить максимум и минимум функции, т.е. её наибольшее и наименьшее значения?
Если знак производной при переходе через критическую точку х0 меняется с «плюса» на «минус», то х0 есть точка максимума; если же знак производной меняется с минуса на плюс, то х0 есть точка минимума; если знак не меняется, то в точке х0 ни максимума, ни минимума нет.
Для рассмотренного примера:
Берём произвольное значение аргумента слева от критической точки: х = -1
При х = -1 значение производной будет у?(-1) = 6*(-1) + 2 = -6 + 2 = -4 (т.е. знак – «минус»).
Теперь берём произвольное значение аргумента справа от критической точки: х = 1
При х = 1 значение производной будет у(1) = 6*1 + 2 = 6 + 2 = 8 (т.е. знак – «плюс»).
Как видим, производная при переходе через критическую точку поменяла знак с минуса на плюс. Значит, при критическом значении х0 мы имеем точку минимума.
Наибольшее и наименьшее значение функции на интервале (на отрезке) находят по такой же процедуре, только с учетом того, что, возможно, не все критические точки будут лежать внутри указанного интервала. Те критические точки, которые находятся за пределом интервала, нужно исключить из рассмотрения. Если внутри интервала находится только одна критическая точка – в ней будет либо максимум, либо минимум. В этом случае для определения наибольшего и наименьшего значений функции учитываем также значения функции на концах интервала.
Например, найдём наибольшее и наименьшее значения функции
y(x) = 3sin(x) — 0,5х
на интервалах:
а) [-9; 9]
б) [-6; -3]
Итак, производная функции —
y?(x) = 3cos(x) — 0,5
Решаем уравнение 3cos(x) — 0,5 = 0
3cos(x) = 0,5
cos(x) = 0,5/3 = 0,16667
х = ±arccos(0,16667) + 2πk.
Находим критические точки на интервале [-9; 9]:
х = arccos(0,16667) — 2π*2 = -11,163 (не входит в интервал)
х = –arccos(0,16667) — 2π*1 = -7,687
х = arccos(0,16667) — 2π*1 = -4,88
х = –arccos(0,16667) + 2π*0 = -1,403
х = arccos(0,16667) + 2π*0 = 1,403
х = –arccos(0,16667) + 2π*1 = 4,88
х = arccos(0,16667) + 2π*1 = 7,687
х = –arccos(0,16667) + 2π*2 = 11,163 (не входит в интервал)
Находим значения функции при критических значениях аргумента:
y(-7,687) = 3cos(-7,687) — 0,5 = 0,885
y(-4,88) = 3cos(-4,88) — 0,5 = 5,398
y(-1,403) = 3cos(-1,403) — 0,5 = -2,256
y(1,403) = 3cos(1,403) — 0,5 = 2,256
y(4,88) = 3cos(4,88) — 0,5 = -5,398
y(7,687) = 3cos(7,687) — 0,5 = -0,885
Видно, что на интервале [-9; 9] наибольшее значение функция имеет при x = -4,88:
x = -4,88, у = 5,398,
а наименьшее – при х = 4,88:
x = 4,88, у = -5,398.
На интервале [-6; -3] мы имеем только одну критическую точку: х = -4,88. Значение функции при х = -4,88 равно у = 5,398.
Находим значение функции на концах интервала:
y(-6) = 3cos(-6) — 0,5 = 3,838
y(-3) = 3cos(-3) — 0,5 = 1,077
На интервале [-6; -3] имеем наибольшее значение функции
у = 5,398 при x = -4,88
наименьшее значение —
у = 1,077 при x = -3
Как найти точки перегиба графика функции и определить стороны выпуклости и вогнутости?
Чтобы найти все точки перегиба линии y = f(x), надо найти вторую производную, приравнять её к нулю (решить уравнение) и испытать все те значения х, для которых вторая производная равна нулю, бесконечна или не существует. Если при переходе через одно из этих значений вторая производная меняет знак, то график функции имеет в этой точке перегиб. Если же не меняет, то перегиба нет.
Корни уравнения f ? (x) = 0, а также возможные точки разрыва функции и второй производной разбивают область определения функции на ряд интервалов. Выпуклость на каждом их интервалов определяется знаком второй производной. Если вторая производная в точке на исследуемом интервале положительна, то линия y = f(x) обращена здесь вогнутостью кверху, а если отрицательна – то книзу.
Как найти экстремумы функции двух переменных?
Чтобы найти экстремумы функции f(x,y), дифференцируемой в области её задания, нужно:
1) найти критические точки, а для этого — решить систему уравнений
fх? (x,y) = 0, fу? (x,y) = 0
2) для каждой критической точки Р0(a;b) исследовать, остается ли неизменным знак разности
f(x,y) – f(a,b)
для всех точек (х;у), достаточно близких к Р0. Если разность сохраняет положительный знак, то в точке Р0 имеем минимум, если отрицательный – то максимум. Если разность не сохраняет знака, то в точке Р0 экстремума нет.
Аналогично определяют экстремумы функции при большем числе аргументов.
Источники:
- Выгодский М.Я. Справочник по высшей математике
- Черненко В.Д. Высшая математика в примерах и задачах. В 3-х томах. Том 1.























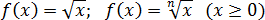
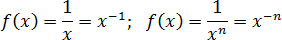
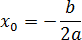
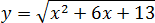
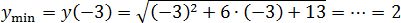
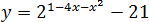
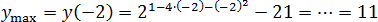
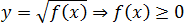
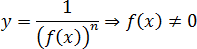
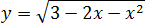
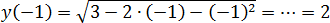



























































![{displaystyle (-infty ;-2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/615ae99698f85cb43b3de7eb156149152b51acc6)


