
Видеоурок по определению экстремума эпюры изгибающих моментов балки
При построении эпюр в сечении где поперечная сила Qy равна нулю, необходимо рассчитать значение экстремума эпюры изгибающих моментов.
На видео показан пример его определения для построенной эпюры M для двухопорной балки.
Предыдущие видео:
- Определение опорных реакций балки
- Расчет и построение эпюр Qy и Mx.
Другие видео
Последующие видео:
- Проверка эпюр Q и M
Пояснения и дополнения:
- Теоретическая механика
- Сопротивление материалов
- Примеры решения задач
Все видео >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Правило построение эпюр – экстремум. Помогите пожалуйста.
Ученик
(129),
на голосовании
9 лет назад
Голосование за лучший ответ
Пунчик
Оракул
(99651)
9 лет назад
все просто – найди координату – расстояние от начала участка до точки в которой эпюра Q проходит через ноль и в этом сечении найди изгибающий момент – в уравнении момента плечи равны этому расстоянию. Значение момента должно получиться наибольшим или наименьшим на ЭТОМ участке. А картинки твои не прорезались, так что конкретнее не получится. Если в математике шаришь, то можно и проще объяснить – эпюра Q – первая производная от М
Купить курс I строительная механика – https://vk.com/stroitelnayamehanika
🌍Также мы предоставляем помощь в решении домашних задач и онлайн на экзаменах
💡3D анимация расчета балки: https://bit.ly/3g5Ou4X
Решение задачи по разделу ‘сопротивление материалов’.
Разбор понятия экстремум.
Определение опорных реакций в балке. Построение эпюр поперечных сил Q и изгибающих моментов М, определение экстремума.
00:00 вступление
00:11 определение опорных реакций
00:24 что такое экстремум?
00:56 определение экстремума
01:44 курс в описании
📝Исполнитель – Скачко Максим
Viber, whatsapp, telegram +37533 328-64-82
#курсстроймех #балка #экстремум
Построение
эпюр поперечной силы и изгибающего
момента для балок
Пример
1.
Построить
эпюры внутренних усилий Qy,
Mx
для балки (см. рис.).
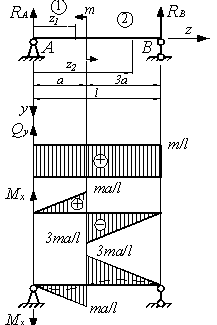
а)
б)
Решение.
1.
Определение опорных реакций
Из
уравнений равновесия
![]()
находим
![]()
.
2.
Определение Qy,
Mx
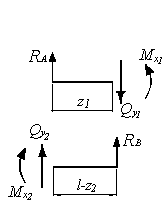
методом сечений (рис. б) и построение
эпюр
Из
уравнений равновесия отсеченных частей
балки находим
![]()
![]()
По
полученным значениям строим эпюры (рис.
а). Отметим, что сосредоточенный момент
не повлиял на характер эпюры Qy.
На эпюре моментов сосредоточенный
момент вызвал скачок на величину этого
момента. Наклон прямых на эпюре моментов
одинаков, что соответствует правилу
Журавского.
Пример
2.
Построить
эпюры Qy,
Mx
для балки (см. рис. а).

а)
б)
Решение.
1.
Определение опорных реакций
Из
уравнений равновесия
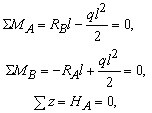
находим
![]()
.
2.
Определение Qy,
Mx
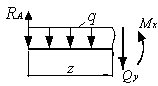
методом сечения и построение эпюр
Из
уравнения равновесия отсеченной части
балки (рис. б) находим
![]()
.
Как
видно, график-эпюра
–
прямая линия, а
– квадратичная парабола. Полагая
![]()
и
![]()
,
находим значения усилий в этих точках.
При
значения внутренних усилий
![]()
а при
:
![]()
Отметим, что в шарнирах моменты всегда
равны нулю. На эпюре
при
![]()
перерезывающая сила
![]()
.
Это признак экстремума на эпюре моментов.
Вычислим при
![]()
максимум изгибающего момента
![]()
Откладываем
полученное значение на графике-эпюре
и проводим через три точки параболу. По
правилу зонтика и дождика выпуклость
параболы обращена к верху, а на перевернутой
эпюре моментов – к низу.
Эпюра моментов напоминает изогнутую
ось балки, изображенную на рис. а
пунктиром.
Пример
3.
Построить
эпюры Qy,
Mx
для балки (см. рис. а).
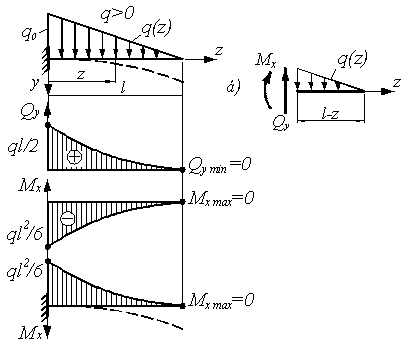
а)
б)
Решение.
Методом
сечений (рис. б)
находим
![]()
![]()
Поскольку
![]()
то эпюра
–
квадратичная парабола, а
![]()
–
кубическая.
При
,
![]()
.
При
имеем
![]()
.
Эпюра
испытывает экстремум при
![]()
,
когда
![]()
Выпуклость эпюры
определяется знаком ее второй производной:
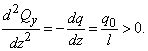
Так как
вторая производная возрастает, то
выпуклость направлена вниз.
Экстремум
эпюры моментов
имеет место в сечении, где
![]()
,
т.е. на конце консоли при
![]()
.
В этом сечении
![]()
.
Выпуклость кривой
определяется по знаку второй производной,
то есть по правилу зонтика:
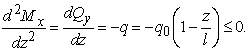
В нашем
случае выпуклость направлена вверх.
Пример
4.
Построить
эпюры перерезывающих сил и изгибающих
моментов Qy,
Mx
для балки (см. рис. а), если
![]()
,
интенсивность нагрузки
![]()
.


а)
б)
Решение.
1.
Определение опорных реакций из уравнений
равновесия
Составим
два независимых уравнения равновесия
моментов относительно опор A,
B:
![]()
Находим
опорные реакции
![]()
.
Для
статической проверки составляем третье
зависимое уравнение равновесия в
проекции на вертикальную ось:
![]()
.
Подставляем в это уравнение значения
найденных реактивных сил и получаем
![]()
Следовательно,
опорные реакции определены правильно.
2.
Определение Qy,
Mx
методом сечения и построение их эпюр
Балка
имеет два участка
![]()
и
![]()
с различными аналитическими выражениями
внутренних силовых факторов.
На
первом участке (рис. б) методом
сечений с учетом
![]()
находим

Эпюра
−
квадратичная парабола, а
− кубическая.
При
![]()
имеем
![]()
,
а при
![]()
имеем
![]()
.
Согласно дифференциальным зависимостям
Журавского экстремум эпюры
имеет место в сечении
![]()
,
где
![]()
,
экстремум эпюры
в сечении, где
![]()
,
что дает
![]()
,
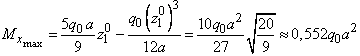
.
На
втором участке (рис. б) методом
сечений получаем
![]()
![]()
При
![]()
![]()
.
Эпюра
− постоянна, а
− наклонная прямая. Максимальный момент
определяется по формуле
![]()
.
3.
Расчет на прочность
Условие
прочности записываем в виде
![]()
Пример
6.
Для
заданной балки (см. рис.) построить эпюры
от силы Q и от момента
М.
Дано:
l1=3,8 м; l2=3,6
м; l3=1,4 м, F=3,8q;
M=14,44q
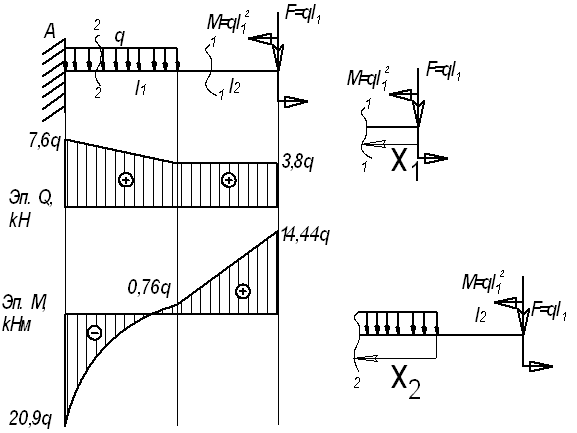
Решение.
Рассмотрим
сечение 1-1:
![]()
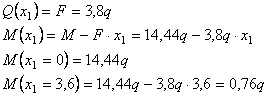
Рассмотрим
сечение 2-2:
![]()

Пример
7.
Для
заданной балки (см. рис.) построить эпюры
от силы Q и от
момента М.
Дано:
l1=3,8 м; l2=3,6
м; l3=1,4 м, F=3,8q;
M=12,96q
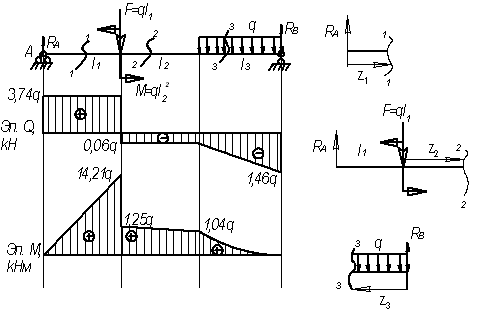
Решение.
Находим
реакции опор
![]()
![]()
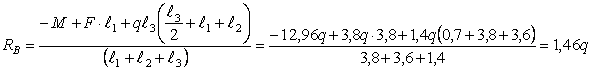
![]()
![]()
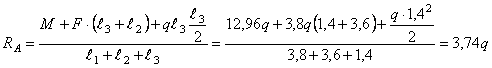
Проверка
![]()
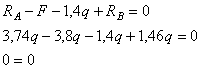
Реакции
опор найдены правильно.
Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Рассмотрим сечение 3-3:

Пример
8.
Для
заданной балки (см. рис.) построить эпюры
от силы Q и от
момента М.
Дано:
l1=2 м; l2=3,4
м; l3=2 м, F=3,4q;
M=4q
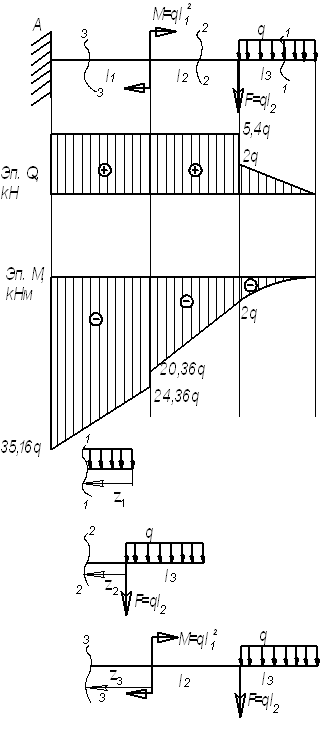
Решение.
Рассмотрим
сечение 1-1:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рассмотрим
сечение 2-2:
![]()
![]()
![]()
![]()
![]()
Рассмотрим
сечение 3-3:
![]()
![]()
![]()
![]()
![]()
Пример
9.
Для
заданной балки (см. рис.) построить эпюры
от силы Q и от момента
М
Дано:
l1=2 м; l2=3,4
м; l3=2 м, F=2q;
M=11,56q
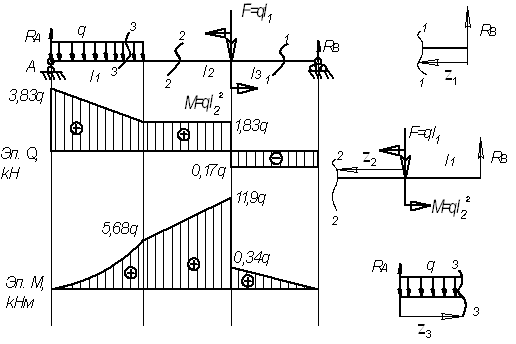
Решение.
Находим
реакции опор
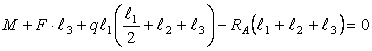
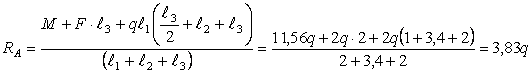
![]()
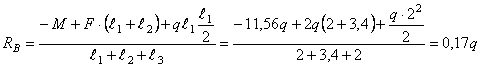
Проверка
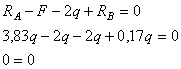
Реакции
опор найдены правильно.
Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Рассмотрим сечение 3-3:
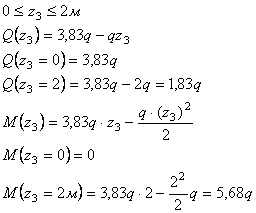
Пример
10.
Для
заданной балки (см. рис.) построить эпюры
от силы Q и от
момента М
Дано:
l1=2,3 м; l2=3,4
м; l3=1,8 м, F=3,4q;
M=2,65q
Решение.
Рассмотрим
сечение 1-1:
![]()
![]()
![]()
Рассмотрим
сечение 2-2:
![]()
![]()
![]()
![]()
![]()
Рассмотрим
сечение 3-3:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
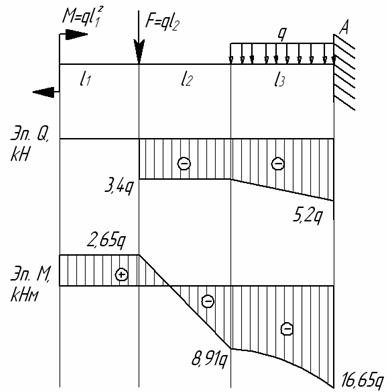
Пример 11.
Для
заданной балки (см. рис.) построить эпюры
от силы Q и от момента
М
Дано:
l1=2,3 м; l2=3,4
м; l3=1,8 м, F=1,8q;
M=2,65q
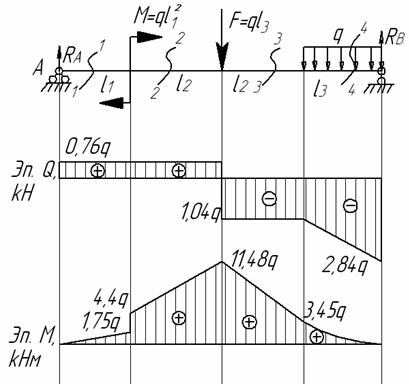
Решение.
Находим
реакции опор
![]()
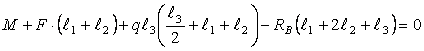

![]()
![]()
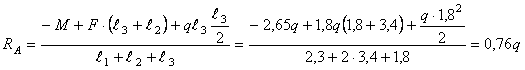
Проверка
![]()
![]()
![]()
0=0
Реакции
опор найдены правильно.
Рассмотрим
сечение 1-1:
![]()
![]()
![]()
![]()
![]()
Рассмотрим
сечение 2-2:
![]()
![]()
![]()
![]()
![]()
Рассмотрим
сечение 3-3:
![]()
![]()
![]()
![]()
![]()
Рассмотрим
сечение 4-4:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Пример
12.
Для
заданной балки (см. рис.) построить эпюры
от силы Q и от момента
М
Дано:
l1=2,4 м; l2=2,8
м; l3=1,8 м, F=2,4q;
M=3,24q
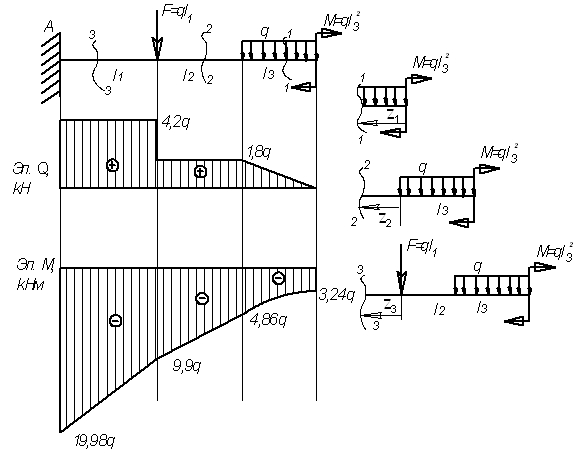
Решение.
Рассмотрим
сечение 1-1:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рассмотрим
сечение 2-2:
![]()
![]()
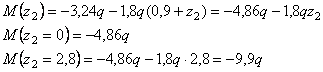
Рассмотрим
сечение 3-3:
![]()
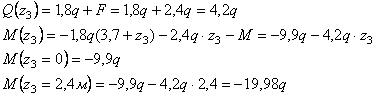
Пример
13.
Для
заданной балки (см. рис.) построить эпюры
от силы Q и от
момента М
Дано:
l1=2,4 м; l2=2,8
м; l3=2 м, F=2,8q;
M=7,84q
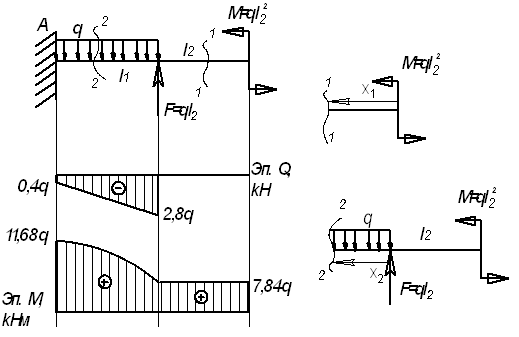
Решение.
Рассмотрим
сечение 1-1:
![]()
![]()
Рассмотрим
сечение 2-2:
![]()
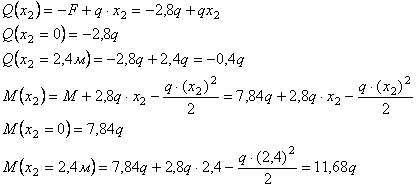
Пример
14.
Для
заданной балки (см.рис.) построить эпюры
от силы Q и от
момента М
Дано:
l1=3,2 м; l2=3
м; l3=2 м, F=3,2q;
M=10,24q
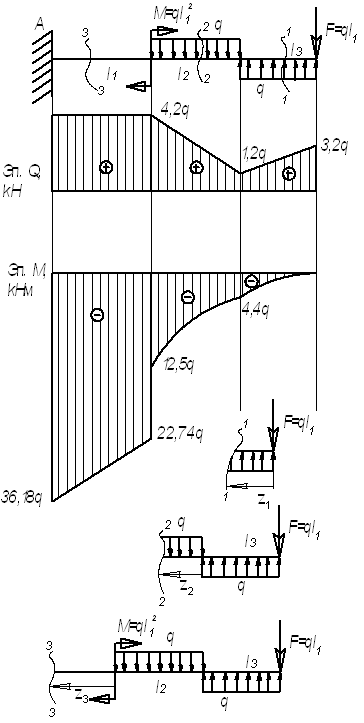
Решение.
Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Рассмотрим
сечение 3-3:

Пример
15.
Для
заданной балки (см. рис.) построить эпюры
от силы Q и от
момента М
Дано:
l1=3,2 м; l2=3
м; l3=2 м, F=3q;
M=10,24q
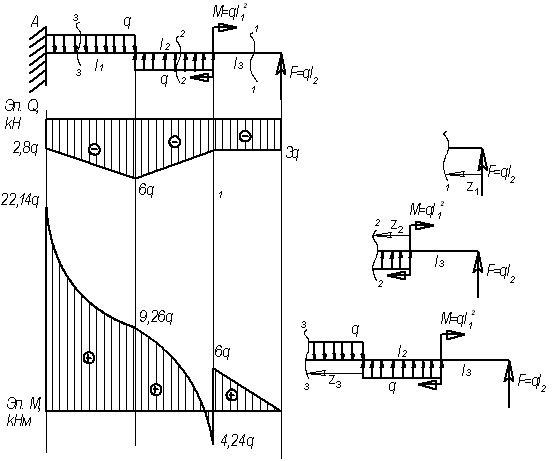
Решение.
Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Рассмотрим
сечение 3-3:

Пример
16.
Для
заданной балки (см. рис.) построить эпюры
от силы Q и от момента
М
Дано:
l1=3,2 м; l2=3
м; l3=2 м, F=3q;
M=4q
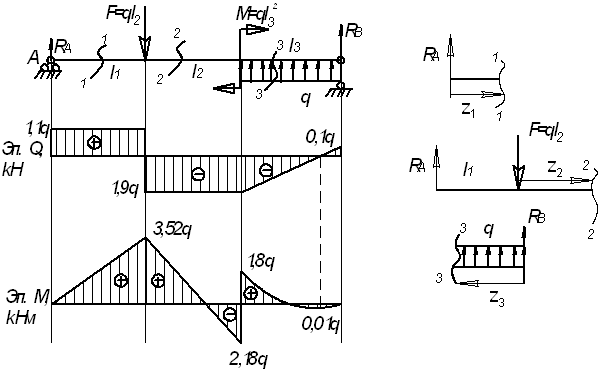
Решение.
Находим
реакции опор
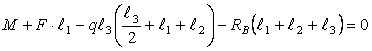
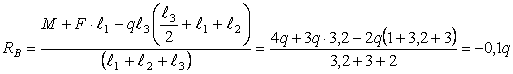
![]()
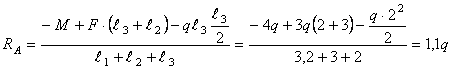
Проверка
![]()
![]()
![]()
0=0
Реакции
опор найдены правильно.
Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Рассмотрим
сечение 3-3:

Пример
17.
Для
заданной балки (см. рис.) построить эпюры
от силы Q и от момента
М
Дано:
l1=3,2 м; l2=2,4
м; l3=2 м, F=3,2q;
M=10,24q
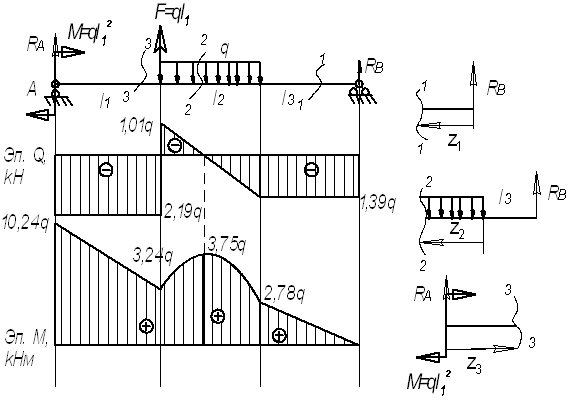
Решение.
Находим
реакции опор

Проверка
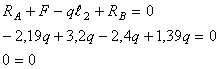
Реакции
опор найдены правильно.
Рассмотрим
сечение 1-1:
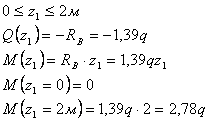
Рассмотрим
сечение 2-2:
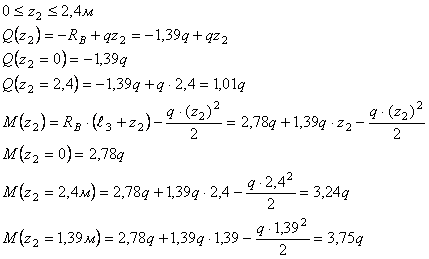
Рассмотрим
сечение 3-3:

Пример
18.
Для
заданной балки (см.рис.) построить эпюры
от силы Q и от момента
М
Дано:
l1=3,6 м; l2=2,6
м; F=3,6q;
M=3,24q
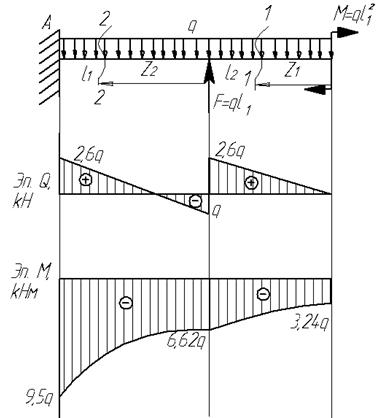
Решение.
Рассмотрим
сечение 1-1:
![]()
![]()
![]()
![]()
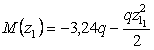
![]()
![]()
Рассмотрим
сечение 2-2:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Пример
19.
Для
заданной балки (см.рис.) построить эпюры
от силы Q и от
момента М
Дано:
l1=3,6 м; l2=3,2
м; l3=1,8 м, F=3,6q;
M=12,96q
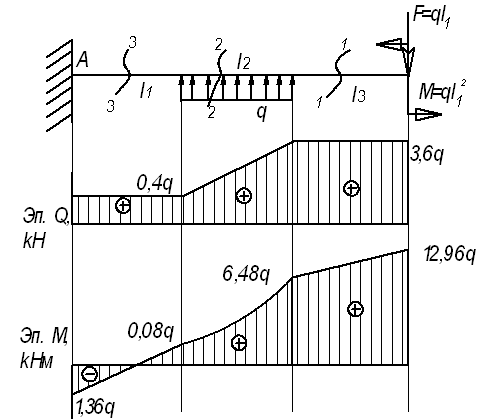
Решение.
Рассмотрим
сечение 1-1:
![]()
![]()
![]()
![]()
![]()
Рассмотрим
сечение 2-2:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рассмотрим
сечение 3-3:
![]()
![]()
![]()
![]()
![]()
![]()
Пример
20.
Построить
эпюры Qy
и Мх для балки с консолью.
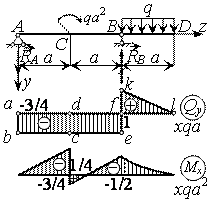
Решение.
1.
Определение опорных реакций. Составляем
уравнения равновесия:
![]()
,
RA![]()
a
–
qa2
–
qa![]()
/2
= 0,
откуда
![]()
,
![]()
,
RВ
a
– qa2–
qa![]()
a/2
= 0,
откуда
![]()
.
Проверка:
![]()
,
RA
– RB
+ qa
= 3qa/4 –
7qa/4 + qa
º
0.
2.
Построение эпюр поперечной силы и
изгибающего момента.
Э п ю
р а Qy.
В сечении А происходит скачок вниз
на величину реакции RA
и QA
= –RA.
На всем протяжении участков АС и СВ
распределенная нагрузка отсутствует
(q = 0), поэтому эпюра
Qy
представляется отрезком прямой,
параллельной оси абсцисс. Наличие пары
сил на эпюре Qy
не отражается. В сечении В происходит
скачок вверх, равный по величине
приложенной реакции RB,
и правее этого сечения имеем QBD
= QBC
+RB=
-3qa/4 + 7qa/4
= qa. На участке BD
поперечная сила изменяется по линейному
закону (Qy
= Qo–qz)
от Qo
= QBD
= qa до QD
= QBD
– qa = 0. По условию
загружения балки в сечении D
нет сосредоточенной силы, поэтому QD=0.
Совпадение значений QD,
полученных независимо друг от друга,
служит проверкой правильности построения
эпюры Qy.
Э п ю
р а Мх. Она строится по
формуле Мх = Мо +
![]()
.
На опоре А нет пары сил, поэтому МА
=0. На участке АС момент изменяется
по линейному закону. Находим момент в
сечении, бесконечно близком слева от
точки С: МСА = Мо
+
![]()
=
-3 qa
/4
= -3qa2/4. По двум
точкам (А и С) строим наклонную
прямую. Пара сил, приложенная в сечении
С, вызывает растяжение нижних волокон
балки при движении слева направо, поэтому
на эпюре Мх скачок вниз и
в бесконечно близком сечении справа
от точки С изгибающий момент
равен: MCB
= MCA
+ qa2 = qa2/4.
Находим момент в сечении В: MB
= MCB
+
![]()
=
qa2/4 – 3qa2/4
= –qa2/2 и по двум
точкам строим наклонную прямую. На
участке BD момент
изменяется по квадратичному закону,
достигая в сечении D
значения, равного MD
= MB
+
![]()
=
–qa2/2 + (1/2)qa
=
0. С другой стороны, по условию загружения
балки на свободном конце MD
= 0. Совпадение результатов служит
проверкой правильности построения
эпюры Мх. По двум точкам
(В и D) приближенно
строим параболу, обращенную выпуклостью
вниз (в направлении нагрузки q).
Вершина параболы совпадает с точкой D,
так как QD
= 0.
Пример
21.
Построить
эпюры Qy
и Мх для простой консоли,
изображенной на рисунке.
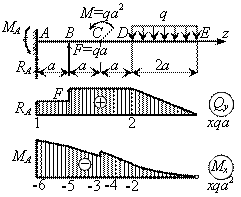
Решение.
1.
Определение опорных реакций. Составляем
уравнения равновесия:
,
MA
+ F
+ M –
q
a![]()
a
= 0,
откуда
MA
= 6qa2;
![]()
,
RA
= q
a
– F = qa.
2.
Построение эпюр поперечной силы и
изгибающего момента.
Э п ю
р а Qy.
В сечении А имеем QA
= RA
(скачок на величину и в направлении
реакции RA
= qa). На участке АВ
погонной нагрузки нет, поэтому поперечная
сила постоянна. В сечении В поперечная
сила меняется скачком от QBA
= QA
= qa до QBC
= QBA
+ F = 2qa
(скачок на величину и в направлении силы
F = qa).
На участках ВС и CD
поперечная сила опять сохраняет
постоянное значение, т.е. QBC
= QCD
= 2qa. На участке DE
поперечная сила изменяется по линейному
закону от QD
= 2qa до QE
= QD
– q
a
= 0.
Э п ю
р а Мх. В сечении А
приложен момент МА,
вызывающий растяжение верхних волокон,
поэтому на эпюре изгибающего момента
происходит скачок вверх на величину
момента MA
= 6qa2.
На
участке АВ Мх изменяется
по линейному закону. Вычисляем момент
в сечении В MB
= MA
+
= -6qa2 + qa×a
= -5qa2 и проводим
наклонную прямую. Аналогично на участках
ВС и СD. В
бесконечно близком сечении слева от
точки С момент равен MСB
= MB
+
=
-5qa2 + 2qa
= -3qa2.
В сечении
С на эпюре Мх скачок
вверх, равный приложенной паре сил M
= qa2, и правее
этого сечения имеем MCD
= MCB
– qa2 = -3qa2
– qa2 = -4qa2.
Момент
в сечении D MD
= MCD
+
= -4qa2 + 2qa
= -2qa2.
На
участке DE изгибающий
момент изменяется по закону квадратной
параболы, обращенной выпуклостью вниз
(в сторону погонной нагрузки q).
В сечении Е по условию загружения
балки МЕ = 0. По двум точкам
D и Е приближенно
строим параболу.
Пример
22.
Построить
эпюры Qy
и Мх для балки.
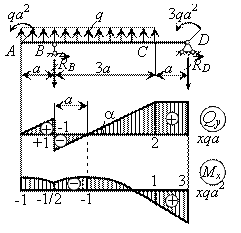
Решение.
1.
Определение опорных реакций. Составляем
уравнения равновесия:
,
q
a
+ qa2
+ 3qa2–RD
a
= 0,
откуда
RD
= 2qa;
![]()
,
RB
a
+ qa2
+3qa2–q
a![]()
a
= 0,
откуда
RB
= 2qa.
П р о в е р к а
,
q×4a
– RB
– RD
= 4qa –
2qa – 2qa
= 0.
2.
Построение эпюр поперечной силы и
изгибающего момента.
Э п ю
р а Qy. Строится по формуле
Qy = Qo ±
qz. В данном случае перед вторым
слагаемым следует взять знак “плюс”,
так как погонная нагрузка положительна
(см. правила построения эпюр). На участках
АВ и ВС эпюра Qy
изображается прямой, наклоненной вверх
(в направлении погонной нагрузки q),
а на участке CD поперечная сила
постоянна (q = 0). В сечениях В и D
на балку действуют сосредоточенные
силы RA и RD,
поэтому на эпюре Qy возникают
скачки. Вычисляем значения поперечной
силы в характерных точках QA
= 0,
QBA
= QA
+ q×a
= qa,
QBC
= QBA
– RB
= qa – 2qa
= –qa,
QC
= QBC
+ q
a
= –qa + 3qa
= 2qa и строим эпюру
Qy.
Э п ю
р а Мх. Она строится по
формуле Мх = Мо +
.
На участках с погонной нагрузкой (АВ
и ВС) изгибающий момент изменяется
по закону квадратной параболы Mx
= Mo + Qoz +
0,5qz2, обращенной выпуклостью
вверх (в сторону погонной нагрузки q).
В сечениях А и D,
где приложены сосредоточенные пары, на
эпюре Мх наблюдаются
скачки, причем момент qa2
вызывает растяжение сверху (при обходе
слева направо), поэтому в сечении А
скачок направлен вверх, а момент 3qa2
вызывает растяжение снизу (при обходе
справа налево), поэтому в сечении D
скачок происходит вниз. На участке АВ
парабола строится по двум точкам А
и В, а на участке ВС – по трем
точкам (к крайним точкам В и С
добавляется точка экстремума). Положение
точки экстремума определяется из условия
zo
= QBC
/![]()
.
Согласно дифференциальной зависимости
=
dQ/dz
= q, поэтому zo
= qa/q
= 0. Вычисляем значения момента в
характерных точках:
MA
= –qa2, MB
= MA
+
= –qa2 + (1/2)![]()
a
= –qa2/2,
Mmax
= MB
+
= –qa2/2
– (1/2)
a
= –qa2,
MC
= Mmax
+
= –qa2
+ (1/2)
qa
a
= qa2
и строим эпюру Мх.
Пример
23.
По
заданной эпюре поперечной силы Qy
установить нагрузку, действующую на
двухопорную балку, и ее опорные реакции.
Построить также эпюру изгибающего
момента, учитывая, что на правой опоре
С приложена пара сил.
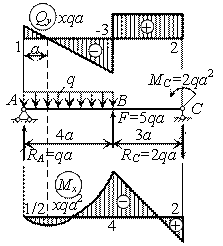
Решение.
Скачки
на эпюре Qy
свидетельствуют о приложенных в этих
сечениях сосредоточенных силах. Приняв
направление обхода слева направо,
получим: реакция в точке А равна RA
= qa и направлена вверх;
в сечении В приложена сосредоточенная
сила F = 5qa,
направленная вверх; наконец, реакция
RB
= 2qa и направлена вниз.
На участке АВ поперечная сила
изменяется по линейному закону, что
связано с наличием погонной нагрузки,
интенсивность которой определяется
как тангенс угла наклона прямой qy
= dQ/dz = (-3qa – qa)/4a = –q.
Знак “минус” означает, что нагрузка
направлена вниз. Для определения
неизвестной пары сил М, приложенной
в сечении С, составим уравнение
моментов относительно этой точки:
![]()
,
–RA![]()
a
– F
a
+ q
a
a
+ MC
= 0,
откуда MC
= 2qa2 и направлен
против часовой стрелки.
Эпюру
Мх строим по формуле Мх
= Мо +
.
На участке АВ изгибающий момент
изменяется по квадратичному закону. На
концевой шарнирной опоре А нет пары
сил, поэтому МА = 0. В
сечении, где Qy
= 0, изгибающий момент принимает
экстремальное значение:
Mmax
= MA
+
=
(1/2)qa
= qa2/2.
Находим
момент в сечении В: MB
= Mmax
+
=
qa2/2- (1/2)3qa
a
= -4qa2 и по трем
точкам приближенно строим параболу,
обращенную выпуклостью вниз. На участке
ВС изгибающий момент изменяется
по линейному закону от MB
= -4qa2 до MC
= MB
+
=
-4qa2 + 2qa
a
= 2qa2. По условию
загружения балки также имеем MC
=2qa2. Совпадение
значений МС, найденных
независимо друг от друга, свидетельствует
о правильности построения эпюры Мх.
Пример
24.
По
заданной эпюре изгибающего момента
построить эпюру поперечной силы и
определить нагрузку, действующую на
балку. Криволинейный участок эпюры Мх
очерчен по квадратной параболе, а кружком
отмечена ее вершина.
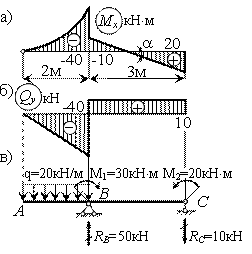
Решение.
На
участке АВ изгибающий момент
изменяется по квадратичному закону:
Mx
= Mo
+ Qoz
– 0,5qz2. Так как
вершина параболы совпадает с точкой
А, то Мо =МА
=0 и Qo
= 0. Следовательно, Мх =
-0,5qz2. Момент в
бесконечно близком сечении слева от
опоры В, судя по приведенной
эпюре, равен МВА = -40 кНм.
С другой стороны, МВА =
-0,5q(2)2.
Следовательно, q = 20
кН/м. Парабола обращена выпуклостью
вниз, поэтому и погонная нагрузка
направлена вниз.
В
сечении В изгибающий момент
изменяется скачком от МВА
= -40 кНм до МВС = -10 кНм, что
свидетельствует о наличии пары сил М1
= 30 кНм, вызывающей растяжение нижних
волокон (при обходе слева направо), т.е.
направленной по часовой стрелке. На
опоре С приложена пара сил с моментом
М2 = 20 кНм, вызывающая растяжение
снизу (при обходе справа налево), т.е.
направленная против часовой стрелки.
На
участке ВС поперечная сила постоянна
и равна тангенсу угла наклона прямой,
т.е. QBC = dM/dz =
=
(20 + 10)/3 = 10 кН. На участке АВ поперечная
сила изменяется по линейному закону
(Qy = Qo – qz)
от Qo
= QA
= 0 до QBA
= –q
= -40 кН. По скачкам на эпюре Qy
находим величины и направления реакций:
RB
= 50 кН (направлена вверх) RC
= 10 кН (направлена вниз).
Пример
25.
Построить
эпюры поперечных сил QY
и изгибающего момента MX
(см. рис.1).
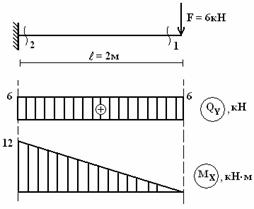
Рис.1
Решение.
1)
Проведем две оси, параллельные оси балки
(одну для эпюры QY,
вторую для эпюры MX).
2) Балка
имеет один участок загружения.
3) Строим
эпюру QY.
Сделаем сечение (1), отбросим жесткую
заделку. Учитывая правило знаков, получим
![]()
.
В сечении (2) получим
![]()
.
Силы
![]()
,
так как сила F
поворачивает оставшуюся часть балки
вокруг сечения по часовой стрелке
(рис.2,а).
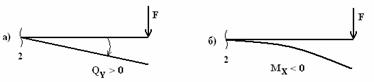
Рис. 2
Положительные
значения поперечной силы откладывают
всегда выше оси.
Соединим
их прямой линией, поставим знак, эпюру
заштрихуем, обозначим.
4) Строим
эпюру МХ. Сделав сечение и отбросив
часть с жесткой заделкой, сосчитаем
момент от силы F относительно
сделанного сечения. Получим
![]()
.
Для эпюры изгибающих моментов принимается
следующее правило: значения моментов
откладываются от оси в сторону растянутого
волокна. Из рис.2,б, следует, что сила F
растягивает верхние волокна, поэтому
полученное значение МХ откладываем
выше оси. Соединяем отложенные значения
прямой линией. Знак на эпюре изгибающих
моментов можно не ставить. Эпюру штрихуем
и обозначаем (рис.1).
5)
Проверка эпюр. К балке не приложена
распределенная нагрузка, следовательно,
на графиках QY
и МХ имеем прямые линии, причем
на эпюре QY
это прямая, параллельная оси. На свободном
конце балки приложена сосредоточенная
сила F = 6кН
![]()
в этом сечении на эпюре QY
образовался скачок, равный 6.
Пример
26.
Построить
эпюры поперечных сил QY
и изгибающего момента MX
(см. рис.).
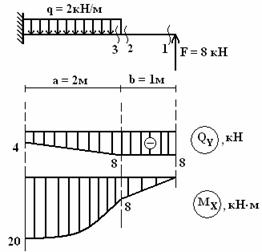
Решение.
1)
Проводим оси для построения эпюр.
2) Делим
балку на два участка загружения.
3) Строим
эпюру QY.
1-й
участок:
![]()
;
![]()
.
Откладываем
значения ниже оси, соединяем прямой
линией.
2-й
участок:
![]()
;
![]()
.
Значение
![]()
откладываем ниже оси, соединяем прямой
линией.
Ставим
знаки, эпюру штрихуем и обозначаем.
4) Строим
эпюру МХ.
1-й
участок:
![]()
;
![]()
.
Откладываем
значения
![]()
ниже оси, так как сила F
растягивает нижние волокна, соединяем
прямой линией.
2-й
участок:
![]()
;
![]()
.
Значения
![]()
откладываем ниже оси и соединяем
параболой. При этом выпуклость параболы
должна быть обращена в сторону действия
распределенной нагрузки. Это правило
называют «правилом паруса». Роль паруса
здесь играет эпюра, а роль ветра –
нагрузка.
5)
Проверка эпюр. На участке балки с
распределенной нагрузкой получаем на
эпюре QY
наклонную прямую, на эпюре MX
– параболу. В сечении с приложенной
сосредоточенной силой F
= 8 кН на эпюре QY
образовался скачек равный 8.
Пример
27.
Построить
эпюры поперечных сил QY
и изгибающего момента MX
(см. рис.).
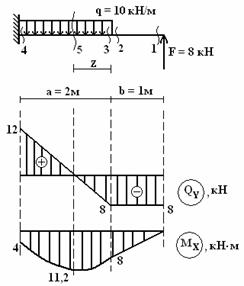
Решение.
1)
Проводим оси для построения эпюр.
2) Делим
балку на два участка загружения.
3) Строим
эпюру QY.
1-й
участок.
;
.
Откладываем
значения ниже оси, соединяем прямой
линией.
2-й
участок.
;
![]()
.
Откладываем
![]()
ниже оси, а
![]()
– выше оси, соединяем прямой линией (см.
рис.).
4) Строим
эпюру МХ.
1-й
участок:
;
![]()
.
Откладываем
ниже оси, соединяем с нулем прямой
линией.
2-й
участок:
Из
рисунка следует, что эпюра поперечных
сил QY
на этом участке пересекает ось, то есть
в некотором сечении (5) сила
![]()
.
Отсюда следует, что в сечении (5) изгибающий
момент МХ достигает экстремального
значения (максимума или минимума). Таким
образом, на этом участке следует
просчитать момент в трех точках.
![]()
.
![]()
.
Определим
экстремальное значение момента. Выясним
сначала, на каком расстоянии Z от
правой границы участка находится сечение
(5), в котором поперечная сила равна нулю.
![]()
.
Найдем
значение момента.
![]()
.
Откладываем
значения
![]()
ниже оси и соединяем параболой по правилу
«паруса», то есть выпуклостью вниз (см.
рис.).
5)
Проверка эпюр. Все линии на эпюрах
соответствуют приложенным нагрузкам,
силе F = 8 кН соответствует
скачок, равный 8 на эпюре QY.
Пример
28.
Построить
эпюры поперечных сил QY
и изгибающего момента MX
(см. рис. 1).
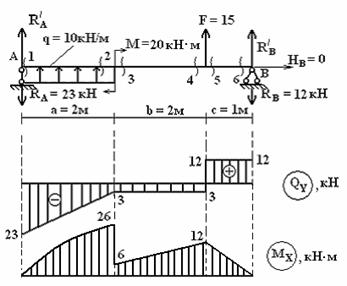
Рис.1
Решение.
1) Расчет
балки с шарнирным закреплением следует
начинать с определения реакций связей.
Расставим эти реакции. В шарнирно
–подвижной опоре А возникает одна
вертикальная реакция R¢A.
В шарнирно-неподвижной опоре В, вообще
говоря, возникает две реакции –
вертикальная R¢B
и горизонтальная НВ, однако,
поскольку в случае вертикального
плоского изгиба все силы действуют
перпендикулярно оси балки, горизонтальная
реакция НВ всегда будет равна
нулю, поэтому в дальнейшем показывать
ее на схеме балки не будем. Вертикальные
реакции найдем из уравнений статики.
![]()
;
![]()
.
![]()
;
![]()
.
При
записи уравнений использовалось
следующее правило знаков: если сила
поворачивает балку вокруг т.А (т.В) по
часовой стрелке, то момент от этой силы
берется со знаком «+».
Для
проверки найденных реакций используем
уравнение статики:
![]()
(сумма всех вертикальных сил должна
быть равна нулю). При этом силы, изображенные
на схеме балки направленными вверх,
берем со знаком «+».
![]()
.
Подставим
сюда найденные значения реакций со
своими знаками.
– 23 + 10
× 2 + 15 – 12 = 0; 35 – 25
=0; 0 = 0.
Поскольку
направления вертикальных реакций
поначалу были взяты произвольно, то
полученные в результате знаки «-» у
реакций RA,
RB
показывают, что мы не угадали направление
реакций, в действительности они направлены
вниз. Удобно изменить направление этих
реакций на обратное и в дальнейшем
считать эти реакции положительными
(см. рис.1).
2)
Проводим оси для построения эпюр.
3) Делим
балку на три участка загружения.
4) Так
как все реакции в закреплениях балки
найдены, то, сделав сечение, можно
отбрасывать любую (обычно более
загруженную) часть балки .
5) Строим
эпюру QY.
1-й
участок.
![]()
(отбросили правую часть балки),
![]()
(отбросили левую часть балки).
Пару
сил М = 20 кНм при вычислении QY,
естественно, не учитываем.
Откладываем
значения от оси, соединяем прямой линией.
2-й
участок.
![]()
;
![]()
.
3-й
участок.
![]()
;
![]()
.
6) Строим
эпюру МХ.
1-й
участок:
![]()
;
![]()
.
Чтобы
не ошибиться в знаке изгибающего момента,
сечение, в котором он определяется,
следует представлять защемленным, а
опоры – отброшенными (рис.2):
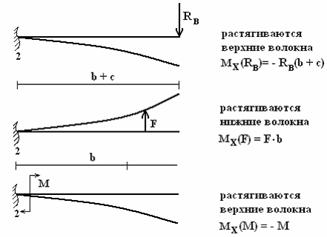
Рис.2
Откладываем
значения от оси и соединяем параболой
по правилу «паруса», то есть направленной
выпуклостью вверх.
2-й
участок:
![]()
![]()
.
Откладываем
значения выше оси, соединяем прямой
линией.
3-й
участок:
![]()
![]()
.
Отложенные
от оси значения соединяем прямой линией
(рис.1).
6)
Проверка эпюр. Все линии на эпюрах
соответствуют действующим нагрузкам.
К балке приложены три сосредоточенные
силы – RA,
F, RB.
На эпюре QY
получили три скачка
на опоре А – равный RA
= 23, на границе 2-го и 3-го участков –
равный F = 3 + 12 = 15, на опоре
В – равный RB
= 12. К балке приложена пара сил М = 20. На
эпюре МХ на границе 1-го и 2-го
участков имеем скачок, равный М = (26 – 6)
= 20.
Пример
29.
Построить
эпюры поперечных сил QY
и изгибающего момента MX
(см. рис.).
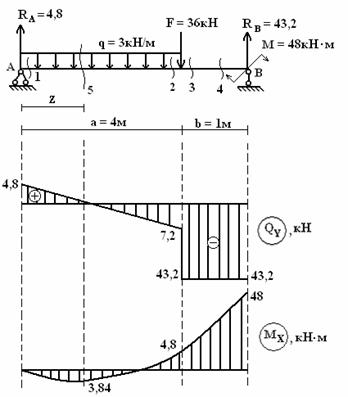
Решение.
1) Найдем
реакции опор RA,
RB.
;
![]()
;
![]()
.
Проверка:
![]()
![]()
.
Обе
реакции получились положительными, то
есть мы угадали их направление, они
действительно направлены вверх.
2) Балка
имеет два участка загружения.
3) Строим
эпюру QY.
1-й
участок.
![]()
;
![]()
.
Откладываем
значения от оси и соединяем прямой
линией.
2-й
участок.
![]()
;
![]()
.
Откладываем
значения от оси и соединяем прямой (см.
рис.).
4) Строим
эпюру МХ.
1-й
участок:
Из эпюры
сил следует, что на этом участке будет
возникать экстремальный момент, поэтому
будем определять МХ в трех сечениях.
(отбрасываем правую часть балки);
![]()
(отбрасываем левую часть балки).
Находим
координату Z сечения (5):
![]()
.
Находим
экстремальный момент.
![]()
.
Откладываем
значения от оси и соединяем параболой
по правилу «паруса», то есть выпуклостью
вниз.
2-й
участок.
![]()
;
![]()
.
Отложенные
от оси значения соединяем прямой (см.
рис.).
5)
Проверка эпюр.
Линии
эпюры соответствуют приложенным
нагрузкам. К балке приложены три
сосредоточенные силы – RA,
F, RB
на эпюре QY
в соответствующих сечениях имеем скачки.
К балке
на опоре В приложена пара сил М: на эпюре
МХ имеем на правом конце скачок,
равный М = 48.
Пример
30.
Дана
балка с действующими на нее нагрузками
(рис. а). Требуется определить
внутренние усилия – поперечную силу Q
и изгибающий момент М в балке,
построить графики их изменения вдоль
оси стержня (эпюры Q и М).
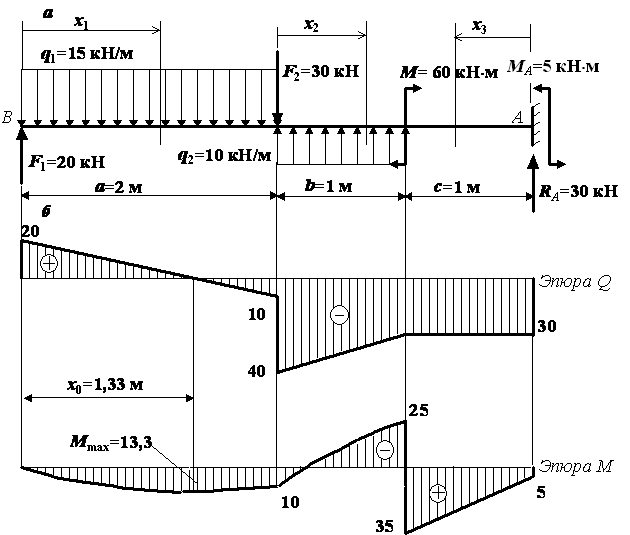
Решение.
Прежде
всего найдем опорные реакции. Балка
имеет жесткое защемление на правом
конце (В балке с заделкой можно строить
эпюры Q и М без определения
опорных реакций, рассматривая все силы
с одной стороны от сечения – со свободного
конца. Но студенту, только начинающему
осваивать построение эпюр, рекомендуем
все же реакции находить. Это дополнительная
проверка правильности решения задачи)
и в этом закреплении при заданной
вертикальной нагрузке возникают две
опорные реакции: вертикальная реакция
RA и реактивный момент MA.
Горизонтальная реакция при действии
вертикальной нагрузки равна нулю. Это
следует из уравнения равновесия “сумма
проекций всех сил на горизонтальную
ось равна нулю”. Определим RA
и MA, используя два других
уравнения статики. Желательно составлять
такие уравнения, в каждое из которых
входит только одна неизвестная. В данном
случае такими уравнениями являются
“сумма проекций всех сил на вертикальную
ось (ось z) равна нулю” и “сумма
моментов всех сил относительно точки
А равна нулю”:
![]()
;
![]()
;
![]()
;
![]()
Из
первого уравнения найдем RA
= 30 кН, из второго – МА
=5 кНм. Полученные положительные знаки
опорных реакций подтверждают выбранные
нами направления опорных реакций: RA
– вверх, а МА – против
часовой стрелки. Для проверки рекомендуем
использовать любое другое уравнение
равновесия, например
![]()
:
– 30×2
– 15×2×1
– 60 + 10×1×2,5
+ 30×4+5 = – 150 + 150 = 0.
Теперь
определяем внутренние усилия: поперечную
силу Q и изгибающий момент М. В
соответствии с методом сечений рассекаем
балку на каждом участке (в данной задаче
их три) произвольным сечением и
рассматриваем все силы, расположенные
с одной стороны от сечения: слева или
справа. Удобно рассматривать все силы
с той стороны от сечения, где сил меньше.
Начало отсчета координаты x на каждом
участке можно выбирать произвольным
образом. Например, на рис. а начало
отсчета x на каждом участке – свое
и находится в начале участка. Запишем
выражения для Q и М на каждом
участке.
Участок
1:
![]()
.
Рассмотрим
силы, расположенные слева от сечения.
По определению поперечной силы и с
учетом правила знаков для Q :
![]()
.
Здесь
![]()
– равнодействующая равномерно
распределенной нагрузки, действующей
слева от сечения.
По
определению изгибающего момента и с
учетом правила знаков для М :
![]()
,
где во
втором слагаемом
![]()
– плечо равнодействующей равномерно
распределенной нагрузки (![]()
),
взятой слева от сечения (равнодействующая
приложена по середине длины отсеченной
части балки x1).
Для
построения эпюр найдем значения Q
и М на границах участка:
в начале
участка (х1 = 0)
![]()
,
а
![]()
;
в конце
участка (![]()
)
![]()
;
![]()
.
Участок
2:
![]()
.
Снова
рассмотрим все силы, расположенные
слева от сечения.
![]()
;
![]()
.
Граничные
значения Q и М:
в начале
участка (![]()
)
![]()
;
,
в конце
участка (![]()
)
![]()
;
![]()
.
Участок
3:
![]()
.
Теперь
рациональнее рассмотреть все силы
справа от сечения. Тогда
![]()
;
![]()
.
Из этих
выражений следует, что поперечная сила
на третьем участке – постоянная величина,
а изгибающий момент меняется по линейному
закону и на границах участка имеет
следующие значения:
в начале
участка (![]()
)
![]()
,
в конце
участка (![]()
)
![]()
.
Запишем
результаты определения внутренних
усилий в таблицу, сосчитав численные
значения Q и М на границах участков
(табл. 1).
Таблица 1

Из
таблицы видно, что поперечная сила на
первом участке меняет свой знак, т. е.
график Q пересекает нулевую линию.
Это значит, что изгибающий момент на
этом участке имеет экстремум. Найдем
максимальное значение М на этом
участке. Сначала определим то значение
координаты х1, при котором
поперечная сила равна нулю. Обозначим
это значение координаты х0
(см. рис. ).
![]()
х0 = 1,33 м.
Чтобы
найти максимальное значение изгибающего
момента, подставим х0 в выражение
для М на первом участке:
![]()
кНм.
По
результатам вычислений в таблице строим
эпюры Q и М на каждом участке
(см. рис. б). Не забываем после
построения эпюр проанализировать
результаты по тем правилам проверки
правильности построения эпюр, которые
перечислены ранее.
Правила построения эпюр поперечных сил и изгибающих моментов
Озвучим правила построения эпюр, вытекающие из метода сечений, и являющиеся следствием дифференциальных и интегральных зависимостей, некоторые из которых справедливы при обходе эпюр 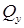 и
и 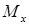 слева направо. Зная правила построения эпюр, можно быстро найти грубую ошибку только по внешнему виду эпюр.
слева направо. Зная правила построения эпюр, можно быстро найти грубую ошибку только по внешнему виду эпюр.
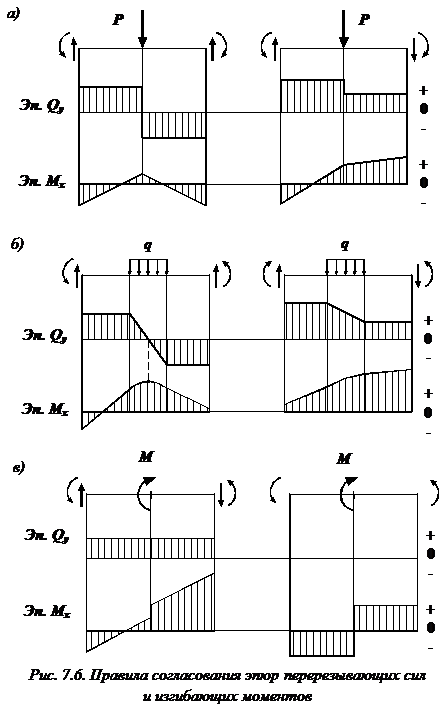
Правило построения эпюр – отсутствующая распределенная нагрузка
Если на участке балки отсутствует распределенная нагрузка (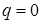 ), то эпюра поперечных сил
), то эпюра поперечных сил 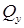 на этом участке представляет собой прямую, параллельную оси балки (рис. 7.6). По дифференциальной зависимости распределенной нагрузки и поперечной силы: поскольку
на этом участке представляет собой прямую, параллельную оси балки (рис. 7.6). По дифференциальной зависимости распределенной нагрузки и поперечной силы: поскольку 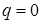 , то и
, то и 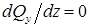 . Следовательно,
. Следовательно, 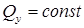 .
.
Эпюра изгибающих моментов на участке, где 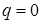 , – прямая линия. Причем, если
, – прямая линия. Причем, если 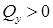 , то прямая идет вверх, а если
, то прямая идет вверх, а если 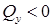 , прямая идет вниз. Если
, прямая идет вниз. Если 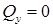 , то изгибающий момент постоянен, поскольку
, то изгибающий момент постоянен, поскольку 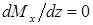 .
.
Правило построение эпюр – скачки и изломы
Под сосредоточенной силой (P) на эпюре поперечных сил 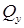 (рис. 7.6, а) имеется скачок на величину этой силы и по ее направлению, а на эпюре изгибающих моментов
(рис. 7.6, а) имеется скачок на величину этой силы и по ее направлению, а на эпюре изгибающих моментов 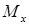 – излом, угол которого направлен навстречу нагрузке.
– излом, угол которого направлен навстречу нагрузке.
Правило построение эпюр – присутствует распределенная нагрузка
Если на участке балки имеется равномерно распределенная нагрузка: эпюра поперечных сил 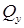 представляет собой наклонную прямую (рис. 7.6, б), идущую вниз, если нагрузка
представляет собой наклонную прямую (рис. 7.6, б), идущую вниз, если нагрузка 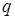 направлена вниз (и наоборот). Эпюра
направлена вниз (и наоборот). Эпюра 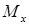 на этом участке, согласно третьей формуле дифференциальных зависимостей, изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке.
на этом участке, согласно третьей формуле дифференциальных зависимостей, изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке.
Правило построение эпюр – экстремум
Если эпюра поперечной силы проходит через нулевое значение, то в этом сечении балки на эпюре изгибающих моментов 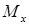 имеется экстремум (последнее вытекает из дифференциальной зависимости
имеется экстремум (последнее вытекает из дифференциальной зависимости 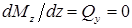 ). В точках, соответствующих началу и концу участка, в пределах которого действует распределенная нагрузка, параболическая и прямолинейная части эпюры
). В точках, соответствующих началу и концу участка, в пределах которого действует распределенная нагрузка, параболическая и прямолинейная части эпюры 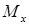 переходят одна в другую плавно (без излома).
переходят одна в другую плавно (без излома).
Правило построение эпюр – внешний момент
Сосредоточенный внешний момент M (рис. 7.6, в) никак не отражается на эпюре 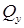 . На эпюре
. На эпюре 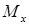 в месте приложения этого момента имеется скачок на его величину.
в месте приложения этого момента имеется скачок на его величину.
Заметим, что построение эпюр поперечных сил и изгибающих моментов ввел в практику расчета балок на изгиб французский ученый Жан Антуан Шарль Бресс (1822 – 1883 гг.) в 1859 г.
