Как найти экстремумы эксель

Как найти экстремумы функции excel

Если функция F(x) непрерывна на отрезке [a, b] и имеет внутри этого отрезка локаль-ный экстремум, то его можно найти, используя надстройку Excel Поиск решения. Рассмотрим последовательность нахождения экстремума функции на примере.

Пример 12. Задана неразрывная функция Y= X 2 +X +2. Требуется найти ее экстремум (минимальное значение) на отрезке [-2, 2].

Решение:

1. В ячейку А3 рабочего листа введите любое число, принадлежащее заданному отрезку, в этой ячейке будет находиться значение Х.

2. В ячейку В3 введите формулу, определяющую заданную функциональную зависимость (рис. 18). Вместо переменной Х в этой формуле должна быть ссылка на ячейку А3: = A2^2 + A2 +2.

3. Выполните команду меню Сервис — Поиск решения.

4. В открывшемся окне диалога Поиск решения в поле Установить целевую ячейку укажите адрес ячейки, содержащей формулу (В3), установите пере-ключатель Минимальному значению, в поле Изменяя значение ячейки укажите адрес ячейки, в которой содержится переменная х.

5. Добавьте два ограничения в соответствующее поле: A3>= -2 и A3<= 2.

6. Щелкните на кнопке Параметры и в от крывшемся диалоговом окне Пара-метры поиска решения установите относительную погрешность вычислений и предельное число итераций.

7. Щелкните на кнопке Выполнить.

В ячейке А3 будет помещено значение аргумента Х функции, при котором она принимает минимальное значение, а в ячейке В3 – минимальное значение функции. В результате выполнения вычислений в ячейке А3 будет получено значение независимой переменной, при котором функция принимает наименьшее значение, а в ячейке В3 – минимальное значение функции, равное 1,75. Постройте график заданной функции и убедитесь, что решение найдено верно.

Источник

Поиск решения MS EXCEL. Экстремум функции с несколькими переменными. Граничные условия заданы уравнениями

history 14 января 2021 г.

Пусть дана функция с несколькими переменными F(x1, x2, . )=a1*x1+a2*x2+. Также даны граничные условия в виде b1*x1+b2*x2+. файл примера ).

Переменные (выделено зеленым) . В качестве переменных модели, очевидно, выступают x1, x2, x3, x4. Эта задача хороша тем, что переменные задаются однозначно, не требуется осмысливать житейскую задачу, например как с оптимизацией затрат . Хотя математически — это эквивалентные задачи, только количество переменных разное.

После запуска Поиск решения будет методично (последовательно) по своему алгоритму подставлять в зеленые ячейки числовые значения и вычислять функцию F (красная ячейка).

Ограничения (выделено серым) . Ограничения модели — это ограничения на область изменения переменных. Они могут задаваться как простыми выражениями для одной переменной, например х1>=0, так и для некой комбинации переменных 5*x1+4*x2-x3-2*x4 =0 ограничения можно ввести прямо в окне Поиска решения (будет показано ниже), для более сложных зависимостей удобно подготовить вспомогательную таблицу (С26:Е29).

Составить модель, особенно первую, непросто. Может помочь такой подход: считать, что переменные (зеленые ячейки) уже содержат некие значения, пусть даже не оптимальные. Так легче составлять огграничения. В нашем случае ограниечение 5*x1+4*x2-x3-2*x4 можно записать с помощью формулы = СУММПРОИЗВ($D$19:$D$22;C26:C29) . В диапазоне D19:D22 содержатся коэффициенты 5; 4; -1; -2. Кроме того, если значения переменных заданы, то и значение целевой функции также автоматически рассчитано (тоже не оптимальное пока, до запуска Поиска решения).

Целевая функция (выделено красным) . Целевая функция — это то, что требуется оптимизировать, т.е. F. Формула для ее вычисления задана в явном виде — не нужно догадываться из условий обычной задачи как ее подсчитать. Это не всегда очевидно (см., например, статью про пропускную способность трубопровода ).

Ниже приведено окно Поиска решения с заполненными полями: целевая функция, переменные и ограничения.

После запуска Поиска решения ответ будет вычислен за доли секунды: F=3.

Источник

Использование Excel для поиска экстремумов функций

Электронные таблицы Excel фирмы Microsoft имеют встроенные средства решения задач поиска экстремума, оформленные в виде так называемой надстройки. Перед началом работы надо убедиться в том, что в составе сгенерированного на вашей ЭВМ пакета Excel требуемая надстройка установлена. Для этого выберите режим Сервис главного меню и проверьте, есть ли в открывшемся ниспадающем меню пункт Поиск решения (рис. 5). Если строка меню Поиск решения отсутствует, то выберите пункт меню Сервис / Надстройки и в открывшейся форме включите режим Поиск решения (рис. 6). Если и в этом окне пункт Поиск решения отсутствует, то это означает, что на вашей машине установлена сокращенная версия электронных таблиц и требуется переустановка пакета Excel.

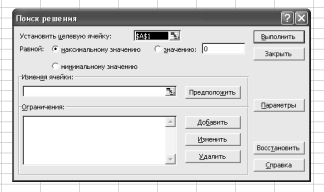
Надстройка Поиск решения (рис. 7) позволяет, задавая некоторую ячейку в виде целевой (Установить целевую ячейку), при условии обеспечения зависимости результата вычислений в ней от значений некоторых изменяемых ячеек (Изменяя ячейки) с учетом заданных ограничений (Ограничения) получить набор переменных в изменяемых ячейках, обеспечивающий или максимальное, или минимальное, или заданное значение целевой ячейки.

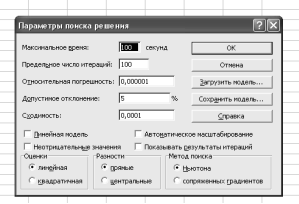
В качестве параметров режима (рис. 8) задаются методы поиска экстремума. Так, при установке флажка Линейная модель надстройка ищет экстремум симплекс-методом. Флажок Неотрицательные значения накладывает дополнительное ограничение на значения переменных задачи. Его установка эквивалентна введению ограничения .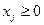

Примечание. Если флажок Линейная модель выключен, решение задачи ведется методом Ньютона или градиентным с использованием прямых или центральных конечных разностей на основе линейной или квадратичной оценки уменьшения приращения экстремума в зависимости от установленных флажков. Эти методы позволяют, в частности, решать нелинейные и целочисленные задачи поиска экстремумов.

Рис. 5. Пункт меню Поиск решения

Рис. 6. Включение надстройки Поиск решения

Режим Автоматическое масштабирование позволяет перейти к отображению данных в относительных единицах, а при установке флажка Показывать результаты итераций включается пошаговый режим. Также к числу параметров относится ограничение по времени процесса поиска решения в секундах (Максимальное время) (максимально 32767) и количеству итераций (Предельное число итераций). Вариант настройки параметров режима Поиск решения может быть сохранен.

Примечание. Точность соответствия результата заданному значению (Относительная погрешность), допустимого отклонения экстремума от оптимального значения при использовании режима целочисленной математики (Допустимое отклонение), а также условие прекращения поиска экстремума (Сходимость), задающее величину относительного приращения экстремума за последние пять итераций относятся к параметрам, используемым при решении задачи методом Ньютона или градиентным.

Рис. 7. Главная форма надстройки Поиск решения

Рассмотрим задачу линейного программирования (1,2), записанную в виде целевой (критериальной) функции и набора ограничений, с конкретными числовыми данными, полученными с помощью датчика случайных чисел.

(4)

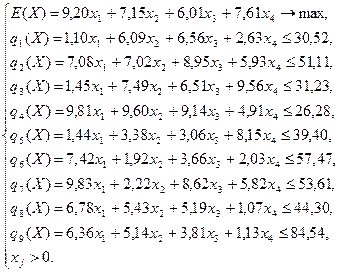
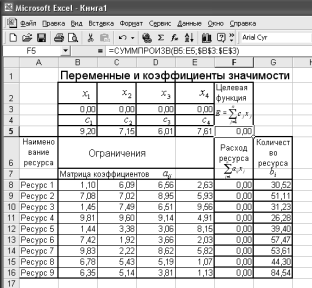
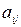
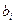
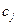
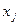
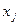
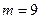
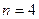
На рис. 9 изображен рабочий лист Excel с данными задачи (4). Для всех ячеек, предназначенных для хранения данных, был задан числовой формат с двумя знаками после запятой режимом Формат/Ячейки…/Число. Матрица размещена в диапазоне ячеек B8:E16. Значения ограничений находятся в диапазоне ячеек G8:G16. Весовые коэффициенты целевой функции занесены в диапазон ячеек B5:E5. Кроме этого, для хранения переменных зарезервирован диапазон ячеек B3:E3. Значения предварительно были обнулены, однако это не является обязательным, поскольку система может начать поиск экстремума с любой начальной комбинации. Очевидно, что в данном случае , .

Рис. 8. Параметры надстройки Поиск решения

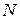
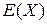
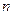
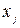
Выражение (3) представляет собой ничто иное, как сумму попарных произведений некоторых наборов чисел, которые должны быть заданы в табличной форме или рассчитаны средствами пакета Excel. Рассчитаем значение целевой функции в ячейке F5. Ее программирование сводится к заданию выражения типа (3), которое можно рассчитать непосредственно на основе формулы Excel =B3*B5+C3*C5+D3*D5+E3*E5. Тем не менее, по ряду причин, более удобно воспользоваться встроенной функцией СУММПРОИЗВ(B5:E5;$B$3:$E$3), которая автоматически определяет количество слагаемых и дает результат вычислений в соответствии с (3). Использование абсолютного формата записи диапазона ячеек, используемого для хранения , не является обязательным, однако удобно для последующих действий, которые могут выполняться способом копирования.

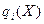
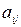
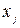
Выражения, определяющие расход ресурсов программируются в ячейки F8, F9,…, F16 аналогично предыдущему с той только разницей, что в качестве первого аргумента функции СУММПРОИЗВ() выступает соответствующая строка матрицы , а второй аргумент по-прежнему есть диапазон ячеек B3:E3, заданный в абсолютом формате и используемый для хранения переменных .

Примечание. Остальная информация, нанесенная на рабочий лист (рис. 9), используется для пояснения принципа размещения данных. Она представляет собой либо текстовые строки, записанные в определенные ячейки, либо внедренные объекты и носит вспомогательный характер. Поэтому при повторении примера на ЭВМ она может быть опущена.

Рис. 9. Вариант размещения данных на рабочем листе

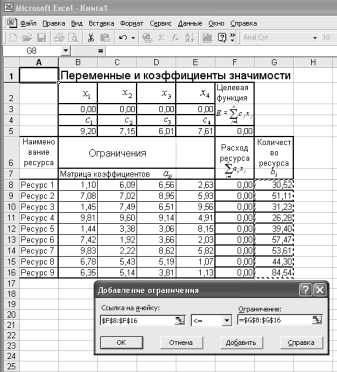
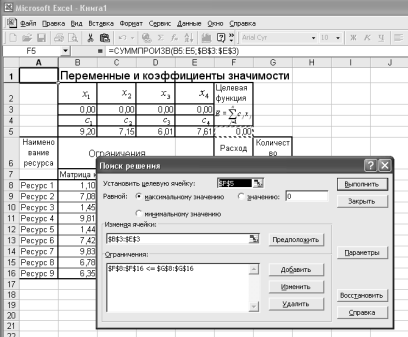
Выполненные ранее в операции (заполнение таблиц данными и программирование формул) позволяют полностью подготовиться собственно к решению задачи оптимизации. Теперь нам необходимо вызвать режим Сервис/Поиск решения. В открывшейся главной форме меню режима Поиск решения (рис. 7) надо указать адрес нашей целевой ячейки F5 и проверить или задать тип экстремума (в нашем случае Установить целевую ячейку равной максимальному значению). 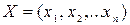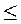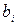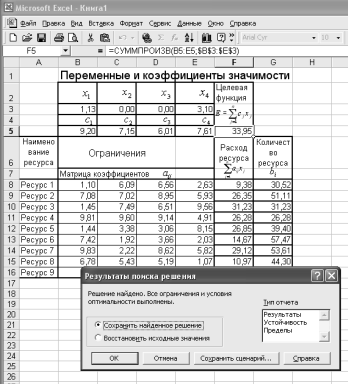В окне Изменяя ячейки задаем адреса ячеек переменных (в нашем случае B3:F3). Нажав кнопку Добавить в открывшейся таблице (рис. 10) Добавление ограничения в поле Ссылка на ячейку вводим адреса левых частей неравенств (2) (в нашем случае F8:F16). Устанавливаем (сохраняем) требуемые знаки неравенств (в нашем случае ). Войдя в окно Ограничение, задаем адреса ячеек, содержащих значения (в нашем случае G8:G16). Нажав кнопку Параметры, в открывшейся таблице (рис. 8) задаем режим Линейная модель и Неотрицательные значения, после чего нажимаем кнопку OK. Результат этих действий отображен на рис11.

Нажимаем кнопку Выполнить и получаем решение задачи, показанное на рис. 12. В результате выполнения команды Поиск решения в таблице Результаты поиска решения могут быть выданы следующие диагностические сообщения:

Решение найдено. Все ограничения и условия оптимальности выполнены (имеет место в рассматриваемом случае).

Поиск не может найти подходящего решения.

Значения целевой ячейки не сходятся.

Если решение найдено, то на рабочем листе Excel в изменяемых ячейках находятся значения переменных 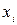(в нашем случае 1,13; 0,00; 0,00; 3,10), обеспечивающие максимальное значение целевой функции (в нашем случае 33,95). Для сохранения результатов вычислений на рабочем листе необходимо выбрать пункт Сохранить найденное решение.

Если в результате решения задачи оптимизации выдается сообщение Поиск не может найти подходящего решения, то это означает, что условия задачи несовместны, т. е. не существует такого набора значений переменных 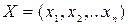, который удовлетворял бы имеющимся ограничениям.

Диагностическое сообщение Значения целевой ячейки не сходятся выдается Excel в том случае, когда при поиске максимума целевой функции область допустимых значений целевой функции не ограничена сверху (целевая функция возрастает неограниченно). Для устранения этой причины целесообразно увеличить количество ограничений на значения переменных.

Рис. 10. Добавление ограничений

Рис. 11. Подготовленная к решению задача линейного программирования

По результатам решения в случае установки режима Линейная модель (симплекс-метод) могут быть представлены три типа отчетов: по результатам, по устойчивости и по пределам. Если они требуются, то в меню результаты поиска решения в окне Тип отчета (рис. 12) необходимо выделить соответствующие строки.

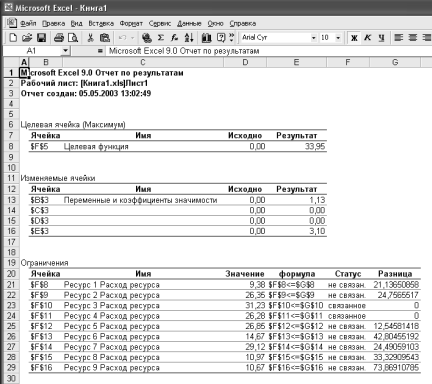
Отчет по результатам (рис. 13) содержит начальные (Исходно) и конечные (Результат) значения целевой функции и изменяемых ячеек, а также сводку результатов использования ресурсов. В этой сводке в столбце Статус символами связанное или несвязанное обозначаются соответственно полное или неполное использование соответствующего ресурса. В рассматриваемом примере полностью израсходованы Ресурс 3 и Ресурс 4.

Рис. 12. Результат решения задачи линейного программирования

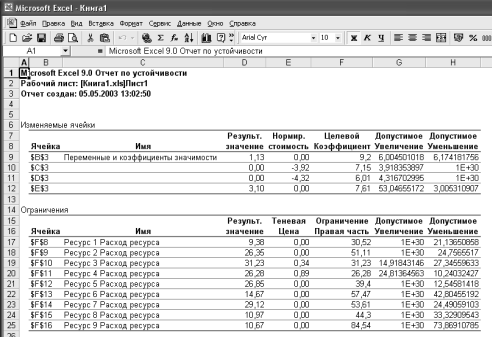
Отчет по устойчивости (рис. 14) показывает значения нормированной стоимости оценок (Нормир. стоимость), определяющих насколько изменится целевая функция при принудительном включении в план единицы продукции. Кроме этого в отчете содержатся величины использованных ресурсов (Результ. значение), их теневые цены, показывающие насколько изменится целевая функция при увеличении соответствующего ресурса на единицу, а также используемые значения ограничений. Колонки Допустимое увеличение (уменьшение) задают диапазон изменения значений переменных и ограничений, сохраняющих общую структуру решения задачи.

Рис. 13. Отчет по результатам

Рис. 14. Отчет по устойчивости

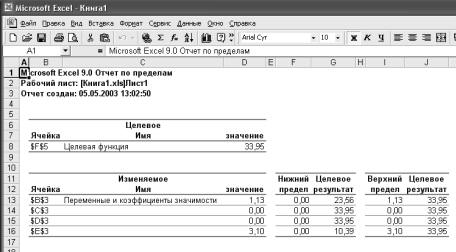
Отчет по пределам (рис. 15) показывает возможный диапазон изменения значений переменных, сохраняющий структуру оптимального решения, а также получающиеся в этом случае значения целевой функции.

Примечание. Конкретные реализации состава таблиц отчетов по пределам и устойчивости могут отличаться от приведенных выше.

Рис. 15. Отчет по пределам

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник

Экстремум функции

Функция y = f(x) называется возрастающей (убывающей) в некотором интервале, если при x₁< x₂ выполняется неравенство(f(x₁) < f (x₂) (f(x₁) >f(x₂)).

Если дифференцируемая функция y = f(x) на отрезке [a,b] возрастает (убывает), то ее производная на этом отрезке f ‘ (x) > 0 , (f ‘ (x) < 0).

Точка x_о называется точкой локального максимума (минимума) функции f(x), если существует окрестность x_о, для всех точек которой верно неравенство f(x) ≤ f(x_о), (f(x) ≥f(x_о)).

Точки максимума и минимума называются точками экстремума, значения функции в них — ее экстремумами.

Точки экстремума

Необходимые условия экстремума. Если x_о является точкой экстремума функции f(x), то либо f ‘ (x_о) = 0, либо f (x_о) не существует. Такие точки называют критическими, причем сама функция в них определена. Экстремумы функции следует искать среди ее критических точек.

Первое достаточное условие. Пусть x_о — критическая точка. Если f ‘ (x) при переходе через x_о меняет знак плюс на минус, то в точке x_о функция имеет максимум, в противном случае — минимум. Если при переходе через критическую точку производная не меняет знак, то в x_о экстремума нет.

Второе достаточное условие. Пусть функция f(x) имеет производную f ‘ (x) в окрестности x_о и вторую производную f » (x₀) в самой точке x_о. Если f ‘ (x_о) = 0, f » (x₀)>0, (f » (x₀) <0), то x_о является точкой локального минимума (максимума) функции f(x). Если же f » (x₀)=0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

На отрезке [a,b] функция y =f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].

Пример 1. Найти экстремумы функции f(x) = 2x 3 — 15x 2 + 36x — 14.

Задачи на нахождения экстремума функции

Пример 2. Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, четвертой стороной примыкала к стене. Для этого имеется a погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?

Пример 3. Требуется изготовить закрытый цилиндрический бак вместимостью V=16p ≈ 50 м 3 . Каковы должны быть размеры бака (радиус R и высота Н), чтобы на его изготовление пошло наименьшее количество материала?

Решение. Площадь полной поверхности цилиндра равна S = 2pR(R+Н). Мы знаем объем цилиндра V = pR 2 Н Þ Н = V/pR 2 =16p/ pR 2 = 16/ R 2 . Значит, S(R) = 2p(R 2 +16/R). Находим производную этой функции:
S ‘ (R) = 2p(2R- 16/R 2 ) = 4p (R- 8/R 2 ). S ‘ (R) = 0 при R 3 = 8, следовательно,
R = 2, Н = 16/4 = 4.

Пример 4. Найти экстремумы функцииf(x) = 2x 3 — 15x 2 + 36x — 14.

Пример 5. Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, четвертой стороной примыкала к стене. Для этого имеется c погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?

[expert_bq id=»1570″]Найти наибольшее и наименьшее значения функции z 5xy-4 , если переменные x и y положительны и удовлетворяют уравнению связи frac frac-1 0. Если же вы хотите что-то уточнить, обращайтесь ко мне![/expert_bq]
Продолжим разбор примеров на нахождение условного экстремума функций нескольких переменных. В первой части мы работали с функциями двух переменных, а здесь обратимся к функциям трёх переменных. Если понадобятся примеры для функций большего количества переменных, отпишите мне, пожалуйста, на форум или в комментариях.

Условный экстремум функций многих переменных. Метод множителей Лагранжа. Первая часть.

Пример 2. Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, четвертой стороной примыкала к стене. Для этого имеется a погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?
[expert_bq id=»1570″]Определяем положение глобального минимума модельной функции , который или принимается в качестве глобального минимума функции f x , или уточняется с помощью какого-либо метода локальной оптимизации. Если же вы хотите что-то уточнить, обращайтесь ко мне![/expert_bq]
Рассмотрим одномерную задачу условной глобальной оптимизации: найти минимум одномерной многоэкстремальной функции f ( x ), определенной в замкнутой области допустимых значений D = [ a ; b ] и имеющей в этой области конечное число минимумов (4.1).

Второй способ

Напомню, что значения функции $f(z)$ при заданных условиях связи совпадают с значениями функции $u(x,y,z)$, т.е. найденный экстремум функции $f(z)$ и есть искомым условным экстремумом функции $u(x,y,z)$. В принципе, несложно также указать остальные координаты точки условного экстремума: