Как найти экстремумы функции двух переменных онлайн

Экстремум функции двух переменных

Назначение сервиса. Онлайн-калькулятор используется для нахождения в онлайн режиме наибольшего и наименьшего значения функции двух переменных (см. пример). Решение оформляется в формате Word.

• Решение онлайн
• Видеоинструкция
• Оформление Word

Для функции трех переменных можно использовать матрицу Гессе.

Алгоритм исследования функции двух переменных на экстремум

Функция z = f(x,y) имеет максимум в точке M₀(x₀;y₀), если f(x₀;y₀) > f(x;y) для всех точек (x;y), достаточно близких к точке (x₀;y₀) и отличных от неё. Функция z = f(x,y) имеет минимум в точке M₀(x₀;y₀), если f(x₀;y₀) < f(x;y) для всех точек (x;y), достаточно близких к точке (x₀;y₀) и отличных от неё. Максимум и минимум функции называются экстремумами функции.

Исследование функции двух переменных на экстремум проводят по следующей схеме.

1. Находят частные производные dz/dx и dz/dy.

2. Решают систему уравнений:

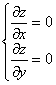
и таким образом находят критические точки функции.

3. Находят частные производные второго порядка:

4. Вычисляют значения этих частных производных второго порядка в каждой из найденных в п.2 критических точках M(x₀;y₀).

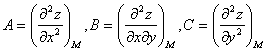
5. Делаю вывод о наличии экстремумов:

а) если AC – B² > 0 и A < 0 , то в точке M имеется максимум;

б) если AC – B² > 0 и A > 0 , то в точке M имеется минимум;

в) если AC – B² < 0, то экстремума нет;

г) если AC – B² = 0, то вопрос о наличии экстремума остается открытым;

Пример №1. Найти экстремумы функции f(x,y)=x³+xy²+x²+y² и определить по критерию Сильвестра их тип.

Решение.

1. Найдем первые частные производные.





2. Решим систему уравнений.

3x²+2x+y²=0

2xy+2y=0

Получим:

а) Из первого уравнения выражаем x и подставляем во второе уравнение:

x = -1

y²+1=0

Данная система уравнений не имеет решения.

б) Из первого уравнения выражаем y и подставляем во второе уравнение:





или





или

Откуда x₁ = -2/3; x₂ = 0; x₃ = -2/3; x₄ = 0

Данные значения x подставляем в выражение для y. Получаем: y₁ = 0; y₂ = 0; y₃ = 0; y₄ = 0

Количество критических точек равно 2: M₁(-2/3;0), M₂(0;0)

3. Найдем частные производные второго порядка.







4. Вычислим значение этих частных производных второго порядка в критических точках M(x₀;y₀).

Вычисляем значения для точки M₁(-2/3;0)







AC – B² = -4/3 < 0, то глобального экстремума нет.

Вычисляем значения для точки M₂(0;0)







AC – B² = 4 > 0 и A > 0 , то в точке M₂(0;0) имеется минимум z(0;0) = 0

Вывод: В точке M₂(0;0) имеется минимум z(0;0) = 0

Пример №2. Исследовать функцию на экстремум классическим методом: Z=8x2+2xy-5x+6.

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

bold{mathrm{Basic}}	bold{alphabetagamma}	bold{mathrm{ABGamma}}	bold{sincos}	bold{gedivrightarrow}	bold{overline{x}spacemathbb{C}forall}	bold{sumspaceintspaceproduct}	bold{begin{pmatrix}square&square\square&squareend{pmatrix}}	bold{H_{2}O}
square^{2} x^{square} sqrt{square} nthroot[msquare]{square} frac{msquare}{msquare} log_{msquare} pi theta infty int frac{d}{dx} ge le cdot div x^{circ} (square) |square| (f:circ:g) f(x) ln e^{square} left(squareright)^{‘} frac{partial}{partial x} int_{msquare}^{msquare} lim sum sin cos tan cot csc sec alpha beta gamma delta zeta eta theta iota kappa lambda mu nu xi pi rho sigma tau upsilon phi chi psi omega A B Gamma Delta E Z H Theta K Lambda M N Xi Pi P Sigma T Upsilon Phi X Psi Omega sin cos tan cot sec csc sinh cosh tanh coth sech arcsin arccos arctan arccot arcsec arccsc arcsinh arccosh arctanh arccoth arcsech begin{cases}square\squareend{cases} begin{cases}square\square\squareend{cases} = ne div cdot times < > le ge (square) [square] ▭:longdivision{▭} times twostack{▭}{▭} + twostack{▭}{▭} – twostack{▭}{▭} square! x^{circ} rightarrow lfloorsquarerfloor lceilsquarerceil overline{square} vec{square} in forall notin exist mathbb{R} mathbb{C} mathbb{N} mathbb{Z} emptyset vee wedge neg oplus cap cup square^{c} subset subsete superset supersete int intint intintint int_{square}^{square} int_{square}^{square}int_{square}^{square} int_{square}^{square}int_{square}^{square}int_{square}^{square} sum prod lim lim _{xto infty } lim _{xto 0+} lim _{xto 0-} frac{d}{dx} frac{d^2}{dx^2} left(squareright)^{‘} left(squareright)^{”} frac{partial}{partial x} (2times2) (2times3) (3times3) (3times2) (4times2) (4times3) (4times4) (3times4) (2times4) (5times5) (1times2) (1times3) (1times4) (1times5) (1times6) (2times1) (3times1) (4times1) (5times1) (6times1) (7times1) mathrm{Радианы} mathrm{Степени} square! ( ) % mathrm{очистить} arcsin sin sqrt{square} 7 8 9 div arccos cos ln 4 5 6 times arctan tan log 1 2 3 – pi e x^{square} 0 . bold{=} +

Подпишитесь, чтобы подтвердить свой ответ

Подписаться

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

• extreme:f(x,y)=3x^{2}y+y^{3}−3x^{2}−3y^{2}+2
  

• extreme:f(x,y)=x^{2}+y^{2}
  

Описание

Шаг за шагом найдите экстремальные и седловые точки функций с несколькими переменными

multi-var-function-extreme-points-calculator

ru

Блог-сообщения, имеющие отношение к Symbolab

High School Math Solutions – Derivative Calculator, the Basics

Differentiation is a method to calculate the rate of change (or the slope at a point on the graph); we will not…

Read More

Введите Задачу

Сохранить в блокнот!

Войти

Ключевые слова: калькулятор экстремумов, найти экстремум функции двух переменных, частные производные первого и второго порядков, стационарные точки, калькулятор частных производных.

Пример 1. Исследовать на экстремум функцию:

Алгоритм решения следующий:

1) находим частные производные первого порядка:

Примечание: найти частные производные онлайн  (первого и второго порядка) можно с помощью калькулятора.

2). Решаем систему уравнений:

и таким образом находим стационарные точки функции.

Точки, в которых значение производной функции равно нулю, называются стационарными точками.

Для данного примера  получаем систему уравнений:

стационарная точка: (-1;1)

3) Находим вторые частные производные

Вычисляем значения этих частных производных второго порядка в каждой из найденных в п.2 стационарных точках M(x₀;y₀).

Для данного примера, получаем

4) Делаем вывод о наличии экстремумов:
а) если AC – B² > 0 и A < 0 , то в точке M имеется максимум;
б) если AC – B² > 0 и A > 0 , то в точке M имеется минимум;
в) если AC – B² < 0, то экстремума нет;
г) если AC – B² = 0, то вопрос о наличии экстремума остается открытым;

Тогда в точке    x=-1, y=1

Следовательно в точке x=-1, y=1 функция имеет локальный минимум

Ответ: min{z}=0

Проверить правильность решения можно с помощью калькулятора “экстремум функции”.

Уважаемые студенты!
Заказать решение задач по 200+ предметам можно здесь всего за 10 минут.

Экстремум функции двух переменных

Как найти?

Постановка задачи

Найти экстремум функции двух переменных $ z = z(x,y) $

План решения

Экстремумы функции двух переменных возможны в стационарных точках функции. Стационарными точками называются точки $ M(x_1,y_1), M(x_2,y_2)… $, в которых первые частные производные функции равны нулю: $ z(x,y) = 0 $

Для нахождения стационарных точек (подозрительных на экстремум) составляем систему:

$$ begin{cases} z’_x = 0 \ z’_y = 0 end{cases} $$

Решая систему получаем точки $ M(x_1,y_1), M(x_2,y_2)… $, каждую из которых нужно проверить на экстремум.

Проверку осуществляется с помощью подстановки точек в выражение, называемое достаточным условием существования экстремума:

$$ A = z”_{xx} cdot z”_{yy} – (z”_{xy})^2 $$

Если в точке $ M(x_1,y_1) $:

1. $ A>0 $ и $ z”_{xx} > 0 $, то $ M(x_1,y_1) $ точка минимума
2. $ A >0 $ и $ z”_{xx} < 0 $, то $ M(x_1,y_1) $ точка максимума
3. $ A < 0 $, то $ M(x_1,y_1) $ не является точкой экстремума
4. $ A = 0 $, то требуется дополнительное исследование (по определению)

Итак, необходимо выполнить действия:

1. Найти частные производные первого порядка. Приравнять их к нулю и решить систему уравнений. Получить точки $ M(x_1,y_1), M(x_2,y_2),… $
2. Найти частные производные второго порядка в точках $ M(x_1,y_1), M(x_2,y_2),… $
3. Используя достаточное условие существования экстремума делаем вывод о наличии экстремума в точках $ M(x_1,y_1), M(x_2,y_2),… $

Примеры решений

Пример 1

Найти экстремумы функции двух переменных $ z = x^2 -xy +y^2 $

Решение

Находим частные производные первого порядка: $$ z’_x = 2x – y $$ $$ z’_y = -x + 2y $$ Приравниваем полученные выражения к нулю и решаем систему двух уравнений: $$ begin{cases} 2x-y = 0 \ -x + 2y = 0 end{cases} $$ Решив систему получаем стационарную точку (подозрительные на экстремум): $$ M (0,0) $$ Далее вычисляем значения частных производных второго порядка в точке $ M $: $$ z”_{xx} Big |_M = 2 $$ $$ z”_{yy} Big |_M= 2 $$ $$ z”_{xy} Big |_M = -1 $$ Подставляя найденные значения в достаточное условие экстремума функции, проводим исследование знаков: $$ A = Big |_M = z”_{xx} Big |_M cdot z”_{yy} Big |_M – (z”_{xy} Big |_M)^2 = 2 cdot 2 – (-1)^2 = 3 $$ Так как получили $ A > 0 $ и $ z”_{xx} > 0 $, то получается $ M(0,0) $ точка минимума. Наименьшее значение находится в минимуме и равно: $$ z_{min} (0,0) = 0^2 – 0 cdot 0 + 0^2 = 0 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

В точке $ M(0,0) $ находится минимум функции; $ z_{min} = 0 $

Пример 2

Найти экстремумы функции двух переменных $ z = x^3 + y^3 – 15xy $

Решение

Составляем систему уравнений из частных производных первого порядка: $$ begin{cases} z’_x = 3x^2 – 15y = 0 \ z’_y = 3y^2 – 15x =0 end{cases} $$ Получаем стационарные точки $ M_1(0,0) $ и $ M_2(5,5) $, которые необходимо проверить через достаточное условие экстремума. Вычисляем значение частных прозводных второго порядка в точке $ M_1 $: $$ z”_{xx} Big |_{M_1} = 6x Big |_{M_1} = 0 $$ $$ z”_{yy} Big |_{M_1} = 6y Big |_{M_2} = 6y Big |_{M_2} = 0 $$ $$ z”_{xy} Big |_{M_1} = -15 $$ Подставляем данные значения в формулу достаточного условия экстремума: $$ A Big |_{M_1} = 0 cdot 0 – (-15)^2 = -225 $$ Так как $ A < 0 $, то в точке $ M_1(0,0) $ экстремума нет. Получаем значения частных производных 2 порядка в $ M_2 $: $$ z”_{xx} Big |_{M_2} = 6x Big |_{M_2} = 6 cdot 5 = 30 $$ $$ z”_{yy} Big |_{M_2} = 6y Big |_{M_2} = 6 cdot 5 = 30 $$ $$ z”_{xy} Big |_{M_2} = -15 $$ Вычисляем значение выражения достаточного условия экстремума: $$ A = 30 cdot 30 – (-15)^2 = 900 – 225 = 675 $$ Получили $ A > 0 $ и $ z”_{xx} > 0 $, то значит, $ M_2(5,5) $ точка минимума. Наименьшее значение функции $ z = x^3 + y^3 – 15xy $ равно: $$ z_{min} |_{M_2} = 5^3 + 5^3 – 15 cdot 5 cdot 5 = 125 + 125 – 375 = -125 $$

Ответ

В $ M_1 (0,0) $ экстремума нет, в $ M_2(5,5) $ минимум функции $ z_{min}=-125 $

Экстремум функции двух переменных. Примеры исследования функций на экстремум.

Пусть функция $z=f(x,y)$ определена в некоторой окрестности точки $(x_0,y_0)$. Говорят, что $(x_0,y_0)$ – точка (локального) максимума, если для всех точек $(x,y)$ некоторой окрестности точки $(x_0,y_0)$ выполнено неравенство $f(x,y)< f(x_0,y_0)$. Если же для всех точек этой окрестности выполнено условие $f(x,y)> f(x_0,y_0)$, то точку $(x_0,y_0)$ называют точкой (локального) минимума.

Точки максимума и минимума часто называют общим термином – точки экстремума.

Если $(x_0,y_0)$ – точка максимума, то значение функции $f(x_0,y_0)$ в этой точке называют максимумом функции $z=f(x,y)$. Соответственно, значение функции в точке минимума именуют минимумом функции $z=f(x,y)$. Минимумы и максимумы функции объединяют общим термином – экстремумы функции.

Алгоритм исследования функции $z=f(x,y)$ на экстремум

1. Найти частные производные $frac{partial z}{partial x}$ и $frac{partial z}{partial y}$. Составить и решить систему уравнений $
   left { begin{aligned}
   & frac{partial z}{partial x}=0;\
   & frac{partial z}{partial y}=0.
   end{aligned} right.$. Точки, координаты которых удовлетворяют указанной системе, называют стационарными.
2. Найти $frac{partial^2z}{partial x^2}$, $frac{partial^2z}{partial xpartial y}$, $frac{partial^2z}{partial y^2}$ и вычислить значение $Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2$ в каждой стационарной точке. После этого использовать следующую схему:
   1. Если $Delta > 0$ и $frac{partial^2z}{partial x^2} > 0$ (или $frac{partial^2z}{partial y^2} > 0$), то в исследуемая точка есть точкой минимума.
   2. Если $Delta > 0$ и $frac{partial^2z}{partial x^2} < 0$ (или $frac{partial^2z}{partial y^2} < 0$), то в исследуемая точка есть точкой максимума.
   3. Если $Delta < 0$, то в расматриваемой стационарной точке экстремума нет.
   4. Если $Delta = 0$, то ничего определённого про наличие экстремума сказать нельзя; требуется дополнительное исследование.

Примечание (желательное для более полного понимания текста): показатьскрыть

Пример №1

Исследовать на экстремум функцию $z=4x^2-6xy-34x+5y^2+42y+7$.

Решение

Будем следовать указанному выше алгоритму. Для начала найдём частные производные первого порядка:

$$
frac{partial z}{partial x}=8x-6y-34; frac{partial z}{partial y}=-6x+10y+42.
$$

Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:

$$
left { begin{aligned}
& 8x-6y-34=0;\
& -6x+10y+42=0.
end{aligned} right.
$$

Сократим каждое уравнение этой системы на $2$ и перенесём числа в правые части уравнений:

$$
left { begin{aligned}
& 4x-3y=17;\
& -3x+5y=-21.
end{aligned} right.
$$

Мы получили систему линейных алгебраических уравнений. Мне в этой ситуации кажется наиболее удобным применение метода Крамера для решения полученной системы.

$$ begin{aligned}
& Delta=left| begin{array} {cc} 4 & -3\ -3 & 5 end{array}right|=4cdot 5-(-3)cdot (-3)=20-9=11;\
& Delta_x=left| begin{array} {cc} 17 & -3\ -21 & 5 end{array}right|=17cdot 5-(-3)cdot (-21)=85-63=22;\
& Delta_y=left| begin{array} {cc} 4 & 17\ -3 & -21 end{array}right|=4cdot (-21)-17cdot (-3)=-84+51=-33.end{aligned} \
x=frac{Delta_{x}}{Delta}=frac{22}{11}=2; ; y=frac{Delta_{y}}{Delta}=frac{-33}{11}=-3.
$$

Значения $x=2$, $y=-3$ – это координаты стационарной точки $(2;-3)$. Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:

$$
frac{partial^2 z}{partial x^2}=8; frac{partial^2 z}{partial y^2}=10; frac{partial^2 z}{partial x partial y}=-6.
$$

Вычислим значение $Delta$:

$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
8cdot 10-(-6)^2=80-36=44.
$$

Так как $Delta > 0$ и $frac{partial^2 z}{partial x^2} > 0$, то согласно алгоритму точка $(2;-3)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $(2;-3)$:

$$
z_{min}=z(2;-3)=4cdot 2^2-6cdot 2 cdot (-3)-34cdot 2+5cdot (-3)^2+42cdot (-3)+7=-90.
$$

Ответ: $(2;-3)$ – точка минимума; $z_{min}=-90$.

Пример №2

Исследовать на экстремум функцию $z=x^3+3xy^2-15x-12y+1$.

Решение

Будем следовать указанному выше алгоритму. Для начала найдём частные производные первого порядка:

$$
frac{partial z}{partial x}=3x^2+3y^2-15; frac{partial z}{partial y}=6xy-12.
$$

Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:

$$
left { begin{aligned}
& 3x^2+3y^2-15=0;\
& 6xy-12=0.
end{aligned} right.
$$

Сократим первое уравнение на 3, а второе – на 6.

$$
left { begin{aligned}
& x^2+y^2-5=0;\
& xy-2=0.
end{aligned} right.
$$

Если $x=0$, то второе уравнение приведёт нас к противоречию: $0cdot y-2=0$, $-2=0$. Отсюда вывод: $xneq 0$. Тогда из второго уравнения имеем: $xy=2$, $y=frac{2}{x}$. Подставляя $y=frac{2}{x}$ в первое уравнение, будем иметь:

$$
x^2+left(frac{2}{x} right)^2-5=0;\
x^2+frac{4}{x^2}-5=0;\
x^4-5x^2+4=0.
$$

Получили биквадратное уравнение. Делаем замену $t=x^2$ (при этом имеем в виду, что $t > 0$):

$$
t^2-5t+4=0;\
begin{aligned}
& D=(-5)^2-4cdot 1 cdot 4=9;\
& t_1=frac{-(-5)-sqrt{9}}{2}=frac{5-3}{2}=1;\
& t_2=frac{-(-5)+sqrt{9}}{2}=frac{5+3}{2}=4.end{aligned}
$$

Если $t=1$, то $x^2=1$. Отсюда имеем два значения $x$: $x_1=1$, $x_2=-1$. Если $t=4$, то $x^2=4$, т.е. $x_3=2$, $x_4=-2$. Вспоминая, что $y=frac{2}{x}$, получим:

begin{aligned}
& y_1=frac{2}{x_1}=frac{2}{1}=2;\
& y_2=frac{2}{x_2}=frac{2}{-1}=-2;\
& y_3=frac{2}{x_3}=frac{2}{2}=1;\
& y_4=frac{2}{x_4}=frac{2}{-2}=-1.
end{aligned}

Итак, у нас есть четыре стационарные точки: $M_1(1;2)$, $M_2(-1;-2)$, $M_3(2;1)$, $M_4(-2;-1)$. На этом первый шаг алгоритма закончен.

Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:

$$
frac{partial^2 z}{partial x^2}=6x; frac{partial^2 z}{partial y^2}=6x; frac{partial^2 z}{partial x partial y}=6y.
$$

Найдём $Delta$:

$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
6xcdot 6x-(6y)^2=36x^2-36y^2=36(x^2-y^2).
$$

Теперь будем вычислять значение $Delta$ в каждой из найденных ранее стационарных точек. Начнём с точки $M_1(1;2)$. В этой точке имеем:

$$Delta(M_1)=36(1^2-2^2)=-108.$$

Так как $Delta(M_1) < 0$, то согласно алгоритму в точке $M_1$ экстремума нет.

Исследуем точку $M_2(-1;-2)$. В этой точке имеем:

$$Delta(M_2)=36((-1)^2-(-2)^2)=-108.$$

Так как $Delta(M_2) < 0$, то согласно алгоритму в точке $M_2$ экстремума нет.

Исследуем точку $M_3(2;1)$. В этой точке получим:

$$
Delta(M_3)=36(2^2-1^2)=108;;; left.frac{partial^2 z}{partial x^2}right|_{M_3}=6cdot 2=12.
$$

Так как $Delta(M_3) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_3} > 0$, то согласно алгоритму $M_3(2;1)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_3$:

$$
z_{min}=z(2;1)=2^3+3cdot 2cdot 1^2-15cdot 2-12cdot 1+1=-27.
$$

Осталось исследовать точку $M_4(-2;-1)$. В этой точке получим:

$$
Delta(M_4)=36((-2)^2-(-1)^2)=108;;; left.frac{partial^2 z}{partial x^2}right|_{M_4}=6cdot (-2)=-12.
$$

Так как $Delta(M_4) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_4} < 0$, то согласно алгоритму $M_4(-2;-1)$ есть точкой максимума функции $z$. Максимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_4$:

$$
z_{max}=z(-2;-1)=(-2)^3+3cdot (-2)cdot (-1)^2-15cdot (-2)-12cdot (-1)+1=29.
$$

Исследование на экстремум завершено. Осталось лишь записать ответ.

Ответ:

• $(2;1)$ – точка минимума, $z_{min}=-27$;
• $(-2;-1)$ – точка максимума, $z_{max}=29$.

Примечание

Вычислять значение $Delta$ в общем случае нет необходимости, потому что нас интересует лишь знак, а не конкретное значение данного параметра. Например, для рассмотренного выше примера №2 в точке $M_3(2;1)$ имеем $Delta=36cdot(2^2-1^2)$. Здесь очевидно, что $Delta > 0$ (так как оба сомножителя $36$ и $(2^2-1^2)$ положительны) и можно не находить конкретное значение $Delta$. Правда, для типовых расчётов это замечание бесполезно, – там требуют довести вычисления до числа 🙂

Пример №3

Исследовать на экстремум функцию $z=x^4+y^4-2x^2+4xy-2y^2+3$.

Решение

Будем следовать алгоритму. Для начала найдём частные производные первого порядка:

$$
frac{partial z}{partial x}=4x^3-4x+4y; frac{partial z}{partial y}=4y^3+4x-4y.
$$

Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:

$$
left { begin{aligned}
& 4x^3-4x+4y=0;\
& 4y^3+4x-4y=0.
end{aligned} right.
$$

Сократим оба уравнения на $4$:

$$
left { begin{aligned}
& x^3-x+y=0;\
& y^3+x-y=0.
end{aligned} right.
$$

Добавим к второму уравнению первое и выразим $y$ через $x$:

$$
y^3+x-y+(x^3-x+y)=0;\
y^3+x^3=0; y^3=-x^3; y=-x.
$$

Подставляя $y=-x$ в первое уравнение системы, будем иметь:

$$
x^3-x-x=0;\
x^3-2x=0;\
x(x^2-2)=0.
$$

Из полученного уравнения имеем: $x=0$ или $x^2-2=0$. Из уравнения $x^2-2=0$ следует, что $x=-sqrt{2}$ или $x=sqrt{2}$. Итак, найдены три значения $x$, а именно: $x_1=0$, $x_2=-sqrt{2}$, $x_3=sqrt{2}$. Так как $y=-x$, то $y_1=-x_1=0$, $y_2=-x_2=sqrt{2}$, $y_3=-x_3=-sqrt{2}$.

Первый шаг решения окончен. Мы получили три стационарные точки: $M_1(0;0)$, $M_2(-sqrt{2},sqrt{2})$, $M_3(sqrt{2},-sqrt{2})$.

Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:

$$
frac{partial^2 z}{partial x^2}=12x^2-4; frac{partial^2 z}{partial y^2}=12y^2-4; frac{partial^2 z}{partial x partial y}=4.
$$

Найдём $Delta$:

$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
(12x^2-4)(12y^2-4)-4^2=\
=4(3x^2-1)cdot 4(3y^2-1)-16=16(3x^2-1)(3y^2-1)-16=16cdot((3x^2-1)(3y^2-1)-1).
$$

Теперь будем вычислять значение $Delta$ в каждой из найденных ранее стационарных точек. Начнём с точки $M_1(0;0)$. В этой точке имеем:

$$Delta(M_1)=16cdot((3cdot 0^2-1)(3cdot 0^2-1)-1)=16cdot 0=0.$$

Так как $Delta(M_1) = 0$, то согласно алгоритму требуется дополнительное исследование, ибо ничего определённого про наличие экстремума в рассматриваемой точке сказать нельзя. Оставим покамест эту точку в покое и перейдём в иным точкам.

Исследуем точку $M_2(-sqrt{2},sqrt{2})$. В этой точке получим:

begin{aligned}
& Delta(M_2)=16cdot((3cdot (-sqrt{2})^2-1)(3cdot (sqrt{2})^2-1)-1)=16cdot 24=384;\
& left.frac{partial^2 z}{partial x^2}right|_{M_2}=12cdot (-sqrt{2})^2-4=24-4=20.
end{aligned}

Так как $Delta(M_2) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_2} > 0$, то согласно алгоритму $M_2(-sqrt{2},sqrt{2})$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_2$:

$$
z_{min}=z(-sqrt{2},sqrt{2})=(-sqrt{2})^4+(sqrt{2})^4-2(-sqrt{2})^2+4cdot (-sqrt{2})sqrt{2}-2(sqrt{2})^2+3=-5.
$$

Аналогично предыдущему пункту исследуем точку $M_3(sqrt{2},-sqrt{2})$. В этой точке получим:

begin{aligned}
& Delta(M_3)=16cdot((3cdot (sqrt{2})^2-1)(3cdot (-sqrt{2})^2-1)-1)=16cdot 24=384;\
& left.frac{partial^2 z}{partial x^2}right|_{M_3}=12cdot (sqrt{2})^2-4=24-4=20.
end{aligned}

Так как $Delta(M_3) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_3} > 0$, то согласно алгоритму $M_3(sqrt{2},-sqrt{2})$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_3$:

$$
z_{min}=z(sqrt{2},-sqrt{2})=(sqrt{2})^4+(-sqrt{2})^4-2(sqrt{2})^2+4cdot sqrt{2}(-sqrt{2})-2(-sqrt{2})^2+3=-5.
$$

Настал черёд вернуться к точке $M_1(0;0)$, в которой $Delta(M_1) = 0$. Согласно алгоритму требуется дополнительное исследование. Под этой уклончивой фразой подразумевается “делайте, что хотите” :). Общего способа разрешения таких ситуаций нет, – и это понятно. Если бы такой способ был, то он давно бы вошёл во все учебники. А покамест приходится искать особый подход к каждой точке, в которой $Delta = 0$. Ну что же, поисследуем поведение функции в окрестности точки $M_1(0;0)$. Сразу отметим, что $z(M_1)=z(0;0)=3$. Предположим, что $M_1(0;0)$ – точка минимума. Тогда для любой точки $M$ из некоторой окрестности точки $M_1(0;0)$ получим $z(M) > z(M_1) $, т.е. $z(M) > 3$. А вдруг любая окрестность содержит точки, в которых $z(M) < 3$? Тогда в точке $M_1$ уж точно не будет минимума.

Рассмотрим точки, у которых $y=0$, т.е. точки вида $(x,0)$. В этих точках функция $z$ будет принимать такие значения:

$$
z(x,0)=x^4+0^4-2x^2+4xcdot 0-2cdot 0^2+3=x^4-2x^2+3=x^2(x^2-2)+3.
$$

В всех достаточно малых окрестностях $M_1(0;0)$ имеем $x^2-2 < 0$, посему $x^2(x^2-2) < 0$, откуда следует $x^2(x^2-2)+3 < 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z < 3$, посему точка $M_1(0;0)$ не может быть точкой минимума.

Но, может быть, точка $M_1(0;0)$ – точка максимума? Если это так, то для любой точки $M$ из некоторой окрестности точки $M_1(0;0)$ получим $z(M) < z(M_1) $, т.е. $z(M) < 3$. А вдруг любая окрестность содержит точки, в которых $z(M) > 3$? Тогда в точке $M_1$ точно не будет максимума.

Рассмотрим точки, у которых $y=x$, т.е. точки вида $(x,x)$. В этих точках функция $z$ будет принимать такие значения:

$$
z(x,x)=x^4+x^4-2x^2+4xcdot x-2cdot x^2+3=2x^4+3.
$$

Так как в любой окрестности точки $M_1(0;0)$ имеем $2x^4 > 0$, то $2x^4+3 > 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z > 3$, посему точка $M_1(0;0)$ не может быть точкой максимума.

Точка $M_1(0;0)$ не является ни точкой максимума, ни точкой минимума. Вывод: $M_1$ вообще не является точкой экстремума.

Ответ: $(-sqrt{2},sqrt{2})$, $(sqrt{2},-sqrt{2})$ – точки минимума функции $z$. В обеих точках $z_{min}=-5$.