Как найти экстремумы функции от трех переменных

1. Экстремумы функций двух и трёх переменных

Определение
1

Точка



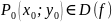
называется
точкой максимума функции

,
если
для любых точек


,
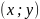
принадлежащих
окрестности точки

,
выполняется неравенство:


.

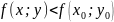
Определение
2

Точка

называется
точкой минимума функции

,
если
для любых точек

,
принадлежащих окрестности точки

,
выполняется
неравенство:



.

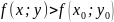
Определение
3

Точки
максимума и минимума называются
точками
экстремума
функции.

Теорема
1 (необходимое условие экстремума)

Если
точка

является точкой экстремума функции

,
то её частные производные в точке

равны нулю или не существуют.

При
доказательстве теоремы 1 используются
определения частных производных и
теорема о необходимых условиях экстремума
функции одной переменной.

Замечание
1.
Аналогично формулируются определения
1 и 2 и теорема 1 для функции трёх и более
переменных.

Теорема
2
(достаточные
условия экстремума функции двух
переменных)

Если
функция

дважды дифференцируема в критической
точке

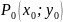
и её окрестности и определитель

,
то в точке

есть экстремум. Причём, если

,
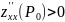
то точка

является точкой минимума функции, а
если

,
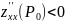
то точка

является точкой максимума.
Замечание
2.
Если определитель

,
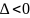
то в точке

нет экстремума, при этом точку

называют седловой точкой. Если

,
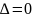
то вопрос об экстремуме в точке

остаётся нерешённым, нужны исследования
функции

по её производным более высокого порядка.

Теорема
3
(достаточные
условия экстремума функции трёх
переменных)

Пусть
функция

дважды дифференцируема в
критической точке

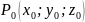
и её окрестности. Определитель

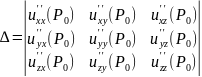
имеет все главные диагональные миноры

,

,

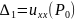
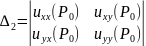
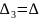
положительные, то

–точка минимума функции

.
Если

,

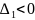
и

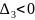
, то точка

– точка максимума функции

.

Замечание
3.
Если


критическая точка функции

и

,
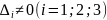
но не выполняются условия теоремы 3, то
в точке

нет экстремума, при этом точка

называется седловой точкой. Если все

,
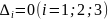
то вопрос об экстремуме в точке

решается с помощью производных более
высокого порядка.

Пример
1.
Найти экстремумы функции:


.

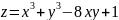
Решение.

;

.

.

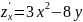
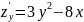
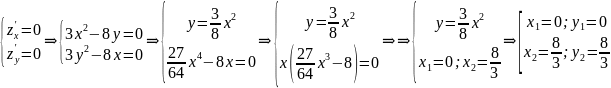
Получили
две точки

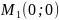
и

;

;

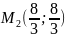
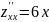
а)
Исследуем точку

:

;

;

.

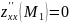
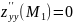
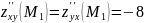
Тогда

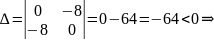
точка

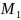
не является точкой экстремума.

б)
Исследуем точку

:

;

;

.

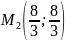
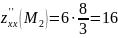
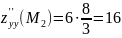
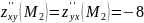
Тогда

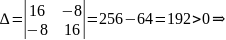
точка

является точкой экстремума. Причём так
как

,
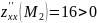
то точка

является точкой минимума функции:

.

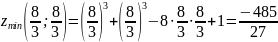
Ответ:

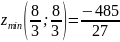
1. Условный экстремум

Пусть
задана функция

на множестве

.
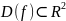
Требуется найти экстремумы функции

,
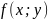
если

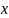
и

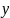
связаны некоторым условием

,
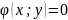
называемым уравнением
связи.

Определение
4.
Точка

называется точкой
условного экстремума
функции

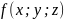
при выполнении дополнительных условий

– уравнений связи.

Для
нахождения точек условного экстремума
существует два метода: метод прямого
отыскания и метод Лагранжа. Прямой
метод состоит в том, что из уравнения
связи

выражается одна из переменных через
другую, и её подставляют в функцию

.
Получают функцию одной переменной, для
которой и решают задачу нахождения
обычного экстремума. Такой метод
применяют тогда, когда удаётся из
уравнения связи выразить одну переменную
через другую.

Пример
2.
Найти условный экстремум функции

при
условии

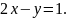
Решение.
Используем метод прямого отыскания
точек условного экстремума. Из условия

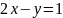
выразим

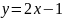
и подставим его в функцию

.
Тогда

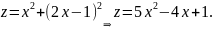
Найдём
для функции

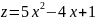
обычный экстремум.

,

– +
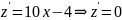
x

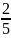
Следовательно,

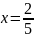
– точка минимума функции

.

Подставляем

в функцию

и получим:

.

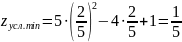
Ответ:

.

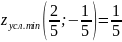
Определение
5.
Функция

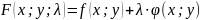
называется функцией
Лагранжа,
а коэффициент λ
–
множителем
Лагранжа.

Замечание
4.
Если связи не одно уравнение, а несколько
(например,

),
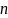
то функция Лагранжа для функции

записывается с

множителями Лагранжа:

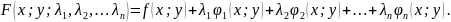
Теорема
4
(необходимое
условие поиска условного экстремума)

Пусть
функции

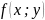
и

,
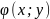
дифференцируемые в точке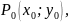

а

является точкой условного экстремума
функции

при условии

.
Тогда найдется такое число

,
при котором точка

является критической для функции
Лагранжа

.

Метод
Лагранжа
поиска условного экстремума состоит в
следующем:

1)
составляют функцию Лагранжа

;

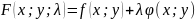
2)
находят её частные производные по

;

3)
приравнять частные производные к нулю
и решают систему уравнений

;

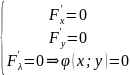
4)
исследуют найденную в результате решения
системы точку

при найденном значении

и решают задачу обычного экстремума
для

.

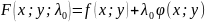
Теорема
5 (достаточное условие поиска условного
экстремума для случая одного уравнения
связи)

Пусть
точка

и

найдены из решения системы

.

Пусть
определитель

.

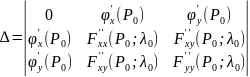
Если

,
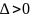
то функция

имеет в точке

условный максимум.

Если

,
то функция

имеет в точке

условный минимум.

Пример
3.
Методом Лагранжа найти условный экстремум
для функции

при условии

.
Решение.
Составим функцию Лагранжа

.

Найдём
её частные производные по

:

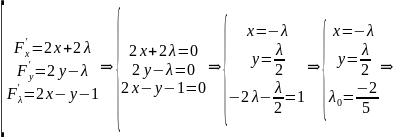
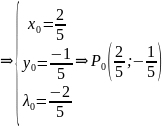
при

.

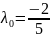
Выясним
характер точки

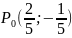
по теореме 5:

;

;

;

;

.

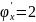
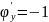
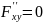
Составим
определитель:

.

Так
как

,
то

– точка условного минимума.

.

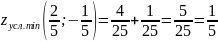
Ответ:

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Условный экстремум. Метод множителей Лагранжа. Вторая часть.

Продолжим разбор примеров на нахождение условного экстремума функций нескольких переменных. В первой части мы работали с функциями двух переменных, а здесь обратимся к функциям трёх переменных. Если понадобятся примеры для функций большего количества переменных, отпишите мне, пожалуйста, на форум или в комментариях.

Пример №4

Найти условный экстремум функции $u=2x+y-z+1$, если переменные $x$ и $y$ удовлетворяют уравнению связи $x^2+y^2+2z^2=22$.

Решение

Обозначим $f(x,y,z)=x^2+y^2+2z^2-22$. Для нахождения условного экстремума функции трёх переменных $u(x,y,z)$ составим функцию Лагранжа, которая будет иметь вид:

$$F(x,y,z)=u(x,y,z)+lambdacdot{f(x,y,z)}=2x+y-z+1+lambdacdotleft(x^2+y^2+2z^2-22right)$$

Составляем систему уравнений:

$$left{begin{aligned}
& F_{x}^{‘}=0;\
& F_{y}^{‘}=0;\
& F_{z}^{‘}=0;\
& f(x,y,z)=0.
end{aligned} right.
Rightarrow
left{begin{aligned}
& 2+2lambda{x}=0;\
& 1+2lambda{y}=0;\
& -1+4lambda{z}=0;\
& x^2+y^2+2z^2=22.
end{aligned} right.
Rightarrow
left{begin{aligned}
& 1+lambda{x}=0;\
& 1+2lambda{y}=0;\
& -1+4lambda{z}=0;\
& x^2+y^2+2z^2=22.
end{aligned} right.
$$

Решая данную систему, получим две точки: $M_1(4;2;-1)$ (при $lambda=-frac{1}{4}$) и $M_2(-4;-2;1)$ (при $lambda=frac{1}{4}$). Процесс решения системы я скрыл под примечание.

Как мы решили систему? показатьскрыть

Характер экстремума в найденных точках можно выяснить либо с помощью знака $d^2F$, либо же с помощью угловых миноров матрицы $L$, о чём говорилось в первой части данной темы. В этом примере и примере №6 определим характер экстремума с помощью угловых миноров матрицы $L$, а в примере №7 – с помощью знака $d^2F$. Для наглядности я запишу матрицу $L$ в общем виде:

$$
L=left(begin{array} {cccc}
0 & frac{partial{f}}{partial{x}} & frac{partial{f}}{partial{y}} & frac{partial{f}}{partial{z}}\
frac{partial{f}}{partial{x}} & frac{partial^2F}{partial{x}^2} & frac{partial^2F}{partial{x}partial{y}} & frac{partial^2F}{partial{x}partial{z}}\
frac{partial{f}}{partial{y}} & frac{partial^2F}{partial{x}partial{y}} & frac{partial^2F}{partial{y}^2}& frac{partial^2F}{partial{y}partial{z}}\
frac{partial{f}}{partial{z}} & frac{partial^2F}{partial{x}partial{z}} & frac{partial^2F}{partial{y}partial{z}} & frac{partial^2F}{partial{z}^2}\
end{array}right)
$$

Находим искомые частные производные и подставляем их в матрицу $L$:

$$f_{x}^{‘}=2x;;f_{y}^{‘}=2y;;f_{z}^{‘}=4z;\
F_{xx}^{”}=2lambda;;F_{xy}^{”}=0;;F_{xz}^{”}=0;;F_{yy}^{”}=2lambda;;F_{yz}^{”}=0;;F_{zz}^{”}=4lambda.$$

Соответственно, матрица $L$ будет такой: $L=left(begin{array}{cccc}0 & 2x & 2y & 4z\2x & 2lambda & 0 & 0\2y & 0 & 2lambda & 0\4z & 0 & 0 & 4lambdaend{array}right)$. Используем правило в первой части темы. Нам нужно найти знаки угловых миноров $H_{2m+1},; H_{2m+2},ldots,H_{m+n}$ матрицы $L$. Параметр $m$ равен количеству условий связи, а параметр $n$ равен количеству переменных. В данной задаче мы имеем одно условие связи и три переменных, поэтому $m=1$ и $n=3$. Так как $2m+1=3$ и $m+n=4$, то нужно найти угловые миноры $H_3$ и $H_4$. Запишем эти миноры (минор $H_4$ совпадает с определителем матрицы $L$). В принципе, указанные миноры несложно вычислить в общем виде, что мы и сделаем. Минор $H_3$ вычислим с помощью готовой формулы, а минор $H_4$ вычислим с помощью разложения по четвёртой строке:

$$H_3=left|begin{array}{ccc} 0 & 2x & 2y\2x & 2lambda & 0\2y & 0 & 2lambdaend{array}right|=-8y^2lambda-8x^2lambda=-8lambdacdotleft(x^2+y^2right);\

H_4=left|begin{array}{cccc}0 & 2x & 2y & 4z\2x & 2lambda & 0 & 0\2y & 0 & 2lambda & 0\4z & 0 & 0 & 4lambdaend{array}right|=-4zcdotleft|begin{array}{ccc}2x & 2y & 4z\2lambda & 0 & 0\0 & 2lambda & 0end{array}right|+4lambdacdotleft|begin{array}{ccc}0 & 2x & 2y\2x & 2lambda & 0\2y & 0 & 2lambdaend{array}right|=\
=-4zcdot{16lambda^2z}+4lambdacdotleft(-8y^2lambda-8x^2lambdaright)=-32lambda^2cdotleft(x^2+y^2+2z^2right).$$

Кстати, по полученным выражениям уже можно сделать вывод, что знак $H_3$ противоположен знаку $lambda$, а $H_4<0$. Поэтому вычислять значения указанных миноров просто нет необходимости, так как нас интересует лишь их знак. Однако в стандартных задачах типовых расчётов требуется считать до конца, поэтому вычислим значения угловых миноров $H_3$ и $H_4$:

$$
begin{aligned}
& H_3(M_1)=-8cdotleft(-frac{1}{4}right)left(4^2+2^2right)=40;;H_4(M_1)=-32cdotleft(-frac{1}{4}right)^2cdotleft(4^2+2^2+2cdot(-1)^2right)=-44;\
& H_3(M_2)=-8cdotfrac{1}{4}left((-4)^2+(-2)^2right)=-40;;H_4(M_2)=-32cdotleft(frac{1}{4}right)^2cdotleft((-4)^2+2^2+(-2)cdot 1^2right)=-44.
end{aligned}
$$

Знаки $H_3(M_1)$ и $H_4(M_1)$ чередуются, причем знак $H_3(M_1)$ совпадает с знаком $(-1)^{m+1}=(-1)^2=1$, поэтому $M_1$ – точка условного максимума. Знаки $H_3(M_2)$ и $H_4(M_2)$ совпадают с знаком $(-1)^{m}=(-1)^1=-1$, поэтому $M_2$ – точка условного минимума.

$$
begin{aligned}
& u_{min}=u(M_2)=-10;\
& u_{max}=u(M_1)=12.
end{aligned}
$$

Ответ: в точке $M_1(4;2;-1)$ функция имеет условный максимум, $u_{max}=12$. В точке $M_2(-4;-2;1)$ функция имеет условный минимум, $u_{min}=-10$.

Пример №5

Найти условный экстремум функции $u=2x+y^2-2z^2$, если переменные $x$ и $y$ удовлетворяют уравнениям связи $2x+y-5z=6$, $-x+3y-z=3$.

Решение

Для нахождения условного экстремума функции трёх переменных $u(x,y,z)$ можно составить функцию Лагранжа, которая будет иметь такой вид:

$$F(x,y,z)=2x+y^2-2z^2+lambda_1cdotleft(2x+y-5z-6right)+lambda_2cdotleft(-x+3y-z-3right)$$

Дальнейшее решение в этом случае предполагало бы составление системы уравнений, аналогичных размещённым в предыдущих задачах:

$$left{begin{aligned}
& F_{x}^{‘}=0;\
& F_{y}^{‘}=0;\
& F_{z}^{‘}=0;\
& 2x+y-5z-6=0;\
& -x+3y-z-3=0.
end{aligned} right.
Rightarrow
left{begin{aligned}
& 2+2lambda_1-lambda_2=0;\
& 2y+lambda_1+3lambda_2=0;\
& -4z-5lambda_1-lambda_2=0;\
& 2x+y-5z-6=0;\
& -x+3y-z-3=0.
end{aligned} right.$$

Решаем данную систему, получив точки возможного экстремума. Затем, после определения знака $d^2F$ в каждой найденной точке, делаем выводы о наличии в означенных точках экстремумов. Однако в данном случае можно поступить проще, выразив из уравнений связи переменные $x$ и $y$ через $z$. Для этого перенесём слагаемые, содержащие $z$, в правые части уравнений связи, а затем применим метод Крамера:

$$left{begin{aligned}
& 2x+y=5z+6;\
& -x+3y=z+3end{aligned}right.$$

$$Delta=left|begin{array} {cc} 2 & 1\ -1 & 3 end{array}right|=7;;
Delta_x=left|begin{array} {cc} 5z+6 & 1\ z+3 & 3 end{array}right|=14z+15;;
Delta_y=left|begin{array} {cc} 2 & 5z+6\ -1 & z+3 end{array}right|=7z+12.$$
$$x=frac{Delta_x}{Delta}=frac{14z+15}{7}=2z+frac{15}{7};;y=frac{Delta_y}{Delta}=frac{7z+12}{7}=z+frac{12}{7}.$$

Полученный результат легко истолковать с геометрической точки зрения. Уравнения $2x+y-5z=6$ и $-x+3y-z=3$ определяют плоскости в трёхмерном пространстве. Линия их пересечения есть прямая, параметрические уравнения которой, по сути, мы и получили выше.

Подставляя $x=2z+frac{15}{7}$ и $y=z+frac{12}{7}$ в заданную функцию $u$, получим функцию одной переменной $z$. Обозначим эту функцию как $f(z)$:

$$f(z)=2left(2z+frac{15}{7}right)+left(z+frac{12}{7}right)^2-2z^2=-z^2+frac{52z}{7}+frac{354}{49}$$

Осталось найти экстремум функции $f(z)$:

$$
f'(z)=-2z+frac{52}{7};\
-2z+frac{52}{7}=0;; z=frac{26}{7}.
$$

Так как $f”(z)=-2<0$, то $z=frac{26}{7}$ – точка максимума функции $f(z)$, при этом максимум равен $f_{max}=fleft(frac{26}{7}right)=frac{1030}{49}$.

Напомню, что значения функции $f(z)$ при заданных условиях связи совпадают с значениями функции $u(x,y,z)$, т.е. найденный экстремум функции $f(z)$ и есть искомым условным экстремумом функции $u(x,y,z)$. В принципе, несложно также указать остальные координаты точки условного экстремума:

$$
x=2z+frac{15}{7}=2cdotfrac{26}{7}+frac{15}{7}=frac{67}{7};\
y=z+frac{12}{7}=frac{26}{7}+frac{12}{7}=frac{38}{7}.\
$$

Итак, $left(frac{67}{7};frac{38}{7};frac{26}{7}right)$ – точка условного максимума функции $u(x,y,z)$. Разумеется, выразить две переменные через третью представляется возможным далеко не всегда. В следующем примере мы разберём такой случай.

Ответ: в точке $left(frac{67}{7};frac{38}{7};frac{26}{7}right)$ функция имеет условный максимум, $u_{max}=frac{1030}{49}$.

Пример №6

Исследовать функцию $u(x,y,z)=xy+yz+3$ на условный экстремум при условиях связи $x^2+y^2=2$, $y+z=2$, если $x>0$, $y>0$, $z>0$.

Решение

Обозначим $f(x,y,z)=x^2+y^2-2$, $g(x,y,z)=y+z-2$. Запишем функцию Лагранжа:

$$F(x,y,z)=u(x,y,z)+lambda_1cdot{f(x,y,z)}+lambda_2cdot{g(x,y,z)}=xy+yz+3+lambda_1cdotleft(x^2+y^2-2right)+lambda_2cdotleft(y+z-2right)$$

Составим систему уравнений:

$$left{begin{aligned}
& F_{x}^{‘}=0;\
& F_{y}^{‘}=0;\
& F_{z}^{‘}=0;\
& x^2+y^2-2=0;\
& y+z-2=0.
end{aligned} right.
Rightarrow
left{begin{aligned}
& y+2lambda_1x=0;\
& x+z+2lambda_1y+lambda_2=0;\
& y+lambda_2=0;\
& x^2+y^2-2=0;\
& y+z-2=0.
end{aligned} right.$$

Из третьего уравнения имеем: $lambda_2=-y$; из пятого уравнения: $z=2-y$; из четвёртого уравнения: $x=sqrt{2-y^2}$ (берём корень со знаком “плюс”, так как по условию $x>0$). Отметим, что $yneqsqrt{2}$, так как если бы $y=sqrt{2}$, то из третьего уравнения получили бы $x^2=0$, $x=0$. А этого быть не может, так как $x>0$ по условию. Так как $yneqsqrt{2}$, то из первого уравнения получим: $lambda_1=-frac{y}{2x}=-frac{y}{2sqrt{2-y^2}}$. Подставляя выражения для $lambda_1$, $lambda_2$, $z$, $x$ во второе уравнение, получим:

$$
sqrt{2-y^2}+2-y+2cdotleft(-frac{y}{2sqrt{2-y^2}}right)cdot{y}+(-y)=0;\
sqrt{2-y^2}+2-2y-frac{y^2}{sqrt{2-y^2}}=0.
$$

Домножая обе части равенства на $sqrt{2-y^2}$ и упрощая, получим:

$$
2-2y^2+(2-2y)sqrt{2-y^2}=0;\
(1-y)(1+y)+(1-y)sqrt{2-y^2}=0;\
(1-y)cdotleft(1+y+sqrt{2-y^2}right)=0.
$$

Так как по условию $y>0$, то $1+y+sqrt{2-y^2}>0$, поэтому последнее равенство возможно лишь при $y-1=0$, т.е. $y=1$. Значения остальных переменных таковы:

$$x=sqrt{2-1^2}=1;;z=2-1=1;;lambda_1=-frac{1}{2cdot{1}}=-frac{1}{2};;lambda_2=-1.$$

Итак, получили точку $M(1;1;1)$. Характер экстремума в данной точке можно выяснить либо с помощью знака $d^2F$ либо же с помощью миноров матрицы $L$, о чём говорилось в первой части данной темы. В этом примере определим характер экстремума с помощью угловых миноров матрицы $L$, а в следующем примере – с помощью знака $d^2F$. Запишем матрицу $L$ в общем виде:

$$
L=left(begin{array} {ccccc}
0 & 0 & frac{partial{f}}{partial{x}} & frac{partial{f}}{partial{y}} & frac{partial{f}}{partial{z}}\
0 & 0 & frac{partial{g}}{partial{x}} & frac{partial{g}}{partial{y}} & frac{partial{g}}{partial{z}}\
frac{partial{f}}{partial{x}} & frac{partial{g}}{partial{x}} & frac{partial^2F}{partial{x}^2} & frac{partial^2F}{partial{x}partial{y}} & frac{partial^2F}{partial{x}partial{z}}\
frac{partial{f}}{partial{y}} & frac{partial{g}}{partial{y}} & frac{partial^2F}{partial{x}partial{y}} & frac{partial^2F}{partial{y}^2}& frac{partial^2F}{partial{y}partial{z}}\
frac{partial{f}}{partial{z}} & frac{partial{g}}{partial{z}} & frac{partial^2F}{partial{x}partial{z}} & frac{partial^2F}{partial{y}partial{z}} & frac{partial^2F}{partial{z}^2}\
end{array}right)
$$

Запишем искомые частные производные и определим их значение в точке $M$.

$$
f_{x}^{‘}=2x;;f_{y}^{‘}=2y;;f_{z}^{‘}=0;\
g_{x}^{prime}=0;;g_{y}^{prime}=1;;g_{z}^{prime}=1;\
F_{xx}^{”}=2lambda_1;;F_{xy}^{”}=1;;F_{xz}^{”}=0;;F_{yy}^{”}=2lambda_1;;F_{yz}^{”}=1;;F_{zz}^{”}=0.
$$

Подставляя $x=y=z=1$, $lambda_1=-frac{1}{2}$ и $lambda_2=-1$, получим:

$$
f_{x}^{‘}(M)=2;;f_{y}^{‘}(M)=2;;f_{z}^{‘}(M)=0;\
g_{x}^{prime}(M)=0;;g_{y}^{prime}(M)=1;;g_{z}^{prime}(M)=1;\
F_{xx}^{”}(M)=-1;;F_{xy}^{”}(M)=1;;F_{xz}^{”}(M)=0;;F_{yy}^{”}(M)=-1;;F_{yz}^{”}(M)=1;;F_{zz}^{”}(M)=0.
$$

Матрица $L$ примет следующий вид: $L=left(begin{array} {ccccc} 0 & 0 & 2 & 2 & 0\0 & 0 & 0 & 1 & 1\2 & 0 & -1 & 1 & 0\2 & 1 & 1 & -1 & 1\0 & 1 & 0 & 1 & 0 end{array}right)$. Обратимся к правилу в первой части темы. Напомню, что нам нужно найти знаки угловых миноров $H_{2m+1},; H_{2m+2},ldots,H_{m+n}$ матрицы $L$. Параметр $m$ равен количеству условий связи, а параметр $n$ равен количеству переменных. В данной задаче мы имеем два условия связи и три переменных, поэтому $m=2$ и $n=3$. Так как $2m+1=5$ и $m+n=5$, то нужно найти лишь один минор $H_5$.

Так как матрица $L$ пятого порядка, то минор $H_5$ совпадает с определителем матрицы $L$. Применяя, к примеру, метод эффективного понижения порядка, будем иметь:

$$H_5=left|begin{array} {ccccc} 0 & 0 & 2 & 2 & 0\0 & 0 & 0 & 1 & 1\2 & 0 & -1 & 1 & 0\2 & 1 & 1 & -1 & 1\0 & 1 & 0 & 1 & 0 end{array}right|
begin{array} {l} phantom{0} \ phantom{0} \ phantom{0} \ phantom{0}\V-IV end{array}=
left|begin{array} {ccccc} 0 & 0 & 2 & 2 & 0\0 & 0 & 0 & 1 & 1\2 & 0 & -1 & 1 & 0\2 & 1 & 1 & -1 & 1\-2 & 0 & -1 & 2 & -1 end{array}right|=
left|begin{array} {cccc} 0 & 2 & 2 & 0\0 & 0 & 1 & 1\2 & -1 & 1 & 0\-2 & -1 & 2 & -1 end{array}right|
begin{array} {l} phantom{0} \ phantom{0} \ phantom{0} \ IV+III end{array}=\
=left|begin{array} {cccc} 0 & 2 & 2 & 0\0 & 0 & 1 & 1\2 & -1 & 1 & 0\0 & -2 & 3 & -1 end{array}right|=
2cdotleft|begin{array} {ccc} 2 & 2 & 0\0 & 1 & 1\-2 & 3 & -1end{array}right|=2cdot(-12)=-24.$$

Так как $(-1)^{m+1}=(-1)^3=-1$, то знаки $H_{2m+1}$ и $(-1)^{m+1}$ совпадают. Следовательно, функция $u$ имеет в точке $(1;1;1)$ условный максимум, при этом $u_{max}=5$. Условный экстремум функции $u$ найден, осталось лишь записать ответ.

Ответ: в точке $left(1;1;1right)$ функция имеет условный максимум, $u_{max}=5$.

Пример №7

Найти условные экстремумы функции $u=xyz+4$, если $x+y+z=5$ и $xy+yz+xz=8$.

Решение

Применим метод множителей Лагранжа для исследования заданной функции трёх переменных. Составим функцию Лагранжа:

$$F=xyz+4+lambda_1(x+y+z-5)+lambda_2(xy+yz+xz-8)$$

Запишем соответствующую систему уравнений:

$$
begin{equation}
left{begin{aligned}
& yz+lambda_1+lambda_2y+lambda_2z=0;\
& xz+lambda_1+lambda_2z+lambda_2x=0;\
& xy+lambda_1+lambda_2y+lambda_2x=0;\
& x+y+z=5;\
& xy+yz+xz=8.
end{aligned}right.
end{equation}
$$

Процесс решения системы (1) довольно громоздкий, поэтому я буду скрывать под примечания некоторые преобразования. Выберем первые два уравнения, из которых выразим $lambda_1$ и $lambda_2$, применив метод Крамера:

$$left{begin{aligned}
& lambda_1+lambda_2(y+z)=-yz;\
& lambda_1+lambda_2(x+z)=-xz.end{aligned}right.$$

$$Delta=left|begin{array} {cc} 1 & y+z\ 1 & x+z end{array}right|=x-y;;
Delta_x=left|begin{array} {cc} -yz & y+z\ -xz & x+z end{array}right|=xz^2-yz^2;;
Delta_y=left|begin{array} {cc} 1 & -yz\ 1 & -xz end{array}right|=yz-xz.$$

Рассмотрим два случая: $Delta=0$ и $Deltaneq{0}$. Если $Delta=0$, т.е. $y=x$, то получим две точки: $M_1left(frac{4}{3};frac{4}{3};frac{7}{3}right)$ (при $lambda_1=frac{16}{9}$, $lambda_2=-frac{4}{3}$) и $M_2(2;2;1)$ (при $lambda_1=4$, $lambda_2=-2$).

Как мы получили эти точки? показатьскрыть

Если же $Deltaneq{0}$, т.е. $x-yneq{0}$, то получим:

$$lambda_1=frac{xz^2-yz^2}{x-y}=frac{z^2(x-y)}{x-y}=z^2;;lambda_1=frac{yz-xz}{x-y}=frac{-z(x-y)}{x-y}=-z.$$

Подставляя $lambda_1=z^2$ и $lambda_2=-z$ в систему уравнений (1), будем иметь:

$$
begin{equation}
left{begin{aligned}
& z^2+xy-xz-yz=0;\
& x+y+z=5;\
& xy+yz+xz=8.
end{aligned} right.
end{equation}
$$

Из данной системы получим: $z_1=frac{4}{3}$ и $z_2=2$.

Как мы получили эти значения? показатьскрыть

Если $z_1=frac{4}{3}$, то $lambda_1=frac{16}{9}$ и $lambda_2=-frac{4}{3}$. Получим две точки: $M_3left(frac{4}{3};frac{7}{3};frac{4}{3}right)$ и $M_4left(frac{7}{3};frac{4}{3};frac{4}{3}right)$.

Как мы получили эти точки? показатьскрыть

Если $z_2=2$, то $lambda_1=4$ и $lambda_2=-2$. Получим две точки: $M_5(1;2;2)$ и $M_6(2;1;2)$.

Как мы получили эти точки? показатьскрыть

Подытожим всё вышеизложенное, записав найденные точки и соответствующие им значения $lambda_1$ и $lambda_2$:

$$begin{aligned}
&M_1left(frac{4}{3};frac{4}{3};frac{7}{3}right),;lambda_1=frac{16}{9},;lambda_2=-frac{4}{3};\
&M_2(2;2;1),;lambda_1=4,;lambda_2=-2;\
&M_3left(frac{4}{3};frac{7}{3};frac{4}{3}right),;lambda_1=frac{16}{9},;lambda_2=-frac{4}{3};\
&M_4left(frac{7}{3};frac{4}{3};frac{4}{3}right),;lambda_1=frac{16}{9},;lambda_2=-frac{4}{3};\
&M_5(1;2;2),;lambda_1=4,;lambda_2=-2;\
&M_6(2;1;2),;lambda_1=4,;lambda_2=-2.end{aligned}$$

Чтобы выяснить характер условного экстремума в данных точках, запишем $d^2F$, предварительно найдя соответствующие частные производные:

$$F_{xx}^{”}=0;; F_{yy}^{”}=0;;F_{zz}^{”}=0;;F_{xy}^{”}=z+lambda_2;;F_{xz}^{”}=y+lambda_2;;F_{yz}^{”}=x+lambda_2.\
d^2F=2left(z+lambda_2right)dxdy+2left(y+lambda_2right)dxdz+2left(x+lambda_2right)dydz$$

Если в рассматриваемой точке $y=z$, то в этой точке $d^2F=-2left(x+lambda_2right)dy^2$. Если в некоторой точке $yneq{z}$, то:

$$d^2F=left(2left(z+lambda_2right)cdotfrac{x-z}{z-y}+2left(y+lambda_2right)frac{y-x}{z-y}+2left(x+lambda_2right)frac{(y-x)(x-z)}{(z-y)^2}right)dx^2$$

Как мы получили эти формулы? показатьскрыть

Теперь осталось лишь подставить в формулы для $d^2F$ координаты найденных точек и соответствующие значения $lambda_1$ и $lambda_2$. Для удобства эти данные я поместил в таблицу:

Ответ: $u_{min}=8$, $u_{max}=frac{220}{27}$.

Экстремум функции трёх переменных