Как найти экстремумы функции python

Время на прочтение
5 мин

Количество просмотров 56K

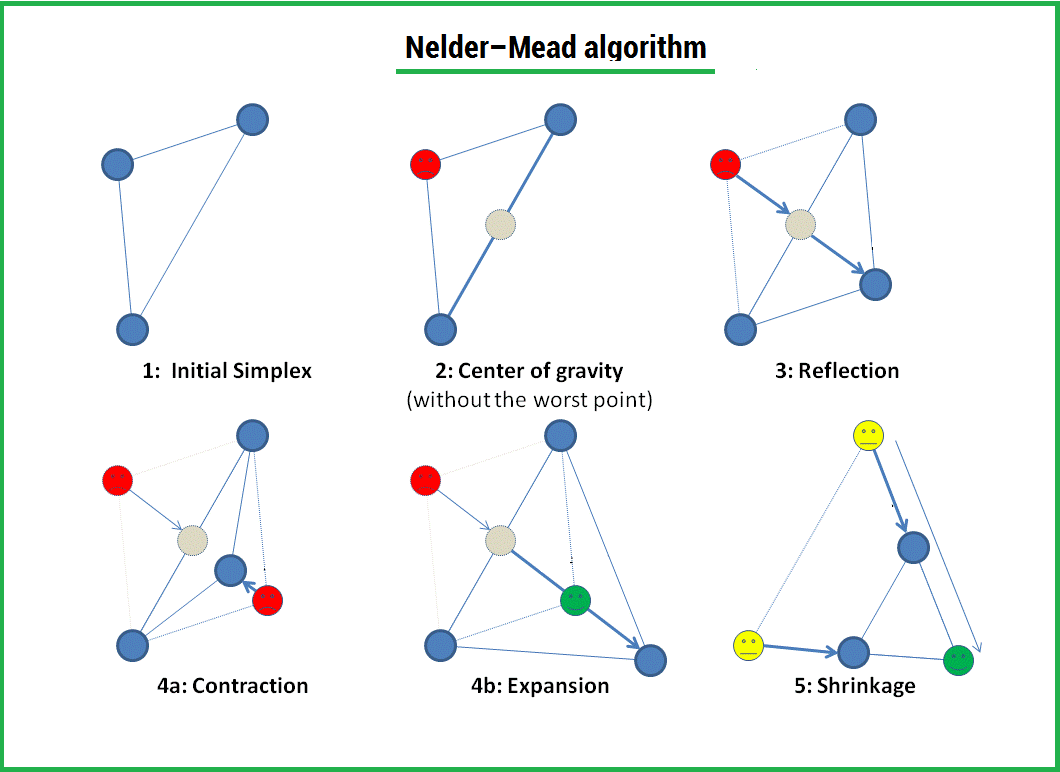
Метод Нелдера — Мида — метод оптимизации (поиска минимума) функции от нескольких переменных. Простой и в тоже время эффективный метод, позволяющий оптимизировать функции без использования градиентов. Метод надежен и, как правило, показывает хорошие результаты, хотя и отсутствует теория сходимости. Может использоваться в функции optimize из модуля scipy.optimize популярной библиотеки для языка python, которая используется для математических расчетов.

Алгоритм заключается в формировании симплекса (simplex) и последующего его деформирования в направлении минимума, посредством трех операций:

1) Отражение (reflection);
2) Растяжение (expansion);
3) Сжатие (contract);

Симплекс представляет из себя геометрическую фигуру, являющуюся n — мерным обобщением треугольника. Для одномерного пространства — это отрезок, для двумерного — треугольник. Таким образом n — мерный симплекс имеет n + 1 вершину.

Алгоритм

1) Пусть

функция, которую необходимо оптимизировать. На первом шаге выбираем три случайные точки (об этом чуть позже) и формируем симплекс (треугольник). Вычисляем значение функции в каждой точке:

,

,

.

Сортируем точки по значениям функции

в этих точках, таким образом получаем двойное неравенство:

Мы ищем минимум функции, а следовательно, на данном шаге лучшей будет та точка, в которой значение функции минимально. Для удобства переобозначим точки следующим образом:

b =

, g =

, w =

, где best, good, worst — соответственно.

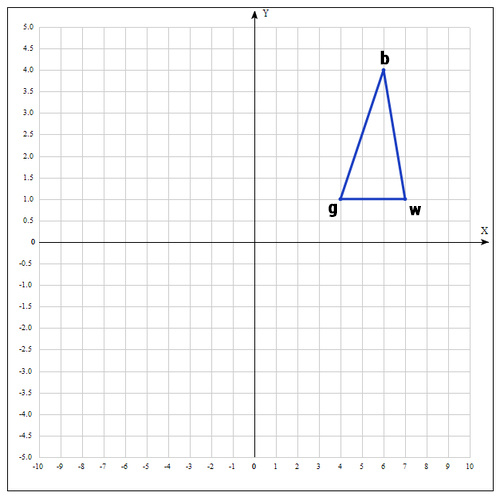
2) На следующем шаге находим середину отрезка, точками которого являются g и b. Т.к. координаты середины отрезка равны полусумме координат его концов, получаем:

В более общем виде можно записать так:

3) Применяем операцию отражения:
Находим точку

, следующим образом:

Т.е. фактически отражаем точку w относительно mid. В качестве коэффициента берут как правило 1. Проверяем нашу точку: если

, то это хорошая точка. А теперь попробуем расстояние увеличить в 2 раза, вдруг нам повезет и мы найдем точку еще лучше.

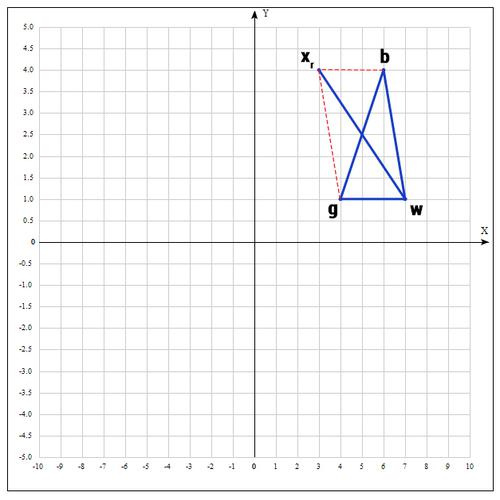
4) Применяем операцию растяжения:
Находим точку

следующим образом:

В качестве γ принимаем γ = 2, т.е. расстояние увеличиваем в 2 раза.

Проверяем точку

:

Если

, то нам повезло и мы нашли точку лучше, чем есть на данный момент, если бы этого не произошло, мы бы остановились на точке

.

Далее заменяем точку w на

, в итоге получаем:

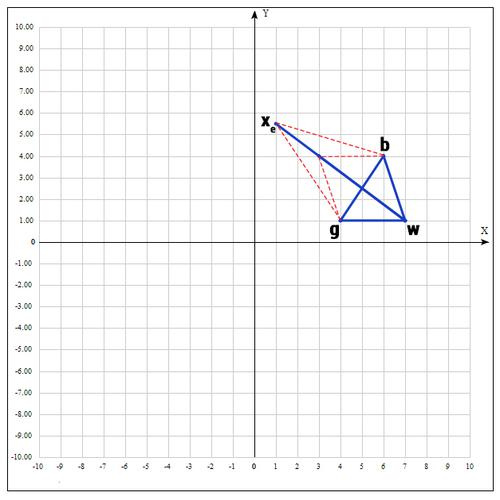
5) Если же нам совсем не повезло и мы не нашли хороших точек, пробуем операцию сжатия.
Как следует из названия операции мы будем уменьшать наш отрезок и искать хорошие точки внутри треугольника.

Пробуем найти хорошую точку

:

Коэффициент β принимаем равным 0.5, т.е. точка

на середине отрезка wmid.

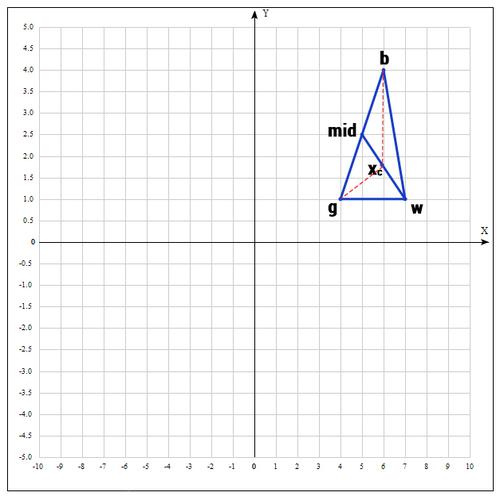
Существует еще одна операция — shrink (сокращение). В данном случае, мы переопределяем весь симплекс. Оставляем только «лучшую» точку, остальные определяем следующим образом:

Коэффициент δ берут равным 0.5.

По существу передвигаем точки по направлению к текущей «лучшей» точке. Преобразование выглядит следующим образом:

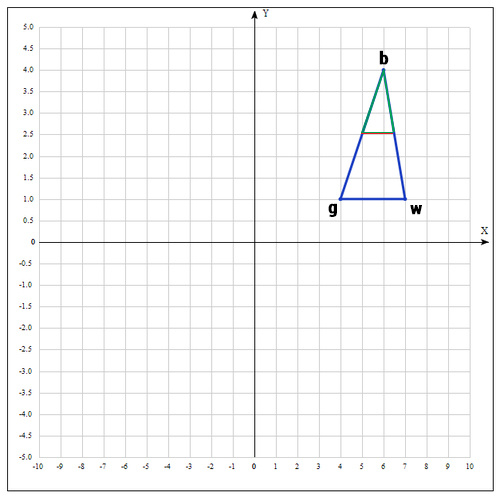
Необходимо отметить, что данная операция дорого обходится, поскольку необходимо заменять точки в симплексе. К счастью было установлено, при проведении большого количества экспериментов, что shrink — трансформация редко случается на практике.

Алгоритм заканчивается, когда:

1) Было выполнено необходимое количество итераций.
2) Площадь симплекса достигла определенной величины.
3) Текущее лучшее решение достигло необходимой точности.

Как и в большинстве эвристических методов, не существует идеального способа выбора инициализирующих точек. Как уже было сказано, можно брать случайные точки, находящиеся недалеко друг от друга для формирования симплекса; но есть решение и получше, которое используется в реализации алгоритма в MATHLAB:

Выбор первой точки

поручаем пользователю, если он имеет некоторое представление о возможном хорошем решении, в противном случае выбирается случайным образом. Остальные точки выбираются исходя из

, на небольшом расстоянии вдоль направления каждого измерения:

где

— единичный вектор.

определяется таким образом:

= 0.05, если коэффициент при

в определении

не нулевой.

= 0.00025, если коэффициент при

в определении нулевой.

Пример:

Найти экстремум следующей функции:

В качестве начальных возьмем точки:

Вычислим значение функции в каждой точке:

Переобозначим точки следующим образом:

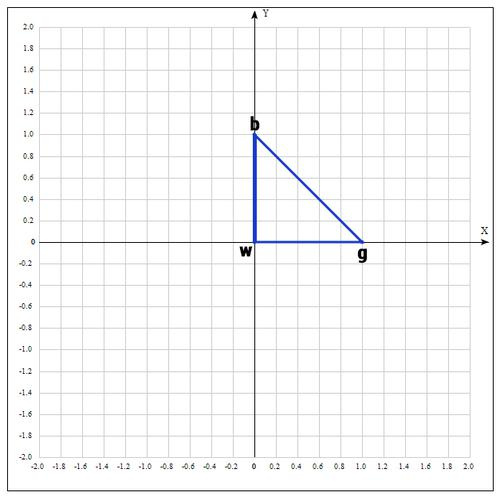
Находим середину отрезка bg:

Находим точку

(операция отражения):

если α=1, тогда:

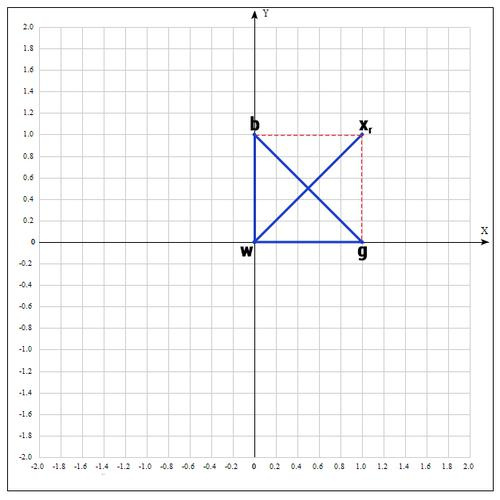
Проверяем точку

:

, т.к.

пробуем увеличить отрезок (операция растяжения).

если γ = 2, тогда:

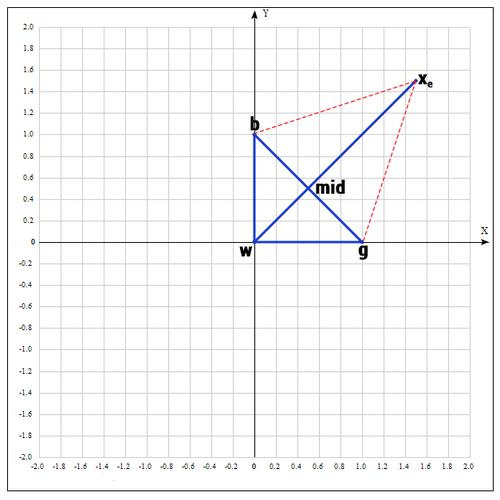
Проверяем значение функции в точке

:

Оказалось, что точка

«лучше» точки b. Следовательно мы получаем новые вершины:

И алгоритм начинается сначала.

Таблица значений для 10 итераций:

Best	Good	Worst

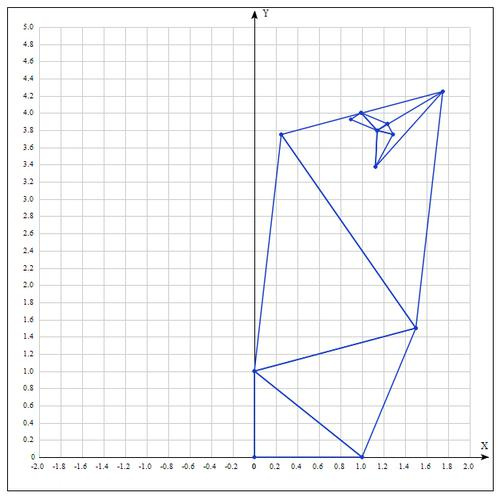
Аналитически находим экстремум функции, он достигается в точке

.
После 10 итераций мы получаем достаточно точное приближение:

Еще о методе:

Алгоритм Нелдера — Мида в основном используется для выбора параметра в машинном обучении. В сущности, симплекс-метод используется для оптимизации параметров модели. Это связано с тем, что данный метод оптимизирует целевую функцию довольно быстро и эффективно (особенно там, где не используется shrink — модификация).

С другой стороны, в силу отсутствия теории сходимости, на практике метод может приводить к неверному ответу даже на гладких (непрерывно дифференцируемых) функциях. Также возможна ситуация, когда рабочий симплекс находится далеко от оптимальной точки, а алгоритм производит большое число итераций, при этом мало изменяя значения функции. Эвристический метод решения этой проблемы заключается в запуске алгоритма несколько раз и ограничении числа итераций.

Реализация на языке программирования python:

Создаем вспомогательный класс Vector и перегружаем операторы для возможности производить с векторами базовые операции. Я намерено не использовал вспомогательные библиотеки для реализации алгоритма, т.к. в таком случае зачастую снижается восприятие.

#!/usr/bin/python
# -*- coding: utf-8 -*-
class Vector(object):
    def __init__(self, x, y):
        """ Create a vector, example: v = Vector(1,2) """
        self.x = x
        self.y = y

    def __repr__(self):
        return "({0}, {1})".format(self.x, self.y)

    def __add__(self, other):
        x = self.x + other.x
        y = self.y + other.y
        return Vector(x, y)

    def __sub__(self, other):
        x = self.x - other.x
        y = self.y - other.y
        return Vector(x, y)

    def __rmul__(self, other):
        x = self.x * other
        y = self.y * other
        return Vector(x, y)

    def __truediv__(self, other):
        x = self.x / other
        y = self.y / other
        return Vector(x, y)

    def c(self):
        return (self.x, self.y)
        
# objective function
def f(point):
    x, y = point
    return x**2 + x*y + y**2 - 6*x - 9*y

def nelder_mead(alpha=1, beta=0.5, gamma=2, maxiter=10):
    
    # initialization
    v1 = Vector(0, 0)
    v2 = Vector(1.0, 0)
    v3 = Vector(0, 1)

    for i in range(maxiter):
        adict = {v1:f(v1.c()), v2:f(v2.c()), v3:f(v3.c())}
        points = sorted(adict.items(), key=lambda x: x[1])
        
        b = points[0][0]
        g = points[1][0]
        w = points[2][0]
        
        
        mid = (g + b)/2

        # reflection
        xr = mid + alpha * (mid - w)
        if f(xr.c()) < f(g.c()):
            w = xr
        else:
            if f(xr.c()) < f(w.c()):
                w = xr
            c = (w + mid)/2
            if f(c.c()) < f(w.c()):
                w = c
        if f(xr.c()) < f(b.c()):

            # expansion
            xe = mid + gamma * (xr - mid)
            if f(xe.c()) < f(xr.c()):
                w = xe
            else:
                w = xr
        if f(xr.c()) > f(g.c()):
            
            # contraction
            xc = mid + beta * (w - mid)
            if f(xc.c()) < f(w.c()):
                w = xc

        # update points
        v1 = w
        v2 = g
        v3 = b
    return b

print("Result of Nelder-Mead algorithm: ")
xk = nelder_mead()
print("Best poits is: %s"%(xk))

Спасибо за чтение статьи. Надеюсь она была Вам полезна и Вы узнали много нового.
С вами был FUNNYDMAN. Удачной оптимизации!)

SciPy – еще одна популярная математическая библиотека Python, реализующая более высокоуровневые математические функции, например из линейной алгебры или теории вероятностей. SciPy использует NumPy (вообще сложно представить, кто не использует NumPy).

Чтобы понять возможности SciPy, нужно знать базовые (а иногда и не совсем базовые) математические понятия. Чтобы посмотреть хоть что-то рассмотрим простейшее понятие – минимум функции.

Минимум функции

Например задача нахождения точки экстремума функции – это задача из области оптимизации. Рассмотрим, что такое экстремум функции на примере функции подсчета погрешности. Функции подсчета погрешности в простейшем случае измеряют отклонение предсказанного результата от проверочных эталонных значений. Чем меньше значение погрешности возвращает проверочная функция, тем точнее результат предсказания. Т.е. мы заинтересованы в нахождении таких параметров для функции, чтобы функция нахождения погрешности возвращала минимальную погрешность. Конкретные значения таких параметров называются точкой минимума. Аналогичные значения параметров функции, при которых она возвращает максимально возможный результат (в данном случае – наибольшую погрешность) называются точкой максимума. Точки минимума и максимума – это точки экстремума функции. Так как нахождение точки экстремума – процесс итеративный, т.е. в простейшем случае пробуем вызвать функцию с произвольными параметрами – смотрим на результат. Далее пробуем увеличить какой-то параметр – смотрим уменьшился результат функции или увеличился.

Таким образом, двигаясь на пути к точки минимума, мы уменьшаем значение функции погрешности, то есть оптимизируем нашу функцию.

Почему точка? Это вопрос геометрического смысла функции. Любая чистая функция – это описанный закон зависимости между входными параметрами и выходным значением функции. Любую математическую зависимость можно визуализировать, например откладывая входной параметр по оси X, а результат по оси Y. Если функция непрерывная, то мы получим график зависимости и если выбрать правильный отрезок X для визуализации, то можно увидеть минимальное значение функции Y – точку экстремума.

Нахождение минимума функции с помощью SciPy

Функционал SciPy разбит на подпакеты по областям. В данном случае нас будет интересовать sub package optimze. Импортируем только его используя следующий Python синтаксис:

Ну а теперь зададим произвольную функцию и найдем ее точку минимума:

Проверить результат можно по-разному, например, визуализировав функцию на небольшом отрезке:

The bounds argument goes [(lower1,upper1),(lower2,upper2)], not [(lower1,lower2),(upper1,upper2)]. If you look at your result (max_x) you will see “ERROR: NO FEASIBLE SOLUTION”, which I am guessing is because your bounds specify an empty set.

Here is a correct way to call the function. I assume the square root is just an example. I used -x**2 instead.

import scipy.optimize as opt
import scipy
from numpy import *
def f(x):
    print x
    return -x**(2)

max_x = opt.fmin_l_bfgs_b(lambda x: -f(x), 1.0, bounds=[(-9,9)],approx_grad=True)

Because you are not specifying a gradient function, you need to set approx_grad=True. The 1.0 is my initial guess for the maximum (although it is obviously zero for this example). I added a print statement so I can see each time the function is called, but that’s normally not necessary. For more details on different ways to call fmin_l_bfgs_b, see here.

The above code results in:

[ 1.]
[ 1.]
[ 1.00000001]
[-0.99999999]
[-0.99999999]
[-0.99999998]
[ 0.001]
[ 0.001]
[ 0.00100001]
[ -5.01108742e-09]
[ -5.01108742e-09]
[  4.98891258e-09]

And max_x looks like this:

(array([ -5.01108742e-09]),
 array([  2.51109971e-17]),
 {'funcalls': 4,
  'grad': array([ -2.21748344e-11]),
  'task': 'CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL',
  'warnflag': 0})