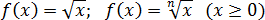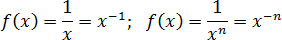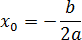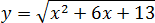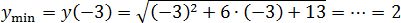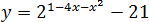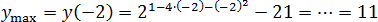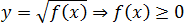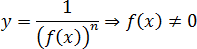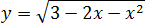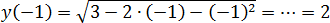Как найти экстремумы функции с корнями

Максимумы, минимумы и экстремумы функций

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.

Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

– Производная положительна там, где функция возрастает.
– Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после – производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.

(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.

(- 9): функция возрастает, а потом убывает – максимум.

Все вышесказанное можно обобщить следующими выводами:

– Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
– Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

1. Найдите производную функции (f'(x)).
2. Найдите корни уравнения (f'(x)=0).
3. Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
4. Определите знак производной в каждом промежутке (методом интервалов).
5. Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
6. Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
   – если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
   – если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
   – если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.

Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:

3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является (-2).

Задание 11 Профильного ЕГЭ по математике

Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.

Вот какие типы задач могут встретиться в этом задании:

Нахождение точек максимума и минимума функций

Исследование сложных функций

Нахождение наибольших и наименьших значений функций на отрезке

Нахождение точек максимума и минимума функций

1. Найдите точку максимума функции

Найдем производную функции.

Приравняем производную к нулю. Получим:

Исследуем знаки производной.

В точке производная меняет знак с «плюса» на «минус». Значит, — точка максимума функции

2. Найдите точку минимума функции

Найдем производную функции.

Приравняем производную к нулю.

Определим знаки производной.

В точке производная меняет знак с «минуса» на «плюс». Значит, — точка минимума функции

Исследование сложных функций

3. Найдите точку максимума функции

Перед нами сложная функция Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.

Так как функция монотонно возрастает, точка максимума функции .будет при том же , что и точка максимума функции А ее найти легко.

при . В точке производная меняет знак с «плюса» на «минус». Значит, — точка максимума функции .

Заметим, что точку максимума функции можно найти и без производной.

Графиком функции является парабола ветвями вниз, и наибольшее значение достигается в вершине параболы, то есть при

4. Найдите абсциссу точки максимума функции

Напомним, что абсцисса — это координата по

Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.

Так как функция монотонно возрастает, точка максимума функции является и точкой максимума функции

Это вершина квадратичной параболы

Нахождение наибольших и наименьших значений функций на отрезке

5. Найдите наибольшее значение функции на отрезке

Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.

Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.

Найдем знаки производной.

В точке производная равна нулю и меняет знак с “+” на “-“. Значит, x = – 2 — точка максимума функции . Поскольку при функция убывает, В этой задаче значение функции на концах отрезка искать не нужно.

6. Найдите наименьшее значение функции на отрезке

Найдем производную функции и приравняем ее к нулю.

Найдем знаки производной.

Точка — точка минимума функции . Точка не лежит на отрезке Поэтому

и Значит, наименьшее значение функции на отрезке достигается при Найдем это значение.

7. Найдите наименьшее значение функции на отрезке

Иногда перед тем, как взять производную, формулу функции полезно упростить.

Мы применили формулу для логарифма произведения. при

Если то Если , то

Значит, — точка минимума функции . В этой точке и достигается наименьшее значение функции на отрезке

8. Найдите наибольшее значение функции на отрезке

Найдем производную функции

Приравняем производную к нулю:

Найдем знаки производной на отрезке

При знак производной меняется с «плюса» на «минус». Значит, — точка максимума функции

Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при и

Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.

9. Найдите наименьшее значение функции на отрезке [0;2].

Снова сложная функция. Запишем полезные формулы:

Найдем производную функции

При знак производной меняется с «минуса» на «плюс». Значит, — точка минимума функции

10. Найдите наибольшее значение функции на отрезке

Как всегда, возьмем производную функции и приравняем ее к нулю.

По условию, . На этом отрезке условие выполняется только для Найдем знаки производной слева и справа от точки

В точке производная функции меняет знак с «плюса» на «минус». Значит, точка — точка максимума функции . Других точек экстремума на отрезке функция не имеет, и наибольшее значение функции на отрезке достигается при

11.Найдите наименьшее значение функции на отрезке

Найдем производную функции и приравняем ее к нулю. — нет решений.

Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.

Поскольку , получим, что для всех , и функция монотонно возрастает при

Значит, наименьшее свое значение функция принимает в левом конце отрезка , то есть при

Как решать задачи B15 без производных

Иногда в задачах B15 попадаются «плохие» функции, для которых сложно найти производную. Раньше такое было лишь на пробниках, но сейчас эти задачи настолько распространены, что уже не могут быть игнорированы при подготовке к настоящему ЕГЭ.

В этом случае работают другие приемы, один из которых — монотонность.

Функция f ( x ) называется на отрезке если для любых точек этого отрезка выполняется следующее:

Функция f ( x ) называется на отрезке если для любых точек этого отрезка выполняется следующее:

Другими словами, для возрастающей функции Для убывающей функции все наоборот:

Например, логарифм монотонно возрастает, если основание и монотонно убывает, если Не забывайте про область допустимых значений логарифма:

f ( x ) = log _a x ( a > 0; a ≠ 1; x > 0)

Арифметический квадратный (и не только квадратный) корень монотонно возрастает на всей области определения:

Показательная функция ведет себя аналогично логарифму: растет и убывает Но в отличие от логарифма, показательная функция определена для всех чисел, а не только

f ( x ) = a x (a > 0)

Наконец, степени с отрицательным показателем. Можно записывать их как дробь. Имеют точку разрыва, в которой монотонность нарушается.

Все эти функции никогда не встречаются в чистом виде. В них добавляют многочлены, дроби и прочий бред, становится тяжело считать производную. Что при этом происходит — сейчас разберем.

Координаты вершины параболы

Чаще всего аргумент функции заменяется на квадратный трехчлен вида Его график — стандартная парабола, в которой нас интересуют:

1. Ветви параболы — могут уходить вверх или вниз Задают направление, в котором функция может принимать бесконечные значения;
2. Вершина параболы — точка экстремума квадратичной функции, в которой эта функция принимает свое наименьшее или наибольшее значение.

Наибольший интерес представляет именно вершина параболы, абсцисса которой рассчитывается по формуле:

Итак, мы нашли точку экстремума квадратичной функции. Но если исходная функция монотонна, для нее тоже будет точкой экстремума. Таким образом, сформулируем ключевое правило:

Точки экстремума квадратного трехчлена и сложной функции, в которую он входит, совпадают. Поэтому можно для квадратного трехчлена, а на функцию — забить.

Из приведенных рассуждений остается непонятным, какую именно точку мы получаем: максимума или минимума. Однако задачи специально составляются так, что это не имеет значения. Судите сами:

1. Отрезок [ a ; b ] в условии задачи отсутствует. Следовательно, вычислять не требуется. Остается рассмотреть лишь точки экстремума;
2. Но таких точек всего одна — это вершина параболы координаты которой вычисляются буквально устно и без всяких производных.

Таким образом, решение задачи резко упрощается и сводится всего к двум шагам:

1. Выписать уравнение параболы и найти ее вершину по формуле:
2. Найти значение исходной функции в этой точке: Если никаких дополнительных условий нет, это и будет ответом.

На первый взгляд, этот алгоритм и его обоснование могут показаться сложными. Я намеренно не выкладываю «голую» схему решения, поскольку бездумное применение таких правил чревато ошибками.

Рассмотрим настоящие задачи из пробного ЕГЭ по математике — именно там данный прием встречается чаще всего. Заодно убедимся, что таким образом многие задачи B15 становятся почти устными.

Задача. Найдите наименьшее значение функции:

Под корнем стоит квадратичная функция График этой функции − парабола ветвями вверх, поскольку коэффициент

x ₀ = − b /(2 a ) = −6/(2 · 1) = −6/2 = −3

Поскольку ветви параболы направлены вверх, в точке функция принимает наименьшее значение.

Корень монотонно возрастает, значит точка минимума всей функции. Имеем:

Задача. Найдите наименьшее значение функции:

Под логарифмом снова квадратичная функция: График — парабола ветвями вверх,

x ₀ = − b /(2 a ) = −2/(2 · 1) = −2/2 = −1

Итак, в точке квадратичная функция принимает наименьшее значение. Но функция монотонная, поэтому:

y _min = y (−1) = log ₂ ((−1) 2 + 2 · (−1) + 9) = . = log ₂ 8 = 3

Задача. Найдите наибольшее значение функции:

В показателе стоит квадратичная функция Перепишем ее в нормальном виде:

Очевидно, что график этой функции — парабола, ветви вниз Поэтому вершина будет точкой максимума:

Исходная функция — показательная, она монотонна, поэтому наибольшее значение будет в найденной точке

Внимательный читатель наверняка заметит, что мы не выписывали область допустимых значений корня и логарифма. Но этого и не требовалось: внутри стоят функции, значения которых всегда положительны.

Следствия из области определения функции

Иногда для решения задачи B15 недостаточно просто найти вершину параболы. Искомое значение может лежать на конце отрезка, а вовсе не в точке экстремума. Если в задаче вообще не указан отрезок, смотрим на область допустимых значений исходной функции. А именно:

Аргумент логарифма должен быть положительным:

y = log _a f ( x ) ⇒ f ( x ) > 0

Арифметический квадратный корень существует только из неотрицательных чисел:

Знаменатель дроби не должен равняться нулю:

Обратите внимание еще раз: ноль вполне может быть под корнем, но в логарифме или знаменателе дроби — никогда. Посмотрим, как это работает на конкретных примерах:

Задача. Найдите наибольшее значение функции:

Под корнем снова квадратичная функция: Ее график — парабола, но ветви вниз, поскольку Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический квадратный корень из отрицательного числа не существует.

Выписываем область допустимых значений (ОДЗ):

3 − 2 x − x 2 ≥ 0 ⇒ x 2 + 2 x − 3 ≤ 0 ⇒

Теперь найдем вершину параболы:

Точка принадлежит отрезку ОДЗ — и это хорошо. Теперь считаем значение функции а также на концах ОДЗ:

Итак, получили числа 2 и 0. Нас просят найти наибольшее — это число 2.

Задача. Найдите наименьшее значение функции:

Внутри логарифма стоит квадратичная функция Это парабола ветвями вниз, но в логарифме не может быть отрицательных чисел, поэтому выписываем ОДЗ:

6 x − x 2 − 5 > 0 ⇒ x 2 − 6 x + 5 x ₀ = − b /(2 a ) = −6/(2 · (−1)) = −6/(−2) = 3

Вершина параболы подходит по ОДЗ: Но поскольку концы отрезка нас не интересуют, считаем значение функции только

y _min = y (3) = log _0,5 (6 · 3 − 3 2 − 5) =

[spoiler title=”источники:”]

http://ege-study.ru/zadanie-12-profilnogo-EGE-po-matematike

http://www.berdov.com/ege/extremum/other_way/

[/spoiler]

Пример 1:

Исследовать функцию на экстремум и вычислить значение функции в точках экстремума:

Решение от преподавателя:

Решение.

Пример 2:

Исследуйте на экстремум функцию.

y = х² – 10х + 5

Решение от преподавателя:

Пример 3:

Найти экстремумы функций двух переменных

z = 2x³ + 6xy² – 30x – 24y.

Решение от преподавателя:

Пример 4:

Исследовать на экстремум:

Решение от преподавателя:

Необходимое условие экстремума функции одной переменной. 

Уравнение f’₀(x*) = 0 – это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x_с, в которых функция не возрастает и не убывает. 

Достаточное условие экстремума функции одной переменной. 
Пусть f₀(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие: 
f’₀(x*) = 0 
f”₀(x*) > 0 
то точка x* является точкой локального (глобального) минимума функции. 
Если в точке x* выполняется условие: 
f’₀(x*) = 0 
f”₀(x*) < 0 
то точка x* – локальный (глобальный) максимум. 
Решение. 
Находим первую производную функции: 
y’ = 6x²+6x 
или 
y’ = 6x(x+1) 
Приравниваем ее к нулю: 
6x²+6x = 0 
x₁ = 0 
x₂ = -1 
Вычисляем значения функции 
f(0) = -11 
f(-1) = -10 
Ответ: 
f_min = -11, f_max = -10 
Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную: 
y” = 12x+6 
Вычисляем: 
y”(0) = 6>0 – значит точка x = 0 точка минимума функции. 
y”(-1) = -6<0 – значит точка x = -1 точка максимума функции. 

Пример 5:

Найти стационарные точки и исследовать на экстремум функцию

z = x² + y² – 2x – 2y+ 8

Решение от преподавателя:

Исследовать на экстремум функцию z = x² + y² – 2x – 2y+ 8

1. Найдем частные производные. 


2. Решим систему уравнений. 
2x-2 = 0 
2y-2 = 0 
Получим: x = 1, y = 1 
критическая  точка   M₁(1;1) 
3. Найдем частные производные второго порядка. 



4. Вычислим значение этих частных производных второго порядка в критических точках M(x₀;y₀). 
Вычисляем значения для точки M₁(1;1) 



AC – B² = 4 > 0 и A > 0 , то в точке M₁(1;1) имеется минимум z(1;1) = 6 
Вывод: В точке M₁(1;1) имеется минимум z(1;1) = 6;

Пример 6:

Исследовать на экстремум функцию:

Решение от преподавателя:

Пример 7:

Исследовать функцию z(x,y) на экстремум

Решение от преподавателя:

Пример 8:

Исследовать на экстремум функцию:

Решение от преподавателя:

Вычислим производную этой функции и найдем стационарные точки, в которых она обращается в нуль:

Решая это уравнение, находим корни x₁ = 1 и x₂ = 2. Они являются подозрительными на экстремум в данной задаче. При этом знаки производной нашей функции распределены следующим образом:

Согласно теореме о достаточном условии экстремума первого порядка, полученные точки являются точками локального экстремума, а именно: x₁ = 1 — точка локального максимума, причем f(x₁) = 11, а x₂ = 2 — точка локального минимума, причем f(x₂) = 10.

Глобальных экстремумов в этой задаче нет. Это видно из того, что

Итак, локальный максимум достигается в точке x = 1 и равен 11, локальный минимум достигается в точке x = 2, и равен 10.

Пример 9:

Исследуйте на экстремум функцию z = z(x;y).

Решение от преподавателя:

Пример 10:

Исследовать на экстремум:

y = (2*x-8)*(9*x+1) 

Решение от преподавателя:

Необходимое условие экстремума функции одной переменной. 

Уравнение f’₀(x*) = 0 – это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x_с, в которых функция не возрастает и не убывает. 
Достаточное условие экстремума функции одной переменной. 

Пусть f₀(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие: 
f’₀(x*) = 0 
f”₀(x*) > 0 
то точка x* является точкой локального (глобального) минимума функции. 
Если в точке x* выполняется условие: 
f’₀(x*) = 0 
f”₀(x*) < 0 
то точка x* – локальный (глобальный) максимум. 
Решение. 
Находим первую производную функции: 
y’ = 36x-70 
Приравниваем ее к нулю: 
36x-70 = 0 

Вычисляем значения функции 

Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную: 
y” = 36 
Вычисляем: 

значит эта точка – минимума функции.

Пример 11:

Найти экстремумы функции z(x,y) при данном условии:

Решение от преподавателя:

Пример 12:

Исследовать на экстремум функцию:

Решение от преподавателя:

Найдем производную f′ (x) = e^x − e^−x . Чтобы найти критические точки функции f(x), приравняем эту производную к нулю:

Очевидно, что точка x = 0 является решением последнего уравнения. Функция f′(x) строго возрастает (поскольку ). Поэтому она отрицательна при x < 0 и положительна при x > 0.

Следовательно, точка x = 0 является точкой строгого локального минимума функции f(x), и f(0) = 2 — соответствующее минимальное значение.

В данной ситуации можно также применить теорему о достаточном условии экстремума второго порядка. Поскольку f′′(0) = 2 > 0, функция f(x) имеет строгий локальный минимум в точке x = 0.

Кроме того, этот минимум глобальный, потому что

Ответ: точка x = 0 является точкой глобального минимума для исследуемой функции и f_min = f(0) = 2.

Пример 13:

Найти наибольшее и наименьшее значения функции z(x,y) в области D:

Решение от преподавателя:

Пример 14:

Исследовать на экстремум функцию:

y = x³+6*x²-4, [-4;1]. 

Решение от преподавателя:

Необходимое условие экстремума функции одной переменной. 

Уравнение f’₀(x*) = 0 – это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x_с, в которых функция не возрастает и не убывает. 
Достаточное условие экстремума функции одной переменной. 

Пусть f₀(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие: 
f’₀(x*) = 0 
f”₀(x*) > 0 
то точка x* является точкой локального (глобального) минимума функции. 
Если в точке x* выполняется условие: 
f’₀(x*) = 0 
f”₀(x*) < 0 
то точка x* – локальный (глобальный) максимум. 
Решение. 
Находим первую производную функции: 
y’ = 3x²+12x 
или 
y’ = 3x(x+4) 
Приравниваем ее к нулю: 
3x(x+4) = 0 
x₁ = 0 
x₂ = -4 
Вычисляем значения функции на концах отрезка 
f(0) = -4 
f(-4) = 28 
f(-4) = 28.0000000000000 
f(1) = 3.00000000000000 

Ответ: f_min = -4, f_max = 28.

Пример 15:

Исследовать на экстремум функцию

Решение от преподавателя:

Как обычно, начнем с нахождения производной исследуемой функции и точек, подозрительных на экстремум:

Легко видеть, что точка x = 0 является критической.

Найдем вторую производную:

Очевидно, f′′(0) = 0. Воспользуемся теоремой о достаточном условии экстремума n-го порядка и будем дифференцировать функцию до того момента, пока не появится отличная от нуля производная:

Значит, x = 0 — точка локального минимума функции f(x).

Из предыдущего примера следует, что при . В то же время . Поэтому f′′(x) > 0 при . Отсюда следует, что производная f′(x) обращается в нуль в единственной точке x = 0.

Так как ,  минимум в точке x = 0 является глобальным.

Ответ: есть один глобальный минимум f(0) = 4.

Пример 16:

С помощью второй производной исследуйте на экстремум функцию . Найдите наибольшее М и наименьшее m значения этой функции на отрезке [-1, 2].

Решение от преподавателя:

Определяем критические точки

Определяем вторую производную функции

Определяем знаки второй производной в критических точках

Т. к. вторая производная положительная, то в точке х=0 минимум

Т. к. вторая производная отрицательная, то в точке х=1 максимум

Наибольшее М и наименьшее m значения этой функции на отрезке [-1, 2]

Т. к. обе критические точки принадлежат указанному отрезку, то определяем значения функции в полученных точках и на концах отрезка

Т. о., М=у(-1)=6 m=у(2)=-3

Пример 17:

Исследовать на экстремум функцию:

Решение от преподавателя:

Подозрительные на экстремум точки найдем с помощью леммы Ферма. Так как

то единственная подозрительная на экстремум точка (в которой все частные производные обращаются в нуль) — это точка a = (3, −2, −1).

Определим, есть ли в этой точке экстремум. Для этого найдем все частные производные второго порядка

и составим из них матрицу полной второй производной f′′(a):

Главные миноры этой матрицы чередуют знаки:

По теореме (достаточное условие экстремума второго порядка) в точке a локальный максимум. Ответ: локальный максимум достигается в точке a = (3, −2, −1) и равен 14.

Ответ: локальный максимум достигается в точке a = (3, −2, −1) и равен 14.

Пример 18:

Найти экстремумы функции:

Решение от преподавателя:

Подозрительные на экстремум точки найдем с помощью леммы Ферма. Так как

то единственной стационарной точкой будет точка a = (0, 0).

Посмотрим, есть ли в ней экстремум. Для этого вычислим частные производные второго порядка

и составим из них матрицу второй производной в точке a:

Очевидно, ее определитель равен нулю. Значит, достаточные условия экстремума из теоремы (достаточное условие экстремума второго порядка) в данном случае не применимы.

Придется использовать определение экстремума. Рассмотрим разность . Она больше нуля при всех y > 0 и меньше нуля при y < 0. Поэтому в точке a = (0, 0) нет экстремума.

Ответ: у функции f нет экстремумов.

Пример 19:

Найти экстремумы функции

Решение от преподавателя:

Очевидно,

и единственная стационарная точка — это a = (0, 0).

Далее вычисляем частные производные второго порядка

и выписываем матрицу второй производной в точке a:

Ее определитель равен нулю. Достаточные условия экстремума опять не работают. С другой стороны, . Поэтому в точке (0, 0) глобальный минимум.

Ответ: есть один глобальный минимум f(0, 0) = 0.

Пример 20:

Исследовать на экстремумы функцию.

Решение от преподавателя:

Как найти экстремум

Экстремумы представляют собой максимальные и минимальные значения функции и относятся к ее важнейшим характеристикам. Экстремумы находятся в критических точках функций. Причем функция в экстремуме минимума и максимума меняет свое направление соответственно знаку. Согласно определению, первая производная от функции в точке экстремума равна нулю или отсутствует. Таким образом, поиск экстремумов функции складывается из двух задач: нахождения производной для заданной функции и определения корней ее уравнения.

Инструкция

Запишите заданную функцию f(x). Определите ее первую производную f’(x). Полученное выражение производной приравняйте к нулю.

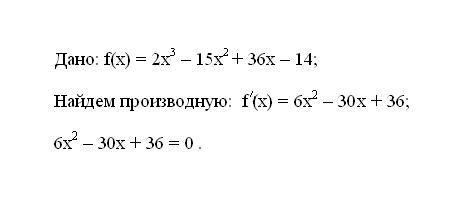
Решите полученное уравнение. Корни уравнения будут являться критическими точками функции.

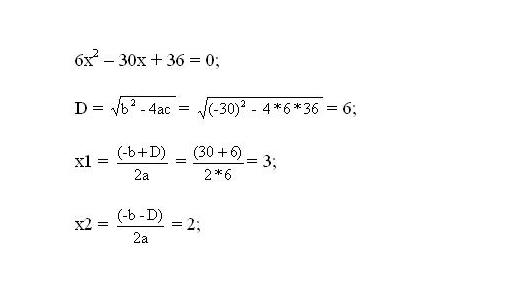
Определите, какими критическими точками – минимума или максимума – являются полученные корни. Для этого найдите вторую производную f’’(x) от исходной функции. Подставьте в нее по очереди значения критических точек и высчитайте выражение. Если вторая производная от функции в критической точке больше нуля, то это будет точка минимума. Иначе – точка максимума.

Посчитайте значение исходной функции в полученных точках минимума и максимума. Для этого подставьте их значения в выражение функции и вычислите. Полученное число будет определять экстремум функции. Причем, если критическая точка была максимумом, экстремум функции также будет максимумом. Также в минимальной критической точке функция будет достигать свой минимальный экстремум.

Видео по теме

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

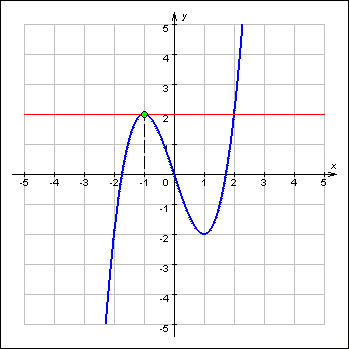
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).

         

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после – производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.

(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.

(- 9): функция возрастает, а потом убывает – максимум.

(-7): минимум.

(3): максимум.

Все вышесказанное можно обобщить следующими выводами:

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

1. Найдите производную функции (f'(x)). 
2. Найдите корни уравнения (f'(x)=0). 
3. Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
4. Определите знак производной в каждом промежутке (методом интервалов). 
5. Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью). 
6. Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
   – если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
   – если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
   – если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.

Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:

(15x^4-60x^2=0)      (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0)       (x^2-4=0)
               (x=±2)

3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является (-2).

Ответ. (-2).

Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов

Скачать статью

Найти экстремумы функции