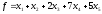Как найти экстремумы линейной функции

Как найти экстремумы линейной функции

Теорема
1.
Если ОДР ЗЛП – ограниченная, то оптимальное
решение ЗЛП существует и совпадает хотя
бы с одним из опорных решений системы
линейных уравнений (1) – ограничений.

Доказательство:

Т.к.
ОДР – ограниченная, то по второй теореме
Вейерштрасса непрерывная функция на
замкнутом и ограниченном интервале
принимает максимальное и минимальное
значение.

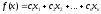
Пусть
х
– допустимое решение.

Доказать,
что Х
– опорное решение.

Пусть
х1,х2,…,xs
– угловые точки (опорные решения) ОДР,
тогда

(*)

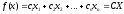
Поскольку
Х
– допустимое решение, то для любой точки
х

Т.к.
xk
– допустимое решение, то
(**)

Из
(*) и (**):

Теорема
2.
Если ОДР ЗЛП – ограниченная, а функция
не ограничена сверху (снизу), то задача
отыскания максимума f
(минимума f)
не имеет решений.

Min
f
(max
f)
существует и достигается по крайней
мере в одном из опорных решений.

Без
доказательства.

Теорема
3. Если
max
(min)
достигается в нескольких опорных
решениях х1,х2,…,хl,
то любая выпуклая линейная комбинация
оптимальн. опорн. реш. есть также
оптимальное решение.

Доказательство:

Рассмотрим
вектор Y,
который является линейной комбинацией
оптим. реш.

Теорема
доказана.

Теоремы
1,2,3 можно обобщить в основную теорему
линейного программирования.

Основная
теорема:
если ЗЛП имеет оптим. реш., то оно
совпадает, по крайней мере, с одним из
опорных решений системы ограничительных
уравнений.

Основная
теорема указывает схему, которая может
быть использована при решении ЗЛП.

Схема
решения ЗЛП.

  1. Найти
    все опорные решения.

  2. Подсчитать
    значения линейной функции на каждом
    опорном решении.

  3. Сравнивая
    найденные значения, установить опорн.
    реш.

Недостаток
схемы: нужно исследовать каждое опорное
решение.

Эта
схема предполагает беспорядочный
перебор опорных решений.

Симплексный
метод предполагает упорядоченный
перебор опорных решений так, что на
каждом следующем опорном решении
значение функции ближе к оптимальному
решению, чем предыдущее (идея
последовательного улучшения решения).

Три
элемента симплексного метода:

  1. Нахождение
    исходного опорного решения.

  2. Правило
    перехода к следующему, лучшему опорному
    решению.

  3. Критерий,
    который позволяет установить оптимальность
    опорного решения или необходимость
    его дальнейшего улучшения, или отсутствия
    решения.

Симплексный
метод.

Пример.

Найти
max
функции при усл.

Умножим
соответствующие уравнения системы (1)
на соответствующие числа (коэф.) и сложим
с равенством (4).

–
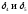числа, оценки свободных переменных

  1. х4=х5=0
    f(Хоп)=

  1. –
    приведённое выражение для линейной
    функции.

Т.к.
для опорн. реш. значения всех свободных
переменных равны нулю, то, положив в
равенстве (5) значения свободных переменных
равными нулю, мы сразу находим значение
линейной функции на данном опорном
решении.

Определение.
Говорят, что ЗЛП приведена к симплексной
форме, если сис. ограничительных уравнений
разрешена относительно базисных
неизвестных, свободные члены уравнений
«≥0», а линейная функция выражена через
свободные неизвестные. ← Отыскав исходн.
опорн. реш., и получив приведённое
выражение лин. функции, мы привели ЗЛП
к симплексной форме.

Перепишем
сист. лин. уравнений (2) в виде таблицы,
добавив к ней в качестве последней
строки строчку с коэффициентами значения
(5), считая что уравнение разрешено
относительно базисной переменной f.

ci

Баз.
неиз.

0

1

1

-2

7

5

bi

x1

x2

x3

x4

x5

1

1

2

x1

x2

x3

6

16

3

1

0

0

0

1

0

0

0

1

-1

2

1

2

3

-1

f

28

-4

-2

Теорема.

Пусть
ЗЛП записана в симплексной форме, тогда:

10.
и в каждом столбце с такой оценкой имеем
хотя бы один положительный элемент,
тогда решение можно улучшить, т.е. перейти
к опорному решениюХ1,
в котором значение линейной функции
будет больше

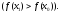
20.
Существует отрицательная оценка
свободных переменных такая, что столбец
которой не содержит положительных
элементов, то ЗЛП
не имеет решения ввиду неограниченности
целевой функции в ОДР.

30.
Все оценки свободных переменных «≥0».
В этом случае соответствующее опорное
решение будет оптимальным.

Все

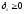
Доказательство:

П.1.
Найдём в симплексной таблице элемент
из следующих условий:

1)
s-й
столбец:

2)
k-я
строка:

С
разрешающим элементом aks
выполним преобразование однократного
замещения.

xs→базисн.,
xk-своб.неизв.

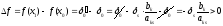
П.2.
Пусть ЗЛП приведена к симплексной форме,
и система ограничительных уравнений
разрешена относительно базисн. неизв.,
и все свободные члены неотрицательны.

Построим
какое-либо неотрицательное решение Х
системы
.

Возьмём
для своб. перем. следующие неотрицательные
значения.

Из
системы
найдём значения базисн. неизв.

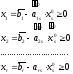
Получим
неотриц. реш. системы
.
Теперь, используя приведённое выражение
для линейной функции, мы получим значение
линейной функции на построенном решении.

Из
этого равенства видно, что если переменной
xs
придать сколь угодно большие значения,
то значение лин. функции можно сделать
сколь угодно большим положительным
числом, т.о. линейная функция не ограничена
сверху в ОДР.

П.3.
Все оценки

Пусть
Х0
– соответствующее опорное решение.
Требуется доказать, что для любого
другого опорного решения Х1

Признак
существования множества оптимальный
решений.

Если
все оценки свободн. перем.
,
то введение любой переменной в базис
приведёт к уменьшению функцииf,
т.к.
и, следовательно, существуеттолько
одно
оптимальное решение.

Если
же какая-то оценка свободной переменной
окажется равной нулю
,
то введение переменнойхs
в базис не изменит значение линейной
функции f,
т.к.
будет «=0», и поэтому можно перейти к
новому опорному решению, для которого,
т.о. признаком существования множества
решений является наличие хотя бы одной
нулевой оценки свободных переменных
при неотрицательности всех остальных
оценок.

Если
нулевых оценок окажется несколько, то
введением в базис кажд. из соотв. своб.
перем. можно найти несколько оптимальных
решений.

Транспортная
задача

Соседние файлы в папке шпоры

  • #
  • #

    03.10.2013265.79 Кб3417.jpg

  • #
  • #
  • #
Источник

Содержание:

Экстремум функции

Функция y=f(x) называется возрастающей (убывающей) в некотором интервале, если при 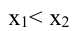Экстремум функции - определение и вычисление с примерами решения

Если дифференцируемая функция у = f(x) на отрезке 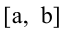Экстремум функции - определение и вычисление с примерами решения возрастает (убывает), то ее производная на этом отрезке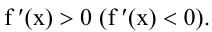 Экстремум функции - определение и вычисление с примерами решения

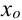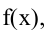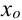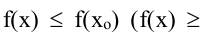
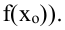
Точка Экстремум функции - определение и вычисление с примерами решения называется точкой локального максимума (минимума) функции Экстремум функции - определение и вычисление с примерами решения если существует окрестность точки Экстремум функции - определение и вычисление с примерами решения для всех точек которой верно неравенство Экстремум функции - определение и вычисление с примерами решенияЭкстремум функции - определение и вычисление с примерами решения

Точки максимума и минимума называются точками экстремума, а значения функции в этих точках – ее экстремумами.

Необходимые условия экстремума. Если точка хо является точкой экстремума функции 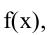Экстремум функции - определение и вычисление с примерами решения то либо 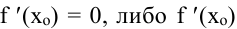Экстремум функции - определение и вычисление с примерами решения не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек. Первое достаточное условие. Пусть 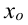Экстремум функции - определение и вычисление с примерами решения – критическая точка. Если f'(х) при переходе через точку Экстремум функции - определение и вычисление с примерами решения меняет знак плюс на минус, то в точке Экстремум функции - определение и вычисление с примерами решения функция имеет максимум, в противном случае – минимум. Если при переходе через критическую точку производная не меняет знак, то в точке хо экстремума нет.

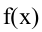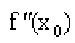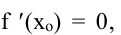
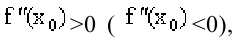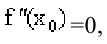Второе достаточное условие. Пусть функция Экстремум функции - определение и вычисление с примерами решения имеет производную f'(х) в окрестности точки Экстремум функции - определение и вычисление с примерами решения и вторую производную Экстремум функции - определение и вычисление с примерами решения в самой точке Экстремум функции - определение и вычисление с примерами решения. Если Экстремум функции - определение и вычисление с примерами решенияЭкстремум функции - определение и вычисление с примерами решения то точка Экстремум функции - определение и вычисление с примерами решения является точкой локального минимума (максимума) функции f(x). Если же Экстремум функции - определение и вычисление с примерами решения то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

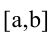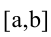На отрезке Экстремум функции - определение и вычисление с примерами решения функция у = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка Экстремум функции - определение и вычисление с примерами решения.

Пример:

Найти экстремумы функции 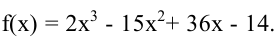Экстремум функции - определение и вычисление с примерами решения

Решение:

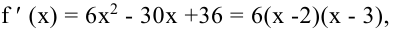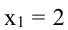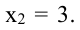Так как Экстремум функции - определение и вычисление с примерами решения то критические точки функции Экстремум функции - определение и вычисление с примерами решения и Экстремум функции - определение и вычисление с примерами решения Экстремумы могут быть только в этих точках. Так как при переходе через точку 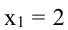Экстремум функции - определение и вычисление с примерами решения производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку 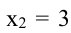Экстремум функции - определение и вычисление с примерами решения производная меняет знак минус на плюс, поэтому в точке 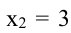Экстремум функции - определение и вычисление с примерами решения у функции минимум. 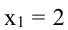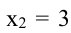Вычислив значения функции в точках Экстремум функции - определение и вычисление с примерами решения и Экстремум функции - определение и вычисление с примерами решения найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) =13.

Пример:

Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, а четвертой стороной примыкала к стене. Для этого имеется а погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?

Решение:

Обозначим стороны площадки через 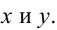Экстремум функции - определение и вычисление с примерами решения Площадь площадки равна 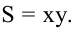Экстремум функции - определение и вычисление с примерами решения Пусть у – это длина стороны, примыкающей к стене. Тогда по условию должно выполняться равенство 2х + у = а. Поэтому 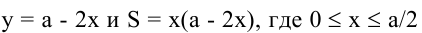Экстремум функции - определение и вычисление с примерами решения (длина и ширина площадки не могут быть отрицательными). 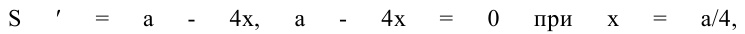Экстремум функции - определение и вычисление с примерами решения откуда 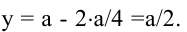Экстремум функции - определение и вычисление с примерами решения Поскольку 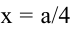Экстремум функции - определение и вычисление с примерами решения– единственная критическая точка, проверим, меняется ли знак производной при переходе через эту точку. При 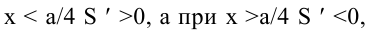Экстремум функции - определение и вычисление с примерами решения значит, в точке 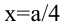Экстремум функции - определение и вычисление с примерами решения функция S имеет максимум. Значение функции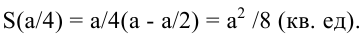 Экстремум функции - определение и вычисление с примерами решения

Поскольку S непрерывна на 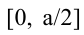Экстремум функции - определение и вычисление с примерами решения и ее значения на концах 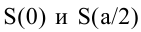Экстремум функции - определение и вычисление с примерами решения равны нулю, то найденное значение будет наибольшим значением функции.

Таким образом, наиболее выгодным соотношением сторон площадки при данных условиях задачи является у = 2х.

Пример:

Требуется изготовить закрытый цилиндрический бак вместимостью 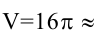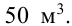Экстремум функции - определение и вычисление с примерами решения Экстремум функции - определение и вычисление с примерами решения Каковы должны быть размеры бака (радиус R и высота Н), чтобы на его изготовление пошло наименьшее количество материала?

Решение:

Площадь полной поверхности цилиндра равна 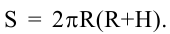Экстремум функции - определение и вычисление с примерами решения Мы знаем объем цилиндра 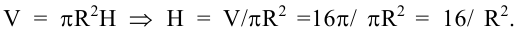Экстремум функции - определение и вычисление с примерами решения Значит, 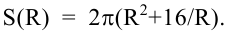Экстремум функции - определение и вычисление с примерами решения Находим производную этой функции: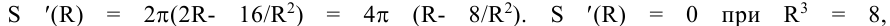Экстремум функции - определение и вычисление с примерами решенияследовательно,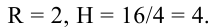 Экстремум функции - определение и вычисление с примерами решения

Экстремумы функции

Введём несколько новых понятий. Окрестностью точки 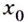Экстремум функции - определение и вычисление с примерами решения называется любой промежуток, для которого 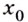Экстремум функции - определение и вычисление с примерами решения является внутренней точкой.

Точка 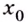Экстремум функции - определение и вычисление с примерами решения называется точкой минимума (максимума) функции 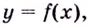Экстремум функции - определение и вычисление с примерами решения если для всех 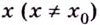Экстремум функции - определение и вычисление с примерами решения из некоторой окрестности точки 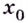Экстремум функции - определение и вычисление с примерами решения выполняется неравенство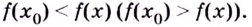 Экстремум функции - определение и вычисление с примерами решения

Точки минимума и максимума обозначают 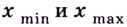Экстремум функции - определение и вычисление с примерами решения соответственно.

Значение функции в точке минимума называется минимумом функции, а в точке максимума — максимумом функции. Обозначают их: 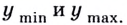Экстремум функции - определение и вычисление с примерами решения

Точки минимума и максимума функции называют точками экстремума (лат. extremum — край, конец). Значения функции в точках её экстремума — её экстремальные значения, или экстремумы.

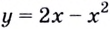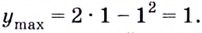
Например, для функции Экстремум функции - определение и вычисление с примерами решения точка Экстремум функции - определение и вычисление с примерами решения является точкой максимума (рис. 77). Её максимум: Экстремум функции - определение и вычисление с примерами решения

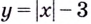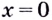Для функции Экстремум функции - определение и вычисление с примерами решения точка Экстремум функции - определение и вычисление с примерами решения является точкой минимума (рис. 78). Её минимум: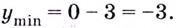 Экстремум функции - определение и вычисление с примерами решения

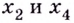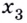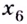Функция, график которой изображён на рисунке 75, имеет четыре экстремальные точки: Экстремум функции - определение и вычисление с примерами решения — точки максимума; Экстремум функции - определение и вычисление с примерами решения и Экстремум функции - определение и вычисление с примерами решения — точки минимума.

Точка экстремума функции не может принадлежать промежутку, на котором эта функция возрастает или убывает (почему?). Следовательно, те точки, в которых производная функции положительная или отрицательная, не могут быть точками её экстремума. Все остальные точки области определения функции являются её критическими точками. Поэтому точками экстремума функции могут быть только её критические точки. Это — необходимое условие существования экстремума.

Выбрать из критических точек функции точки экстремума позволяет достаточное условие существования экстремума.

Экстремум функции - определение и вычисление с примерами решения

Экстремум функции - определение и вычисление с примерами решения

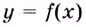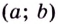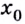Пусть функция Экстремум функции - определение и вычисление с примерами решения непрерывна на промежутке Экстремум функции - определение и вычисление с примерами решения и Экстремум функции - определение и вычисление с примерами решения — её критическая точка, 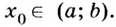Экстремум функции - определение и вычисление с примерами решения Тогда: точка 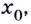Экстремум функции - определение и вычисление с примерами решения при переходе через которую в направлении роста аргумента производная меняет знак с «плюса» на «минус», является точкой максимума, а точка, при переходе через которую производная меняет знак с «минуса» на «плюс» — точкой минимума.

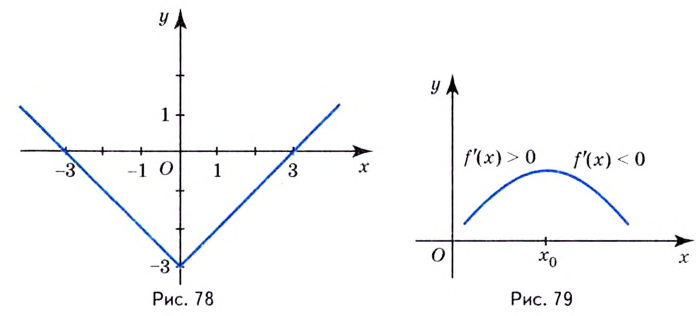
Действительно, если производная функции 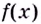Экстремум функции - определение и вычисление с примерами решения отрицательная, то при переходе через точку 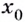Экстремум функции - определение и вычисление с примерами решения возрастание функции изменяется на убывание (рис. 79). В этом случае 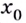Экстремум функции - определение и вычисление с примерами решения — точка максимума. Если же при переходе через точку 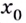Экстремум функции - определение и вычисление с примерами решения убывание функции изменяется на возрастание, то 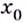Экстремум функции - определение и вычисление с примерами решения — точка минимума (рис. 80).

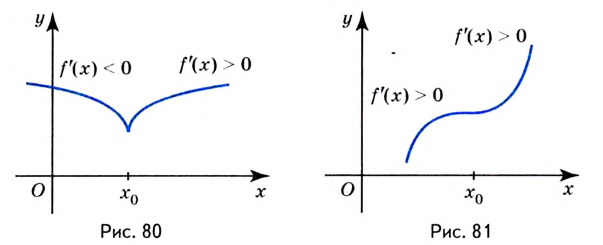
Если же производная функции в точке 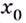Экстремум функции - определение и вычисление с примерами решения равна нулю, а слева и справа от 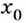Экстремум функции - определение и вычисление с примерами решения производная функции положительная (рис.81) или слева и справа отрицательная, то 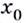Экстремум функции - определение и вычисление с примерами решения не является точкой экстремума.

  • Заказать решение задач по высшей математике

Пример №552

Найдите точки экстремума и экстремальные значения функции 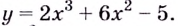Экстремум функции - определение и вычисление с примерами решения

Решение:

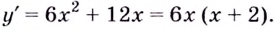
 Экстремум функции - определение и вычисление с примерами решения

Критические точки функции: 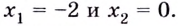Экстремум функции - определение и вычисление с примерами решения При переходе через точку 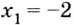Экстремум функции - определение и вычисление с примерами решения производная меняет знаке 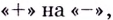Экстремум функции - определение и вычисление с примерами решения поэтому 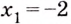Экстремум функции - определение и вычисление с примерами решения —точка максимума. При переходе через точку 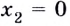Экстремум функции - определение и вычисление с примерами решения производная меняет знак с 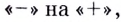Экстремум функции - определение и вычисление с примерами решения поэтому 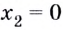Экстремум функции - определение и вычисление с примерами решения — точка минимума (рис. 82).

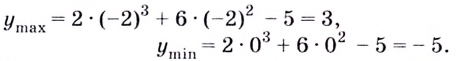
Экстремум функции - определение и вычисление с примерами решения

Ответ. 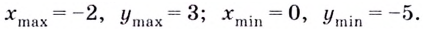Экстремум функции - определение и вычисление с примерами решения

Нахождение экстремумов функции можно оформлять в виде таблицы, как на с. 176. Особенно это удобно при общем исследовании функции, когда находят не только её экстремумы, но и другие свойства, строят её график.

Чтобы исследовать функцию, можно пользоваться следующей схемой:

  1. найти область определения функции;
  2. исследовать функцию на чётность, нечётность, периодичность;
  3. найти точки пересечения графика функции с осями координат;
  4. исследовать функцию на монотонность, то есть найти промежутки возрастания и убывания функции;
  5. найти точки экстремума и экстремальные значения функции;
  6. найти асимптоты графика функции;
  7. построить график функции.

Пример №553

Исследуйте функцию 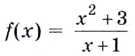Экстремум функции - определение и вычисление с примерами решения и постройте её график.

Решение:

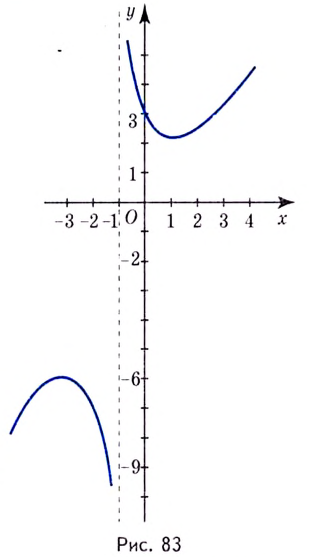
Область определения функции — все действительные числа, кроме 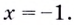Экстремум функции - определение и вычисление с примерами решения Поскольку она не симметрична относительно нуля, то функция не может быть чётной или нечётной. Функция непериодическая.

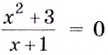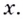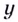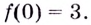
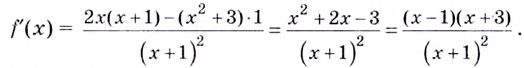
Уравнение Экстремум функции - определение и вычисление с примерами решения не имеет решений, поэтому график функции не пересекает ось Экстремум функции - определение и вычисление с примерами решения Ось Экстремум функции - определение и вычисление с примерами решения он пересекает в точке с ординатой Экстремум функции - определение и вычисление с примерами решения

Экстремум функции - определение и вычисление с примерами решения

Критические точки: 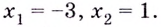Экстремум функции - определение и вычисление с примерами решения

Составим и заполним таблицу.
Экстремум функции - определение и вычисление с примерами решения

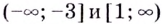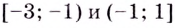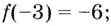
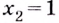На промежутках Экстремум функции - определение и вычисление с примерами решения функция возрастает, на промежутках  Экстремум функции - определение и вычисление с примерами решения функция убывает. Экстремум функции - определение и вычисление с примерами решения — точка максимума,  Экстремум функции - определение и вычисление с примерами решения Экстремум функции - определение и вычисление с примерами решения —точка минимума,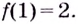 Экстремум функции - определение и вычисление с примерами решения 

Область значений функции: 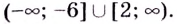Экстремум функции - определение и вычисление с примерами решения

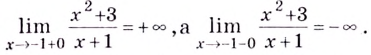
График функции имеет вертикальную асимптоту Экстремум функции - определение и вычисление с примерами решения так как Экстремум функции - определение и вычисление с примерами решения

График этой функции изображён на рисунке 83.

Экстремум функции - определение и вычисление с примерами решения

Пример №554

Может ли нечётная функция иметь экстремум в точке 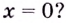Экстремум функции - определение и вычисление с примерами решения А чётная функция?

Решение:

Нечётная функция не может. Если в окрестности точки 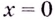Экстремум функции - определение и вычисление с примерами решения функция имеет экстремум, то с одной стороны от нуля она возрастает, а с другой — убывает, или наоборот. А нечётная функция — или только возрастает, или только убывает в окрестности точки Экстремум функции - определение и вычисление с примерами решения Чётная функция может. Например, функция 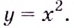Экстремум функции - определение и вычисление с примерами решения

Пример №555

Существуют ли такие числа 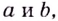Экстремум функции - определение и вычисление с примерами решения при которых имеет экстремум функция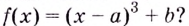 Экстремум функции - определение и вычисление с примерами решения

Решение:

При любых действительных значениях 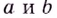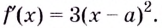Экстремум функции - определение и вычисление с примерами решенияЭкстремум функции - определение и вычисление с примерами решения В каждой точке 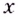Экстремум функции - определение и вычисление с примерами решенияпроизводная данной функции неотрицательная. Функция 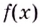Экстремум функции - определение и вычисление с примерами решениявозрастает на 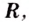Экстремум функции - определение и вычисление с примерами решения поэтому не может иметь экстремумов.

Ответ. Не существуют.

Пример №556

Исследуйте функцию 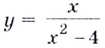Экстремум функции - определение и вычисление с примерами решения и постройте её график.

Решение. 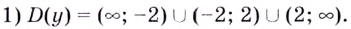Экстремум функции - определение и вычисление с примерами решения

2) Функция — нечётная, поскольку 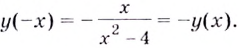Экстремум функции - определение и вычисление с примерами решения

Следовательно, её график симметричен относительно начала координат и достаточно исследовать функцию на промежутке 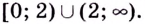Экстремум функции - определение и вычисление с примерами решения

3) если 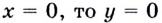Экстремум функции - определение и вычисление с примерами решения — график пересекает оси координат только в точке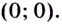 Экстремум функции - определение и вычисление с примерами решения

4) Найдём производную функции:

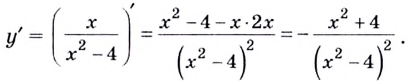
Экстремум функции - определение и вычисление с примерами решения

Очевидно, что 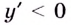Экстремум функции - определение и вычисление с примерами решения для всех х из области определения. Следовательно, функция убывает на каждом из промежутков 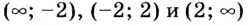Экстремум функции - определение и вычисление с примерами решения и не имеет максимумов и минимумов.

Для более точного построения вычислим значение функции в нескольких точках:

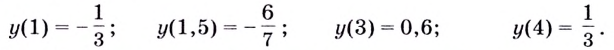
Экстремум функции - определение и вычисление с примерами решения

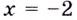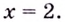График функции имеет вертикальные асимптоты Экстремум функции - определение и вычисление с примерами решения и Экстремум функции - определение и вычисление с примерами решения (Убедитесь самостоятельно.)

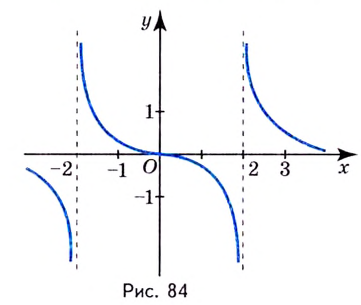
График функции изображён на рисунке 84.

Экстремум функции - определение и вычисление с примерами решения

  • Методы решения систем линейных алгебраических уравнений (СЛАУ)
  • Скалярное произведение и его свойства
  • Векторное и смешанное произведения векторов
  • Преобразования декартовой системы координат
  • Определитель матрицы
  • Критерий совместности Кронекера-Капелли
  • Формулы Крамера
  • Матричный метод
Источник

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

на графике функции отмечены локальные минимумы и максимумы

Минимумы и максимумы вместе именуют экстремумами функции.

Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

найдите количество точек экстремумов функции

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).

на графике функции отмечены локальные минимумы и максимумы         график производной и отмеченные на ней точки минимумов и максимумов функции

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

– Производная положительна там, где функция возрастает.
– Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

найдите количество точек экстремумов функции

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

по графику производной определить минимумы и максимумы функции

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после – производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.

(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.

(- 9): функция возрастает, а потом убывает – максимум.

(-7): минимум.

(3): максимум.

Все вышесказанное можно обобщить следующими выводами:

– Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
– Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

  1. Найдите производную функции (f'(x)). 
  2. Найдите корни уравнения (f'(x)=0). 
  3. Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
  4. Определите знак производной в каждом промежутке (методом интервалов). 
  5. Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью). 
  6. Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
    – если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
    – если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
    – если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

нахождение минимума и максимума

Всё! Точки максимумов и минимумов найдены.

Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

схематичное изображение функции

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:

(15x^4-60x^2=0)      (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0)       (x^2-4=0)
               (x=±2)

3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

поиск минимумов и максимумов

Теперь очевидно, что точкой максимума является (-2).

Ответ. (-2).

Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов

Скачать статью

Источник

Как найти точки минимума и максимума функции

Содержание:

  • Минимум и максимум функции

    • Точка минимума, минимум функции
    • Точка максимума, максимум функции
  • Исследование функций на экстремумы
  • Примеры задач

Минимум и максимум функции

Минимумом и максимумом функции, другими словами экстремумами, называют точки, в которых функция меняет характер монотонности (с возрастания на убывание и наоборот). Важно понимать, что экстремумы это не максимальные и минимальные значения функции. Обозначаются следующим образом: 

  • (y_{min}, y_{max}) — минимум, максимум функции или экстремумы;
  • (x_{min}, x_{max}) — точки минимума, максимума функции;
  • (y_{наиб}, y_{наим}) — наибольшее (максимальное), наименьшее (минимальное) значение функции.

Точка минимума, минимум функции

Точка минимума — такая точка (x_0), если у неё существует окрестность, для всех точек которой выполняется неравенство (f(x)geq f(x_0))

Минимум функции — значение функции в точке минимума (x_0)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Простыми словами, точка минимума — это та, где убывание функции меняется на возрастание.

Точка максимума, максимум функции

Точка максимума — такая точка (x_0), если у неё существует окрестность, для всех точек которой выполняется неравенство (f(x)leq f(x_0))

Максимум функции — значение функции в точке максимума (x_0)

Простыми словами, точка максимума — это та, где возрастание функции меняется на убывание.

Точки максимума и минимума на графике:

Точка экстремума

Источник: school-collection.edu.ru

Исследование функций на экстремумы

Теорема. Если функция f(x) имеет экстремум в точке (x=x_0,) то в ней производная либо равна 0, либо не существует.

Алгоритм нахождения экстремумов с помощью производной:

  1. Найти область определения функции — D(y).

  2. Определить производную — f ‘(x).

  3. Определить стационарные точки y = f(x), т.е. те, которые принадлежат D(y), f ‘(x) в них обращается в ноль, отыскать критические точки, в которых производной не существует (пример: (f^,(x)=frac1{2sqrt x}), производной не существует при x = 0).

  4. Исследовать характер изменения функции f (x) и знак f ‘(x) в промежутках, на которые найденные критические точки делят область определения (при отрицательном знаке производной функция убывает, при положительном — возрастает).

  5. Относительно каждой критической точки определить, является ли она точкой максимума, минимума  (возрастание меняется на убывание — точка максимума, убывание на возрастание — минимума) или не является точкой экстремума (то есть, меняется ли знак производной при переходе через исследуемую точку).

  6. Вычислить значения функции в точках экстремума.

Примеры задач

Задача 1

Исследовать на экстремумы функцию (f(x)=x^3-3x^2.)

Решение задачи по алгоритму:

1) (D(y): xin(-infty;+infty)), т.е. x — любое число.

2) Производная: (f'(x)=3x^2-6x) .

3) Из пункта 1 следует, что критических точек нет. Найдем стационарные:

Приравниваем f ‘(x) к 0, решаем квадратное уравнение (3x^2-6x=0), получаем (x_1=0),(;x_2=2.)

4) Отметим на горизонтальной оси координат точки 0 и 2. Подставим любое x из интервала ((-infty;0)) в f'(x), например, пусть x = -1, тогда (f'(x)=3{(-1)}^2-6(-1)=3+6=9). Получаем f ‘(x)>0, значит на исследуемом интервале f(x) возрастает. Аналогично рассмотрим оставшиеся интервалы. Итого, на отрезке (0;2) производная отрицательна, функция убывает, а на интервале ((2;+infty)) производная положительна, возрастает. Из этого следует, что x=0 – точка максимума, а x=2 – минимума.

5) Найдем значение экстремумов функции.

(f(0)=0-3times0=0)

(f(2)=2^3-3times2^2=8-12=-4)

Ответ: (x_{min}=2,;y_{min}=-4;;x_{max}=0,;y_{max}=0) или (0;0) – минимум функции, (2;-4) – максимум.

Задача 2

Найти промежутки монотонности функции (f(x)=frac x{x^2-4}).

1) (D(y): xinmathbb{R},;)кроме(;pm2)

2) (f'(x)=frac{1(x^2-4)-xtimes2x}{{(x^2-4)}^2}=-frac{x^2+4}{{(x^2-4)}^2})

3) Итак, как выяснилось в пункте 1, критические точки 2 и -2. Если мы приравняем f ‘(x) к 0, чтобы найти стационарные точки, то увидим, что уравнение не будет иметь корней. Значит, стационарных точек нет. Из этого следует, что функция монотонна на всей области определения. Проверим, возрастает она или убывает. Для этого решаем неравенство (-frac{x^2+4}{{(x^2-4)}^2}leq0) и получим, что неравенство верно при любом x, значит функция убывает.

Не забываем, что в ответе, указывая промежуток, обязательно нужно исключить критические точки -2 и 2 т.к. в них функция не определена.

Ответ: f(x) убывает на промежутке ((-infty;-2)cup(-2;2)cup(2;+infty)).

Задача 3

Докажите, что функция (f(x)=x^5+2x^3-4) возрастает на всех числовой прямой.

1) (D(y): xinmathbb{R}), значит критических точек нет.

2) (f'(x)=5x^4+6x)

3) Приравняем f'(x) к 0 и найдем корень: x = 0. Отметим 0 на числовой прямой и определим знак производной на промежутках ((-infty;0)) и ((0;+infty)). Получим, что производная положительна на обоих промежутках, следовательно функция возрастает на всей числовой прямой.

Утверждение доказано

Источник

Экстремумы функции

С помощью данного сервиса можно найти наибольшее и наименьшее значение функции одной переменной f(x) с оформлением решения в Word. Если же задана функция f(x,y), следовательно, необходимо найти экстремум функции двух переменных. Также можно найти интервалы возрастания и убывания функции.

  • Решение онлайн
  • Видеоинструкция
  • Оформление Word
  • Также решают

Необходимое условие экстремума функции одной переменной

Уравнение f’0(x*) = 0 – это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки xс, в которых функция не возрастает и не убывает.

Достаточное условие экстремума функции одной переменной

Пусть f0(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие:

f’0(x*) = 0

f”0(x*) > 0

то точка x* является точкой локального (глобального) минимума функции.

Если в точке x* выполняется условие:

f’0(x*) = 0

f”0(x*) < 0

то точка x* – локальный (глобальный) максимум.

Пример №1. Найти наибольшее и наименьшее значения функции:
Наибольшее и наименьшее значения функции. Пример на отрезке [1; 3].

Решение.



Критическая точка одна x1 = 2 (f’(x)=0). Эта точка принадлежит отрезку [1;3]. (Точка x=0 не является критической, так как 0∉[1;3]).

Вычисляем значения функции на концах отрезка и в критической точке.

f(1)=9, f(2)=5/2, f(3)=3 8/81

Ответ: fmin=5/2 при x=2; fmax=9 при x=1

Пример №2. С помощью производных высших порядков найти экстремум функции y=x-2sin(x).

Решение.

Находим производную функции: y’=1-2cos(x). Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=±π/3+2πk, k∈Z. Находим y’’=2sin(x), вычисляем Наибольшее и наименьшее значения функции. Пример, значит x=π/3+2πk, k∈Z – точки минимума функции; Наибольшее и наименьшее значения функции. Пример, значит x=-π/3+2πk, k∈Z – точки максимума функции.

Пример №3. Исследовать на экстремум фцнкцию в окрестностях точки x=0.

Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0, то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).

Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x0 или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.

Пример №4. Разбить число 49 на два слагаемых, произведение которых будет наибольшим.

Решение. Обозначим x – первое слагаемое. Тогда (49-x) – второе слагаемое.

Произведение будет максимальным: x·(49-x) → max

или

49x – x2

Наибольший объем цилиндра

Найти размеры цилиндра наибольшего объема, изготовленного из заготовки в форме шара радиуса R.

Решение:



Объем цилиндра равен: V = πr2H

где H = 2h,

Подставим эти значения в целевую функцию.



V → max

Найдем экстремум функции. Поскольку функция объема V(h) зависит только от одной переменной, то найдем производную с помощью сервиса Производная онлайн и приравняем ее к нулю.

dV/dh = 2πR2 – 6πh2

dV/dh = 0

2πR2 – 6πh2 = 0 или R2 = 3h2

Откуда





При высоте и радиусе основания размеры цилиндра будут наибольшими.

Источник

Добавить комментарий