Как найти экстремумы поверхности - Сайт, где вы сможете решить свои вопросы

Применение поверхностей первого и второго порядков
в задачах на экстремум функций

Общая постановка задачи поиска экстремума функций приведена здесь. Рассмотрим задачу поиска безусловного экстремума функций двух переменных.

Аналитический метод поиска локального безусловного экстремума

Пусть задана дважды непрерывно дифференцируемая функция f(x)=f(x_1,x_2) двух переменных.

Точка $x^{ast}$ называется точкой локального минимума, если существует такая окрестность этой точки, для всех точек которой выполняется условие

$f(x^{ast})leqslant f(x).$

Если знак неравенства заменить на знак , то получится определение локального максимума. Точки локального минимума или максимума называются точками локального экстремума функции.

Требуется найти точки локального экстремума функции f(x) .

Порядок решения поставленной задачи содержит два этапа.

На первом этапе при помощи необходимых условий экстремума первого порядка:

$left.frac{partial f(x)}{partial x_1}right|_{x=x^{ast}}=0,quad left.frac{partial f(x)}{partial x_2}right|_{x=x^{ast}}=0,$

(4.74)

находятся стационарные точки $x^{ast}$ , “подозрительные” на наличие локального экстремума (частные производные первого порядка в точке $x^{ast}$ равны нулю).

На втором этапе проверяются достаточные условия экстремума, а если они не выполняются, то и необходимые условия второго порядка. Они следуют из формулы Тейлора для приращения функции в точке $x^{ast}$ (учитывая члены до второго порядка включительно):

$Delta f=f(x_1^{ast}+Delta x_1,,x_2^{ast}+Delta x_2)-f(x_1^{ast},x_2^{ast})= frac{1}{2}Bigl[a_{11}cdotDelta x_1^2+2cdot a_{12}cdotDelta x_1Delta x_2+a_{22}cdotDelta x_2^2Bigr],$

где

$a_{11}=left.frac{partial^2f(x)}{partial x_1^2}right|_{x=x^{ast}},quad a_{12}=left.frac{partial^2f(x)}{partial x_1partial x_2}right|_{x=x^{ast}},quad a_{22}=left.frac{partial^2f(x)}{partial x_2^2}right|_{x=x^{ast}},$

а члены с производными первого порядка отсутствуют, так как точка $x^{ast}$ удовлетворяет (4.74).

Равенство

$Delta f=frac{1}{2}Bigl[a_{11}cdotDelta x_1^2+2cdot a_{12}cdotDelta x_1Delta x_2+a_{22}cdotDelta x_2^2Bigr]$

(4.75)

можно рассматривать как уравнение поверхности второго порядка относительно неизвестных Delta x_1, Delta x_2, Delta f . Уравнение (4.75) можно записать в матричной форме

$Delta f=frac{1}{2}begin{pmatrix}Delta x_1&Delta x_2end{pmatrix}cdot H(x^{ast})cdot begin{pmatrix}Delta x_1\Delta x_2end{pmatrix},$

(4.76)

где $H(x^{ast})$ — матрица квадратичной формы, называемая матрицей Гессе.

Она составлена из частных производных второго порядка, вычисленных в стационарной точке $x^{ast}:$

$H(x^{ast})= begin{pmatrix}a_{11}&a_{12}\a_{12}&a_{22}end{pmatrix}= left.{begin{pmatrix}dfrac{partial^2f(x)}{partial x_1^2}&dfrac{partial^2f(x)}{partial x_1partial x_2}\ dfrac{partial^2f(x)}{partial x_1partial x_2}& dfrac{partial^2f(x)}{partial x_1^2}end{pmatrix}}right|_{Large{x=x^{ast}}}$

Как показано в разд.4.4.1, при помощи поворота системы координат вокруг оси Delta f можно квадратичную форму в правой части (4.76) привести к каноническому виду

$Delta f=frac{1}{2}Bigl[lambda_1cdot(Delta x'_1)^2+lambda_2cdot(Delta x'_2)^2Bigr],$

(4.77)

где lambda_1,,lambda_2 — собственные значения матрицы Гессе $H(x^{ast})$ .

В зависимости от знаков собственных значений возможны следующие случаи:

1) если собственные значения одного знака, то поверхность (4.77) представляет собой эллиптический параболоид: выпуклый при lambda_1>0, lambda_2>0 (рис.4.58,а), или вогнутый при lambda_1<0, lambda_2<0 (рис.4.58,б);

2) если собственные значения имеют разные знаки, то поверхность (4.77) представляет собой гиперболический параболоид (рис.4.58,в при lambda_1>0, lambda_2<0 );

3) если одно из собственных значений равно нулю (например, при lambda_2=0 ), то поверхность (4.77) представляет собой параболический цилиндр: выпуклый при lambda_1>0 (рис.4.58,2) или вогнутый при lambda_1<0 (рис.4.58,д).

Критические (стационарные) точки поверхностей второго порядка

В случае эллиптического параболоида стационарная точка $x^{ast}$ является либо точкой локального минимума функции при lambda_1>0, lambda_2>0 , либо точкой локального максимума функции при lambda_1<0, lambda_2<0 . В случае гиперболического параболоида ( и имеют разные знаки) в стационарной точке $x^{ast}$ нет экстремума. В случае выпуклого параболического цилиндра можно сказать, что точка $x^{ast}$ не может быть точкой максимума, но может быть точкой минимума, в случае вогнутого параболического цилиндра точка $x^{ast}$ не может быть точкой минимума, но может быть точкой максимума. Таким образом, если хотя бы одно собственное значение равно нулю, судить о наличии экстремума в точке $x^{ast}$ нельзя, так как нужны дополнительные исследования, учитывающие в формуле Тейлора члены выше второго порядка.

Алгоритм исследования функции на локальный экстремум

1. Составить и решить систему (4.74) — найти стационарные точки $x^{ast}$ . Если система не имеет решения, то точек локального экстремума нет.

2. Составить матрицу Гессе $H(x^{ast})$ и найти ее собственные значения lambda_1 и lambda_2 , решая характеристическое уравнение

$detBigl(H(x^{ast})-lambdacdot EBigr)=0.$

3. Проверить выполнение следующих условий.

а) Если lambda_1>0, lambda_2>0 , то $x^{ast}$ — точка локального минимума.

б) Если lambda_1<0, lambda_2<0 , то $x^{ast}$ — точка локального максимума.

в) Если lambda_1geqslant0, lambda_2geqslant0 , то $x^{ast}$ может быть точкой локального минимума (требуется дополнительное исследование).

г) Если lambda_1leqslant0, lambda_2leqslant0 , то $x^{ast}$ может быть точкой локального максимума (требуется дополнительное исследование).

д) Если lambda_1 и lambda_2 разных знаков (lambda_1cdotlambda_2<0) , то $x^{ast}$ не является точкой локального экстремума.

Пример 4.25. Найти экстремумы функции f(x)=x_1^3+x_2^3-3x_1x_2 .

Решение.. Решая систему уравнений

$frac{partial f(x)}{partial x_1}=3cdot x_1^2-3cdot x_2=0,quad frac{partial f(x)}{partial x_2}=3cdot x_2^2-3cdot x_1=0,$

находим стационарные точки O(0,0) и M(1,1) .

Составляем матрицу Гессе $H(x)=begin{pmatrix}6x_1&-3\-3&6x_2end{pmatrix}$ .

В стационарной точке O(0,0) матрица Гессе $H(x)|_{O}=begin{pmatrix}0&-3\-3&0end{pmatrix}$ . Найдем собственные значения матрицы Гессе. Характеристическое уравнение

$begin{vmatrix},-lambda&-3\-3&-lambda,end{vmatrix}=0 quadLeftrightarrowquad lambda^2-9=0$

имеет корни lambda_1=3,~lambda_2=-3 разных знаков. Следовательно, точка O(0,0) не является точкой экстремума (см. п.3,”д” алгоритма).

В стационарной точке M(1,1) матрица Гессе $H(x)|_{M}=begin{pmatrix}6&-3\-3&6end{pmatrix}$ . Характеристическое уравнение

$begin{vmatrix},6&-3\-3&6,end{vmatrix} quadLeftrightarrowquad (6-lambda)^2-9=0$

имеет два положительных корня lambda_1=3,~lambda_2=9 . Следовательно, точка M(1,1) является точкой минимума (см. п.3,”а” алгоритма).

Применение графических методов поиска экстремума функции

Рассмотрим постановку задачи поиска условного экстремума функции трех переменных. Пусть заданы:

а) функция f(x)=f(x_1,x_2,x_3) трех переменных $(xinmathbb{R}^3)$ ;

б) множество допустимых решений $M~(Msubsetmathbb{R}^3)$ .

Требуется найти такую точку $x^{ast}$ из множества допустимых решений, которой соответствует минимальное значение функции f(x) на этом множестве:

$f(x^{ast})=min_{xin M}f(x).$

Алгоритм графического метода поиска условного (или безусловного экстремума) функции аналогичен алгоритму, рассмотренному ранее для функции двух переменных. Однако его применение на практике ограничивается возможностями изображения пространственных фигур. Как правило, используется плоское изображение пространственных фигур, т.е. проекции этих фигур на плоскость, что не дает полного представления о взаимном их расположении.

Ниже рассматриваются задачи, в которых минимизируемая функция и функции, задающие ограничения, являются многочленами трех переменных первой или второй степени. Построение множества допустимых решений и поверхностей уровня функции f(x) сводится к построению алгебраических поверхностей первого или второго порядков. В этих задачах применение графического метода упрощается.

Напомним, что поверхностью уровня функции f(x)=f(x_1,x_2,x_3) называется геометрическое место точек пространства, в которых функция принимает постоянное значение, т.е. f(x)=text{const} .

Если функция f(x)=f(x_1,x_2,x_3) является многочленом первой степени, то ее поверхности уровня f(x)=text{const} при разных значениях постоянной (text{const}) представляют собой семейство параллельных плоскостей (несобственный пучок плоскостей).

Если функция f(x)=f(x_1,x_2,x_3) является многочленом второй степени, то ее поверхности уровня f(x)=text{const} при разных значениях постоянной (text{const}) представляют собой поверхности второго порядка. Поскольку уравнения разных поверхностей уровня отличаются только свободными членами, то собственные векторы, собственные значения lambda_1,,lambda_2,,lambda_3 , а также инварианты tau_1,,tau_2,,delta остаются постоянными для всех поверхностей уровня f(x)=text{const} . Следовательно, тип поверхности и канонический базис остаются постоянными для всех поверхностей уровня квадратичной функции.

Пример 4.26. Графическим методом найти экстремумы:

$mathsf{1)}~f(x)=x_1^2+frac{x_2^2}{4}+x_3^2totext{extr},;quad mathsf{2)},begin{cases}f(x)=x_3totext{extr},\dfrac{x_1}{2}+dfrac{x_2}{3}+x_3=1,\ x_1,x_2,x_3geqslant0;end{cases}mathsf{3)},begin{cases}f(x)=x_1^2+x_2^2-x_3^2totext{extr},\x_1^2+x_2^2+x_3^2=1.end{cases}$

Решение.

1) 1. Множество допустимых решений строить не нужно, так как оно совпадает со всем пространством: $M=mathbb{R}^3$ .

2. Поверхность уровня $x_1^2+frac{x_2^2}{4}+x_3^2=text{const}$ при text{const}>0 представляет собой эллипсоид (рис.4.59,а), при text{const}=0 — мнимый конус с единственной вещественной точкой O(0,0,0) , при text{const}<0 — мнимый эллипсоид. При увеличении постоянной (text{const}) полуоси эллипсоида пропорционально увеличиваются. На рис.4.59,а изображены эллипсоиды

$x_1^2+frac{x_2^2}{4}+x_3^2=1~(a=1,~b=2,~c=1)$ и $frac{x_1^2}{4}+frac{x_2^2}{16}+frac{x_3^2}{4}=1~(a=2,~b=4,~c=2).$

Стрелками указаны направления наискорейшего возрастания функции.

3. Из пункта 2 следует, что допустимые значения функции определяются не равенством 0leqslant f(x)<+infty .

4. В точке O(0,0,0) достигается безусловный минимум функции, так как в этой точке функция принимает наименьшее значение по сравнению со значениями в других точках пространства, а наибольшего значения функция не достигает.

Поверхности уровня эллипсоида и плоскости

2) Решается задача поиска условного экстремума с ограничениями типа равенств и неравенств.

1. Строим множество допустимых решений — часть плоскости $frac{x_1}{2}+frac{x_2}{3}+x_3=1$ в первом октанте, т.е. плоский треугольник с вершинами A(2,0,0), B(0,3,0), C(0,0,1) (рис.4.59,б).

2. Поверхности уровня $x_3=text{const}$ функции f(x_1,x_2,x_3)=x^3 представляют собой семейство параллельных плоскостей, каждая из которых перпендикулярна оси аппликат. На рис.4.59,б изображены три плоскости уровня x_3=0, x_3=1, x_3=2 . При text{const}<0 или text{const}>1 плоскость $x_3=text{const}$ не имеет общих точек с треугольником ABC ; при 0leqslanttext{const}leqslant1 плоскость $x_3=text{const}$ имеет общие точки с треугольником ABC , в частности, при text{const}=0 плоскости x_3=0 принадлежит сторона треугольника, при text{const}=1 плоскости x_3=1 принадлежит вершина треугольника.

3. Из пункта 2 следует, что допустимые значения функции определяются неравенством 0leqslant f(x)leqslant1 .

4. Наименьшее значение на множестве , равное нулю, функция достигает в любой точке отрезка ; наибольшее значение на множестве , равное единице, функция достигает в точке C(0,0,1) .

3) Решается задача поиска условного экстремума с ограничением типа равенств.

1. Строим множество допустимых решений — сфера x_1^2+x_2^2+x_3^2=1 единичного радиуса с центром в начале координат (рис.4.60).

2. Поверхности уровня $x_1^2+x_2^2-x_3^2=text{const}$ представляют собой либо однополостный гиперболоид вращения при text{const}>0 (например, однополостный гиперболоид x_1^2+x_2^2-x_3^2=1 (рис.4.60,а)), либо круговой конус x_1^2+x_2^2-x_3^2=0 при text{const}=0 (рис.4.60,б), либо двуполостный гиперболоид вращения при text{const}<0 (например, двуполостный гиперболоид x_1^2+x_2^2-x_3^2=-1 (рис.4.60,в)). При text{const}>1 поперечные полуоси однополостного гиперболоида $x_1^2+x_2^2-x_3^2=text{const}$ больше единицы, и он не имеет общих точек со сферой единичного радиуса. При text{const}<-1 продольная полуось двуполостного гиперболоида $x_1^2+x_2^2-x_3^2=text{const}$ больше единицы, и он не имеет общих точек со сферой x_1^2+x_2^2+x_3^2=1 . При -1leqslanttext{const}leqslant1 поверхность уровня $x_1^2+x_2^2-x_3^2=text{const}$ имеет общие точки с заданной сферой.

3. Из п.2 следует, что допустимые значения функции определяются неравенством -1leqslant f(x)leqslant1 .

4. Наименьшее значение на множестве , равное –1, функция достигает в точках (0,0,pm1) — вершинах двуполостного гиперболоида x_1^2+x_2^2-x_3^2=-1 (рис.4.60,в); наибольшее значение на множестве , равное единице, функция достигает в точках окружности $begin{cases}x_1^2+x_2^2=1,\x_3=0,end{cases}$ т.е. в точках горлового эллипса (в данном случае окружности) однополостного гиперболоида вращения x_1^2+x_2^2-x_3^2=1 (рис.4.60,а).

Поверхности уровня гиперболоидов и конуса

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Экстремум функции двух переменных

Понятия max, min,
экстремума функции двух переменных
аналогичны соответствующим понятиям
функции одной переменной. Пусть функция
Z= f(x; у) определена в
некоторой области D и т.
М
принадлежит к этой области. Точка М
называется точкой max
функции Z= f(x; у), если
существует такая δ-окрестность точки
,
что для каждой точки из этой окрестности
выполняется неравенство
.
Аналогичным образом определяется и
точка min, только знак
неравенства при этом изменится
.
Значение функции в точке max
(min) называется максимумом
(минимумом). Максимум и минимум функции
называются экстремумами.

Необходимые и достаточные условия экстремума

Теорема: (Необходимые условия
экстремума). Если в точке М
дифференцируемая функция Z= f(x;
у) имеет экстремум, то ее частные
производные в этой точке равны нулю:
,.

Доказательство: зафиксировав одну
из переменных x или y,
превратим Z= f(x; у) в функцию
одной переменной, для экстремума которой
вышеописанные условия должны выполняться.
Геометрически равенства

и

означают, что в точке экстремума функции
Z= f(x; у), касательная
плоскость к поверхности, изображающую
функцию f(x,y)=Z
параллельна плоскости OXY,
т.к. уравнение касательной плоскости
есть Z=Z_0.Точка, в которой частные производные
первого порядка функции Z= f(x;
у) равны нулю, т.е.
,,
называются стационарной точкой функции.
Функция может иметь экстремум в точках,
где хотя бы одна из частных производных
не существует. Например Z=|-|
имеет max в точке O(0,0),
но не имеет в этой точке производных.

Стационарные точки и точки, в которых
хотя бы одна частная производная не
существует, называются критическими
точками. В критических точках функция
может иметь экстремум, а может и не
иметь. Равенство нулю частных производных
является необходимым, но не достаточным
условием существования экстремума.
Например, при Z=xy
точка O(0,0) является
критической. Однако экстремума в ней
функция Z=xy
не имеет. (Т.к. в I и III
четвертях Z>0, а в II
и IV – Z<0).
Таким образом для нахождения экстремумов
функции в данной области необходимо
подвергнуть каждую критическую точку
функции дополнительному исследованию.

Теорема: (Достаточное условие
экстремумов). Пусть в стационарной точке

и некоторой окрестности функция f(x;
у) имеет непрерывные частные производные
до 2^ого порядка включительно.
Вычислим в точке

значения
,
и
.
Обозначим

Тогда:

если
,
то f(x; у) в точке

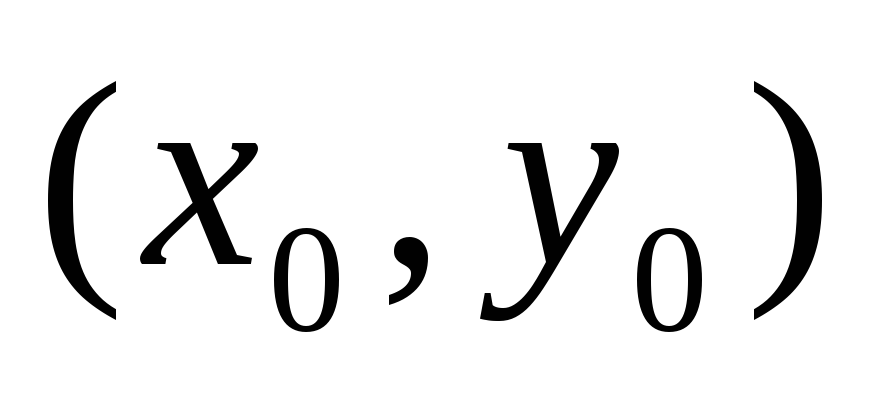
имеет экстремум max, если
А<0 и min, если А>0.
если
,
то f(x; у) в точке
экстремума
не имеет.

В случае если
,
экстремум в точке

может быть, а может и не быть. Необходимы
дополнительные исследования.

II. Неопределенный интеграл

Понятие неопределенного интеграла

В дифференцируемом исчислении мы решали
задачу как по данной функции f(x)
найти ее производную (или дифференциал).
Интегральное исчисление решает обратную
задачу: найти функцию F(x),
зная ее производную

(или дифференциал). Искомую функцию F(x)
называют первообразной функции
f(x).

F(x) –
называется первообразной функции f(x)
на интервале (a, b),
если для любого

выполняется равенство

(или.

Например, первообразной функции

является функция
,
так как
.

Очевидно, что первообразными будут
также любые функции
,
где С – постоянная, поскольку
.

Теорема 1. Если F(x)
является первообразной функции f(x)
на
,
то множество всех первообразных для
f(x) задается
формулой
,
где С – постоянное число.

Док-во. Функция

– первообразная f(x).
Действительно,
.
Пусть

некоторая другая отличная от

первообразная функции
,
т.е.
=.
Тогда для любого

имеем
,
а это означает, что
,
где С –
.
Следовательно,
.

Множество всех первообразных функций

для

называется неопределенным интегралом
от функции

и обозначается символом
.
Таким образом
=.

Здесь

– называется подынтегральной функцией,

– подынтегральным выражением, x
– переменной интегрирования,
–
знаком неопределенного интеграла.
Операция нахождения неопределенного
интеграла – интегрированием этой
функции.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Содержание:

Точки максимума и минимума называются точками экстремума.
Пример с решением

Внутренняя область каждого круга с центром и радиусом называется окрестностью точки

Рассмотрим функцию непрерывную в окрестности точки Строгим максимумом {строгим локальным максимумом) функции называется такое ее значение которое больше всех других значений, принимаемых в точках достаточно близких к точке и отличных от нее (рис. 15.1), т. е.

Пусть функция непрерывна в окрестности точки Строгим минимумом (строгим локальным минимумом) функции называется такое ее значение в точке которое меньше всех других значений, принимаемых в точках достаточно близких к точке и отличных от нее (рис. 15.1), т. е.

Если рассмотренные выше неравенства являются нестрогими, то говорят о нестрогих локальных максимуме и минимуме соответственно.

В случаях, когда упоминание о том, является ли максимум или минимум строгим или нестрогим, локальным или глобальным, не является существенным, то соответствующие прилагательные опускают.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Точки максимума и минимума называются точками экстремума.

Приведем теоремы, облегчающие нахождение экстремумов функции двух переменных.

Теорема 1 (необходимое условие экстремума). Если функция имеет в точке экстремум и

первые частные производные непрерывны, в некоторой окрестности этой точки, то

Если в точке функция имеет максимум, то функция одной переменной имеет в точке максимум, и, следовательно, ее производная равна нулю. Функция одной переменной также имеет в точке максимум, и, следовательно, ее производная равна нулю. Следовательно, одновременно должно иметь место:

Аналогично доказывается случай, когда функция имеет в точке минимум.

Точки, при которых выполняются (15.1), называются стационарными точками функции

Возможно вам будут полезны данные страницы:

Теорема 2 (геометрический смысл необходимых условий экстремума). В стационарной точке касательная плоскость к поверхности параллельна плоскости

Пусть есть стационарная точка функции Уравнение касательной плоскости в этой точке имеет вид

Так как частные производные равны нулю, то получаем

Заметим, что точки экстремума могут быть не только в тех точках, в которых частные производные функции равны нулю. Экстремум функции может быть и в тех точках, где хотя бы одна из частных производных не существует или равна бесконечности. На рис. 15.2 изображена функция с конусообразным графиком. В вершине конуса — точке — находится максимальная точка функции, однако частные производные там не существуют (в соответствующей точке невозможно провести касательную плоскость).

Более того, обращение в нуль или же несуществование частных производных первого порядка является более общим необхо-димымым условием экстремума.

Однако это необходимое условие недостаточно для существования экстремума. Например, у седловидной поверхности изображенной на рис. 15.2, частные производные равны нулю в точке но эта точка не является экстремумом. Рис. 15.2. В точке максимум, однако частные производные не существуют. В точке нет экстремума, однако частные производные равны нулю.

Теорема 3 (достаточные условия экстремума). Если функция имеет, в окрест,ноет,и точки первые и вторые непрерывные частные производные, то в точке о которой выполняются необходимые условия {15.1), имеет место экстремум в случае, когда в этой точке

Функция имеет максимум в точке если в этой точке и минимум, если

Если же то функция не имеет экстремума в точке

Таким образом, схема исследования функции имеющей непрерывные первые и вторые частные производные, на экстремум такова. Вначале сужаем область поиска. Находим стационарные точки (только они могут быть точками экстремума). Далее, пусть является стационарной точкой функции. Значения производных второго порядка в точке обозначим так:

Составим определитель Если то в стационарной точке нет экстремума (в этом случае является так называемой седловиной, или точкой минимакса ( рис. 15.2).

Если то в точке есть экстремум, причем максимум, если и минимум, если

Если то требуется дополнительное исследование. (В этом случае возможны оба случая. Для одних функций в стационарной есть экстремум, для других нет.) Поэтому при проводят исследование, используя определение.