Как найти экв сопротивление

Сопротивления
в электрических цепях могут быть
соединены последовательно, параллельно,
по смешанной схеме и по схемам «звезда»,
«треугольник». Расчет сложной схемы
упрощается, если сопротивления в этой
схеме заменяются одним эквивалентным
сопротивлением R_экв,
и вся схема представляется в виде схемы
на рис. 1.3, где R=R_экв,
а расчет токов и напряжений производится
с помощью законов Ома и Кирхгофа.

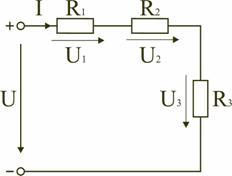
Электрическая
цепь с последовательным соединением
элементов

Рис. 1.4

Рис. 1.5

Последовательным
называют такое соединение элементов
цепи, при котором во всех включенных в
цепь элементах возникает один и тот же
ток I (рис. 1.4).

На
основании второго закона Кирхгофа (1.5)
общее напряжение U всей цепи равно сумме
напряжений на отдельных участках:

U
= U₁
+ U₂
+ U₃ или
IR_экв
= IR₁
+ IR₂
+ IR₃,

откуда
следует

(1.5)

R_экв
= R₁
+ R₂
+ R₃.

Таким
образом, при последовательном соединении
элементов цепи общее эквивалентное
сопротивление цепи равно арифметической
сумме сопротивлений отдельных участков.
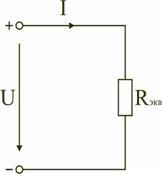
Следовательно, цепь с любым числом
последовательно включенных сопротивлений
можно заменить простой цепью с одним
эквивалентным сопротивлением R_экв
(рис. 1.5). После этого расчет цепи
сводится к определению тока I всей цепи
по закону Ома

,

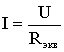и
по вышеприведенным формулам рассчитывают
падение напряжений U₁,
U₂,
U₃
на соответствующих участках электрической
цепи (рис. 1.4).

Недостаток
последовательного включения элементов
заключается в том, что при выходе из
строя хотя бы одного элемента, прекращается
работа всех остальных элементов цепи.

Электрическая
цепь с параллельным соединением элементов

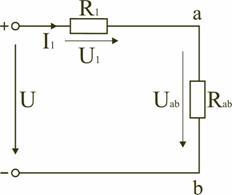
Параллельным
называют такое соединение, при котором
все включенные в цепь потребители
электрической энергии, находятся под
одним и тем же напряжением (рис. 1.6).

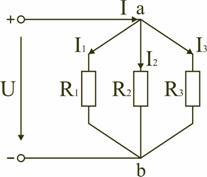
Рис.
1.6

В
этом случае они присоединены к двум
узлам цепи а и b, и на основании первого
закона Кирхгофа (1.3) можно записать, что
общий ток I всей цепи равен алгебраической
сумме токов отдельных ветвей:

I
= I₁
+ I₂
+ I₃,
т.е.
,

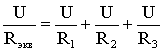откуда
следует, что

(1.6)

.

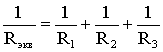В
том случае, когда параллельно включены
два сопротивления R₁
и R₂,
они заменяются одним эквивалентным
сопротивлением

(1.7)

.

Из
соотношения (1.6), следует, что эквивалентная
проводимость цепи равна арифметической
сумме проводимостей отдельных ветвей:

g_экв
= g₁
+ g₂
+ g₃.

По
мере роста числа параллельно включенных
потребителей проводимость цепи gэкв
возрастает, и наоборот, общее сопротивление
R_экв
уменьшается.

Напряжения
в электрической цепи с параллельно
соединенными сопротивлениями (рис. 1.6)

U
= IR_экв
= I₁R₁
= I₂R₂ =
I₃R₃.

Отсюда
следует, что

,

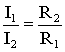т.е.
ток в цепи распределяется между
параллельными ветвями обратно
пропорционально их сопротивлениям.

По
параллельно включенной схеме работают
в номинальном режиме потребители любой
мощности, рассчитанные на одно и то же
напряжение. Причем включение или
отключение одного или нескольких
потребителей не отражается на работе
остальных. Поэтому эта схема является
основной схемой подключения потребителей
к источнику электрической энергии.

Электрическая
цепь со смешанным соединением элементов

Смешанным
называется такое соединение, при котором
в цепи имеются группы параллельно и
последовательно включенных сопротивлений.

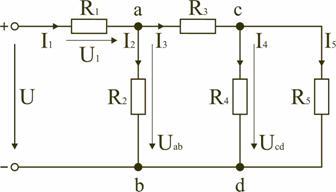
Рис.
1.7

Для
цепи, представленной на рис. 1.7, расчет
эквивалентного сопротивления начинается
с конца схемы. Для упрощения расчетов
примем, что все сопротивления в этой
схеме являются одинаковыми: R₁=R₂=R₃=R₄=R₅=R.
Сопротивления R₄
и R₅
включены параллельно, тогда сопротивление
участка цепи cd равно:

.

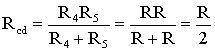В
этом случае исходную схему (рис. 1.7)
можно представить в следующем виде
(рис. 1.8):

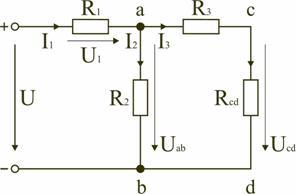
Рис.
1.8

На
схеме (рис. 1.8) сопротивление R₃
и R_cd
соединены последовательно, и тогда
сопротивление участка цепи ad равно:

.

Тогда
схему (рис. 1.8) можно представить в
сокращенном варианте (рис. 1.9):

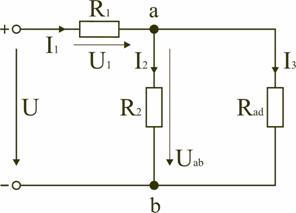
Рис.
1.9

На
схеме (рис. 1.9) сопротивление R₂
и R_ad
соединены параллельно, тогда сопротивление
участка цепи аb равно

.

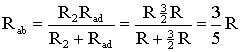Схему
(рис. 1.9) можно представить в упрощенном
варианте (рис. 1.10), где сопротивления
R₁
и R_ab
включены последовательно.

Тогда
эквивалентное сопротивление исходной
схемы (рис. 1.7) будет равно:

.

Рис. 1.10

Рис. 1.11

В
результате преобразований исходная
схема (рис. 1.7) представлена в виде
схемы (рис. 1.11) с одним сопротивлением
R_экв.
Расчет токов и напряжений для всех
элементов схемы можно произвести по
законам Ома и Кирхгофа.

Соединение
элементов электрической цепи по схемам
«звезда» и «треугольник»

В
электротехнических и электронных
устройствах элементы цепи соединяются
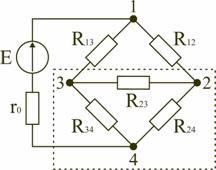
по мостовой схеме (рис. 1.12). Сопротивления
R₁₂,
R₁₃,
R₂₄,
R₃₄
включены в плечи моста, в диагональ 1–4
включен источник питания с ЭДС Е, другая
диагональ 3–4 называется измерительной
диагональю моста.

Рис. 1.12

Рис. 1.13

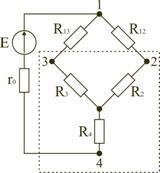
В
мостовой схеме сопротивления R₁₃,
R₁₂,
R₂₃
и R₂₄,
R₃₄,
R₂₃
соединены по схеме «треугольник».
Эквивалентное сопротивление этой схемы
можно определить только после замены
одного из треугольников, например
треугольника R₂₄
R₃₄
R₂₃
звездой R₂
R₃
R₄
(рис. 1.13). Такая замена будет
эквивалентной, если она не вызовет
изменения токов всех остальных элементов
цепи. Для этого величины сопротивлений
звезды должны рассчитываться по следующим
соотношениям:

(1.8)

;

;

.

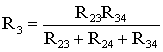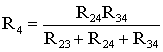Для
замены схемы «звезда» эквивалентным
треугольником необходимо рассчитать
сопротивления треугольника:

(1.9)

;

;

.

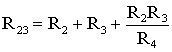После
проведенных преобразований (рис. 1.13)
можно определить величину эквивалентного
сопротивления мостовой схемы (рис. 1.12)

.

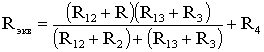Эквивалентное сопротивление резисторов определить эквивалентное

Расчет реальной электрической цепи в идеальном виде невозможен по причине отсутствия математических методик учета индивидуальных параметров каждого составляющего элемента. Это естественно, так как любая деталь имеет свои паразитные характеристики, которые нереально учесть при расчетах. Для устранения этой проблемы было введено понятие эквивалентной замены. При этом в расчет принимается только одна определяющая характеристика элемента. Так, например, эквивалентное сопротивление резисторов в электрической схеме, отображает только величину сопротивления без влияния на него сторонних факторов.

В электротехнике существует два основных варианта включения деталей в электрической цепи – это последовательное и параллельное соединение. Объединяющей для них является смешанная схема, которая по сути может быть разбита на участки с вышеприведенными характеристиками.

Рассмотрим эквивалентное соединение резисторов в каждом отдельном случае.

Эквивалентное сопротивление при последовательно соединенных резисторов

При данном типе размещения резисторов в цепи условная схема будет соответствовать рис. 1.

Рисунок 1

Для того чтобы определить эквивалентное сопротивление
резисторов необходимо вспомнить закон Ома. Для последовательного соединения он
гласит что общее, а в нашем случае эквивалентное сопротивление, соответствует
следующему уравнению:

R_экв=
R₁+R₂+R₃+R_N-1+R_N

Рассмотрим пример последовательного соединения трех резисторов, сопротивление которых равно 10, 20 и 30 Ом, соответственно. Согласно выше приведенной формуле общее сопротивление всех этих резисторов на данном участке цепи будет равно 60 Ом. Таким образом, при расчетах параметров электрической схемы нет надобности использовать индивидуальные характеристики отдельных элементов. Их можно просто заменить одним значением эквивалентным их сумме.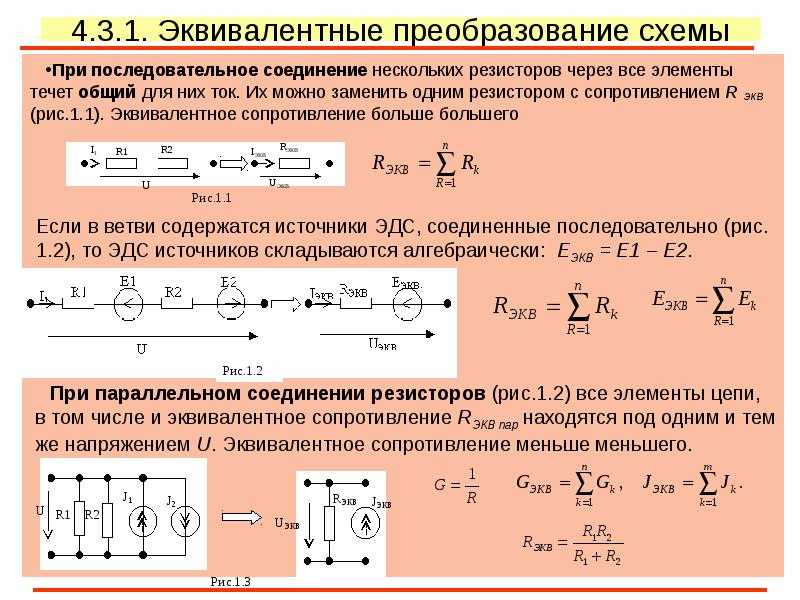

Кроме теории, данное суммирование значений сопротивлений
элементов, имеет и практическое применение – в случае необходимости всегда можно
заменить несколько резисторов одним. Также имеет место и обратное утверждение –
при отсутствии деталей с требуемой характеристикой ее можно заменить на
несколько других, эквивалентное сопротивление которых будет соответствовать
требуемому значению.  Все это справедливо
и для параллельного соединения резисторов, только с некоторыми особенности.

Эквивалентное сопротивление при параллельном соединении резисторов

Общая схема при данном включении резисторов в цепь соответствует рис. 2.

Рисунок 2

Определить эквивалентное сопротивление параллельно
соединенных резисторов позволяет закон Ома согласно которому, в данном варианте,
справедливо равенство:

1/R _экв =1/R₁+1/R₂+1/R₃+1/R
_N-1+1/R_N

Возвращаясь к нашему примеру с резисторами 10, 20 и 30 Ом.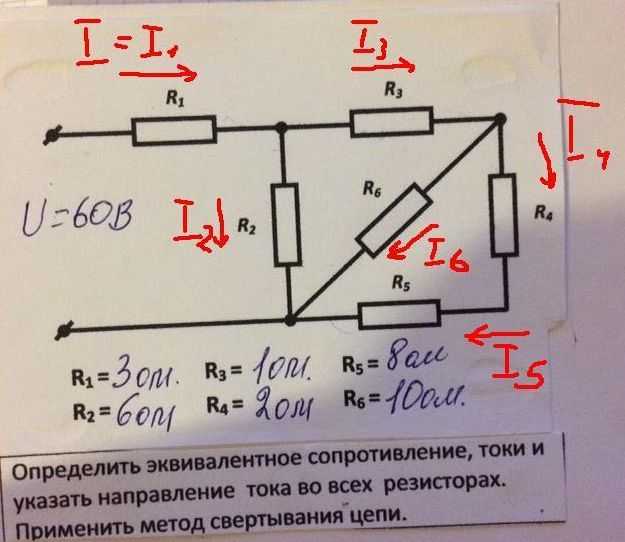

Можно
определить эквивалентное сопротивление для данного случая, преобразуя уравнение
и получаем следующую формулу:

R _экв = R₁ х R₂
х R₃ / (R₁ x R₂) + (R₁
x R₃) + (R₂ x R₃) = 5,45
Ом

Важный момент: При параллельном включении резисторов в цепь эквивалентное сопротивление будет всегда меньше наименьшего значения отдельного элемента. При последовательном соединении R _экв обязательно больше самого большого параметра.

Эквивалентное сопротивление при смешанном соединении резисторов

Определение эквивалентного сопротивления при смешанном соединении резисторов не представляет особых сложностей. Для этого достаточно разбить существующую цепочку на логические составляющие – блоки. Т.е.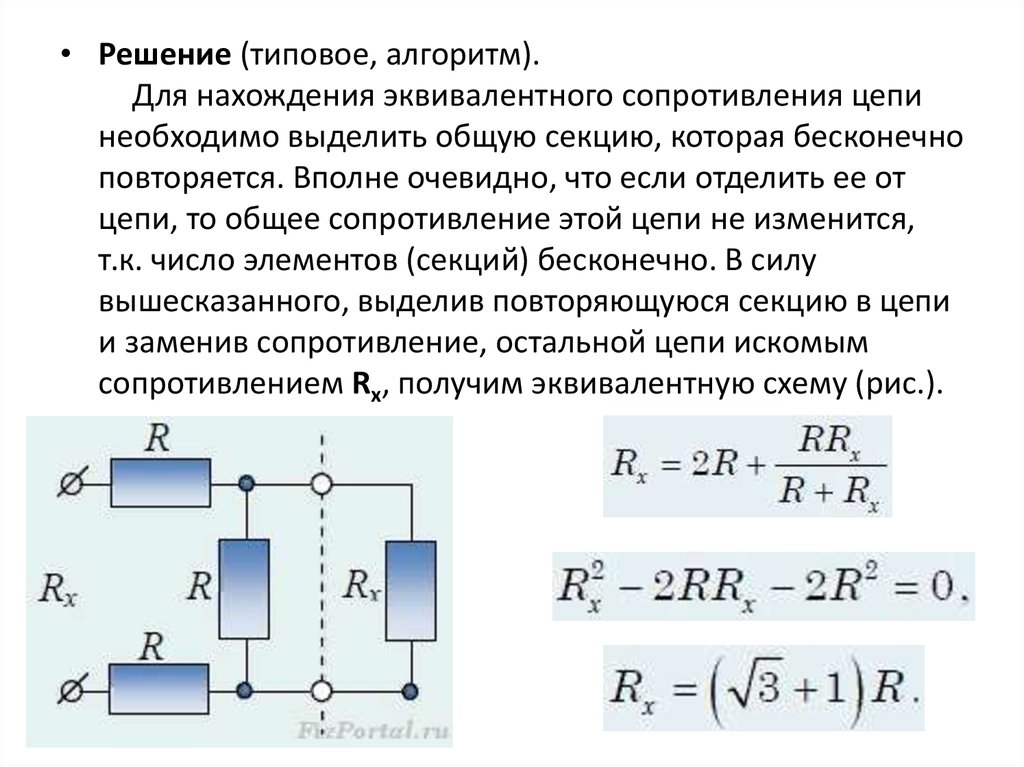

максимально упростить схему, приведя ее в соответствие с характеристиками свойственных тому или иному типу соединения. На рис. 3 приведена типичная схема упрощения, которая получила название метод свертывания цепи.

Рисунок 3

Данная схема позволяет наглядно понять, как можно определить эквивалентное сопротивление резисторов при смешанном соединении. Обращаем внимание, что начинать процесс упрощения можно в произвольном порядке. Так, например, объединение резисторов R₁ и R₂ не обязательно должно быть первым шагом. Можно совершенно смело на первом этапе найти R _экв сумме сопротивлений последовательно включенных в цепь резисторов R₄ и R₅.  Определение эквивалентного сопротивления для резисторов необходимо осуществлять в зависимости от типа соединения.

В заключение вернемся к самому понятию эквивалентной замены резисторов. В рассмотренных нами случаях речь шла об идеальном варианте. То есть в расчет принимается только величина сопротивления при нулевых значениях остальных характеристик. Также обращаем внимание, что при составлении эквивалентной схемы любых элементов электрической цепи, не только резисторов, можно вводить дополнительные переменные, которые будут влиять на конечные итоги.

Добавить отзыв

Как найти сопротивление эквивалентное?

Параллельное соединение резисторов. Калькулятор для расчета

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом. Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.

Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны. Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Расчёт при смешанном соединении устройств

Произвести расчет сопротивления цепи, когда она разветвлена и наполнена разными видами резистивных соединений, просто не получится. Затрудняет решение задачи множество участков, где детали подключены друг другу в разных комбинациях. В таких обстоятельствах желательно выполнять ряд преобразований, добиваясь упрощения схемы вводом отдельных эквивалентных элементов. Выявляют при этом подходящие контуры последовательных и параллельных присоединений.

Например, выискав некоторое количество последовательных подключений резисторов, заменяют их на один эквивалентный компонент. Определив элементы, соединённые последовательно, также рисуют вместо него эквивалент. Вновь начинают искать подобные простые соединения.

Метод называют «методом свёртывания». Схему упрощают до тех пор, пока в ней не останется одно Rэкв.

Параллельное и последовательное соединение элементов

В разделе электротехники присутствует несколько вариантов того, как подключить детали в электрическую цепь. Есть параллельное и попеременное подсоединения. Их объединяет смешанная схема, которая представлена ниже.

Последовательное подключение — это когда все источники соединяются друг с другом последовательно. Получаемая цепь не обладает никакими разветвлениями. Сила тока в данном случае проходит через каждый источник. Она постоянная, общее напряжение одинаковое.

В случае препятствия резисторов заряду при последовательном подключении получится, что сопротивляемость будет равна сумме всех взаимозаменяемых пассивных элементов цепи. Рассчитывая параметры электротехнической схемы, не нужно применять частные параметры устройств. Их можно заменить одним значением, которое равно их суммарному показателю.

Вам это будет интересно Определение резонанса

Обратите внимание! Польза взаимозаменяемости компонентов заключается в возможности замены нескольких пассивных элементов электрической сети одним.

Соединение элементов

Параллельное подключение — это такое подсоединение источников, в котором входы всех устройств находятся в одних местах, а выходы — в других. Этими местами служат узлы.

В случае эквивалентного препятствия заряду при параллельном соединении определить его можно благодаря закону Ома с преобразованием формулировки подсчета. Так, сделать необходимый расчет можно, основываясь на следующей формуле: R · R / N·R = R / N.

Если это соединение нескольких индуктивных катушек, то их индуктивный показатель сопротивляемости будет рассчитываться по той же формуле, что для резисторных устройств.

Важно! В случае с параллельным подключением общий показатель будет меньше любого показателя резистора. При последовательном подсоединении все наоборот.

Эквивалентные преобразования

При падении напряжения между двумя точками цепи в их разность включают свободное число значений потенциалов, имеющих противоположные знаки. После чего их попарно объединяют.

Ты эксперт в этой предметной области? Предлагаем стать автором Справочника Условия работы

$Uab = phi a — phi b$, где $a$ и $b$ – точки.

После преобразований у нас получается внушительная формула:

$U_{ab} = phi a — phi b = phi a -phi с +phi с -phi d +phi d -…-phi i +phi i -phi k +phi k-… -phi q +phi q — phi b = (phi a -phi с) + (phi с-phi d) + (phi d -…-phi i) + (phi i -phi k) + (phi k-… -phi q) + (phi q — phi b) = U_{ac}+ U_{cd} + U_{de} +…+ U_{ik} + U_{kl} + U_{lm} +…+ U_{qb} = Ir_1+ Ir_2 + … + Ir_m + E_1 + E_2 +… –E_n = I(r_1 + r_2 + r_3 + … + r_m) + ( E_1 + E_2 +… –E_n) = IR + E$

Всякое последовательное соединения электрической цепи можно преобразовать при помощи последовательного соединения:

• эквивалентного резистора;
• источника электродвижущей силы.

В нашем случае сопротивление эквивалентного резистора равняется сумме сопротивлений, которые входят в соединение. Электродвижущая сила эквивалентного источника будет равна сумме ЭДС источников, входящих в это соединение.

Определение 2

Любые элементы соединения цепи возможно переставлять в разном порядке. Все действия должны осуществляться в пределах соединения. Такой процесс называют свойством коммутативности последовательного соединения элементов.

Готовые работы на аналогичную тему

Курсовая работа Эквивалентные электрические цепи 440 ₽ Реферат Эквивалентные электрические цепи 270 ₽ Контрольная работа Эквивалентные электрические цепи 200 ₽

Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость

Если взять за основу эквивалентное сопротивление ($R$), которое представляет собой сумму положительных слагаемых, тогда получим, что $R geq r$, где $r$ — максимальное значение из всех сопротивлений, входящих в соединение.

При подключении последовательного соединения к узлам электрической цепи его значение будет равно определению ветви цепи. В этом случае ветвь образовывается исключительно последовательным соединением.

В параллельном соединении элементов совокупность частей электрической цепи не имеет связи с другими узлами, при этом объединена с двумя узлами. Параллельное соединение ветви и элементов параллельного соединения цепи существенно отличается от последовательного соединения.

В параллельное соединение входят также резисторы и источники тока, однако в цепи не могут присутствовать больше одного источника электродвижущей силы.

Преобразования цепей поддерживают еще одну особую задачу в физике. Она состоит в определении сопротивления цепи относительно точек разрыва. Такая ситуация возникает, когда используется метод эквивалентного генератора при анализе электрических цепей, находящихся в неподвижном режиме, а также при решении уравнения для анализа переходных процессов.

Эквивалентное сопротивление является входным сопротивлением определенной цепи.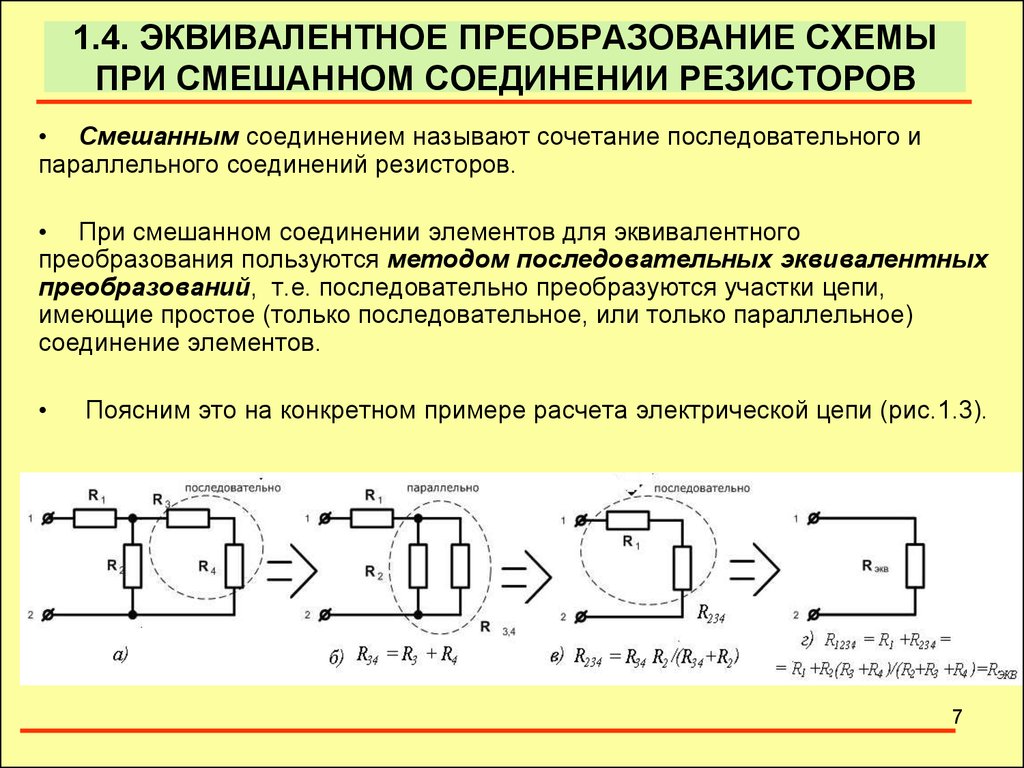 До начала эквивалентных преобразований необходимо в изучаемой цепи заменить источники электродвижущей силы на эквивалентное сопротивление тока и ЭДС. После этого нужно определить само эквивалентное сопротивление. При этом сопротивление источника электродвижущей силы равняется нулю. Сопротивление источника тока имеет бесконечные значения.

Простые электрические цепи содержат исключительно последовательное или параллельное соединение элементов.

Сложный участок цепи содержит последовательное и параллельное соединение элементов (смешанное соединение).

Эквивалентные преобразования имеют смысл, если при их выполнении токи и напряжения не изменяются на конкретных участках цепи. При преобразовании сложных электрических цепей пользуются последовательным методом. Он состоит в последовательном преобразовании участков цепи, которые имеют простое соединение элементов.

ЭКВИВАЛЕНТНАЯ СХЕМА РЕЗИСТОРА. SMD – РЕЗИСТОР.

Резистор обычно составляет 80-40% от общего числа элементов электронных аппаратов. Резисторы всех типов являются источниками напряжения шумов, обусловленных тепловым и контактным шумом. Важнейшим фактором, влияющим на шумы резистора, является его номинальная мощность рассеяния. Резисторы выпускаются на определенную номинальную мощность рассеяния, которая выбирается исходя из допустимого превышения температуры сопротивления над температурой окружающей среды. Мощность, рассеиваемая в резисторе всегда должна быть минимальной. Далее на рисунке приведена эквивалентная схема резистора.

В реальных резисторах, кроме основных параметров, присутствуют паразитные параметры, обусловленные конструктивными особенностями резистора: Cв1, Св2- емкости выводов резистора относительно общего провода; Cr – емкость между выводами резистора;Rr – сопротивление резистивного слоя: Rk – сопротивление контактов, Rиз – сопротивление защитного покрытия;Lr– индуктивность выводов резистора и его резистивного слоя.

Наиболее вредным параметром является паразитная индуктивность, немного меньшее значение имеет паразитная емкость резистора. Оба этих параметра ограничивают maxf до которой можно применить конкретный тип резистора. Наилучшими частотными параметрами в настоящее время обладают резисторы поверхностного монтажа SMD. Основным несущим элементом резистора является подложка, изготовленная из окиси аллюминия (Al2O3). Этот материал обладает хорошими диэлектрическими свойствами, но помимо этого имеет очень высокую теплопроводность, что необходимо для отвода тепла, выделяющегося в резистивном слое, в окружающую среду. Основные электрические характеристики резистора определяются резистивным элементом, в качестве которого чаще всего используется пленка металла или окисла, например, чистого хрома или двуокиси рутения, нанесенная на подложку. Состав, технология нанесения на подложку и характер обработки этой пленки являются важнейшими элементами, определяющими характеристики резистора. Для соединения резистивного элемента с проводниками печатной платы служат несколько слоев контактных элементов.

ЭКВИВАЛЕНТНАЯ СХЕМА КОНДЕНСАТОРА. ПОНЯТИЕ ДОБРОТНОСТИ.

Конденсатор обычно составляет 20-30% от общего числа элементов электронных аппаратов. Важнейшим параметром С

является его частотная характеристика.
С
различных типов имеет характеристики, делающие их пригодными для одних и непригодными для других применений. Реальный
С
не является чистой емкостью, а обладает также сопротивлением и индуктивностью. Индуктивность L создается как выводами, так и структурой самого конденсатора. . Ry — сопротивление, определяющееся током утечки. Величина Ry зависит от объемного удельного сопротивления материала диэлектрика. Rп – сопротивление определяющее потери мощности в диэлектрике под действием приложенного к нему напряжения, которое зависит от tg угла потерь диэлектрика
С
. Эквивалентная схема
С
представляет собой колебательный контур.

На практике для фильтрации и развязки используется электролитические конденсаторы, которые имеют большую емкость в малом корпусе. Однако, из-за своей конструкции они имеют большие индуктивности, поэтому являются низкочастотными C

и на f>10кГц они начинают терять емкостные свойства. На практике С характеризуются параметрами
С
и . Величина, обратная
tgδ
называется добротностью . Добротность – параметр колебательности системы, определяющая ширину резонанса и характеризующий во сколько раз запас энергии в системе больше чем потери энергии за 1 период колебаний. Колебательность обратна пропорциональна скорости затухания собственных колебаний. Чем выше
Q
, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.

Эквивалентное сопротивление сложных, последовательных и параллельных цепей

Базовая электроника

Энгр Фахад
Отправить письмо
2 января 2021 г.

5 609

Допустим, у вас есть два резистора R1 = 10 и R2 = 20, соединенные последовательно.

Допустим, это резистор на 10 Ом, а это резистор на 20 Ом. Чему равно эквивалентное сопротивление или полное сопротивление цепи? В последовательной цепи общее сопротивление равно сумме всех сопротивлений. Таким образом, 10 + 20 равно 30. Таким образом, мы можем описать это как резистор на 30 Ом. Таким образом, эти две схемы эквивалентны. Вы можете просто заменить два резистора одним резистором.

Теперь, что если у нас есть два резистора параллельно. Допустим, это резистор на 10 Ом, а это резистор на 10 Ом. Мы назовем их R1 и R2. Так каково эквивалентное сопротивление этой цепи? Теперь, когда у вас есть два резистора, подключенных параллельно, и если они имеют одинаковое значение, эквивалентное сопротивление будет просто равно половине этого значения, поэтому эквивалентное сопротивление будет равно 5 Ом. Чтобы рассчитать общее сопротивление двух резисторов в параллельной цепи, это (1/R1 + 1/R2)

-1 . Так что это будет (1/10 + 1/10) ^-1 . Теперь 1 + 1 равно 2, так что это становится 2 из 10, и когда вы возводите дробь в отрицательную степень 1, вы в основном переворачиваете дробь, и получается половина 10 или 10, деленное на 2, что равно 5.

А что, если мы подключим три резистора параллельно? Допустим, это резистор на четыре Ома, резистор на шесть Ом и резистор на 8 Ом. Каково эквивалентное сопротивление этой цепи?

Назовем это R1, R2 и R3. Таким образом, мы можем использовать эту формулу, чтобы получить ответ, который будет (1/R1 + 1/R2 + 1/R3) ^-1 . Итак, это (1/4 + 1/6 + 1/8) ^-1 , и поэтому для этой схемы эквивалентное сопротивление составляет 1,846 Ом, и это ответ.

Вот еще один пример. Рассчитайте эквивалентное сопротивление этой цепи. Допустим, у нас есть два резистора на 20 Ом, которые соединены параллельно, и еще один резистор на 15 Ом. Обратите внимание, что эти два резистора параллельны друг другу и имеют одинаковое значение, поэтому эквивалентное сопротивление этих двух резисторов вы можете заменить на резистор 10 Ом.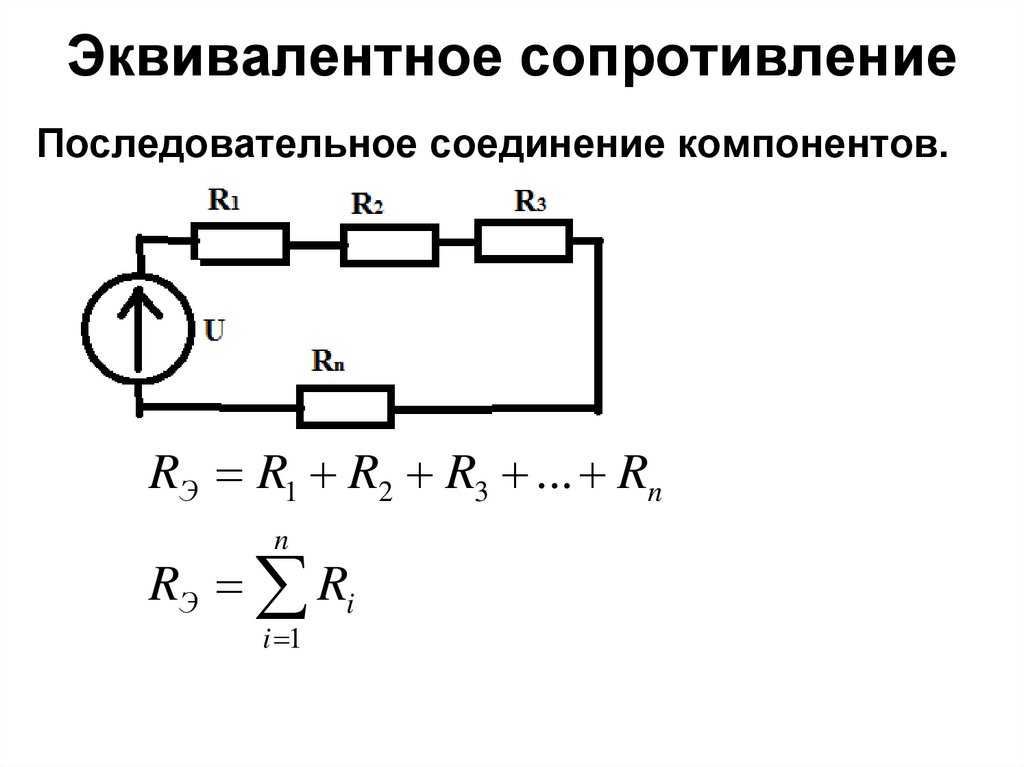 Итак, в этот момент вы можете заменить два резистора одним резистором на 10 Ом. Теперь это создаст последовательную цепь с резистором 15 Ом. Теперь резисторы 10 Ом и 15 Ом соединены последовательно, и теперь вы можете просто добавить два сопротивления, и вы получите общее сопротивление. Итак, 15 + 10 = 25 Ом. Таким образом, эквивалентное сопротивление для этой цепи составляет 25 Ом, и на этом все.

Вот еще один, допустим, три резистора 40 Ом, 40 Ом и 20 Ом соединены параллельно, и в той же цепи есть еще три резистора 5 Ом, 15 Ом и 30 Ом. Как объяснялось ранее, если два резистора соединены параллельно и имеют одинаковые значения, мы можем просто уменьшить значение вдвое. Итак, как вы можете видеть, два резистора по 40 Ом соединены параллельно, поэтому мы просто заменим его резистором на 20 Ом, другим резистором на 20 Ом, так что если эти два резистора вместе составляют 20, и это становится одним резистором, а это 20, то эти два становятся 10. Таким образом, эквивалентное сопротивление для всех трех резисторов равно 10, и чтобы подтвердить это, вы можете ввести его (1/40 +  1/40 + 1/20) ^-1 Это даст вам 10 Ом.

Итак, я могу заменить всю эту параллельную цепь резистором на 10 Ом, так что теперь оставшиеся четыре резистора замечают, что они все последовательно, и есть только один путь для протекания тока, так что это будет 5 плюс 15, что 20 плюс 10 плюс 30, поэтому эквивалентное сопротивление для этой цепи составляет 60 Ом, и это все для этой проблемы.

Давайте попробуем этот пример. Итак, скажем, это резистор 10 Ом, это 20, а это 30, поэтому не стесняйтесь остановиться здесь и вычислить эквивалентное сопротивление цепи. Обратите внимание, что эти два элемента соединены последовательно, потому что ток течет только по одному пути, поэтому 10 + 20 равно 30 Ом. так что я могу заменить эти два резистора резистором 30 м, теперь я могу написать этот резистор, как показано внизу, или если вы нарисуете его как-то иначе, не имеет значения, что важно, это понять, что эти два, когда вы их комбинируете в один резистор, они параллельны другому резистору на 30 Ом, поэтому, как только вы это осознаете, и тот факт, что у вас есть два параллельных резистора с одинаковым значением, вы знаете, что эквивалентное сопротивление будет половина от 30, так что это 15 Ом и это ответ.

Теперь давайте попробуем аналогичный пример, но с большим количеством шагов. Резисторы обведены красным, если это 10, это 20, и это всего лишь 30, мы собираемся сказать, что это 60. Во-первых, мы должны понять, что эти три резистора всерьез, есть только один путь для тока, протекающего в этой ветви, поэтому мы можем добавить 10, 20 и 30, чтобы получить 60, поэтому давайте заменим его собственным резистором 60. Итак, когда вы замените все три резистора одним резистором на 60 Ом, вы обнаружите, что этот резистор будет подключен параллельно резистору на 60 Ом. Таким образом, резисторы одинакового номинала соединены параллельно, и вы знаете, что если резисторы одного номинала, просто половина номинала, то есть это будет 30 Ом.

Теперь у нас есть три резистора в сериях 10, 30 и 20, что дает нам эквивалентное сопротивление или общее сопротивление 60 Ом для этой цепи.

Давайте рассмотрим еще один пример. Это будет сложнее, чем другие, но вы обязательно должны попробовать.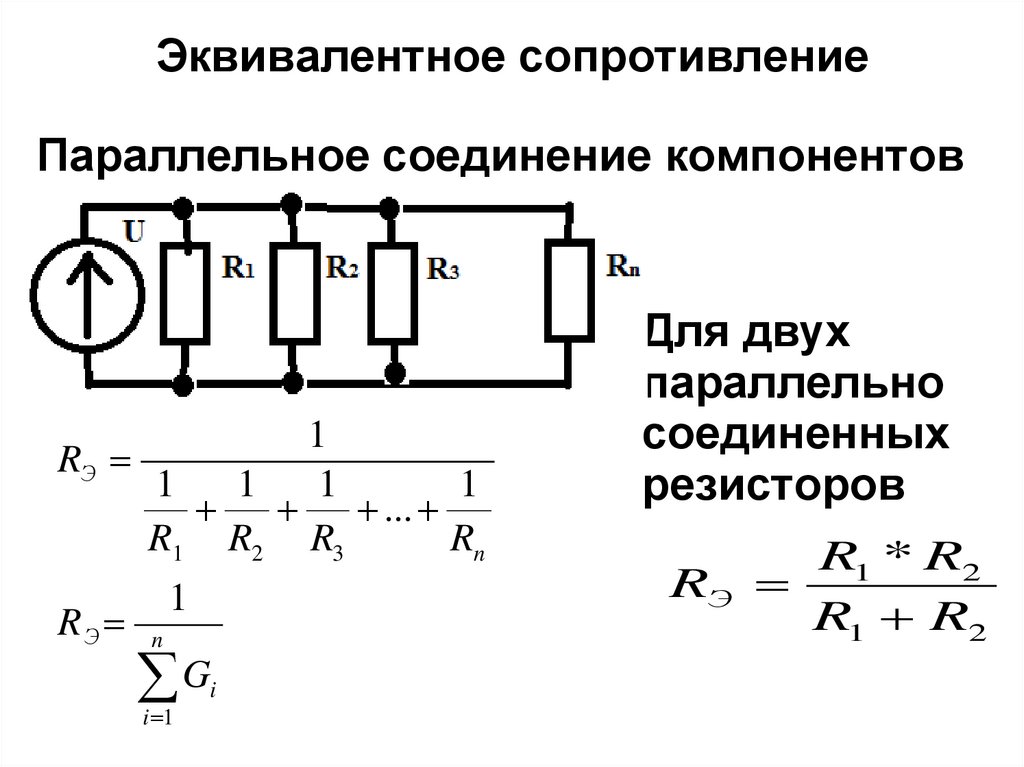 Слишком много резисторов подключены параллельно и последовательно. Всякий раз, когда вы пытаетесь решить схему, подобную той, которую вы видите на экране, прежде всего, посмотрите на схему и попытайтесь понять, какие резисторы соединены последовательно, а какие резисторы подключены параллельно. Если вам все еще трудно понять, вы можете перерисовать схему, чтобы лучше понять соединения. На изображении выше вы можете видеть, что другая схема представляет собой упрощенную версию исходной схемы, которую довольно легко понять.

Итак, в правой части схемы вы видите резисторы 15 Ом и 5 Ом, соединенные последовательно, поэтому решите, 15 + 5 = 20. Вы можете заменить эти два резистора одним резистором 20 Ом. Теперь можно перерисовать схему.

Теперь вы можете видеть, что два резистора имеют одинаковое значение и подключены параллельно. Вы знаете, что если два резистора подключены параллельно и имеют одинаковые значения, то просто разделите значение на 2 или простыми словами просто половина значения, которое будет составлять 10 Ом. Теперь можно дополнительно перерисовать схему и заменить два резистора одним резистором на 10 Ом между точками D и E.

Теперь вы обнаружите, что резистор на 10 Ом включен последовательно с резисторами на 20 Ом. Вы можете добавить два резистора, и вы получите 30 Ом.

Далее вы обнаружите, что резистор на 30 Ом теперь подключен параллельно другому резистору на 30 Ом. Так как резисторы одинаковые и подключены параллельно, то половина значения и вы получите 15 Ом.

Теперь вы обнаружите, что резисторы 5, 15 и 20 включены последовательно. Итак, продолжайте и добавьте их 5 + 15 + 20 = 40.

Теперь этот резистор, который составляет 40 Ом, теперь будет параллелен резистору, подключенному между точками A и B. Так как оба резистора подключены параллельно и того же значения, поэтому мы просто уменьшим вдвое значение. Таким образом, мы получим 20 Ом. Теперь можно перерисовать схему.

Теперь все три резистора соединены последовательно, и теперь вы знаете, что вам нужно сделать, это просто добавить эти резисторы. Итак, 30+20+50=100 Ом.

Как рассчитать эквивалентное сопротивление

Ключевые понятия

• Чистое сопротивление при последовательном соединении
• Чистое сопротивление при параллельном соединении

Введение: больше, так как общее сопротивление уменьшается при параллельном соединении. В этом разделе мы собираемся вывести формулу для расчета чистого сопротивления при последовательном и параллельном соединении. Мы также собираемся рассчитать напряжение и ток в каждой цепи. Объяснение:   Последовательное соединение резисторов:  

Когда резисторы соединены так, что один конец резистора соединен с концом другого и т. д., то образованная цепь представляет собой последовательное соединение резисторов. .

В этой цепи один и тот же ток протекает через разные резисторы, и напряжение на каждом из них разное. Если какой-либо из резисторов перестает работать, то вся цепь разрывается.

В приведенной выше схеме общее сопротивление указано как  

R = R ₁ + R ₂ + ………. + R _N

Теперь с той же точки все уравнение с током, I.  

I × R = (I × R ₁ ) + (I × R ₂ ) + …….. _п )  

þ V = V ₁ + V ₂ + …… .. + V _N

, в эфире, в серии. Подключение A -necials Cniestors,

92

. R = R ₁ + R ₂ +……….+ R _n  

I =

12𝟏𝟐

V = V ₁ + В ₂ + …… .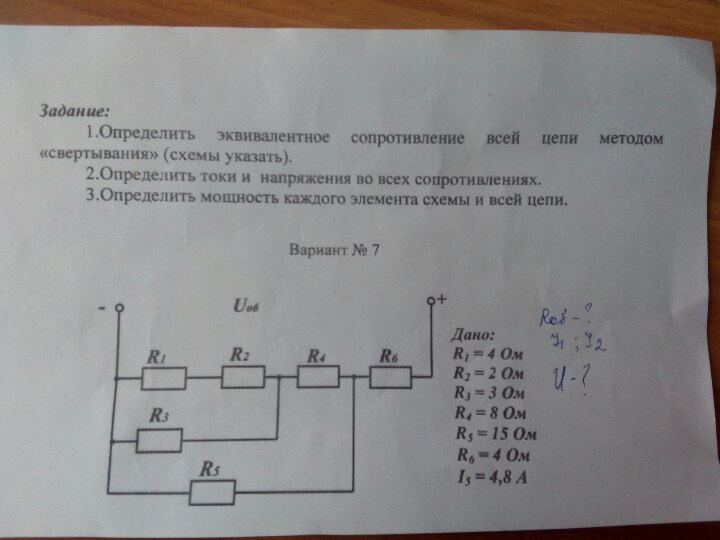 . + V _N

Параллельное соединение резисторов:

. точка и аналогично, другой конец всех резисторов соединяется с одной точкой, тогда образующаяся цепь представляет собой параллельное соединение резисторов.

В этой цепи напряжение одинаково на всех резисторах, а ток разветвляется, когда входит в одну точку соединения, и рекомбинирует, когда выходит из другого конца. Если какой-либо из резисторов перестанет работать, это не повлияет на всю схему.

В приведенной выше схеме общее сопротивление указано как  

1R=1R1+1R2+ . . . . . + 1Rn𝟏𝑹=𝟏𝑹𝟏+𝟏𝑹𝟐+ . . . . . + 𝟏𝑹𝒏

Теперь, поскольку напряжение на каждом резисторе одинаково, мы умножим все уравнение на напряжение, В. 

(V×1R)=VR1+VR2+ . . . . . + VRn𝑽×𝟏𝑹=𝑽𝑹𝟏+𝑽𝑹𝟐+ . . . . . + 𝑽𝑹𝒏

þ I = I ₁ + I ₂ + …… . . + _{N + ……0115}  

Следовательно, при параллельном соединении резисторов

1R=1R1+1R2+. . . . . + 1Rn𝟏𝑹=𝟏𝑹𝟏+𝟏𝑹𝟐+ . . . . . + 𝟏𝑹𝒏

V = same 

I = I ₁ + I ₂ + …….. + I _n  

Questions and answers  

Вопрос 1: Узнайте чистое сопротивление, ток и напряжение на каждом резисторе.  

Ответ:  

Вопрос 2: Определите чистое сопротивление, ток и напряжение на каждом резисторе.  

 Рисунок 4: Вопрос 2 рисунок  

Ответ:  

Вопрос 3: Найдите чистое сопротивление в данной электрической цепи.  

Ответ:  

Резюме

Последовательное соединение:

1. Ток одинаков на каждом резисторе.

Equivalent resistance is defined as the total resistance of the circuit for the resistors connected in series or parallel combination. Resistors are electrical devices that limit the current flow in a circuit and obey Ohm’s law, V = IR. A circuit may have more than one resistor present due to which equivalent resistance is evaluated accordingly. The value of current and voltage depends on the orientation of resistors in the circuit. 

In this article, we will learn about the Equivalent Resistance Formula in Series and Parallel combinations in detail.

What is the Equivalent Resistance?

Equivalent Resistance is the total resistance of the combination of all the resistances in the circuit. Suppose there are n resistance added in the circuit either in series or in parallel combination and if we replace all the resistance with a single resistance such that the current and the voltage difference in the circuit do not change it is called equivalent resistance.

Unit of Equivalent Resistance

Equivalent resistance is denoted by the symbol R_eq. SI unit of the measurement of Equivalent Resistance is Ohm (Ω) and the dimensional formula of the Equivalent Resistance [M¹L²A⁻²T⁻³].

Formula for Equivalent Resistance

Equivalent Resistance is calculated using the Equivalent Resistance Formula, and the equivalent resistance formula is different in series and parallel combinations, i.e., we have two different equivalent resistance formulas they are,

• Equivalent Resistance Formula for Series Combination.
• Equivalent Resistance Formula for Parallel Combination.

Now, let’s learn about both formulas in detail in this article,

Equivalent Resistance Formula for Series Combination

In a series circuit of resistors, n resistors (n > 1) are connected adjacently one after the other, such that the collection of these resistors can be replaced by a single equivalent resistor to give the same resistance value. Here, the sum of the individual resistances will be the equivalent resistance of a series of resistors. The current through each resistor is the same but the voltage gets divided into n parts among the resistors.

R_eq = R₁ + R₂ + R₃ + ….. + R_n

where,
R_eq is the equivalent resistance,
R₁ is the resistance of the first resistor,
R₂ is the resistance of the second resistor,
R₃ is the resistance of the third resistor,
R_n is the resistance of the n^th resistor,

Equivalent Resistance Formula for Parallel Combination

In a parallel circuit of resistors, n resistors (n > 1) are connected parallelly via wires that start from a common point. Here, the sum of the reciprocals of individual resistances equals the reciprocal of the equivalent resistance. The voltage through each resistor is the same but the current gets divided into n parts among the resistors.

1/R_eq = 1/R₁ + 1/R₂ + 1/R₃ + ….. + 1/R_n

where,
R_eq is the equivalent resistance,
R₁ is the resistance of the first resistor,
R₂ is the resistance of the second resistor,
R₃ is the resistance of the third resistor,
R_n is the resistance of the n^th resistor,

How to find Equivalent Resistance?

The equivalent resistance of any circuit can easily be calculated using the steps given below,

Step 1: Study the electric circuit and mark all the resistance in the circuit along with the voltage of the battery.

Step 2: Check whether the resistance added is in series or parallel combination or both.

Step 3: Use the Equivalent Resistance Formula for Series Combination or Parallel combination accordingly.

Step 4: Simplify the formula in step 3 to get the Equivalent Resistance.

Read, More

• Electrical Resistance and Resistivity
• Temperature Dependence of Resistance
• Electrical Resistance Formula

Solved Examples on Equivalent Resistance Formula

Example 1: What is the equivalent resistance if three resistances of 4 Ω, 2 Ω, and 5 Ω are connected in series?

Solution:

We have,

R₁ = 4 Ω
R₂ = 2 Ω
R₃ = 5 Ω

Using the formula we get,

R_eq = R₁ + R₂ + R₃

      = 4 + 2 + 5

      = 11 Ω

Example 2: Find the unknown resistance if three resistances of 2 Ω, 5 Ω, and x Ω are connected in series to give an equivalent resistance of 10 Ω.

Solution:

We have,

R₁ = 2 Ω
R₂ = 5 Ω

R_eq = 10 Ω

Using the formula we get,

R_eq = R₁ + R₂ + R₃

10 = 2 + 5 + x

10 = 7 + x

x = 3 Ω

Example 3: Find the unknown resistance if three resistances of 7 Ω, 3 Ω, and X Ω are connected in series to give an equivalent resistance of 15 Ω.

Solution:

We have,

R₁ = 7 Ω
R₂ = 3 Ω

R_eq = 15 Ω

Using the formula we get,

R_eq = R₁ + R₂ + R₃

15 = 7 + 3 + X

15 = 10 + 

x = 5 Ω

Example 4: What is the equivalent resistance if three resistances of 6 Ω, 3 Ω, and 8 Ω are connected in parallel?

Solution:

We have,

R₁ = 6 Ω
R₂ = 3 Ω
R₃ = 8 Ω

Using the formula we get,

1/R_eq = 1/R₁ + 1/R₂ + 1/R₃

1/R_eq = 1/6 + 1/3 + 1/8

1/R_eq = (4+8+3)/24

1/R_eq = 15/24

R_eq = 24/15 Ω = 1.6 Ω

Example 5: Find the unknown resistance if three known resistances of 4 Ω, 2 Ω, and 1 Ω connected in series with an unknown resistance of X Ω give an equivalent resistance of 0.5 Ω.

Solution:

We have,

R₁ = 4 Ω
R₂ = 2 Ω
R₃ = 1 Ω

R_eq = 0.5 Ω 

Using the formula we get,

1/R_eq = 1/R₁ + 1/R₂ + 1/R₃ + 1/R₄ 

1/0.5 = 1/4 + 1/2 + 1/1 + 1/R₄ 

1/R₄ = 1/4 + 1/2 + 1/1 – 1/0.5

1/R₄ = 1/4

R₄ = 4 Ω

FAQs on Equivalent Resistance Formula

Question 1: What is the “equivalent resistance” formula in the Series combination?

Answer:

The “equivalent resistance” formula in the Series combination is given below,

R_eq = R₁ + R₂ + R₃ + ….. + R_n

Question 2: What is the condition for the series combination of resistance?

Answer:

For the resistor to be connected in series combination the important conditions are,

• The current passing through each resistor is the must be same.
• The resistors are connected in a linear manner.

Question 3: What is the “equivalent resistance” formula in the Parallel combination?

Answer:

The “equivalent resistance” formula in the Parallel combination is given below,

1/R_eq = 1/R₁ + 1/R₂ + 1/R₃ + ….. + 1/R_n

Question 4: What is the condition for the parallel combination of resistance?

Answer:

For the resistor to be connected in parallel combination the important conditions are,

• The voltage difference across each resistor is the same.
• The resistors are connected parallel to each other.

Last Updated :
21 Mar, 2023

Like Article

Save Article

Как найти эквивалентное сопротивление в цепи?

Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:

1. параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
2. последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.

Чему равно эквивалентное сопротивление?

Резисторы соединены последовательно, если по ним течет один и тот же ток. Эквивалентное сопротивление цепи, состоящей из n последовательно соединенных резисторов, равно сумме их сопротивлений: .

Общее сопротивление цепи при параллельном соединении проводников определяется по формуле: 1 R = 1 R 1 + 1 R 2 . Обратное значение общего сопротивления равно сумме обратных значений сопротивлений отдельных проводников. Для проверки формулы можно использовать омметр.

Как найти общее R?

Если известны значения общей силы тока и напряжения в цепи, общее сопротивление вычисляется по закону Ома: R = V/I. Например, напряжение в параллельной цепи равно 9 В, а общая сила тока равна 3 А. Общее сопротивление: RO = 9 В / 3 А = 3 Ом.

Как найти эквивалентное сопротивление?

3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R, где I — ток во внешней цепи (до точки разветвления), U — напряжение внешней цепи, R — сопротивление внешней цепи, т. е. эквивалентное сопротивление.

Как найти общий ток в цепи?

Если известен общий ток, то можно найти ток ветви, умножив общий ток на сопротивление противоположной ветви и разделить на сумму сопротивлений ; .

Как найти напряжение в электрической цепи?

Закон Ома для участка цепи:

1. I — сила тока (в системе СИ измеряется — Ампер)
2. Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
3. Формула: I=frac.
4. U — напряжение (в системе СИ измеряется — Вольт)

Как складывается сопротивление?

R = R1 + R2. При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников. Этот результат справедлив для любого числа последовательно соединенных проводников.

Что называется эквивалентным сопротивлением?

Если несколько сопротивлений соединенных последовательно, параллельно заменяется одним равным по значению, то такое сопротивление — эквивалентное.

Как найти ток в параллельной цепи?

Общая сила тока в параллельной цепи равна сумме силы тока на каждом элементе этой цепи. То есть, если известна сила тока на каждом резисторе, сложите эти силы тока, чтобы найти общую силу тока в параллельной цепи: IT = I1 + I2 + I3 + … Общее сопротивление в параллельной цепи.

Как складываются сопротивления при параллельном соединении?

Из закона Ома и первого и второго правил Кирхгофа следует: При параллельном соединении величина обратная полному сопротивлению, равна сумме величин, обратных сопротивлений ветвей. При параллельном соединении полное сопротивление цепи меньше самого малого из сопротивлений ветвей.

Как найти емкость конденсатора при параллельном соединении?

C = Q / U = (Q1 + Q2 + Q3) / U = C1 + C2 + C3, т. е. при параллельном соединении конденсаторов общая емкость равна сумме емкостей отдельных конденсаторов.

Как найти сопротивление R?

Сопротивление проводника прямо пропорционально напряжению на его концах и обратно пропорционально величине силы тока, протекающего через него. Формула для нахождения сопротивления по закону Ома, если известны сила тока и напряжение: R = U I {R= dfrac{U}{I}} R=IU, где R — сопротивление, U — напряжение, I — сила тока.

Как найти коэффициент сопротивления воздуха?

Pv = cx·S·v2·ρ/2, где S – площадь фронтальной проекции автомобиля, м2; v – скорость движения автомобиля относительно воздуха, м/с; ρ – плотность воздуха, кг/м3; cх – коэффициент аэродинамического сопротивления.

Параллельное соединение резисторов. Калькулятор для расчета

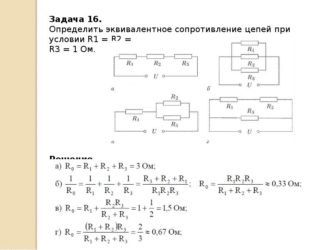
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Пример  №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление  R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.

Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи  можно определить как:

I = I1 + I2

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

Отправить сообщение об ошибке.

Источник: http://www.joyta.ru/7362-parallelnoe-soedinenie-rezistorov/

Эквивалентное сопротивление

> Теория > Эквивалентное сопротивление

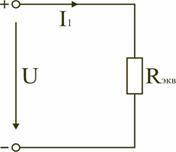
Если электрическая цепь содержит несколько резисторов, то для подсчёта её основных параметров (силы тока, напряжения, мощности) удобно все резистивные устройства заменить на одно эквивалентное сопротивление цепи. Только для него должно выполняться следующее требование: его сопротивление должно быть равным суммарному значению сопротивлений всех элементов, то есть показания амперметра и вольтметра в обычной схеме и в преобразованной не должны измениться. Такой подход к решению задач называется методом свёртывания цепи.

Внимание! Расчёт эквивалентного (общего или суммарного) сопротивления в случае последовательного или параллельного подключения выполняется по разным формулам.

Последовательное соединение элементов

В случае последовательного подключения все приборы соединяются последовательно друг с другом, а собранная цепь не имеет разветвлений.

При таком подключении сила тока, проходящая через каждый резистор, будет одинаковая, а общее падение напряжения складывается из суммарных падений напряжения на каждом из приборов.

Последовательное подключение приборов

Чтобы определить суммарное значение в этом случае, воспользуемся законом Ома, который записывается следующим образом:

I = U/R.

Из вышестоящего выражения получаем значение R:

R = U/I (1).

Поскольку при последовательном соединении:

• I = I1 = I2 =…= IN (2),
• U = U1 + U2 +…+ UN (3),

формула для расчёта эквивалентного сопротивления (Rобщ или Rэкв) из (1) – (3) будет иметь вид:

• Rэкв = (U1 + U2 + …+ UN)/I,
• Rэкв = R1 + R2 + … + RN (4).

Таким образом, если имеется N последовательно соединённых одинаковых элементов, то их можно заменить на одно устройство, у которого:

Rобщ = N·R (5).

Параллельное соединение

При таком подключении входы от всех устройств соединены в одной точке, выходы – в другой точке. Эти точки в физике и электротехнике называются узлами. На электрических схемах узлы представляют собой места разветвления проводников и обозначаются точками.

Расчет эквивалентного сопротивления также выполняем с помощью закона Ома.

В этом случае общее значение силы тока складывается из суммы сил токов, протекающих по каждой ветви, а величина падения напряжения для каждого устройства и общее напряжение одинаковые.

Если имеются N резистивных устройств, подключенных таким образом, то:

I = I1 + I2  + … + IN (6),

U = U1 = U2 = … = UN (7).

Из выражений (1), (6) и (7) имеем:

• Rобщ = U/(I1 + I2 + …+ IN),
• 1/Rэкв = 1/R1 + 1/R2 +…+ 1/RN (8).

Если имеется N одинаковых резисторов, имеющих подключение данного типа, то формула (8) преобразуется следующим образом:

Rобщ = R · R / N·R = R / N (9).

Если соединены несколько катушек индуктивности, то их суммарное индуктивное сопротивление рассчитывается так же, как и для резисторов.

Расчёт при смешанном соединении устройств

В случае смешанного подключения присутствуют участки с последовательным и параллельным подключениями элементов.

При решении задачи используют метод сворачивания цепи (метод эквивалентных преобразований). Его используют для вычисления параметров в том случае, если есть один источник энергии.

Предположим, задана следующая задача. Электрическая схема (см. рис. ниже) состоит из 7 резисторов. Рассчитайте токи на всех резисторах, если имеются следующие исходные данные:

• R1 = 1Ом,
• R2 = 2Ом,
• R3 = 3Ом,
• R4 = 6Ом,
• R5 = 9Ом,
• R6 = 18Ом,
• R7 = 2,8Ом,
• U = 32В.

Из закона Ома имеем: 

I = U/R,

где R – суммарное сопротивление всех приборов.

Его будем находить, воспользовавшись методом сворачивания цепи.

Элементы R2 и R3 подключены параллельно, поэтому их можно заменить на R2,3, величину которого можно рассчитать по формуле:

R2,3= R2·R3 / (R2+R3).

R4, R5 и R6 также включены параллельно, и их можно заменить на R4,5,6, которое вычисляется следующим образом:

1/R4,5,6 = 1/R4+1/R5+1/R6.

Таким образом, схему, изображённую на картинке выше, можно заменить на эквивалентную, в которой вместо резисторов R2, R3 и R4, R5, R6 используются R2,3 и R4,5,6.

Согласно картинке выше, в результате преобразований получаем последовательное соединение резисторов R1, R2,3, R4,5,6 и R7.

Rобщ может быть найдено по формуле:

Rобщ = R1 + R2,3 + R4,5,6 + R7.

Подставляем числовые значения и рассчитываем R для определённых участков:

• R2.3 = 2Ом·3Ом / (2Ом + 3Ом) = 1,2Ом,
• 1/R4,5,6 = 1/6Ом + 1/9Ом + 1/18Ом = 1/3Ом,
• R4,5,6 = 3Ом,
• Rэкв = 1Ом + 1,2Ом + 3Ом + 2,8Ом= 8Ом.

Теперь, после того, как нашли Rэкв, можно вычислять значение I:

I = 32В / 8Ом = 4А.

После того, как мы получили величину общего тока, можно вычислить силу тока, протекающую на каждом участке.

Поскольку R1, R2,3, R4,5,6 и R7 соединены последовательно, то:

I1 = I2,3 = I4,5,6 = I7 = I = 4А.

На участке R2,3 напряжение находим по формуле:

• U2,3 = I2,3·R2,3,
• U2,3 = 4А·1,2Ом = 4,8В.

Поскольку R2 и R3 подключены параллельно, то U2,3 = U2 = U3, следовательно:

• I2 = U2 / R2,
• I2 = 4,8В / 2Ом = 2,4А,
• I3 = U3 / R3,
• I3 = 4,8В / 3Ом = 1,6А.

Проверяем правильность решения:

• I2,3 = I2 + I3,
• I2,3 = 2,4А + 1,6А = 4А.

На участке R4,5,б напряжение также находим, исходя из закона Ома:

• U4,5,6 = I4,5,6·R4,5,6,
• U4,5,6 = 4А·3Ом = 12В.

Так как R4, R5, Rб подключены параллельно друг к другу, то:

U4,5,6 = U4 = U5 = U6 = 12В.

Вычисляем I4, I5, I6:

• I4 = U4 / R4,
• I4 = 12В / 6Ом = 2А,
• I5 = U5 / R5,
• I5 = 12В / 9Ом » 1,3А,
• I6 = U6 / R6,
• I5 = 12В / 18Ом » 0,7А.

Проверяем правильность решения:

I4,5,6 = 2А + 1,3А + 0,7А = 4А.

Чтобы автоматизировать выполнение расчётов эквивалентных значений для различных участков цепи, можно воспользоваться сервисами сети Интернет, которые предлагают на их сайтах выполнить онлайн вычисления нужных электрических характеристик. Сервис обычно имеет встроенную специальную программу – калькулятор, которая помогает быстро выполнить расчет сопротивления цепи любой сложности.

https://www.youtube.com/watch?v=OP6nJnzO1Sc

Таким образом, использование метода эквивалентных преобразований при расчёте смешанных соединений различных устройств позволяет упростить и ускорить выполнение вычислений основных электрических параметров.

Источник: https://elquanta.ru/teoriya/ehkvivalentnoe-soprotivlenie.html

Эквивалентное сопротивление резисторов

Расчет реальной электрической цепи в идеальном виде невозможен по причине отсутствия математических методик учета индивидуальных параметров каждого составляющего элемента. Это естественно, так как любая деталь имеет свои паразитные характеристики, которые нереально учесть при расчетах.

Для устранения этой проблемы было введено понятие эквивалентной замены. При этом в расчет принимается только одна определяющая характеристика элемента.

Так, например, эквивалентное сопротивление резисторов в электрической схеме, отображает только величину сопротивления без влияния на него сторонних факторов.

В электротехнике существует два основных варианта включения деталей в электрической цепи – это последовательное и параллельное соединение. Объединяющей для них является смешанная схема, которая по сути может быть разбита на участки с вышеприведенными характеристиками.

Рассмотрим эквивалентное соединение резисторов в каждом отдельном случае.

Эквивалентное сопротивление при последовательно соединенных резисторов

При данном типе размещения резисторов в цепи условная схема будет соответствовать рис. 1.

Рисунок 1

Для того чтобы определить эквивалентное сопротивлениерезисторов необходимо вспомнить закон Ома. Для последовательного соединения онгласит что общее, а в нашем случае эквивалентное сопротивление, соответствуетследующему уравнению:

Rэкв=R1+R2+R3+RN-1+RN

Кроме теории, данное суммирование значений сопротивленийэлементов, имеет и практическое применение – в случае необходимости всегда можнозаменить несколько резисторов одним. Также имеет место и обратное утверждение –при отсутствии деталей с требуемой характеристикой ее можно заменить нанесколько других, эквивалентное сопротивление которых будет соответствоватьтребуемому значению.  Все это справедливои для параллельного соединения резисторов, только с некоторыми особенности.

Эквивалентное сопротивление при параллельном соединении резисторов

Общая схема при данном включении резисторов в цепь соответствует рис. 2.

Рисунок 2

Определить эквивалентное сопротивление параллельносоединенных резисторов позволяет закон Ома согласно которому, в данном варианте,справедливо равенство:

1/R экв =1/R1+1/R2+1/R3+1/RN-1+1/RN

Возвращаясь к нашему примеру с резисторами 10, 20 и 30 Ом. Можноопределить эквивалентное сопротивление для данного случая, преобразуя уравнениеи получаем следующую формулу:

R экв = R1 х R2х R3 / (R1 xR2) + (R1x R3) + (R2 xR3) = 5,45Ом

Важный момент: При параллельном включении резисторов в цепь эквивалентное сопротивление будет всегда меньше наименьшего значения отдельного элемента. При последовательном соединении R экв обязательно больше самого большого параметра.

Эквивалентное сопротивление при смешанном соединении резисторов

Определение эквивалентного сопротивления при смешанном соединении резисторов не представляет особых сложностей. Для этого достаточно разбить существующую цепочку на логические составляющие – блоки. Т.е. максимально упростить схему, приведя ее в соответствие с характеристиками свойственных тому или иному типу соединения. На рис. 3 приведена типичная схема упрощения, которая получила название метод свертывания цепи.

Рисунок 3

Данная схема позволяет наглядно понять, как можно определить эквивалентное сопротивление резисторов при смешанном соединении. Обращаем внимание, что начинать процесс упрощения можно в произвольном порядке.

 Определение эквивалентного сопротивления для резисторов необходимо осуществлять в зависимости от типа соединения.

В заключение вернемся к самому понятию эквивалентной замены резисторов. В рассмотренных нами случаях речь шла об идеальном варианте. То есть в расчет принимается только величина сопротивления при нулевых значениях остальных характеристик. Также обращаем внимание, что при составлении эквивалентной схемы любых элементов электрической цепи, не только резисторов, можно вводить дополнительные переменные, которые будут влиять на конечные итоги.

Источник: http://podvi.ru/elektrokompanenty/ekvivalentnoe-soprotivlenie-rezistorov.html