Как найти экваториальные координаты светил

Принципы экваториальной системы небесных координат и примеры навигационных расчетов.

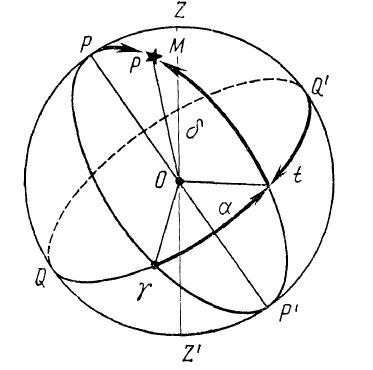
В отличие от горизонтальной системы небесных координат, где за основную плоскость принят истинный горизонт небесной сферы, в экваториальной системе небесных координат основной плоскостью является плоскость небесного экватора, а полюсами являются полюсы мира. Положение светила в этой системе координат определяется склонением и часовым углом светила.

Принцип экваториальной системы небесных координат

Склонением светила δ называется угол, заключенный между плоскостью небесного экватора и направлением на светило из центра небесной сферы. Склонение светила измеряется от 0 до ±90°.
Положительное склонение отсчитывается в направлении к Северному полюсу мира, а отрицательное — к Южному. Склонение Солнца, Луны и планет обычно берется из авиационного астрономического ежегодника для каждого часа гринвичского времени, а навигационных звезд — в таблице экваториальных координат звезд на начало каждого года ввиду изменения его за год на 1—2 градуса. Иногда вместо склонения светила пользуются другой координатой — полярным расстоянием.

Полярным расстоянием Р называется угол в плоскости круга склонения, заключенный между осью мира и направлением на светило из центра небесной сферы. Полярное расстояние отсчитывается от Северного полюса мира к Южному от 0 до 180°. Между полярным расстоянием и склонением светила имеется следующая зависимость:

Р + δ = 90°, откуда Р = 90° — δ; δ = 90° — Р

Светила, находящиеся на одной суточной параллели, имеют одинаковые склонения и одинаковые полярные расстояния. Склонение, или полярное расстояние, определяет положение светила на круге склонения. Положение же самого круга склонения на небесной сфере определяется часовым углом светила.

Часовым углом светила t называется двугранный угол в плоскости небесного экватора, заключенный между плоскостью небесного меридиана и плоскостью круга склонения светила.
Часовой угол отсчитывается от южного направления небесного меридиана по ходу часовой стрелки (к западу) до круга склонения светила от 0 до 360°. Важно знать, что отсчет часового угла светила ведется в направлении суточного вращения небесной сферы.

При решении некоторых задач для удобства часовые углы светил отсчитывают от 0 до 180° к западу и востоку и соответственно обозначают их t3 и tB. В Авиационном астрономическом ежегоднике даны западные часовые углы светил от 0 до 360°, а в расчетных таблицах для Солнца, Луны и планет — от 0 до 180°.

Важное значение имеет зависимость между часовым углом светила и долготой места наблюдателя. Выше указывалось, что часовой угол светила принято отсчитывать к западу от небесного меридиана. Так как плоскость небесного меридиана совпадает с географическим меридианом наблюдателя, то в один и тот же момент времени часовые углы одного и того же светила для наблюдателей, находящихся на разных меридианах, будут различны.
Очевидно, что в один и тот же момент времени разность местных часовых углов светила равна разности долгот наблюдателей t2-t1=λ2-λ1. Если принять в данном соотношении λ1=0, то t1 = tгр. Принимая λ1=λ и t2=t, получаем t=tгр+-λ^b₃.

Как видно из полученной формулы, местный часовой угол светила отличается от гринвичского на значение долготы наблюдателя. В практике часто вместо часового угла светила пользуются другой координатой — прямым восхождением светила.

Прямым восхождением светила α называется угол, заключенный между плоскостью круга склонения точки весеннего равноденствия (начального круга склонения) и плоскостью круга склонения светила.

Точкой весеннего равноденствия называется точка пересечения плоскости небесного экватора центром Солнца (21 марта) при его видимом годовом движении по небесной сфере. Эту точку принято обозначать символом созвездия Овен, в котором она находилась в эпоху зарождения астрономии.

Прямое восхождение светила отсчитывается в плоскости небесного экватора от точки весеннего равноденствия против хода часовой стрелки (к востоку) до круга склонения светила от 0 до 360°. Прямое восхождение светила и его часовой угол можно измерять не только углом, но и дугой небесного экватора, а склонение и полярное расстояние светила — дугой круга склонения.

Особенности экваториальной системы небесных координат

В авиационной астрономии экваториальная система небесных координат дополнительно подразделяется на две системы.

В первой экваториальной системе положение светила на небесной сфере определяется склонением и часовым углом, а во второй — прямым восхождением и склонением светила. Первая экваториальная система берется в основу при разработке и создании астрономических компасов, а также при составлении расчетных таблиц. Вторую экваториальную систему используют для составления звездных карт и таблиц экваториальных координат звезд.

Экваториальная система небесных координат является более практичной по сравнению с горизонтальной. Она имеет большое практическое значение в авиационной астрономии. С этой системой связано измерение времени и определение места самолета, т. е. решение главных вопросов практической авиационной астрономии.

Основным ее достоинством является то, что экваториальные координаты светил не зависят от места наблюдателя на земной поверхности, за исключением местного часового угла. Часовой угол светила зависит не только от долготы места наблюдателя, но и от времени наблюдения. Он непрерывно изменяется пропорционально времени, и это позволяет учитывать в астрокомпасах при помощи часового механизма его изменение за счет вращения Земли.

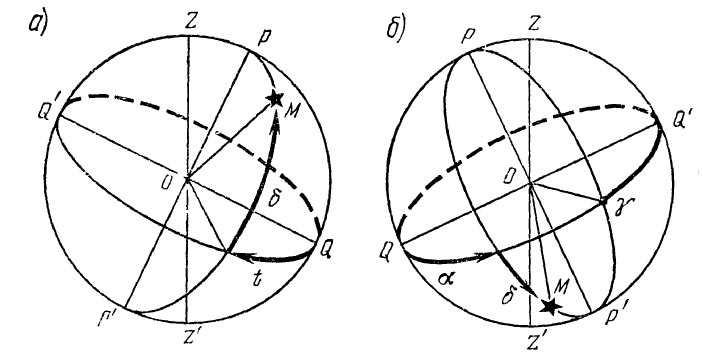
Ниже приведены примеры графического изображения положения светил на небесной сфере по заданным экваториальным координатам.

• Пример 1. Западный часовой угол светила t3 = 230°; склонение светила δ = +60°.
• Пример 2. Прямое восхождение светила α =300°; склонение светила δ = -60°.

---

источник: по книге “Авиационная астрономия”

Экваториа́льная систе́ма координа́т — система небесных координат, в которой фундаментальной плоскостью является плоскость небесного экватора. Экваториальная система координат имеет две формы: первую и вторую экваториальные системы. Первая из них связана с земным шаром и вращается вместе с ним, вторая неподвижна относительно удалённых звёзд^[1].

Используемые координаты[править | править код]

Одной из координат является либо склонение , либо, реже — полярное расстояние .

Склонение светила лежит в диапазоне от −90° до +90° и равно углу между плоскостью экватора и направлением на светило, причём для светил в северном полушарии эта величина положительна, а в южном — отрицательна.

Полярное расстояние равняется углу между светилом и северным полюсом мира и меняется в диапазоне от 0° до +180°. Склонение и полярное расстояние взаимозаменяемы и тесно связаны: ^[1].

Другой координатой может быть либо часовой угол , либо прямое восхождение .

Часовой угол равен длине дуги экватора от небесного меридиана до круга склонения светила и отсчитывается в направлении вращения небесной сферы. Иногда используется понятие «гринвичский часовой угол»: в этом случае вместо небесного меридиана используется гринвичский меридиан.

Прямое восхождение равно длине дуги экватора от точки весеннего равноденствия до круга склонения светила и отсчитывается против направления вращения небесной сферы. С прямым восхождением также связано так называемое звёздное дополнение , используемое в навигации: оно также равно длине дуги от точки весеннего равноденствия до круга склонения светила, но отсчитывается в направлении вращения небесной сферы. Таким образом, ^[1].

Как правило, эти величины измеряются в часах и лежат в диапазоне от 0^h до 24^h не включительно. Соответственно, в градусной мере это от 0° до 360°. Однако, иногда считают, что они лежат в пределах от 0° до 180° (от 0^ч до 12^ч) к западу и от 0° до −180° (от 0^ч до −12^ч) к востоку^[1][2].

Первая экваториальная система координат[править | править код]

В первой экваториальной системе координат используется склонение (или полярное расстояние) и часовой угол. В этой системе координаты неподвижных звёзд непостоянны: у них меняется часовой угол из-за суточного вращения Земли. Однако, в отличие от горизонтальных координат, часовой угол равномерно меняется со временем, а склонение остаётся постоянным. Кроме того, часовой угол точки весеннего равноденствия по определению равен местному звёздному времени^[1][3].

Вторая экваториальная система координат[править | править код]

Во второй экваториальной системе координат используется склонение (или полярное расстояние) и прямое восхождение. В отличие от первой экваториальной системы, во второй координаты из-за суточного движения не изменяются, так как точка весеннего равноденствия неподвижна. По этой причине координаты небесных тел удобно хранить и записывать во второй экваториальной системе координат^[1].

Связь первой и второй экваториальной системы координат[править | править код]

Связь первой и второй экваториальной систем определяется в первую очередь связью часового угла и прямого восхождения. Эти величины связаны со звёздным временем : . Строго говоря, сумма часового угла и прямого восхождения может быть больше 24^h, и в таком случае оказывается верным равенство по модулю 24^h[1].

Связь с другими системами координат[править | править код]

Для связи с другими системами координат, к примеру, горизонтальной или эклиптической, используется параллактический треугольник^[4].

Общие характеристики[править | править код]

• Склонение измеряется в градусах, минутах и секундах дуги. Положительное направление — к северу от небесного экватора, отрицательное — к югу. При склонениях следует указывать знак.
• Объект на небесном экваторе имеет склонение 0°.
• Склонение северного полюса небесной сферы равно +90°.
• Склонение южного полюса равно −90°.
• Склонение небесного объекта, который проходит через зенит, равно широте наблюдателя.

В Северном полушарии Земли для заданной широты :

• Небесные объекты со склонением не заходят за горизонт.
• Если склонение объекта , то такой объект не будет наблюдаться на этой широте.

Поскольку расположение плоскости небесного экватора вследствие прецессии постепенно изменяется, то для экваториальной системы координат всегда указывают эпоху, которая определяет некоторое расположение основной плоскости и, соответственно, направление на точку весеннего равноденствия.

Примечания[править | править код]

Ссылки[править | править код]

Астрономический энциклопедический словарь

§ 4. Небесные координаты и звёздные карты

ВОПРОСЫ 

1. Какие координаты светила называются экваториальными?

2. Меняются ли экваториальные координаты звезды в течение суток?

3. Какие особенности суточного движения светил позволяют использовать систему экваториальных координат?

4. Почему на звёздной карте не показано положение Земли?

5. Почему на звёздной карте изображены только звёзды, но нет ни Солнца, ни Луны, ни планет?

6. Какое склонение — положительное или отрицательное — имеют звёзды, находящиеся к центру карты ближе, чем небесный экватор?

Упражнение 3

1. Выразите в часовой мере 90°, 103°.

2. Выразите в угловой мере прямое восхождение, равное 5 ч 24 мин, 18 ч 36 мин.

3. Угловое расстояние Сириуса (а Большого Пса) от Полярной звезды составляет 106°. Положительное или отрицательное склонение имеет Сириус?

4. По координатам, приведённым в списке ярких звёзд (приложение V), найдите некоторые из них на звёздной карте.

5. Определите по карте координаты нескольких ярких звёзд. Сравните полученные данные с координатами, приведёнными в их списке.

Задание 5. Найдите на модели небесной сферы её основные круги, линии и точки: горизонт, небесный экватор, небесный меридиан, отвесную линию, ось мира, зенит, юг, запад, север, восток.

Часть 3.
Астролябии и как ими астроляпить пользоваться.

Начало ЗДЕСЬ.

Продолжим разбирать нашу Астролябию.
Как по ней определить координаты Светила, Звезды?

Рис.1

Измерив высоту Солнца или звезды с помощью алидады, поворачивают паук так, чтобы изображение точки эклиптики, в которой Солнце находится в данный момент года, либо изображение звезды попало на изображение альмукантарата, соответствующего этой высоте. При этом на лицевой стороне астролябии получается стереографическое изображение неба в момент наблюдения, после чего определяется азимут, координаты светила и точное время, а также гороскоп (букв. «указатель часа») — градус эклиптики, восходящий над горизонтом в момент наблюдения.

Согласно данной простой инструкции:
Определим звезду под номером 6 в правом верхнем углу, на которую указывает алибада, и ее координаты.

Рис.2

Это звезда

СПИКА

(6) из созвездия Девы.

Определим экваториальные координаты звезды.

Склонение  можно легко определить по шкале, нанесенной на Линейку.
Ориентировочно  –11° с небольшим (по картинке сложно точно определить).

Экваториальные координаты Звезды Спика на 2000 год:
прямое восхождение α = 13 ч. 25 м. (долгота);  склонение δ = – 11°10′(широта).
Видим, что склонение звезды, а соответственно широта ее на небосводе практически не изменилась.

А вот с определением долготы дело обстоит сложнее.
Прямое восхождение (долгота) равно 16,5 часов, визуально по шкале с римскими цифрами. Алибада-линейка указывает на середину между XVI и XVII на внешнем лимбе круга.
То есть α = 16 ч. 30 м. – прямое восхождение, которое на 3 часа больше, по сравнению с 13,5 ч. в 2000 году?? Разница очень большая (1 час = 15°)!!

Разберемся с данной нестыковкой.

Часовой отсчет идет от Севера (NORD) – «0» часов, далее по часовой стрелке.
На Эклиптическом круге паука (Рис.1) северное направление соответствует знаку Рака (♋).
Это указывает на июнь месяц, а переход из Близнецов в Рак на день Летнего солнцестояния (ЛС).

Посмотрим внимательно на Рис.2.
Видим, что звезда Спика находится рядом с Западом (на шкале QUEST).
Логически, звезда находится на Заходе – закате.

А вот и картинка неба 22.06.2000 в полночь 0.00 ч.

Скрин 2. Точка наблюдения Лондон – Гринвич.

Справа на закате на Западе видим звезду

Спика

(6). Она как раз находится немного за пределами Эклиптики, как и на Рис. 2. Эклиптика здесь указана белой дугой внизу.

По сути, Вид этой карты полностью соответствует Зодиакальному (эклиптическому) кругу на пауке Астролябии (Рис. 1 и 2), только с «эффектом перевернутого листа», в зеркальном отображении. Север с Югом поменян местами.

Есть и существенное Различие. Это градация часового Прямого Восхождения.

Вспомним, что такое Экваториальные координаты светила https://youtu.be/CdF8DNZWjno
Прямым восхождением (α) светила называется дуга небесного экватора от точки весеннего равноденствия до круга склонения светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга склонения светила.
Прямые восхождения отсчитываются в сторону, противоположную суточному вращению небесной сферы, в пределах от 0° до 360° (в градусной мере) или от 0 ч. до 24 ч. (в часовой мере).

Это значит, что Точка отсчета прямого восхождения находится на Востоке (Солнце встает в день весеннего равноденствия) – «0» (24) часов. Далее координата движется по часовой стрелке.
Что мы собственно и наблюдаем на современной Карте астрокалькулятора.

Такой Вид (Скрин 2.) карта – небосвод имеет 21 марта в день ВР, в 6.00 до восхода Солнца; 22 июня в день ЛС, в полночь 0.00 ч. А также 22 сентября в 18.00 ч., ОР и 21 декабря в 12.00 ч., ЗС.

Произведем небольшой расчет.

Рассмотрим Скрин 2. Отсчет от «0» часов на Востоке, по часовой вверх +6 часов – Север, далее +6 часов – Запад, далее +1 час 25 минут. Итого 13 часов 25 минут.

Скрин 3. Эфемериды звезды Спика

По астрокалькулятору на 22.06. 2000 г. Спика имела Прямое восхождение  α = 13 ч. 25 м.
Азимут Спики равен 246°. Так и есть.

Рассмотрим Рис.1. Если взять Отсчет от «0» часов на Востоке, вниз +6 часов до Севера, далее +6 часов до Запада, далее +1 час 30 минут. Отсчет здесь мы производим против часовой стрелки, в зеркальном отражении.  Итого α = 13 часов 30 минут. Данное Прямое восхождение ближе к истине, если его определять современным научным методом.

Однако, ранее, по шкале внешнего лимба астролябии мы определили α = 16 ч. 30 м.?
Это связано исключительно с точкой отсчета. Отсчет велся от северного направления.
На астролябии реперный «0» жестко закреплен за Севером.

Проверить правильность расчетов можно, используя координату  Часовой угол t из первой экваториальной системы координат, вместо Прямого восхождения.

Часовым углом t светила называется дуга небесного экватора от верхней точки небесного экватора  (то есть точки пересечения небесного экватора с небесным меридианом) до круга склонения светила,   или  двугранный  угол между плоскостями небесного меридиана и круга склонения светила.   
Часовые углы отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от верхней точки небесного экватора, в пределах от 0° до 360° (в градусной мере) или от 0 ч. до 24 ч. (в часовой мере). Иногда часовые углы отсчитываются от 0° до +180° (от 0h до +12h) к западу и от 0° до −180° (от 0h до −12h) к востоку.

На Скрин 3, вверху, в эфемеридах записан округленно Часовой угол  t = 04 ч. 33 м. и зеленой линией отражен отсчет угла согласно вышеизложенному правилу.

Для астролябии на Рис.2 Часовой угол  t = 04 ч. 30 м., тоже отмечен зеленой линией. Отсчет угла произведен к западу по правилу, только по часовой стрелке – в зеркальном отражении.

Итак, мы вычислили экваториальные координаты звезды Спика на Астролябии. Они приближенно и округленно такие же, как в 2000 году:
Прямое восхождение α = 13 ч. 30 м. (или Часовой угол  t = 04 ч. 30 м.):
Склонение δ = – 11°10′.
Картинка Астролябии нарисована в современную эпоху.

По астролябии можно вычислить точное время в момент наблюдения.
Звёздное время , s — часовой угол точки весеннего равноденствия. Звёздное время используется астрономами, чтобы определить, куда надо направить телескоп, чтобы увидеть нужный объект.
Зная прямое восхождение звезды и, измерив ее часовой угол, можно определить звездное время. Между звездным временем, часовым углом и прямым восхождением светила имеется очевидная зависимость, которую через координаты звезды можно записать в виде: S =  t + a.
Из этой зависимости следует, что звездное время в любой момент равно сумме часового угла звезды и ее прямого восхождения.
Обычно в астрономических обсерваториях звездные часы проверяют по кульминирующей звезде. Поскольку в этот момент часовой угол звезды равен нулю, то звездное время будет соответствовать прямому восхождению данной звезды, т. е. S = a.
Не буду утомлять читателя более сложными расчетами Звездного времени, перевода его в Местное.
Для особо интересующихся можно посмотреть Астрономический калькулятор и ЗВЕЗДНОЕ ВРЕМЯ В РЕШЕНИИ ЗАДАЧ ПО АСТРОМЕТРИИ.

Склонение δ и прямое восхождение α светил при вращении небесной сферы не изменяются, но они могут меняться из-за движений светил, не связанных с суточным вращением.
Высота h, азимут A и часовой угол t светил постоянно изменяются вследствие вращения небесной сферы, так как отсчитываются от точек, не связанных с этим вращением.

Для закрепления понимания принципа работы подобных инструментов рассмотрим реальную простенькую Астролябию.

Рис. 3. Астролябия парижская
Полный круг Астролябии очерчивает границу Южного Тропика.

Надписи на данной Астролябии понятны. Стрелочками на «пауке» указаны важные звезды:
(Стрелки, указывающие на звезды на пауках могут быть различными, дугообразными с разными изысками – см. начало Части 3)

Spi – Спика (Дева)
Arc – Арктур (Волопас)
Den – Денеб (Лебедь)
Veg – Вега (Лира)
Alt – Альтаир (Орел)
Ald – Альдебаран (Телец)
Rig – Ригель (Орион)
Sir – Сириус (Большой Пес)

В какое время возможно наблюдение за данными звездами в Париже?

Воспользуемся Астрокалькулятором.

20 июня, ЛС, полночь 0.00 по Гринвичу или 1.00 по Парижу (взят 1800 год).

Скрин 4.

Альтаир – Денеб – Вега – Арктур (красная линия) видны на небосводе. Спика находится над горизонтом, чуть ниже эклиптики. Звезды Альдебаран, Ригель, Сириус (отмечены голубым) не попадают в обозрение неба на широте Парижа в данный момент времени.

Здесь мы видим Звездное небо для Наблюдателя с Земли.
Изображение развернуто на 90° для лучшего восприятия соответствия с наблюдаемым небосводом на диске Астролябии (Рис.3).

Мы вновь наблюдаем «эффект перевернутого листа», зеркальное отображение. Для наглядности – проведена красная линия звезд Арктур – Денеб – Вега – Альтаир.
Небосвод Астролябии исполнен в Проекции на Землю.

Однако, нас интересует Сириус, на него направлена алибада.

Определим экваториальные координаты звезды Сириус.

Рис. 4

«0» отсчет начинается внизу, с Севера, чему соответствует конец Марта (Mars) и 0 градусов Эклиптики, указанные на колесе «паука».
«Паук» на Астролябии указывает на день весеннего равноденствия 21 марта.

Сириус на Астролябии находится на Западе (противоположной Востоку, подписанного на диске EST), причем у самого Южного тропика. Наблюдать в Париже мы его не сможем, он будет за линией горизонта.

Склонение определяем по шкале, нанесенной на Линейку.
Ориентировочно  –16° (нет мелкой градации шкалы, сложно точно определить).

Вид звездного неба 21 марта, день ВР, 1.00 час ночи, Париж (взят 1800 год).

Скрин 5.

«0» отсчет будет на Востоке в 6.00 во время восхода Солнца. В полночь 0 (24) часов Прямого восхождения начинается сверху, с Севера.

Запад на 6 часов. Сириус ниже Западной точки.

Скрин 6.

На 1800 г.: Прямое восхождение α = 06 ч.36 м. (синим цветом)
Часовой угол  t = 5 ч. 24 м. (зеленым цветом).
Склонение δ = – 16°27′ (Сириус ниже точки горизонта).
Азимут Сириуса равен 260°.

На Астралябии Прямое восхождение Сириуса указано на отметке 17, 5 часов (между 17 и 18 часами).

Если к Рис.3,4 применить «эффект перевернутого листа», получим картинку небосвода, полностью соответствующую на Скрин 5, а отсчет часов от Севера произвести с учетом зеркального отражения, получим искомые 06 ч.36 м. – Прямое восхождение.

Итак, мы стали немного понимать, как раньше использовалась Астролябия, как по ней можно было определить координаты небесных объектов, вычислить звездное и местное время наблюдения.

Выводы тоже сделали.
Главное, стоит отметить:
Прямое восхождение светил и Азимут на астролябиях и Картах до конца 18 века было другим, в связи с тем, что использовалась Проекция звездного неба на Землю.
Прямое восхождение и Азимут реально имели другое числовое значение (интересно было бы посмотреть эти наблюдаемые координаты звезд, например в Альфонсовых таблицах и соотнести их с современными вычислениями?!).
Реперную точку на астролябиях использовали «0» часов – направление на Север (неплохо было бы исследовать арабские и греческие астролябии).

Известны Универсальные астролябии.
В этой астролябии, изобретённой аз-Заркали, за центр проектирования взята одна из точек равноденствия. В этом случае небесный экватор и эклиптика изображаются на тимпане прямыми линиями. Тимпан этой астролябии, в отличие от тимпанов обычных астролябий, пригоден для любой широты. Функции паука обычной астролябии здесь выполняет линейка, вращающаяся вокруг центра тимпана и называемая «подвижным горизонтом».

Компоненты универсальной астролябии.

Рис.5
1 – трон, как на планесферной астролябии, позволяет пользователю удерживать его вертикально, указывая звезду с алидадой.
2 – окружность масштабируется в градусах.
3 – на табличке показаны меридианы и параллели.
4 – эклиптика масштабируется в долготе эклиптики и обозначается именами созвездий Зодиака.
5 – линейка вращается вокруг оси, масштабируется в эклиптической долготе.
6 – точка, также называемая брахиолусом, шарнирно соединена и вращается с линейкой. Его конец можно переместить в точку на пластине на пересечении меридиана и параллели.

Основное использование универсальной астролябии – преобразование астрономических координат, например, между экваториальными и эклиптическими координатами.

Сферическая астролябия.
Небесная сфера представлена в этой астролябии в виде сферы, и её паук также имеет сферическую форму.

Принцип работы и приминение Армиллярных сфер разберем в следующей части.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #