Перевод систем счисления

В решении определенного класса задач иногда удобно записывать числовые значения в разных системах счисления. Разработан ряд унифицированных правил перевода чисел между системами. О том, как выполняется перевод систем счисления, рассказано в статье.
Что такое перевод систем счисления
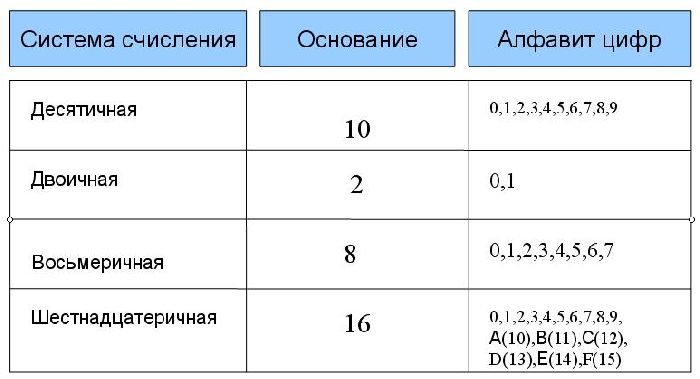
Основанием системы счисления является величина, определяющая количество символов для записи числового значения. Например, основанием двоичной системы является число 2, пятеричной, соответственно – 5.
Число 15 в десятичной системе при переводе в пятеричную равно 30, а в восьмеричной будет равно 17. Шестнадцатеричный эквивалент пятнадцати представляет собой букву F. Как так получается?
Перевод чисел с участием десятичной системы счисления
В преобразовании чисел с участием десятичной системы приняты три строгих правила перевода.
1. Пересчет числового значения из десятичного формата в эквивалент другой системы счисления заключается в делении целой части и полученных частных, на величину основания будущей системы счисления. При этом остатки от деления записываются начиная с последнего.
Например, 15 из десятичной системы в восьмеричную переводится так: 15 / 8 = 1 (в остатке 7). Записываем итог, начиная с конечного и в данном случае единственного частного, и затем остаток. Получим 17.
Еще один пример: десятичное 125 в восьмеричной системе: 125 / 8 = 15 (5). Полученное частное больше, чем основание 8.
Продолжаем делить: 15 / 8 = 1 (7). Ответ записывается с последнего частного, а затем остатки от деления: 175.
Следует запомнить, что запись результата всегда начинает с последнего частного и остатков от деления в обратном порядке.
2. Преобразование части десятичного числа, записанной после запятой, выполняется с помощью обратной процедуры, то есть умножения, вычисляя одно за другим произведения дробных частей на основание будущей системы счисления и записывая последовательно цифры, полученные в целой части. Например, дробная часть числа 0,134 в двоичную систему переводится так (удобнее это делать столбиком):
0,134 * 2 = 0,268 (в целой части 0)
0,268 * 2 = 0,536 (0)
0,536 * 2 = 1,072 (слева от запятой 1)
0,072 * 2 = 0,144 (в целой части 0)
0,144 * 2 = 0,288 (0)
Произведения вычисляют до тех пор, пока не будет обеспечена заданная точность или в остатке не получится ноль.
Ответ: десятичное 0,134 в двоичной системе равно 0,00100.
При умножении следует брать только остатки, не учитывая полученную цифру в целой части.
3. Перевод чисел из разных систем счисления в десятичную удобнее всего представлять с помощью развернутой записи числа, или при использовании формулы полинома, который формируется путем сложения одночленов, возведенных в степень и умноженных на некоторые коэффициенты:
a1 * x^(n-1) + a2 * x^(n-2) + a3 * x^(n-3) + …+an * x^0
Например, 137 = 1 * 10^2 + 3 * 10^1 + 7 * 10^0.
Рассмотрим примеры перевода чисел:
2 →10: 11011 = 1 * 2^4 + 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0 = 27
8 →10: 134 = 1 * 8^2 + 3 * 8^1 + 4 * 8^0 = 92
16 → 10: 1AF = 1 * 16^2 + 10 * 16^1 + 15 * 16^0 = 431
Перевод чисел в системах счислении, построенных на бинарном основании
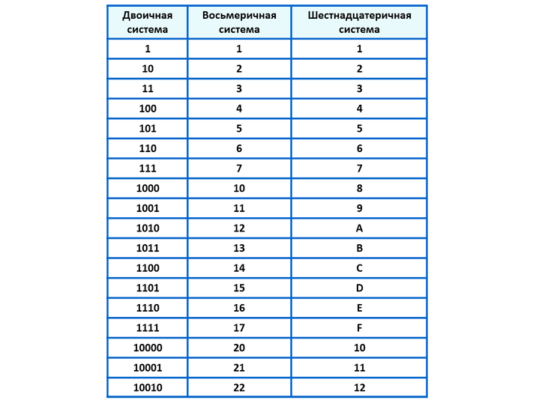
Восьмеричная и шестнадцатеричные системы счисления построены на бинарном базисе. Основанием восьмеричной системы является число 8, то есть 2^3, а основание шестнадцатеричной системы 16 = 2^4. Перевод между этими системами и двоичной системой удобнее всего выполнять с помощью таблицы перевода систем счисления:
Каждое восьмеричное число представляется триадой (тремя элементами) двоичных знаков, каждое шестнадцатеричное – двоичной тетрадой (четыре элемента).
Например, 8 → 2: 134 ⇔ 001011100
16 → 2: 8F ⇔ 10001111
2 → 8: 110101 ⇔ 65
2 → 16: 11011000 ⇔ D8
Что мы узнали?
Переход между различными системами счисления выполняется по строго определенным правилам. Десятичные числа преобразуются в другие системы путем последовательного деления целой части и умножения дробной, обратный перевод выполняется с помощью полинома. Перевод между 2-, 8- и 16-ми системами выполняется по таблице.
Оценка статьи
А какая ваша оценка?
Эквиваленты чисел в разных системах счисления
10с/с
n = 2 n = 3 n = 5 n = 8 n = 16
0 0000
000 00 00 0
1
0001 001 01 01 1
2
0010 002 02 02 2
3
0011 010 03 03 3
4
0100 011 04 04 4
5
0101 012 10 05 5
6
0110 020 11 06 6
7
0111 021 12 07 7
8
1000 022 13 10 8
9
1001 100 14 11 9
10
1010 101 20 12 A
11
1011 102 21 13 B
12
1100 110 22 14 C
13
1101 111 23 15 D
14
1110 112 24 16 E
15
1111 120 30 17 F
Другой вид табличного
метода заключается в том, что имеются
таблицы эквивалентов в каждой системе
счисления только для цифр этих систем
и степеней основания; задача перевода
сводится к тому, что в выражение ряда
N=, для исходной системы счисления надо
подставить эквиваленты из новой системы
для всех цифр и степеней основания и
произвести соответствующие действия
( умножения и сложения ) по правилам n –
арифметики. Полученный результат этих
действий будет изображать число в
новой системе счисления.
Pассмотрим пример.
Переведем десятичное число 113 в двоичную
систему cчисления, используя таблицу
эквивалентов цифр и степеней основания.
Табл.
2
Таблица
двоичных эквивалентов
Десятичное число
Двоичный эквивалент
100
0 001
101
1 010
102
1 1 00 100
Подставив
значения двоичных эквивалентов десятичных
цифр и степеней основания в ряд
N=an3+bn2+cn1+dn0,
получим
11310=1102+1101+3100=0011100100+00011010+00110001=
1110001(2с/с).
Метод использования
промежуточной системы счисления
применяют при переводе из десятичной
системы в двоичную и наоборот. В качестве
промежуточной системы счисления можно
использовать, например, восьмеричную
систему.
Pассмотрим
примеры, в которых перевод одного и того
же числа в разные системы счисления
осуществляется методом деления на
основание новой системы. Переведем
десятичное число 121 в двоичную систему
счисления, используя в качестве
промежуточной восьмеричную систему
счисления.
n
= 8
n = 2
121
¦ 1 121 ¦ 1 12110=1718=11110012
15 ¦ 7
60 ¦ 0
1
¦ 1
30 ¦ 0
15
¦ 1
3 шага
7 ¦ 1
3
¦ 1
1
¦ 1
7
шагов
Сравнивая эти
примеры, видим, что при переводе числа
из десятичной системы в восьмеричную
требуется в два с лишним раза меньше
шагов, чем при переводе в двоичную
систему. Если при этом учесть, что
восьмеpичная система связана с двоичной
соотношением
8k
= (2 3)
k,
то пеpевод из
восьмеpичной системы в двоичную и
наобоpот можно осуществить пpостой
заменой восьмеpичных цифp их двоичными
эквивалентами в соответствии с табл.
1.
Тpиада
– двоичный эквивалент восьмеpичных цифp.
В
качестве пpомежуточных систем счисления
целесообpазно использовать системы
счисления с основанием 2
k.
Пpи этом существенно упpощается
пpеобpазование инфоpмации из системы
счисления с основанием 2k
в двоичную систему и наобоpот.
Пpеобpазование фактически сводится к
тому, что символы пеpвоначальной
инфоpмации, заданной в системе с основанием
2k,
заменяются соответствующими двоичными
эквивалентами. Обpатное пpеобpазование
из двоичной системы в систему с основанием
2 k
сводится к тому, что двоичный код
pазбивается на гpуппы по k двоичных
pазpядов в каждой; эти гpуппы (диады,
тpиады, тетpады и т.д.) заменяются
соответствующими символами исходной
системы счисления. Системы счисления
с основанием 2k
шиpоко используют для записи пpогpамм
pешения задач, а также в ЭВМ для ускоpения
выполнения аpифметических опеpаций.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Paul Norman
Мыслитель
(6963)
6 лет назад
Для нас привычна десятичная система счисления. Т. е. нам знакомы числа, записанные в десятичной системе, где легко назвать привычные разряды числа.
Но, существуют другие системы счисления ( двоичная, шестнадцатиричная и т. д.)
Любое число нетрудно из одной системы перевести в другую.
Например, 100100_2=36_10, т. е число 100100 в двоичной системе равно 36 в десятичной. Число 36 есть десятичный эквивалент для 100100
Фатима СефералиеваУченик (124)
3 года назад
спасибо вам большое
Вася РомеоУченик (154)
1 год назад
здравствуйте, а как вы это решили?
Как найти десятичные эквиваленты чисел по их прямым кодам?
На этой странице сайта, в категории Информатика размещен ответ на вопрос
Как найти десятичные эквиваленты чисел по их прямым кодам?. По уровню сложности вопрос рассчитан на учащихся
5 – 9 классов. Чтобы получить дополнительную информацию по
интересующей теме, воспользуйтесь автоматическим поиском в этой же категории,
чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы
расположена кнопка, с помощью которой можно сформулировать новый вопрос,
который наиболее полно отвечает критериям поиска. Удобный интерфейс
позволяет обсудить интересующую тему с посетителями в комментариях.
Задание 2. Как в памяти компьютера представляются целые положительные и целые отрицательные числа?
При представлении со знаком самый старший (левый) разряд отводится под знак числа, а остальные разряды – под само число.
Когда число положительное, то в знаковый разряд помещается 0, когда число отрицательное, то 1.
Задание 3. Любое число можно рассматривать как вещественное, но с нулевой дробной частью. Обоснуйте целесообразность наличия особых способов компьютерного представления целых чисел.
Обычно вещественные числа важны при решении научных и инженерных задач. Алгоритм обработки таких чисел более трудоёмки по сравнению с алгоритмами обработки целых чисел. Для хранения в компьютере вещественных чисел выделяются разряды на хранение порядка числа, самого порядка, знака мантиссы и мантиссы.
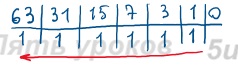
Задание 4. Представьте число 6310 в беззнаковом 8-разрядном формате.
6310 = 1111112
В восьмиразрядном представлении имеет вид:
Задание 5. Найдите десятичные эквиваленты чисел по их прямым кодам, записанным в 8-разрядном формате со знаком:
а) 01001100
Так как в знаковом разряде стоит 0, значит число положительное. Переведём 1001100 в десятичную систему счисления:
10011002 = 1*26 + 1*23 + 1*22 = 64 + 8 + 4 = 7610
Ответ: +76
б) 00010101
Так как в знаковом разряде стоит 0, значит число положительное. Переведём 10101 в десятичную систему счисления:
101012 = 1*24 + 1*22 + 1*20 = 16 + 4 + 1 = 2110
Ответ: +21
Задание 6. Какие из чисел 4438, 1010102, 25610 можно сохранить в 8-разрядном формате?
Максимальное значение в 8-разрядном формате 255 (таблица приведена в учебнике с минимальным и максимальным значением в различных разрядностях).
1) 4438 = 4*82 + 4*81 + 3*80 = 4*64 + 32 + 3 = 29110 Число нельзя сохранить в 8-разрядном формате.
2) 1010102 можно сохранить в 8-разрядном формате, так как задействованы 6 разрядом из 8-ми.
3) Число 25610 нельзя сохранить в данном формате.
Задание 7. Запишите следующие числа в естественной форме.
а) 0,3800456*102 = 38,00456
б) 0,245*10-3 = 0,000245
в) 1,256900Е+5 = 1,256900*105 = 125690
г) 9,569120Е-3 = 9,569120*10-3 = 0,00956912
Задание 8. Запишите число 2010,010210 пятью различными способами в экспоненциальной форме.
1) 20100102Е-4
2) 201001,02Е-2
3) 0,20100102Е+4
4) 2,0100102Е+3
5) 201,00102Е+1
Задание 9. Запишите следующие числа в экспоненциальной форме с нормализованной мантиссой – правильной дробью, имеющей после запятой цифру, отличную от нуля.
а) 217,93410 = 0,217934*103
б) 7532110 = 0,75321*105
в) 0,0010110 = 0,101*10-2
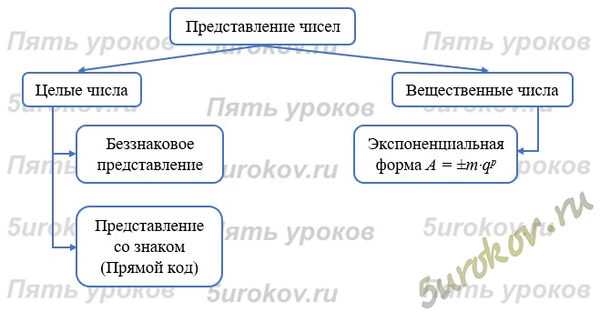
Задание 10. Изобразите схему, связывающую основные понятия, рассмотренные в данном параграфе.
Решение заданий из учебника Информатика 8 класс Босова, параграф 1.2. Представление целых чисел, представление вещественных чисел.