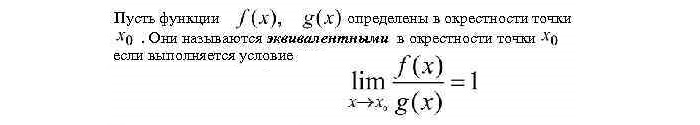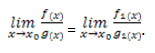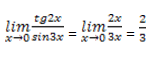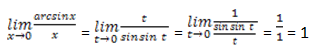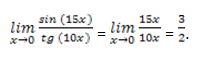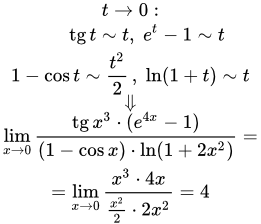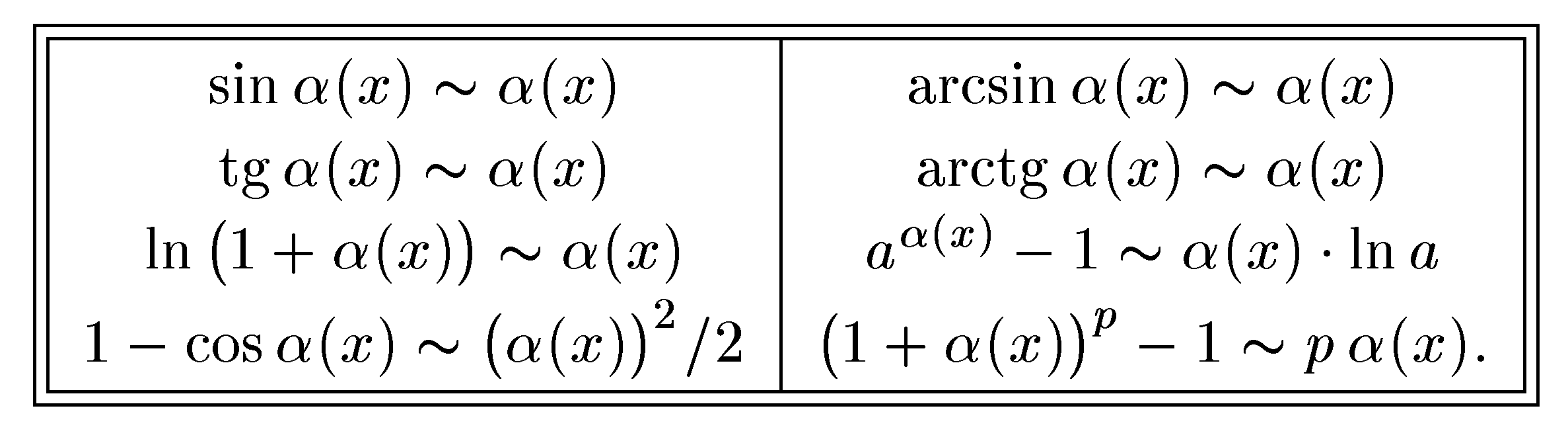Как найти эквивалент функции - Сайт, где вы сможете решить свои вопросы

Определение эквивалентных функций

Эквивалентные функции – это функции, имеющие одинаковое значение. Они могут представлять собой бесконечность малых и больших величин.

Функция может иметь такое понятие лишь при наличии предела. Следует понимать, что одна и та же функция принимает значение малой или большой до бесконечности лишь в единственной точке.

Теорема о замене функций эквивалентными в пределе частного

Если при x₁, стремящимся к x₂, f(x)~f₁(x) и g(x)~g₁(x) существует предел:

то существует и предел:

Доказательство

Допустим, что следствие этой теоремы часто применяемое. Если мы имеем частное, являющееся результатом произведения функций:

в этом случае, при нахождении предела, можно сделать замену этих функций на эквивалентные:

при этом:

f(x) ~ f₁(x), p(x) ~ p₁(x), … , r(x) ~ r₁(x), g(x) ~ g₁(x), q(x) ~ q₁(x), … , s(x) ~ s₁(x).

Выражения равны друг другу, это значит, что при существовании одного из таких пределов, применимо существование выражения, равного первому. Соответственно, если не существует такой предел, то не может существовать и второй.

Следует отметить, что можно делать замену как одной величины функции, так и нескольких одновременно.

Таблица эквивалентных функций

Ниже приведена таблица равнозначных функций и формул при t → 0. В данном случае величина t может представлять собой как переменную, так и до бесконечности малую функцию t = t(x) при x → x₀:

Эквивалентность при t → 0	Равенство при t → 0
sin t ~ t	sin t = t + 0(t)
arsin t ~ t	arsin t = t + 0(t)
tg t ~ t	tg t = t + 0(t)
artg t ~ t	artg t = t + 0(t)
1-cos t ~	1-cos t = + 0(t²)
e^t – 1 ~ t	e^t – 1 = t + 0(t)
a^t – 1 ~ t ln a	a^t – 1 = t ln a + 0(t)
ln (1 + t) ~ t	ln (1 + t) = t + 0(t)
log_a (1 + t) ~	log_a (1 + t) = + 0(t)
(1 + t)^b – 1 ~ bt	(1 + t)^b – 1 = bt + 0(t)
sh t ~ t	sh t = t + 0(t)
arsh t ~ t	arsh t = t + 0(t)
th t ~ t	th t = t + 0(t)
arsh t ~ t	arsh t= t + 0(t)
ch t – 1 ~ t²/2	ch t – 1 ~ t²/2 + 0(t²)

Свойства замены функций равносильными доступны для дробных выражений с перемножаемыми величинами и произведений, где необходимо найти предел.

В этом случае величины в числителе или знаменателе допускается заменить равнозначными функциями. Если математическое выражение представляет собой сумму чисел, замену сделать нельзя.

Примеры решения пределов с помощью эквивалентных функций

Для сравнения рассмотрим несколько примеров.

Пример 1

Вычислить

Начнём решение, учитывая, что tg2x ~ 2x, sin3x ~ 3x при x → 0, тогда

Пример 2

Найти

Пусть arcsin x = t, тогда x = sin t и t → 0 при x → 0. Исходя из этого:

Значит, arcsin x ~ x при x → 0.

Пример 3

Вычислить

Решение: если sin (15x) ~ 15x, tg (10x) ~ 10x, тогда

Для решения пределов можно использовать онлайн калькуляторы, размещенные на ресурсах в свободном доступе.

Источник

Эквивалентные функции

Говорят, что функции ff и gg, определенные в некоторой проколотой окрестности точки x0x_0 (возможно, x0=±∞x_0=pminfty) эквивалентны, если

lim⁡x→x0f(x)g(x)=1.
limlimits_{xto x_0}frac{f(x)}{g(x)}=1.

Если функции эквивалентны, то мы пишем

f(x)∼g(x)при x→x0.f(x)sim g(x)quadtext{при },, xto x_0.

Если существует конечный предел lim⁡x→x0f(x)=A≠0limlimits_{xto x_0 }f(x)=Ane 0, то, очевидно,

f(x)∼A при x→x0.f(x)sim A,,text{при},,xto x_0.

Если lim⁡x→x0f(x)=0limlimits_{xto x_0 }f(x)= 0, то говорят, что величина f(x)f(x) бесконечно малая при x→x0xto x_0.

Пример 1

Как следует из статьи замечательные пределы, имеют место следующие эквивалентности

sin⁡x∼tg⁡x∼arcsin⁡x∼arctg⁡x∼x, 1−cos⁡x∼x22sin xsimoperatorname{tg} xsimoperatorname{arcsin} xsimoperatorname{arctg} x sim x,,, 1-cos xsimfrac{x^2}{2}

ln⁡(1+x)∼x, (1+x)a∼1ax, ex∼1+xпри x→0.
ln(1+x)sim x,,,(1+x)^asim 1 ax,,,e^xsim 1+xquadtext{при },, xto 0.

При вычислении пределов функции можно заменять на эквивалентные.

Пример 2

Вычислить предел

lim⁡x→01+sin⁡x−1arcsin⁡x.
limlimits_{xto 0}frac{sqrt{1+sin x}-1}{arcsin{x}}.

Заменяем функции на эквивалентные:

1+sin⁡x−1arcsin⁡x∼1+x−1x∼1+12x−1x=12
frac{sqrt{1+sin x}-1}{arcsin{x}}simfrac{sqrt{1+ x}-1}{{x}}simfrac{1+frac{1}{2}x-1}{x}=frac{1}{2}

Таким образом,

lim⁡x→01+sin⁡x−1arcsin⁡x=12.
limlimits_{xto 0}frac{sqrt{1+sin x}-1}{arcsin{x}}=frac{1}{2}.

Однако, как показывает следующий предел, замена выражений на эквивалентные при вычислении пределов может привести к неопределенности:

lim⁡x→0x−sin⁡xarcsin⁡x−x=lim⁡x→0x−xx−x=00.
limlimits_{xto 0}frac{x-sin x}{arcsin x-x}=limlimits_{xto 0}frac{x- x}{ x-x}=frac{0}{0}.

O-большое

Пусть функции f(x)f(x) и g(x)g(x) определены в некоторой проколотой окрестности точки x0x_0 (или определены для достаточно больших значений ∣x∣|x|, если x0=±∞x_0=pminfty), причем функция g(x)g(x) строго положительна.

Говорят, что f(x)=O(g(x))f(x)=O(g(x)) при x→x0xto x_0, если существует постоянная C>0C>0 для которой

∣f(x)∣<Cg(x).
|f(x)|<Cg(x).

Заметим, что запись f(x)=O(1)f(x)=O(1), x→x0xto x_0 означает, что f(x)f(x) ограничена в некоторой проколотой окрестности точки x0x_0.

Пример 3

x=O(ex)x=O(e^x) при x→+∞xto+infty, так как x<exx<e^x для всех x>0x>0;
ex=O(∣x∣)e^x=O(|x|) при x→−∞xto -infty, так как ex<∣x∣e^x<|x| для всех x<−1x<-1;
1x=O(1×2)frac{1}{x}=Oleft(frac{1}{x^2}right) при x→0xto 0, так как 1∣x∣<1x2frac{1}{|x|} < frac{1}{x^2} для всех x∈(−1;0)∪(0;1)xin (-1;0)cup(0;1);
1×2=O(1∣x∣)frac{1}{x^2}=Oleft(frac{1}{|x|}right) при x→±∞xto pminfty, так как 1×2<1∣x∣frac{1}{x^2}<frac{1}{|x|} для всех ∣x∣>1|x|>1.

Из определения следует, что условие f(x)=O(g(x))f(x)=O(g(x)) при x→x0xto x_0 равносильно тому, что

∣f(x)g(x)∣<Cleft|frac{f(x)}{g(x)}right|<C

в некоторой проколотой окрестности точки x0x_0.

Если f(x)=O(g(x))f(x)=O(g(x)) и g(x)=O(f(x))g(x)=O(f(x)) при x→x0xto x_0, то пишут

f(x)≍g(x),x→x0.f(x)asymp g(x),quad xto x_0.

Данное отношение равносильно существованию положительных констант c,C>0c,C>0, для которых в некоторой проколотой окрестности точки x0x_0 выполнено

c<f(x)g(x)<C.
c<frac{f(x)}{g(x)}<C.

Например, x≍3×2−1,x→+∞xasymp sqrt{3x^2-1},quad xto +infty.

Свойства O-большого

f1(x)=O(g1(x))f_1(x)=O(g_1(x)), f2(x)=O(g2(x))f_2(x)=O(g_2(x)) ⇒Rightarrow f1(x)f2(x)=O(g1(x)g2(x))f_1(x)f_2(x)=O(g_1(x)g_2(x)),

в частности если функция h(x)h(x) положительна, то h(x)O(g(x))=O(h(x)g(x))h(x)O(g(x))=O(h(x)g(x));

f1(x)=O(g1(x))f_1(x)=O(g_1(x)), f2(x)=O(g2(x))f_2(x)=O(g_2(x)) ⇒Rightarrow f1(x)+f2(x)=O(g1(x)+g2(x))f_1(x)+f_2(x)=O(g_1(x)+g_2(x)),

в частности f1(x),f2(x)=O(g(x))f_1(x), f_2(x)=O(g(x)) ⇒Rightarrow f1(x)+f2(x)=O(g(x))f_1(x)+f_2(x)=O(g(x));

Говорят, что f(x)=o(g(x))f(x)=o(g(x)) при x→x0xto x_0 (f(x)f(x) является бесконечно малой от g(x)g(x)), если

lim⁡x→x0f(x)g(x)=0.
limlimits_{xto x_0}frac{f(x)}{g(x)}=0.

Заметим, что запись f(x)=o(1)f(x)=o(1), x→x0xto x_0 означает, что lim⁡x→x0f(x)=0limlimits_{xto x_0}f(x)=0.

Пример 4

xa=o(ex)x^a=o(e^x) при x→+∞xto+infty для любого a∈Rainmathbb{R};
ex−1=o(1)e^x-1=o(1) при x→0xto 0;
sin⁡x−x=o(x)sin x-x=o(x) при x→0xto 0;
1−cos⁡x=o(x)1-cos x=o(x) при x→0xto 0.

Свойства o-малого

Свойства o-малого аналогичны свойствам O-большого. Кроме того

o(O(g(x)))=O(o(g(x)))=o(g(x)).
oleft(O(g(x))right)=Oleft(o(g(x))right)=o(g(x)).

Пример 5

Покажем, что

sin⁡x−x=o(x2).sin x-x=oleft(x^2right).

Действительно, используя неравенство xcos⁡x<sin⁡x<xxcos x<sin x<x, (см. Пример 2 статьи Предел функции в точке), имеем

0<x−sin⁡x<x(1−cos⁡x)=xo(x)=o(x2).0<x-sin x<x(1-cos x)=xo(x)=oleft(x^2right).

Откуда следует sin⁡x−x=o(x2)sin x-x=oleft(x^2right).

На самом деле имеет место более сильное равенство

x−sin⁡x=O(x3).x-sin x=Oleft(x^3right).

Следствия формулы Маклорена

Используя ряд Маклорена для элементарных функций, можно получить следующие формулы (ряд Маклорена с остаточным членом в форме Пеано)

sin⁡x=x+x36+o(x4)sin x=x+frac{x^3}{6}+o(x^4)
arcsin⁡x=x−x36+o(x4)arcsin x=x-frac{x^3}{6}+o(x^4)
tg⁡x=x+x33+o(x4)tg x=x+frac{x^3}{3}+o(x^4)
arctg⁡x=x−x33+o(x4)operatorname{arctg} x=x-frac{x^3}{3}+o(x^4)
ln⁡(1+x)=x−x22+o(x2)ln(1+ x)=x-frac{x^2}{2}+o(x^2)
(1+x)a=1+ax+a(a−1)x22+o(x2)(1+x)^a=1+ax+frac{a(a-1)x^2}{2}+o(x^2)

Пример 6
lim⁡x→0x−sin⁡xarcsin⁡x−x=lim⁡x→0x36+o(x3)x36+o(x3)=lim⁡x→01+o(1)1+o(1)=1.limlimits_{xto 0}frac{x-sin x}{arcsin x-x}=limlimits_{xto 0}frac{frac{x^3}{6}+oleft(x^3right)}{frac{x^3}{6}+oleft(x^3right)}=limlimits_{xto 0}frac{1+o(1)}{1+o(1)}=1.

Тест по теме “Сравнение функций”

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 февраля 2020 года; проверки требуют 8 правок.

Асимптотическое равенство (эквивалентность) в математическом анализе — отношение эквивалентности между функциями, определёнными в некоторой проколотой окрестности точки, означающее равенство функций вблизи этой точки со сколь угодно малой относительной погрешностью. Асимптотические равенства широко используются при вычислении пределов. Часто асимптотически эквивалентные функции называют просто эквивалентными, опуская слово асимптотически. Также довольно распространённым является термин эквивалентные бесконечно малые, что есть не что иное как частный случай асимптотической эквивалентности для бесконечно малых функций.

Мотивировка[править | править код]

Про многие функции часто говорят, что они примерно равны или ведут себя одинаково вблизи некоторой точки. Однако такая терминология слишком расплывчата, и если мы действительно хотим говорить про одинаковое поведение функций, этому нужно дать формальное определение.

Определим следующий термин: будем говорить, что функция g(x) приближает или аппроксимирует функцию f(x) вблизи точки $x_{0}$ , если для сколь угодно малого числа можно взять такую окрестность, где эти функции будут отличаться не более чем на это число. На -языке:

${displaystyle forall varepsilon >0 exists delta >0 forall xin (x_{0}-delta ;x_{0})cup (x_{0};x_{0}+delta ):|f(x)-g(x)|<varepsilon }$

Не трудно увидеть, что это определение означает равенство предела разности функций нулю при стремлении к точке $x_{0}$ . есть не что иное как абсолютная погрешность приближения функции f(x) функцией g(x) . При определении аппроксимирующей в точке функции мы требуем того, чтобы абсолютную погрешность можно было сделать сколь угодно малой. При этом относительная погрешность совсем не обязательно будет мала. Простой пример: функция аппроксимирует функцию в точке , так как у них равный предел. Однако относительная погрешность этой аппроксимации во всех точках кроме равна .

Можно вместо условия малости абсолютной погрешности потребовать малость относительной. Функции с таким условием и называются асимптотически эквивалентными^[1]^{[нет в источнике]}. Относительная погрешность (для неравной нулю f(x) в некоторой проколотой окрестности точки $x_{0}$ ) функций f(x) и g(x) считается по формуле ${displaystyle left|{frac {f(x)-g(x)}{f(x)}}right|}$ . Условие асимптотической эквивалентности формулируется тогда так:

${displaystyle forall varepsilon >0 exists delta >0 forall xin (x_{0}-delta ;x_{0})cup (x_{0};x_{0}+delta ):left|{frac {f(x)-g(x)}{f(x)}}right|<varepsilon }$

Это, очевидно, эквивалентно условию ${displaystyle lim _{xto x_{0}}{frac {g(x)}{f(x)}}=1}$ , которое чаще всего и принимается за определение асимптотической эквивалентности.

Определение[править | править код]

Классическое определение

Пусть f(x) и g(x) определены в некоторой проколотой окрестности точки $x_{0}$ ( $x_{0}$ также может быть бесконечностью, как с определённым знаком, так и беззнаковой) и g(x) не равна в некоторой проколотой окрестности. Функции f(x) и g(x) называются асимптотически равными при ${displaystyle xto x_{0}}$ , если:

${displaystyle lim _{xto x_{0}}{frac {f(x)}{g(x)}}=1}$

Эквивалентность по базе

Конечно, асимптотическое равенство можно рассматривать не только для простого стремления аргумента к некоторому значению. Можно рассматривать предел и по другим базам: при стремлении аргумента справа, слева, по какому-то подмножеству и вообще по любой базе. Поэтому имеет смысл определить асимптотическую эквивалентность для любой базы . Пусть f(x) и g(x) определены на некотором элементе базы и g(x) не равна на некотором элементы базы. Функции f(x) и g(x) называются асимптотически равными по базе , если:^[2]^{[нет в источнике]}

${displaystyle lim _{mathfrak {B}}{frac {f(x)}{g(x)}}=1}$

Общий случай

Понятие асимптотического равенства может быть обобщено и на случай, если условие неравенства нулю g(x) не выполняется ни в какой окрестности. Пусть f(x) и g(x) определены на некотором элементе базы . Функции f(x) и g(x) называются асимптотически равными по базе , если функцию f(x) можно представить в виде , где ${displaystyle lim _{mathfrak {B}}varepsilon (x)=1}$ ^[3].

Через о-малое

Эквивалентное определение асимптотическому равенству может быть дано с использованием понятия о-малого. Пусть f(x) и g(x) определены на некотором элементе базы и g(x) не равна на некотором элементы базы. Функции f(x) и g(x) называются асимптотически равными по базе , если функцию f(x) можно представить в виде , где есть о-малое от f(x) по базе .

Через бесконечно малое

Для общего случая приведённое выше определение через о-малое можно сформулировать используя понятие бесконечно малое. Пусть f(x) и g(x) определены на некотором элементе базы . Функции f(x) и g(x) называются асимптотически равными по базе , если функцию f(x) можно представить в виде , где o(1) есть бесконечно малое по базе ^[3].

Для обозначения асимптотического равенства используется тильда: .

Отношение эквивалентности[править | править код]

Асимптотическое равенство по некоторой базе в полном смысле является отношением эквивалентности на множестве определённых на некотором элементе базы функций, то есть оно рефлексивно, симметрично и транзитивно. Поэтому множество таких функций может быть разбито на классы эквивалентности.

Любые две функции, имеющие одинаковый конечный ненулевой предел, эквивалентны между собой. С другой стороны, эквивалентность функции некоторой функции с ненулевым конечным пределом, автоматически влечёт за собой равенство их предела. Таким образом, множество функций с одинаковым ненулевым конечным пределом образует класс эквивалентности.

Совсем не так обстоит дело с бесконечно малыми, бесконечно большими и не имеющими предела функциями. Именно такие эквивалентности и представляют интерес. Эквивалентность двух функций влечёт за собой равенство их пределов (либо их несуществование), поэтому можно рассматривать отдельно классы эквивалентности бесконечно больших и бесконечно малых функций^[3].

Примеры[править | править код]

Полином при эквивалентен своему ненулевому слагаемому со старшей степенью, а при с младшей.

${displaystyle a_{n}x^{n}+a_{n-1}x^{n-1}+dots +a_{1}x+a_{0}sim a_{n}x^{n}}$

при ${displaystyle xto infty ,a_{n}neq 0}$

${displaystyle a_{n}x^{n}+a_{n-1}x^{n-1}+...+a_{m+1}x^{m+1}+a_{m}x^{m}sim a_{m}x^{m}}$

при ${displaystyle xto 0,a_{m}neq 0}$

При вычислении пределов во многих учебниках часто приводят таблицы эквивалентностей для некоторых элементарных функций:

Эквивалентные бесконечно малые при

Функция 1	Функция 2




	${displaystyle {frac {x^{2}}{2}}}$
${displaystyle e^{x}-1}$

${displaystyle (1+x)^{alpha }-1}$




	${displaystyle {frac {x^{2}}{2}}}$

Довольно известной является формула Стирлинга, приближающая факториал непрерывной функцией:

${displaystyle n!sim {sqrt {2pi n}}left({frac {n}{e}}right)^{n}}$

при

Асимптотики полезны при оценке комбинаторных величин с достаточно большими параметрами. Например, подставив формулу Стирлинга в явную формулу вычисления биномиального коэффициента, можно получить, что:

${displaystyle {binom {2n}{n}}sim {sqrt {frac {1}{pi n}}}2^{2n}}$

при

Количество простых чисел, меньших некоторого заданного числа, также имеет простое асимптотическое приближение:

${displaystyle pi (n)sim {frac {n}{ln {n}}}}$

при

где pi (n) — количество простых чисел, меньших

Свойства[править | править код]

Это свойство позволяет заменять выражение под знаком предела на эквивалентное. Именно на нём основана техника вычисления пределов с помощью эквивалентностей.

${displaystyle f(x)g(x)sim f_{1}(x)g_{1}(x)}$

по базе

${displaystyle {frac {f(x)}{g(x)}}sim {frac {f_{1}(x)}{g_{1}(x)}}}$

по базе

${displaystyle (f(x))^{m}sim (f_{1}(x))^{m}}$

по базе

Все равенства тут в смысле пределы либо равны, либо оба не существуют. Последнее свойство может быть обобщено и на случай дробной степени, однако так как отрицательные числа возводить в нецелую степень нельзя, необходимо предварительно проверить, будут ли итоговые функции определены на каком-либо элементе базы. Для арифметических корней нечётной степени свойство может быть применено без дополнительных проверок.

Эти свойства широко используются на практике для вычисления предела. Пример:

${displaystyle lim _{xto 0}{frac {sin x(e^{x}-1)}{(ln(x+1))^{2}cdot e^{x-1}}}=lim _{xto 0}{frac {xcdot x}{x^{2}cdot e^{-1}}}=e}$

Заметим, что аналогичного свойства для суммы нет: сумма эквивалентных не обязана быть эквивалентна сумме.

Представление через о-малое.

Так как это альтернативное определение эквивалентности, его можно использовать и в обратную сторону. К примеру:

при

, поскольку

. Это позволяет в эквивалентностях избавляться от малых слагаемых. Пример:

${displaystyle lim _{xto +infty }(e^{x}-x^{1}0-lnx)=lim _{xto +infty }e^{x}=+infty }$

Это свойство в прямую сторону часто используется в комбинации со следующим:

o-малое есть о-малое от эквивалентного.

Несмотря на то, что в сумме на эквивалентные заменять нельзя, можно воспользоваться последними двумя свойствами:

${displaystyle lim _{xto 0}{frac {sin x+ln(x+1)}{e^{x}-1+operatorname {arctg} {x}}}=lim _{xto 0}{frac {x+o(sin x)+x+o(ln(x+1))}{x+o(e^{x}-1)+o(operatorname {arctg} {x})}}=lim _{xto 0}{frac {2x+o(x)}{2x+o(x)}}=lim _{xto 0}{dfrac {2x+o(1)x}{2x+o(1)x}}=lim _{xto 0}{dfrac {2+o(1)}{2+o(1)}}={frac {2}{2}}=1}$

Теорема об эквивалентности сложных функций как и теорема о пределе сложной функции имеет непростую формулировку. Сформулируем 3 варианта этой теоремы:

Эквивалентность сложных функций.

Версия теоремы для непрерывных функций, впрочем, покрывает большинство примеров, встречающихся на практике. К примеру: ${displaystyle sin {dfrac {1}{x}}sim {dfrac {1}{x}}}$

при

. Для разрывных функций требуется дополнительное условие.

Оба этих свойства являются следствием общей теоремы для пределов по произвольной базе.

${displaystyle sum limits _{n=0}^{infty }{a_{n}}}$

и ${displaystyle sum limits _{n=0}^{infty }{b_{n}}}$

если ${displaystyle forall n: b_{n}>0}$

и ряд:

${displaystyle sum limits _{n=0}^{infty }{b_{n}}}$

расходится, то из ${displaystyle a_{n}sim b_{n}}$

следует, что:

${displaystyle sum limits _{k=0}^{n}{a_{k}}sim sum limits _{k=0}^{n}{b_{k}}}$

Порядок[править | править код]

Сходным по смыслу с асимптотическим равенством, но менее строгим отношением является наличие одинакового порядка функций. Говорят, что функции f(x) и g(x) имеют одинаковый порядок, если . В этом случае используют обозначение или . В случае если эти функции бесконечно малые порядок обычно называют порядком малости, а если бесконечно большие, то порядком роста.

При этом из одинаковости порядка отнюдь не следует существование константы такой, что . Для примера достаточно заметить, что
, так как
, однако не существует такой константы , что .

Примечания[править | править код]

↑ Кудрявцев, 2003, с. 264.
↑ Архипов, 2004, с. 73.
↑ ¹ ² ³ encyclopediaofmath.

Литература[править | править код]

Кудрявцев Л. Д. Курс математического анализа. В 3-х томах. Том 1. — М.: Дрофа, 2003. — 704 p.
Архипов, Г. И. Лекции по математическому анализу : учеб. для вузов / Г. И. Архипов, В. А. Садовничий, В. Н. Чубариков ; под ред. В. А. Садовничего. — 5-е изд., испр.. — М.: Дрофа, 2004. — 640 с. — (Классический университетский учебник). — ISBN 5-7107-8900-3.
Asymptotic equality. Encyclopedia of Mathematics.

Источник

09.5. Эквивалентные функции

В тех случаях, когда функциональная зависимость имеет довольно сложный вид, возникают большие трудности при изучении ее свойств. Простой просчет значений функции на ЭВМ порой может оказаться неосуществимым, так как даже современные ЭВМ допускают значительные погрешности в расчетах с очень большими или же малыми числами. Мы рассмотрим весьма интересный подход к изучению функциональных зависимостей, основанный на их замене более простыми функциями в окрестности некоторых предельных точек.

Будем говорить, что функции и ЭКВИВАЛЕНТНЫ в окрестности предельной точки (конечной или бесконечной), если найдется такая функция в окрестности этой предельной точки, что

Очевидно, новое определение обобщает данное ранее для бесконечно малых функций.

Данное условие не является необходимым. Проиллюстрируйте это примером.

Докажите эту теорему.

Теорема. Для эквивалентности функций и при достаточно, чтобы предел их отношения при был равен единице:

Рассмотрим пример. Пусть

То в качестве функции, эквивалентной данной при , может быть взята

Действительно .

Найдем, для каких x эквивалентная функция будет отличаться от данной менее чем на :

(9. 35)

Можно провести вычислительный эксперимент и достаточно точно определить, с каких x более сложную функцию

Допустимо заменить более простой

Сделаем приближенную оценку этих значений x, усиливая рассматриваемое неравенство (9.35):

Значения x, соответствующие неравенству

Тем более будет удовлетворять неравенству (9.35).

Поэтому искомые значения х определяются неравенством:

Положим, к примеру, что . Тогда

Это означает, что для x > 2,43 и x < –2,43 данная функция будет отличаться по абсолютной величине от функции менее чем на 0,002.

Может показаться, что в качестве функции, эквивалентной данной, для достаточно больших по модулю x можно взять функцию

Она действительно проще, чем . Однако при той же абсолютной погрешности E, заменив более сложную функцию на такую простую функцию как , мы получим, что неравенство

Путем аналогичных рассуждений

Дает допустимый диапазон значений x:

Если принять то же значение , то для и значения данной функции можно полагать равными нулю. Как видим, при заданной абсолютной погрешности диапазон допустимых значений меняется. Выигрывая в простоте эквивалентной функции, мы, вместе с тем, теряем часть промежутка, на котором осуществляется упрощение.

Найдем функцию, эквивалентную данной, в окрестности предельной точки . Для этого представим иначе данную функцию:

То эквивалентная функция в окрестности нуля будет иметь вид:

Определим, при каких x, близких к нулю, функция отличается от данной по абсолютной величине менее, чем на E :

Найдем искомые значения x с некоторым “запасом”:

Будет ли лучше для отыскания необходимых значений х другая оценка

При той же погрешности вычислений получим

Рис. 9.22. Функция и ей эквивалентные.

На рис. 9.22 изображены данная функция и эквивалентные ей. Мы видим, что на весьма значительной части области определения функции при абсолютной погрешности расчета можно использовать на практике более простые функциональные зависимости.

Рассмотрим другой пример. Функция

Как несложно установить, при имеет эквивалентную:

Значения x, допускающие такую замену при абсолютной погрешности E, определяются следующим образом:

Находим с некоторым запасом требуемые значения x:

При получаем , то есть или .

Если же данную функцию непосредственно табулировать с использованием вычислительных средств, то переполнение порядка на ЭВМ для практически неизбежно, однако эта функция ведет себя, как эквивалентная ей . Отметим также, что отыскание путем вычислительного эксперимента допустимых x, упрощающих при заданной абсолютной погрешности вычисления, едва ли осуществимо в полной мере, так как этому могут воспрепятствовать вычислительные возможности ЭВМ. Следовательно, полученная аналитически оценка более значима.

Применение эквивалентных функций при решении пределов

Применение эквивалентных функций позволяет упростить вычисление пределов. Если нам нужно вычислить предел дроби, то мы можем заменить множители в числителе и знаменателе эквивалентными функциями и вычислять предел от более простого выражения. Подчеркнем, что речь идет именно о множителях в дробях и произведениях. Замена эквивалентными функциями в других выражениях, например в суммах, может привести к неправильному результату. Однако, ошибки не будет, если выразить любую функцию в виде суммы эквивалентной ей функции и о малого (см. пример ⇓).

Все связанные с этим определения и теоремы приводятся на странице «О большое и о малое. Сравнение функций». Напомним некоторые из них.

Применяемые определения и теоремы

Определение эквивалентных функций
Функции f и g называются эквивалентными (асимптотически равными) при :
при ,
если на некоторой проколотой окрестности точки ,
при , причем
.

Если при , то ;
если , то .
При этом функцию называют главной частью при . См. теорему о связи эквивалентных функций с о малым

Теорема о замене функций эквивалентными в пределе частного
Если, при , и и существует предел
, то существует и предел
.
Доказательство

Отметим часто применяемое следствие этой теоремы. Пусть мы имеем частное, составленное из конечного произведения функций: . Тогда, при вычислении предела, эти функции можно заменить на эквивалентные:
,
где . Знак равенства означает, что если существует один из этих пределов, то существует и равный ему второй. Если не существует один из пределов, то не существует и второй.

Таблица эквивалентных функций

Далее приводится таблица функций, эквивалентных при . Здесь t может быть как переменной, так и бесконечно малой функцией при : ; .

Эквивалентность при

Равенство при

Предостережение

Как указывалось в самом начале, производить замену функций эквивалентными можно только в множителях дробей и произведений, предел которых мы хотим найти. В других выражениях, например в суммах, делать такую замену нельзя.

В качестве примера рассмотрим следующий предел:
.
При . Но если заменить в числителе на x , то получим ошибку:
.
Ошибки не будет, если выразить синус через эквивалентную функцию и о малое, :
.
Поскольку и , то мы снова получили неопределенность 0/0 . Это указывает на то, что для вычисления этого предела применение эквивалентной функции не достаточно. Нужно применить другой метод.

Примеры

Все примеры Далее мы приводим подробные решения следующих пределов, упрощая вычисления с помощью эквивалентных функций.
⇓, ⇓, ⇓, ⇓.

Пример 1

Из таблицы эквивалентных функций ⇑ имеем:
. Поскольку исходная функция является дробью и каждая из этих функций входит в нее в виде множителя в числителе или знаменателе, то заменим их на эквивалентные.
.

Пример 2

Из таблицы эквивалентных функций ⇑ находим:
.
Преобразуем квадрат логарифма:
.
Поскольку исходная функция является дробью и каждая из этих функций входит в нее в виде множителя в числителе или знаменателе, то заменим их на эквивалентные.
.

Пример 3

Здесь мы имеем неопределенность вида один в степени бесконечность. Приводим ее к неопределенности вида 0/0 . Для этого воспользуемся тем, что экспонента и натуральный логарифм являются взаимно обратными функциями.
.
Теперь в показателе экспоненты у нас неопределенность вида 0/0 .

Вычисляем предел:
.
Поскольку у нас дробь, то заменим некоторые множители в числителе и знаменателе эквивалентными функциями, пользуясь приведенной выше таблицей ⇑.
;
;

Поскольку экспонента непрерывна для всех значений аргумента, то по теореме о пределе непрерывной функции от функции имеем:
.

Пример 4

При . Выясним, к чему стремится . Поскольку здесь дробь, то заменим логарифм эквивалентной функцией: . Тогда
. Таким образом, мы имеем неопределенность вида ∞–∞ .

Преобразуем ее к неопределенности вида 0/0 . Для этого приводим дроби к общему знаменателю.
.
Здесь мы также воспользовались формулой . После преобразований, наш предел принимает следующий вид:
.

В знаменателе мы сразу можем заменить натуральный логарифм эквивалентной функцией, как это сделали выше:
.

В числителе имеется произведение двух множителей, каждый из которых тоже можно заменить эквивалентной функцией и, таким образом, упростить вычисления. В качестве эквивалентных, попробуем найти степенные функции:
.
Тогда . Считаем, что . Раскрываем неопределенность по правилу Лопиталя.
.
Если положить , то . Тогда
.
Тот же результат можно получить, применяя разложение в ряд Тейлора при :
.
Отсюда .

Найдем эквивалентную функцию для второго множителя, используя разложение в ряд Тейлора при :
.
Отсюда .

Теперь заменим множители эквивалентными функциями:
.

Примечание. Заметим, что делать замену функций на эквивалентные можно, только если функция, от которой ищется предел, является дробью или произведением. Тогда часть множителей в числителе или знаменателе можно заменить эквивалентными функциями. Так, если бы мы с самого начала заменили ln (1+x) на x, то получили бы ошибку.

Использованная литература:
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, 2003.

Эквивалентные бесконечно малые функции. Таблица эквивалентных б.м. функций

Обозначают: $alpha(x) sim beta(x)$ при $x rightarrow a$.

Задание. Проверить, являются ли функции $alpha(x) = 5(x^2-5x+6)$ и $beta(x) = x^2-x-6$ эквивалентными бесконечно малыми при $x rightarrow 3$.

Решение. Проверим вначале, что данные функции являются бесконечно малыми функциями в точке $x=3$:

Найдем предел отношения этих функций:

Ответ. Заданные функции $alpha(x) = 5(x^2-5x+6)$ и $beta(x) = x^2-x-6$ являются эквивалентными бесконечно малыми.

Таблица эквивалентных б.м. функций

Таблица эквивалентных б.м. функций при $x rightarrow 0$

Предельные равенства для эквивалентных б.м. функций

Предел отношения двух б.м. функций $alpha(x)$ и $beta(x)$ при $x rightarrow a$ равен пределу отношения эквивалентных им б.м. функций $alpha^(x)$ и $beta^(x)$ при $x rightarrow a$, то есть верны предельные равенства:

Задание. Найти предел $lim _ frac>$

Решение. При $x rightarrow 0$: $sin 2 x sim 2 x$

Разность двух эквивалентных б.м. функций есть б.м. функция более высокого порядка, чем каждая из них.

Верно и обратное утверждение.

Сумма конечного числа б.м. функций разных порядков эквивалентна слагаемому низшего порядка.

Слагаемое, которое эквивалентно сумме б.м. функций, называется главной частью указанной суммы.

Замена суммы б.м. функций ее главной частью называется отбрасыванием б.м. высшего порядка.

Решение. При $x rightarrow 0$: $5 x-6 x^ sim 5 x,$ tg $3 x sim 3 x$

Источник

Пусть α(х) и β(х) — бесконечно
малые приха. Их частное может и не быть бесконечно
малым. Более того, предел отношения двух
бесконечно малых величин является
неопределенной величиной.
В зависимости от того, какие конкретные
бесконечно малые рассматриваются, этот
символ может быть равен произвольному
числу, или символу бесконечности.

Опр. 1.Если отношениедвух бесконечно малых величин само
бесконечно мало, то α(х) называетсявеличиной более высокого порядка
малости, чем β(х); при этом β(х)
называется величиной более низкого
порядка малости, чем α(х).

Если отношение
двух бесконечно малых величин стремится
к конечному пределу, не равному нулю,
то α(х) и β(х) называютсябесконечно
малыми одного порядка малости. В
частности, если отношениедвух бесконечно малых величин стремится
к 1, то α(х) и β(х) называютсяэквивалентными. В этом случае
пишут α(х) ~ β (х).

Таблица эквивалентных бесконечно
малых функций.Пусть α(х) – бесконечно
малая прих0.
Тогда

Принцип замены эквивалентных.Если
функции α(х) и β(х) являются
бесконечно малыми прихаи если α(х) ~(x),
β (х) ~(x),
то

§ 8. Односторонние пределы

Опр.
1. Если любая
последовательность х_n→а,
х_n<а
(а–число
или символ -∞) при любом
,
то говорят, что функцияf(x)
при х→а-0
(слева) имеет левый
односторонний предел
Говорят, что функцияf(x)
при х_n→а+0
(справа) имеет правый
односторонний предел
если функцияf(х)
была определена правее точки а,
и любая последовательность х_n→а,
х_n>а
(а–число
или символ +∞)
при любом

.

Если
f(х)
имеет в точке а
(а
– число) односторонние пределы f(a-0)
и f(a+0)
и f(a-0)=f(a+0)=b
(b
– число или один из символов – ∞ или +
∞), тогда f(x)
имеет в точке а
обычный (двусторонний) предел
Если односторонние пределы различны,
т.е.f(a-0)≠f(a+0),
то не существует предела функции при
х→а.

§ 9. Непрерывность функции

Опр.
1. Функция
f(x)
называется непрерывной
в точке а,
если функция имеет конечный предел в
точке а
и этот предел совпадает со значением
функции в этой точке, т. е.

Опр.
2. Функция
называется непрерывной
на промежутке
X,
если она непрерывна в каждой точке этого
промежутка.

Теорема
1. Основные
элементарные функции непрерывны в
областях их определения.

§ 10. Точки разрыва функции

Пусть
функция b₁
– левосторонний предел функции f(x)
в точке х=а,
b₂
– правосторонний предел функции f(x)
в точке х=а.
Рассмотрим функцию у=f(x),
определенную на интервале X,
кроме, быть может, точки
.
Точкаа
называется точкой
разрыва
данной функции, если в ней функция
определена, но не является непрерывной,
или не определена в этой точке.

В зависимости от
характера поведения функции в окрестности
точки разрыва различают три основных
вида разрывов.

Опр.
1. Точка а
называется точкой
устранимого разрыва
функции f(x),
если существует конечный
,
но либо функция не определена в точкеа,
либо

Опр.
2. Разрыв
I рода –
в этом случае существуют конечные
пределыи,
ноВеличина |b₂–b₁|
называется скачком.

Опр.
3. Разрыв
II рода —
в этом случае хотя бы один из пределов
ине существует или бесконечен.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Определение эквивалентных функций

Теорема о замене функций эквивалентными в пределе частного

Доказательство

Таблица эквивалентных функций

Примеры решения пределов с помощью эквивалентных функций

Пример 1

Пример 2

Пример 3

Эквивалентные функции

O-большое

Свойства O-большого

Свойства o-малого

Следствия формулы Маклорена

Тест по теме “Сравнение функций”

Мотивировка[править | править код]

Определение[править | править код]

Отношение эквивалентности[править | править код]

Примеры[править | править код]

Свойства[править | править код]

Порядок[править | править код]

Примечания[править | править код]

Литература[править | править код]

09.5. Эквивалентные функции

Применение эквивалентных функций при решении пределов

Применяемые определения и теоремы

Таблица эквивалентных функций

Предостережение

Примеры

Пример 1

Пример 2

Пример 3

Пример 4

Эквивалентные бесконечно малые функции. Таблица эквивалентных б.м. функций

Таблица эквивалентных б.м. функций

Предельные равенства для эквивалентных б.м. функций

§ 8. Односторонние пределы

§ 9. Непрерывность функции

§ 10. Точки разрыва функции

Вам также может понравиться

Как найти географические координаты точки по карте

Майнкрафт как найти тундру в майнкрафт

Как найти беспроводную зарядку на телефоне

Добавить комментарий Отменить ответ