Как найти эквивалентная электротехника

Главная
→
Примеры решения задач ТОЭ
→
Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Основными законами, определяющими расчет электрической цепи, являются законы Кирхгофа.

На основе законов Кирхгофа разработан ряд практических методов расчета электрических цепей постоянного тока, позволяющих сократить вычисления при расчете сложных схем.

Существенно упростить вычисления, а в некоторых случаях и снизить трудоемкость расчета, возможно с помощью эквивалентных преобразований схемы.

Преобразуют параллельные и последовательные соединения элементов, соединение «звезда» в эквивалентный «треугольник» и наоборот. Осуществляют замену источника тока эквивалентным источником ЭДС. Методом эквивалентных преобразований теоретически можно рассчитать любую цепь, и при этом использовать простые вычислительные средства. Или же определить ток в какой-либо одной ветви, без расчета токов других участков цепи.

В данной статье по теоретическим основам электротехники рассмотрены примеры расчета линейных электрических цепей постоянного тока с использованием метода эквивалентных преобразований типовых схем соединения источников и потребителей энергии, приведены расчетные формулы.

Решение задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований

---

Задача 1. Для цепи (рис. 1), определить эквивалентное сопротивление относительно входных зажимов a−g, если известно: R₁ = R₂ = 0,5 Ом, R₃ = 8 Ом, R₄ = R₅ = 1 Ом, R₆ = 12 Ом, R₇ = 15 Ом, R₈ = 2 Ом, R₉ = 10 Ом, R₁₀= 20 Ом.

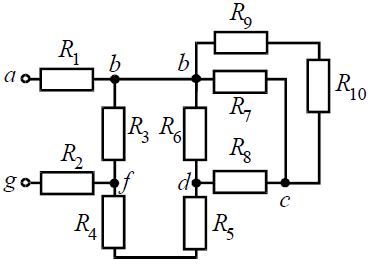
Рис. 1

Решение

Начнем эквивалентные преобразования схемы с ветви наиболее удаленной от источника, т.е. от зажимов a−g:

---

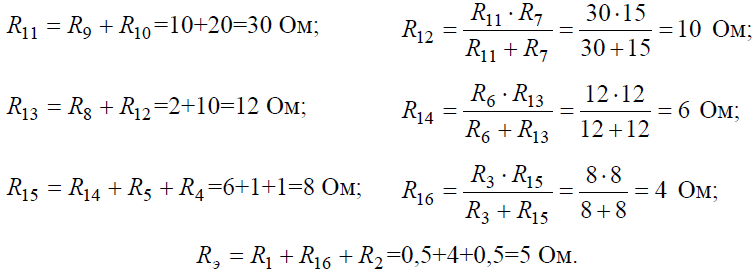
Задача 2. Для цепи (рис. 2, а), определить входное сопротивление если известно: R₁ = R₂ = R₃ = R₄= 40 Ом.

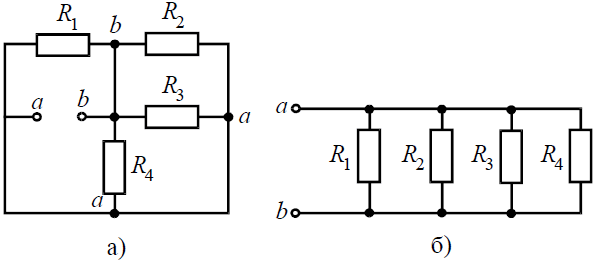Рис. 2

Решение

Исходную схему можно перечертить относительно входных зажимов (рис. 2, б), из чего видно, что все сопротивления включены параллельно. Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивленияможно воспользоваться формулой:

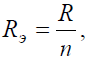где R — величина сопротивления, Ом;

n — количество параллельно соединенных сопротивлений.

---

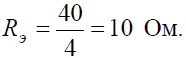
Задача 3. Определить эквивалентное сопротивление относительно зажимов a–b, если R₁ = R₂ = R₃ = R₄ = R₅ = R₆ = 10 Ом (рис. 3, а).

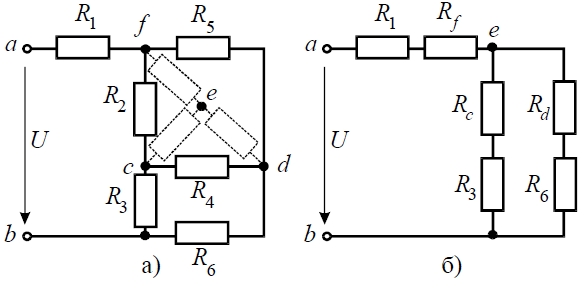
Рис. 3

Решение

Преобразуем соединение «треугольник» f−d−c в эквивалентную «звезду». Определяем величины преобразованных сопротивлений (рис. 3, б):

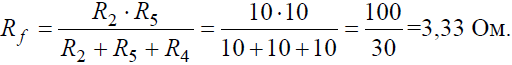По условию задачи величины всех сопротивлений равны, а значит:

На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно:

И тогда эквивалентное сопротивление исходной схемы представляет последовательное соединение сопротивлений:

---

Задача 4. В заданной цепи (рис. 4, а) определить методом эквивалентных преобразований входные сопротивления ветвей a−b, c–d и f−b, если известно, что: R₁ = 4 Ом, R₂ = 8 Ом, R₃ =4 Ом, R₄ = 8 Ом, R₅ = 2 Ом, R₆ = 8 Ом, R₇ = 6 Ом, R₈ =8 Ом.

Решение

Для определения входного сопротивления ветвей исключают из схемы все источники ЭДС. При этом точки c и d, а также b и f соединяются накоротко, т.к. внутренние сопротивления идеальных источников напряжения равны нулю.

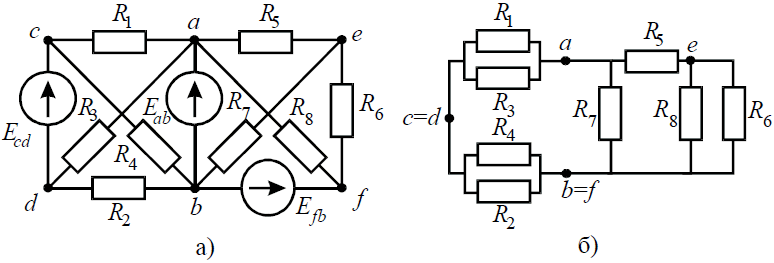
Рис. 4

Ветвь a−b разрывают, и т.к. сопротивление R_a–b = 0, то входное сопротивление ветви равно эквивалентному сопротивлению схемы относительно точек a и b (рис. 4, б):

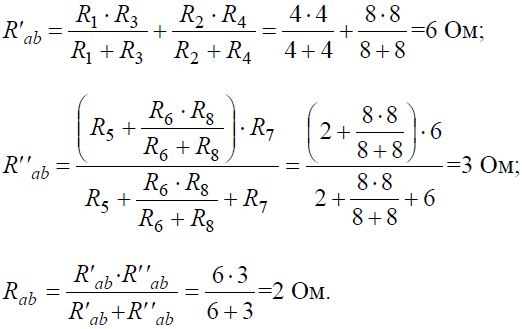
Аналогично методом эквивалентных преобразований определяются входные сопротивления ветвей R_cd и R_bf. Причем, при вычислении сопротивлений учтено, что соединение накоротко точек a и b исключает ( «закорачивает») из схемы сопротивления R₁, R₂, R₃, R₄ в первом случае, и R₅, R₆, R₇, R₈ во втором случае.

---

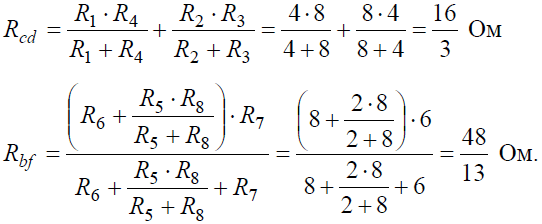
Задача 5. В цепи (рис. 5) определить методом эквивалентных преобразований токи I₁, I₂, I₃ и составить баланс мощностей, если известно: R₁ = 12 Ом, R₂ = 20 Ом, R₃ = 30 Ом, U = 120 В.

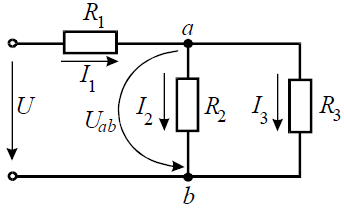
Рис. 5

Решение

Эквивалентное сопротивлениедля параллельно включенных сопротивлений:

Эквивалентное сопротивление всей цепи:

американские сигареты парламент.

Ток в неразветвленной части схемы:

Напряжение на параллельных сопротивлениях:

Токи в параллельных ветвях:

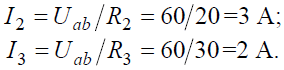
Баланс мощностей:

---

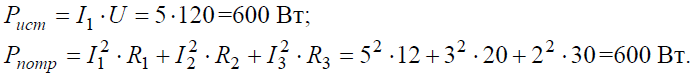
Задача 6. В цепи (рис. 6, а), определить методом эквивалентных преобразований показания амперметра, если известно: R₁ = 2 Ом, R₂ = 20 Ом, R₃ = 30 Ом, R₄ = 40 Ом, R₅ = 10 Ом, R₆ = 20 Ом, E = 48 В. Сопротивление амперметра можно считать равным нулю.

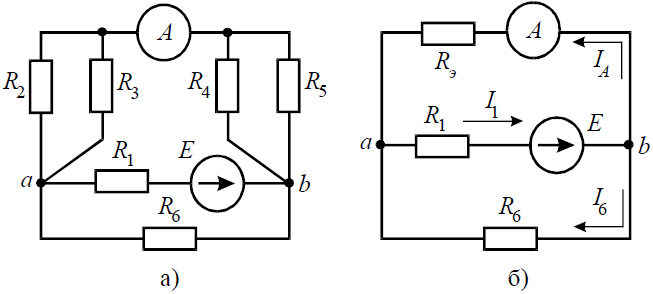
Рис. 6

Решение

Если сопротивления R₂, R₃, R₄, R₅ заменить одним эквивалентным сопротивлением R_Э, то исходную схему можно представить в упрощенном виде (рис. 6, б).

Величина эквивалентного сопротивления:

проститутки академическая. Смотри здесь строительство и ремонт деревянного дома.

Преобразовав параллельное соединение сопротивлений R_Э и R₆ схемы (рис. 6, б), получим замкнутый контур, для которого по второму закону Кирхгофа можно записать уравнение:

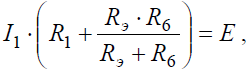
откуда ток I₁:

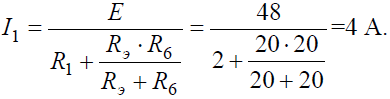
Напряжение на зажимах параллельных ветвей U_ab выразим из уравнения по закону Ома для пассивной ветви, полученной преобразованием R_Э и R₆:

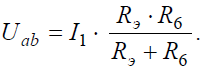
Тогда амперметр покажет ток:

---

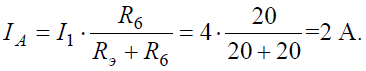
Задача 7. Определить токи ветвей схемы методом эквивалентных преобразований (рис. 7, а), если R₁ = R₂ = R₃ = R₄ = 3 Ом, J = 5 А, R₅ = 5 Ом.

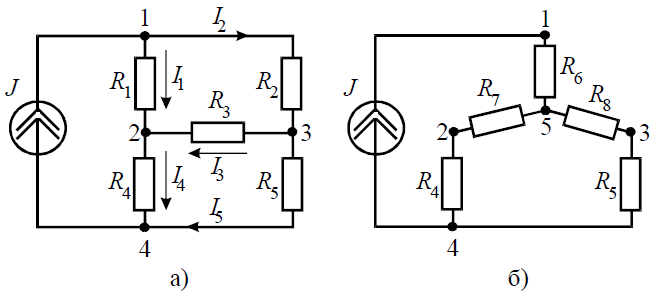
Рис. 7

Решение

Преобразуем «треугольник» сопротивлений R₁, R₂, R₃ в эквивалентную «звезду» R₆, R₇, R₈ (рис. 7, б) и определим величины полученных сопротивлений:

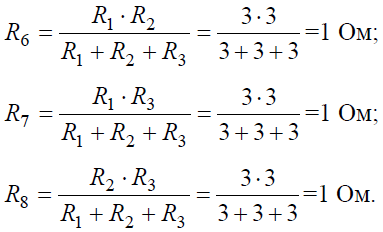
Преобразуем параллельное соединение ветвей между узлами 4 и 5

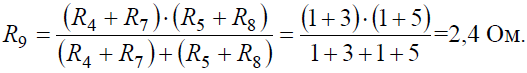
Ток в контуре, полученном в результате преобразований, считаем равным току источника тока J, и тогда напряжение:

И теперь можно определить токи I₄ и I₅:

Возвращаясь к исходной схеме, определим напряжение U₃₂ из уравнения по второму закону Кирхгофа:

Тогда ток в ветви с сопротивлением R₃ определится:

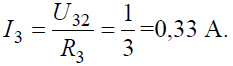
Величины оставшихся неизвестными токов можно определить из уравнений по первому закону Кирхгофа для узлов 3 и 1:

---

Электронная версия статьи Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Примеры решения задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Расчет электрических цепей постоянного тока методом эквивалентных преобразований

---

Метод эквивалентных преобразований

Сопротивления
в электрических цепях могут быть
соединены последовательно, параллельно,
по смешанной схеме и по схемам «звезда»,
«треугольник». Расчет сложной схемы
упрощается, если сопротивления в этой
схеме заменяются одним эквивалентным
сопротивлением R_экв,
и вся схема представляется в виде схемы
на рис. 1.3, где R=R_экв,
а расчет токов и напряжений производится
с помощью законов Ома и Кирхгофа.

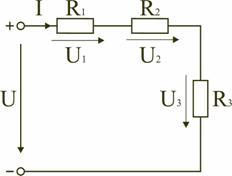
Электрическая
цепь с последовательным соединением
элементов

Рис. 1.4

Рис. 1.5

Последовательным
называют такое соединение элементов
цепи, при котором во всех включенных в
цепь элементах возникает один и тот же
ток I (рис. 1.4).

На
основании второго закона Кирхгофа (1.5)
общее напряжение U всей цепи равно сумме
напряжений на отдельных участках:

U
= U₁
+ U₂
+ U₃ или
IR_экв
= IR₁
+ IR₂
+ IR₃,

откуда
следует

(1.5)

R_экв
= R₁
+ R₂
+ R₃.

Таким
образом, при последовательном соединении
элементов цепи общее эквивалентное
сопротивление цепи равно арифметической
сумме сопротивлений отдельных участков.
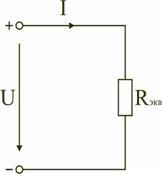
Следовательно, цепь с любым числом
последовательно включенных сопротивлений
можно заменить простой цепью с одним
эквивалентным сопротивлением R_экв
(рис. 1.5). После этого расчет цепи
сводится к определению тока I всей цепи
по закону Ома

,

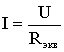и
по вышеприведенным формулам рассчитывают
падение напряжений U₁,
U₂,
U₃
на соответствующих участках электрической
цепи (рис. 1.4).

Недостаток
последовательного включения элементов
заключается в том, что при выходе из
строя хотя бы одного элемента, прекращается
работа всех остальных элементов цепи.

Электрическая
цепь с параллельным соединением элементов

Параллельным
называют такое соединение, при котором
все включенные в цепь потребители
электрической энергии, находятся под
одним и тем же напряжением (рис. 1.6).

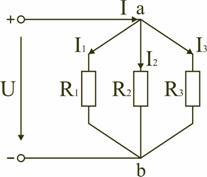
Рис.
1.6

В
этом случае они присоединены к двум
узлам цепи а и b, и на основании первого
закона Кирхгофа (1.3) можно записать, что
общий ток I всей цепи равен алгебраической
сумме токов отдельных ветвей:

I
= I₁
+ I₂
+ I₃,
т.е.
,

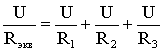откуда
следует, что

(1.6)

.

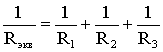В
том случае, когда параллельно включены
два сопротивления R₁
и R₂,
они заменяются одним эквивалентным
сопротивлением

(1.7)

.

Из
соотношения (1.6), следует, что эквивалентная
проводимость цепи равна арифметической
сумме проводимостей отдельных ветвей:

g_экв
= g₁
+ g₂
+ g₃.

По
мере роста числа параллельно включенных
потребителей проводимость цепи gэкв
возрастает, и наоборот, общее сопротивление
R_экв
уменьшается.

Напряжения
в электрической цепи с параллельно
соединенными сопротивлениями (рис. 1.6)

U
= IR_экв
= I₁R₁
= I₂R₂ =
I₃R₃.

Отсюда
следует, что

,

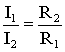т.е.
ток в цепи распределяется между
параллельными ветвями обратно
пропорционально их сопротивлениям.

По
параллельно включенной схеме работают
в номинальном режиме потребители любой
мощности, рассчитанные на одно и то же
напряжение. Причем включение или
отключение одного или нескольких
потребителей не отражается на работе
остальных. Поэтому эта схема является
основной схемой подключения потребителей
к источнику электрической энергии.

Электрическая
цепь со смешанным соединением элементов

Смешанным
называется такое соединение, при котором
в цепи имеются группы параллельно и
последовательно включенных сопротивлений.

Рис.
1.7

Для
цепи, представленной на рис. 1.7, расчет
эквивалентного сопротивления начинается
с конца схемы. Для упрощения расчетов
примем, что все сопротивления в этой
схеме являются одинаковыми: R₁=R₂=R₃=R₄=R₅=R.
Сопротивления R₄
и R₅
включены параллельно, тогда сопротивление
участка цепи cd равно:

.

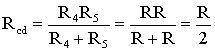В
этом случае исходную схему (рис. 1.7)
можно представить в следующем виде
(рис. 1.8):

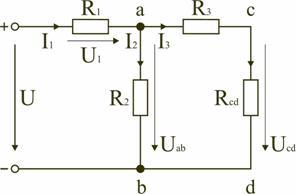
Рис.
1.8

На
схеме (рис. 1.8) сопротивление R₃
и R_cd
соединены последовательно, и тогда
сопротивление участка цепи ad равно:

.

Тогда
схему (рис. 1.8) можно представить в
сокращенном варианте (рис. 1.9):

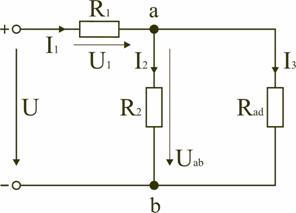
Рис.
1.9

На
схеме (рис. 1.9) сопротивление R₂
и R_ad
соединены параллельно, тогда сопротивление
участка цепи аb равно

.

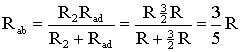Схему
(рис. 1.9) можно представить в упрощенном
варианте (рис. 1.10), где сопротивления
R₁
и R_ab
включены последовательно.

Тогда
эквивалентное сопротивление исходной
схемы (рис. 1.7) будет равно:

.

Рис. 1.10

Рис. 1.11

В
результате преобразований исходная
схема (рис. 1.7) представлена в виде
схемы (рис. 1.11) с одним сопротивлением
R_экв.
Расчет токов и напряжений для всех
элементов схемы можно произвести по
законам Ома и Кирхгофа.

Соединение
элементов электрической цепи по схемам
«звезда» и «треугольник»

В
электротехнических и электронных
устройствах элементы цепи соединяются
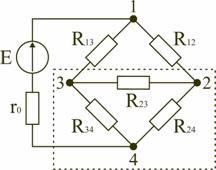
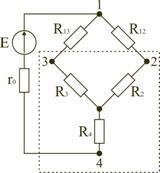
по мостовой схеме (рис. 1.12). Сопротивления
R₁₂,
R₁₃,
R₂₄,
R₃₄
включены в плечи моста, в диагональ 1–4
включен источник питания с ЭДС Е, другая
диагональ 3–4 называется измерительной
диагональю моста.

Рис. 1.12

Рис. 1.13

В
мостовой схеме сопротивления R₁₃,
R₁₂,
R₂₃
и R₂₄,
R₃₄,
R₂₃
соединены по схеме «треугольник».
Эквивалентное сопротивление этой схемы
можно определить только после замены
одного из треугольников, например
треугольника R₂₄
R₃₄
R₂₃
звездой R₂
R₃
R₄
(рис. 1.13). Такая замена будет
эквивалентной, если она не вызовет
изменения токов всех остальных элементов
цепи. Для этого величины сопротивлений
звезды должны рассчитываться по следующим
соотношениям:

(1.8)

;

;

.

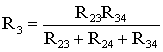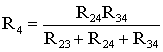Для
замены схемы «звезда» эквивалентным
треугольником необходимо рассчитать
сопротивления треугольника:

(1.9)

;

;

.

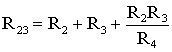После
проведенных преобразований (рис. 1.13)
можно определить величину эквивалентного
сопротивления мостовой схемы (рис. 1.12)

.

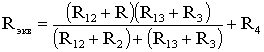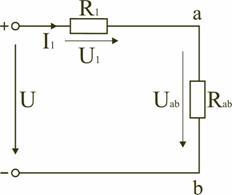
Метод эквивалентного генератора применяется для определения тока одной из ветвей электрической цепи в том случае, когда расчет всей схемы не требуется. В основу метода положена теорема об активном двухполюснике (теорема Гельмгольца-Тевенена). Основная идея метода заключается в том, что часть цепи, параметры которой определять нет необходимости, заменяется эквивалентным генератором с известной эдс и сопротивлением. Метод часто применяется для расчета режима электрической цепи.

Алгоритм состоит из следующих шагов:

1. Выбранная для расчета ветвь удаляется из схемы, а места образовавшегося разрыва обозначаются буквами. Оставшаяся часть схемы будет представлять собой эквивалентный генератор.
2. Рассчитывается эквивалентная эдс генератора.
3. Определяется эквивалентное сопротивление генератора.
4. По найденным в пунктах 2 и 3 параметрам генератора определяется ток через исключенную в пункте 1 ветвь.

Метод эквивалентного генератора: примеры решения

Рассмотрим пример расчета электрической схемы методом эквивалентного генератора (рисунок 1).

Допустим, что необходимо рассчитать ток I_ab через резистор R4. Тогда преобразования схема будет иметь вид, представленный на рисунке 2.

После преобразования ток через резистор R_ab (R4) определяется по формуле

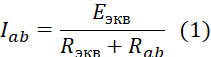
Для того, чтобы рассчитать значения Еэкв и Rэкв необходимо рассмотреть режим холостого хода генератора. Для этого необходимо обеспечить его работу без нагрузки, то есть условно отсоединить от цепи исследуемую ветвь ab (рисунок 3).

Для представленной схемы напряжение Еэкв будет равно

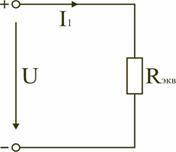
Далее требуется определить эквивалентное сопротивление. Для этого воспользуемся методом пассивного двухполюсника. В этом случае необходимо исключить из схемы источник эдс и найти общее сопротивление цепи (рисунок 4).

Эквивалентное сопротивление полученной схемы определяется по формуле

Теперь можно определить ток, проходящий через резистор ab согласно выражению (1).

Поставленная задача решена.

Методы расчета электрических цепей

Основными методами расчета электрических цепей являются:

1. Метод наложения.
2. Расчет электрических цепей с использованием законов Кирхгофа и Ома.
3. Метод эквивалентного генератора.
4. Метод эквивалентных преобразований.
5. Метод узловых потенциалов.
6. Метод контурных токов.

Большинство методов расчета электрических цепей основано на упрощении процедуры нахождения тока в ее ветвях. Некоторые из них основаны на упрощении систем уравнений, по которым осуществляется расчет, а в других случаях упрощается сама схема. Упрощение схемы применяется тогда, когда есть необходимость в определении электрического тока только в одной ветви.

Метод эквивалентных преобразований. Примеры расчета

Преобразование электрической цепи считается эквивалентным, в том случае, если при замене участка рассматриваемой электрической цепи более простыми электрические токи и напряжения участка, который не был преобразован, остаются неизменными. На практике, при расчетах электрических цепей используется преобразование со смешанным соединением элементов, представляющее собой сочетание простых параллельных и последовательных соединений. При помощи метода эквивалентных преобразований можно рассчитать практически любую цепь, при этом используются простые вычислительные средства и операции. Данный метод также позволяет рассчитать ток в ветви цепи, без расчета других участков.

Рассмотри схему, которая представлена на рисунке ниже.

«Метод эквивалентных преобразований» 👇

Так как в представленной схеме всего один источник, то можно определить истинные направления токов, как и показано на рисунке. Таким образом мы можем рассчитать эквивалентное сопротивление всей схемы:

$Rэк = ((((R3*R4)/(R3+R4)+R5))/R2) / ((R3*R4)/(R3+R4)+R5+R2))+R1$

Поэтому эквивалентная схема будет иметь следующий вид

Так как при эквивалентности замены участка схемы необходима неизменность токов и напряжений остальной цепи, то электрический ток будет везде одинаков. Таким образом электрический ток источника можно рассчитать следующим образом:

$I1 = E/Rэкв$

Так как нам известно сопротивление на первом участке, то мы можем рассчитать напряжение на элементе R1:

$U1 = I1*R1$

Согласно второму закону Кирхгофа запишем уравнение для контура R1-E-R2:

$E = U1+U2 = I*=I1*R1+I2*R2$

Откуда

$U2 = E-U1$

Теперь согласно закону Ома можно рассчитать ток на втором участке:

$I2 = U2/R2$

Применяя закон на третьем участке рассчитываем электрический ток на третьем участке:

$I3 = I1-I2$

Напряжение на резисторе 3 рассчитывается по второму закону Кирхгофа, действительного для контура R2-R5-R3:

$U4 = U2-U3$

Так как в рассматриваемой схеме сопротивления 3 и 4 соединены параллельно, то напряжение на них будет одинаково, поэтому можно рассчитать токи I4 и I5 по следующим формулам:

$I4 = U4/R3$

$I5 = U4/R4$

Рассмотрим схему, которая представлена на рисунке ниже.

Предположим, что нам известны следующие величины R1, R2, R3, R4, R5, R6, E1, E2, J. На рисунках ниже изображено поэтапное преобразование исходной схемы, задачей которого является расчет I3.

На схеме б резисторы 4 и 6 соединены последовательно и могут быть заменены на один резистор R46, который рассчитывается следующим образом:

$R46 = R4+R6$

В схеме в источник электродвижущей силы 1 пересчитывается в эквивалентный источник тока следующим образом:

$Jэ = Е1/R3$

Затем сопротивление R2 и R3 могут быть заменены эквивалентны R23, которое рассчитывается по формуле:

$R23 = (R2*R3) / (R2+R3)$

Затем производится (рисунок д) обратный расчет эквивалентного источника электрического тока в эквивалентный источник электродвижущей силы:

$Eэ = Jэ*R23$

Рассмотрим рисунок е, на котором изображен пересчет электродвижущей силы Е2 в эквивалентный источник тока:

$Jэ1 = Е2/R46$

Теперь Jэ1 с источником J объединяется в один эквивалентный источник тока, суммарный ток которого можно рассчитать по следующей формуле:

$Jэ2 = J + Jэ1$

В данном случае сопротивление (рисунок з) R5 не будет учитываться, потому что сопротивление источника тока бесконечно. В последнем рисунке производится обратный переход к источнику электродвижущей силы:

$Еэ1 = Jэ2*R46$

В итоге получается одноконтурная схема, по которой можно рассчитать I3

$I3 = (Eэ+Еэ1) / (R1+R23+R46)$

Из схемы д можно рассчитать электрический ток I4, для чего используется первый закон Кирхгофа:

$I4+J-I3=0$
Отсюда

$I4 = I3-J$
Так как теперь известны токи I3 и I4, то по рисунку б можно рассчитать электрический ток I1, для чего составляется уравнение по второму закону Кирхгофа для внешнего контура схемы:

$I1*R3+I4*R46+I3*R1 = E1+E2$

Из вышепредставленного уравнения находится I1, а затем по второму закону рассчитывается электрический ток I2:

$I2+I3-I1 = 0$

Отсюда

$I2 = I1-I3$

Содержание:

Преобразование схем электрических цепей:

При расчете электрических цепей часто возникает целесообразность преобразования схем этих цепей в более простые и удобные для расчета. Так, при одном или нескольких источниках электрической энергии в ряде случаев удается преобразовать электрическую схему в одноконтурную или в схему с двумя узлами, что весьма упрощает последующий расчет.

Описываемые ниже приемы преобразования схем электрических цепей применимы для цепей постоянного и переменного тока-, ради общности изложения они приводятся в комплексной записи.

Одним из основных видов преобразования электрических схем, часто применяемых на практике, является преобразование схемы со смешанным соединением элементов. Смешанное соединение элементов представляет собой сочетание более простых соединений — последовательного и параллельного, рассмотрению которых и посвящен данный параграф.

Последовательное соединение

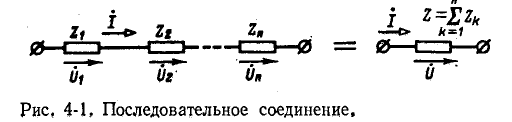
На рис. 4-1 изображена ветвь электрической цепи, в которой последовательно включены комплексные сопротивления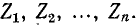

Напряжения на отдельных участках цепи обозначены через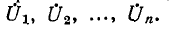

По второму закону Кирхгофа

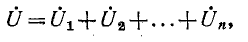
или, что то же,

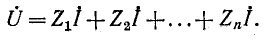
Сумма комплексных сопротивлений всех последовательно соединенных участков цепи

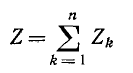
называется эквивалентным комплексным сопротивлением.

Если мнимые части комплексов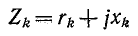

представляют собой сопротивления одинакового характера— индуктивного или емкостного (рис. 4-2), то эквивалентное комплексное сопротивление Z находится в результате

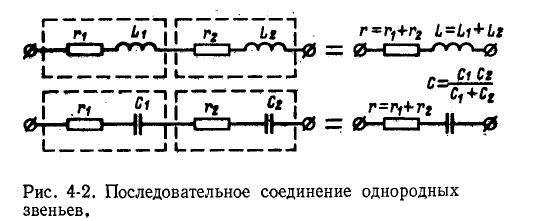
арифметического сложения в отдельности сопротивлений индуктивностей или величин обратных емкостям:

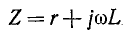
или

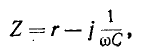
где

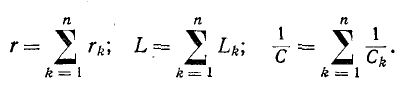
Ток в цепи равен:

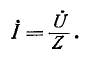
Напряжения на участках цепи, соединенных последовательно, относятся как комплексные сопротивления этих участков: напряжение на k-м участке равно произведению суммарного напряжения 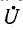на отношение комплексного сопротивления 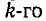участка к эквивалентному комплексному сопротивлению цепи:

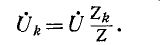
Приведенные выше формулы справедливы при любых значениях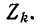

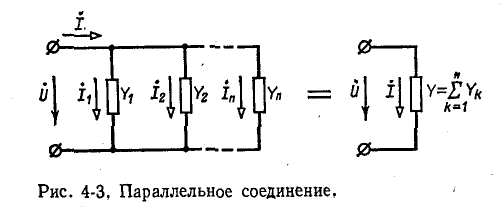
Параллельное соединение

На рис. 4-3 изображена схема электрической цепи с двумя узлами. Между этими узлами параллельно соединены ветви с комплексными проводимостями 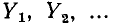 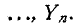Напряжение на всех ветвях одинаковое, равное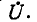

Токи в ветвях обозначены через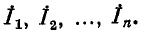

По первому закону Кирхгофа

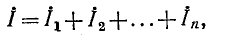
или, что то же,

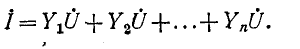
Сумма комплексных проводимостей всех ветвей, соединенных параллельно,

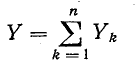
называется эквивалентной комплексной проводимостью.

Если мнимые части комплексов 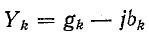представляют собой проводимости одинакового характера — емкостного или индуктивного (рис. 4-4), то эквивалентная

комплексная проводимость Y находится в результате арифметического сложения отдельных активных проводимостей 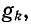, емкостей 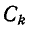или величин 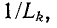обратных индуктивностям:

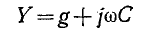
или

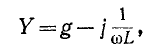
где

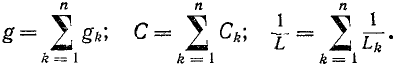
Суммарный ток в цепи равен:

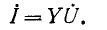
Токи в ветвях относятся, как их комплексные проводимости: ток в 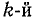 ветви равен произведению суммарного тока всех ветвей на отношение комплексной проводимости 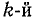ветви к эквивалентной комплексной проводимости:

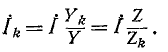
Данным выражением особенно удобно пользоваться при n > 2. При этом значения 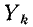могут быть любыми.

В случае параллельного соединения двух ветвей (n = 2) обычно пользуются выражениями, в которые входят сопротивления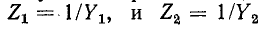 ветвей; эквивалентное комплексное сопротивление равно: v 1    1    Z,Z2

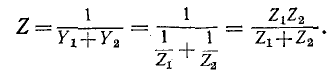
Токи в параллельных ветвях:

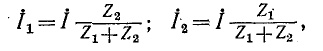
t. e. ток одной из двух параллельных ветвей равен суммарному току, умноженному на сопротивление другой ветви и деленному на сумму сопротивлений обеих ветвей.
 

Смешанное соединение

Электрические схемы, имеющие смешанное соединение, могут быть преобразованы в более простую электрическую схему путем замены параллельных ветвей одной ветвью и соответственно последовательно соединенных участков цепи — одним участком.

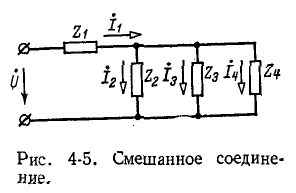
На рис. 4-5 показан пример электрической цепи со смешанным соединением. Эта схема легко приводится к одноконтурной. Первоначально вычисляется эквивалентная комплексная проводимость параллельных ветвей; затем находится величина, обратная проводимости, т. е. общее комплексное сопротивление параллельных ветвей; найденное комплексное сопротивление суммируется с комплексным сопротивлением последовательно включенного участка. Полученное суммарное

комплексное сопротивление эквивалентно сопротивлению исходной цепи со смешанным соединением.

Расчетные выражения для рассматриваемого случая будут следующие:

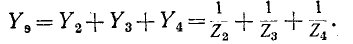
Суммарное комплексное сопротивление всей цепи равно:

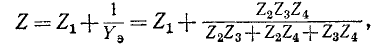
а суммарный ток

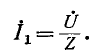
Токи в ветвях относятся, как комплексные проводимости ветвей:

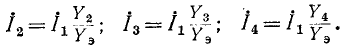
Таким юбразом, многоконтурная электрическая схема со смешанным соединением приводится к одноконтурной,

имеющей суммарное комплексное сопротивление Z или соответственно суммарную комплексную проводимость Y. Распределение токов и напряжений в смешанной цепи подчиняется правилам, указанным в предыдущем параграфе.

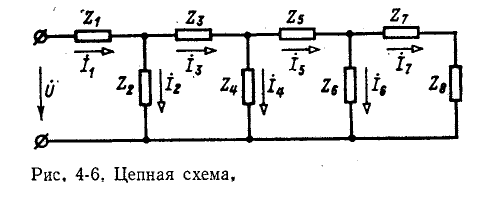
Описанный выше порядок преобразования схемы и нахождения распределения токов принципиально применим и для так называемой цепной схемы, показанной на рис. 4-6. Просуммировав комплексные сопротивления 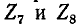в последней ветви, найдем комплексную проводимость ветви, которую алгебраически сложим с 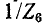и получим суммарную комплексную проводимость двух последних ветвей; вычислив обратную величину, т. е. комплексное сопротивление, прибавим к ней 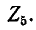Продолжая

таким образом дальше, получим в итоге результирующее комплексное сопротивление цепи и соответственно суммарный ток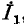 который может быть путем последовательных вычислений распределен между всеми ветвями сложной цепи.

Однако такой способ расчета цепной схемы является достаточно трудоемким и утомительным. Более целесообразно в этом случае воспользоваться другим методом, который известен под названием метода подобия или единичного тока.

Задавшись током в последней ветви, равным единице 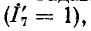находим напряжение на комплексном сопротивлении 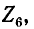равное 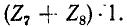При этом ток  .

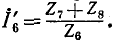Следовательно,

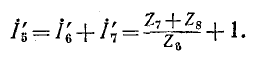
Прибавив к напряжению на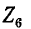 падение напряжения от тока 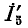в комплексном сопротивлении 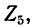получим напряжение на 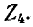Продолжая таким образом дальше, найдем в конечном итоге ток 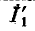и напряжение 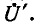Ввиду того что ток 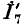был произвольно выбран равным единице, полученное напряжение не будет равно заданному напряжению 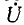на выводах цепи. Для нахождения действительного распределения токов в схеме необходимо все вычисленные значения токов умножить на отношение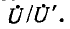
 

Эквивалентные участки цепи с последовательным и параллельным соединениями

Обозначим комплексное сопротивление участка цепи, состоящего из двух последовательно соединенных элементов, через 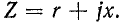Комплексная проводимость данного участка цепи равна 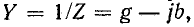причем активная и реактивная проводимости:

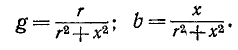
Если два элемента с проводимостями g и b, вычисленными по этим формулам, соединить параллельно, то суммарная комплексная проводимость будет равна Y и соответственно комплексное сопротивление будет равно Z,

Такие две цепи с последовательным и параллельным соединениями, имеющие одинаковые сопротивления на выводах, называются эквивалентными.

Ввиду того что реактивное сопротивление х, входящее в расчетные формулы, в общем случае зависит от частоты, условие эквивалентности этих цепей выполняется только при той частоте, для которой вычислено х.

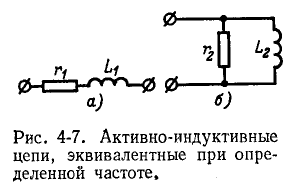
Пусть, например, задана схема с последовательным соединением сопротивления 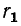и индуктивности 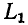(рис. 4-7, а). Преобразуем ее в схему с параллельным соединением элементов (рис. 4-7, б).

Активная и реактивная проводимости исходной цепи:

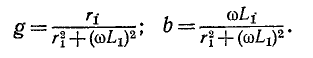
Из условия эквивалентности цепей следует, что параметры новой цепи будут:

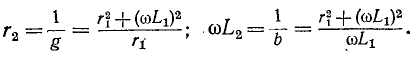
Вычислив по этим формулам 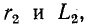получим схему цепи, эквивалентной исходной при данной частоте 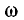При других значениях частоты параметры будут иметь другие значения, следовательно эквивалентность цепей нарушится.

При 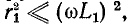например, при достаточно высокой частоте:

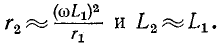
Если исходной является схема рис. 4-7, б и заданными параметрами являются 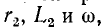то параметры эквивалентной цепи (рис. 4-7, а) определятся из выражений:

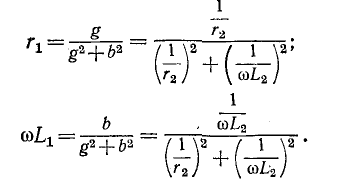
Из полученных выражений видно, что числовые значения 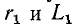эквивалентной цепи зависят от частоты.

Условия эквивалентности для цепей с последовательным и параллельным соединением сопротивления и емкости имеют вид:

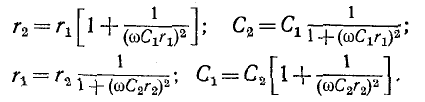
При достаточно высокой частоте 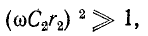и тогда

 

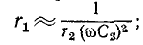
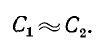
Преобразование треугольника в эквивалентную звезду

Преобразованием треугольника в эквивалентную звезду называется такая замена части цепи, соединенной по схеме треугольником, цепью, соединенной по схеме звезды, при которой токи и напряжения в остальной части цепи

сохраняются неизменными. Иначе говоря, эквивалентность треугольника и звезды понимается в том смысле, что при одинаковых напряжениях между одноименными выводами токи, входящие в одноименные выводы, одинаковы. Это равносильно тому, что мощности в этих цепях одинаковы.

На рис. 4-8 показан случай, когда преобразование треугольника в эквивалентную звезду дает возможность преобразовать многоконтурную схему в одноконтурную.

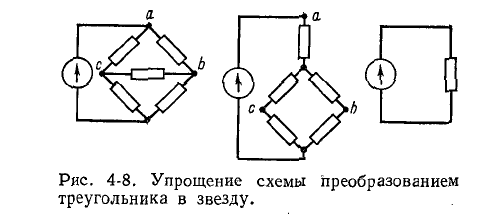
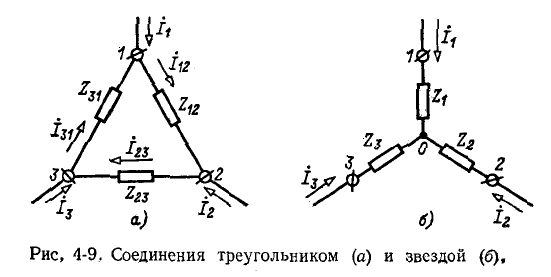
Для вывода расчетных выражений, служащих для преобразования треугольника в эквивалентную звезду, ниже приняты следующие обозначения (рис. 4-9):

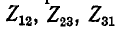• — сопротивления сторон треугольника;
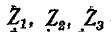• — сопротивления лучей звезды;
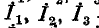• — токи, подходящие к выводам 1, 2, 3
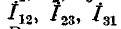• — Токи в ветвях треугольника.

Выразим токи в ветвях треугольника через приходящие токи.

По второму закону Кирхгофа сумма напряжений в контуре треугольника равна нулю:

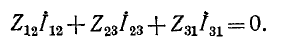
По первому закону Кирхгофа для узлов 2 и 1

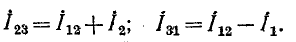
Решение этих уравнений относительно 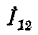Дает:

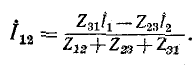
Напряжение между выводами 1 и 2 схемы рис. 4-9, а будет:

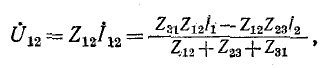
a в схеме рис. 4-9, б оно равно:

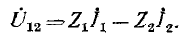
Для эквивалентности необходимо равенство напряжений 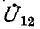при всяких токах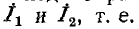

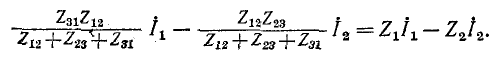
Это возможно при условии:

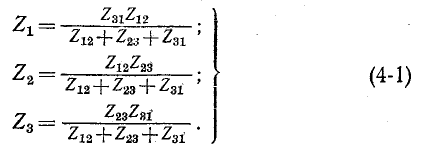
Третье выражение получается в результате круговой замены индексов.

Итак, комплексное сопротивление луча звезды равно произведению комплексных сопротивлений прилегающих сторон треугольника, деленному на сумму комплексных сопротивлений трех сторон треугольника.

Выше было получено выражение для тока в стороне 1—2 треугольника в зависимости от токов 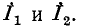Круговой заменой индексов можно получить токи в двух других сторонах треугольника:

 

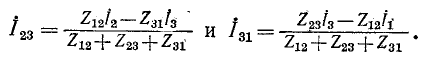
Преобразование звезды в эквивалентный треугольник

В расчетах также возникает необходимость замены звезды эквивалентным треугольником. На рис. 4-10 показан, например, случай, когда такая замена позволяет

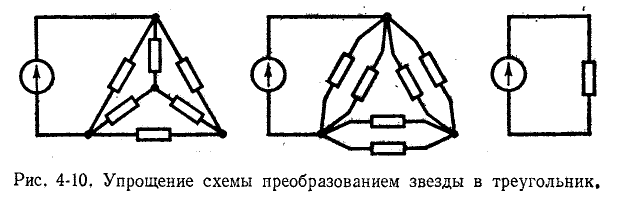
преобразовать сложную электрическую схему в одноконтурную.

При переходе от звезды к треугольнику заданными являются сопротивления звезды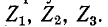 Выражения для искомых сопротивлений треугольника находятся в результате совместного решения трех уравнений (4-1).

Деление третьего уравнения на первое, а затем на второе дает:

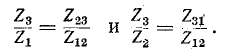
Выражая отсюда 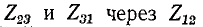и подставляя их в первое уравнение (4-1), получим:

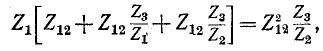
откуда

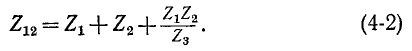
Аналогично круговой заменой индексов получим:

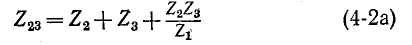
И

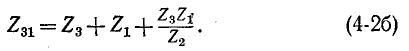
Отедовательно, комплексное сопротивление стороны треугольника равно сумме комплексных сопротивлений прилегающих лучей звезды и произведения их, деленного на сопротивление третьего луча.

Токи в лучах звезды легко выражаются через токи в сторонах треугольника. С учетом положительных направлений на рис. 4-9 имеем:

 

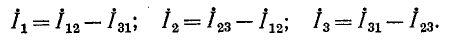
Эквивалентные источники э. д. с. и тока

Два разнородных источника электрической энергии — источник э. д. с. и источник тока — считаются эквивалентными,, если при замене одного источника другим токи и напряжения во внешней электрической цепи, с которой эти источники соединяются, остаются неизменными. На рис. 4-11 изображены эквивалентные источники тока, посылающие во внешнюю цепь ток 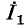и поддерживающие на своих выводах одинаковое напряжение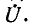

Условием эквивалентности источников, именуемым в дальнейшем правилом об эквивалентных источниках э.д.с. и тока, служит следующее соотношение между э. д. с. Ё источника э. д. с. и током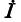

источника тока:

где Z — внутреннее комплексное сопротивление как источника э. д. с., так и источника тока.

Действительно, напряжение 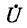на источнике э. д. с. получается в результате вычитания из э. д. с. 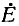падения напряжения от тока 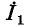в комплексном сопротивлении Z источника (рис. 4-11, а).

Соответственно напряжение 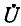на источнике тока при том же токе 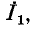посылаемом во внешнюю цепь, равно падению напряжения от тока 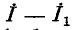в комплексном сопротивлении Z источника (рис. 4-11,6).

В обоих случаях напряжения на выводах обоих источников одинаковы:

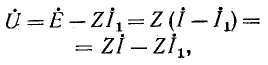
т. е. получается условие (4-3), не зависящее от тока 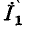нагрузки.

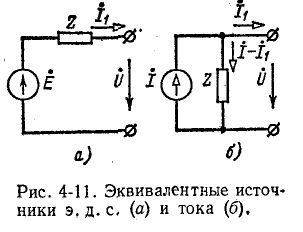
При отсоединении эквивалентных источников э. д. с.

и тока от внешней цепи 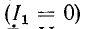напряжение на выводах обоих источников равно Ё. Именно это обстоятельство и равенство внутренних комплексных сопротивлений обоих источников и обеспечивают их эквивалентность при любом режиме работы.

Следует заметить, что мощности, расходуемые во внутренних сопротивлениях эквивалентных источников э. д. с. и тока, неодинаковы. В первом случае полная мощность, расходуемая в источнике, равна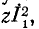 во втором случае

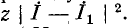
Например, при отсоединении источников от внешней цепи в первом случае мощность в источнике не расходуется, а во втором случае она составляет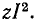

Поэтому эквивалентность источников следует понимать только в смысле неизменности токов, напряжений и мощностей во внешней электрической цепи, присоединенной к источникам.

Если внутреннее сопротивление источника э. д. с. равно нулю, то непосредственное применение формулы (4-3) для нахождения эквивалентного источника тока по, заданной э. д. с. источника не представляется возможным. В таких случаях сопротивление внешней цепи, включенной последовательно с э. д. с., можно рассматривать в качестве внутреннего сопротивления источника, что позволит применить формулу (4-3).

В случае сложной электрической цепи замена источника э. д. с. эквивалентным источником тока или обратно может иногда упростить расчет.

Целесообразность такой замены проиллюстрирована, в частности, в следующем параграфе.
 

Преобразование схем с двумя узлами

Применим правило об эквивалентных источниках э. д. с. и тока к преобразованию схемы с параллельным соединением n ветвей, содержащих источники э. д. с. (рис. 4-12, а).

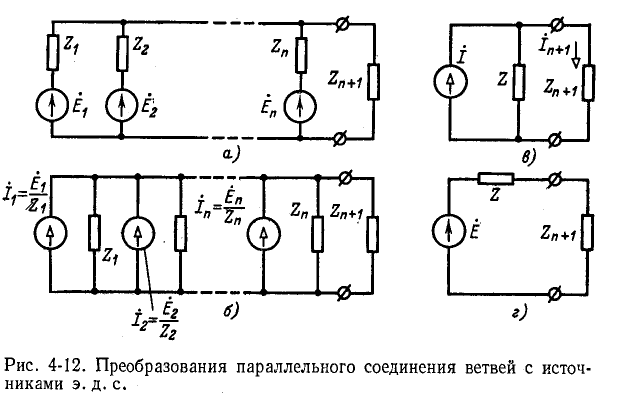
Заменяя заданные источники э. д. с. источниками тока, получаем схему рис. 4-12, б. Источники тока в совокупности образуют эквивалентный источник тока 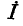(рис. 4-12, в), причем

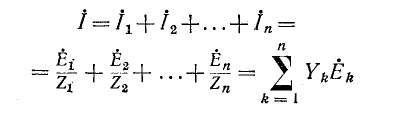
и

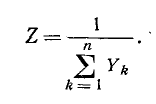
Пользуясь этим соотношением, можно в конечном итоге перейти от схемы рис. 4-12, в к схеме рис. 4-12, s, являющейся эквивалентом исходной схемы рис. 4-21, а. Здесь

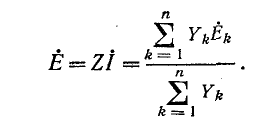
Таким образом, n параллельных ветвей с источниками э. д. с. между двумя узлами могут быть заменены одним источником тока (рис. 4-12, в) или источником э. д. с. (рис. 4-12, s).

Ток во внешней цепи (в ветви с сопротивлением 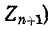равен:

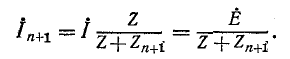
Напряжение между двумя узлами находится по формуле

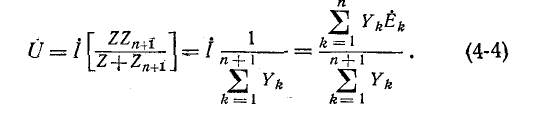
Выведенные здесь выражения широко используются для расчета электрических цепей с двумя узлами, а также более сложных цепей, приводящихся к двум узлам.
 

Перенос источников в схеме

Расчет электрической цепи облегчается в ряде случаев в результате переноса в схеме источников э. д. с. или тока. Как это видно из уравнений Кирхгофа, токи в схеме определяются заданными величинами суммарных э. д. с. в контурах независимо от того, из каких отдельных слагающих они состоят. Поэтому изменение расположения в схеме источников э. д. с., при котором суммарные э. д. с. во всех контурах сохраняются неизменными, не влияет на токи в ветвях. Аналогично напряжения на ветвях определяются заданными суммарными токами источников тока в узлах, и поэтому изменение расположения в схеме источников тока, при котором их суммарные токи во всех узлах сохраняются неизменными, не влияет на напряжения в схеме.

Если, например, требуется исключить источник э. д. с. из какой-либо ветви, то в данную ветвь вводится компенсирующая э. д. с., причем точно такая же э. д. с. вводится одновременно во все остальные ветви, сходящиеся

в одном из узлов данной ветви. Компенсирующая и дополнительные э. д. с. имеют одинаковое направление по отношению к рассматриваемому узлу. В результате этого источник э. д. с. из ветви исключается и появляются источники э. д. с. в других ветвях схемы. Суммарные э. д. с. во всех контурах и соответственно токи в ветвях остаются прежними.

Итак, источник э. д. с. может быть перенесен из какой-либо ветви схемы во все другие ветви, присоединенные к узлу данной ветви, без изменения токов в схеме.

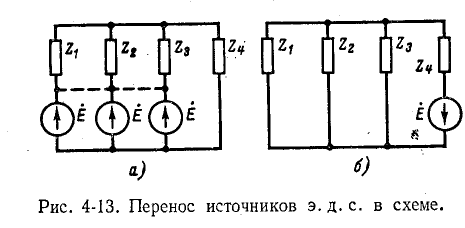
Справедливо и обратное положение: если во всех ветвях, кроме одной, сходящихся в узле, имеются одинаковые источники э. д. с. (рис. 4-13, а), направленные все к одному узлу или все от узла, то они могут быть заменены одним источником э. д. с. в ветви, в которой источник отсутствовал (рис. 4-13, б).

Это положение подтверждается тем, что суммарные э. д. с. в контурах схем на рис. 4-13, а и б одинаковы.

Имеется и другое доказательство данного положения: ввиду равенства э. д. с. всех источников вторые выводы

их могут быть объединены, как имеющие одинаковый потенциал. В результате такого объединения, показанного на рис. 4-13, а пунктиром, получается схема рис. 4-13, б.

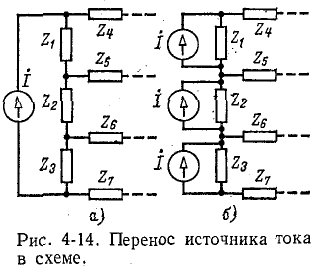
В случае переноса источников тока они присоединяются к узлам схемы так, чтобы оставались неизменными их суммарные токи в узлах.

Так, например, несмотря на то, что источники тока размещены в схемах рис.

4-14, а и б различно, суммарные токи источников в узлах обеих схем одинаковы. Поэтому и напряжения между узлами не изменились.

Итак, источник тока может быть заменен источниками тока, подключенными. параллельно всем

ветвям, которые составляли контур с рассматриваемым источником.

• Перенос источников в схеме успешно сочетается на практике с различными методами преобразований и расчетов (см. пример 4-1).

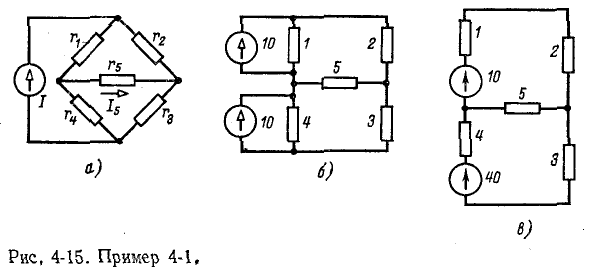
Пример 4-1.

Вычислить ток в диагональной ветви мостовой схемы рис. 4-15, а.

Дано: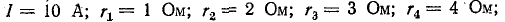

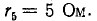
Заданный источник тока может быть заменен двумя источниками, подключенными параллельно сопротивлениям 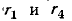(рис. 4-15, б). Пользуясь условием эквивалентности источников э, д, с, и тока, получаем схему рис, 4-15, в с двумя узлами. По формуле (4-4) напряжение на ветви 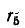равно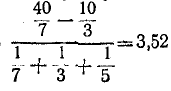

В. Искомый ток

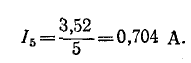
Преобразование симметричных схем

Схема электрической цепи, в которой имеется ось симметрии, называется симметричной. Например, схема рис. 4-16, а симметрична относительно вертикальной оси. В симметричных схемах легко выявляются точки или узлы с одинаковым потенциалом. В ветвях, присоединенных к таким узлам, токи равны нулю. Поэтому эти ветви

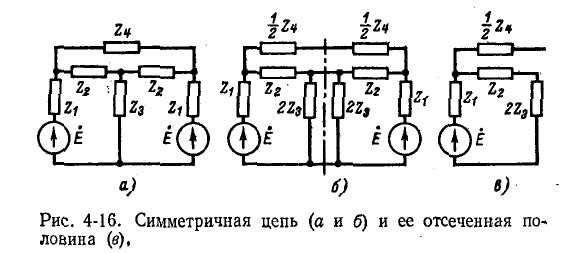
можно разрезать, не нарушая распределения токов и напряжений в схеме. Точки, имеющие одинаковый потенциал, могут быть объединены. Рассечение ветвей, по которым не проходит ток, и объединение точек равного потенциала упрощают схему и облегчают расчет.

Так, в симметричной схеме рис. 4-16, б токи в соединениях, пересекающих ось симметрии, отсутствуют. Разрезав схему по оси симметрии, получим с обеих сторон одноконтурную схему рис. 4-16, в, которая легко рассчитывается.

Допустим теперь, что полярность источников в симметричной схеме неодинакова (рис. 4-17, а). В этом случае (равенство э. д. с. источников и различие их полярности) токи в симметричных ветвях (например, и напряжения между соответствующими парами выводов, симметрично расположенными относительно оси, равны и противоположны по знаку. Отсюда следует, что напряжения между всеми точками, лежащими на оси симметрии, равны нулю 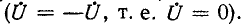Поэтому все точки схемы на оси симметрии могут быть замкнуты накоротко (рис. 4-17, б).

Таким образом, расчет сложных симметричных схем приводится к расчету более простых схем.

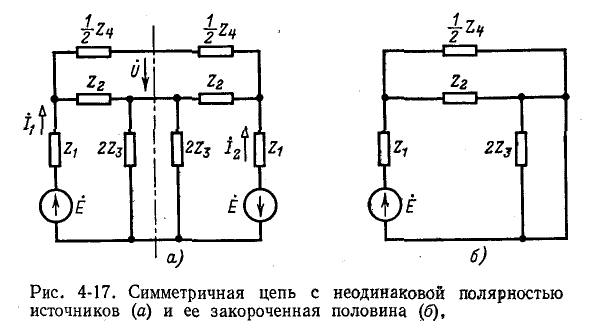
На рис. 4-18, а и б показана симметричная мостовая схема, имеющая две оси симметрии — вертикальную и

горизонтальную. В продольных ветвях ток отсутствует; потенциалы средних точек поперечных (перекрещенных) ветвей одинаковы.

Поэтому продольные ветви могут быть рассечены, а средние точки поперечных ветвей — объединены. В результате с обеих сторон получится одноконтурная схема (рис. 4-18, в), расчет которой крайне прост.

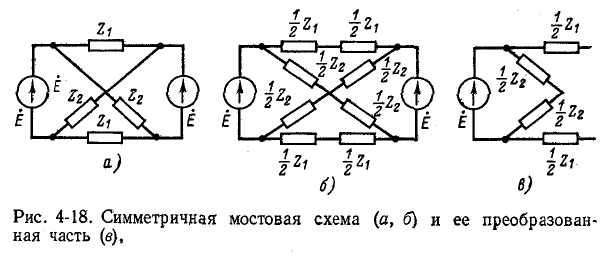
Если изменить полярность одного из источников (рис. 4-19, а), то роли продольных и поперечных ветвей поменяются и преобразованная часть схемы примет вид, показанный на рис. 4-19, б.

В разобранных выше примерах э. д. с. источников были равны. В случае неравенства э. д. с. источников преобразование симметричной схемы удобно сочетается с методом наложения (см. пример 7-5).