Главная
→
Примеры решения задач ТОЭ
→
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Основными законами, определяющими расчет электрической цепи, являются законы Кирхгофа.
На основе законов Кирхгофа разработан ряд практических методов расчета электрических цепей постоянного тока, позволяющих сократить вычисления при расчете сложных схем.
Существенно упростить вычисления, а в некоторых случаях и снизить трудоемкость расчета, возможно с помощью эквивалентных преобразований схемы.
Преобразуют параллельные и последовательные соединения элементов, соединение «звезда» в эквивалентный «треугольник» и наоборот. Осуществляют замену источника тока эквивалентным источником ЭДС. Методом эквивалентных преобразований теоретически можно рассчитать любую цепь, и при этом использовать простые вычислительные средства. Или же определить ток в какой-либо одной ветви, без расчета токов других участков цепи.
В данной статье по теоретическим основам электротехники рассмотрены примеры расчета линейных электрических цепей постоянного тока с использованием метода эквивалентных преобразований типовых схем соединения источников и потребителей энергии, приведены расчетные формулы.
Решение задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Задача 1. Для цепи (рис. 1), определить эквивалентное сопротивление относительно входных зажимов a−g, если известно: R1 = R2 = 0,5 Ом, R3 = 8 Ом, R4 = R5 = 1 Ом, R6 = 12 Ом, R7 = 15 Ом, R8 = 2 Ом, R9 = 10 Ом, R10= 20 Ом.
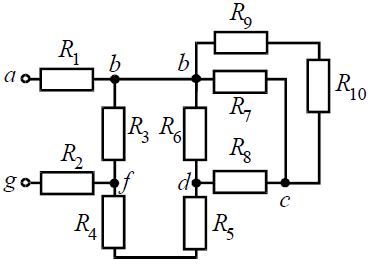
Рис. 1
Решение
Начнем эквивалентные преобразования схемы с ветви наиболее удаленной от источника, т.е. от зажимов a−g:
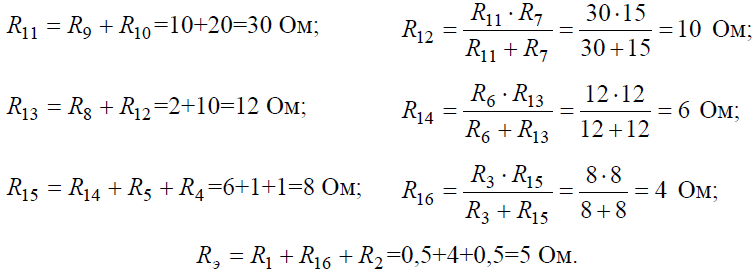
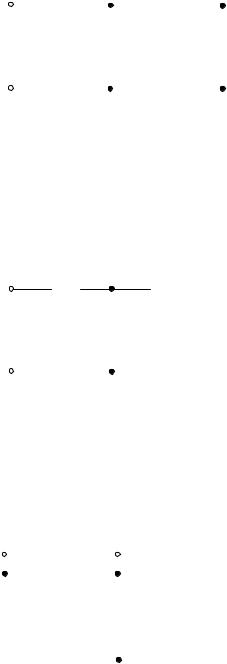
Задача 2. Для цепи (рис. 2, а), определить входное сопротивление если известно: R1 = R2 = R3 = R4= 40 Ом.
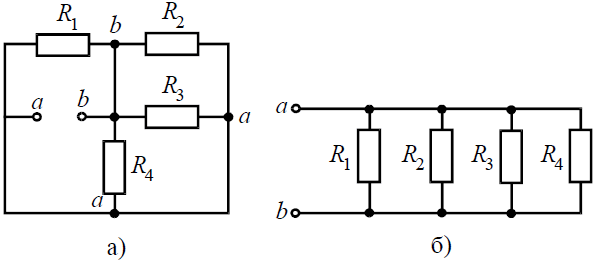 Рис. 2
Рис. 2
Решение
Исходную схему можно перечертить относительно входных зажимов (рис. 2, б), из чего видно, что все сопротивления включены параллельно. Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивленияможно воспользоваться формулой:
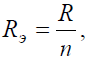 где R — величина сопротивления, Ом;
где R — величина сопротивления, Ом;
n — количество параллельно соединенных сопротивлений.
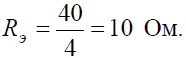
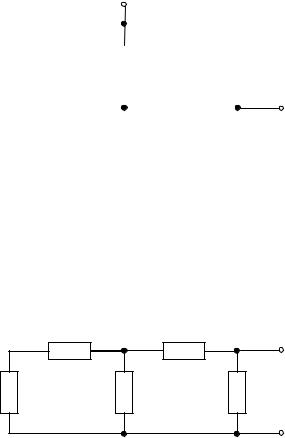
Задача 3. Определить эквивалентное сопротивление относительно зажимов a–b, если R1 = R2 = R3 = R4 = R5 = R6 = 10 Ом (рис. 3, а).
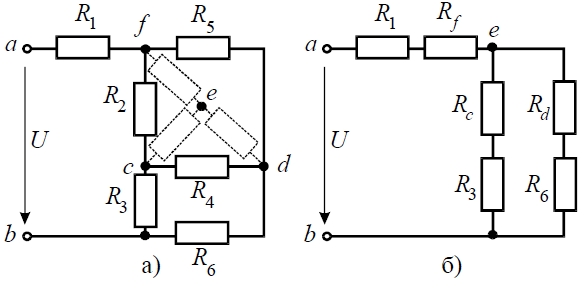
Рис. 3
Решение
Преобразуем соединение «треугольник» f−d−c в эквивалентную «звезду». Определяем величины преобразованных сопротивлений (рис. 3, б):
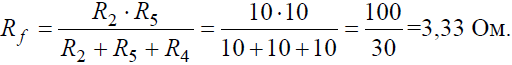 По условию задачи величины всех сопротивлений равны, а значит:
По условию задачи величины всех сопротивлений равны, а значит:
![]() На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно:
На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно:
![]()
И тогда эквивалентное сопротивление исходной схемы представляет последовательное соединение сопротивлений:
![]()
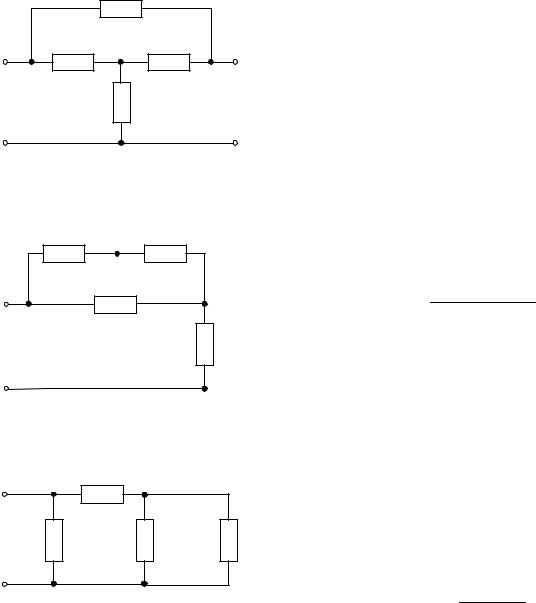
Задача 4. В заданной цепи (рис. 4, а) определить методом эквивалентных преобразований входные сопротивления ветвей a−b, c–d и f−b, если известно, что: R1 = 4 Ом, R2 = 8 Ом, R3 =4 Ом, R4 = 8 Ом, R5 = 2 Ом, R6 = 8 Ом, R7 = 6 Ом, R8 =8 Ом.
Решение
Для определения входного сопротивления ветвей исключают из схемы все источники ЭДС. При этом точки c и d, а также b и f соединяются накоротко, т.к. внутренние сопротивления идеальных источников напряжения равны нулю.
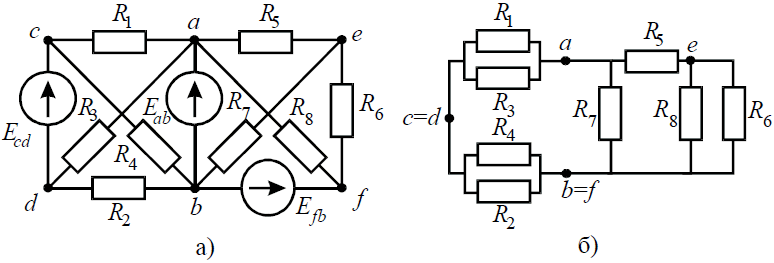
Рис. 4
Ветвь a−b разрывают, и т.к. сопротивление Ra–b = 0, то входное сопротивление ветви равно эквивалентному сопротивлению схемы относительно точек a и b (рис. 4, б):
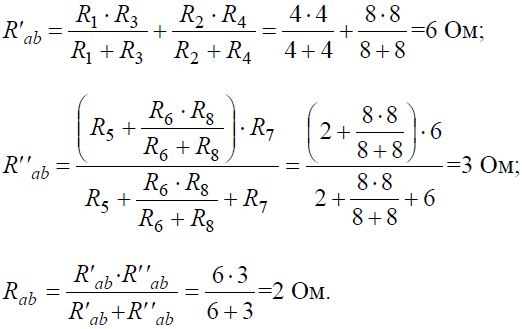
Аналогично методом эквивалентных преобразований определяются входные сопротивления ветвей Rcd и Rbf. Причем, при вычислении сопротивлений учтено, что соединение накоротко точек a и b исключает ( «закорачивает») из схемы сопротивления R1, R2, R3, R4 в первом случае, и R5, R6, R7, R8 во втором случае.
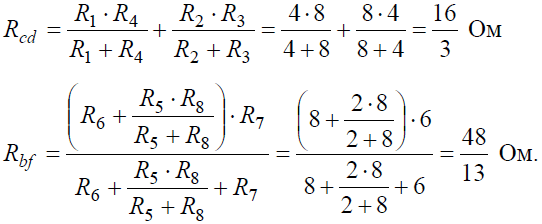
Задача 5. В цепи (рис. 5) определить методом эквивалентных преобразований токи I1, I2, I3 и составить баланс мощностей, если известно: R1 = 12 Ом, R2 = 20 Ом, R3 = 30 Ом, U = 120 В.
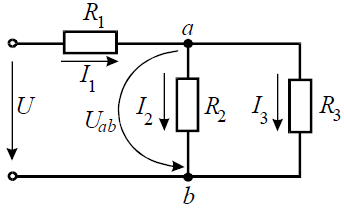
Рис. 5
Решение
Эквивалентное сопротивлениедля параллельно включенных сопротивлений:
![]()
Эквивалентное сопротивление всей цепи:
американские сигареты парламент.
![]()
Ток в неразветвленной части схемы:
![]()
Напряжение на параллельных сопротивлениях:
![]()
Токи в параллельных ветвях:
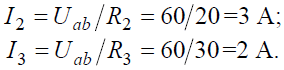
Баланс мощностей:
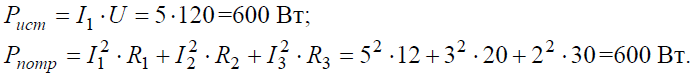
Задача 6. В цепи (рис. 6, а), определить методом эквивалентных преобразований показания амперметра, если известно: R1 = 2 Ом, R2 = 20 Ом, R3 = 30 Ом, R4 = 40 Ом, R5 = 10 Ом, R6 = 20 Ом, E = 48 В. Сопротивление амперметра можно считать равным нулю.
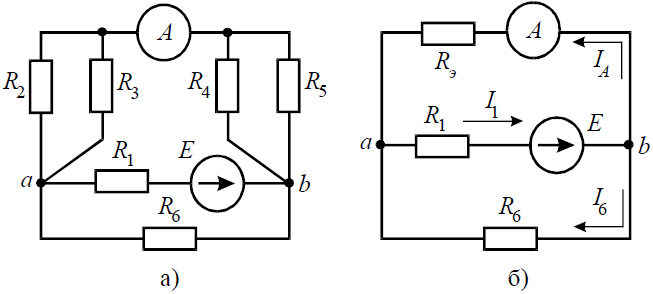
Рис. 6
Решение
Если сопротивления R2, R3, R4, R5 заменить одним эквивалентным сопротивлением RЭ, то исходную схему можно представить в упрощенном виде (рис. 6, б).
Величина эквивалентного сопротивления:
проститутки академическая. Смотри здесь строительство и ремонт деревянного дома.
![]()
Преобразовав параллельное соединение сопротивлений RЭ и R6 схемы (рис. 6, б), получим замкнутый контур, для которого по второму закону Кирхгофа можно записать уравнение:
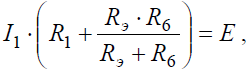
откуда ток I1:
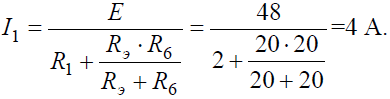
Напряжение на зажимах параллельных ветвей Uab выразим из уравнения по закону Ома для пассивной ветви, полученной преобразованием RЭ и R6:
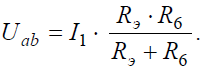
Тогда амперметр покажет ток:
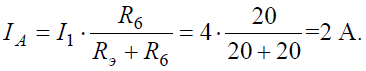
Задача 7. Определить токи ветвей схемы методом эквивалентных преобразований (рис. 7, а), если R1 = R2 = R3 = R4 = 3 Ом, J = 5 А, R5 = 5 Ом.
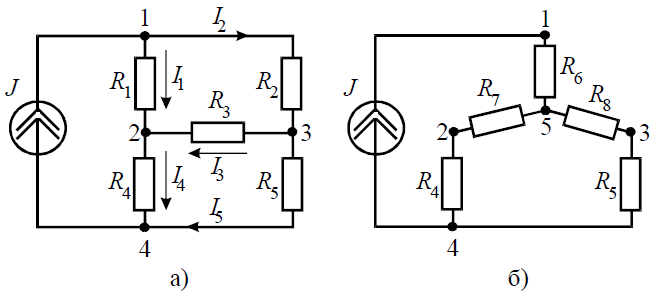
Рис. 7
Решение
Преобразуем «треугольник» сопротивлений R1, R2, R3 в эквивалентную «звезду» R6, R7, R8 (рис. 7, б) и определим величины полученных сопротивлений:
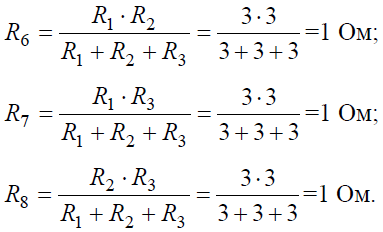
Преобразуем параллельное соединение ветвей между узлами 4 и 5
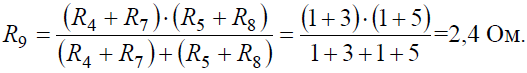
Ток в контуре, полученном в результате преобразований, считаем равным току источника тока J, и тогда напряжение:
![]()
И теперь можно определить токи I4 и I5:

Возвращаясь к исходной схеме, определим напряжение U32 из уравнения по второму закону Кирхгофа:
![]()
Тогда ток в ветви с сопротивлением R3 определится:
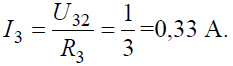
Величины оставшихся неизвестными токов можно определить из уравнений по первому закону Кирхгофа для узлов 3 и 1:
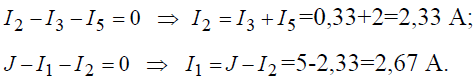
Электронная версия статьи Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Примеры решения задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
 Метод эквивалентных преобразований
Метод эквивалентных преобразований
2) В случае, если цепь содержит непреобразованные источники напряжения и источники тока, то элементы матрицы узловых токов [Jy] рассчитывают следующим образом:
Jyk Jk Gk Ek ,
где Jk – алгебраическая сумма токов источника тока, подключенных к рассматриваемому узлу. Токи Jk записывают под знаком суммы со знаком плюс, если они направлены к k-му узлу и со знаком минус, если они направлены от k- го узла; GkEk – алгебраическая сумма произведений ЭДС ветвей, сходящихся в k-м узле, на проводимости этих ветвей. Слагаемое записывается со знаком плюс (минус), если ЭДС направлена к узлу (от узла).
1.7 Краткая характеристика методов расчета электрических цепей
Наиболее универсальным методом анализа и расчёта электрических цепей является метод, основанный на применении I и II – го законов Кирхгофа.
Первый закон применяют для описания баланса токов в узлах электрической цепи, согласно которому: “Алгебраическая сумма токов, сходящихся в узле электрической цепи, должна быть равна нулю”:
n
Ik 0. k 1
Если бы условие (3) не выполнялось, то в узлах электрической цепи происходило бы накопление электрических зарядов, что экспериментально не подтверждается.
Второй закон применяют для описания замкнутых (условно или, безусловно) контуров, согласно которому: “Алгебраическая сумма ЭДС, действующих в замкнутом контуре, должна уравновешиваться алгебраической суммой падений напряжений на элементах замкнутого контура”:
n m m
Ek Up IpRp. k 1 p 1 p 1
Оба закона Кирхгофа являются следствиями закона сохранения энергии применительно к электрическим цепям.
Метод наложения (суперпозиции) применяют для анализа и расчёта только линейных электрических цепей, содержащих несколько источников энергии. Здесь токи в ветвях определяются путем алгебраического суммирования “частичных” токов, получающихся в ветвях под воздействием каждой частичной ЭДС схемы в отдельности.
Наиболее эффективен метод наложения тогда, когда в цепи содержатся источники тока (с Rвн ) и источники ЭДС (с Rвн 0), так как при рассмотрении “частичных” режимов работы схемы (только с каким – то одним источником) – идеальные источники ЭДС закорачиваются (из-за Rвн 0), а ветви с ис-
21
точником тока обрываются (из-за Rвн ), что вызывает максимальное упрощение схемы в конкретном “частичном” режиме.
1.8 Потенциальная диаграмма
Второй закон Кирхгофа наглядно иллюстрируется с помощью потенциальной диаграммы (ПД). Если по оси абсцисс прямоугольной системы координат отложить сопротивления участков в той последовательности, в которой они включены в цепь, а по оси ординат – потенциалы соответствующих точек, то получится график распределения потенциала вдоль неразветвленной цепи. Пользуясь этим графиком, можно определить напряжение между двумя любыми точками цепи. Порядок построения потенциальной диаграммы (предварительно необходимо выполнить расчет электрической цепи) состоит в следующем:
1)Выбираем опорный узел и принимаем его потенциал равным нулю;
2)Задаем положительное направление обхода контура;
3)Если направление обхода контура и направление тока совпадают на участке цепи, то потенциал при прохождении через сопротивление уменьшается, при направлении обхода контура и противоположном направлении тока потенциал при прохождении через сопротивление увеличится;
4)Идеальный источник ЭДС вызывает скачкообразное изменение потенциала. Скачок потенциала положительный, если направление ЭДС совпадает по направлению с обходом контура и отрицательный, если направления обхода контура и ЭДС противоположны.
При построении ПД необходимо соблюдать следующие правила:
1)Если направление обхода выбранного замкнутого контура и направление тока на участке цепи совпадают, то потенциал будет уменьшаться при прохождении через сопротивление, на величину падения в нём напряжения;
2)Если направление обхода выбранного замкнутого контура и направление тока на участке цепи противоположны, то потенциал будет увеличиваться при прохождении через сопротивление, на величину падения в нём напряжения;
3)Идеальный источник ЭДС вызывает скачок потенциала на величину
ЭДС источника (т.к. его Rвн =0);
4)Скачок потенциала после источника ЭДС положительный, если направление ЭДС совпадает с направлением обхода и отрицательный, если направление ЭДС и направление обхода противоположны;
5)Источник ЭДС повышает потенциал в той точке, в которую направлена его стрелка.
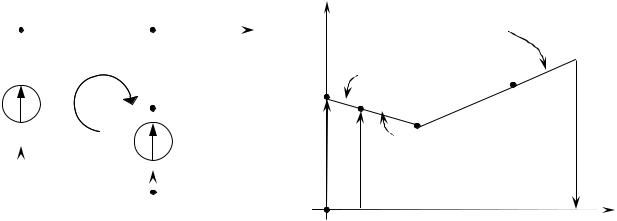
Для примера построим потенциальную диаграмму для контура “a – b – c – d – a” в схеме представленной на рис. 1.8.1.
Примем потенциал точки “а” равным нулю ( a) и найдём последовательно потенциалы точек “b”, “c”, “d”:
b = a + E1 – I1R01 ,
22
|
c = b – I1R1 = a + E1 – I1R01 + I1R1 , |
||||||||||||||||
|
d = c + I2R2 = a + E1 – I1R01 – I1R1 + I2R2 , |
||||||||||||||||
|
a = d – E2 = 0. |
||||||||||||||||
|
а затем построим потенциальную диаграмму (рис. 1.8.2). |
||||||||||||||||
|
b |
R1 |
c |
R3 |
I |
φ, В |
|||||||||||
|
3 |
ΔU2 = I1·R02 |
|||||||||||||||
|
E1 |
R2 |
ΔU1 = –I1·R01 |
d’ |
|||||||||||||
|
d |
b’ |
b |
||||||||||||||
|
R01 |
c |
|||||||||||||||
|
E2 |
E1 |
I2·R2 |
||||||||||||||
|
I1 |
–I1·R1 |
|||||||||||||||
|
R02 |
||||||||||||||||
|
I3 |
а |
|||||||||||||||
|
a |
||||||||||||||||
|
0 |
R01 |
|||||||||||||||
 d
d
–E2
d R, Ом
Замечание: При построении ПД один из узлов схемы принимается за опорный и заземляется, то есть его потенциал обнуляется. При этом токи в ветвях не изменяются, так как их величина зависит от разности потенциалов, а не от абсолютной величины потенциала одного отдельно взятого узла схемы.
23
2 РАСЧЕТ ПРОСТЫХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
2.1 Примеры решения задач цепей с источниками постоянного напряжения и тока
2.1.1 Найти эквивалентное сопротивление для цепей рис. 2.1.1 относительно зажимов a, b?
|
2R |
2R |
РЕШЕНИЕ: в схеме представленной на |
|||||||||||||||
|
рис. 2.1.1.а резисторы R и 2R попарно соеди- |
|||||||||||||||||
|
R |
R |
нены между собой параллельно: эквивалентное |
|||||||||||||||
|
сопротивление состоит из суммы этих двух со- |
|||||||||||||||||
|
единений: |
|||||||||||||||||
|
a |
b |
2RR |
2RR |
4 |
|||||||||||||
|
Rab |
R Ом. |
||||||||||||||||
|
Рис. 2.1.1.а |
2R R |
2R R |
3 |
||||||||||||||
|
R |
R |
РЕШЕНИЕ: в схеме представленной на |
|||||||||||||||
|
рис. 2.1.1.б перемычка закорачивает резистор |
|||||||||||||||||
|
4R, и он как бы исключается из схемы. Экви- |
|||||||||||||||||
|
валентное сопротивление состоит из парал- |
|||||||||||||||||
|
4R |
3R |
||||||||||||||||
|
лельного соединения резисторов 3R и (R+2R): |
|||||||||||||||||
R 2R 3R
Rab R 2R 3R 1,5R Ом.
Рис. 2.1.1.б
|
а |
РЕШЕНИЕ: в схеме представленной на |
||||||||||||||
|
рис. 2.1.1.в резисторы R1 и R2 соединены по- |
|||||||||||||||
|
R3 |
R1 |
следовательно: R12=R1+R2; резисторы R4 и R5 |
|||||||||||||
|
соединены параллельно, их общее сопротивле- |
|||||||||||||||
|
ние рассчитывается по формуле: |
|||||||||||||||
|
R5 |
R4 R2 |
R45 |
R4 R5 |
. |
|||||||||||
|
R4 R5 |
|||||||||||||||
|
b |
Эквивалентное сопротивление состоит из двух |
||||||||||||||
|
параллельно соединенных ветвей с резисто- |
|||||||||||||||
|
Рис. 2.1.1.в |
рами: R12 в одной ветви и последовательно со- |
||||||||||||||
|
единенных R3 и R45 в другой. Эквивалентное |
|||||||||||||||
|
сопротивление рассчитывается по формуле: |
|||||||||||||||
|
R12 R3 R45 |
|||||||||||||||
|
Rab |
. |
||||||||||||||
|
R12 R3 R45 |
24
25
2.1.2 Найти эквивалентное сопротивление цепи (рис. 2.1.2) относительно зажимов “a” и “b”, если: R1=600 Ом, R2=360 Ом, R3=400 Ом, R4=300 Ом.
а
R4
R2
R3
R1
b
Рис. 2.1.2
|
а |
|
|
R2 |
|
|
R4 |
|
|
b |
R13 |
|
Рис. 2.1.2.б |
а

 R2
R2
R4
b
Рис. 2.1.2.а
РЕШЕНИЕ: Заданную схему можно представить в ином виде (рис. 2.1.2.а, рис. 2.1.2.б).
Резисторы R1 и R3 соединены параллельно, их сопротивление рассчитывается по формуле:
|
R13 |
R1 R3 |
600 400 |
240 Ом, |
||
|
R1 R3 |
600 400 |
||||
с резистором R2 сопротивление R13 соединено последовательно, то есть их общее сопротивление R123:
R123 R13 R2 240 360 600 Ом,
Эквивалентное сопротивление цепи Rab состоит из двух соединенных парал-
|
лельно резисторов R123 |
и R4: |
R123 R4 |
600 300 |
||
|
Rab |
R123 R4 |
600 300 200 Ом. |
|||
|
2.1.3 Чему равно сопротивление цепи (рис. 2.1.3) Rab при разомкнутом и |
|||||
|
замкнутом рубильнике? |
РЕШЕНИЕ: |
||||
|
а |
1 |
||||
|
R |
Решение данной задачи распадается на два от- |
||||
|
R |
дельных случая: |
||||
|
K |
1-й случай – ключ “К” разомкнут. Перемычка |
||||
|
2 |
|||||
|
между узлами 1 и 3 шунтирует два резистора, |
|||||
|
поэтому реальная схема имеет вид, представ- |
|||||
|
b |
R |
R |
ленный на рис. 2.1.3.а. Следовательно, эквива- |
||
|
лентное сопротивление состоит из двух после- |
|||||
|
3 |
|||||
|
Рис. 2.1.3 |
довательно соединенных резисторов: Rab=2R; |
||||
a R 1
b R
2
Рис. 2.1.3.а
а 1
R
R 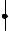 2
2
R
b R
3
Рис. 2.1.3.б
2-й случай – ключ “К” замкнут (рис. 2.3.1.б). Наличие в цепи двух перемычек приводит к тому, что три резистора между точками 1 и “b” включены параллельно между собой: каждый резистор одним полюсом подключен к узлу 1, что равносильно подключению к узлу 3, а вторым полюсом подключен к узлу “b”, что равносильно подключению к узлу 2.
В этом случае эквивалентное сопротивление преобразованной схемы представленной на рис. 2.1.3.в можно найти как:
|
Rab R |
1 |
R |
R |
4 |
R Ом. |
||||||||||||||||||
|
1 |
1 |
1 |
3 |
3 |
|||||||||||||||||||
|
R |
R |
R |
|||||||||||||||||||||
|
а |
R |
1 |
3 |
||||||||||||||||||||
|
R |
R |
R |
|||||||||||||||||||||
|
b |
|||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||
|
Рис. 2.1.3.в |
2.1.4 Пусть требуется найти эквивалентное сопротивление цепи представленной на рис. 2.1.4 между различными зажимами “a” – “b”, “c” – “d”, “d”
– “f”, “a” – “f”, “e” – “f”, если: R1=6 Ом, R2=5 Ом, R3=15 Ом, R4=30 Ом, R5=3 Ом, R6=3 Ом.
|
а |
R1 |
c |
R2 |
d |
R5 |
e |
|
R3 |
R4 |
R6 |
||||
|
b |
f |
|||||
|
Рис. 2.1.4 |
РЕШЕНИЕ:
а) Для расчета сопротивления Rab между зажимами “а” и “b” представим схему в ином виде (рис. 2.1.4.а). Эта схема представляет собой лестничное соединение сопротивлений.
26
|
а |
R1 |
R2 |
R5 |
Резисторы R5 |
и R6 |
соединены по- |
||||||||||||||
|
следовательно и |
эквивалентное |
|||||||||||||||||||
|
сопротивление резисторов R5 и R6 |
||||||||||||||||||||
|
R5 |
R4 |
R6 |
найдем как: |
|||||||||||||||||
|
b |
R56 R5 R6 |
3 3 6 Ом. |
||||||||||||||||||
|
Рис. 2.1.4.а |
Сопротивление R56 соединено параллельно R4, поэтому их общее сопротивление найдем по формуле:
|
R456 |
R4 R56 |
30 6 |
5 Oм. |
|||||||||||||
|
R4 R56 |
||||||||||||||||
|
30 6 |
||||||||||||||||
|
а |
R1 |
R2 |
После этого преобразования схему мож- |
|||||||||||||
|
но свернуть и представить в виде (рис. |
||||||||||||||||
|
2.1.4.б). Резисторы R2 |
и R456 соединены |
|||||||||||||||
|
R3 |
R456 |
последовательно, тогда |
их общее сопро- |
|||||||||||||
|
b |
тивление R’ будет равно: |
|||||||||||||||
|
R R2 R456 5 5 10Oм. |
||||||||||||||||
|
Рис. 2.1.4.б |
||||||||||||||||
Полное эквивалентное сопротивление цепи Rab состоит из резистора R1, последовательно с которым соединены параллельно включенные резисторы R3 и R’:
|
Rab R1 |
||||||||||||||
|
c R2 |
d |
R5 |
||||||||||||
|
R3 |
R4 |
R6 |
||||||||||||
Рис. 2.1.4.в
|
R3R |
15 10 |
||
|
6 |
12 Oм; |
||
|
R3 R |
15 10 |
б) Для расчета сопротивления Rcd между зажимами “с” и “d” перечертим схему и представим в виде (рис. 2.1.4.в). Резистор R1 не следует учитывать, так как он подключен к разомкнутым зажимам “a” – “b”. Резисторы R5, R6 включены между собой последовательно, а с резистором R4 параллельно:
|
R456 |
R4 R5 R6 |
30 3 3 |
5 Oм, |
||
|
R4 R5 R6 |
|||||
|
30 3 3 |
с результирующим сопротивлением R456 последовательно соединен резистор R3 и их общее сопротивление R” будет равно: R”=R3+R456 =15+5=20 Ом, Эквивалентное сопротивление Rcd состоит из параллельно соединенных резисторов R2 и R”:
|
R |
2 R |
5 20 |
|||
|
Rcd |
4Oм. |
||||
|
R2 R |
|||||
|
5 20 |
27
|
R2 |
d |
R5 |
в) Для расчета сопротивления Rdf |
ме- |
||||||||||||||
|
жду зажимами “d” и “f” представим |
||||||||||||||||||
|
схему в виде, как показано на |
рис. |
|||||||||||||||||
|
R3 |
R4 |
R6 |
2.1.4.г. |
|||||||||||||||
|
f |
Резистор R1 не будем учитывать, так |
|||||||||||||||||
|
как он подключен к разомкнутым за- |
||||||||||||||||||
|
Рис. 2.1.4.г |
жимам “a” и “b”. |
|||||||||||||||||
Эквивалентное сопротивление цепи между зажимами “d” – “f” состоит из трех параллельно соединенных ветвей: R2+R3; R4 и R5+R6. Поэтому найдем вначале сумму проводимостей 3-х параллельных ветвей:
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
См, откуда Rdf =4 Ом. |
|||||||
|
R2 R3 |
R5 R6 |
5 15 |
|||||||||||||
|
Rdf |
R4 |
30 3 3 4 |
|
R2 |
R5 |
e |
|
R3 |
R4 |
R6 |
|
f |
||
|
Рис. 2.1.4.д |
г) Для расчета сопротивления Ref между зажимами “e” и “f” рассчитаем схему, представленную (рис. 2.1.4.д). Резистор R1 так же не будем учитывать, т.к. он включен на разомкнутые зажи-
мы “a” и “b”.
Резисторы R2 и R3 соединены последовательно, то есть R23=R2+R3=5+15=20 Ом, а параллельно с ними соединен резистор R4; тогда их общее сопротивление
R234:
|
R234 |
R23 R4 |
20 30 |
12Oм, |
|||
|
R23 R4 |
20 30 |
|||||
последовательно с R234 соединен резистор R5: R2-5=R234 + R5=12 + 3 =15 Ом,
Эквивалентное сопротивление Ref состоит из параллельного соединения
|
R2-5 и R6: |
R2 5 R6 |
15 3 |
|||
|
Ref |
2,5Oм. |
||||
|
R2 5 R6 |
|||||
|
15 3 |
2.1.5 Пусть требуется найти сопротивление между зажимами “a” и “b” схемы представленной на рис. 2.1.5 в двух режимах:
1)при холостом ходе зажимов “c” и “d”;
2)коротком замыкании зажимов “c” и “d”, если: R1=16 Ом, R2=4 Ом, R3=4 Ом, R4=12 Ом.
28
|
R4 |
||||
|
а |
R1 |
e |
R2 |
c |
|
R3 |
||||
|
b |
d |
|||
|
f |
||||
|
Рис. 2.1.5 |
||||
|
R4 |
c |
R2 |
||
|
а |
R1 |
e |
||
|
b |
R3 |
|||
|
f |
||||
|
Рис. 2.1.5.а |
||||
|
а |
R1 |
e |
||
|
R4 |
R3 |
R2 |
||
|
b |
||||
|
c |
||||
|
Рис. 2.1.5.б |
РЕШЕНИЕ:
а) Зажимы “c” и “d” разомкнуты (режим холостого хода – хх). Схема для этого случая представлена на рис. 2.1.5.а. В этом режиме резисторы R4 и R2 соединены последовательно.
Результирующий резистор R42 = R4 + R2 соединен параллельно с резистором R1, тогда их общее сопротивление R’ найдем как:
|
R |
R42 R1 |
(12 4) 16 |
8Oм, |
|
|
R42 R1 |
||||
|
12 4 16 |
R’ оказывается соединен последовательно с R3 и эквивалентное сопротивление между зажимами а и b будет равно:
Rab R’ R3 (R4 R2)R1 R3 R4 R2 R1
8 4 12Oм.
б) Зажимы “c” и “d” закорочены. Для режима К.З. схема представлена на рис. 2.1.5.б. Здесь точки “c”, “d”, “f”, и “b” имеют одинаковые потенциалы, причем резистор R4 при коротком замыкании зажимов “c” и “d” оказывается включенным параллельно зажимам “а” и “b”. “Свернем” схему от конца к началу: резисторы R2 и R3 соединены параллельно между собой, их общее сопротивление R23 включено последовательно с R1:
R123 R1 R2 R3 .
R2 R3
Эквивалентное сопротивление схемы относительно зажимов “a” и “b” представляет параллельное соединение R4 и R123:
|
R4 |
(R1 |
R2 |
R3 |
) |
4 4 |
|||||||||||||||
|
R |
R123 |
12 (16 |
) |
|||||||||||||||||
|
R2 R3 |
||||||||||||||||||||
|
Rab |
4 |
4 4 |
7,2Oм. |
|||||||||||||||||
|
R4 |
R123 |
R4 |
R1 |
R |
2 R3 |
12 16 |
4 4 |
|||||||||||||
|
R2 R3 |
4 4 |
|||||||||||||||||||
2.1.6 Найти входное сопротивление цепи, представленной на рис. 2.1.6, при разомкнутом и замкнутом ключе, если: R1=40 Ом, R2=20 Ом, R3=10 Ом, R4=30 Ом, R5=40 Ом.
29
|
R3 |
R1 |
РЕШЕНИЕ: |
||||||||||
|
а) Пусть ключ “K” разомкнут (рис. 2.1.6). В |
||||||||||||
|
этом режиме входное сопротивление цепи оп- |
||||||||||||
|
а |
||||||||||||
|
K |
R5 |
ределяется параллельным соединением двух |
||||||||||
|
c |
d |
ветвей, в которые |
последовательно включены |
|||||||||
|
R4 |
резисторы R1 с R2 |
и R3 с R4. Найдем последова- |
||||||||||
|
R2 |
||||||||||||
|
b |
тельно включенные сопротивления: |
|||||||||||
|
R12 R1 R2, R34 R3 R4, |
||||||||||||
Рис. 2.1.6
R3 а R1
R5
c 
R4 b R2
Рис. 2.1.6.a
R3 а R1
c 
R4 b R2
Рис. 2.1.6.б
тогда, эквивалентное сопротивление схемы:
|
Rвх |
R12 R34 |
(R1 R2) (R3 R4) |
||
|
R12 R34 |
R1 R2 R3 R4 |
(40 20) (10 30) 24Oм. 40 20 30 10
б) Пусть ключ “К” замкнут (рис. 2.1.6.а). В этом случае резисторы схемы образуют два “треугольника” или две “звезды”. Так резисторы R1, R3, R5 и R2, R4, R5 соединены “треугольником”, а R1, R2, R5 и R3, R4, R5 – “звез-
 d дой”. Задачу определения Rвх можно решить преобразованием “треугольника” в “звезду”, или “звезды” в “треугольник”.
d дой”. Задачу определения Rвх можно решить преобразованием “треугольника” в “звезду”, или “звезды” в “треугольник”.
1 способ:
Преобразуем “треугольник” R2, R4, R5 в эквивалентную “звезду” с сопротивлениями Rb, Rc, Rd. После преобразования схема принимает вид (рис. 2.1.6.б).
Сопротивления звезды:
|
Rb |
R2 R4 |
20 30 |
6Ом, |
|||||||||||||
|
R2 R4 R5 |
20 30 50 |
|||||||||||||||
|
d |
||||||||||||||||
|
R2 R5 |
20 |
50 |
||||||||||||||
|
Rd |
10 Ом, |
|||||||||||||||
|
R2 R4 R5 |
20 30 50 |
|||||||||||||||
|
Rc |
R4 R5 |
30 50 |
15 Ом. |
|||||||||||||
|
R2 R4 R5 |
20 30 50 |
|||||||||||||||
|
Входное сопротивление цепи Rвх: |
||||||||||||||||
|
R |
вх Rb |
(R3 Rc)(R1 Rd) |
||||||||||||||
|
R3 Rc R1 Rd |
6 (10 15) (40 10) 22,7 Oм. 10 15 40 10
30
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением Rэкв, и вся схема представляется в виде схемы на рис. 1.3, где R=Rэкв, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа.
Электрическая цепь с последовательным соединением элементов
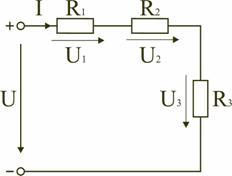 Рис. 1.4
Рис. 1.4
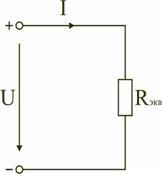 Рис. 1.5
Рис. 1.5
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).
На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:
Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением Rэкв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома
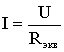 ,
,
и по вышеприведенным формулам рассчитывают падение напряжений U1, U2, U3 на соответствующих участках электрической цепи (рис. 1.4).
Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.
Электрическая цепь с параллельным соединением элементов
Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).
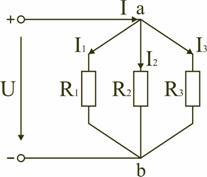
В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа (1.3) можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:
I = I1 + I2 + I3, т.е. 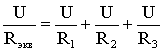 ,
,
откуда следует, что
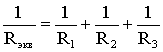 .
.
В том случае, когда параллельно включены два сопротивления R1 и R2, они заменяются одним эквивалентным сопротивлением
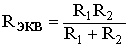 .
.
Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:
По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление Rэкв уменьшается.
Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)
Отсюда следует, что
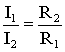 ,
,
т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.
По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.
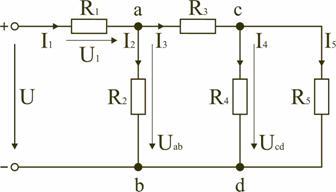
Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R1=R2=R3=R4=R5=R. Сопротивления R4 и R5 включены параллельно, тогда сопротивление участка цепи cd равно:
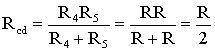 .
.
В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):
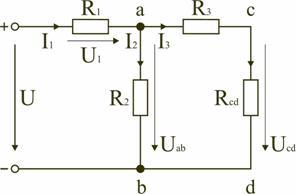
На схеме (рис. 1.8) сопротивление R3 и Rcd соединены последовательно, и тогда сопротивление участка цепи ad равно:
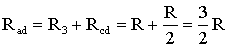 .
.
Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):
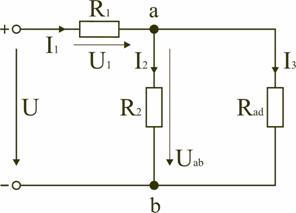
На схеме (рис. 1.9) сопротивление R2 и Rad соединены параллельно, тогда сопротивление участка цепи аb равно
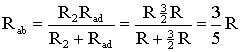 .
.
Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R1 и Rab включены последовательно.
Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:
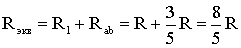 .
.
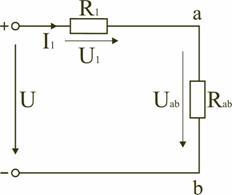 Рис. 1.10
Рис. 1.10
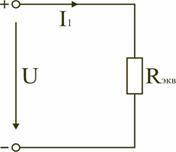 Рис. 1.11
Рис. 1.11
В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением Rэкв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.
Соединение элементов электрической цепи по схемам «звезда» и «треугольник»
В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 1.12). Сопротивления R12, R13, R24, R34 включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.
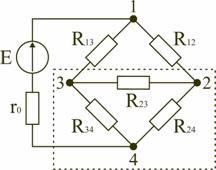 Рис. 1.12
Рис. 1.12
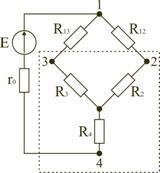 Рис. 1.13
Рис. 1.13
В мостовой схеме сопротивления R13, R12, R23 и R24, R34, R23 соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника R24 R34 R23 звездой R2 R3 R4 (рис. 1.13). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям:
 ;
; 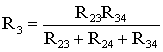 ;
; 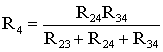 .
.
Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника:
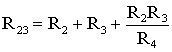 ;
; 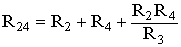 ;
; 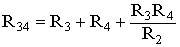 .
.
После проведенных преобразований (рис. 1.13) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 1.12)
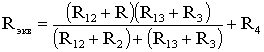 .
.
Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением Rэкв, и вся схема представляется в виде схемы на рис. 1.3, где R=Rэкв, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа.
Электрическая цепь с последовательным соединением элементов
 Рис. 1.4
Рис. 1.4
 Рис. 1.5
Рис. 1.5
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).
На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:
Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением Rэкв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома
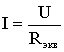 ,
,
и по вышеприведенным формулам рассчитывают падение напряжений U1, U2, U3 на соответствующих участках электрической цепи (рис. 1.4).
Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.
Электрическая цепь с параллельным соединением элементов
Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).

В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа (1.3) можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:
I = I1 + I2 + I3, т.е. 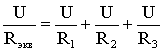 ,
,
откуда следует, что
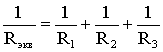 .
.
В том случае, когда параллельно включены два сопротивления R1 и R2, они заменяются одним эквивалентным сопротивлением
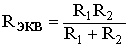 .
.
Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:
По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление Rэкв уменьшается.
Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)
Отсюда следует, что
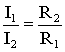 ,
,
т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.
По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.

Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R1=R2=R3=R4=R5=R. Сопротивления R4 и R5 включены параллельно, тогда сопротивление участка цепи cd равно:
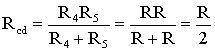 .
.
В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):

На схеме (рис. 1.8) сопротивление R3 и Rcd соединены последовательно, и тогда сопротивление участка цепи ad равно:
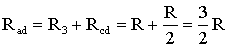 .
.
Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):

На схеме (рис. 1.9) сопротивление R2 и Rad соединены параллельно, тогда сопротивление участка цепи аb равно
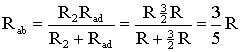 .
.
Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R1 и Rab включены последовательно.
Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:
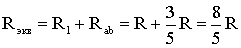 .
.
 Рис. 1.10
Рис. 1.10
 Рис. 1.11
Рис. 1.11
В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением Rэкв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.
Соединение элементов электрической цепи по схемам «звезда» и «треугольник»
В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 1.12). Сопротивления R12, R13, R24, R34 включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.
 Рис. 1.12
Рис. 1.12
 Рис. 1.13
Рис. 1.13
В мостовой схеме сопротивления R13, R12, R23 и R24, R34, R23 соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника R24 R34 R23 звездой R2 R3 R4 (рис. 1.13). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям:
 ;
; 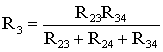 ;
; 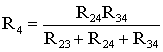 .
.
Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника:
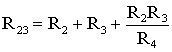 ;
; 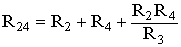 ;
; 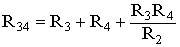 .
.
После проведенных преобразований (рис. 1.13) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 1.12)
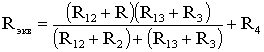 .
.
Расчёт электрических схем, содержащих несколько сопротивлений (резисторов), при нахождении силы тока в цепи, напряжения или мощности, производится с использованием метода свёртывания. Метод заключается в том, чтобы найти эквивалентное сопротивление выделенных участков цепи. Основная задача – замена резисторов, имеющих различное подключение относительно друг друга, на эквивалент (Rэкв.).

Определение эквивалентного сопротивления
При рассмотрении схем любых электрических или электронных устройств можно увидеть, что такие компоненты, как резисторы, имеют разные типы соединений между собой. Чтобы определить эквивалентное соединение, необходимо рассматривать два элемента, включенных в определённом порядке. Несмотря на то, что на чертеже их может быть несколько десятков, и соединены они по-разному, есть только два типа включения их друг с другом: последовательное и параллельное. Остальные конфигурации – это лишь их вариации.
Последовательное соединение элементов
Подобное включение подразумевает комбинацию деталей в прямой последовательности. Выход одного сопротивления подключается к входу другого. При этом отсутствуют какие-либо ответвления на участке. Величина тока, который проходит через все соединённые последовательно компоненты, будет одна и та же.
Внимание! Снижение потенциала на каждом резистивном элементе в сумме даст полное напряжение, приложенное к последовательной цепи.

В случае постоянного тока формула закона Ома для отрезка цепи имеет вид:
Сила тока зависит от приложенного напряжения и оказанного ему сопротивления. Если выразить R, его формула:
Параметры последовательной цепи, включающей n соединённых друг с другом элементов, имеют свои особенности.
Проходящий по цепи ток везде одинаковый:
Прикладываемое напряжение является суммой напряжений на каждом резисторе:
Следовательно, рассчитать можно общее:
Rэкв.= U1/I + U2/I + … +Un/I) = R1 + R2 + … +Rn.
Важно! Последовательная цепь, имеющая в своём составе N резисторов равного номинала, имеет эквивалентное сопротивление Rэкв. = N*R.
Параллельное соединение
Когда условные выходы деталей имеют общий контакт в одной точке (узле) схемы, а условные входы так же объединены во второй, говорят о параллельном соединении. Узел на чертеже обозначается графической точкой. Это место, где происходят разветвления цепей в схемах. Такой вариант подключения резисторов обеспечивает одинаковое падение напряжения U для всех параллельных элементов. Ток в этой позиции будет равен сумме токов, идущих по каждому компоненту.
Когда в параллельное подключение входит n резистивных элементов, то разность потенциалов, ток и общее сопротивление будут иметь следующие выражения:
- общий ток: I = I1 + I2 + … + In;
- общее напряжение: U = U1 = U2 = … = Un;
- Rобщ. = Rэкв. = U/I1 + U/I2 + …+ U/In) = 1/R1 + 1/R2 +…+ 1/Rn.
Величину, обратно пропорциональную сопротивлению 1/R, называют проводимостью.
Если n равных по номиналу сопротивлений включить параллельно, то Rэкв. = (R*R)/n*R = R/n. Формула подходит и для индуктивных сопротивлений проволочных катушек и ёмкостных сопротивлений конденсаторов.

Расчёт при смешанном соединении устройств
Произвести расчет сопротивления цепи, когда она разветвлена и наполнена разными видами резистивных соединений, просто не получится. Затрудняет решение задачи множество участков, где детали подключены друг другу в разных комбинациях. В таких обстоятельствах желательно выполнять ряд преобразований, добиваясь упрощения схемы вводом отдельных эквивалентных элементов. Выявляют при этом подходящие контуры последовательных и параллельных присоединений.
Например, выискав некоторое количество последовательных подключений резисторов, заменяют их на один эквивалентный компонент. Определив элементы, соединённые последовательно, также рисуют вместо него эквивалент. Вновь начинают искать подобные простые соединения.
Метод называют «методом свёртывания». Схему упрощают до тех пор, пока в ней не останется одно Rэкв.

Важно! Метод эквивалентных преобразований применяется тогда, когда питание рассматриваемого участка цепи осуществляется от одного источника электрического тока, а также при определении Rэкв. в замкнутом контуре с одной ЭДС.
Такой относительный способ определения Rэкв используют и для изучения зависимости токов в некоторой цепи от значения R нагрузки. Это метод эквивалентного генератора, при котором сложный двухполюсник, являющийся активным, представляют эквивалентным генератором. При этом считают, что ЭДС его соответствует Uх.х. (холостого хода) на зажимах, R внутреннее соответствует R входному двухполюсника пассивного на тех же зажимах. Для такого определения источники тока разъединяют, а канал ЭДС закорачивают.
Физические формулы и примеры вычислений
Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
- параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
- последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.
У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.
Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:
- R1 = 1 Ом;
- R2 = 2 Ом;
- R3 = 3 Ом;
- R4 = 6 Ом;
- R5 = 9 Ом;
- R6 = 18 Ом;
- R7 = 2Ом;
- R8 = 2Ом;
- R9 = 8 Ом;
- R10 = 4 Ом.
Напряжение, поданное на схему:
Требуется рассчитать токи на всех резистивных элементах.

Для расчётов применяется закон Ома:
I = U/R, подставляя вместо R эквивалентное сопротивление.
Внимание! Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте.
Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком.
На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:
- АВ – участок, имеющий две параллельных ветви;
- ВС – отрезок, вмещающий в себя последовательное сопряжение;
- CD – отрезок схемы с расположением трёх параллельных цепочек.
Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте.

Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов.

Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов. Выполняют это в следующем порядке:
- Rэкв.2,3 = R2+R3=2 + 3 = 5 Ом;
- Rэкв.7,8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ом;
- Rэкв.7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.
Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже.

Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:
- Rэкв.AB = (R1*Rэкв 2,3)/R1 + Rэкв 2,3 = (1*5)/1 + 5 = 0,83 Ом;
- Rэкв.BC = R4 + R5 = 6 + 9 = 15 Ом;
- 1/Rэкв.CD = 1/R6 + 1/Rэкв.7,8,9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0,05 + 0,11 + 0,25 = 0,41 Ом.
В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже.

Теперь можно определить эквивалентное сопротивление всей первоначальной схемы, сложив эквивалентные значения всех трёх участков:
Rэкв. = Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом.
Далее, используя закон Ома, находят ток в последнем последовательном участке:
I = U/ Rэкв. = 24/56,83 = 0,42 А.
Зная силу тока, можно найти, какое падение напряжения на рассмотренных участках AB, BC, CD. Это выполняется следующим образом:
- UAB = I* Rэкв.AB= 0,42*0,83 = 0,35 В;
- UBC = I* Rэкв.BC= 0,42*15 = 6,3В;
- UCD = I* Rэкв.CD = 0,42*0,41 = 0,17 В.
Следующим шагом станет определение токов на параллельных отрезках AB и CD:
- I1 = UAB/R1 = 0,35/1 = 0,35 А;
- I2 = UAB/Rэкв.2,3 = 0,35/5 = 0,07 А;
- I3 = UCD/R6 = 0,17/18 = 0,009 А;
- I6 = UCD/Rэкв.7,8,9= 0,17/9 = 0,02 А;
- I7 = UCD/R10 = 0,17/4 = 0,04 А.
Далее, чтобы найти значения токов, проходящих через R7 и R8, нужно рассчитать напряжение на этих двух резисторах. Предварительно находят падение напряжения на R9.
U9 = R9*I6 = 8*0,02 = 0,16 В.
Теперь напряжение, падающее на Rэкв.7,8, будет разностью между U CD и U9.
U7,8 = UCD – U9= 0,17 – 0,16 = 1 В.
После этого можно уже узнать значение токов, движущихся по резисторам R7 и R8, используя формулы:
- I4 = U7,8/R7 = 1/2 = 0,5 A;
- I5 = U7,8/R8 = 1/2 = 0,5 A.
Стоит заметить! Ток, протекающий через R4 и R5, по своему значению равен току на отрезке, не имеющем разветвления.
Рассчитывая схемы и решая задачи по нахождению значений электрических параметров, необходимо использовать эквивалентные сопротивления. С помощью такой замены сложные построения превращаются в элементарные цепи, которые сводятся к параллельным и последовательным соединениям резистивных элементов.
Видео
Расчет электрической цепи методом эквивалентных преобразований
Содержание:
- Расчет линейных электрических цепей постоянного тока методом эквивалентных преобразований
- Задача с примером решения 1.1.1
- Задача с примером решения 1.1.2
- Задача с примером решения 1.1.3
- Задача с примером решения 1.1.4
- Задача с примером решения 1.1.12
Расчет линейных электрических цепей постоянного тока методом эквивалентных преобразований
Задача с примером решения 1.1.1
Для цепи (рисунок 1), определить эквивалентное сопротивление относительно входных зажимов  , если
, если

известно:

Решение:
Начнем преобразование схемы с ветви наиболее удаленной от источника, т.е. зажимов  :
:

Задача с примером решения 1.1.2
Для цепи (рисунок 2а), определить входное сопротивление если известно: 
 Решение:
Решение:
Исходную схему можно перечертить относительно входных зажимов (рисунок 26), из чего видно, что все сопротивления включены параллельно. Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивления можно воспользоваться формулой:

где  – величина сопротивления, Ом;
– величина сопротивления, Ом;
 – количество параллельно соединенных сопротивлений.
– количество параллельно соединенных сопротивлений.

Задача с примером решения 1.1.3
Найти эквивалентное сопротивление цепи (рисунок За), которая образована делением нихромовой проволоки сопротивлением 0,3 Ом на пять равных частей и припайкой в полученных точках медных перемычек 1-3, 2-4, 4-6. Сопротивлениями перемычек и переходных контактов пренебречь.
 Решение:
Решение:
При сопротивлении проволоки 0,3 Ом и при условии равенства всех пяти частей, сопротивление каждого отдельного участка проволоки равно:

Обозначим каждый участок проволоки и изобразим исходную цепь эквивалентной схемой замещения (рисунок 36).
Возможно вам будут полезны данные страницы:
Из рисунка видно, что схема представляет собой последовательное соединение двух параллельно соединенных групп сопротивлений. Тогда величина эквивалентного сопротивления определится:

Задача с примером решения 1.1.4
Определить эквивалентное сопротивление относительно зажимов  , если
, если  (рисунок 4а).
(рисунок 4а).
Преобразуем соединение «треугольник»  в эквивалентную «звезду», определяем величины преобразованных сопротивлений (рисунок 46):
в эквивалентную «звезду», определяем величины преобразованных сопротивлений (рисунок 46):
 По условию задачи величины всех сопротивлений равны, а значит:
По условию задачи величины всех сопротивлений равны, а значит:

 На преобразованной схеме получили параллельное соединение ветвей между узлами
На преобразованной схеме получили параллельное соединение ветвей между узлами  , тогда эквивалентное сопротивление равно:
, тогда эквивалентное сопротивление равно:
И тогда эквивалентное сопротивление исходной схемы представляет последовательное соединение сопротивлений:
 На примере данной схемы рассмотрим преобразование «звезда»-«треугольник». Соединение «звезда» с сопротивлениями
На примере данной схемы рассмотрим преобразование «звезда»-«треугольник». Соединение «звезда» с сопротивлениями  преобразуем в эквивалентный «треугольник» с сопротивлениями
преобразуем в эквивалентный «треугольник» с сопротивлениями  и
и  (рисунок 5а):
(рисунок 5а):
 Затем преобразуем параллельные соединения ветвей с сопротивлениями
Затем преобразуем параллельные соединения ветвей с сопротивлениями  (рисунок 5б):
(рисунок 5б):
 Величина сопротивления
Величина сопротивления  определяется преобразованием параллельного соединения
определяется преобразованием параллельного соединения  :
:
 Тогда эквивалентное сопротивление представляет собой сумму сопротивлений
Тогда эквивалентное сопротивление представляет собой сумму сопротивлений  :
:

Задача с примером решения 1.1.12
Методом эквивалентных преобразований найти ток  (рисунок 16а), если
(рисунок 16а), если  Ом
Ом
Решение: Для преобразования активной «звезды» введем дополнительные узлы
. Образовавшуюся пассивную «звезду» преобразуем в пассивный «треугольник» (рисунок 166), сопротивления которого равны:

 Перенесем источники ЭДС через дополнительные узлы (рисунок 17а) и определим параметры эквивалентных источников ЭДС.
Перенесем источники ЭДС через дополнительные узлы (рисунок 17а) и определим параметры эквивалентных источников ЭДС.
 Очевидно, что при одинаковых значениях ЭДС и их разнонаправленности, величины эквивалентных источников ЭДС равны нулю. Полученный пассивный «треугольник» преобразуем с «треугольником»
Очевидно, что при одинаковых значениях ЭДС и их разнонаправленности, величины эквивалентных источников ЭДС равны нулю. Полученный пассивный «треугольник» преобразуем с «треугольником»  (рисунок 17б):
(рисунок 17б):

 Заменяем соединение полученных сопротивлений одним эквивалентным:
Заменяем соединение полученных сопротивлений одним эквивалентным:
 Для образовавшегося контура запишем уравнение по второму закону Кирхгофа, из которого выразим ток
Для образовавшегося контура запишем уравнение по второму закону Кирхгофа, из которого выразим ток  :
:

Сопротивления
в электрических цепях могут быть
соединены последовательно, параллельно,
по смешанной схеме и по схемам «звезда»,
«треугольник». Расчет сложной схемы
упрощается, если сопротивления в этой
схеме заменяются одним эквивалентным
сопротивлением Rэкв,
и вся схема представляется в виде схемы
на рис. 1.3, где R=Rэкв,
а расчет токов и напряжений производится
с помощью законов Ома и Кирхгофа.
Электрическая
цепь с последовательным соединением
элементов
|
Рис. |
Рис. |
Последовательным
называют такое соединение элементов
цепи, при котором во всех включенных в
цепь элементах возникает один и тот же
ток I (рис. 1.4).
На
основании второго закона Кирхгофа (1.5)
общее напряжение U всей цепи равно сумме
напряжений на отдельных участках:
U
= U1
+ U2
+ U3 или
IRэкв
= IR1
+ IR2
+ IR3,
откуда
следует
(1.5)
Rэкв
= R1
+ R2
+ R3.
Таким
образом, при последовательном соединении
элементов цепи общее эквивалентное
сопротивление цепи равно арифметической
сумме сопротивлений отдельных участков.
Следовательно, цепь с любым числом
последовательно включенных сопротивлений
можно заменить простой цепью с одним
эквивалентным сопротивлением Rэкв
(рис. 1.5). После этого расчет цепи
сводится к определению тока I всей цепи
по закону Ома
,
и
по вышеприведенным формулам рассчитывают
падение напряжений U1,
U2,
U3
на соответствующих участках электрической
цепи (рис. 1.4).
Недостаток
последовательного включения элементов
заключается в том, что при выходе из
строя хотя бы одного элемента, прекращается
работа всех остальных элементов цепи.
Электрическая
цепь с параллельным соединением элементов
Параллельным
называют такое соединение, при котором
все включенные в цепь потребители
электрической энергии, находятся под
одним и тем же напряжением (рис. 1.6).
Рис.
1.6
В
этом случае они присоединены к двум
узлам цепи а и b, и на основании первого
закона Кирхгофа (1.3) можно записать, что
общий ток I всей цепи равен алгебраической
сумме токов отдельных ветвей:
I
= I1
+ I2
+ I3,
т.е.
,
откуда
следует, что
(1.6)
.
В
том случае, когда параллельно включены
два сопротивления R1
и R
2,
они заменяются одним эквивалентным
сопротивлением
(1.7)
.
Из
соотношения (1.6), следует, что эквивалентная
проводимость цепи равна арифметической
сумме проводимостей отдельных ветвей:
gэкв
= g1
+ g2
+ g3.
По
мере роста числа параллельно включенных
потребителей проводимость цепи gэкв
возрастает, и наоборот, общее сопротивление
Rэкв
уменьшается.
Напряжения
в электрической цепи с параллельно
соединенными сопротивлениями (рис. 1.6)
U
= IRэкв
= I1R1
= I2R2 =
I3R3.
Отсюда
следует, что
,
т.е.
ток в цепи распределяется между
параллельными ветвями обратно
пропорционально их сопротивлениям.
По
параллельно включенной схеме работают
в номинальном режиме потребители любой
мощности, рассчитанные на одно и то же
напряжение. Причем включение или
отключение одного или нескольких
потребителей не отражается на работе
остальных. Поэтому эта схема является
основной схемой подключения потребителей
к источнику электрической энергии.
Электрическая
цепь со смешанным соединением элементов
Смешанным
называется такое соединение, при котором
в цепи имеются группы параллельно и
последовательно включенных сопротивлений.
Рис.
1.7
Для
цепи, представленной на рис. 1.7, расчет
эквивалентного сопротивления начинается
с конца схемы. Для упрощения расчетов
примем, что все сопротивления в этой
схеме являются одинаковыми: R1=R2=R3=R4=R5=R.
Сопротивления R4
и R5
включены параллельно, тогда сопротивление
участка цепи cd равно:
.
В
этом случае исходную схему (рис. 1.7)
можно представить в следующем виде
(рис. 1.8):
Рис.
1.8
На
схеме (рис. 1.8) сопротивление R3
и Rcd
соединены последовательно, и тогда
сопротивление участка цепи ad равно:
.
Тогда
схему (рис. 1.8) можно представить в
сокращенном варианте (рис. 1.9):
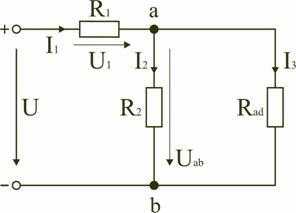
Рис.
1.9
На
схеме (рис. 1.9) сопротивление R2
и Rad
соединены параллельно, тогда сопротивление
участка цепи аb равно
.
Схему
(рис. 1.9) можно представить в упрощенном
варианте (рис. 1.10), где сопротивления
R1
и Rab
включены последовательно.
Тогда
эквивалентное сопротивление исходной
схемы (рис. 1.7) будет равно:
.
|
Рис. |
Рис. |
В
результате преобразований исходная
схема (рис. 1.7) представлена в виде
схемы (рис. 1.11) с одним сопротивлением
Rэкв.
Расчет токов и напряжений для всех
элементов схемы можно произвести по
законам Ома и Кирхгофа.
Соединение
элементов электрической цепи по схемам
«звезда» и «треугольник»
В
электротехнических и электронных
устройствах элементы цепи соединяются
по мостовой схеме (рис. 1.12). Сопротивления
R12,
R13,
R24,
R34
включены в плечи моста, в диагональ 1–4
включен источник питания с ЭДС Е, другая
диагональ 3–4 называется измерительной
диагональю моста.
|
Рис. |
Рис. |
В
мостовой схеме сопротивления R13,
R12,
R23
и R24,
R34,
R23
соединены по схеме «треугольник».
Эквивалентное сопротивление этой схемы
можно определить только после замены
одного из треугольников, например
треугольника R24
R34
R23
звездой R2
R3
R4
(рис. 1.13). Такая замена будет
эквивалентной, если она не вызовет
изменения токов всех остальных элементов
цепи. Для этого величины сопротивлений
звезды должны рассчитываться по следующим
соотношениям:
(1.8)
;
;
.
Для
замены схемы «звезда» эквивалентным
треугольником необходимо рассчитать
сопротивления треугольника:
(1.9)
;
;
.
После
проведенных преобразований (рис. 1.13)
можно определить величину эквивалентного
сопротивления мостовой схемы (рис. 1.12)
.
studfiles.net
Расчет эквивалентного сопротивления электрической цепи — Мегаобучалка
Любое последовательное соединение можно преобразовать к последовательному соединению одного эквивалентного резистора и одного источника ЭДС. Причем, сопротивление эквивалентного резистора равно сумме всех сопротивлений входящих в соединение, а ЭДС эквивалентного источника равна алгебраической сумме ЭДС источников входящих в соединение.
R4=20 Ом, R5=40 Ом, R6=15 Ом (пример)

Путем сворачивания цепи с помощью преобразований последовательно и параллельно соединенных проводников, можно максимально упростить для дальнейшего расчета сколь угодно сложную схему. Исключением служат цепи содержащие сопротивления, соединенные по схеме звезда и треугольник.
9. СОЕДИНЕНИЕ ЗВЕЗДОЙ И ТРЕУГОЛЬНИКОМ
Схему еоедииения трех ветвей, образующих замкнутый контур с тремя узлами называют треугольником.

взаимные замены треугольника и звезды сопротивлений должны быть эквивалентными, т. е. при соответственно равных напряжениях между вершинами А, Б и В треугольника и звезды токи IA, IБ, 1В в подводящих проводах, соединяющих эти вершины с остальной частью цепи, должны остаться без изменений. Равенство токов должно выполняться при любых изменениях и переключениях в остальной части цепи и, в частности, при обрывах некоторых ее ветвей.

Рис 2.8 Соединение резисторов треугольником (а) и звездой (б)
Сопротивления эквивалентной звезды rа, rб, rв находятся в определенных соотношениях с сопротивлениями треугольника r
аб, rбв, rва. Для выяснения этой зависимости допустим сначала, что в вершине А произошел обрыв подводящего провода и, следовательно, ток Iа=0. Сопротивления между двумя оставшимися присоединенными вершинами Б и В для обеих схем должны быть одинаковы, чтобы были соответственно равны токи IБ и Iв в обеих схемах.
Чтобы преобразовать треугольник в звезду при заданных сопротивлениях сторон треугольника rаб,rбв, rва, требуется определить сопротивления лучей эквивалентной звезды rа, rб, rв . Для этого составим полусумму левых и правых частей уравнений (2.15) и (2.16):
и вычтем из полученного выражения уменьшенные вдвое левую и правую части (2.14). В результате получим
(2.17)
Аналогично получим
(2.18)
(2.19)
сли сопротивления треугольника равны друг другу: rаб = rбв=rва=rΔ, то будут равны друг другу и сопротив
ления звезды, т. е. rа = rб=rв=r λ, причем из формул (2.17)—(2.19) получается простое соотношение
(2.20)
При обратном преобразовании звезды в эквивалентный треугольник, т. е. при заданных сопротивленияхrа, rб, rв, надо решить три уравнения (2.17)—(2 19) относительно сопротивлений rаб, rбв:
Таким образом, сопротивление стороны эквивалентного треугольника равно сумме сопротивлений двух лучей звезды, присоединенных к тем же вершинам, что и сторона треугольника, и их произведения, деленного на сопротивление третьего луча звезды.
11. Режимы работы электрической цепи
· Режим короткого замыкания ( КЗ )
В режиме короткого замыкания источник питания замкнут накоротко. Режим является аварийным. Ток короткого замыкания КЗ во много раз превышает значение номинального тока.
Rн = 0 I = max
· Режим холостого хода ( ХХ )
В режиме холостого хода источник питания отсоединен от нагрузки и работает вхолостую. Сопротивление внешнего участка цепи и ток равен 0. Rн = ∞
· Режим согласованной нагрузки
Свойства электрической цепи – наибольшая мощность нагрузки развивается источником, когда сопротивление нагрузки ровно внутреннему сопротивлению источника.
Rн = I0

Из графика видно с ростом сопротивления нагрузки растёт мощность на нагрузке при Rн = I0 мощность нагрузки наибольшая при дальнейшем росте Rн – PRн уменьшается.
Мощность электрического тока
P = UI
megaobuchalka.ru
Физическая формула расчета (определения) эквивалентного сопротивления в цепи
Если электрическая цепь содержит несколько резисторов, то для подсчёта её основных параметров (силы тока, напряжения, мощности) удобно все резистивные устройства заменить на одно эквивалентное сопротивление цепи. Только для него должно выполняться следующее требование: его сопротивление должно быть равным суммарному значению сопротивлений всех элементов, то есть показания амперметра и вольтметра в обычной схеме и в преобразованной не должны измениться. Такой подход к решению задач называется методом свёртывания цепи.
Метод свёртывания цепи
Внимание! Расчёт эквивалентного (общего или суммарного) сопротивления в случае последовательного или параллельного подключения выполняется по разным формулам.
Последовательное соединение элементов
В случае последовательного подключения все приборы соединяются последовательно друг с другом, а собранная цепь не имеет разветвлений.
При таком подключении сила тока, проходящая через каждый резистор, будет одинаковая, а общее падение напряжения складывается из суммарных падений напряжения на каждом из приборов.
Последовательное подключение приборов
Чтобы определить суммарное значение в этом случае, воспользуемся законом Ома, который записывается следующим образом:
I = U/R.
Из вышестоящего выражения получаем значение R:
R = U/I (1).
Поскольку при последовательном соединении:
- I = I1 = I2 =…= IN (2),
- U = U1 + U2 +…+ UN (3),
формула для расчёта эквивалентного сопротивления (Rобщ или Rэкв) из (1) – (3) будет иметь вид:
- Rэкв = (U1 + U2 + …+ UN)/I,
- Rэкв = R1 + R2 + … + RN (4).
Таким образом, если имеется N последовательно соединённых одинаковых элементов, то их можно заменить на одно устройство, у которого:
Rобщ = N·R (5).
Параллельное соединение
При таком подключении входы от всех устройств соединены в одной точке, выходы – в другой точке. Эти точки в физике и электротехнике называются узлами. На электрических схемах узлы представляют собой места разветвления проводников и обозначаются точками.
Параллельное соединение
Расчет эквивалентного сопротивления также выполняем с помощью закона Ома.
В этом случае общее значение силы тока складывается из суммы сил токов, протекающих по каждой ветви, а величина падения напряжения для каждого устройства и общее напряжение одинаковые.
Если имеются N резистивных устройств, подключенных таким образом, то:
I = I1 + I2 + … + IN (6),
U = U1 = U2 = … = UN (7).
Из выражений (1), (6) и (7) имеем:
- Rобщ = U/(I1 + I2 + …+ IN),
- 1/Rэкв = 1/R1 + 1/R2 +…+ 1/RN (8).
Если имеется N одинаковых резисторов, имеющих подключение данного типа, то формула (8) преобразуется следующим образом:
Rобщ = R · R / N·R = R / N (9).
Если соединены несколько катушек индуктивности, то их суммарное индуктивное сопротивление рассчитывается так же, как и для резисторов.
Расчёт при смешанном соединении устройств
В случае смешанного подключения присутствуют участки с последовательным и параллельным подключениями элементов.
При решении задачи используют метод сворачивания цепи (метод эквивалентных преобразований). Его используют для вычисления параметров в том случае, если есть один источник энергии.
Предположим, задана следующая задача. Электрическая схема (см. рис. ниже) состоит из 7 резисторов. Рассчитайте токи на всех резисторах, если имеются следующие исходные данные:
- R1 = 1Ом,
- R2 = 2Ом,
- R3 = 3Ом,
- R4 = 6Ом,
- R5 = 9Ом,
- R6 = 18Ом,
- R7 = 2,8Ом,
- U = 32В.
Электрическая схема
Из закона Ома имеем:
I = U/R,
где R – суммарное сопротивление всех приборов.
Его будем находить, воспользовавшись методом сворачивания цепи.
Элементы R2 и R3 подключены параллельно, поэтому их можно заменить на R2,3, величину которого можно рассчитать по формуле:
R2,3= R2·R3 / (R2+R3).
R4, R5 и R6 также включены параллельно, и их можно заменить на R4,5,6, которое вычисляется следующим образом:
1/R4,5,6 = 1/R4+1/R5+1/R6.
Таким образом, схему, изображённую на картинке выше, можно заменить на эквивалентную, в которой вместо резисторов R2, R3 и R4, R5, R6 используются R2,3 и R4,5,6.
Эквивалентная схема
Согласно картинке выше, в результате преобразований получаем последовательное соединение резисторов R1, R2,3, R4,5,6 и R7.
Rобщ может быть найдено по формуле:
Rобщ = R1 + R2,3 + R4,5,6 + R7.
Подставляем числовые значения и рассчитываем R для определённых участков:
- R2.3 = 2Ом·3Ом / (2Ом + 3Ом) = 1,2Ом,
- 1/R4,5,6 = 1/6Ом + 1/9Ом + 1/18Ом = 1/3Ом,
- R4,5,6 = 3Ом,
- Rэкв = 1Ом + 1,2Ом + 3Ом + 2,8Ом= 8Ом.
Теперь, после того, как нашли Rэкв, можно вычислять значение I:
I = 32В / 8Ом = 4А.
После того, как мы получили величину общего тока, можно вычислить силу тока, протекающую на каждом участке.
Поскольку R1, R2,3, R4,5,6 и R7 соединены последовательно, то:
I1 = I2,3 = I4,5,6 = I7 = I = 4А.
На участке R2,3 напряжение находим по формуле:
- U2,3 = I2,3·R2,3,
- U2,3 = 4А·1,2Ом = 4,8В.
Поскольку R2 и R3 подключены параллельно, то U2,3 = U2 = U3, следовательно:
- I2 = U2 / R2,
- I2 = 4,8В / 2Ом = 2,4А,
- I3 = U3 / R3,
- I3 = 4,8В / 3Ом = 1,6А.
Проверяем правильность решения:
- I2,3 = I2 + I3,
- I2,3 = 2,4А + 1,6А = 4А.
На участке R4,5,б напряжение также находим, исходя из закона Ома:
- U4,5,6 = I4,5,6·R4,5,6,
- U4,5,6 = 4А·3Ом = 12В.
Так как R4, R5, Rб подключены параллельно друг к другу, то:
U4,5,6 = U4 = U5 = U6 = 12В.
Вычисляем I4, I5, I6:
- I4 = U4 / R4,
- I4 = 12В / 6Ом = 2А,
- I5 = U5 / R5,
- I5 = 12В / 9Ом » 1,3А,
- I6 = U6 / R6,
- I5 = 12В / 18Ом » 0,7А.
Проверяем правильность решения:
I4,5,6 = 2А + 1,3А + 0,7А = 4А.
Чтобы автоматизировать выполнение расчётов эквивалентных значений для различных участков цепи, можно воспользоваться сервисами сети Интернет, которые предлагают на их сайтах выполнить онлайн вычисления нужных электрических характеристик. Сервис обычно имеет встроенную специальную программу – калькулятор, которая помогает быстро выполнить расчет сопротивления цепи любой сложности.
Таким образом, использование метода эквивалентных преобразований при расчёте смешанных соединений различных устройств позволяет упростить и ускорить выполнение вычислений основных электрических параметров.
Видео
Оцените статью:
elquanta.ru
Расчет сопротивления цепи
Расчет сопротивления цепи необходим при решении различных задач по электротехнике. Суть заключается в приведении сложной разветвленной электрической цепи к цепи с единственным эквивалентным сопротивлением, которую называют простой электрической цепью.
Пример 1
Цепь в данном примере состоит из двух последовательно соединенных сопротивлений, следовательно, их общее сопротивление будет равно сумме их сопротивлений. Подробнее о видах соединений тут.
Допустим, что R1=10 Ом R2=20 Ом, тогда
Пример 2

Два сопротивления соединены параллельно, значит при сворачивании схемы, общее сопротивление будет равно (значения R1,R2 такие же как и в примере 1)
Можно заметить, что при параллельном соединении общее сопротивление меньше, чем при последовательном в несколько раз.
Пример 3

В данном примере ситуация аналогична примеру 2, за тем лишь исключением, что сопротивлений три. Тогда общее сопротивление будет равно (R1,R2 прежние, R3=105 Ом)
Пример 4

Чтобы рассчитать общее сопротивление смешанного соединения проводников, необходимо для начала найти общее сопротивление резисторов R1 и R2 соединенных параллельно, а затем общее сопротивление, как сумму R12 и R3 соединенных последовательно.
Пример 5

Данная электрическая цепь сложнее, чем предыдущие, но как можно увидеть, она также состоит из последовательно или параллельно соединенных сопротивлений, которые можно постепенно сворачивать, приводя цепь к единственному эквивалентному сопротивлению R.
R4=20 Ом, R5=40 Ом, R6=15 Ом

Путем сворачивания цепи с помощью преобразований последовательно и параллельно соединенных проводников, можно максимально упростить для дальнейшего расчета сколь угодно сложную схему. Исключением служат цепи содержащие сопротивления, соединенные по схеме звезда и треугольник.
electroandi.ru
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Главная
→
Примеры решения задач ТОЭ
→
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Основными законами, определяющими расчет электрической цепи, являются законы Кирхгофа.
На основе законов Кирхгофа разработан ряд практических методов расчета электрических цепей постоянного тока, позволяющих сократить вычисления при расчете сложных схем.
Существенно упростить вычисления, а в некоторых случаях и снизить трудоемкость расчета, возможно с помощью эквивалентных преобразований схемы.
Преобразуют параллельные и последовательные соединения элементов, соединение «звезда» в эквивалентный «треугольник» и наоборот. Осуществляют замену источника тока эквивалентным источником ЭДС. Методом эквивалентных преобразований теоретически можно рассчитать любую цепь, и при этом использовать простые вычислительные средства. Или же определить ток в какой-либо одной ветви, без расчета токов других участков цепи.
В данной статье по теоретическим основам электротехники рассмотрены примеры расчета линейных электрических цепей постоянного тока с использованием метода эквивалентных преобразований типовых схем соединения источников и потребителей энергии, приведены расчетные формулы.
Решение задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Задача 1. Для цепи (рис. 1), определить эквивалентное сопротивление относительно входных зажимов a−g, если известно: R1 = R2 = 0,5 Ом, R3 = 8 Ом, R4 = R5 = 1 Ом, R6 = 12 Ом, R7 = 15 Ом, R8 = 2 Ом, R9 = 10 Ом, R10= 20 Ом.

Рис. 1
Решение
Начнем эквивалентные преобразования схемы с ветви наиболее удаленной от источника, т.е. от зажимов a−g:

Задача 2. Для цепи (рис. 2, а), определить входное сопротивление если известно: R1 = R2 = R3 = R4= 40 Ом.
 Рис. 2
Рис. 2
Решение
Исходную схему можно перечертить относительно входных зажимов (рис. 2, б), из чего видно, что все сопротивления включены параллельно. Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивленияможно воспользоваться формулой:
где R – величина сопротивления, Ом;
n – количество параллельно соединенных сопротивлений.
Задача 3. Определить эквивалентное сопротивление относительно зажимов a–b, если R1 = R2 = R3 = R4 = R5 = R6 = 10 Ом (рис. 3, а).

Рис. 3
Решение
Преобразуем соединение «треугольник» f−d−c в эквивалентную «звезду». Определяем величины преобразованных сопротивлений (рис. 3, б):
По условию задачи величины всех сопротивлений равны, а значит:
На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно:
И тогда эквивалентное сопротивление исходной схемы представляет последовательное соединение сопротивлений:
Задача 4. В заданной цепи (рис. 4, а) определить методом эквивалентных преобразований входные сопротивления ветвей a−b, c–d и f−b, если известно, что: R1 = 4 Ом, R2 = 8 Ом, R3 =4 Ом, R4 = 8 Ом, R5 = 2 Ом, R6 = 8 Ом, R7 = 6 Ом, R8 =8 Ом.
Решение
Для определения входного сопротивления ветвей исключают из схемы все источники ЭДС. При этом точки c и d, а также b и f соединяются накоротко, т.к. внутренние сопротивления идеальных источников напряжения равны нулю.

Рис. 4
Ветвь a−b разрывают, и т.к. сопротивление Ra–b = 0, то входное сопротивление ветви равно эквивалентному сопротивлению схемы относительно точек a и b (рис. 4, б):

Аналогично методом эквивалентных преобразований определяются входные сопротивления ветвей Rcd и Rbf. Причем, при вычислении сопротивлений учтено, что соединение накоротко точек a и b исключает ( «закорачивает») из схемы сопротивления R1, R2, R3, R4 в первом случае, и R5, R6, R7, R8 во втором случае.

Задача 5. В цепи (рис. 5) определить методом эквивалентных преобразований токи I1, I2, I3 и составить баланс мощностей, если известно: R1 = 12 Ом, R2 = 20 Ом, R3 = 30 Ом, U = 120 В.

Рис. 5
Решение
Эквивалентное сопротивлениедля параллельно включенных сопротивлений:
Эквивалентное сопротивление всей цепи:
Ток в неразветвленной части схемы:
Напряжение на параллельных сопротивлениях:
Токи в параллельных ветвях:
Баланс мощностей:
Задача 6. В цепи (рис. 6, а), определить методом эквивалентных преобразований показания амперметра, если известно: R1 = 2 Ом, R2 = 20 Ом, R3 = 30 Ом, R4 = 40 Ом, R5 = 10 Ом, R6 = 20 Ом, E = 48 В. Сопротивление амперметра можно считать равным нулю.
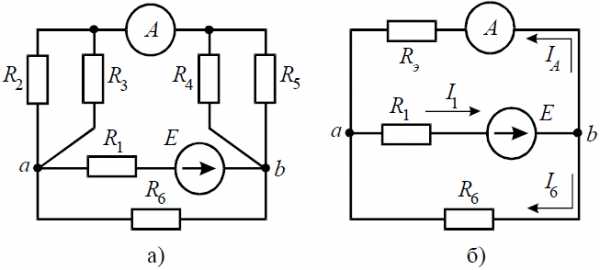
Рис. 6
Решение
Если сопротивления R2, R3, R4, R5 заменить одним эквивалентным сопротивлением RЭ, то исходную схему можно представить в упрощенном виде (рис. 6, б).
Величина эквивалентного сопротивления:
Преобразовав параллельное соединение сопротивлений RЭ и R6 схемы (рис. 6, б), получим замкнутый контур, для которого по второму закону Кирхгофа можно записать уравнение:
откуда ток I1:
Напряжение на зажимах параллельных ветвей Uab выразим из уравнения по закону Ома для пассивной ветви, полученной преобразованием RЭ и R6:
Тогда амперметр покажет ток:
Задача 7. Определить токи ветвей схемы методом эквивалентных преобразований (рис. 7, а), если R1 = R2 = R3 = R4 = 3 Ом, J = 5 А, R5 = 5 Ом.

Рис. 7
Решение
Преобразуем «треугольник» сопротивлений R1, R2, R3 в эквивалентную «звезду» R6, R7, R8 (рис. 7, б) и определим величины полученных сопротивлений:
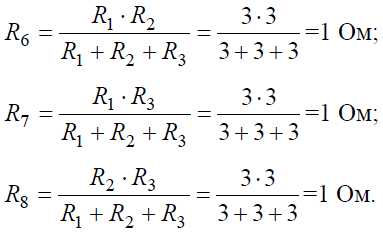
Преобразуем параллельное соединение ветвей между узлами 4 и 5
Ток в контуре, полученном в результате преобразований, считаем равным току источника тока J, и тогда напряжение:
И теперь можно определить токи I4 и I5:
Возвращаясь к исходной схеме, определим напряжение U32 из уравнения по второму закону Кирхгофа:
Тогда ток в ветви с сопротивлением R3 определится:
Величины оставшихся неизвестными токов можно определить из уравнений по первому закону Кирхгофа для узлов 3 и 1:
Электронная версия статьи Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Примеры решения задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Метод эквивалентных преобразований
02.09.2011, 237358 просмотров.
rgr-toe.ru
1. Законы электрических цепей постоянного тока
1.1 Определения.
Законы
электрических цепей постоянного тока
подробно изучаются в школьном и вузовском
курсах физики, поэтому в данном учебном
пособии излагаются кратко. Приведем
лишь некоторые определения и формулировки
основных законов.
Узлом
электрической
цепи называется
точка, в
которой соединяется не менее трех
проводников. Однородный участок
цепи – это
такой участок, на котором не действуют
сторонние силы.
Эквивалентным
сопротивлением
участка цепи называется сопротивление,
которым можно заменить все сопротивления
рассматриваемого участка, при этом
параметры других участков цепи не
изменятся.
1.2 Основные законы.
Закон Ома
для участка цепи:
Сила тока на
участке цепи прямо пропорциональна
напряжению на этом участке и обратно
пропорциональна его эквивалентному
сопротивлению.
 (1.1)
(1.1)
Закон Ома
для полной цепи:
Сила тока прямо
пропорциональна электродвижущей силе
(э.д.с.) источника тока и обратно
пропорциональна полному сопротивлению
этой цепи :

 .
.
(1.2)
Здесь r
– внутреннее сопротивление источника
тока.
Рассчитать
электрическую цепь – значит определить
токи и падения напряжения на всех ее
участках. Часто при расчете электрических
цепей применяют законы Кирхгофа.
1-й закон
Кирхгофа: Алгебраическая
сумма токов, сходящихся в узле электрической
цепи, равна нулю:
ΣIk
= 0 (1.3)
При этом токи,
входящие в узел, и выходящие из него,
берутся с разными знаками.
Другая формулировка
этого закона: Сумма
входящих в узел токов равна сумме токов,
выходящих из него.
2-й закон
Кирхгофа: Алгебраическая
сумма э.д.с., входящих в замкнутый контур,
равна сумме падений напряжений на
элементах этого контура:
ΣЕk
= ΣUk
(1.4)
При этом э.д.с.,
совпадающие по направлению с обходом
контура, берутся со знаком «+», а
противоположного направления – со
знаком «-».
Закон баланса
мощности электрической
цепи: Алгебраическая сумма мощностей,
генерируемых источниками напряжения,
равна сумме мощностей, потребляемых
приемниками электрической энергии:
ΣРист=
ΣРпр
(1.5)
Закон баланса
мощности являются универсальным
инструментом, с помощью которого можно
проверить правильность расчета
электрической цепи.
1.3 Правила расчета эквивалентных сопротивлений.
Рассмотрим различные
схемы соединения электрических элементов.
-
Последовательное
соединение элементов.
Последовательное
соединение элементов изображено на
рис.1.1.
Цепь, через все
элементы которой протекают один и тот
же ток, называется неразветвленной.
Эквивалентное
сопротивление последовательно соединенных
элементов равно сумме сопротивлений
этих элементов:
Rэкв=
ΣRk
,
(1.6)
или :
Rэкв=R1
+ R2
+…+ Rk
(1.7)
Падение
напряжения на любом из k
элементов может быть найдено по формуле:
Uk=I·
Rk
(1.8)
а)
б)
Рис.1.1
Схема последовательного соединения
(а)
и
ее эквивалентная схема (б)
Применив 2-й
закон Кирхгофа и закон баланса мощности,
можно проверить правильность
расчета электрической цепи с
последовательным
соединением элементов. Должны выполняться
соотношения (1.4) и (1.5) в следующем виде
:
Uист
= ΣUк
=U1
+ U2
+…+Uk
(1.9)
и
Рист
=I·Uист=
ΣРпр к
=
Р1+Р2+…+Рk
(1.10)
здесь
Рпр
к= Ik2·Rk
— мощность,
потребляемая k-тым
приемником;
Рист
– мощность
источника тока.
studfiles.net
Способы соединения сопротивлений и расчет эквивалентного сопротивления электрической цепи
Поиск Лекций
Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник».
Электрическая цепь с последовательным соединением элементов
Рис. 2.1
Рис. 2.2
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 2.1).
На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:
или ,
откуда следует
(1.6).
Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением (рис. 2.2). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома , и по вышеприведенным формулам рассчитывают падение напряжений , , на соответствующих участках электрической цепи (рис. 2.1).
Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.
Электрическая цепь с параллельным соединением элементов
Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 2.3).
Рис. 2.3
В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа (1.3) можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:
, т.е. ,
откуда следует, что
(1.7).
В том случае, когда параллельно включены два сопротивления и , они заменяются одним эквивалентным сопротивлением
(1.8).
Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:
.
По мере роста числа параллельно включенных потребителей проводимость цепи возрастает, и наоборот, общее сопротивление уменьшается.
Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 2.3)
.
Отсюда следует, что
,т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.
По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.
Рис. 2.4
Для цепи, представленной на рис. 2.4, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: . Сопротивления и , R5 включены параллельно, тогда сопротивление участка цепи равно:
.
В этом случае исходную схему (рис. 2.4) можно представить в следующем виде (рис. 2.5):
Рис. 2.5
На схеме (рис. 2.5) сопротивление и соединены последовательно, и тогда сопротивление участка цепи равно:
.
Тогда схему (рис. 2.5) можно представить в сокращенном варианте (рис. 2.6):
Рис. 2.6
На схеме (рис. 2.6) сопротивление и соединены параллельно, тогда сопротивление участка цепи равно:
.
Схему (рис. 2.6) можно представить в упрощенном варианте (рис. 2.7), где сопротивления и включены последовательно.
Тогда эквивалентное сопротивление исходной схемы (рис. 2.4) будет равно:
Рис. 2.7
Рис. 2.8
В результате преобразований исходная схема (рис. 2.4) представлена в виде схемы (рис. 2.8) с одним сопротивлением . Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.
Соединение элементов электрической цепи по схемам «звезда» и «треугольник»
В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 2.9). Сопротивления , , , включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.
Рис. 2.9
Рис. 2.10
В мостовой схеме сопротивления , , и , , соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника звездой (рис. 2.10). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям:
, , (1.9)
Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника:
, , (1.10)
После проведенных преобразований (рис. 2.10) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 2.9)
.
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
