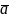Как найти эквивалентность формула

Эквивалент – это реальная или условная
частица, которая в кислотно-основных реакциях присоединяет
(или отдает) один ион Н⁺ или ОН^–, в
окислительно-восстановительных реакциях принимает (или отдает) один
электрон, реагирует с одним атомом водорода или с одним эквивалентом
другого вещества. Например, рассмотрим следующую
реакцию: 

H₃PO₄ + 2KOH
®
K₂HPO₄ + 2H₂O. 

В
ходе этой реакции только два атома водорода замещаются на атомы
калия, иначе, в реакцию вступают два иона Н⁺ (кислота
проявляет основность 2). Тогда по определению эквивалентом
H₃PO₄
будет являться условная частица 1/2H₃PO₄,
т.к. если одна молекула H₃PO₄
предоставляет два иона Н⁺, то один ион Н⁺ дает
половина молекулы H₃PO₄.

С
другой стороны, на реакцию с одной молекулой ортофосфорной кислотой
щелочь отдает два иона ОН^–, следовательно, один ион ОН^–
потребуется на взаимодействие с 1/2 молекулы кислоты. Эквивалентом
кислоты является условная частица 1/2Н₃РО₄, а
эквивалентом щелочи частица КОН.

Число, показывающее, какая часть молекулы
или другой частицы вещества соответствует эквиваленту, называется
фактором эквивалентности (f_Э).
Фактор эквивалентности – это безразмерная величина, которая меньше,
либо равна 1. Формулы расчета фактора эквивалентности приведены в
таблице 1.1.

Таким образом, сочетая фактор эквивалентности и формульную единицу
вещества, можно составить формулу эквивалента какой-либо частицы,
где фактор эквивалентности записывается как химический коэффициент
перед формулой частицы:

В примере, рассмотренном выше, фактор эквивалентности для кислоты,
соответственно, равен 1/2, а для щелочи КОН равен 1.

Между H₃PO₄
и КОН также могут происходить и другие реакции. При этом кислота
будет иметь разные значения фактора эквивалентности:

H₃PO₄ + 3KOH
®
K₃PO₄ + 3H₂O        
f_Э(H₃PO₄)
= 1/3

 H₃PO₄ + KOH
®
KН₂PO₄
+ H₂O        f_Э(H₃PO₄)
= 1.

Следует учитывать, что эквивалент одного
и того же вещества может меняться в зависимости от того, в какую
реакцию оно вступает. Эквивалент элемента также может быть
различным в зависимости от вида соединения, в состав которого он
входит. Эквивалентом может являться как сама молекула или
какая-либо другая формульная единица вещества, так и ее часть.

Таблица 1.1 –
Расчет фактора эквивалентности 

Пример.
Определите фактор эквивалентности и эквивалент у солей: а)
ZnCl₂, б) КНСО₃, в)
(MgOH)₂SO₄.

Решение: Для расчетов воспользуемся формулами, приведенными в
таблице 1.1.

а)
ZnCl₂ (средняя соль):

. 

f_Э(ZnCl₂)
= 1/2, поэтому эквивалентом ZnCl₂
является частица 1/2ZnCl₂.

б) КНСО₃
(кислая соль): 

. 

f_Э(КНСО₃) = 1,
поэтому эквивалентом КНСО₃ является частица КНСО₃.

в) (MgOH)₂SO₄
(основная соль): 

. 

f_Э(
(MgOH)₂SO₄
) = 1/2, поэтому эквивалентом
(MgOH)₂SO₄
является частица 1/2(MgOH)₂SO₄.

Эквивалент, как частица, может быть охарактеризован молярной массой
(молярным объемом) и определенным
количеством вещества
n_э.
Молярная масса эквивалента (М_Э)
– это масса одного моль эквивалента. Она равна
произведению молярной массы вещества на фактор эквивалентности:

Молярная масса
эквивалента имеет размерность «г/моль».

Молярная масса эквивалента сложного
вещества равна сумме молярных масс эквивалентов образующих его
составных частей, например:

Газообразные вещества помимо молярной массы эквивалента имеют
молярный объем эквивалента (
или V_Э)
– объем, занимаемый молярной массой эквивалента или объем одного
моль эквивалента. Размерность «л/моль».
При н.у. получаем:

 Закон
эквивалентов был открыт в 1792 г. И. Рихтером.
Современная формулировка закона:
вещества реагируют и образуются согласно их эквивалентам.
Все вещества в уравнении реакции связаны законом эквивалентов,
поэтому:

Из закона эквивалентов следует, что массы (или объемы)
реагирующих и образующихся веществ пропорциональны молярным массам
(молярным объемам) их эквивалентов. Для любых двух веществ,
связанных законом эквивалентов, можно записать:

  
      
где m₁ и
m₂ – массы реагентов и
(или) продуктов реакции, г;

,  –
молярные массы эквивалентов реагентов и (или) продуктов реакции,
г/моль;

V₁, V₂
– объемы реагентов и (или) продуктов реакции, л;

,–
молярные объемы эквивалентов реагентов и (или) продуктов реакции,
л/моль.

Л.А. Яковишин

МАТЕМАТИЧЕСКАЯ ЛОГИКА

Высказывание
– всякое связное, осмысленное
повествовательное предложение, о котором
вполне определенно можно сказать,
истинно оно или ложно; ни одно высказывание
не может быть одновременно истинным и
ложным. Высказывания обозначаются
большими и малыми буквами латинского
алфавита.

Логические
операции над высказываниями:

1)


– “не a”, отрицание

a
1	0
0	1

2) a
ʌ b – “a и
b”, конъюнкция

a	b	a ʌ b
1	1	1
1	0	0
0	1	0
0	0	0

3) a
v b – “a или b”, дизъюнкция

a	b	a v b
1	1	1
1	0	1
0	1	1
0	0	0

4) a
→ b – “из a
следует b”, импликация;
a – условие, посылка; b
– следствие, заключение;

a	b	a → b
1	1	1
1	0	0
0	1	1
0	0	1

5) a
↔ b – “а эквивалентно
b”, эквиваленция

a	b	a ↔ b
1	1	1
1	0	0
0	1	0
0	0	1

Высказывание,
представляющее собой одно утверждение,
называется простым (элементарным,
пропозициональным).

Формулы
алгебры высказываний – выражения,
полученные из символов высказывательных
переменных, знаком пяти операций (˥, ʌ,
v, →,↔) и скобок, определяющих
порядок действий.

1)
пропозициональные переменные –
формулы;

2)
если x и y –
формулы, то ¬x, x
v y, x
ʌ y, x → y,
x ↔ y тоже
формулы;

3)
других высказываний нет.

Если
формула для любых значений высказывательных
переменных принимает значение истина,
то она называется тождественно
истинной. ТИ формула – тавтология.

Если
формула для любых значений высказывательных
переменных принимает значение ложь, то
она называется тождественно ложной.
ТЛ формула – противоречие.

Формулы,
принимающие значение истина хотя бы
для одного набора переменных называются
выполнимыми.

A
и B равносильны,
если для любого x₁,
x₂, … , x_n,
где это совокупность всех переменных,
входящих в A и B,
эти формулы принимают одинаковые
значения.

Свойства
равносильности: 1) рефлексивность A
~ A; 2) симметричность A
~ B <-> B ~
A; 3) транзитивность A
~ B ʌ B ~ C
-> A ~ C.

Основные формулы эквивалентности:

1)
¬(¬X) = Y

2) X
ʌ Y = Y ʌ X
– коммутативность

3) X
v Y = Y
v X –
коммутативность

4) X
ʌ (Y ʌ Z) = (X
ʌ Y) ʌ Z –
ассоциативность

5) X
v (Y v
Z) = (X v
Y) v Z
– ассоциативность

6) X
ʌ (Y v Z)
= (X ʌ Y) v
(X ʌ Z) –
дистрибутивность

7) X
v (Y ʌ Z)
= (X v Y)
ʌ (X v Z)
– дистрибутивность

8)
¬(X ʌ Y) = ¬X
v ¬Y –
Де-Моргана

9)
¬(X v Y)
= ¬X ʌ ¬Y –
Де-Моргана

10)
X v ¬X
= 1

11)
X ʌ ¬X = 0

12)
X ʌ 1 = X

13)
X v 1 = 1

14)
X ʌ 0 = 0

15)
X v 0 = X

16)
X ʌ X = X
– идемпотентность

17)
X v X
= X – идемпотентность

18)
X ʌ (X v
Y) = X – закон
поглощения

19)
X v (X
ʌ Y) = X –
закон поглощения

20)
X -> Y = ¬X v Y

21)
X -> Y = ¬Y -> ¬X

22)
X <-> Y = (X -> Y) ʌ (Y -> X)

23)
X <-> Y =
(¬X v Y)
ʌ (X v ¬Y)

Рассмотрим
множество элементов любой природы M,
в котором определены операции “+”, “×”,
“˥”, “=” подчиняются следующим аксиомам:

1) x + y = y + x	1) xy = yx
2) x + (y + z) = (x + y) + z	2) (xy)z = x(yz)
3)	3)
4) x + yz = (x + y)(x + z)	4) x(y + z) = xy + xz
5) ¬(¬x)
6) ¬(x + y) = ¬x¬y	6) ¬(xy)
7) x + xy = x	7) x(x + y) = x

Такое
множество называется булевой алгеброй.

В
тех случаях, когда для некоторой системы
аксиом удается подобрать конкретные
объекты и конкретные соотношения между
ними так, что все конкретные аксиомы
выполняются, то говорят, что найдена
модель данной системы аксиом.

Формулы,
в которые входят операции ʌ, v,
˥, причем ˥ относится лишь к высказывательным
переменным, называются приведенными.

Назовем
систему логических операций ∑ полной,
если всякая формула эквивалентна
некоторой формуле, в которую входят
только операции из системы ∑.

Введем
новые операции:

1)
Стрелка Пирса A↓B

A	B	A↓B
1	1	0
1	0	0
0	1	0
0	0	1

2)
Штрих Шеффера A|B

A	B	A|B
1	1	0
1	0	1
0	1	1
0	0	1

Закон двойственности

Эквивалентности
2 и 3, 4 и 5, 6 и 7, 8 и 9 таковы, что могут быть
получены друг из друга заменой ʌ на v
и наоборот. При этом справедлив общим
закон двойственности, позволяющий с
помощь описанного выше преобразования
из любых 2-х эквивалентных формул,
состоящих из высказывательных переменных,
с помощью ʌ, v, ¬ получить
формулы тоже эквивалентные.

Формула
А* называется двойственной формуле
А, если она получается из А заменой ʌ на
v и v на ʌ.

Если
формула A – тавтология,
то A* – противоречие.

Функцией
алгебры логики или функцией Буля
f(x₁,
x₂, … , x_n)
называется функция, принимающая значения
1 и 0, аргументы которых принимают значения
1 и 0.

Такая
функция имеет тип {0; 1}ⁿ
-> {0; 1}.

ТИ
И ТЛ функции АЛ – постоянные функции,
а 2 равносильные функции – одна и та же
функция.

f(x₁,
… , x_i-1,
x_i,
x_i+1,
… , x_n)
существенно зависит от x_i,
если существует такой набор a₁,
… , a_{i
– 1}, a_i,
a<sub>i
+ 1</sub>, … , a_n
из 0 и 1 таких, что f(a₁,
…, a_i-1,
a, a_i+1,
…, a_n)
!= f(a₁,
…, a_i-1,
1, a_i+1,
…, a_n).

Переменные,
от которых функция f
существенно зависит, называются
существенными, а остальные –
фиктивными.

Пусть
f и g –
функции. f и g
равны (f = g),
если для любых значений аргументов
функции f и g
совпадают.

Каждой
формуле A в алгебре
высказываний можно сопоставить функцию
фи(A) такую, что фи(А) =
фи(B).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Таблица эквивалентности пределов

Для раскрытия неопределенностей ноль делить на ноль $[frac{0}{0}]$ очень удобно использовать таблицу эквивалентности пределов. Важно, чтобы аргумент функции стремился к нулю. Только в этом случае возможно делать замену.

Формулы эквивалентности пределов
$ sin x sim x $	$ e^x – 1 sim x $
$ tg ;x sim x $	$ a^x – 1 sim xln a $
$ arcsin x sim x $	$ ln (1+x) sim x $
$ arctg ; x sim x $	$log_a (1+x) sim frac{x}{ln a}$
$ 1- cos x sim frac{x^2}{2} $	$(1+x)^a – 1 sim ax $

Пример 1

Найти пределы используя эквивалентные бесконечно малые функции $limlimits_{xto 0} frac{x sin x^2}{arcsin x} $

Решение

Подставляем точку $x=0$ в предел и получаем неопределенность. $$limlimits_{xto 0} frac{x sin x^2}{arcsin x} = bigg [frac{0}{0} bigg ] $$ Замечаем под пределом две функции, для которых можно использовать формулы эквивалентных бесконечно малых функций. Но перед этим проверим, что аргументы их стремятся к нулю. $$ sin 0^2 = sin 0 = 0 $$ $$ arcsin 0 = 0 $$ Значит для нашей задачи получаем следующие замены. $$ sin x^2 sim x^2 $$ $$ arcsin x sim x $$ Подставим эквивалентности в предел, чтобы вычислить ответ. $$limlimits_{xto 0} frac{x sin x^2}{arcsin x} = lim limits_{x to 0} frac{x cdot x^2}{x} = $$ Сокращаем знаменатель и подставляем в оставшееся выражение под числителем $x=0$. $$ = limlimits_{xto 0} x^2 = 0^2 = 0 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ limlimits_{xto 0} frac{x sin x^2}{arcsin x} = 0 $$

Пример 2

Заменяя эквивалентными бесконечно малыми найдите предел $ limlimits_{xto 0} frac{1-cos 4x}{x} $

Решение

В пределе получаем неопределенность ноль делить на ноль $[frac{0}{0}]$. Замечаем, что числитель похож на формулу из таблицы эквивалентности пределов. Подставим в него точку $x=0$. $$ 1- cos (4 cdot 0) = 1-cos 0 = 1 – 1 = 0 $$ Получили, что числитель равен нулю при $x=0$, а это значит допустима замена на бесконечно малую функцию. $$ 1-cos 4x = frac{(4x)^2}{2} = frac{16x^2}{2} = 8x^2 $$ Возвращаемся к пределу, подставляя в него полученное выражение для числителя. $$limlimits_{xto 0} frac{1-cos 4x}{x} = limlimits_{xto 0} frac{8x^2}{x} = limlimits_{xto 0} 8x = 0 $$

Ответ

$$ limlimits_{xto 0} frac{1-cos 4x}{x} = 0 $$

Пример 3

Вычислить предел функции используя эквивалентно малые величины $limlimits_{xto 1} frac{sin (x-1)}{x^2-1} $

Решение

Подставив $x=1$ получаем неопределенность $[ frac{0}{0} ] $. Замечаем, что в числителе присутствует синус, который есть в таблице эквивалентностей. По необходимому условию аргумент синуса должен стремиться к нулю, чтобы применить формулу эквивалентности. Проверим это подставив $x=1$ в него. $$ sin (1-1) = sin 0 = 0 $$ Проверка показала, что формулу можно применить, так как аргумент равен нулю. $$ sin (x-1) sim x-1 $$ $$limlimits_{xto 1} frac{sin (x-1)}{x^2} = limlimits_{xto 1} frac{x-1}{x^2-1} = $$ Применяя формулу разности квадратов $a^2-b^2 = (a-b)(a+b)$ для знаменателя упрощаем его. $$ = limlimits_{xto 1} frac{x-1}{(x-1)(x+1)} = limlimits_{xto 1} frac{1}{x+1} = frac{1}{2} $$

Ответ

$$ limlimits_{xto 1} frac{sin (x-1)}{x^2-1} = frac{1}{2} $$

Формулы. Равенство функций и эквивалентность формул. Основные эквивалентности

Формулы. Как и в анализе, исходя из элементарных функций, можно строить формулы.

Определение. Пусть $F$ — некоторое { не обязательно конечное } подмножество функций из $P_2$

а) Базис индукции. Каждая функция $f(x_1, x_2,…, x_n)$ из $F$ называется формулой над $F$.

б) Индуктивный переход. Пусть $f_0(x_1, …, x_n)$ — функция из $F$ и $A1,…, An$ — выражения, являющиеся либо формулами над $F$, либо символами переменных из алфавита $U$. Тогда выражение $f_0(A_1, …, A_n)$ называется формулой над $F$.

Замечание. В дальнейшем будем обозначать формулы заглавными готическими буквами (mathfrak { M } , mathfrak { N } ), а системы функций — заглавными каллиграфическими буквами $(A, B, F)$.

Пример 1.1. Пусть $F$ — множество элементарных функций. Следующие выражения являются формулами над $F$:

1) $((x_1x_2) + x_1) rightarrow x_2$;

2) $ bar { x_1 } (x_2 vee x_3)$;

3) $overline { x_1 vee ((x_2 wedge x_3)(x_3 wedge x_2)) } $.

Сопоставим теперь каждой формуле $mathfrak { M } $ над $F$ функцию из $P_2$, опираясь на индуктивное определение формул.

а) Базис индукции. Если $mathfrak { M } = f(x_1 ,…, x_n)$, где $f in F$, то формуле $mathfrak { M } $ сопоставим функцию $f(x_1 ,…, x_n)$.

б) Индуктивный переход. Пусть $mathfrak { M } = f_0(A_1 ,…, A_n)$, гдe $A_1 ,…, A_n$ — выражения, являющиеся либо формулами над $F$, либо символами переменных из алфавита $U$. Тогда по предположению индукции каждому $A_i$ сопоставлена либо функция $f_i$ из $P_2$, либо тождественная функция $f_i = x_s$. Сопоставим формуле $mathfrak { M } $ функцию $f(x_1 ,…, x_n) = f_0(f_1 ,…, f_n)$.

Пример 1.2. Формула $((x_1x_2) + x_1)rightarrow x_2$, строится за три шага. Мы имеем следующие подформулы:

$((x_1x_2) + x_1, ((x_1x_2) + x_1)rightarrow x_2$

$x_1$	$x_2$	$x_1x_2$	$(x_1x_2)+x_1$	$((x_1x_2)+x_1)rightarrow x_2$
0	0	0	0	1
0	1	0	0	1
1	0	0	1	0
1	1	1	0	1

Таблица 4. Построение таблицы функции, заданной формулой $((x_1x_2) + x_1)rightarrow x_2$

Равенство функций и эквивалентность формул

Введенное понятие функции не позволяет рассматривать функции от меньшего числа аргументов как функции от большего числа аргументов.

Определение. Функция $f(x_1,…,x_ { i—1 } ,x_i,x_ { i+1 } ,… ,x_n)$ из $P_2$ существенно зависит от переменной $x_i$, если существуют такие значения $alpha ,1,…, alpha_ { i—1 } , alpha_ { i+1 } ,…, alpha_n$ переменных $x_1,…,x_ { i—1 } , x_ { i+1 } ,…,x_n$, что

$f(alpha_1,…,alpha_ { i-1 } ,0,alpha_ { i+1 } ,…,alpha_n) neq f(alpha_1,…,alpha_ { i-1 } ,1,alpha_ { i+1 } ,…,alpha_n)$.

В этом случае переменная $x_i$ называется существенной. Если $x_i$ не является существенной переменной, то она называется фиктивной.

Пусть для функции $f(x_1,…, x_n)$ перемениая $x_i$ является фиктивной. По таблице функции $f(x_1,… ,x_n)$ построим новую таблицу, вычеркивая все строки вида $(alpha_1,…,alpha_ { i-1 } ,1,alpha_ { i+1 } ,…,alpha_n)$ и вычеркивая столбец переменной $x_i$. Полученная таблица определяет некоторую функцию $g(x_1,…, x_ { i—1 } ,x_ { i+1 } ,…, x_n)$. Будем говорить, что функция $g$ получена из $f$ путем удаления фиктивной переменной $x_i$ а также, что функция $f$ получается из $g$ путем введения фиктивной переменной $x_i$.

Определение. Функции $f_1$ и $f_2$ называются равными, если функцию $f_2$ можно получить из $f_1$ путем введения и удаления фиктивных переменных.

Напомним, что каждой формуле над $F$ соответствует функция алгебры логики, причем различным формулам могут соответствовать равные функции.

Определение. Формулы $mathfrak { M } $ и $mathfrak { N } $ над $F$ называются эквивалентными, если соответствующие им функции равны. Записи $mathfrak { M } $ = $mathfrak { N } $ будет означатв, что формулы $mathfrak { M } $ и $mathfrak { N } $ эквивалентны.

Пример 1.3. $xbar { x } = 0$

Приведем список основных эквивалентностей, характеризующих некоторые свойства элементарных функций. Обозначим через $x_icirc x_2$ любую из функций $x_1wedge x_2$, $x_1vee x_2$, $x_1 + x_2$.

1. Ассоциативность. $(x_1circ x_2)circ x_3 = x_1circ (x_2circ x_3)$.
2. Коммутативность. $x_1circ x_2 = x_2circ x_1$.
3. Дистрибутивность. $x_1wedge(x_2vee x_3) = (x_1wedge x_2) vee (x_1wedge x_3)$, $x_1vee (x_2 wedge x_3) = (x_1 vee x_2) wedge (x_1 vee x_3)$, $x_1 wedge (x_2 + x_3) = (x_1 wedge x_2) + (x_1 wedge x_3)$.
4. Правила де Моргана. $overline { x_1 wedge x_2 } = bar { x_1 } vee bar { x_2 } $, $overline { x_1 vee x_2 } = bar { x_1 } wedge bar { x_2 } $.
5. $0 = x wedge bar { x } = x wedge 0 = x + x$, $1 = x vee bar { x } = x vee 1 = x sim x$, $x = bar { bar { x } } = x wedge x = x vee x = x wedge 1 = x vee 0$, $bar { x } = x + 1, x_1 sim x_2 = overline { x_1 + x_2 } $, $x_1 rightarrow x_2 = bar { x_1 } vee x_2$.

Замечание. С целью упрощения записи формул мы условимся, что конъюнкция сильнее других элементарных функций. Более того, знак конъюнкции можно не писать. Например, записи $x_1x_2 vee x_3$ означает $(x_1 wedge x_2) vee x_3$.

Замечание. Очевидно, что если $mathfrak { M } $ — подформула формулы $mathfrak { M } $ и если заменитв любое из ее вхождений на эквивалентную формулу $mathfrak { N } $, то формула $mathfrak { M } $ перейдет в формулу $mathfrak { N } $, которая будет эквивалентна $mathfrak { M } $.

Пример 1.4. $x_1 vee x_1 x_2 = x_1 wedge 1 vee x_1x_2 = x_1(1 vee x_2) = x_1 wedge 1 = x_1$.

Как найти эквивалент

Эквивалентом называется частица, которая химически равноценна (эквивалентна) в кислотно-основных реакциях одному иону водорода, а в реакциях окислительно-восстановительного типа – одному электрону. Эквивалент выражается числом без размерности, тогда как эквивалентная масса измеряется в г/моль.

Вам понадобится

• – калькулятор;
• – периодическая таблица

Инструкция

Чтобы можно было найти эквивалент того или иного вещества, вы должны использовать формулу: 1/z (какое-то вещество),где 1/z – фактор эквивалентности (fэ), то есть число, которое показывает, какая доля частицы вещества равноценна эквиваленту. Эта величина всегда меньше или равна единице. Проще говоря, фактор эквивалентности – это некий коэффициент, который записывается непосредственно перед формулой вещества при нахождении эквивалента. Например, вам надо найти эквивалент фосфорной кислоты при ее взаимодействии с гидроксидом натрия. Запишите уравнение реакции:2NaOH + H3PO4 = Na2HPO4 + 2H2OОтсюда видно, что на атомы натрия замещаются только два атома водорода, то есть кислота является двуосновной (в реакции участвуют 2 иона Н+). Таким образом, согласно определению, эквивалентом фосфорной кислоты будет условная частица ½ H3PO4.

Учтите, что эквивалент одного и того же вещества изменяется в зависимости типа реакции, в которую это вещество вступает. Кроме того, эквивалент элемента находится в зависимости от вида соединения, в состав которого входит. Возьмите те же вещества, что и в предыдущем случае, но реакция пусть пойдет по-другому:3NaOH + H3PO4 = Na 3PO4 + 3H2O.Здесь fэ(H3PO4) = 1/3, fэ(NaOH) =1. Следовательно, эквивалент фосфорной кислоты – частица 1/3 H3PO4, а эквивалент щелочи равен единице.

Для успешного нахождения эквивалентов различных веществ вам необходимо запомнить формулы для нахождения fэ в зависимости от типа химического соединения. Так для простых элементов fэ = 1/ валентность элемента. Пример: fэ ( H2SO4) = 1/6, а эквивалент серы в H2SO4 равен 6.Для солей – fэ = 1/n (мет.) – B(мет.) = 1/ n (к.о.) – B(к.о.), гдеn (мет.) – количество атомов металла,B(мет.) – валентность металла,n (к.о.) – количество кислотных остатков,B(к.о.) – валентность кислотного остатка и т.д.

Сложнее находить эквивалент вещества в реакциях окислительно-восстановительного типа, так как расчет вы будете вести по числу электронов, которые принимают участие в процессе восстановления или окисления. Дано задание найти эквивалент гидроксида марганца в реакции: 2Mn(OH)2 + 12NaOH + 5Cl2 = 2NaMnO4 + 10NaCl + 8H2OИз уравнения видно, что марганец отдает 5 электронов и переходит из Mn +2 в Mn +7. Значит, фактор эквивалентности Mn(OH)2 – 1/5, а эквивалент гидроксида равен 5.

Полезный совет

При расчете не забывайте о том, что эквивалентом может быть сама молекула или же какая-нибудь другая единица вещества.

Источники:

• эквивалент кислоты

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?