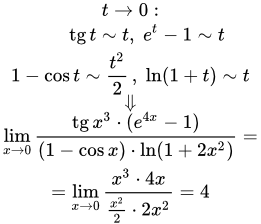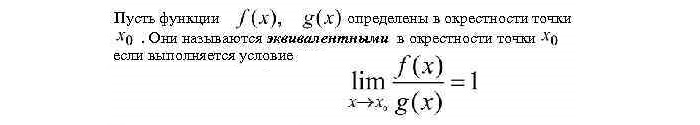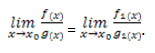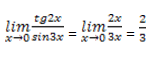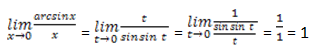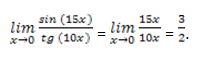Как найти эквивалентную функцию онлайн - Сайт, где вы сможете решить свои вопросы

Содержание:

Таблица эквивалентных б.м. функций
Предельные равенства для эквивалентных б.м. функций

Определение

Б.м. функции $alpha(x)$ и $beta(x)$ называются эквивалентными или равносильными б.м.
одного порядка при $x rightarrow a$, если $lim _{x rightarrow a} frac{alpha(x)}{beta(x)}=1$

Обозначают: $alpha(x) sim beta(x)$ при
$x rightarrow a$.

Пример

Задание. Проверить, являются ли функции $alpha(x) = 5(x^2-5x+6)$ и
$beta(x) = x^2-x-6$ эквивалентными бесконечно малыми при
$x rightarrow 3$.

Решение. Проверим вначале, что данные функции являются
бесконечно малыми функциями в точке
$x=3$:

$$begin{aligned} lim _{x rightarrow 3} alpha(x) &=lim _{x rightarrow 3} 5left(x^{2}-5 x+6right)=0 \ lim _{x rightarrow 3} beta(x) &=lim _{x rightarrow 3}left(x^{2}-x-6right)=0 end{aligned}$$

Найдем предел отношения этих функций:

$$begin{aligned}
lim _{x rightarrow 3} frac{alpha(x)}{beta(x)}=lim _{x rightarrow 3} frac{5left(x^{2}-5 x+6right)}{x^{2}-x-6} &=lim _{x rightarrow 3} frac{5(x-3)(x-2)}{(x-3)(x+2)}=\
&=lim _{x rightarrow 3} frac{5(x-2)}{x+2}=frac{5}{5}=1
end{aligned}$$

Ответ. Заданные функции $alpha(x) = 5(x^2-5x+6)$ и
$beta(x) = x^2-x-6$ являются эквивалентными бесконечно малыми.

Таблица эквивалентных б.м. функций

Таблица эквивалентных б.м. функций при $x rightarrow 0$

$$begin{array}{|l|c|c|c|}
hline 1 . & sin x sim x & 6 . & ln (1+x) sim x \
hline 2 . & arcsin x sim x & 7 . & log _{a} x sim frac{x}{ln a} \
hline 3 . & operatorname{tg} x sim x & 8 . & a^{x}-1 sim x ln a \
hline 4 . & operatorname{arctg} x sim x & 9 . & e^{x}-1 sim x \
hline 5 . & 1-cos x sim frac{x^{2}}{2} & 10 . & (1+x)^{m}-1 sim m x \
hline
end{array}$$

Предельные равенства для эквивалентных б.м. функций

Теорема

Предел отношения двух б.м. функций $alpha(x)$ и
$beta(x)$ при
$x rightarrow a$ равен пределу отношения эквивалентных им б.м.
функций $alpha^{*}(x)$ и $beta^{*}(x)$ при
$x rightarrow a$, то есть верны предельные равенства:

$$lim _{x rightarrow a} frac{alpha(x)}{beta(x)}=lim _{x rightarrow a} frac{alpha^{*}(x)}{beta(x)}=lim _{x rightarrow a} frac{alpha(x)}{beta^{*}(x)}=lim _{x rightarrow a} frac{alpha^{*}(x)}{beta^{*}(x)}$$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти предел $lim _{x rightarrow 0} frac{3 x+7 x^{2}}{sin 2 x}$

Решение. При $x rightarrow 0$:
$sin 2 x sim 2 x$

$$lim _{x rightarrow 0} frac{3 x+7 x^{2}}{sin 2 x}=lim _{x rightarrow 0} frac{x(3+7 x)}{2 x}=lim _{x rightarrow 0} frac{3+7 x}{2}=frac{3}{2}$$

Ответ. $lim _{x rightarrow 0} frac{3 x+7 x^{2}}{sin 2 x}=frac{3}{2}$

Теорема

Разность двух эквивалентных б.м. функций есть б.м. функция более высокого порядка, чем каждая из них.

Верно и обратное утверждение.

Теорема

Сумма конечного числа б.м. функций разных порядков эквивалентна слагаемому низшего порядка.

Слагаемое, которое эквивалентно сумме б.м. функций, называется главной частью указанной суммы.

Замена суммы б.м. функций ее главной частью называется отбрасыванием б.м. высшего порядка.

Пример

Задание. Найти предел $lim _{x rightarrow 0} frac{5 x-6 x^{3}}{operatorname{tg} 3 x}$

Решение. При $x rightarrow 0$:
$5 x-6 x^{3} sim 5 x,$ tg $3 x sim 3 x$

$lim _{x rightarrow 0} frac{5 x-6 x^{3}}{operatorname{tg} 3 x}left[frac{0}{0}right]=lim _{x rightarrow 0} frac{5 x}{3 x}=lim _{x rightarrow 0} frac{5}{3}=frac{5}{3}$

Ответ. $lim _{x rightarrow 0} frac{5 x-6 x^{3}}{operatorname{tg} 3 x}=frac{5}{3}$

Читать дальше: признаки существования пределов.

Источник

09.5. Эквивалентные функции

В тех случаях, когда функциональная зависимость имеет довольно сложный вид, возникают большие трудности при изучении ее свойств. Простой просчет значений функции на ЭВМ порой может оказаться неосуществимым, так как даже современные ЭВМ допускают значительные погрешности в расчетах с очень большими или же малыми числами. Мы рассмотрим весьма интересный подход к изучению функциональных зависимостей, основанный на их замене более простыми функциями в окрестности некоторых предельных точек.

Будем говорить, что функции и ЭКВИВАЛЕНТНЫ в окрестности предельной точки (конечной или бесконечной), если найдется такая функция в окрестности этой предельной точки, что

Очевидно, новое определение обобщает данное ранее для бесконечно малых функций.

Данное условие не является необходимым. Проиллюстрируйте это примером.

Докажите эту теорему.

Теорема. Для эквивалентности функций и при достаточно, чтобы предел их отношения при был равен единице:

Рассмотрим пример. Пусть

То в качестве функции, эквивалентной данной при , может быть взята

Действительно .

Найдем, для каких x эквивалентная функция будет отличаться от данной менее чем на :

(9. 35)

Можно провести вычислительный эксперимент и достаточно точно определить, с каких x более сложную функцию

Допустимо заменить более простой

Сделаем приближенную оценку этих значений x, усиливая рассматриваемое неравенство (9.35):

Значения x, соответствующие неравенству

Тем более будет удовлетворять неравенству (9.35).

Поэтому искомые значения х определяются неравенством:

Положим, к примеру, что . Тогда

Это означает, что для x > 2,43 и x < –2,43 данная функция будет отличаться по абсолютной величине от функции менее чем на 0,002.

Может показаться, что в качестве функции, эквивалентной данной, для достаточно больших по модулю x можно взять функцию

Она действительно проще, чем . Однако при той же абсолютной погрешности E, заменив более сложную функцию на такую простую функцию как , мы получим, что неравенство

Путем аналогичных рассуждений

Дает допустимый диапазон значений x:

Если принять то же значение , то для и значения данной функции можно полагать равными нулю. Как видим, при заданной абсолютной погрешности диапазон допустимых значений меняется. Выигрывая в простоте эквивалентной функции, мы, вместе с тем, теряем часть промежутка, на котором осуществляется упрощение.

Найдем функцию, эквивалентную данной, в окрестности предельной точки . Для этого представим иначе данную функцию:

То эквивалентная функция в окрестности нуля будет иметь вид:

Определим, при каких x, близких к нулю, функция отличается от данной по абсолютной величине менее, чем на E :

Найдем искомые значения x с некоторым “запасом”:

Будет ли лучше для отыскания необходимых значений х другая оценка

При той же погрешности вычислений получим

Рис. 9.22. Функция и ей эквивалентные.

На рис. 9.22 изображены данная функция и эквивалентные ей. Мы видим, что на весьма значительной части области определения функции при абсолютной погрешности расчета можно использовать на практике более простые функциональные зависимости.

Рассмотрим другой пример. Функция

Как несложно установить, при имеет эквивалентную:

Значения x, допускающие такую замену при абсолютной погрешности E, определяются следующим образом:

Находим с некоторым запасом требуемые значения x:

При получаем , то есть или .

Если же данную функцию непосредственно табулировать с использованием вычислительных средств, то переполнение порядка на ЭВМ для практически неизбежно, однако эта функция ведет себя, как эквивалентная ей . Отметим также, что отыскание путем вычислительного эксперимента допустимых x, упрощающих при заданной абсолютной погрешности вычисления, едва ли осуществимо в полной мере, так как этому могут воспрепятствовать вычислительные возможности ЭВМ. Следовательно, полученная аналитически оценка более значима.

Применение эквивалентных функций при решении пределов

Применение эквивалентных функций позволяет упростить вычисление пределов. Если нам нужно вычислить предел дроби, то мы можем заменить множители в числителе и знаменателе эквивалентными функциями и вычислять предел от более простого выражения. Подчеркнем, что речь идет именно о множителях в дробях и произведениях. Замена эквивалентными функциями в других выражениях, например в суммах, может привести к неправильному результату. Однако, ошибки не будет, если выразить любую функцию в виде суммы эквивалентной ей функции и о малого (см. пример ⇓).

Все связанные с этим определения и теоремы приводятся на странице «О большое и о малое. Сравнение функций». Напомним некоторые из них.

Применяемые определения и теоремы

Определение эквивалентных функций
Функции f и g называются эквивалентными (асимптотически равными) при :
при ,
если на некоторой проколотой окрестности точки ,
при , причем
.

Если при , то ;
если , то .
При этом функцию называют главной частью при . См. теорему о связи эквивалентных функций с о малым

Теорема о замене функций эквивалентными в пределе частного
Если, при , и и существует предел
, то существует и предел
.
Доказательство

Отметим часто применяемое следствие этой теоремы. Пусть мы имеем частное, составленное из конечного произведения функций: . Тогда, при вычислении предела, эти функции можно заменить на эквивалентные:
,
где . Знак равенства означает, что если существует один из этих пределов, то существует и равный ему второй. Если не существует один из пределов, то не существует и второй.

Таблица эквивалентных функций

Далее приводится таблица функций, эквивалентных при . Здесь t может быть как переменной, так и бесконечно малой функцией при : ; .

Эквивалентность при

Равенство при

Предостережение

Как указывалось в самом начале, производить замену функций эквивалентными можно только в множителях дробей и произведений, предел которых мы хотим найти. В других выражениях, например в суммах, делать такую замену нельзя.

В качестве примера рассмотрим следующий предел:
.
При . Но если заменить в числителе на x , то получим ошибку:
.
Ошибки не будет, если выразить синус через эквивалентную функцию и о малое, :
.
Поскольку и , то мы снова получили неопределенность 0/0 . Это указывает на то, что для вычисления этого предела применение эквивалентной функции не достаточно. Нужно применить другой метод.

Примеры

Все примеры Далее мы приводим подробные решения следующих пределов, упрощая вычисления с помощью эквивалентных функций.
⇓, ⇓, ⇓, ⇓.

Пример 1

Из таблицы эквивалентных функций ⇑ имеем:
. Поскольку исходная функция является дробью и каждая из этих функций входит в нее в виде множителя в числителе или знаменателе, то заменим их на эквивалентные.
.

Пример 2

Из таблицы эквивалентных функций ⇑ находим:
.
Преобразуем квадрат логарифма:
.
Поскольку исходная функция является дробью и каждая из этих функций входит в нее в виде множителя в числителе или знаменателе, то заменим их на эквивалентные.
.

Пример 3

Здесь мы имеем неопределенность вида один в степени бесконечность. Приводим ее к неопределенности вида 0/0 . Для этого воспользуемся тем, что экспонента и натуральный логарифм являются взаимно обратными функциями.
.
Теперь в показателе экспоненты у нас неопределенность вида 0/0 .

Вычисляем предел:
.
Поскольку у нас дробь, то заменим некоторые множители в числителе и знаменателе эквивалентными функциями, пользуясь приведенной выше таблицей ⇑.
;
;

Поскольку экспонента непрерывна для всех значений аргумента, то по теореме о пределе непрерывной функции от функции имеем:
.

Пример 4

При . Выясним, к чему стремится . Поскольку здесь дробь, то заменим логарифм эквивалентной функцией: . Тогда
. Таким образом, мы имеем неопределенность вида ∞–∞ .

Преобразуем ее к неопределенности вида 0/0 . Для этого приводим дроби к общему знаменателю.
.
Здесь мы также воспользовались формулой . После преобразований, наш предел принимает следующий вид:
.

В знаменателе мы сразу можем заменить натуральный логарифм эквивалентной функцией, как это сделали выше:
.

В числителе имеется произведение двух множителей, каждый из которых тоже можно заменить эквивалентной функцией и, таким образом, упростить вычисления. В качестве эквивалентных, попробуем найти степенные функции:
.
Тогда . Считаем, что . Раскрываем неопределенность по правилу Лопиталя.
.
Если положить , то . Тогда
.
Тот же результат можно получить, применяя разложение в ряд Тейлора при :
.
Отсюда .

Найдем эквивалентную функцию для второго множителя, используя разложение в ряд Тейлора при :
.
Отсюда .

Теперь заменим множители эквивалентными функциями:
.

Примечание. Заметим, что делать замену функций на эквивалентные можно, только если функция, от которой ищется предел, является дробью или произведением. Тогда часть множителей в числителе или знаменателе можно заменить эквивалентными функциями. Так, если бы мы с самого начала заменили ln (1+x) на x, то получили бы ошибку.

Использованная литература:
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, 2003.

Эквивалентные бесконечно малые функции. Таблица эквивалентных б.м. функций

Обозначают: $alpha(x) sim beta(x)$ при $x rightarrow a$.

Задание. Проверить, являются ли функции $alpha(x) = 5(x^2-5x+6)$ и $beta(x) = x^2-x-6$ эквивалентными бесконечно малыми при $x rightarrow 3$.

Решение. Проверим вначале, что данные функции являются бесконечно малыми функциями в точке $x=3$:

Найдем предел отношения этих функций:

Ответ. Заданные функции $alpha(x) = 5(x^2-5x+6)$ и $beta(x) = x^2-x-6$ являются эквивалентными бесконечно малыми.

Таблица эквивалентных б.м. функций

Таблица эквивалентных б.м. функций при $x rightarrow 0$

Предельные равенства для эквивалентных б.м. функций

Предел отношения двух б.м. функций $alpha(x)$ и $beta(x)$ при $x rightarrow a$ равен пределу отношения эквивалентных им б.м. функций $alpha^(x)$ и $beta^(x)$ при $x rightarrow a$, то есть верны предельные равенства:

Задание. Найти предел $lim _ frac>$

Решение. При $x rightarrow 0$: $sin 2 x sim 2 x$

Разность двух эквивалентных б.м. функций есть б.м. функция более высокого порядка, чем каждая из них.

Верно и обратное утверждение.

Сумма конечного числа б.м. функций разных порядков эквивалентна слагаемому низшего порядка.

Слагаемое, которое эквивалентно сумме б.м. функций, называется главной частью указанной суммы.

Замена суммы б.м. функций ее главной частью называется отбрасыванием б.м. высшего порядка.

Решение. При $x rightarrow 0$: $5 x-6 x^ sim 5 x,$ tg $3 x sim 3 x$

Источник

Эквивалентные функции

Говорят, что функции ff и gg, определенные в некоторой проколотой окрестности точки x0x_0 (возможно, x0=±∞x_0=pminfty) эквивалентны, если

lim⁡x→x0f(x)g(x)=1.
limlimits_{xto x_0}frac{f(x)}{g(x)}=1.

Если функции эквивалентны, то мы пишем

f(x)∼g(x)при x→x0.f(x)sim g(x)quadtext{при },, xto x_0.

Если существует конечный предел lim⁡x→x0f(x)=A≠0limlimits_{xto x_0 }f(x)=Ane 0, то, очевидно,

f(x)∼A при x→x0.f(x)sim A,,text{при},,xto x_0.

Если lim⁡x→x0f(x)=0limlimits_{xto x_0 }f(x)= 0, то говорят, что величина f(x)f(x) бесконечно малая при x→x0xto x_0.

Пример 1

Как следует из статьи замечательные пределы, имеют место следующие эквивалентности

sin⁡x∼tg⁡x∼arcsin⁡x∼arctg⁡x∼x, 1−cos⁡x∼x22sin xsimoperatorname{tg} xsimoperatorname{arcsin} xsimoperatorname{arctg} x sim x,,, 1-cos xsimfrac{x^2}{2}

ln⁡(1+x)∼x, (1+x)a∼1ax, ex∼1+xпри x→0.
ln(1+x)sim x,,,(1+x)^asim 1 ax,,,e^xsim 1+xquadtext{при },, xto 0.

При вычислении пределов функции можно заменять на эквивалентные.

Пример 2

Вычислить предел

lim⁡x→01+sin⁡x−1arcsin⁡x.
limlimits_{xto 0}frac{sqrt{1+sin x}-1}{arcsin{x}}.

Заменяем функции на эквивалентные:

1+sin⁡x−1arcsin⁡x∼1+x−1x∼1+12x−1x=12
frac{sqrt{1+sin x}-1}{arcsin{x}}simfrac{sqrt{1+ x}-1}{{x}}simfrac{1+frac{1}{2}x-1}{x}=frac{1}{2}

Таким образом,

lim⁡x→01+sin⁡x−1arcsin⁡x=12.
limlimits_{xto 0}frac{sqrt{1+sin x}-1}{arcsin{x}}=frac{1}{2}.

Однако, как показывает следующий предел, замена выражений на эквивалентные при вычислении пределов может привести к неопределенности:

lim⁡x→0x−sin⁡xarcsin⁡x−x=lim⁡x→0x−xx−x=00.
limlimits_{xto 0}frac{x-sin x}{arcsin x-x}=limlimits_{xto 0}frac{x- x}{ x-x}=frac{0}{0}.

O-большое

Пусть функции f(x)f(x) и g(x)g(x) определены в некоторой проколотой окрестности точки x0x_0 (или определены для достаточно больших значений ∣x∣|x|, если x0=±∞x_0=pminfty), причем функция g(x)g(x) строго положительна.

Говорят, что f(x)=O(g(x))f(x)=O(g(x)) при x→x0xto x_0, если существует постоянная C>0C>0 для которой

∣f(x)∣<Cg(x).
|f(x)|<Cg(x).

Заметим, что запись f(x)=O(1)f(x)=O(1), x→x0xto x_0 означает, что f(x)f(x) ограничена в некоторой проколотой окрестности точки x0x_0.

Пример 3

x=O(ex)x=O(e^x) при x→+∞xto+infty, так как x<exx<e^x для всех x>0x>0;
ex=O(∣x∣)e^x=O(|x|) при x→−∞xto -infty, так как ex<∣x∣e^x<|x| для всех x<−1x<-1;
1x=O(1×2)frac{1}{x}=Oleft(frac{1}{x^2}right) при x→0xto 0, так как 1∣x∣<1x2frac{1}{|x|} < frac{1}{x^2} для всех x∈(−1;0)∪(0;1)xin (-1;0)cup(0;1);
1×2=O(1∣x∣)frac{1}{x^2}=Oleft(frac{1}{|x|}right) при x→±∞xto pminfty, так как 1×2<1∣x∣frac{1}{x^2}<frac{1}{|x|} для всех ∣x∣>1|x|>1.

Из определения следует, что условие f(x)=O(g(x))f(x)=O(g(x)) при x→x0xto x_0 равносильно тому, что

∣f(x)g(x)∣<Cleft|frac{f(x)}{g(x)}right|<C

в некоторой проколотой окрестности точки x0x_0.

Если f(x)=O(g(x))f(x)=O(g(x)) и g(x)=O(f(x))g(x)=O(f(x)) при x→x0xto x_0, то пишут

f(x)≍g(x),x→x0.f(x)asymp g(x),quad xto x_0.

Данное отношение равносильно существованию положительных констант c,C>0c,C>0, для которых в некоторой проколотой окрестности точки x0x_0 выполнено

c<f(x)g(x)<C.
c<frac{f(x)}{g(x)}<C.

Например, x≍3×2−1,x→+∞xasymp sqrt{3x^2-1},quad xto +infty.

Свойства O-большого

f1(x)=O(g1(x))f_1(x)=O(g_1(x)), f2(x)=O(g2(x))f_2(x)=O(g_2(x)) ⇒Rightarrow f1(x)f2(x)=O(g1(x)g2(x))f_1(x)f_2(x)=O(g_1(x)g_2(x)),

в частности если функция h(x)h(x) положительна, то h(x)O(g(x))=O(h(x)g(x))h(x)O(g(x))=O(h(x)g(x));

f1(x)=O(g1(x))f_1(x)=O(g_1(x)), f2(x)=O(g2(x))f_2(x)=O(g_2(x)) ⇒Rightarrow f1(x)+f2(x)=O(g1(x)+g2(x))f_1(x)+f_2(x)=O(g_1(x)+g_2(x)),

в частности f1(x),f2(x)=O(g(x))f_1(x), f_2(x)=O(g(x)) ⇒Rightarrow f1(x)+f2(x)=O(g(x))f_1(x)+f_2(x)=O(g(x));

Говорят, что f(x)=o(g(x))f(x)=o(g(x)) при x→x0xto x_0 (f(x)f(x) является бесконечно малой от g(x)g(x)), если

lim⁡x→x0f(x)g(x)=0.
limlimits_{xto x_0}frac{f(x)}{g(x)}=0.

Заметим, что запись f(x)=o(1)f(x)=o(1), x→x0xto x_0 означает, что lim⁡x→x0f(x)=0limlimits_{xto x_0}f(x)=0.

Пример 4

xa=o(ex)x^a=o(e^x) при x→+∞xto+infty для любого a∈Rainmathbb{R};
ex−1=o(1)e^x-1=o(1) при x→0xto 0;
sin⁡x−x=o(x)sin x-x=o(x) при x→0xto 0;
1−cos⁡x=o(x)1-cos x=o(x) при x→0xto 0.

Свойства o-малого

Свойства o-малого аналогичны свойствам O-большого. Кроме того

o(O(g(x)))=O(o(g(x)))=o(g(x)).
oleft(O(g(x))right)=Oleft(o(g(x))right)=o(g(x)).

Пример 5

Покажем, что

sin⁡x−x=o(x2).sin x-x=oleft(x^2right).

Действительно, используя неравенство xcos⁡x<sin⁡x<xxcos x<sin x<x, (см. Пример 2 статьи Предел функции в точке), имеем

0<x−sin⁡x<x(1−cos⁡x)=xo(x)=o(x2).0<x-sin x<x(1-cos x)=xo(x)=oleft(x^2right).

Откуда следует sin⁡x−x=o(x2)sin x-x=oleft(x^2right).

На самом деле имеет место более сильное равенство

x−sin⁡x=O(x3).x-sin x=Oleft(x^3right).

Следствия формулы Маклорена

Используя ряд Маклорена для элементарных функций, можно получить следующие формулы (ряд Маклорена с остаточным членом в форме Пеано)

sin⁡x=x+x36+o(x4)sin x=x+frac{x^3}{6}+o(x^4)
arcsin⁡x=x−x36+o(x4)arcsin x=x-frac{x^3}{6}+o(x^4)
tg⁡x=x+x33+o(x4)tg x=x+frac{x^3}{3}+o(x^4)
arctg⁡x=x−x33+o(x4)operatorname{arctg} x=x-frac{x^3}{3}+o(x^4)
ln⁡(1+x)=x−x22+o(x2)ln(1+ x)=x-frac{x^2}{2}+o(x^2)
(1+x)a=1+ax+a(a−1)x22+o(x2)(1+x)^a=1+ax+frac{a(a-1)x^2}{2}+o(x^2)

Пример 6
lim⁡x→0x−sin⁡xarcsin⁡x−x=lim⁡x→0x36+o(x3)x36+o(x3)=lim⁡x→01+o(1)1+o(1)=1.limlimits_{xto 0}frac{x-sin x}{arcsin x-x}=limlimits_{xto 0}frac{frac{x^3}{6}+oleft(x^3right)}{frac{x^3}{6}+oleft(x^3right)}=limlimits_{xto 0}frac{1+o(1)}{1+o(1)}=1.

Тест по теме “Сравнение функций”

Источник

Предел функции при ( x to x_0 )

Пусть функция ( f(x) ) определена на некотором множестве (X) и пусть точка ( x_0 in X ) или ( x_0 notin X )

Возьмем из (X) последовательность точек, отличных от (x_0) :
(x_1 ;, ; x_2 ;, ; x_3 ;, …, ; x_n ; , ; … tag{1} )
сходящуюся к (x^*).
Значения функции в точках этой последовательности также образуют числовую последовательность
( f(x_1) ;, ; f(x_2) ;, ; f(x_3) ;, …, ; f(x_n) ; , ; … tag{2} )
и можно ставить вопрос о существовании ее предела.

Определение. Число (A) называется пределом функции (f(x)) в точке ( x = x_0 ) (или при ( x to x_0 ) ), если для
любой сходящейся к (x_0) последовательности (1) значений аргумента (x), отличных от (x_0) соответствующая
последовательность (2) значений функции сходится к числу (A).

Символически это записывается так:
$$ lim_{xto x_0}{ f(x)} = A $$

Функция (f(x)) может иметь в точке (x_0) только один предел. Это следует из того, что последовательность ( left{ f(x_n) right} )
имеет только один предел.

Существует другое определение предела функции.

Определение Число (A) называется пределом функции (f(x)) в точке (x_0), если для любого числа ( varepsilon > 0 )
существует число ( delta > 0 ) такое, что для всех ( x in X, ; x neq x_0 ), удовлетворяющих неравенству ( |x-x_0| < delta ),
выполняется неравенство ( |f(x)-A| < varepsilon )

Используя логические символы, это определение можно записать в виде
( (forall varepsilon > 0) (exists delta > 0) (forall x in X, ; x neq x_0, ; |x-x_0| < delta): |f(x)-A| < varepsilon )

Отметим, что неравенства ( x neq x_0, ; |x-x_0| < delta ) можно записать в виде ( 0 < |x-x_0| < delta )

<>Первое определение основано на понятии предела числовой последовательности, поэтому его часто называют определением
«на языке последовательностей».
Второе определение называют определением «на языке ( varepsilon – delta )».
Эти два определения предела функции эквивалентны и можно использовать любое из них в зависимости от того, какое более
удобно при решении той или иной задачи.

Заметим, что определение предела функции «на языке последовательностей» называют также определением предела функции по Гейне,
а определение предела функции «на языке ( varepsilon – delta )» — определением предела функции по Коши.

Предел функции при ( x to x_{0-} ) и при ( x to x_{0+} )

В дальнейшем будут использованы понятия односторонних пределов функции, которые определяются следующим образом.

Определение Число (A) называется правым (левым) пределом функции (f(x)) в точке (x_0), если для любой сходящейся
к (x_0) последовательности (1), элементы (x_n) которой больше (меньше) (x_0), соответствующая
последовательность (2) сходится к (A).

Символически это записывается так:
$$ lim_{x to x_{0+}} f(x) = A ; left( lim_{x to x_{0-}} f(x) = A right) $$

Можно дать равносильное определение односторонних пределов функции «на языке ( varepsilon – delta )»:

Определение число (A) называется правым (левым) пределом функции (f(x)) в точке (x_0), если для любого
( varepsilon > 0 ) существует ( delta > 0 ) такое, что для всех (x), удовлетворяющих неравенствам
( x_0 < x < x_0 + delta ; (x_0 -delta < x < x_0 ) ) , выполняется неравенство ( |f(x)-A| < varepsilon ).

Символические записи:

( (forall varepsilon > 0) (exists delta > 0) (forall x, ; x_0 < x < x_0 + delta ): |f(x)-A| < varepsilon )

( (forall varepsilon > 0) (exists delta > 0) (forall x, ; x_0 -delta < x < x_0 ): |f(x)-A| < varepsilon )

Связь между односторонними пределами и пределом функции устанавливает следующая теорема.

Теорема
Функция (f(x)) имеет в точке (x_0) предел тогда и только тогда, когда в этой точке существуют как правый, так и левый пределы,
и они равны. В этом случае предел функции равен односторонним пределам.

Предел функции при ( x to infty ), при ( x to -infty ) и при ( x to +infty )

Кроме рассмотренных понятий предела функции при ( x to x_0 ) и односторонних пределов существует также понятие предела функции
при стремлении аргумента к бесконечности.

Определение. Число (A) называется пределом функции (f(x)) при ( x to infty ), если для любой бесконечно большой
последовательности (1) значений аргумента соответствующая последовательность (2) значений функции сходится к (A).

Символическая запись:
$$ lim_{x to infty} f(x) = A $$

Определение. Число (A) называется пределом функции (f(x)) при ( x to +infty ; (x to -infty) ) , если для любой бесконечно
большой последовательности значений аргумента, элементы (x_n) которой положительны (отрицательны), соответствующая
последовательность значений функции сходится к (A).

Символическая запись:
$$ lim_{x to +infty} f(x) = A ; left( lim_{x to -infty} f(x) = A right) $$

Теоремы о пределах функций

Определение предела функции «на языке последовательностей» дает возможность перенести доказанные выше теоремы о пределах
последовательностей на функции. Покажем это на примере двух теорем.

Теорема. Пусть функции (f(x)) и (g(x)) имеют в точке (x_0) пределы (B) и (C). Тогда функции ( f(x) pm g(x) ; , ; f(x) cdot g(x) ) и
( frac{f(x)}{g(x)} ) (при ( C neq 0 ) ) имеют в точке (x_0) пределы, равные соответственно ( B pm C ; , ; B cdot C ), и ( frac{B}{C} ).

Теорема. Пусть функции ( f(x) ; , ; g(x) ) и ( h(x) ) определены в некоторой окрестности точки (x_0), за исключением, быть
может, самой точки (x_0), и функции ( f(x) ; , ; h(x) ) имеют в точке (x_0) предел, равный (A), т.е.
$$ lim_{x to x_0} f(x) = lim_{x to x_0} h(x) = A $$

Пусть, кроме того, выполняются неравенства ( f(x) leqslant g(x) leqslant h(x) ).
Тогда $$ lim_{x to x_0} g(x) = A $$

Теорема Лопиталя. Если $$ lim_{x to x_0} f(x) = lim_{x to x_0} g(x) = 0 $$ или (infty ), (f(x)) и (g(x))
дифференцируемы в окрестности (x_0) , и ( g'(x) neq 0 ) в окрестности (x_0) ,
и существует $$ lim_{x to x_0} frac{f'(x)}{g'(x)} $$ то существует $$ lim_{x to x_0} frac{f(x)}{g(x)} = lim_{x to x_0} frac{f'(x)}{g'(x)} $$

Т.е. теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Теорема Лопиталя позволяет раскрывать неопределённости вида ( frac{0}{0} ) и ( frac{infty}{infty} ).

Первый замечательный предел

$$ lim_{x to 0} frac{sin x}{x} = 1 $$

Второй замечательный предел

$$ lim_{x to infty} left( 1+ frac{1}{x} right)^x = e $$

Источник

Определение эквивалентных функций

Эквивалентные функции – это функции, имеющие одинаковое значение. Они могут представлять собой бесконечность малых и больших величин.

Функция может иметь такое понятие лишь при наличии предела. Следует понимать, что одна и та же функция принимает значение малой или большой до бесконечности лишь в единственной точке.

Теорема о замене функций эквивалентными в пределе частного

Если при x₁, стремящимся к x₂, f(x)~f₁(x) и g(x)~g₁(x) существует предел:

то существует и предел:

Доказательство

Допустим, что следствие этой теоремы часто применяемое. Если мы имеем частное, являющееся результатом произведения функций:

в этом случае, при нахождении предела, можно сделать замену этих функций на эквивалентные:

при этом:

f(x) ~ f₁(x), p(x) ~ p₁(x), … , r(x) ~ r₁(x), g(x) ~ g₁(x), q(x) ~ q₁(x), … , s(x) ~ s₁(x).

Выражения равны друг другу, это значит, что при существовании одного из таких пределов, применимо существование выражения, равного первому. Соответственно, если не существует такой предел, то не может существовать и второй.

Следует отметить, что можно делать замену как одной величины функции, так и нескольких одновременно.

Таблица эквивалентных функций

Ниже приведена таблица равнозначных функций и формул при t → 0. В данном случае величина t может представлять собой как переменную, так и до бесконечности малую функцию t = t(x) при x → x₀:

Эквивалентность при t → 0	Равенство при t → 0
sin t ~ t	sin t = t + 0(t)
arsin t ~ t	arsin t = t + 0(t)
tg t ~ t	tg t = t + 0(t)
artg t ~ t	artg t = t + 0(t)
1-cos t ~	1-cos t = + 0(t²)
e^t – 1 ~ t	e^t – 1 = t + 0(t)
a^t – 1 ~ t ln a	a^t – 1 = t ln a + 0(t)
ln (1 + t) ~ t	ln (1 + t) = t + 0(t)
log_a (1 + t) ~	log_a (1 + t) = + 0(t)
(1 + t)^b – 1 ~ bt	(1 + t)^b – 1 = bt + 0(t)
sh t ~ t	sh t = t + 0(t)
arsh t ~ t	arsh t = t + 0(t)
th t ~ t	th t = t + 0(t)
arsh t ~ t	arsh t= t + 0(t)
ch t – 1 ~ t²/2	ch t – 1 ~ t²/2 + 0(t²)

Свойства замены функций равносильными доступны для дробных выражений с перемножаемыми величинами и произведений, где необходимо найти предел.

В этом случае величины в числителе или знаменателе допускается заменить равнозначными функциями. Если математическое выражение представляет собой сумму чисел, замену сделать нельзя.