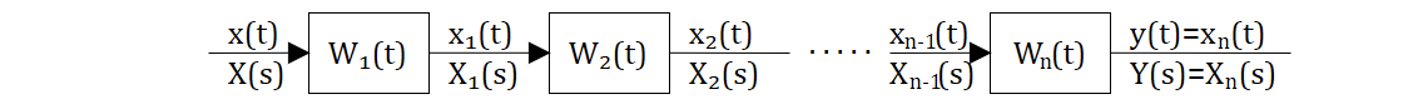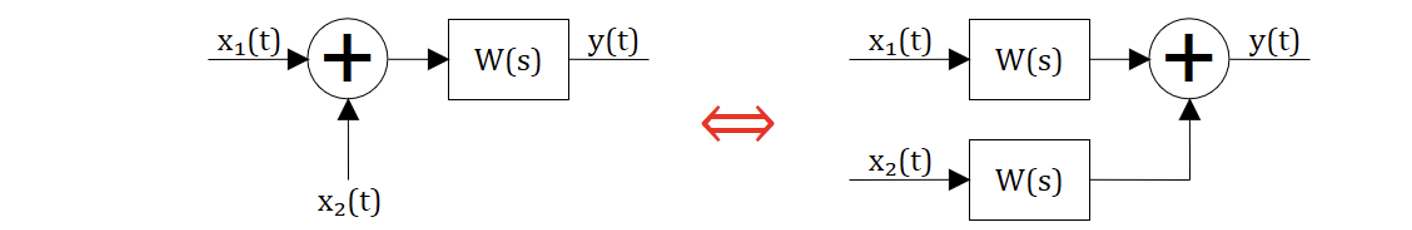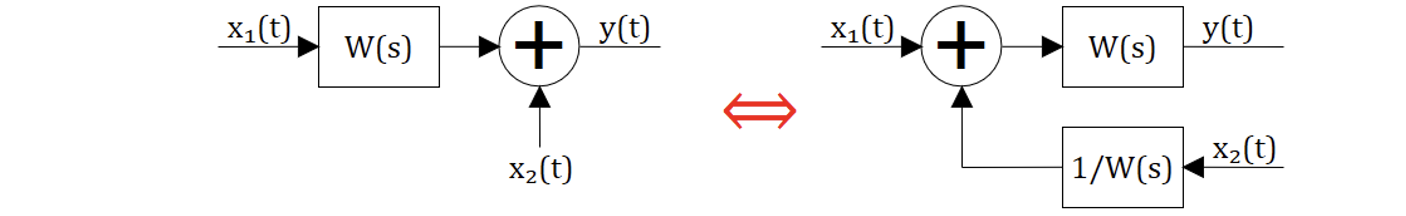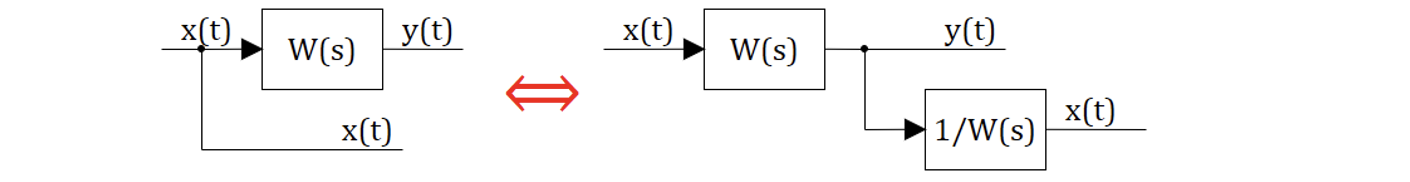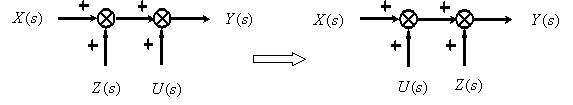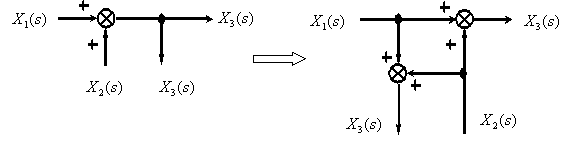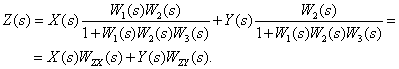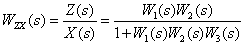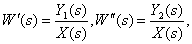Как найти эквивалентную передаточную функцию - Сайт, где вы сможете решить свои вопросы

Время на прочтение
8 мин

Количество просмотров 7K

Для решения задач расчета и моделирования систем автоматического регулирования зачастую приходится рассматривать достаточно сложные системы, состоящие из множества звеньев (передаточных функций). Так, например, поворот закрылок у самолета обеспечивается следующим набором механизмов:

Два электродвигателя постоянного тока, каждый из которых имеет по четыре обмотки возбуждения (две последовательные и две параллельные).
Электромагнитные муфты сцепления-торможения.
Планетарный редуктор с суммирующей дифференциальной передачей.

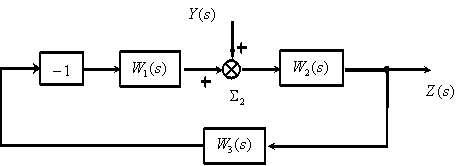
И это только для обеспечения механизма поворота! Так же нужно учитывать, что до электродвигателей существует непосредственно система автоматического регулирования, которая вырабатывает необходимые сигналы управления. На рисунке 1. приведена структурная схема системы управления двигателем с постоянными магнитами. При этом в качестве входа в эту систему используется значение заданного положения, которое, в свою очередь, тоже должно быть определено исходя из решения уравнений динамики летательного аппарата.

Рисунок 1. Структурная схема управления двигателем с постоянными магнитами

При прямом физическом моделировании подобных систем приходится выполнять множество математических вычислений, и скорость вычислений снижается до неприемлемого уровня. Если мы хотим исследовать движение летательного аппарата в целом, необходимо представить модель сложной системы в упрощенном виде, желательно, не теряя качества и сохраняя необходимую точность. В предыдущей лекции при выводе уравнений динамики ядерного реактора мы показывали, каким образом, пренебрегая малыми величинами, мы получаем компактное выражение, и сохраняем точность в заданном диапазоне изменений.

В этой лекции мы покажем каким образом сократить количество вычислений, используя преобразования передаточных функций в сложной системе.

Большинство реальных систем автоматического регулирования являются сложными. При анализе часто приходится рассматривать как “фрагменты”, так полные системы САР, и выполнять над ними некоторые операции, упрощающие их структуру.

Определение. Действия, упрощающие математическое или графическое изображение САР (структуры) или упрощающие последующий анализ динамических свойств САР, называются структурными преобразованиями.

Различают несколько типовых упрощающих действий:

замена цепи из последовательно соединенных звеньев эквивалентным звеном;
замена цепи из параллельно соединенных звеньев эквивалентным звеном;
замена цепи с местной обратной связью эквивалентным звеном;
замена цепи с местной обратной связью на единичною обратную связь;
перенос точек включения обратной связи “вперед”- “назад”;
перенос точек суммирования или ветвления “вперед”- “назад”.

4.1 Замена цепи из последовательно параллельно соединенных звеньев

Рисунок 4.1.1. Последовательное соединение звеньев.

Цепь преобразований: Получить эквивалентную передаточную функцию:

$W_{экв}(s)=frac{Y(s)}{X(s)}=frac{X_n(s)}{X(s)};$

Запишем ряд очевидных равенств:

$left { begin{align}W_1(s) = frac{X_1(s)}{X(s)}; \ W_2(s)=frac{X_2(s)}{X_1(s)}; \ ................\W_n(s)=frac{X_n(s)}{X_{n-1}(s)};end{align} right.$

Перемножим, соответсвенно правые и левые части этих равентсв:

$W_1(s)cdot W_2(s)cdot cdots cdot W_n(s) = frac{X_1(s)}{X(s)}cdot frac{X_2(s)}{X_1(s)}cdot cdots cdot frac{X_n(s)}{X_{n-1}(s)};$ $frac{X_n(s)}{X(s)} =W_{экв}(s)=W_1(s)cdot W_2(s)cdots W_n(s);$

Эквивалентная передаточная функция:

$W_{экв}=prod _{j=1}^{j=n}W_j(s); mathbf{(4.1)}$

Найдем эквивалентную АФЧХ. (Подробнее см. лекцию Частотные характеристики систем автоматического управления (АФЧХ, ЛАХ, ФЧХ)).

$s = i cdot omega Rightarrow W_{экв}(icdotomega)=prod_{j=1}^{j=n}W_j(icdot omega) mathbf{(4.2)}$

Учитвая, что
$W_j = A_j(omega)cdot e^{icdot phi_i(omega)}Rightarrow$

$left { begin{align} A_{экв}(omega)=prod_{j=1}^{j=n} A_j(omega); \ phi_{экв}(omega)=sum_{j=1}^{j=n} phi_j(omega); end{align} right. mathbf{(4.3)}$

Эквивалентная логарифмическая амплитудная характеристика ЛАХ:

$Lm_{экв}(omega)=20 cdot lg [A_{экв}(omega)]=sum_{j=1}^nLm_j(omega) mathbf{(4.4)}$

Если каждое из звеньев имеет передаточную функцию в виде $W_j(s) =K_jcdot frac{N(s)}{L(s)}$ , где у свободный член равен 1, а у свободный член = 0, то

$K_{экв}= prod_{j=1}^n K_j mathbf{(4.5)}$

Пример 1.

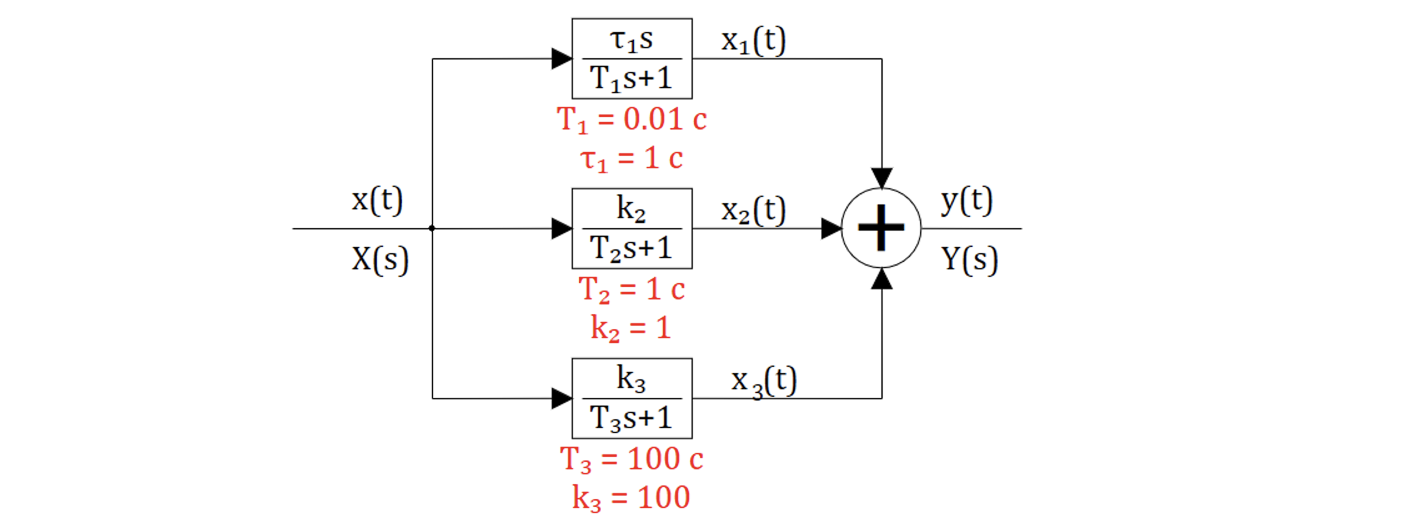
Заменить последовательные звенья структуры на рисунке 4.1.2 эквивалентным звеном и построить его логарифмическую амплитудную характеристику.

Рисунок 4.1.2 Последовательно соединенные звенья

Для начала вполним расчет эквивалентной передаточной функции по формуле 4.1:

$W_{экв}=frac{tau_1cdot s}{T_1cdot s+1}cdot frac{k_2}{T_2cdot s+1}cdot frac{k3}{T_3cdot s+1}Rightarrow$ $W_{экв}=frac{(tau_1cdot k_2cdot k_3) s}{(T_1cdot T_2cdot T_3)s^3+(T_1cdot T_2+T_1cdot T_3+T_2cdot T_3) s^2+(T_1+T_2+T_3) s+1}$

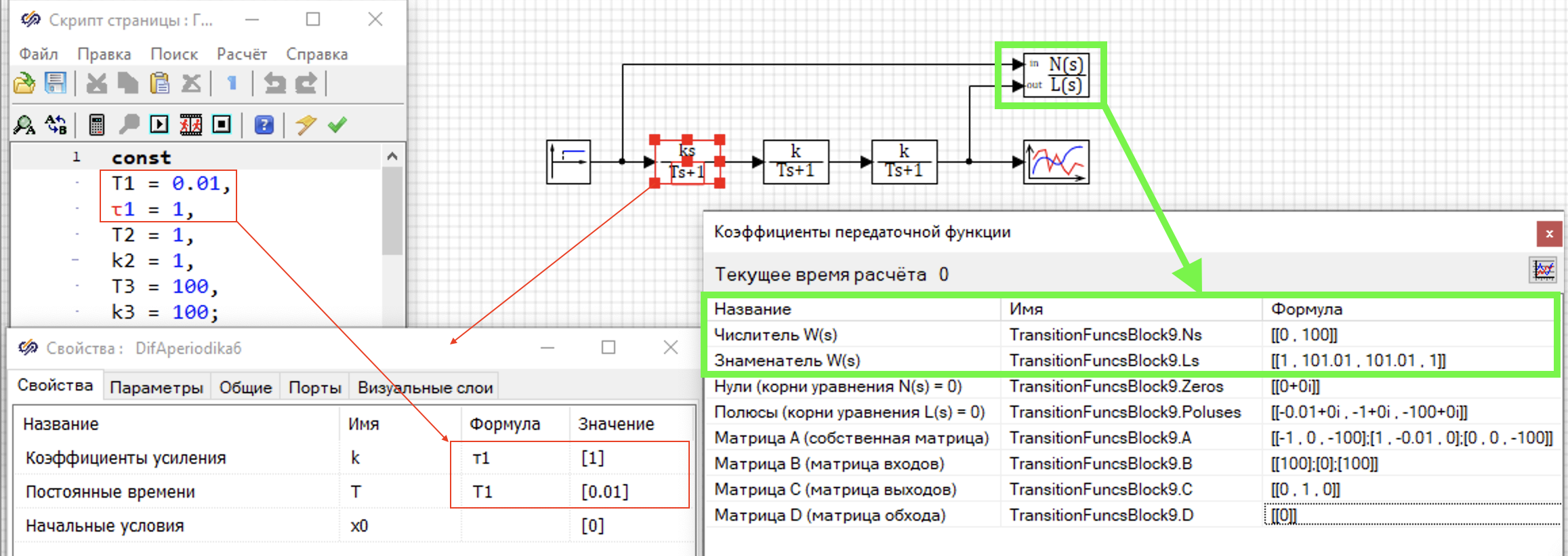
Если подставить вместо символьных коэффициентов их значение (см. рисунок 4.1.3) эквивалентаня передаточная функция примет вид:

$W_{экв}=frac{100cdot s}{s^3+101.01cdot s^2+101.01cdot s+1}$

Выполним аналогичное преобразование с помощью блока “Построение передаточных функций“. На рисунке 4.1.3 представлена схема модели в которой выполняется расчет эквивалентной передаточной функции для трех последовательных звеньев.

Рисунок 4.1.3 Схема расчета эквивалентоно передаточной функции

Численные значения коффициентов задаются в скрипте программы в секции констант, а затем используются в столбце формула, для свойств блоков – звеньев на схеме (красные прямоугольники на рис. 4.1.3). Блок “Построение передаточных функций” выполняет расчет коэффициентов, и результаты рассчета совппадают с аналитическим решением (зеленые прямоугольники на рис. 4.1.3).

Можно так же построить ЛАХ данной системы из трех звеньев, если сообразить, что на схема 4.1.2 испольуются блоки “Апереодическое звено первого порядка” и “Инерционно-дифференцирующее звено”, которые мы рассматривали в соотвествующих лекциях ранее. Для каждого блока мы можем построить ЛАХ, используя формулы для точек перегиба функций, как это было показано ранее, а затем графически сложить для получения эквивалентной согласно формуле 4.4. Решение представлено на рисунке 4.1.4

Рисунок4.1.4 Построение эквивалентной ЛАХ

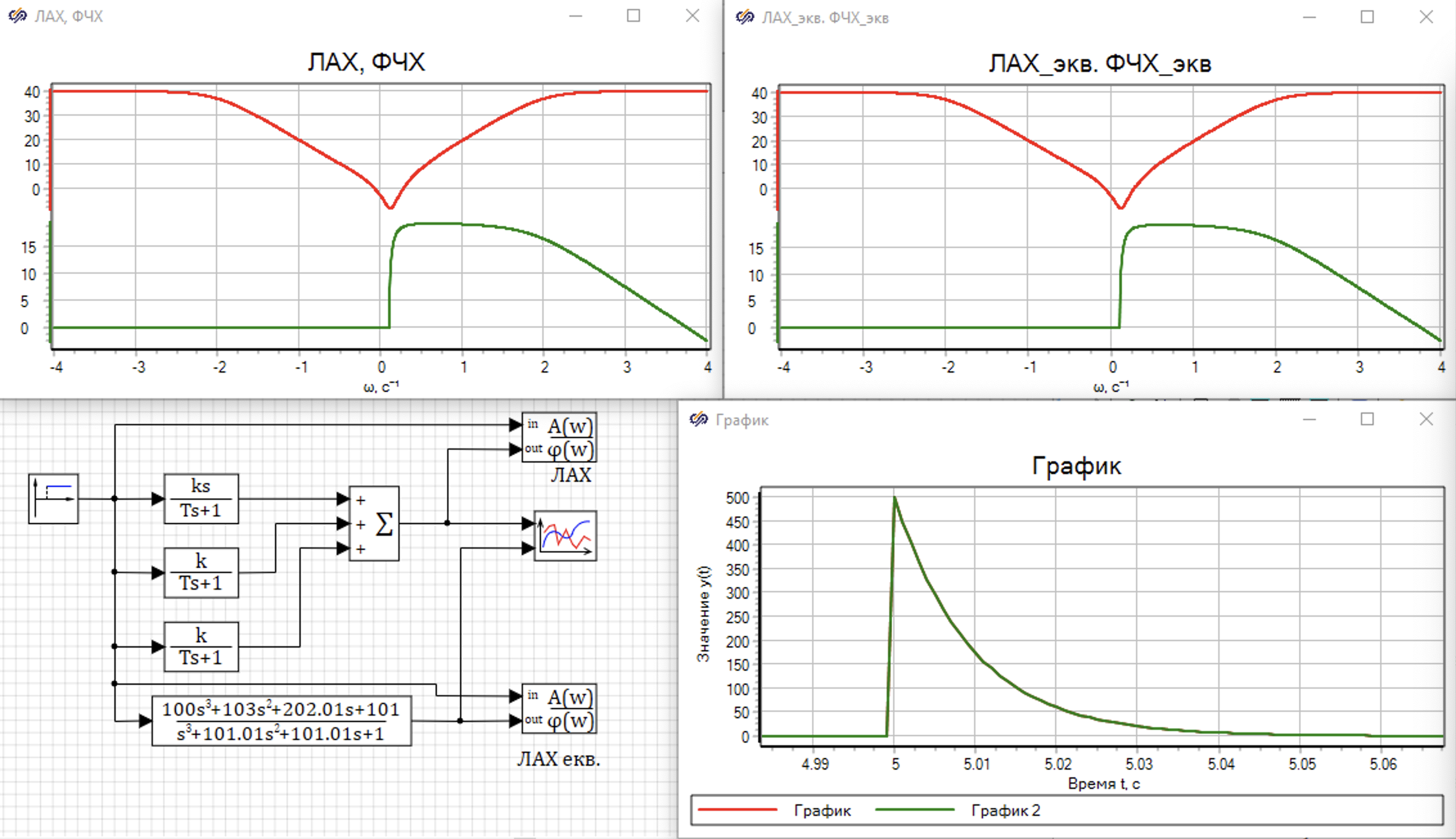
Проверим графическое аналитическое решение построекнием ЛАХ с помощью блока “Построение частотных характеристие“. На рисунке 4.1.5 Представлена расчетная схема из трех последовательных звеньев и еквивалентное звено. Для каждого блока построена ЛАХ, и мы видим что точки перегиба и углы наклона функции совпадают.

Рисунок 4.1.5 ЛАХ последовательных звеньев и эквивалентного звена

4.2. Замена цепи из параллельно соединенных звеньев эквивалентным звеном

Рисунок 4.2.1 Система паралельных звеньев

Выходное значение является сумммой выходов из всех звеньев (см. рис. 4.2.1):

$y(t)=sum^n_{j=1}x(t) Rightarrow$ $Y(s)=sum_{j=1}^n X_j(s)$

Запишем ряд очевидных равенства для передаточных функций:

$left { begin{align}X_1(s) = W_1(s)cdot X(s); \ X_2(s)=W_2(s)cdot X(s); \ ................\X_n(s)=W_n(s)X(s);end{align} right.$

Складывая, получаем:

$underbrace{X_1(s)+X_2(s)+...+X_n(s)}_{Y(s)}=X(s)cdotunderbrace{[W_1(s)+W_2(s)+...+W_n(s)]}_{W_{экв}(S)}Rightarrow$ $W_{экв}(s)=sum_{j=1}^n W_j(s) mathbf{(4.6)}$

Найдем эквивиалентную АФЧХ, подставляя вместо значение :

$W_{экв}(icdot omega)=sum_{j=1}^nW_j(icdotomega) = sum_{j=1}^nU_j(omega)+icdot sum_{j=1}^nV_j(omega); mathbf{(4.7)}$ $left { begin{align} U_{экв}(omega)=sum_{j=1}^{j=n} U_j(omega); \ V_{экв}(omega)=sum_{j=1}^{j=n} V_j(omega); end{align} right. mathbf{(4.8)}$

Модуль АФЧХ эквивалентной передаточной функции:

$A_{экв}(omega)=sqrt{left[sum_{j=1}^nU_j(omega)right]^2+left[sum_{j=1}^nV_j(omega)right]^2} mathbf{(4.9)}$

Фазовый сдвиг для эквивалентной передаточной функции:

$phi (omega)=-picdot m+arctfrac{V_{экв}(omega)}{U_{экв}(omega)} mathbf{(4.10)}$

где занчения m, зависит от положения вектора АФЧХ на векторной плоскости:

если вектор находится в 2 и 3 квадрантах комплексной плоскости,

если вектор находится в 1 и 4 квадрантах комплексной плоскости.

Логарифмическая амплитудная характеристика:

$Lm_{экв}(omega)=20cdot lg[A_{экв}(omega)]=20cdot lgsqrt{left[sum_{j=1}^nU_j(omega)right]^2+left[sum_{j=1}^nV_j(omega)right]^2} mathbf{(4.11)}$

Наиболее простые соотношения имеют место для переходной и весовой эквивалентных функций:

$h_{экв}(t)=sum_{j=1}^nh_j(t); w_{экв}(t)=sum_{j=1}^n w_j(t); mathbf{(4.12)}$

Последовательное и параллельное соединение звеньев в значительной степени похожи на аналогичные соединения в электротехнике, гидравлики, и т.д.

Пример 2

Заменить паралельные звенья структуры на рисунке 4.2.2 эквивалентным звеном .

Рисунок 4.2.2 Паралельные звенья

Согласно формуле 4.6 получим выражения для эквивалентной функции:

$W_{экв}=frac{tau_1cdot s}{T_1cdot s+1}+ frac{k_2}{T_2cdot s+1}+ frac{k_3}{T_3cdot s+1}Rightarrow$ $W_{экв}=frac{N_3cdot s^3+N_2cdot s^2+N_1cdot s+N_0}{(T_1cdot T_2cdot T_3)s^3+(T_1cdot T_2+T_1cdot T_3+T_2cdot T_3) s^2+(T_1+T_2+T_3) s+1}$

где значения многочлена числителя получаются путем приведения к общему знаменателю:

$N_3=tau_1cdot T_2cdot T_3;\ N_2=k_2cdot T_1 cdot T_3+k_3cdot T_1 cdot T_2+tau_1cdot T_3+tau_1cdot T_2;\N_1 = tau_1+k_2cdot T_3+k_3cdot T_2+k_3cdot T_1; \N_0=k_2+k_3.$

При подстановке численных значений коэффициентов с рисунка 4.2.2 получаем следующее значение эквивалентной передаточной функции:

$W_{экв}=frac{100cdot s^3+103cdot s^2+202.01cdot s+101}{s^3+101.01cdot s^2+101.01cdot s+1}$

Точно такое же значение получится при исползовании блока “Построение передаточных функций“, для автоматически построения функций. Для сравнения построим переходный процесс для параллельных звеньев и эквивалентного звена:

Рисунок 4.2.3 Сравнение трех паралельных звеньев с эквивалетным звеном.

4.3 Цепь с обратной связью

Определение Связь выходного сигнала системы с входным, при которой отклонение выходного сигнала системы (т.е. объекта) вызывает соответствующее изменение ее входного сигнала, называется обратная связь.

Цепь с обратной связью имеет следующий структурный вид:

Рисунок 4.3.1 Струкутура системы с обратной связью

Определение: если обратная связь охватывает только часть цепи или одно звено, то такая связь называется местная обратная связь.

Если занчение сигнала обратной связи вычитается из входного сигнала, то такая связь называется отрицательной и может обозначатся на схема как “сравнивающее устройство” или просто знаком минус (см. рис. 4.3.2):

Рисунок 4.3.2 Обозначение отрицательной обратной связи

Если заначение сигнала обратной связи складывается с входным сигналом, то такая связь называется положительной, и обозначается знаком + (см. рис. 4.3.3).

Рисунок 4.3.3 Обзначение положительной обратной связи

Рассмотрим преобразование на примере отрицательной обратной связи см. рис. 4.3.4, которую нужно преобразовать в одно звено с эквивалентной передаточной функцией:

Рисунок 4.3.4 Преобрзование струкутруы с обратной связью.

На выходе из блока “Сравнивающее устройство” получается рассогласование:

$varepsilon(t)=x(t)-x_{ос}(t) Rightarrow E(s)=X(s)-X_{oc}(s)$

Выполним преобразования в изображениях обходя структуру по контору:

$Y(s)=E(s)cdot W(s)=[X(s)-X_{oc}(s)]cdot W(s) =\ =[X(s)-Y(s)cdot W_{oc}(s)]cdot W(s) Rightarrow \ (1+W_{oc}(s)cdot W(s))cdot Y(s)=X(s)cdot W(s);$

Эквивалентная передаточная функция для отрицательной обратной связи:

$W_{экв}(s)=frac{Y(s)}{X(s)}=frac{W(s)}{1+W_{ос}(s)cdot W(s)} mathbf{(4.13)}$

Для положительной обратной связи преобразование аналогичные, за исключением знака обратной связи для величины “рассогласование” $varepsilon(t) = x(t)+x_{oc}(t)$ тогда выражение эквивалентной функции для положительной обратаной связи по аналогии:

$W_{экв}(s)=frac{Y(s)}{X(s)}=frac{W(s)}{1-W_{ос}(s)cdot W(s)} mathbf{(4.14)}$

Можно так же записать общее выражение для системы с обратной связью:

$W_{экв}(s)=frac{W(s)}{1 pm W_{ос}(s)cdot W(s)} mathbf{(4.15)}$

где: знак ” ” – для отрицательной обратной свзязи, а знак ” ” – для положителеной

Как правило в регуляторах используется отрицательная обратная свзязь.

Опредление: обратная связь у которой значение сигнала выхода передается непосредственно на вход без передаточного зена, назвается единичная обратная связь.

В случае когда обратная связь единичная $W_{оc} = 1$ выражение для эквивалентной функции принимает вид:

$W_{экв}(s)=frac{W(s)}{1 pm W(s)} mathbf{(4.15)}$

Для единичной отрицательной обратной связи изображенной на рисунке 4.3.5 эквивалентная функция:

$W_{экв}=frac{W(s)}{1+W(s)}$

Рисунок 4.3.5 Отрицательная единичная обратная связь.

Пример 3

Заменить звено с обратной связью структуры на рисунке 4.3.6 эквивалентным звеном.

4.3.6 Звено с обратной связью.

Согласно формуле 4.13

$W_{экв}=frac{frac{tau_1cdot s}{T_1cdot s+1}}{1+frac{k_2}{T_2cdot s+1}cdotfrac{tau_1cdot s}{T_1cdot s+1}}=frac{tau_1cdot T_2cdot s^2+tau_1cdot s}{T_1cdot T_2cdot s^2+(T_2+T_1+k_2cdottau_1)cdot s+1}$

Подставляя значения коэффициентов с рисунка 4.3.6 получаем следующие выражение передаточной функции:

$W_{экв}=frac{s^2+s}{0.01cdot s^2+2.01cdot s+1}$

Рисунок 4.3.7 Сравнение системы с обратной связью и эквивалентной

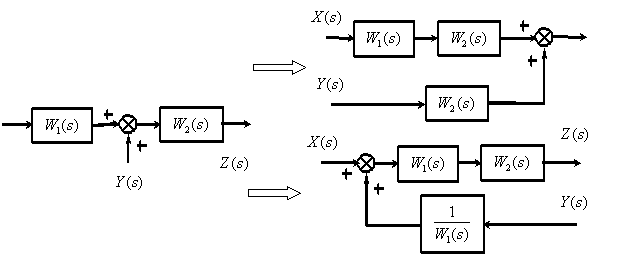
4.3.1. Замена звена с местной обратной связью на единичную

Существуют два способа замены местной обратной связи на единичную:

Способ 1. Добавление последовательного звена после обратной связи, таким образом, что бы общая передаточная функция не изменилась (см. рис. 4.3.8):

Рисунок 4.3.8 Замена местной обратной связи.

Исходная передаточная функция согласно формулы 4.13:

$W_{ис}=frac{W(s)}{1+W(s)cdot W_{oc}(s)}$

Общая передаточная функция новой системы получается по формуле 4.1 для последовательных звенье, где первая часть это формула звена с единичной обратной связью, а вторая часть – новая неизвестная передаточная функция Z(s) см. рис. 4.3.8:

$W_{экв}=frac{W(s)cdot W_{oc}(s)}{1+W_{oc}(s)cdot W(s)}cdot Z(s);$

Приравнивая $W_{ис}=W_{экв}$ получаем выражение для добавленного звена:

$Z(s)=frac{1}{W_{oc}(s)} mathbf{(4.18)}$

Cпособ 2. Добавление звена в контур до обратной связи так, что бы обратная единичная связь охватывала все звенья (см. рис. 4.3.9):

4.3.9 Замена обратной местной связи на единичную

Исходная передаточная функция согласно формулы 4.13:

$W_{ис}=frac{W(s)}{1+W(s)cdot W_{oc}(s)}$

Эквивалентаня функция для преобразованной схемы по формуле для последовательных звеньев 4.1 и для единичной обратной связи 4.15:

$W_{экв}=frac{W(s)cdot Z(s)}{1 +W(s)cdot Z(s)}$

Приравнивая $W_{ис}=W_{экв}$ получаем выражение для добавленного звена:

$frac{W(s)}{1+W(s)cdot W_{oc}(s)}=frac{W(s)cdot Z(s)}{1+W(s)cdot Z(s)} Rightarrow$ $Rightarrow 1+W(s)cdot Z(s)=Z(s)+W(s)cdot W_{oc}(s)cdot Z(s) Rightarrow$ $Z(s)=frac{1}{1-W(s)+W(s)cdot W_{oc}(s)} mathbf{(4.19)}$

4.3.2. Перенос места обратной связи “вперед” или “назад”

Перенос обратной связи вперед. Исходная и эквивалентная САР представлены на рисунке 4.3.10

4.3.10 Перенос обратной связи вперед.

Эквивалентная функция для исходной системы получим используя формулы для звена с обратной связью 4.13 и последовательного соединения 4.1:

$W_{исх}(s)=frac{W_1(s)}{1+W_1(s)cdot W_{oc}(s)}cdot W_2(s)$

Эквиваланетная функция для преобразованной системы:

$W_{экв}=frac{W_1(s)cdot W_2(s)}{1+W_{ос}(s)cdot Z(s)cdot W_1(s)cdot W_2}$

Приравнивая $W_{исх}=W_{экв}$ получаем:

$Z(s)=frac{1}{W_2(s)} mathbf{(4.20)}$

Перенос обратной свзяи назад. Исходная и эквивалентная схемы представлены на рисунке 4.3.11

Рисунок 4.3.11 Перенос обратной связи назад

Аналогично запишем уравнения для обоих систем и определим значение добавленной передаточной функции:

$W_{исх}(s)=frac{W_1(s)cdot W_2}{1+W_1(s)cdot W_{oc}(s)cdot W_2(s)}=$ $=W_{экв}=frac{W_1(s)cdot W_2(s)}{1+W_{1}(s)cdot W_{oc}(s)cdot Z(s)}Rightarrow$ $Z(s)= W_2(s) mathbf{(4.21)}$

4.4. Перенос точек суммирования “вперед” или “назад”

Такие преобразования достаточно просто илюстирируются графически.

На рисунке 4.4.1 перенос точки суммирования вперед:

4.4.1 Перенос точки сумирования вперед

На рисунке 4.4.2 перенос точки суммирования назад:

Рисунок 4.4.2 Перенос точки сумирования назад

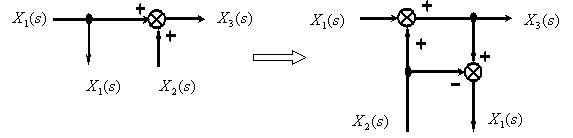
4.5. Перенос точек ветвления “вперед” или “назад”

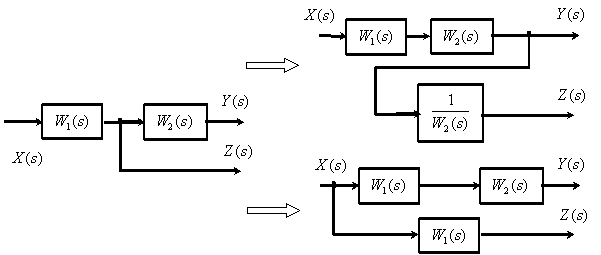
На рисунках 4.5.1 и 4.5.2 представлены схемы переноса точек ветвления вперед и назад соответвенно:

Рисунок 4.5.1 Перенос точки ветвеления вперед

Рисунок 4.5.2 Перенос точки ветвления назад

Данные рисунки очевидны и не требуют дополнительных комментариев. Иногда этот прием называется “перенос внешнего воздействия”.

Как всегда, примеры разобранные в лекции можно взять по ссылке здесь.

Предыдущие лекции:

1. Введение в теорию автоматического управления.
2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.
3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕГУЛИРОВАНИЯ.
3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2. Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3. Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4. Апериодическое звено 2-го порядка. 3.5. Колебательное звено. 3.6. Инерционно-дифференцирующее звено. 3.7. Форсирующее звено. 3.8. Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9. Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности.

Источник

Как найти эквивалентную передаточную функцию схемы

Правила эквивалентных преобразований структурных схем систем автоматического управления

Выше были рассмотрены математические модели отдельных динамических звеньев. САУ представляет собой систему, состоящую из функциональных элементов, каждый из которых может быть представлен в виде динамического звена. То есть САУ можно представить в виде совокупности динамических звеньев с известными математическими моделями. Рассмотрим структуру типичной САУ

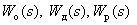
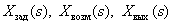
где передаточные функции соответственно объекта, датчика и регулятора, изображения задающего, возмущающего и выходного сигналов.

В процессе анализа и синтеза САУ необходимо получать передаточные функции САУ, которые связывают выходную переменную с заданием и возмущением в САУ, по известным структурной схеме и передаточным функциям динамических звеньев, входящих в состав САУ.

Аналогичная задача возникает в том случае, когда известны частотные характеристики динамических звеньев, а необходимо определить частотные характеристики САУ, характеризующие связи между выходом и входом САУ.

Решением этих задач мы и займемся в дальнейшем.

Эта задача решается путем преобразования (сворачивания) структурной схемы к одному динамическому звену с искомой передаточной функцией на основе использования правил эквивалентных преобразований структурных схем и принципа суперпозиции (наложения).

Правила эквивалентных преобразований позволяют найти необходимую передаточную функцию САУ, свернув структурную схему к одному динамическому звену с искомой передаточной функцией.

Рассмотрим правила эквивалентных преобразований, не изменяющих свойств систем и необходимых для нахождения передаточной функции:

Последовательное соединение динамических звеньев.

Параллельное соединение динамических звеньев.

Замкнутый контур с отрицательной обратной связью.

Замкнутый контур с положительной обратной связью.

Перенос точки ветвления через динамическое звено.

Перенос суммирующего звена через динамическое звено.

Перестановка суммирующих звеньев.

Перенос точки ветвления с выхода на вход суммирующего звена.

Перенос точки ветвления с входа на выход суммирующего звена.

Принцип суперпозиции (наложения)

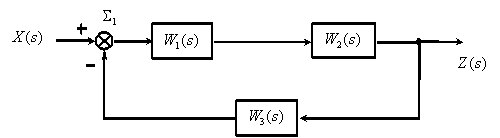
Применим рассмотренные правила для упрощения структурной схемы

Процесс преобразования, который часто называют свертыванием структурной схемы, выглядит следующим образом.

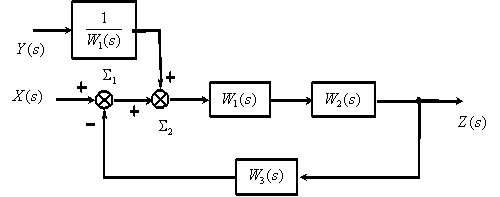
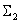
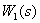
Перенесем суммирующее звено через динамическое звено .

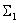
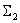
Поменяем местами суммирующие звенья и.

Преобразуем последовательно включенные динамические звенья и .

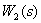
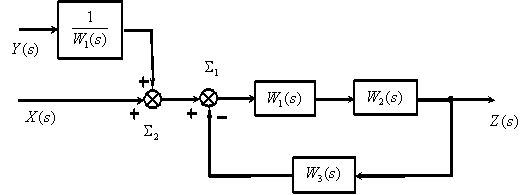
Преобразуем замкнутый контур с отрицательной обратной связью ().

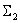
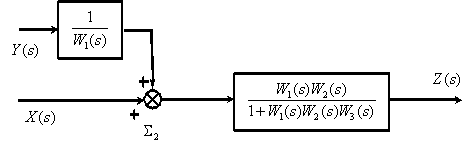
Перенесем суммирующее звено вправо.

Преобразуем последовательно включенные звенья..

В соответствии с полученной структурной схемой запишем операторное уравнение

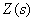
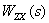
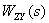
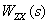
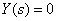
Уравнение показывает, что является линейной комбинацией изображений входных сигналов, взятых с коэффициентами и . Выясним смысл этих коэффициентов на примере коэффициента . Для этого положим в (1) , тогда получим

Таким образом, из (2) следует, это передаточная функция динамического звена, к которому свернута структурная схема в предположении, что изображения всех входных сигналов, кроме , равны нулю.

Теперь становится ясным смысл и самого операторного уравнения (1), описывающего систему. Он заключается в том, что реакция линейной системы на совместно действующие входные сигналы может быть определена в виде суммы частичных реакций, каждая из которых вычисляется в предположении, что на систему действует только один входной сигнал, а остальные равны нулю.

По сути это формулировка фундаментального принципа, который называют принципом наложения или суперпозиции. Этот принцип можно рассматривать как дополнение к правилам эквивалентных преобразований структурных схем и активно использовать на практике.

Практически принцип суперпозиции для нахождения конкретной передаточной функции используют следующим образом. Полагают равными нулю все входные сигналы, кроме необходимого сигнала, а затем выполняют преобразование структурной схемы в одно динамическое звено.

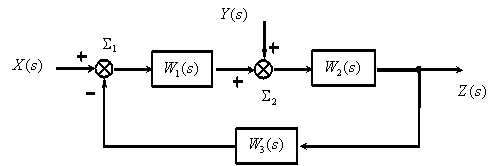
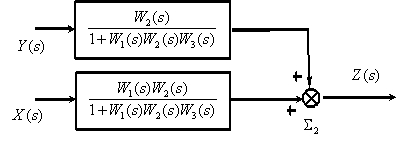
Рассмотрим использование принципа суперпозиции на примере показанной на рис. 1 структурной схемы.

Полагаем 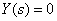и изобразим соответствующую этому случаю структурную схему.

Используя эквивалентные преобразования, получим

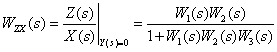
Полагаем 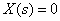и изобразим соответствующую этому случаю структурную схему.

Используя эквивалентные преобразования, получим

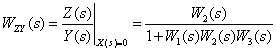
Имея 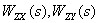, в соответствии с принципом суперпозиции получим «свернутую» структурную схему САУ.

Контрольные вопросы и задачи

Какие задачи позволяют решать правила эквивалентных преобразований структурных схем?

Дайте определение принципа суперпозиции применительно к структурным схемам систем автоматического управления.

Как используют принцип суперпозиции на практике?

Определите передаточные функции

по следующей структурной схеме

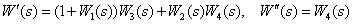
Определите передаточную функцию, эквивалентную структурной схеме.

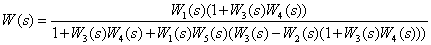
Определите передаточные функции

по следующей структурной схеме

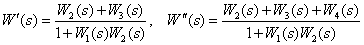
Источник

Как найти эквивалентную передаточную функцию схемы

4.1. Эквивалентные преобразования структурных схем

Структурная схема САУ в простейшем случае строится из элементарных динамических звеньев. Но несколько элементарных звеньев могут быть заменены одним звеном со сложной передаточной функцией. Для этого существуют правила эквивалентного преобразования структурных схем. Рассмотрим возможные способы преобразований.

1. Последовательное соединение (рис.28) — выходная величина предшествующего звена подается на вход последующего. При этом можно записать:

y ₁ = W ₁ y o ; y ₂ = W ₂ y ₁ ; . ; y _n = W _n y _{n — 1} = >

y _n = W 1 W 2 . W n .y o = W_эквy o ,

где.

То есть цепочка последовательно соединенных звеньев преобразуется в эквивалентное звено с передаточной функцией, равной произведению передаточных функций отдельных звеньев.

2. Параллельно — согласное соединение (рис.29) — на вход каждого звена подается один и тот же сигнал, а выходные сигналы складываются. Тогда:

y = y ₁ + y ₂ + . + y _n = (W ₁ + W ₂ + . + W3)y _o = W_эквy _o ,

где .

То есть цепочка звеньев, соединенных параллельно — согласно, преобразуется в звено с передаточной функцией, равной сумме передаточных функций отдельных звеньев.

3. Параллельно — встречное соединение (рис. 30а) — звено охвачено положительной или отрицательной обратной связью. Участок цепи, по которому сигнал идет в противоположном направлении по отношению к системе в целом (то есть с выхода на вход) называется цепью обратной связи с передаточной функцией W _ос . При этом для отрицательной ОС:

где .

Аналогично: — для положительной ОС.

Если W _oc = 1 , то обратная связь называется единичной (рис.30б), тогда W_экв = W _п /(1 ± W _п ).

Замкнутую систему называют одноконтурной , если при ее размыкании в какой либо точке получают цепочку из последовательно соединенных элементов (рис.31а). Участок цепи, состоящий из последовательно соединенных звеньев, соединяющий точку приложения входного сигнала с точкой съема выходного сигнала называется прямой цепью (рис.31б, передаточная функция прямой цепи W _п = WoW ₁ W ₂ ) . Цепь из последовательно соединенных звеньев, входящих в замкнутый контур называют разомкнутой цепью (рис.46в, передаточная функция разомкнутой цепи W _p = W ₁ W ₂ W ₃ W ₄ ).

Исходя из приведенных выше способов эквивалентного преобразования структурных схем, одноконтурная система может быть представлена одним звеном с передаточной функцией: W_экв = W _п /(1 ± W _p ) — передаточная функция одноконтурной замкнутой системы с отрицательной ОС равна передаточной функции прямой цепи, деленной на единицу плюс передаточная функция разомкнутой цепи. Для положительной ОС в знаменателе знак минус. Если сменить точку снятия выходного сигнала, то меняется вид прямой цепи. Так, если считать выходным сигнал y ₁ на выходе звена W ₁ , то W _p = WoW ₁ . Выражение для передаточной функции разомкнутой цепи не зависит от точки снятия выходного сигнала.

Замкнутые системы бывают одноконтурными и многоконтурной (рис.32).Чтобы найти эквивалентную передаточную функцию для данной схемы нужно сначала осуществить преобразование отдельных участков.

Если многоконтурная система имеет перекрещивающиеся связи (рис.33), то для вычисления эквивалентной передаточной функции нужны дополнительные правила:

4. При переносе сумматора через звено по ходу сигнала необходимо добавить звено с передаточной функцией того звена, через которое переносится сумматор. Если сумматор переносится против хода сигнала, то добавляется звено с передаточной функцией, обратной передаточной функции звена, через которое переносим сумматор (рис.34).

Так с выхода системы на рис.34а снимается сигнал

Такой же сигнал должен сниматься с выходов систем на рис.34б:

При подобных преобразованиях могут возникать неэквивалентные участки линии связи (на рисунках они заштрихованы).

5. При переносе узла через звено по ходу сигнала добавляется звено с передаточной функцией, обратной передаточной функции звена, через которое переносим узел. Если узел переносится против хода сигнала, то добавляется звено с передаточной функцией звена, через которое переносится узел (рис.35). Так с выхода системы на рис.35а снимается сигнал

Такой же сигнал снимается с выходов рис.35б:

6. Возможны взаимные перестановки узлов и сумматоров: узлы можно менять местами (рис. 36а); сумматоры тоже можно менять местами (рис.36б); при переносе узла через сумматор необходимо добавить сравнивающий элемент (рис.36в: y = y ₁ + f ₁ = > y ₁ = y — f ₁ ) или сумматор (рис.36г: y = y ₁ + f ₁ ).

Во всех случаях переноса элементов структурной схемы возникают неэквивалентные участки линии связи, поэтому надо быть осторожным в местах съема выходного сигнала.

При эквивалентных преобразованиях одной и той же структурной схемы могут быть получены различные передаточные функции системы по разным входам и выходам. Так на рис.48 имеется два входа: по управляющему воздействию u и возмущению f при одном выходе y . Такая схема может быть преобразована к одному звену с двумя передаточными функциями W _uy и W _fy .

4.2. САР напряжения генератора постоянного тока

Для примера рассмотрим схему САР напряжения генератора постоянного тока (рис.37).

Выведем дифференциальное уравнение исполнительного двигателя постоянного тока. Его схема замещения изображена на рис. 38.

Для якорной цепи справедливо уравнение

Если принять, что , гдеj – угол поворота вала двигателя, то

где – постоянная времени якорной цепи; , – коэффициенты пропорциональнсти.

Если учесть, что , где J – момент инерции якоря, M — электромагнитный момент, М _с – момент сторонних сил, то получим

= >

Здесь – электромеханическая постоянная времени;

; ; ; – коэффициенты пропорциональности;

, – передаточные функции по напряжению и моменту сторонних сил.

Структурная схема двигателя постоянного тока показана на рис.39.

Аналогичным образом выводится передаточная функция генератора постоянного тока, которая с учетом пренебрежения индуктивностью обмотки якоря имеет вид, показанный на рис.40, где

Усилитель можно представить пропорциональным звеном с коэффициентом усиления K _у . В окончательном виде структурная схема САР напряжения генератора постоянного тока показана на рис.41.

Перечислите типичные схемы соединения звеньев САУ?
Как преобразовать цепь последовательно соединенных звеньев к одному звену?
Как преобразовать цепь параллельно соединенных звеньев к одному звену?
Как преобразовать обратную связь к одному звену?
Что называется прямой цепью САУ?
Что называется разомкнутой цепью САУ?
Как перенести сумматор через звено по ходу и против движения сигнала?
Как перенести узел через звено по ходу и против движения сигнала?
Как перенести узел через узел по ходу и против движения сигнала?
Как перенести сумматор через сумматор по ходу и против движения сигнала?
Как перенести узел через сумматор и сумматор через узел по ходу и против движения сигнала?
Что называется неэквивалентными участками линий связи в структурных схемах?
Каково назначение САР напряжения генератора постоянного тока?

Источник

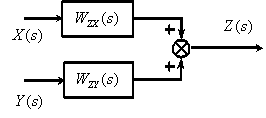
Получение эквивалентной передаточной функции системы.

Используем
систему MatLab
(Matrix Laboratory).

Для
того чтобы определить передаточную
функцию
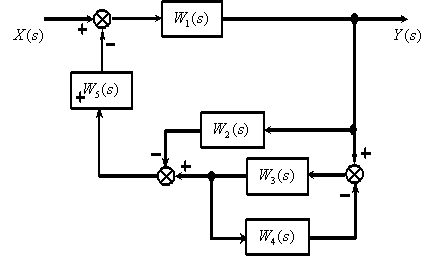
системы ее необходимо привести к
одноконтурному виду. Для этого используются
правила структурных преобразований.

Если
имеется структурная схема, которую
нужно преобразовать к одноконтурному
виду, то основные правила таких
преобразований следующие:

Если
имеется цепочка из последовательно
соединенных звеньев, то эквивалентная
передаточная функция такой цепочки
равна произведению передаточных
функций, входящих в эту цепочку.
Если
звенья соединены параллельно, то
эквивалентная передаточная функция
такой цепочки равна сумме передаточных
функций, входящих в цепочку.
Если
звено с передаточной функцией

охвачено обратной связью с передаточной
функцией

,
то эквивалентная передаточная функция
такой связки определяется по
следующей формуле:

В
данной формуле знак «+»
соответствует отрицательной обратной
связи, а знак «–»
– положительной.

Система
MatLab
представляет собой интерактивную
компьютерную систему для выполнения
инженерных и научных расчетов,
ориентированную на работу с массивами
данных. Для нахождения передаточной
функции системы нам понадобятся следующие
команды:

»W_1

2=
W₁*W₂
– преобразование последовательного
соединения звеньев;

»W_1

2=
W₁+W₂
– преобразование параллельного
соединения звеньев;

»
feedback
– преобразование встречно-параллельного
соединения звеньев.

»
W1=tf([4],[0.001 1]);

»
W2=tf([0.24 12],[1 0]);

»
W3=tf([6],[0.005 1]);

»
W4=tf([5],[0.04 1]);

»
W5=tf([1],[0.006 0]);

»
W6=tf([1],[65 0]);

»
W7=0.3;

»
W8=0.07;

»
W457 = feedback(W4*W5,W7);

»
W234578 = feedback(W2*W3*W457,W8);

»
Wsystem = feedback(W1*W234578*W6,1)

Transfer
function:

28.8
s + 1440

7.8e-008
s^6 + 9.555e-005 s^5 + 0.01843 s^4 + 1.008 s^3 + 131.9 s^2 + 1667 s +
1440

Используем
систему MathCAD.

MathCAD
– это специфический язык программирования,
который позволяет облегчить решение
математических уравнений. Для нахождения
передаточной функции в системе MathCAD,
необходимо воспользоваться следующим
уравнением:

Рис.
3. Получение передаточной функции в
системе MathCAD

Преобразуем
получившееся выражение, умножив числитель
и знаменатель передаточной функции на

.
Тогда передаточная функция системы
запишется следующим образом:

Эта
передаточная функция полностью совпадает
с передаточной функцией, полученной в
системе MatLab.

Таким
образом, эквивалентная передаточная
функция исследуемой системы имеет
следующий вид:

Определение фробениусовой канонической формы уравнений состояния.

Любое
звено динамической системы может быть
описано с помощью одного дифференциального
уравнения. Однако одной и той же
передаточной функции может соответствовать
множество структур моделей. Отсюда
вытекает необходимость выбора наиболее
рациональной модели при математическом
описании динамических систем. На практике
отдают предпочтение так называемым
каноническим формам. С инженерной точки
зрения канонические
формы
– это модели исходной системы, отличающиеся
простотой математического описания и
регулярной структурой. Это обеспечивается
переходом от исходного описания с
помощью замены переменных к такой
системе координат, что большинство
элементов матриц

в
новой системе координат становятся
равными нулю или единице.

Наиболее
распространенными в практике каноническими
формами являются:

каноническая
форма Фробениуса;
каноническая
форма Жордана.

Наибольший
интерес представляют канонические
формы, при которых структура матриц

имеет наиболее простой вид. Причем, при
приведении уравнений к канонической
форме простую структуру принимают две
матрицы из трех:

матрицы

управляемые канонические формы;
матрицы

наблюдаемые канонические формы.

Основу
реализации фробениусовой канонической
формы составляет цепочка последовательно
включенных интеграторов, охваченных
обратными связями, причем, коэффициенты
обратных связей совпадают с коэффициентами
характеристического полинома динамической
системы.

Для
формирования уравнения состояния во
фробениусовой канонической форме,
необходима передаточная функция
исследуемой системы:

Здесь

Запишем
дифференциальное уравнение исследуемой
системы:

Произведем
следующие замены:

Пусть

;

Тогда
из уравнения (16)
следует, что

Таким
образом,

Из
уравнения (17)
следует, что

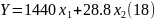
Объединим
получившиеся дифференциальные уравнения
и уравнение выхода (16)
в систему

Матричная
запись этих уравнений имеет следующий
вид:

(21)

Полученная
форма уравнений состояния носит название
фробениусовой канонической формы.

Построим
граф, соответствующий данной канонической
форме. Графы используются для наглядного
изображения зависимостей в САУ. Граф –
это условное графическое изображение
системы уравнений. Граф представляет
собой совокупность вершин (узлов) и
соединяющих их ветвей (дуг) с обозначением
направления передачи сигналов и их
пропускной способности. В данном случае
вершинами графа являются переменные

входной
сигнал

,
выходной сигнал

Связи между переменными изображаются
в виде дуг с проставленными коэффициентами
при переменных и направлениями передачи
сигнала.

Рис.
4. Граф системы для фробениусовой
канонической формы.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

4.1. Эквивалентные преобразования структурных схем

Структурная схема САУ в простейшем случае строится из элементарных динамических звеньев. Но несколько элементарных звеньев могут быть заменены одним звеном со сложной передаточной
функцией. Для этого существуют правила эквивалентного преобразования структурных схем. Рассмотрим возможные способы преобразований.

1. Последовательное соединение (рис.28) – выходная величина предшествующего звена подается на вход последующего. При этом можно записать:

y₁ = W₁y_o;
y₂ = W₂y₁;
…; y_n = W_ny_{n

– 1} = >

y_n = W₁W₂…..W_n.y_o
= W_эквy_o,

где.

2. Параллельно – согласное соединение (рис.29) – на вход каждого звена подается один и тот же сигнал, а выходные сигналы складываются. Тогда:

y = y₁ + y₂
+ … + y_n = (W₁
+ W₂ + … + W3)y_o
= W_эквy_o,

где .

То есть цепочка звеньев,
соединенных параллельно – согласно, преобразуется в звено с передаточной функцией,
равной сумме передаточных функций отдельных звеньев.

3. Параллельно – встречное соединение
(рис. 30а) – звено охвачено положительной или отрицательной обратной связью.
Участок цепи, по которому сигнал идет в противоположном направлении по отношению
к системе в целом (то есть с выхода на вход) называется цепью обратной связи
с передаточной функцией W_ос. При этом
для отрицательной ОС:

y = W_пu;
y₁ = W_осy;
u = y_o – y₁,

следовательно

y
= W_пy_o – W_пy₁
= W_пy_o – W_пW_ocy
= >

y(1 + W_пW_oc)
= W_пy_o = > y
= W_эквy_o,

где .

Аналогично: – для положительной ОС.

Если
W_oc = 1, то обратная связь называется
единичной (рис.30б), тогда W_экв = W_п
/(1 ± W_п).

Замкнутую систему называют одноконтурной, если при ее размыкании в какой либо точке получают цепочку из последовательно
соединенных элементов (рис.31а). Участок цепи, состоящий из последовательно соединенных звеньев, соединяющий точку приложения входного сигнала с точкой
съема выходного сигнала называется прямой цепью (рис.31б, передаточная
функция прямой цепи W_п = WoW₁W₂).
Цепь из последовательно соединенных звеньев, входящих в замкнутый контур называют
разомкнутой цепью (рис.46в, передаточная функция разомкнутой цепи W_p
= W₁W₂W₃W₄).

Исходя из приведенных выше способов эквивалентного преобразования структурных
схем, одноконтурная система может быть представлена одним звеном с передаточной
функцией: W_экв = W_п/(1 ± W_p)
– передаточная функция одноконтурной замкнутой системы с отрицательной ОС равна
передаточной функции прямой цепи, деленной на единицу плюс передаточная функция
разомкнутой цепи. Для положительной ОС в знаменателе знак минус. Если сменить
точку снятия выходного сигнала, то меняется вид прямой цепи. Так, если считать
выходным сигнал y₁ на выходе звена
W₁, то W_p
= WoW₁.
Выражение для передаточной функции разомкнутой цепи не зависит от точки снятия
выходного сигнала.

Замкнутые системы бывают одноконтурными
и многоконтурной (рис.32).Чтобы найти эквивалентную передаточную
функцию для данной схемы нужно сначала осуществить преобразование отдельных
участков.

Если многоконтурная система имеет перекрещивающиеся связи (рис.33), то для вычисления эквивалентной передаточной
функции нужны дополнительные правила:

4. При переносе сумматора через звено по ходу сигнала необходимо добавить звено
с передаточной функцией того звена, через которое переносится сумматор. Если
сумматор переносится против хода сигнала, то добавляется звено с передаточной
функцией, обратной передаточной функции звена, через которое переносим сумматор
(рис.34).

Так с выхода системы на рис.34а снимается сигнал

y₂
= (f + y_oW₁)W₂.

Такой же сигнал должен сниматься с выходов
систем на рис.34б:

y₂
= fW₂ + y_oW₁W₂
= (f + y_oW₁)W₂,

и
на рис.34в:

y₂
= (f(1/W₁) + y_o)W₁W₂
= (f + y_oW₁)W₂.

При подобных преобразованиях могут возникать неэквивалентные
участки линии связи (на рисунках они заштрихованы).

y₁
= y_oW₁.

Такой же сигнал снимается с выходов рис.35б:

y₁
= y_oW₁W₂/W₂
= y_oW₁

и
рис.35в:

y₁
= y_oW₁.

6.
Возможны взаимные перестановки узлов и сумматоров: узлы можно менять местами (рис.
36а); сумматоры тоже можно менять местами (рис.36б); при переносе узла через сумматор
необходимо добавить сравнивающий элемент (рис.36в: y = y₁
+ f₁ = > y₁
= y – f₁) или сумматор (рис.36г: y =
y₁ + f₁).

Во
всех случаях переноса элементов структурной схемы возникают неэквивалентные
участки линии связи, поэтому надо быть осторожным в местах съема выходного сигнала.

При эквивалентных преобразованиях одной и той же структурной схемы
могут быть получены различные передаточные функции системы по разным входам и
выходам. Так на рис.48 имеется два входа: по управляющему воздействию u
и возмущению f при одном выходе y. Такая схема может быть преобразована
к одному звену с двумя передаточными функциями W_uy
и W_fy.

4.2.
САР напряжения генератора постоянного тока

Для примера рассмотрим схему САР напряжения генератора постоянного тока (рис.37).

Для якорной цепи справедливо уравнение

Если принять, что , гдеj
– угол поворота вала двигателя, то

то есть

где – постоянная времени якорной
цепи; , – коэффициенты пропорциональнсти.

Если
учесть, что , где J – момент инерции
якоря, M – электромагнитный момент, М_с
– момент сторонних сил, то получим

Следовательно

= >

Здесь – электромеханическая постоянная времени;

; ; ; – коэффициенты пропорциональности;

, – передаточные функции по напряжению
и моменту сторонних сил.

Структурная схема двигателя постоянного тока показана на рис.39.

Усилитель можно представить пропорциональным звеном с коэффициентом усиления K_у. В окончательном виде структурная схема САР напряжения генератора постоянного тока показана на рис.41.

Вопросы

Перечислите типичные схемы соединения звеньев САУ?
Как преобразовать цепь последовательно
соединенных звеньев к одному звену?
Как преобразовать цепь параллельно
соединенных звеньев к одному звену?
Как преобразовать обратную связь к
одному звену?
Что называется прямой цепью САУ?
Что называется
разомкнутой цепью САУ?
Как перенести сумматор через звено по ходу и против
движения сигнала?
Как перенести узел через звено по ходу и против движения
сигнала?
Как перенести узел через узел по ходу и против движения сигнала?
Как
перенести сумматор через сумматор по ходу и против движения сигнала?
Как
перенести узел через сумматор и сумматор через узел по ходу и против движения
сигнала?
Что называется неэквивалентными участками линий связи в структурных
схемах?
Каково назначение САР напряжения генератора постоянного тока?

Далее…

Источник

4.1 Замена цепи из последовательно параллельно соединенных звеньев

Пример 1.

4.2. Замена цепи из параллельно соединенных звеньев эквивалентным звеном

Пример 2

4.3 Цепь с обратной связью

Пример 3

4.3.1. Замена звена с местной обратной связью на единичную

4.3.2. Перенос места обратной связи “вперед” или “назад”

4.4. Перенос точек суммирования “вперед” или “назад”

4.5. Перенос точек ветвления “вперед” или “назад”

Как найти эквивалентную передаточную функцию схемы

Как найти эквивалентную передаточную функцию схемы

Получение эквивалентной передаточной функции системы.

Определение фробениусовой канонической формы уравнений состояния.

Вам также может понравиться

Как найти угол в математике 5 класс

Как найти нотариуса в ставрополе

Как найти мастера тату по фото

Добавить комментарий Отменить ответ