Как найти эквивалентную схему электрической цепи

Введение

Решение задач – неотъемлемая часть обучения
физике, поскольку в процессе решения задач
происходит формирование и обогащение физических
понятий, развивается физическое мышление
учащихся и совершенствуется их навыки
применения знаний на практике.

В ходе решения задач могут быть поставлены и
успешно реализованы следующие дидактические
цели:

• Выдвижение проблемы и создание проблемной
  ситуации;
• Обобщение новых сведений;
• Формирование практических умений и навыков;
• Проверка глубины и прочности знаний;
• Закрепление, обобщение и повторение материала;
• Реализация принципа политехнизма;
• Развитие творческих способностей учащихся.

Наряду с этим при решении задач у школьников
воспитываются трудолюбие, пытливость ума,
смекалка, самостоятельность в суждениях, интерес
к учению, воля и характер, упорство в достижении
поставленной цели. Для реализации перечисленных
целей особенно удобно использовать
нетрадиционные задачи.

§1. Задачи по расчету электрических
цепей постоянного тока

По школьной программе на рассмотрение данной
темы очень мало отводится времени, поэтому
учащиеся более или менее успешно овладевают
методами решения задач данного типа. Но часто
такие типы задач встречаются олимпиадных
заданиях, но базируются они на школьном курсе.

К таким, нестандартным задачам по расчету
электрических цепей постоянного тока можно
отнести задачи, схемы которых:

1) содержат большое число элементов –
резисторов или конденсаторов;

2) симметричны;

3) состоят из сложных смешанных соединений
элементов.

В общем случае всякую цепь можно рассчитать,
используя законы Кирхгофа. Однако эти законы не
входят в школьную программу. К тому же, правильно
решить систему из большого числа уравнений со
многими неизвестными под силу не многим учащимся
и этот путь не является лучшим способом тратить
время. Поэтому нужно уметь пользоваться
методами, позволяющими быстро найти
сопротивления и емкости контуров.

§2. Метод эквивалентных схем

Метод эквивалентных схем заключается в том, что
исходную схему надо представить в виде
последовательных участков, на каждом из которых
соединение элементов схемы либо
последовательно, либо параллельно. Для такого
представления схему необходимо упростить. Под
упрощением схемы будем понимать соединение или
разъединение каких-либо узлов схемы, удаление
или добавление резисторов, конденсаторов,
добиваясь того, чтобы новая схема из
последовательно и параллельно соединенных
элементов была эквивалентна исходной.

Эквивалентная схема – это такая схема, что при
подаче одинаковых напряжений на исходную и
преобразованную схемы, ток в обеих цепях будет
одинаков на соответствующих участках. В этом
случае все расчеты производятся с
преобразованной схемой.

Чтобы начертить эквивалентную схему для цепи
со сложным смешанным соединением резисторов
можно воспользоваться несколькими приемами. Мы
ограничимся рассмотрением в подробностях лишь
одного из них – способа эквипотенциальных узлов.

Этот способ заключается в том, что в
симметричных схемах отыскиваются точки с
равными потенциалами. Эти узлы соединяются между
собой, причем, если между этими точками был
включен какой-то участок схемы, то его
отбрасывают, так как из-за равенства потенциалов
на концах ток по нему не течет и этот участок
никак не влияет на общее сопротивление схемы.

Таким образом, замена нескольких узлов равных
потенциалов приводит к более простой
эквивалентной схеме. Но иногда бывает
целесообразнее обратная замена одного узла

несколькими узлами с равными потенциалами, что
не нарушает электрических условий в остальной
части.

Рассмотрим примеры решения задач эти методом.

З а д а ч а №1

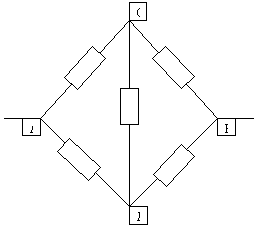
Рассчитать сопротивление между точками А и В
данного участка цепи. Все резисторы одинаковы и
их сопротивления равны r.

Решение:

В силу симметричности ветвей цепи точки С И Д
являются эквипотенциальными. Поэтому резистор
между ними мы можем исключить. Эквипотенциальные
точки С и Д соединяем в один узел. Получаем очень
простую эквивалентную схему:

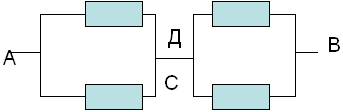
Сопротивление которой равно:

RАВ=Rac+Rcd=r*r/r*r+r*r/r+r=r.

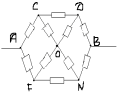
З а д а ч а № 2

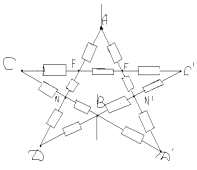
Решение:

В точках F и F` потенциалы равны, значит
сопротивление между ними можно отбросить.
Эквивалентная схема выглядит так:

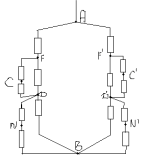
Сопротивления участков DNB;F`C`D`; D`, N`, B`; FCD равны
между собой и равны R1:

1/R1=1/2r+1/r=3/2r

R1=2/3*r

С учетом этого получается новая эквивалентная
схема:

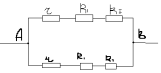
Ее сопротивление и сопротивление исходной цепи
RАВ равно:

1/RАВ=1/r+R1+R1+1/r+R1+R1=6/7r

RАВ=(7/6)*r.

З а д а ч а № 3.

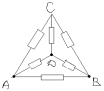
Решение:

Точки С и Д имеют равные потенциалы.
Исключением сопротивление между ними. Получаем
эквивалентную схему:

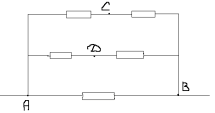
Искомое сопротивление RАВ равно:

1/RАВ=1/2r+1/2r+1/r=2/r

RАВ=r/2.

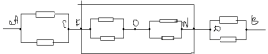
З а д а ч а № 4.

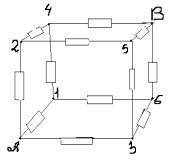
Решение:

Как видно из схемы узлы 1,2,3 имеют равные
потенциалы. Соединим их в узел 1. Узлы 4,5,6 имеют
тоже равные потенциалы- соединим их в узел 2.
Получим такую эквивалентную схему:

Сопротивление на участке А-1, R 1-равно
сопротивлению на участке 2-В,R3 и равно:

R1=R3=r/3

Сопротивление на участке 1-2 равно: R2=r/6.

Теперь получается эквивалентная схема:

Общее сопротивление RАВ равно:

RАВ= R1+ R2+ R3=(5/6)*r.

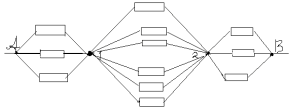
З а д а ч а № 5.

Решение:

Точки C и F-эквивалентные. Соединим их в один
узел. Тогда эквивалентная схема будет иметь
следующий вид:

Сопротивление на участке АС:

Rас=r/2

Сопротивление на участке FN:

R_FN =

Сопротивление на участке DB:

R_DB =r/2

Получается эквивалентная схема:

Искомое общее сопротивление равно:

R_AB= r.

Задача №6

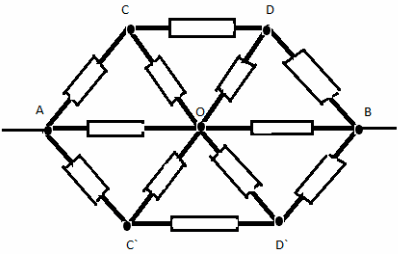
Решение:

Заменим общий узел О тремя узлами с равными
потенциалами О, О₁ , О₂. Получим
эквивалентную систему:

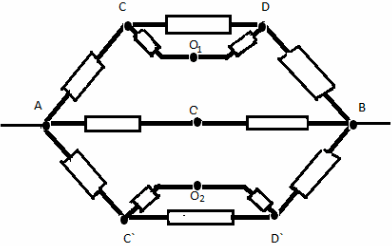
Сопротивление на участке ABCD:

R₁=(3/2)*r

Сопротивление на участке A`B`C`D`:

R₂= (8/3)*r

Сопротивление на участке ACВ

R₃ = 2r.

Получаем эквивалентную схему:

Искомое общее сопротивление цепи R_AB
равно:

R_AB= (8/10)*r.

Задача №7.

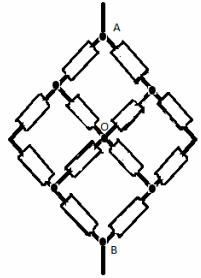
Решение:

“Разделим” узел О на два эквипотенциальных
угла О₁ и О₂. Теперь схему можно
представить, как параллельные соединение двух
одинаковых цепей. Поэтому достаточно подробно
рассмотреть одну из них:

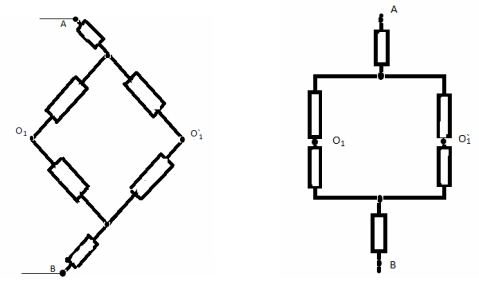
Сопротивление этой схемы R₁ равно:

R₁ = 3r

Тогда сопротивление всей цепи будет равно:

R_AB = (3/2)*r

З а д а ч а №8

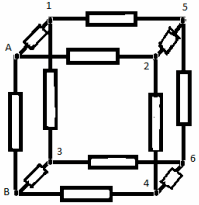
Решение:

Узлы 1 и 2 – эквипотенциальные, поэтому соединим
их в один узел I. Узлы 3 и 4 также эквипотенциальные
– соединимих в другой узел II. Эквивалентная
схема имеет вид:

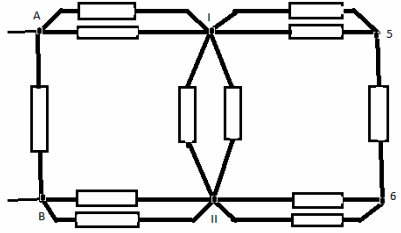
Сопротивление на участке A- I равно
сопротивлению на участке B- II и равно:

R_I =

Сопротивление участка I-5-6- II равно:

R_II = 2r

Cопротивление участка I- II равно:

R_III =

Получаем окончательную эквивалентную схему:

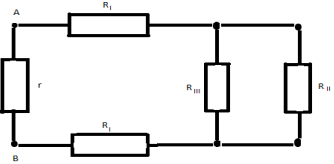
Искомое общее сопротивление цепи R_AB=(7/12)*r.

З а д а ч а №9

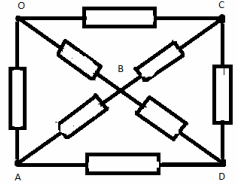
В ветви ОС заменим сопротивление на два
параллельно соединенных сопротивления по 2r.
Теперь узел С можно разделить на 2
эквипотенциальных узла С₁ и С₂.
Эквивалентная схема в этом случае выглядит так:

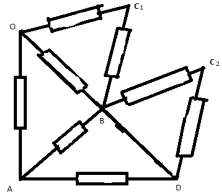
Сопротивление на участках ОС_IB и DC_IIB
одинаковы и равны, как легко подсчитать 2r. Опять
чертим соответствующую эквивалентную схему:

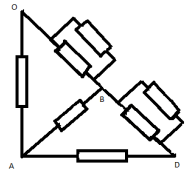
Сопротивление на участке AOB равно
сопротивлению на участке ADB и равно (7/4)*r. Таким
образом получаем окончательную эквивалентную
схему из трех параллельно соединенных
сопротивлений:

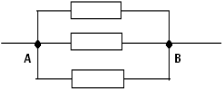
Ее общее сопротивление равно R_AB= (7/15)*r

З а д а ч а № 10

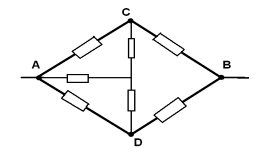
Точки СОD имеют равные потенциалы – соединим их
в один узел О^I .Эквивалентная схема
изображена на рисунке :

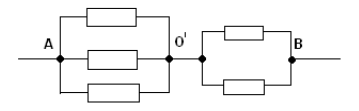
Сопротивление на участке А О^I равно . На участке
О^IВ сопротивление равно .Получаем совсем
простую эквивалентную схему:

ЕЕ сопротивление равно искомому общему
сопротивлению

R_AB=(5/6)*r

Задачи № 11 и № 12 решаются несколько иным
способом, чем предыдущие. В задаче №11 для ее
решения используется особое свойство
бесконечных цепей, а в задаче № 12 применяется
способ упрощения цепи.

Задача № 11

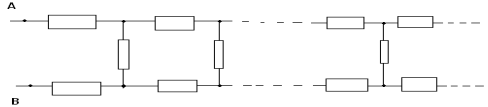
Решение

Выделим в этой цепи бесконечно повторяющееся
звено, оно состоит в данном случае из трех первых
сопротивлений. Если мы отбросим это звено, то
полное сопротивление бесконечной цепи R не
измениться от этого , так как получится точно
такая же бесконечная цепь. Так же ничего не
измениться, если мы выделенное звено подключим
обратно к бесконечному сопротивлению R, но при
этом следует обратить внимание , что часть звена
и бесконечная цепь сопротивлением R соединены
параллельно. Таким образом получаем
эквивалентную схему :

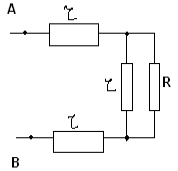
Получается уравнения

R_AB=2ч +

R_AB = R

Решая систему этих уравнений, получаем:

R=ч (1+ ).

§3. Обучение решению задач по расчету
электрических цепей способом эквипотенциальных
узлов

Задача – это проблема, для разрешения которой
ученику потребуются логические рассуждения и
выводы. Строящиеся на основе законов и методов
физики. Таким образом, с помощью задач происходит
активизация целенаправленного мышления
учащихся.

В то же время. Теоретические знания можно
считать усвоенными только тогда, когда они
удачно применяются на практике. Задачи по физике
описывают часто встречающиеся в жизни и на
производстве проблемы, которые могут быть решены
с помощью законов физики и, если ученик успешно
решает задачи, то можно сказать, что он хорошо
знает физику.

Для того, чтобы ученики успешно решали задачи,
недостаточно иметь набор методов и способов
решения задач, необходимо еще специально учить
школьников применению этих способов.

Рассмотрим план решения задач по расчету
электрических цепей постоянного тока методом
эквипотенциальных узлов.

1. Чтение условия.
2. Краткая запись условия.
3. Перевод в единицы СИ.
4. Анализ схемы:
1. установить, является ли схема симметричной;
2. установить точки равного потенциала;
3. выбрать, что целесообразнее сделать –
   соединить точки равных потенциалов или же,
   наоборот, разделить одну точку на несколько
   точек равных потенциалов;
4. начертить эквивалентную схему;
5. найти участки только с последовательным или
   только с параллельным соединением и рассчитать
   общее сопротивление на каждом участке по законам
   последовательного и параллельного соединения;
6. начертить эквивалентную схему, заменяя участки
   соответствующими им расчетными сопротивлениями;
7. пункты 5 и 6 повторять до тех пор, пока не
   останется одно сопротивление, величина которого
   и будет решением задачи.
5. Анализ реальности ответа.

Подробнее об анализе схемы

а) установить, является ли схема симметричной.

Определение. Схема симметрична, если одна ее
половина является зеркальным отражением другой.
Причем симметрия должна быть не только
геометрической, но должны быть симметричны и
численные значения сопротивлений или
конденсаторов.

Примеры:

1)

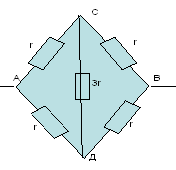
Схема симметричная, так как ветви АСВ и АДВ
симметричны геометрически и отношение
сопротивления на одном участке АС:АД=1:1 такое же,
как и на другом участке СД:ДВ=1:1.

2)

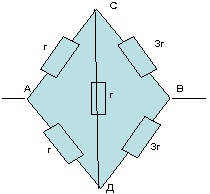
Схема симметричная, так как отношение
сопротивлений на участке АС:АД=1:1 такое же, как и
на другом участке СВ:ДВ=3:3=1:1

3)

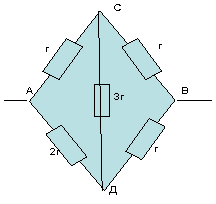
Схема не симметрична, так как отношения
сопротивлений численно

не симметричны -1:2 и 1:1.

б) установить точки равных потенциалов.

Пример:

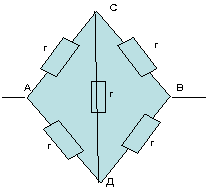
Из соображений симметрии делаем вывод, что в
симметричных точках потенциалы равны. В данном
случае симметричными точками являются точки С и
Д. Таким образом, точки С и Д – эквипотенциальные
точки.

в) выбрать, что целесообразно сделать –
соединить точки равных потенциалов или же,
наоборот, разделить одну точку на несколько
точек равных потенциалов.

Мы видим в этом примере, что между точками
равных потенциалов С и Д включено сопротивление,
по которому ток не будет течь. Следовательно, мы
можем отбросить это сопротивление, а точки С и Д
соединить в один узел.

г) начертить эквивалентную схему.

Чертим эквивалентную схему. При этом получаем
схему с соединенными в одну точку точками С и Д.

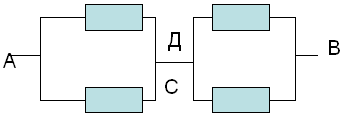
д) найти участки только с последовательным или
только с параллельным соединением и рассчитать
общее сопротивление на каждом таком участке по
законам последовательного и параллельного
соединения.

Из полученной эквивалентной схемы видно, что на
участке АС мы имеем два параллельно соединенных
резистора. Их общее сопротивление находится по
закону параллельного соединения:

1/ Rобщ=1/R1+1/R2+1/R3+…

Таким образом 1/RAC=1/r+1/r=2/r,откуда RAC= r/2.

На участке СВ картина аналогичная:

1/RCB= 1/r+1/r =2/r, откуда RCB=r/2.

е)начертить эквивалентную схему, заменяя
участки соответствующими им расчетными
сопротивлениями.

Чертим эквивалентную схему подставляя в нее
рассчитанные сопротивления участков RAC и RCB:

ж)пункты д) и е) повторять до тех пор, пока
останется одно сопротивление, величина которого
и будет решением задачи.

Повторяем пункт д): на участке АВ имеем два
последовательно соединенных сопротивления. Их
общее сопротивление находим по закону
последовательного соединения:

Rобщ= R1+R2+R3+… то есть, RAB=RAC+RCB = r/2+r/2 =2r/2 = r.

Повторяем пункт е): чертим эквивалентную
схему:

Мы получили схему с одним сопротивлением,
величина которого равна сопротивлению исходной
схемы. Таким образом, мы получили ответ RAB = r.

Далее, для проверки усвоения данного материала
можно учащимся предложить задания для
самостоятельной работы, взятые из
дидактического материала. (см. приложение)

Литература

1. Балаш. В.А. задачи по физике и методы их решения. –
   М: Просвещение,1983.
2. Лукашик В.И. Физическая олимпиада.- М:
   Просвещение, 2007
3. Усова А.В., Бобров А.А. Формирование учебных
   умений и навыков учащихся на уроках физики.- М:
   Просвещение,1988
4. Хацет А. Методы расчета эквивалентных схем
   //Квант.
5. Чертов А. Г. Задачник по физике. – М.: Высшая
   школа,1983
6. Зиятдинов Ш.Г., Соловьянюк С.Г. (методические
   рекомендации) г. Бирск,1994г
7. Марон А.Е., Марон Е.А. Физика. Дидактические
   материалы. Москва, “Дрофа”, 2004г

Главная
→
Примеры решения задач ТОЭ
→
Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Основными законами, определяющими расчет электрической цепи, являются законы Кирхгофа.

На основе законов Кирхгофа разработан ряд практических методов расчета электрических цепей постоянного тока, позволяющих сократить вычисления при расчете сложных схем.

Существенно упростить вычисления, а в некоторых случаях и снизить трудоемкость расчета, возможно с помощью эквивалентных преобразований схемы.

Преобразуют параллельные и последовательные соединения элементов, соединение «звезда» в эквивалентный «треугольник» и наоборот. Осуществляют замену источника тока эквивалентным источником ЭДС. Методом эквивалентных преобразований теоретически можно рассчитать любую цепь, и при этом использовать простые вычислительные средства. Или же определить ток в какой-либо одной ветви, без расчета токов других участков цепи.

В данной статье по теоретическим основам электротехники рассмотрены примеры расчета линейных электрических цепей постоянного тока с использованием метода эквивалентных преобразований типовых схем соединения источников и потребителей энергии, приведены расчетные формулы.

Решение задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований

---

Задача 1. Для цепи (рис. 1), определить эквивалентное сопротивление относительно входных зажимов a−g, если известно: R₁ = R₂ = 0,5 Ом, R₃ = 8 Ом, R₄ = R₅ = 1 Ом, R₆ = 12 Ом, R₇ = 15 Ом, R₈ = 2 Ом, R₉ = 10 Ом, R₁₀= 20 Ом.

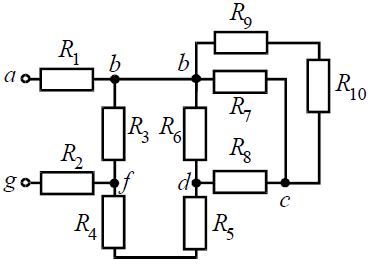
Рис. 1

Решение

Начнем эквивалентные преобразования схемы с ветви наиболее удаленной от источника, т.е. от зажимов a−g:

---

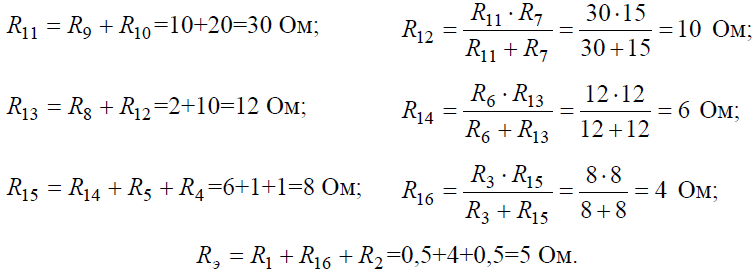
Задача 2. Для цепи (рис. 2, а), определить входное сопротивление если известно: R₁ = R₂ = R₃ = R₄= 40 Ом.

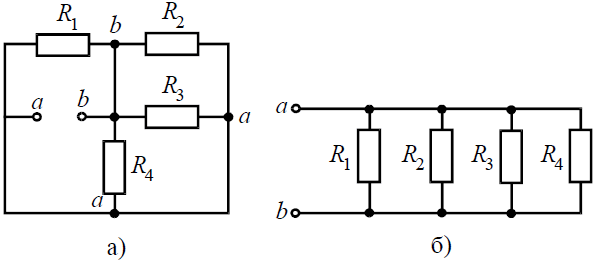Рис. 2

Решение

Исходную схему можно перечертить относительно входных зажимов (рис. 2, б), из чего видно, что все сопротивления включены параллельно. Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивленияможно воспользоваться формулой:

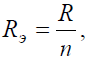где R — величина сопротивления, Ом;

n — количество параллельно соединенных сопротивлений.

---

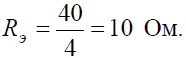
Задача 3. Определить эквивалентное сопротивление относительно зажимов a–b, если R₁ = R₂ = R₃ = R₄ = R₅ = R₆ = 10 Ом (рис. 3, а).

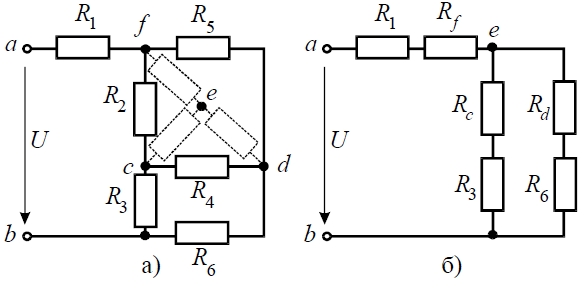
Рис. 3

Решение

Преобразуем соединение «треугольник» f−d−c в эквивалентную «звезду». Определяем величины преобразованных сопротивлений (рис. 3, б):

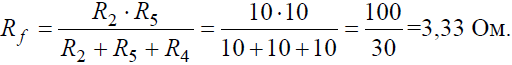По условию задачи величины всех сопротивлений равны, а значит:

На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно:

И тогда эквивалентное сопротивление исходной схемы представляет последовательное соединение сопротивлений:

---

Задача 4. В заданной цепи (рис. 4, а) определить методом эквивалентных преобразований входные сопротивления ветвей a−b, c–d и f−b, если известно, что: R₁ = 4 Ом, R₂ = 8 Ом, R₃ =4 Ом, R₄ = 8 Ом, R₅ = 2 Ом, R₆ = 8 Ом, R₇ = 6 Ом, R₈ =8 Ом.

Решение

Для определения входного сопротивления ветвей исключают из схемы все источники ЭДС. При этом точки c и d, а также b и f соединяются накоротко, т.к. внутренние сопротивления идеальных источников напряжения равны нулю.

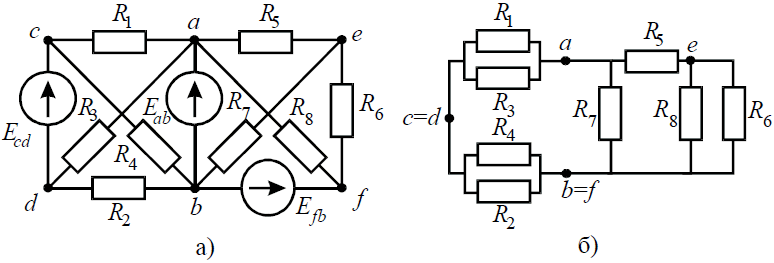
Рис. 4

Ветвь a−b разрывают, и т.к. сопротивление R_a–b = 0, то входное сопротивление ветви равно эквивалентному сопротивлению схемы относительно точек a и b (рис. 4, б):

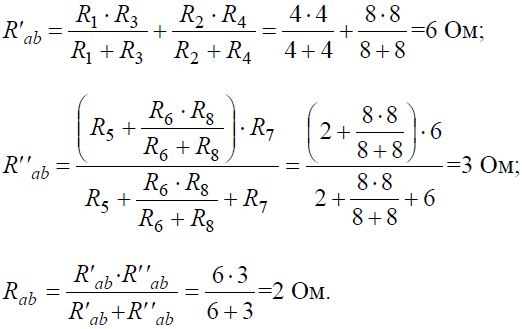
Аналогично методом эквивалентных преобразований определяются входные сопротивления ветвей R_cd и R_bf. Причем, при вычислении сопротивлений учтено, что соединение накоротко точек a и b исключает ( «закорачивает») из схемы сопротивления R₁, R₂, R₃, R₄ в первом случае, и R₅, R₆, R₇, R₈ во втором случае.

---

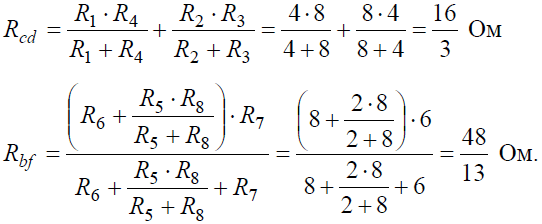
Задача 5. В цепи (рис. 5) определить методом эквивалентных преобразований токи I₁, I₂, I₃ и составить баланс мощностей, если известно: R₁ = 12 Ом, R₂ = 20 Ом, R₃ = 30 Ом, U = 120 В.

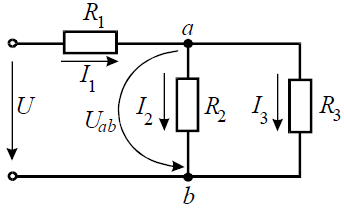
Рис. 5

Решение

Эквивалентное сопротивлениедля параллельно включенных сопротивлений:

Эквивалентное сопротивление всей цепи:

американские сигареты парламент.

Ток в неразветвленной части схемы:

Напряжение на параллельных сопротивлениях:

Токи в параллельных ветвях:

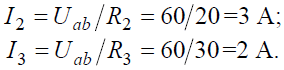
Баланс мощностей:

---

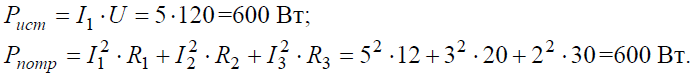
Задача 6. В цепи (рис. 6, а), определить методом эквивалентных преобразований показания амперметра, если известно: R₁ = 2 Ом, R₂ = 20 Ом, R₃ = 30 Ом, R₄ = 40 Ом, R₅ = 10 Ом, R₆ = 20 Ом, E = 48 В. Сопротивление амперметра можно считать равным нулю.

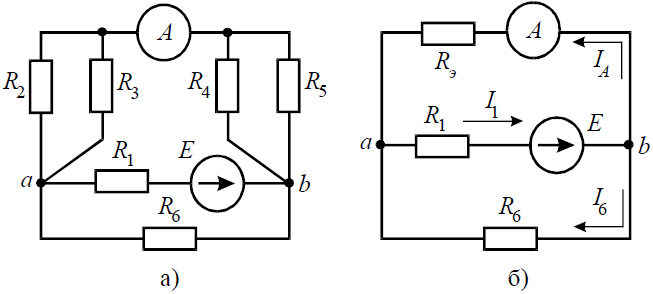
Рис. 6

Решение

Если сопротивления R₂, R₃, R₄, R₅ заменить одним эквивалентным сопротивлением R_Э, то исходную схему можно представить в упрощенном виде (рис. 6, б).

Величина эквивалентного сопротивления:

проститутки академическая. Смотри здесь строительство и ремонт деревянного дома.

Преобразовав параллельное соединение сопротивлений R_Э и R₆ схемы (рис. 6, б), получим замкнутый контур, для которого по второму закону Кирхгофа можно записать уравнение:

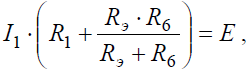
откуда ток I₁:

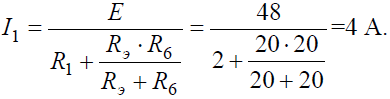
Напряжение на зажимах параллельных ветвей U_ab выразим из уравнения по закону Ома для пассивной ветви, полученной преобразованием R_Э и R₆:

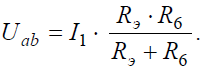
Тогда амперметр покажет ток:

---

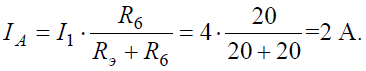
Задача 7. Определить токи ветвей схемы методом эквивалентных преобразований (рис. 7, а), если R₁ = R₂ = R₃ = R₄ = 3 Ом, J = 5 А, R₅ = 5 Ом.

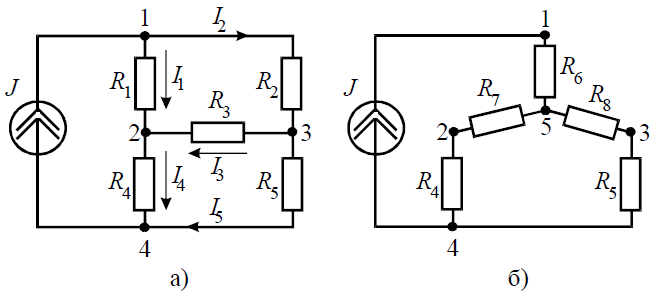
Рис. 7

Решение

Преобразуем «треугольник» сопротивлений R₁, R₂, R₃ в эквивалентную «звезду» R₆, R₇, R₈ (рис. 7, б) и определим величины полученных сопротивлений:

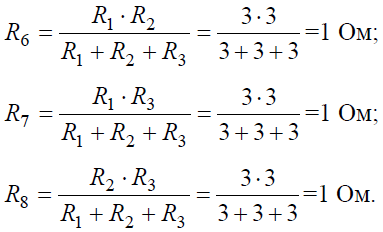
Преобразуем параллельное соединение ветвей между узлами 4 и 5

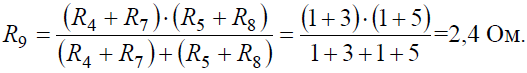
Ток в контуре, полученном в результате преобразований, считаем равным току источника тока J, и тогда напряжение:

И теперь можно определить токи I₄ и I₅:

Возвращаясь к исходной схеме, определим напряжение U₃₂ из уравнения по второму закону Кирхгофа:

Тогда ток в ветви с сопротивлением R₃ определится:

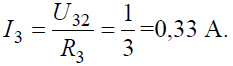
Величины оставшихся неизвестными токов можно определить из уравнений по первому закону Кирхгофа для узлов 3 и 1:

---

Электронная версия статьи Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Примеры решения задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Расчет электрических цепей постоянного тока методом эквивалентных преобразований

---

Метод эквивалентных преобразований

Содержание:

Преобразование схем электрических цепей:

При расчете электрических цепей часто возникает целесообразность преобразования схем этих цепей в более простые и удобные для расчета. Так, при одном или нескольких источниках электрической энергии в ряде случаев удается преобразовать электрическую схему в одноконтурную или в схему с двумя узлами, что весьма упрощает последующий расчет.

Описываемые ниже приемы преобразования схем электрических цепей применимы для цепей постоянного и переменного тока-, ради общности изложения они приводятся в комплексной записи.

Одним из основных видов преобразования электрических схем, часто применяемых на практике, является преобразование схемы со смешанным соединением элементов. Смешанное соединение элементов представляет собой сочетание более простых соединений — последовательного и параллельного, рассмотрению которых и посвящен данный параграф.

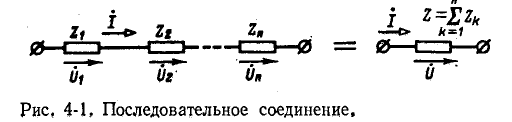
Последовательное соединение

На рис. 4-1 изображена ветвь электрической цепи, в которой последовательно включены комплексные сопротивления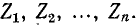

Напряжения на отдельных участках цепи обозначены через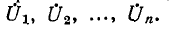

По второму закону Кирхгофа

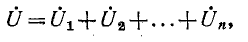
или, что то же,

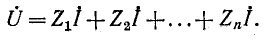
Сумма комплексных сопротивлений всех последовательно соединенных участков цепи

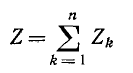
называется эквивалентным комплексным сопротивлением.

Если мнимые части комплексов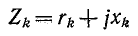

представляют собой сопротивления одинакового характера— индуктивного или емкостного (рис. 4-2), то эквивалентное комплексное сопротивление Z находится в результате

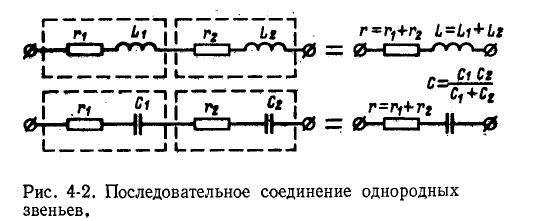
арифметического сложения в отдельности сопротивлений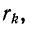 индуктивностей 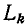или величин 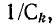обратных емкостям:

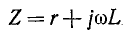
или

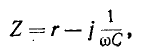
где

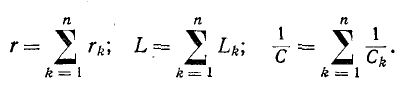
Ток в цепи равен:

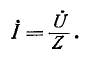
Напряжения на участках цепи, соединенных последовательно, относятся как комплексные сопротивления этих участков: напряжение на k-м участке равно произведению суммарного напряжения 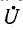на отношение комплексного сопротивления 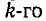участка к эквивалентному комплексному сопротивлению цепи:

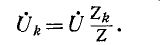
Приведенные выше формулы справедливы при любых значениях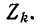

Параллельное соединение

На рис. 4-3 изображена схема электрической цепи с двумя узлами. Между этими узлами параллельно соединены ветви с комплексными проводимостями 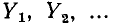 Напряжение на всех ветвях одинаковое, равное

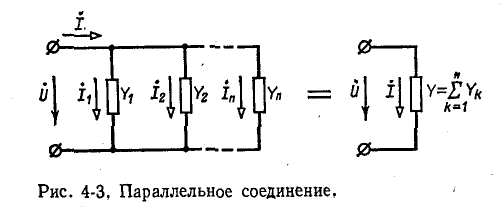
Токи в ветвях обозначены через

По первому закону Кирхгофа

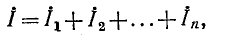
или, что то же,

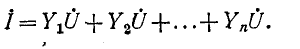
Сумма комплексных проводимостей всех ветвей, соединенных параллельно,

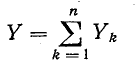
называется эквивалентной комплексной проводимостью.

Если мнимые части комплексов 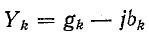представляют собой проводимости одинакового характера — емкостного или индуктивного (рис. 4-4), то эквивалентная

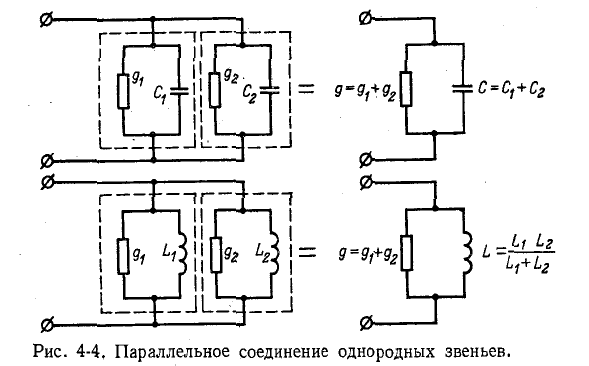
комплексная проводимость Y находится в результате арифметического сложения отдельных активных проводимостей 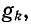, емкостей 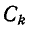или величин 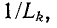обратных индуктивностям:

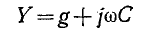
или

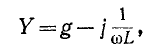
где

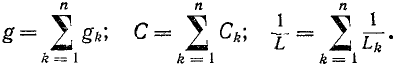
Суммарный ток в цепи равен:

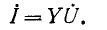
Токи в ветвях относятся, как их комплексные проводимости: ток в 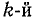 ветви равен произведению суммарного тока всех ветвей на отношение комплексной проводимости 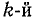ветви к эквивалентной комплексной проводимости:

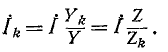
Данным выражением особенно удобно пользоваться при n > 2. При этом значения 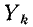могут быть любыми.

В случае параллельного соединения двух ветвей (n = 2) обычно пользуются выражениями, в которые входят сопротивления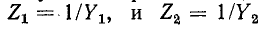 ветвей; эквивалентное комплексное сопротивление равно: v 1    1    Z,Z2

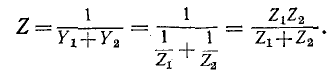
Токи в параллельных ветвях:

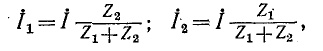
t. e. ток одной из двух параллельных ветвей равен суммарному току, умноженному на сопротивление другой ветви и деленному на сумму сопротивлений обеих ветвей.
 

Смешанное соединение

Электрические схемы, имеющие смешанное соединение, могут быть преобразованы в более простую электрическую схему путем замены параллельных ветвей одной ветвью и соответственно последовательно соединенных участков цепи — одним участком.

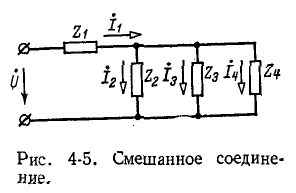
На рис. 4-5 показан пример электрической цепи со смешанным соединением. Эта схема легко приводится к одноконтурной. Первоначально вычисляется эквивалентная комплексная проводимость параллельных ветвей; затем находится величина, обратная проводимости, т. е. общее комплексное сопротивление параллельных ветвей; найденное комплексное сопротивление суммируется с комплексным сопротивлением последовательно включенного участка. Полученное суммарное

комплексное сопротивление эквивалентно сопротивлению исходной цепи со смешанным соединением.

Расчетные выражения для рассматриваемого случая будут следующие:

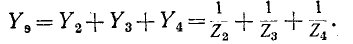
Суммарное комплексное сопротивление всей цепи равно:

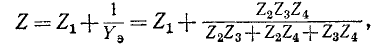
а суммарный ток

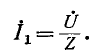
Токи в ветвях относятся, как комплексные проводимости ветвей:

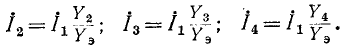
Таким юбразом, многоконтурная электрическая схема со смешанным соединением приводится к одноконтурной,

имеющей суммарное комплексное сопротивление Z или соответственно суммарную комплексную проводимость Y. Распределение токов и напряжений в смешанной цепи подчиняется правилам, указанным в предыдущем параграфе.

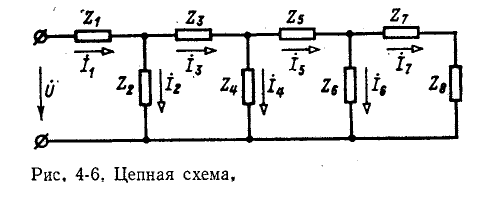
Описанный выше порядок преобразования схемы и нахождения распределения токов принципиально применим и для так называемой цепной схемы, показанной на рис. 4-6. Просуммировав комплексные сопротивления 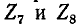в последней ветви, найдем комплексную проводимость ветви, которую алгебраически сложим с 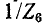и получим суммарную комплексную проводимость двух последних ветвей; вычислив обратную величину, т. е. комплексное сопротивление, прибавим к ней 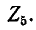Продолжая

таким образом дальше, получим в итоге результирующее комплексное сопротивление цепи и соответственно суммарный ток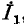 который может быть путем последовательных вычислений распределен между всеми ветвями сложной цепи.

Однако такой способ расчета цепной схемы является достаточно трудоемким и утомительным. Более целесообразно в этом случае воспользоваться другим методом, который известен под названием метода подобия или единичного тока.

Задавшись током в последней ветви, равным единице 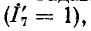находим напряжение на комплексном сопротивлении 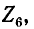равное 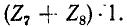При этом ток  .

Следовательно,

Прибавив к напряжению на падение напряжения от тока в комплексном сопротивлении 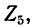получим напряжение на 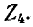Продолжая таким образом дальше, найдем в конечном итоге ток 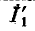и напряжение 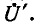Ввиду того что ток 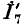был произвольно выбран равным единице, полученное напряжение не будет равно заданному напряжению 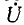на выводах цепи. Для нахождения действительного распределения токов в схеме необходимо все вычисленные значения токов умножить на отношение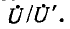
 

Эквивалентные участки цепи с последовательным и параллельным соединениями

Обозначим комплексное сопротивление участка цепи, состоящего из двух последовательно соединенных элементов, через 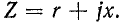Комплексная проводимость данного участка цепи равна 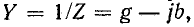причем активная и реактивная проводимости:

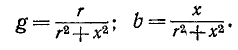
Если два элемента с проводимостями g и b, вычисленными по этим формулам, соединить параллельно, то суммарная комплексная проводимость будет равна Y и соответственно комплексное сопротивление будет равно Z,

Такие две цепи с последовательным и параллельным соединениями, имеющие одинаковые сопротивления на выводах, называются эквивалентными.

Ввиду того что реактивное сопротивление х, входящее в расчетные формулы, в общем случае зависит от частоты, условие эквивалентности этих цепей выполняется только при той частоте, для которой вычислено х.

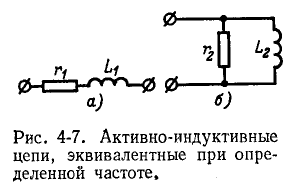
Пусть, например, задана схема с последовательным соединением сопротивления 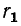и индуктивности 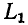(рис. 4-7, а). Преобразуем ее в схему с параллельным соединением элементов (рис. 4-7, б).

Активная и реактивная проводимости исходной цепи:

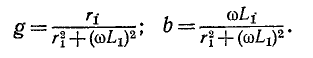
Из условия эквивалентности цепей следует, что параметры новой цепи будут:

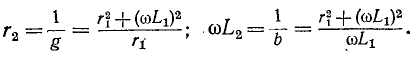
Вычислив по этим формулам 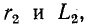получим схему цепи, эквивалентной исходной при данной частоте 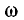При других значениях частоты 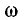параметры 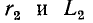будут иметь другие значения, следовательно эквивалентность цепей нарушится.

При 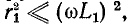например, при достаточно высокой частоте:

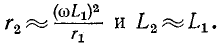
Если исходной является схема рис. 4-7, б и заданными параметрами являются 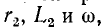то параметры эквивалентной цепи (рис. 4-7, а) определятся из выражений:

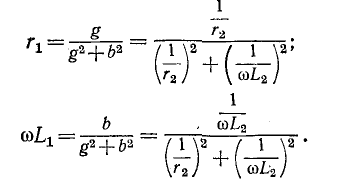
Из полученных выражений видно, что числовые значения 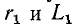эквивалентной цепи зависят от частоты.

Условия эквивалентности для цепей с последовательным и параллельным соединением сопротивления и емкости имеют вид:

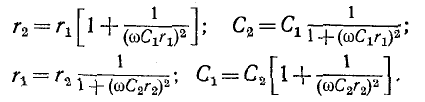
При достаточно высокой частоте 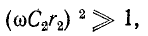и тогда

 

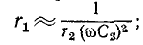
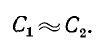
Преобразование треугольника в эквивалентную звезду

Преобразованием треугольника в эквивалентную звезду называется такая замена части цепи, соединенной по схеме треугольником, цепью, соединенной по схеме звезды, при которой токи и напряжения в остальной части цепи

сохраняются неизменными. Иначе говоря, эквивалентность треугольника и звезды понимается в том смысле, что при одинаковых напряжениях между одноименными выводами токи, входящие в одноименные выводы, одинаковы. Это равносильно тому, что мощности в этих цепях одинаковы.

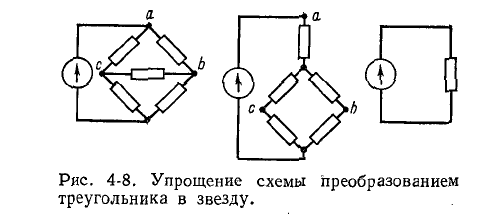
На рис. 4-8 показан случай, когда преобразование треугольника в эквивалентную звезду дает возможность преобразовать многоконтурную схему в одноконтурную.

Для вывода расчетных выражений, служащих для преобразования треугольника в эквивалентную звезду, ниже приняты следующие обозначения (рис. 4-9):

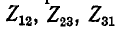• — сопротивления сторон треугольника;
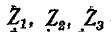• — сопротивления лучей звезды;
• — токи, подходящие к выводам 1, 2, 3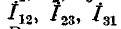
• — Токи в ветвях треугольника.

Выразим токи в ветвях треугольника через приходящие токи.

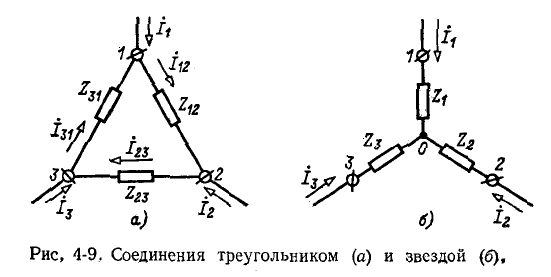
По второму закону Кирхгофа сумма напряжений в контуре треугольника равна нулю:

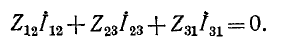
По первому закону Кирхгофа для узлов 2 и 1

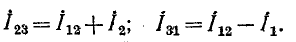
Решение этих уравнений относительно 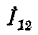Дает:

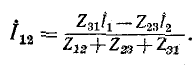
Напряжение между выводами 1 и 2 схемы рис. 4-9, а будет:

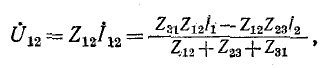
a в схеме рис. 4-9, б оно равно:

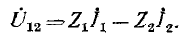
Для эквивалентности необходимо равенство напряжений 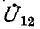при всяких токах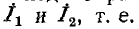

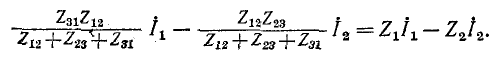
Это возможно при условии:

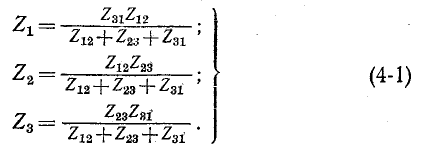
Третье выражение получается в результате круговой замены индексов.

Итак, комплексное сопротивление луча звезды равно произведению комплексных сопротивлений прилегающих сторон треугольника, деленному на сумму комплексных сопротивлений трех сторон треугольника.

Выше было получено выражение для тока в стороне 1—2 треугольника в зависимости от токов 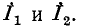Круговой заменой индексов можно получить токи в двух других сторонах треугольника:

 

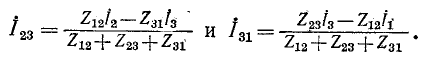
Преобразование звезды в эквивалентный треугольник

В расчетах также возникает необходимость замены звезды эквивалентным треугольником. На рис. 4-10 показан, например, случай, когда такая замена позволяет

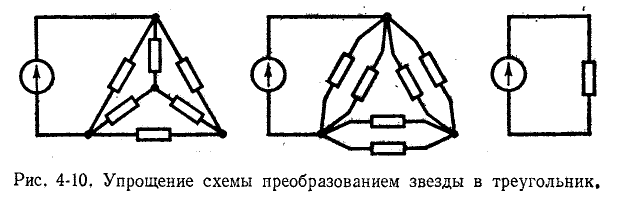
преобразовать сложную электрическую схему в одноконтурную.

При переходе от звезды к треугольнику заданными являются сопротивления звезды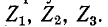 Выражения для искомых сопротивлений треугольника находятся в результате совместного решения трех уравнений (4-1).

Деление третьего уравнения на первое, а затем на второе дает:

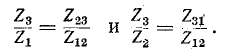
Выражая отсюда 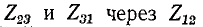и подставляя их в первое уравнение (4-1), получим:

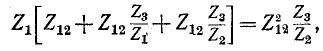
откуда

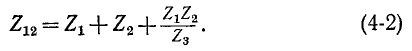
Аналогично круговой заменой индексов получим:

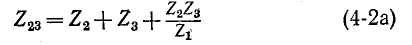
И

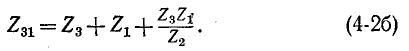
Отедовательно, комплексное сопротивление стороны треугольника равно сумме комплексных сопротивлений прилегающих лучей звезды и произведения их, деленного на сопротивление третьего луча.

Токи в лучах звезды легко выражаются через токи в сторонах треугольника. С учетом положительных направлений на рис. 4-9 имеем:

 

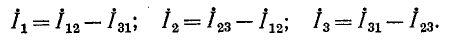
Эквивалентные источники э. д. с. и тока

Два разнородных источника электрической энергии — источник э. д. с. и источник тока — считаются эквивалентными,, если при замене одного источника другим токи и напряжения во внешней электрической цепи, с которой эти источники соединяются, остаются неизменными. На рис. 4-11 изображены эквивалентные источники тока, посылающие во внешнюю цепь ток 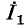и поддерживающие на своих выводах одинаковое напряжение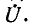

Условием эквивалентности источников, именуемым в дальнейшем правилом об эквивалентных источниках э.д.с. и тока, служит следующее соотношение между э. д. с. Ё источника э. д. с. и током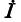

источника тока:

где Z — внутреннее комплексное сопротивление как источника э. д. с., так и источника тока.

Действительно, напряжение 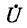на источнике э. д. с. получается в результате вычитания из э. д. с. 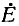падения напряжения от тока 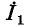в комплексном сопротивлении Z источника (рис. 4-11, а).

Соответственно напряжение 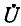на источнике тока при том же токе 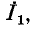посылаемом во внешнюю цепь, равно падению напряжения от тока 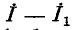в комплексном сопротивлении Z источника (рис. 4-11,6).

В обоих случаях напряжения на выводах обоих источников одинаковы:

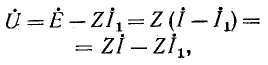
т. е. получается условие (4-3), не зависящее от тока 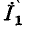нагрузки.

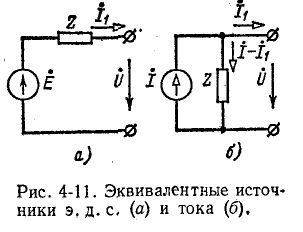
При отсоединении эквивалентных источников э. д. с.

и тока от внешней цепи 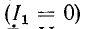напряжение на выводах обоих источников равно Ё. Именно это обстоятельство и равенство внутренних комплексных сопротивлений обоих источников и обеспечивают их эквивалентность при любом режиме работы.

Следует заметить, что мощности, расходуемые во внутренних сопротивлениях эквивалентных источников э. д. с. и тока, неодинаковы. В первом случае полная мощность, расходуемая в источнике, равна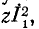 во втором случае

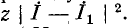
Например, при отсоединении источников от внешней цепи в первом случае мощность в источнике не расходуется, а во втором случае она составляет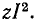

Поэтому эквивалентность источников следует понимать только в смысле неизменности токов, напряжений и мощностей во внешней электрической цепи, присоединенной к источникам.

Если внутреннее сопротивление источника э. д. с. равно нулю, то непосредственное применение формулы (4-3) для нахождения эквивалентного источника тока по, заданной э. д. с. источника не представляется возможным. В таких случаях сопротивление внешней цепи, включенной последовательно с э. д. с., можно рассматривать в качестве внутреннего сопротивления источника, что позволит применить формулу (4-3).

В случае сложной электрической цепи замена источника э. д. с. эквивалентным источником тока или обратно может иногда упростить расчет.

Целесообразность такой замены проиллюстрирована, в частности, в следующем параграфе.
 

Преобразование схем с двумя узлами

Применим правило об эквивалентных источниках э. д. с. и тока к преобразованию схемы с параллельным соединением n ветвей, содержащих источники э. д. с. (рис. 4-12, а).

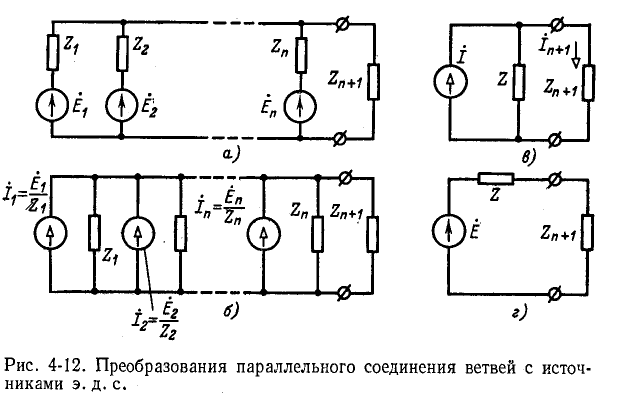
Заменяя заданные источники э. д. с. источниками тока, получаем схему рис. 4-12, б. Источники тока в совокупности образуют эквивалентный источник тока 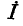(рис. 4-12, в), причем

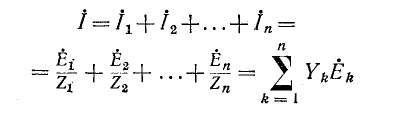
и

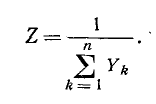
Пользуясь этим соотношением, можно в конечном итоге перейти от схемы рис. 4-12, в к схеме рис. 4-12, s, являющейся эквивалентом исходной схемы рис. 4-21, а. Здесь

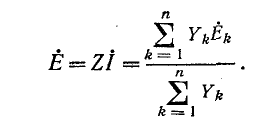
Таким образом, n параллельных ветвей с источниками э. д. с. между двумя узлами могут быть заменены одним источником тока (рис. 4-12, в) или источником э. д. с. (рис. 4-12, s).

Ток во внешней цепи (в ветви с сопротивлением 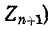равен:

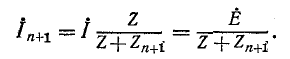
Напряжение между двумя узлами находится по формуле

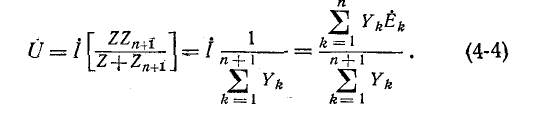
Выведенные здесь выражения широко используются для расчета электрических цепей с двумя узлами, а также более сложных цепей, приводящихся к двум узлам.
 

Перенос источников в схеме

Расчет электрической цепи облегчается в ряде случаев в результате переноса в схеме источников э. д. с. или тока. Как это видно из уравнений Кирхгофа, токи в схеме определяются заданными величинами суммарных э. д. с. в контурах независимо от того, из каких отдельных слагающих они состоят. Поэтому изменение расположения в схеме источников э. д. с., при котором суммарные э. д. с. во всех контурах сохраняются неизменными, не влияет на токи в ветвях. Аналогично напряжения на ветвях определяются заданными суммарными токами источников тока в узлах, и поэтому изменение расположения в схеме источников тока, при котором их суммарные токи во всех узлах сохраняются неизменными, не влияет на напряжения в схеме.

Если, например, требуется исключить источник э. д. с. из какой-либо ветви, то в данную ветвь вводится компенсирующая э. д. с., причем точно такая же э. д. с. вводится одновременно во все остальные ветви, сходящиеся

в одном из узлов данной ветви. Компенсирующая и дополнительные э. д. с. имеют одинаковое направление по отношению к рассматриваемому узлу. В результате этого источник э. д. с. из ветви исключается и появляются источники э. д. с. в других ветвях схемы. Суммарные э. д. с. во всех контурах и соответственно токи в ветвях остаются прежними.

Итак, источник э. д. с. может быть перенесен из какой-либо ветви схемы во все другие ветви, присоединенные к узлу данной ветви, без изменения токов в схеме.

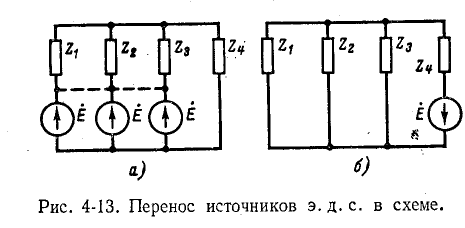
Справедливо и обратное положение: если во всех ветвях, кроме одной, сходящихся в узле, имеются одинаковые источники э. д. с. (рис. 4-13, а), направленные все к одному узлу или все от узла, то они могут быть заменены одним источником э. д. с. в ветви, в которой источник отсутствовал (рис. 4-13, б).

Это положение подтверждается тем, что суммарные э. д. с. в контурах схем на рис. 4-13, а и б одинаковы.

Имеется и другое доказательство данного положения: ввиду равенства э. д. с. всех источников вторые выводы

их могут быть объединены, как имеющие одинаковый потенциал. В результате такого объединения, показанного на рис. 4-13, а пунктиром, получается схема рис. 4-13, б.

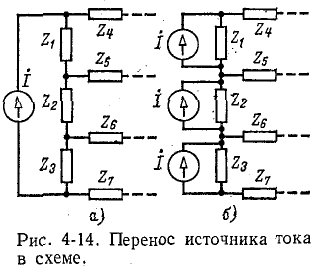
В случае переноса источников тока они присоединяются к узлам схемы так, чтобы оставались неизменными их суммарные токи в узлах.

Так, например, несмотря на то, что источники тока размещены в схемах рис.

4-14, а и б различно, суммарные токи источников в узлах обеих схем одинаковы. Поэтому и напряжения между узлами не изменились.

Итак, источник тока может быть заменен источниками тока, подключенными. параллельно всем

ветвям, которые составляли контур с рассматриваемым источником.

• Перенос источников в схеме успешно сочетается на практике с различными методами преобразований и расчетов (см. пример 4-1).

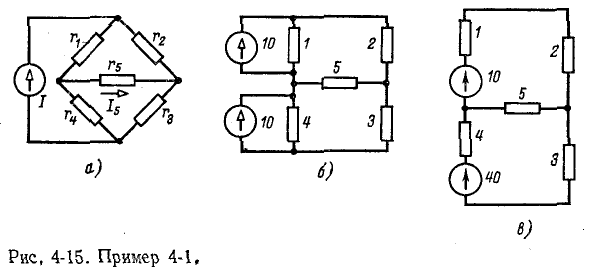
Пример 4-1.

Вычислить ток в диагональной ветви мостовой схемы рис. 4-15, а.

Дано: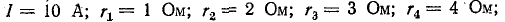

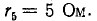
Заданный источник тока может быть заменен двумя источниками, подключенными параллельно сопротивлениям 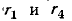(рис. 4-15, б). Пользуясь условием эквивалентности источников э, д, с, и тока, получаем схему рис, 4-15, в с двумя узлами. По формуле (4-4) напряжение на ветви равно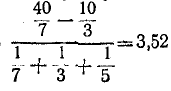

В. Искомый ток

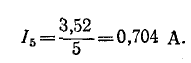
Преобразование симметричных схем

Схема электрической цепи, в которой имеется ось симметрии, называется симметричной. Например, схема рис. 4-16, а симметрична относительно вертикальной оси. В симметричных схемах легко выявляются точки или узлы с одинаковым потенциалом. В ветвях, присоединенных к таким узлам, токи равны нулю. Поэтому эти ветви

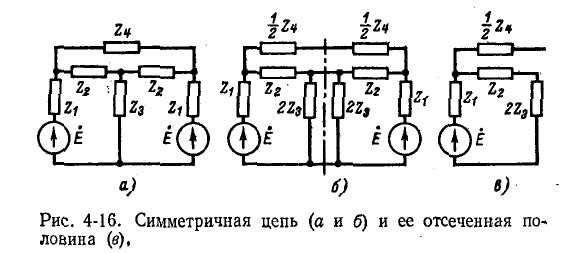
можно разрезать, не нарушая распределения токов и напряжений в схеме. Точки, имеющие одинаковый потенциал, могут быть объединены. Рассечение ветвей, по которым не проходит ток, и объединение точек равного потенциала упрощают схему и облегчают расчет.

Так, в симметричной схеме рис. 4-16, б токи в соединениях, пересекающих ось симметрии, отсутствуют. Разрезав схему по оси симметрии, получим с обеих сторон одноконтурную схему рис. 4-16, в, которая легко рассчитывается.

Допустим теперь, что полярность источников в симметричной схеме неодинакова (рис. 4-17, а). В этом случае (равенство э. д. с. источников и различие их полярности) токи в симметричных ветвях (например, 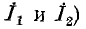и напряжения между соответствующими парами выводов, симметрично расположенными относительно оси, равны и противоположны по знаку. Отсюда следует, что напряжения между всеми точками, лежащими на оси симметрии, равны нулю 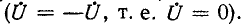Поэтому все точки схемы на оси симметрии могут быть замкнуты накоротко (рис. 4-17, б).

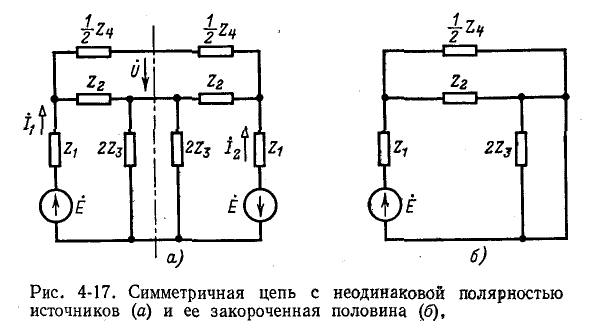
Таким образом, расчет сложных симметричных схем приводится к расчету более простых схем.

На рис. 4-18, а и б показана симметричная мостовая схема, имеющая две оси симметрии — вертикальную и

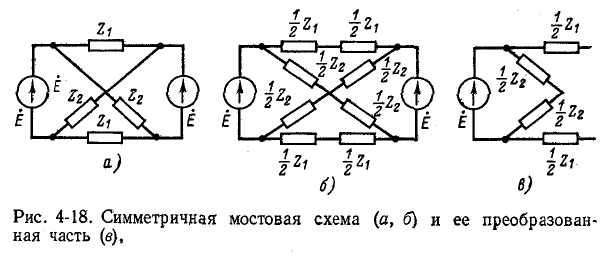
горизонтальную. В продольных ветвях ток отсутствует; потенциалы средних точек поперечных (перекрещенных) ветвей одинаковы.

Поэтому продольные ветви могут быть рассечены, а средние точки поперечных ветвей — объединены. В результате с обеих сторон получится одноконтурная схема (рис. 4-18, в), расчет которой крайне прост.

Если изменить полярность одного из источников (рис. 4-19, а), то роли продольных и поперечных ветвей поменяются и преобразованная часть схемы примет вид, показанный на рис. 4-19, б.

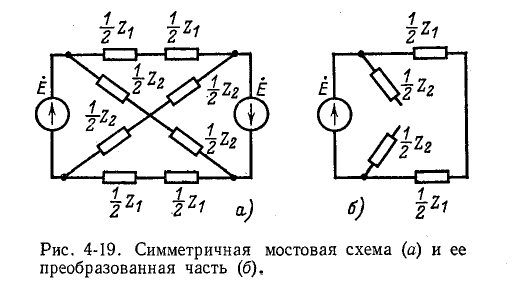
В разобранных выше примерах э. д. с. источников были равны. В случае неравенства э. д. с. источников преобразование симметричной схемы удобно сочетается с методом наложения (см. пример 7-5).

Эквивале́нтная схе́ма (схема замещения, эквивалентная схема замещения) цепи — электрическая схема, в которой все реальные элементы заменены их эквивалентными схемами.

Эквивалентная схема (схема замещения, эквивалентная схема замещения) реального элемента цепи — электрическая схема цепи, состоящая из идеализированных элементов цепи, рассчитанные напряжения и токи на зажимах которой совпадают с какой-то погрешностью с измеренными токами и напряжениями на зажимах реального элемента. Уравнения для токов и напряжений эквивалентной схемы реального элемента являются его математической моделью.

Необходимость эквивалентных схем[править | править код]

Одной из основных задач электроники является расчет электрических цепей, то есть получение детальной количественной информации о процессах, происходящих в этой цепи. Однако рассчитать произвольную цепь, состоящую из реальных электронных компонент, практически невозможно. Мешает расчету то обстоятельство, что попросту не существует методик математического описания поведения реальных электронных компонентов (например, транзистора) как единого целого. Имеются значения отдельных параметров и экспериментально снятые зависимости, но связать их в единую точную формулу, полностью описывающую поведение компоненты, в большинстве случаев не представляется возможным.

С другой стороны, исключительно простым математическим аппаратом описываются идеализированные базовые элементы электронных схем (например, идеальный резистор). Однако они не существуют в реальном мире. Так, любой резистор (реальный элемент) имеет множество паразитных параметров: индуктивность, ёмкость, температурные зависимости и т. п.

Введение понятия эквивалентная схема позволяет «связать» мир реальных компонентов и мир их идеальных приближений. Эквивалентная схема представляет собой цепь только из идеальных компонент, которая функционирует примерно так же, как и исходная схема. В эквивалентной схеме реального элемента могут быть отражены, при необходимости, различные паразитные эффекты: утечки, внутренние сопротивления и т. д. В зависимости от требуемой точности разработаны и продолжают разрабатываться множество схем замещения одного и того же реального элемента. Например, известны сотни схем замещения (моделей) разных типов транзисторов.

Идеальные элементы[править | править код]

В эквивалентных схемах используются перечисленные ниже идеальные элементы. Предполагается также, что геометрические размеры эквивалентной схемы настолько малы, что какие-либо эффекты длинных линий отсутствуют, то есть эквивалентная схема рассматривается как система с сосредоточенными параметрами.

• Резистор. Идеальный резистор характеризуется только сопротивлением. Индуктивность, ёмкость, а также сопротивление выводов равны нулю.
• Конденсатор. Идеальный конденсатор характеризуется только ёмкостью. Индуктивность, утечка, тангенс угла потерь, диэлектрическое поглощение а также сопротивление выводов равны нулю.
• Катушка индуктивности. Идеальная катушка индуктивности характеризуется только индуктивностью. Ёмкость, сопротивление потерь, а также сопротивление выводов равны нулю.
• Источник ЭДС. Идеальный источник ЭДС характеризуется только своим напряжением. Внутреннее сопротивление и сопротивление выводов равны нулю.
• Источник тока. Идеальный источник тока характеризуется только своим током. Утечка равна нулю.
• Проводники. Элементы эквивалентной схемы соединены идеальными проводниками, то есть индуктивность, ёмкость и сопротивление проводников равны нулю.

Составление эквивалентных схем[править | править код]

Этот раздел статьи ещё не написан. Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (31 августа 2016)

Неоднозначность[править | править код]

Для любой электрической схемы можно составить сколько угодно различных эквивалентных схем — количество их ограничивается только соображениями целесообразности. Для одной схемы имеет смысл составлять несколько эквивалентных схем по следующим причинам:

• Учёт различных эффектов. Эквивалентная схема составляется тем или иным образом в зависимости от того, какие эффекты мы хотим с её помощью описать. Например, для нахождения рабочей точки по постоянному току требуется одна эквивалентная схема, а для расчета АЧХ — совершенно другая.
• Поэтапное упрощение. В процессе расчета схемы целесообразно заменять её сложные участки простыми эквивалентными цепями. Например, цепь из последовательно включенных резисторов можно заменить одним резистором с суммарным сопротивлением. В полученной упрощенной схеме можно вновь применить некоторую замену и т. д.

Ограничения[править | править код]

Эквивалентная схема является линейной системой, поэтому нелинейные эффекты реальных схем не могут быть смоделированы путём составления эквивалентных схем.

Частичным выходом из этого затруднения является рассмотрение нелинейной системы в малосигнальном приближении для конкретной рабочей точки, при этом нелинейные эффекты малы и ими можно пренебречь. Данный подход позволяет не описать нелинейные эффекты, а всего лишь ограничиться случаем, когда они пренебрежимо малы.

Эквивалентная схема реального элемента, описываемая дифференциальными уравнениями в обыкновенных производных, не может абсолютно точно соответствовать реальному элементу, электрические процессы в котором описываются дифференциальными уравнениями в частных производных (например, многие характеристики полупроводникового диода могут быть получены из решения уравнения Пуассона для p — n-перехода).

Литература[править | править код]

• Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — М.: Высшая школа, 1996. — 224 с. — ISBN 5-8297-0159-6
• Попов В. П. Основы теории цепей . — М.: Высшая школа, 2003. — 575 с. — ISBN 5-06-003949-8

Метод эквивалентного преобразования электрических цепей

Сущность и цель преобразований

Цель преобразования электрических цепей состоит в упрощении схем путем эквивалентных преобразований, приводящих к уменьшению числа ветвей и узлов. Эквивалентные преобразования входят во все методы расчета в качестве первого шага в последовательностях расчета. Под эквивалентными преобразованиями мы будем понимать преобразования одной части схемы, при которых в остальной части величины токов и напряжений остаются неизменными, как и сама схема.

Расчет цепи при последовательном соединении элементов и закон Ома для ветви, содержащей ЭДС

Рассмотрим электрическую цепь при последовательном соединении и ЭДС и резисторов, когда величина тока во всех элементах одинакова.

Все величины ЭДС и резисторов известны, как и напряжение на входе цепи. Необходимо упростить цепь до двух элементов (рисунок 3.6) и определить величину тока.

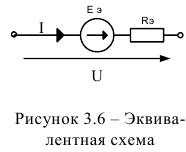
Для решения задачи выберем произвольное направление тока 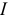и обхода контура и на основании второго закона Кирхгофа составим уравнение:

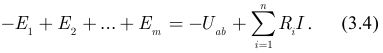
Учитывая, что ток 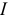одинаковый во всех резисторах, выносим его за знак суммы и вводим обозначения:

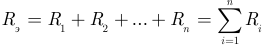— эквивалентное сопротивление, определяемое в виде арифметической суммы всех последовательно соединенных сопротивлении;

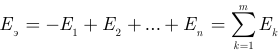— эквивалентная ЭДС, определяемая как алгебраическая сумма ЭДС.

С учетом выполненных обозначений, уравнение приобретает вид:

Схема имеет вид (рисунок 3.6), а величина тока:

Расчет цепи при параллельном соединении элементов

Задана электрическая цепь, содержащая параллельно соединенные элементы, т.е. на всех элементах напряжения одинаковые (рисунок 3.7). Величины сопротивлений резисторов заданы 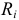и токи источников тока 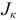. Необходимо рассчитать ток .

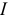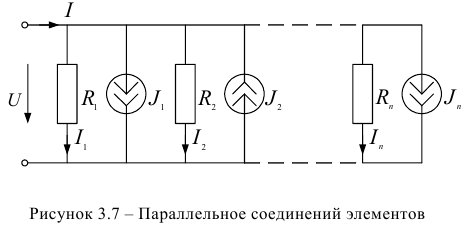
Решение задачи выполним на основании первого закона Кирхгофа, предварительно выбрав направления токов в ветвях, с резисторами от верхнего узла с большим потенциалом к нижнему с меньшим потенциалом:

В представленном уравнении все подтекающие токи взяты со знаком «+», а оттекающие — со знаком «-». Т.к. величина тока в любом резисторе может быть найдена по закону Ома:

то ток 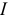на входе цепи может быть вычислен по выражению:

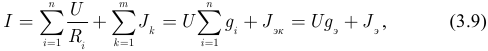
где 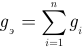— эквивалентная проводимость всех ветвей с резисторами определяемая как арифметическая сумма проводимостей всех параллельно соединенных резисторов; 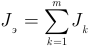— ток эквивалентного источника тока, определяемый как алгебраическая сумма всех параллельно соединенных источников тока. Знак тока источника тока положителен, если он направлен от узла и отрицателен, если он направлен к узлу.

В соответствии с последним уравнением можно зарисовать эквивалентную схему замещения (рисунок 3.8).

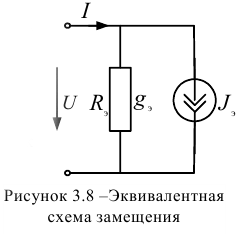
Расчет цепи при смешанном соединении элементов

Под смешанным соединением элементов понимают такие соединения, при которых цепь содержит одновременно последовательно соединенные элементы и параллельно соединенные элементы.

Задача 3.1.

Рассчитать эквивалентное сопротивление для схемы, представленной на рисунке 3.9, если:

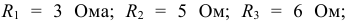
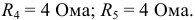
Решение:

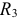На первом этапе объединим последовательно соединенные элементы и и параллельно соединенные элементы и :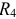

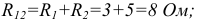
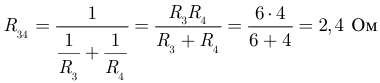
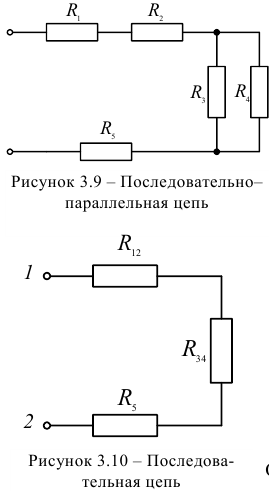
В результате получаем упрощенную схему (рисунок 3.10).

На втором этапе суммируем сопротивления 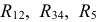и получаем эквивалентное сопротивление всей схемы относительно входных зажимов 1 и 2: 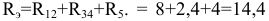Ом.

Задача 3.2.

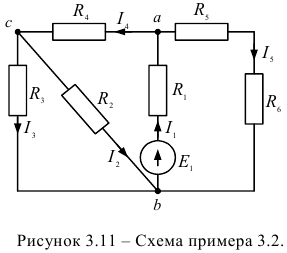
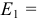
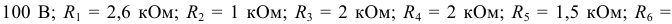
Задана электрическая цепь (рисунок 3.11.). Для величин элементов: 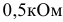выполнить расчет величин токов в ветвях электрической цепи.

Решение:

Выбираем направления токов в ветвях электрической цепи с учетом направления ЭДС 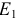. На первом этапе объединяем резисторы 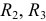и .

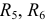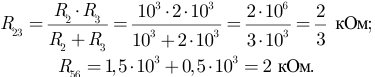
На рисунке 3.12 представлена упрощенная схема. Объединяем сопротивления ветвей, подключенных параллельно, к узлам и :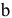

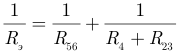
Следовательно:

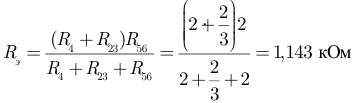
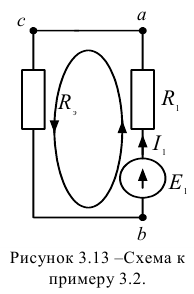
На рисунке 3.13 получена неразветвленная электрическая цепь.

Применяем второй закон Кирхгофа для замкнутого контура:

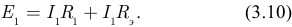
Решаем уравнение относительно тока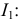

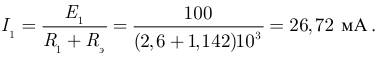
Вычисляем напряжение 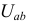по закону Ома:

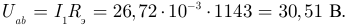
Тогда:

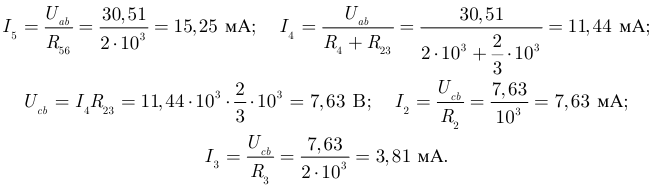
Выполним проверку вычислений по балансу мощностей:

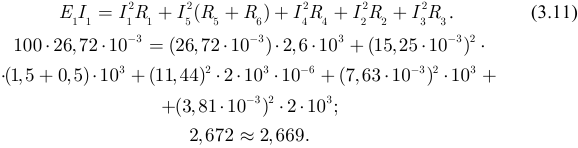
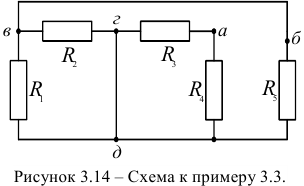
Задача 3.3.

Пользуясь методом преобразования, рассчитать эквивалентное входное сопротивление электрической цепи (рисунок 3.14.) относительно точек и 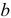если величины элементов имеют значения:

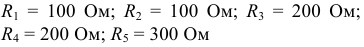
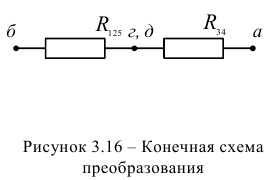
Решение:

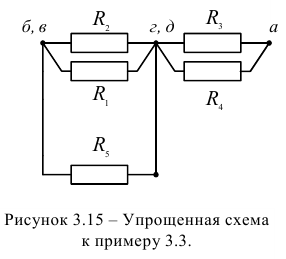
Так как схема содержит ветви без элементов, то узлы и точки с равными потенциалами можно объединить. Объединяем точку в и б и узел г с узлом д. Упрощенная схема представлена на рисунке 3.15. Рассчитаем эквивалентные сопротивления 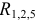и :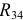

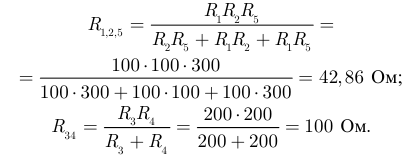
Эквивалентное сопротивление всей цепи относительно точек а и б, в соответствии с новой схемой (рисунок 3.16):

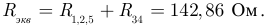
Эта страница взята со страницы задач по электротехнике:

Электротехника — решения задач и примеры выполнения заданий

Возможно эти страницы вам будут полезны: